WOJSKOWA AKADEMIA TECHNICZNA
INSTYTUT SYSTEMÓW MECHATRONICZNYCH
ZAKŁAD SYSTEMÓW STEROWANIA
INSTRUKCJA
DO PRZEPROWADZENIA WICZENIA LABORATORYJNEGO
NA TEMAT:
ANALIZA KINEMATYCZNA MANIPULATORÓW
– ZADANIE PROSTE KINEMATYKI
Mjr dr in . Wojciech KACZMAREK
Dr in . Jarosław PANASIUK
WARSZAWA 2008
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
3
I. CZ
TEORETYCZNA
1. C
EL WICZENIA
Celem
wiczenia jest zapoznanie studentów z kinematyk manipulatorów robotów
przemysłowych oraz problemami powstaj cymi podczas analizy kinematyki w trybie symulacji
komputerowej. Studenci podczas wiczenia zapoznaj si ze rodowiskiem MATLAB oraz wykorzystaj
jego podstawowe funkcje do analizy kinematycznej manipulatora.
2. K
INEMATYKA MANIPULATORÓW
Kinematyka to nauka zajmuj ca si opisem ruchu bez uwzgl dnienia sił wywołuj cych ten
ruch. W jej ramach bada si zmiany poło enia, pr dko ci i przyspiesze członów manipulatora.
W zagadnieniach zwi zanych z kinematyk manipulatorów robotów mo na wyró ni dwa typy zada :
•
zadanie bezpo rednie (proste) kinematyki, które polega na wyznaczeniu pozycji i orientacji
efektora manipulatora wzgl dem układu podstawy przy znanych współrz dnych
konfiguracyjnych (odwzorowanie opisu poło enia manipulatora z przestrzeni współrz dnych
konfiguracyjnych do przestrzeni współrz dnych kartezja skich);
•
zadanie odwrotne kinematyki, które polega na wyznaczeniu wszystkich mo liwych zbiorów
współrz dnych konfiguracyjnych umo liwiaj cych osi gni cie zadanych pozycji i orientacji
manipulatora.
Przy rozwa aniach dotycz cych kinematyki obowi zuj nast puj ce zasady:
•
robota opisuje si za pomoc struktury kinematycznej (szkicu schematu kinematycznego), na
której zaznacza si człony oraz poł czenia;
•
oznaczenia osi współrz dnych, kierunków i zespołów ruchu, konieczne do jednoznaczno ci
opracowanego szkicu zapisane s w normie PN-93/M-55251;
•
robota opisuje si w trzech układach odniesienia:
o
globalnym (bazowym oznaczonym cyfr 0) – opis przemieszczenia robota wzgl dem
inercjalnego (nieruchomego) układu współrz dnych (najcz ciej wzgl dem stanowiska
roboczego);
o
regionalnym (oznaczonym cyframi k=1,2,3,,, rozpoczynaj c numeracj od członu
znajduj cego si najbli ej) – opis przemieszczenia manipulatora;
o
lokalnym (oznaczonym liter C) – opis przemieszczenia i orientacji chwytaka.
•
podstawowy układ osi jest prawoskr tnym układem kartezja skim (prostok tnym), gdzie osie x
i y tworz płaszczyzn poziom .
•
za dodatni przyjmuje si zwroty ruchów:
o
w ruchu liniowym na zewn trz mechanizmów (od pocz tku układów globalnego,
regionalnego, lokalnego);
o
w ruchu obrotowym w kierunku prawoskr tnym, zgodnie z przyj tym układem
współrz dnych.
•
numeracj ła cucha kinematycznego nale y rozpocz od podstawy (układu bazowego),
a zako czy przed efektorem (układem lokalnym).
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
4
Przemieszczenie układu lokalnego wzgl dem bazowego opisuje wektor miejsca (
0
r
c
rys.2.1).
Łatwo zauwa y , e układ lokalny mo e by nie tylko przesuni ty wzgl dem układu bazowego, ale
równie obrócony (wzgl dem poszczególnych osi układu rys.2.1c). T drug operacj (obrót) mo na
opisa poprzez, tworzon za pomoc cosinusów kierunkowych macierz obrotu o wymiarach 3x3.
Rys.2.1. Widok wzajemnego poło enia układów współrz dnych:
a) układ i-tego ciała jest przemieszczony wzgl dem układu bazowego
b) układ i-tego ciała jest obrócony wzgl dem układu bazowego
c) układ i-tego ciała jest przemieszczony i obrócony wzgl dem układu bazowego
Oznaczenia:
•
prawy, dolny indeks oznacza nowy układ lub nowe poło enie po transformacji;
•
lewy górny indeks oznacza układ, wzgl dem którego dokonano transformacji;
•
0
i
– pocz tek układu współrz dnych ciała i;
•
C – zmienny punkt ciała;
•
z
y
x
e
e
e
0
0
0
,
,
– wektory jednostkowe układu inercjalnego;
•
z
i
y
i
x
i
e
e
e
)
(
0
)
(
0
)
(
0
,
,
– wektory jednostkowe układu ciała i przedstawione w układzie bazowym;
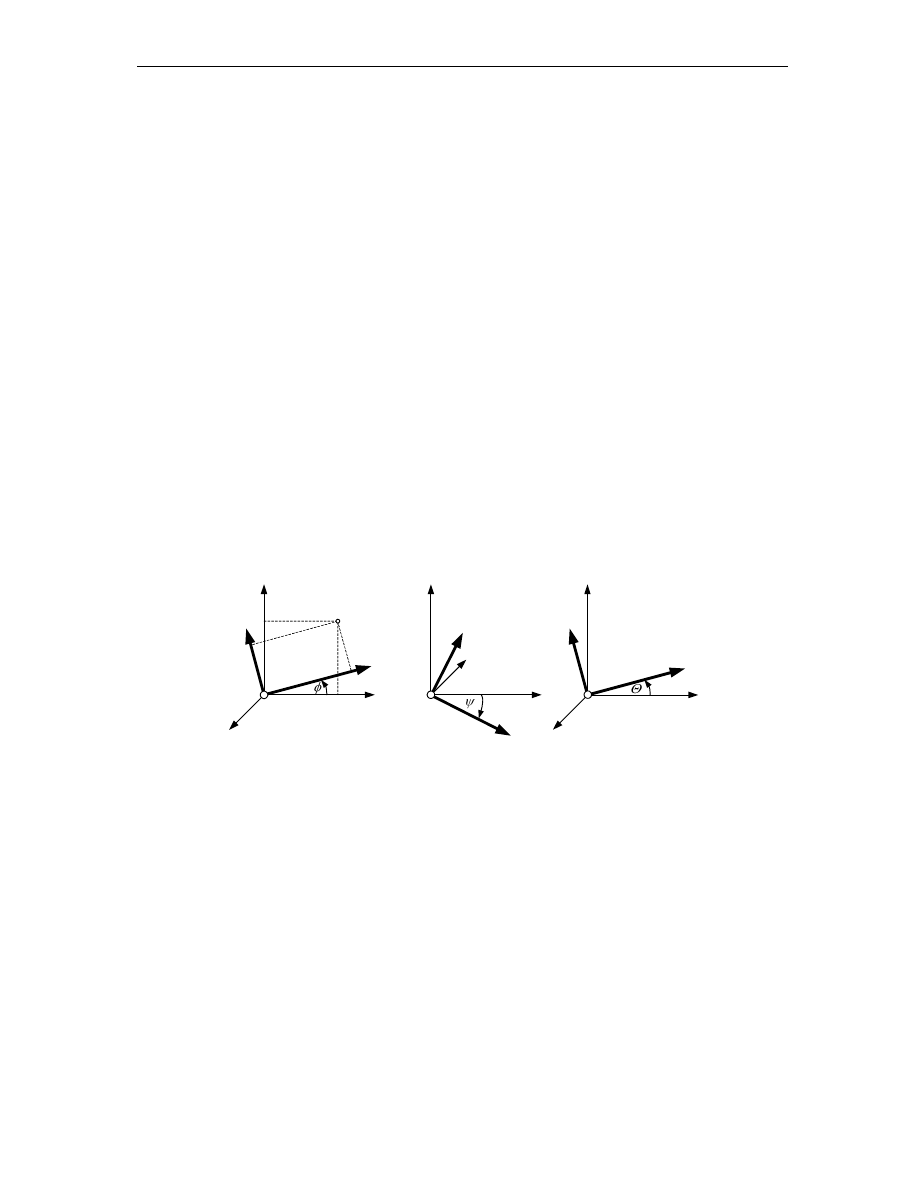
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
5
•
C
r
0
– wektor miejsca w układzie bazowym;
•
C
i
r
– wektor miejsca w układzie lokalnym.
Dla przypadków szczególnych mo na zapisa nast puj ce zale no ci:
•
je li i-ty układ jest przesuni ty wzgl dem układu bazowego, a jego orientacja jest taka sama jak
układu bazowego (poszczególne osie układu s do siebie równoległe – rys.2.1a):
C
i
i
C
r
r
r
+
=
0
0
(1.1)
•
je li i-ty układ jest obrócony wzgl dem układu bazowego, a jego pocz tek układu pokrywa si z
pocz tkiem układu bazowego – rys.2.1b:
C
i
i
C
r
rot
r
⋅
=
0
0
(1.2)
Pełn transformacj współrz dnych (rys.2.1c) mo na przedstawi jako poł czenie przemieszczenia
(translacji) i obrotu (rotacji):
C
i
i
i
C
r
rot
r
r
⋅
+
=
0
0
0
(1.3)
Obroty elementarne
Zgodnie z ogólnie panuj cymi zasadami przyj to prawoskr tny układ współrz dnych (rys.2.2).
Rys.2.2. Obroty elementarne wzgl dem poszczególnych osi:
a) – osi x; b) – osi y; c) – osi z.
Dla poszczególnych obrotów elementarnych mo na zapisa nast puj ce zale no ci:
Obrót wokół osi x (rys.2.2a).
macierz obrotu wokół osi x mo na jest opisana wyra eniem:
−
=
φ
φ
φ
φ
φ
cos
sin
0
sin
cos
0
0
0
1
)
(
x
rot
(1.4)
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
6
Obrót wokół osi y (rys.2.2b).
macierz obrotu wokół osi y mo na opisa wyra eniem:
( )
−
=
ψ
ψ
ψ
ψ
ψ
cos
0
sin
0
1
0
sin
0
cos
y
rot
(1.5)
Obrót wokół osi z (rys.2.2c).
macierz obrotu wokół osi z mo na opisa wyra eniem:
( )
−
=
1
0
0
0
cos
sin
0
sin
cos
θ
θ
θ
θ
θ
z
rot
(1.6)
Obroty zło one
Obroty zło one mog by tworzone z trzech kolejno po sobie wykonywanych obrotów
elementarnych. Nale y pami ta o tym, i mno enie macierzy nie jest przemienne, dlatego kolejno
wykonywania obrotów elementarnych jest wa na i wpływa na wynik ko cowy (posta macierzy obrotów
zło onych). Dowodem tego s macierze przedstawione poni ej jako wzory (1.7) i (1.8).
Dla uproszczenia zapisu u yto skrótów s
φ
=sin
φ
, c
φ
= cos
φ
itd.
( )
( )
( )
+
−
−
−
+
−
=
=
⋅
⋅
=
ψ
φ
θ
ψ
φ
θ
φ
θ
ψ
φ
θ
φ
ψ
φ
θ
ψ
φ
θ
φ
θ
ψ
φ
θ
φ
ψ
θ
ψ
θ
ψ
θ
ψ
φ
θ
ψ
φ
c
c
s
s
c
c
s
c
s
c
s
s
c
s
s
s
s
c
c
c
s
s
s
c
s
s
c
c
c
rot
rot
rot
rot
z
y
x
)
,
,
(
(1.7)
( )
( )
( )
−
+
−
+
+
+
−
=
=
⋅
⋅
=
ψ
φ
ψ
φ
ψ
θ
ψ
φ
θ
φ
θ
ψ
φ
θ
φ
ψ
θ
φ
ψ
θ
θ
φ
θ
ψ
φ
θ
φ
θ
ψ
φ
ψ
θ
φ
ψ
θ
s
c
c
s
s
s
s
c
c
s
s
s
s
c
c
c
s
c
s
c
s
s
c
s
s
s
c
c
s
rot
rot
rot
rot
x
y
z
)
,
,
(
(1.8)
Współrz dne i transformacje jednorodne.
Do analizy kinematycznej u ywa si tzw. współrz dnych jednorodnych. Punkt o współrz dnych
kartezja skich x,y,z opisuje si liczbami x
1
,x
2
,x
3
,x
4
, przy czym nie wszystkie z nich mog by
jednocze nie równe zero. Zale no mi dzy współrz dnymi prostok tnymi (x,y,z) i współrz dnymi
jednorodnymi mo na zapisa nast puj co:
4
3
4
2
4
1
x
x
z
x
x
y
x
x
x
=
=
=
(1.9)
Współrz dne jednorodne mo na okre li za pomoc wektora:
[
]
T
x
x
x
x
R
4
3
2
1
=
,
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
7
Wprowadzenie współrz dnych jednorodnych umo liwiło utworzenie tzw., jednorodnej macierzy
transformacji o postaci:
4
4
1
1
1
000
000
x
i
i
i
i
R
r
rot
skali
czynnik
translacji
wektor
rotacji
macierz
T
∈
=
=
−
−
(1.10)
Czynnik skali (wzór 1.10) mo e opisywa np. odkształcenie obiektu w trójwymiarowej
przestrzeni jednak w robotyce, ze wzgl du na rozpatrywanie ciał sztywnych przyj to, i jest on równy
jeden.
W zwi zku z tym, i w kartezja skim układzie współrz dnych ciało mo e posiada sze stopni
swobody, zbiór wszystkich transformacji jednorodnych mo na przedstawi za pomoc sze ciu
elementarnych macierzy transformacji:
−
=
−
=
−
=
1
0
0
0
0
1
0
0
0
0
cos
sin
0
0
sin
cos
1
0
0
0
0
cos
0
sin
0
0
1
0
0
sin
0
cos
1
0
0
0
0
cos
sin
0
0
sin
cos
0
0
0
0
1
θ
θ
θ
θ
ψ
ψ
ψ
ψ
φ
φ
φ
φ
z
y
x
Rot
Rot
Rot
(1.11)
=
=
=
1
0
0
0
1
0
0
0
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
0
1
0
0
0
0
1
1
0
0
0
0
1
0
0
0
0
1
0
0
0
1
z
z
y
y
x
x
r
P
r
P
r
P
(1.12)
gdzie: r
x
, r
y
, r
z
– składowe wektora przemieszczenia.
Zadanie bezpo rednie (proste) kinematyki
Konfiguracja układu manipulatora jest realizowana poprzez zmienne konfiguracyjne
q=(q
1
,q
2
,..,q
n
) tzn. e ka dej warto ci zmiennej konfiguracyjnej odpowiada jedno poło enie chwytaka R
w układzie bazowym. Je li zało y si , i chwytak C jest zdefiniowany miejscem na ciele i układu
wielociałowego to mo na zapisa :
C
i
i
C
R
T
R
⋅
=
0
0
(1.13)
Zadanie bezpo rednie kinematyki mo na podzieli na etapy:
1. Usytuowanie manipulatora w poło eniu pocz tkowym i wprowadzenie układu bazowego.
2. Wprowadzenie układów regionalnych dla wszystkich członów manipulatora.
3. Wprowadzenie współrz dnych konfiguracyjnych.
4. Wyznaczenie wzajemnych poło e poszczególnych członów za pomoc jednorodnych macierzy
transformacji
n
i
T
i
i
,...
2
,
1
1
=
−
.
5. Wyznaczenie poło enia ko cówki manipulatora wzgl dem układu bazowego
i
i
i
T
T
T
T
1
2
1
1
0
0
...
−
⋅
⋅
⋅
=
.
6. Wyznaczenie zale no ci pomi dzy współrz dnymi bazowymi i współrz dnymi lokalnymi ko cówki
manipulatora
C
i
i
C
R
T
R
⋅
=
0
0
.
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
8
II. CZ
PRAKTYCZNA
3. O
PIS STANOWISKA LABORATORYJNEGO
wiczenie laboratoryjne nale y wykona na komputerze PC w rodowisku MATLAB.
4. W
YKONANIE WICZENIA
wiczenie nale y wykona zgodnie z zaleceniami prowadz cego. Dla podanego typu
manipulatora (np. rys.4.1) nale y okre li transformacje układów współrz dnych w poszczególnych
zł czach i napisa program umo liwiaj cy analiz zadania bezpo redniego kinematyki.
Rys.4.1. Przykładowy widok manipulatora
UWAGA:
Podczas pracy w rodowisku MATLAB:
•
nie u ywaj specjalnych i polskich znaków nadaj c nazwy tworzonym plikom;
•
indeksy wpisuj zwykł czcionk .
Na zaj cia nale y przynie dyskietk 3,5”.
5. S
CHEMAT OBLICZE W RODOWISKU
MATLAB
i=1,2,3,……..
Pocz tek programu:
clear all
wyczy
wszystkie zmienne
close all
zamknij wszystkie okna
Zmienne wej ciowe
t
i
=0; i=1,2,3…
warto
pocz tkowa k ta
…….
tk
i
=50; i=1,2,3…
warto
ko cowa k ta
…….
t
i
=t
i
*pi/180; i=1,2,3…
przeliczenie warto ci pocz tkowej k ta na radiany
…….
tk
i
=tk
i
*pi/180; i=1,2,3… przeliczenie warto ci ko cowej k ta na radiany
…….
l
i
=15; i=1,2,3…
długo ci ramion manipulatora
…….
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
9
Obszar wy wietlania
set(gca,'XlimMode','manual','YLimMode','manual','ZLimMode','manual'); umo liwia manualne definiowanie
przestrzeni roboczej
set(gca,'Xlim',[-50,50],'Ylim',[-50,50],'Zlim',[0,50]); definiowanie przestrzeni roboczej
i-ty człon manipulatora
Rx
i
=[1,0,0,0;0,cos(t
i
),-sin(t
i
),0;0,sin(t
i
),cos(t
i
),0;0,0,0,1]; zdefiniowanie macierzy obrotów wzgl dem osi x
Ry
i
=[ cos(t
i
),0, sin(t
i
),0;0,1,0,0;-sin(t
i
),0,cos(t
i
),0;0,0,0,1]; zdefiniowanie macierzy obrotów wzgl dem osi y
Rz
i
=[cos(t
i
),-sin(t
i
),0,0;sin(t
i
),cos(t
i
),0,0;0,0,1,0;0,0,0,1]; zdefiniowanie macierzy obrotów wzgl dem osi z
P
i
=[1,0,0, l
i
;0,1,0, l
i
;0,0,1,l
i
;0,0,0,1];
zdefiniowanie macierzy przesuni
T
i
=Rxyz
i
*P
i
;
wyznaczenie jednorodnej macierzy transformacji
x
i
=T
i
(1,4);
wyznaczenie warto ci współrz dnej x
y
i
=T
i
(2,4);
wyznaczenie warto ci współrz dnej y
z
i
=T
i
(3,4);
wyznaczenie warto ci współrz dnej z
i+1 człon manipulatora
Rx
i+1
=[1,0,0,0;0,cos(t
i+1
),-sin(t
i+1
),0;0,sin(t
i+1
),cos(t
i+1
),0;0,0,0,1]; zdefiniowanie macierzy obrotów
wzgl dem osi x
Ry
i+1
=[ cos(t
i+1
),0, sin(t
i+1
),0;0,1,0,0;-sin(t
i+1
),0,cos(t
i+1
),0;0,0,0,1]; zdefiniowanie macierzy obrotów
wzgl dem osi y
Rz
i+1
=[cos(t
i+1
),-sin(t
i+1
),0,0;sin(t
i+1
),cos(t
i+1
),0,0;0,0,1,0;0,0,0,1]; zdefiniowanie macierzy obrotów
wzgl dem osi z
P
i+1
=[1,0,0, l
i+1
;0,1,0, l
i+1
;0,0,1,l
i+1
;0,0,0,1] zdefiniowanie macierzy przesuni
T
i+1
=T
i
*Rxyz
i+1
*P
i+1
;
wyznaczenie jednorodnej macierzy transformacji
x
i+1
=T
i+1
(1,4);
wyznaczenie warto ci współrz dnej x
y
i+1
=T
i+1
(2,4);
wyznaczenie warto ci współrz dnej y
z
i+1
=T
i+1
(3,4);
wyznaczenie warto ci współrz dnej z
view(-27.5,30)
ustawienie k ta nachylenia wy wietlania układu współrz dnych
grid on
wy wietlenie siatki
ld
i
=line([0,x
i
],[0,y
i
],[0,z
i
],'LineWidth',6,'Color','red'); wykre
_
lenie i-tego członu manipulatora
ld
i+1
=line([x
i
,x
i+1
],[ y
i
,y
i+1
],[ z
i
,z
i+1
],'LineWidth',6,'Color','red'); wykre
_
lenie i+1 członu manipulatora
Ruch i-tego członu manipulatora
for t
i
=t
i
:0.05:tk
i
delete (ld
i
);
delete (ld
i+1
);
Tk1
i
=t
i
;
Rx
i
=[1,0,0,0;0,cos(Tk1
i
),-sin(Tk1
i
),0;0,sin(Tk1
i
),cos(Tk1
i
),0;0,0,0,1];
Ry
i
=[ cos(Tk1
i
),0, sin(Tk1
i
),0;0,1,0,0;-sin(Tk1
i
),0,cos(Tk1
i
),0;0,0,0,1];
Rz
i
=[cos(Tk1
i
),-sin(Tk1
i
),0,0;sin(Tk1
i
),cos(Tk1
i
),0,0;0,0,1,0;0,0,0,1];
P
i
=[1,0,0,0;0,1,0,0;0,0,1,l
i
;0,0,0,1];
T
i
=Rxyz
i
*P
i
;
x
i
=T
i
(1,4);
y
i
=T
i
(2,4);
z
i
=T
i
(3,4);
Rx
i+1
=[1,0,0,0;0,cos(t
i+1
),-sin(t
i+1
),0;0,sin(t
i+1
),cos(t
i+1
),0;0,0,0,1];
Ry
i+1
=[ cos(t
i+1
),0, sin(t
i+1
),0;0,1,0,0;-sin(t
i+1
),0,cos(t
i+1
),0;0,0,0,1];
Rz
i+1
=[cos(t
i+1
),-sin(t
i+1
),0,0;sin(t
i+1
),cos(t
i+1
),0,0;0,0,1,0;0,0,0,1];
P
i+1
=[1,0,0,0;0,1,0,0;0,0,1,l
i+1
;0,0,0,1];
T
i+1
=T
i
*Rxyz
i+1
*P
i+1
;
x
i+1
=T
i+1
(1,4);
y
i+1
=T
i+1
(2,4);
z
i+1
=T
i+1
(3,4);
grid on
ld
i
=line([0,x
i
],[0,y
i
],[0,z
i
],'LineWidth',6,'Color','red');
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
10
ld
i+1
=line([x
i
,x
i+1
],[ y
i
,y
i+1
],[ z
i
,z
i+1
],'LineWidth',6,'Color','red');
pause(0.1);
end
Ruch i-tego członu manipulatora
for t
i+1
=t
i+1
:0.05:tk
i+1
delete (ld
i
);
delete (ld
i+1
);
Tk1
i+1
=t
i+1
;
Rx
i
=[1,0,0,0;0,cos(Tk1
i
),-sin(Tk1
i
),0;0,sin(Tk1
i
),cos(Tk1
i
),0;0,0,0,1];
Ry
i
=[ cos(Tk1
i
),0, sin(Tk1
i
),0;0,1,0,0;-sin(Tk1
i
),0,cos(Tk1
i
),0;0,0,0,1];
Rz
i
=[cos(Tk1
i
),-sin(Tk1
i
),0,0;sin(Tk1
i
),cos(Tk1
i
),0,0;0,0,1,0;0,0,0,1];
P
i
=[1,0,0,0;0,1,0,0;0,0,1,l
i
;0,0,0,1];
T
i
=Rxyz
i
*P
i
;
x
i
=T
i
(1,4);
y
i
=T
i
(2,4);
z
i
=T
i
(3,4);
Rx
i+1
=[1,0,0,0;0,cos(Tk1
i+1
),-sin(Tk1
i+1
),0;0,sin(Tk1
i+1
),cos(Tk1
i+1
),0;0,0,0,1];
Ry
i+1
=[ cos(Tk1
i+1
),0, sin(Tk1
i+1
),0;0,1,0,0;-sin(Tk1
i+1
),0,cos(Tk1
i+1
),0;0,0,0,1];
Rz
i+1
=[cos(Tk1
i+1
),-sin(Tk1
i+1
),0,0;sin(Tk1
i+1
),cos(Tk1
i+1
),0,0;0,0,1,0;0,0,0,1];
P
i+1
=[1,0,0,0;0,1,0,0;0,0,1,l
i+1
;0,0,0,1];
T
i+1
=T
i
*Rxyz
i+1
*P
i+1
;
x
i+1
=T
i+1
(1,4);
y
i+1
=T
i+1
(2,4);
z
i+1
=T
i+1
(3,4);
grid on
ld
i
=line([0,x
i
],[0,y
i
],[0,z
i
],'LineWidth',6,'Color','red');
ld
i+1
=line([x
i
,x
i+1
],[ y
i
,y
i+1
],[ z
i
,z
i+1
],'LineWidth',6,'Color','red');
pause(0.1);
end
UWAGA:
W programie nale y uwzgl dni tylko macierze obrotów i przesuni , które opisuj faktycznie tworzony
manipulator, tzn. je eli ruch pierwszego ramienia nast puje tylko wzgl dem osi x do programu nale y
wpisa tylko macierz rotacji wzgl dem tej osi.
W wyniku wiczenia powinien powsta program umo liwiaj cy przedstawienie ruchu manipulatora
(animacja) zgodnie z zaleceniami prowadz cego (m.in. zakresy ruchu poszczególnych osi).
6. W
YKONANIE SPRAWOZDANIA
W sprawozdaniu nale y zamie ci :
•
cel wiczenia;
•
szkic manipulatora;
•
przykłady zastosowa analizowanego typu robota;
•
wydruk programu z komentarzem;
•
widok manipulatora ze rodowiska MATLAB (skopiowany zrzut ekranu - Alt+PrtScr);
•
program w wersji elektronicznej.
7. P
YTANIA KONTROLNE
ANALIZA KINEMATYCZNA MANIPULATORÓW – ZADANIE PROSTE KINEMATYKI
11
1. Co to s współrz dne jednorodne podaj przykład?
2. Co to jest i jaka ma posta jednorodna macierz transformacji ?
3. Jakie maj postacie macierze obrotów elementarnych?
4. Co to jest czynnik skali (w mcierzy transformacj ijednorodnej) i do czego słu y?
5. Co to jest: zadanie bezposrednie/odwrotne kinematyki?
8. L
ITERATURA
1. Kaczmarek W., Panasiuk J..: „Podstawy robotyki” – opracowanie własne 2006.
2. Podr cznik u ytkownika pakietu Matlab.