WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
1
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
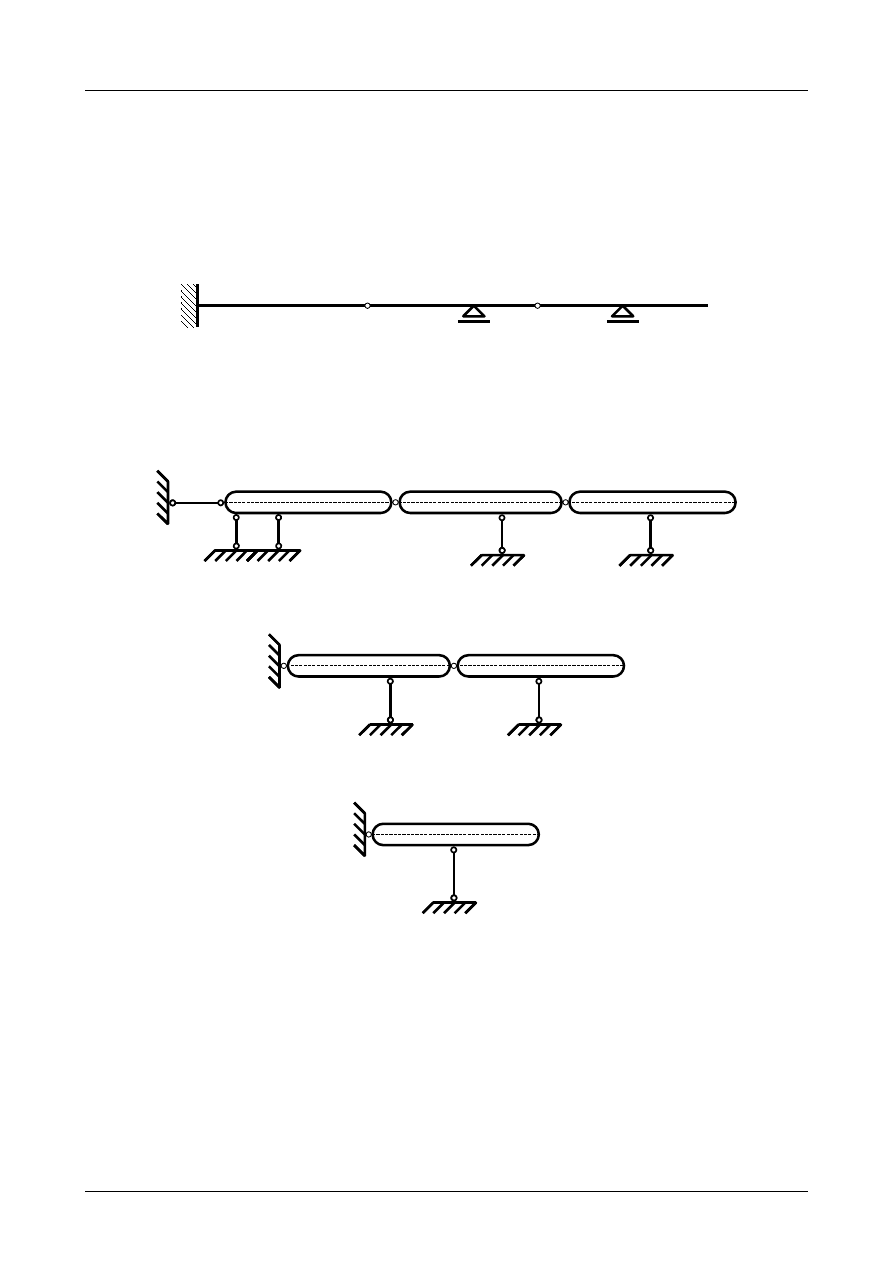
Z2/2.1. Belka złożona numer 1
Sprawdzić czy belka złożona przedstawiona na rysunku Z2/2.1 jest układem geometrycznie niezmien-
nym.
Rys. Z2/2.1. Belka złożona
W pierwszej kolejności musimy pręty belki zamienić na tarcze sztywne a podpory na układ prętów
podporowych. Przedstawia to rysunek Z2/2.2.
4
5
1
2
3
A
B
I
II
III
Rys. Z2/2.2. Zastępczy układ tarcz sztywnych
4
5
A
B
II
III
Rys. Z2/2.3. Zastępczy układ tarcz sztywnych
5
B
III
Rys. Z2/2.4. Zastępcza tarcza sztywna
Jak widać na rysunku Z2/2.2 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅3=5⋅12⋅2
.
(Z2/2.1)
Warunek konieczny geometrycznej niezmienności został spełniony. Belka może być układem geometrycznie
niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić warunki dosta-
teczne geometrycznej niezmienności.
Dr inż. Janusz Dębiński
WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
2
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/2.3.
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić
podłoże dla pozostałej tarczy sztywnej. Przedstawia to rysunek Z2/2.4.
Tarcza numer III jest podparta przegubem rzeczywistym B oraz prętem podporowym numer 5. Prze-
gub B nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
belka złożona jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
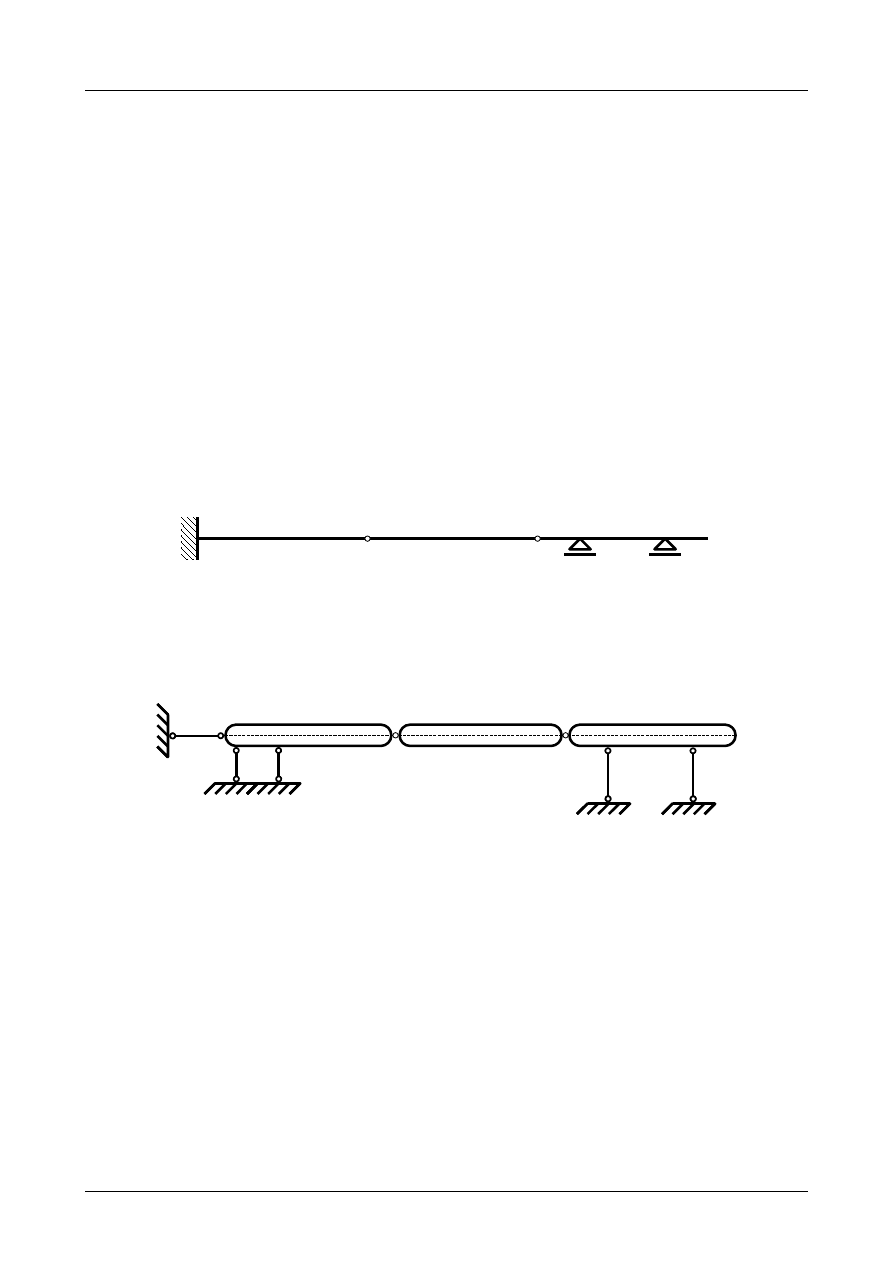
Z2/2.2. Belka złożona numer 2
Sprawdzić czy belka złożona przedstawiona na rysunku Z2/2.5 jest układem geometrycznie niezmien-
nym.
Rys. Z2/2.5. Belka złożona
W pierwszej kolejności musimy pręty belki zamienić na tarcze sztywne a podpory na układ prętów
podporowych. Przedstawia to rysunek Z2/2.6.
4
5
1
2
3
A
B
I
II
III
Rys. Z2/2.6. Zastępczy układ tarcz sztywnych
Jak widać na rysunku Z2/2.6 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅3=5⋅12⋅2
.
(Z2/2.2)
Warunek konieczny geometrycznej niezmienności został spełniony. Belka może być układem geometrycznie
niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić warunki
dostateczne geometrycznej niezmienności.
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/2.7.
Dr inż. Janusz Dębiński
WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
3
4
5
A
B
C
∞
II
III
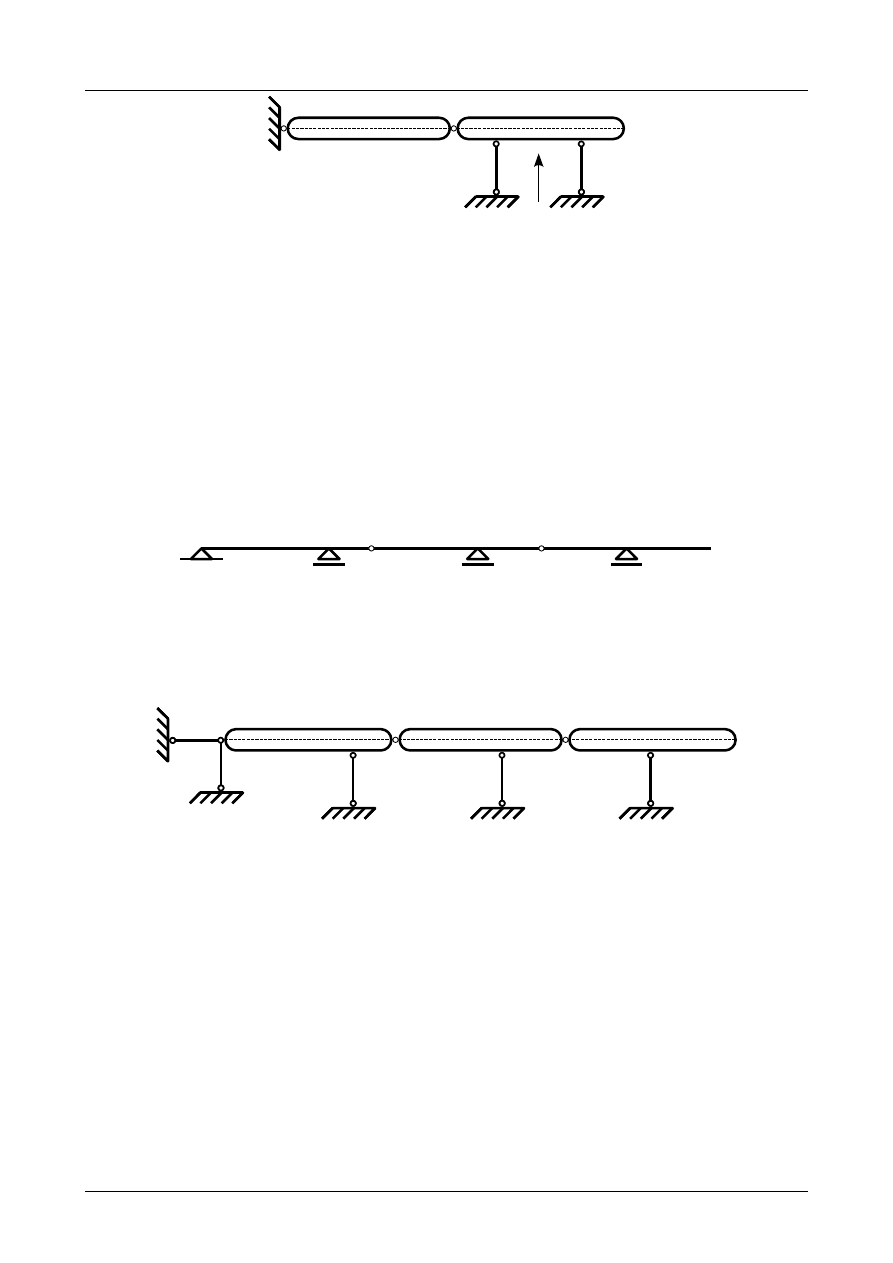
Rys. Z2/2.7. Zastępczy układ tarcz sztywnych
Tarcze numer II i III tworzą układ trójprzegubowy z przegubami rzeczywistymi A i B oraz przegubem
niewłaściwym C utworzonym z prętów podporowych numer 4 i 5. Wszystkie przeguby nie leżą na jednaj
prostej. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz sztywnych.
Wobec tego są one geometrycznie niezmienne.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
belka złożona jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Z2/2.3. Belka złożona numer 3
Sprawdzić czy belka złożona przedstawiona na rysunku Z2/2.8 jest układem geometrycznie niezmien-
nym.
Rys. Z2/2.8. Belka złożona
W pierwszej kolejności musimy pręty belki zamienić na tarcze sztywne a podpory na układ prętów
podporowych. Przedstawia to rysunek Z2/2.9.
4
5
1
2
3
A
B
I
II
III
Rys. Z2/2.9. Zastępczy układ tarcz sztywnych
Jak widać na rysunku Z2/2.9 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅3=5⋅12⋅2
.
(Z2/2.3)
Warunek konieczny geometrycznej niezmienności został spełniony. Belka może być układem geometrycznie
niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić warunki
dostateczne geometrycznej niezmienności.
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/2.10.
Dr inż. Janusz Dębiński
WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
4
4
5
A
B
II
III
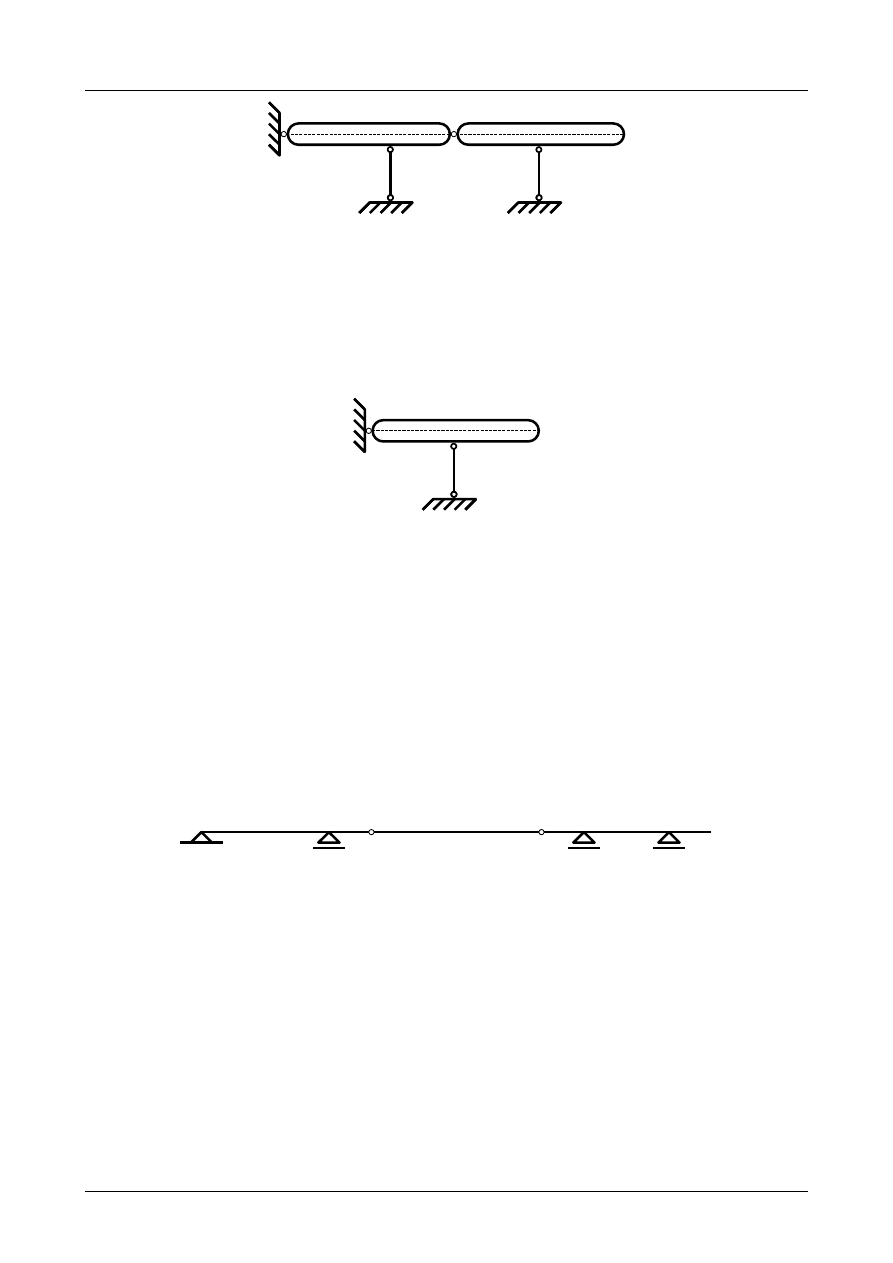
Rys. Z2/2.10. Zastępczy układ tarcz sztywnych
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić
podłoże dla pozostałej tarczy sztywnej. Przedstawia to rysunek Z2/2.11.
5
B
III
Rys. Z2/2.11. Zastępcza tarcza sztywna
Tarcza numer III jest podparta przegubem rzeczywistym B oraz prętem podporowym numer 5. Prze-
gub B nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
belka złożona jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
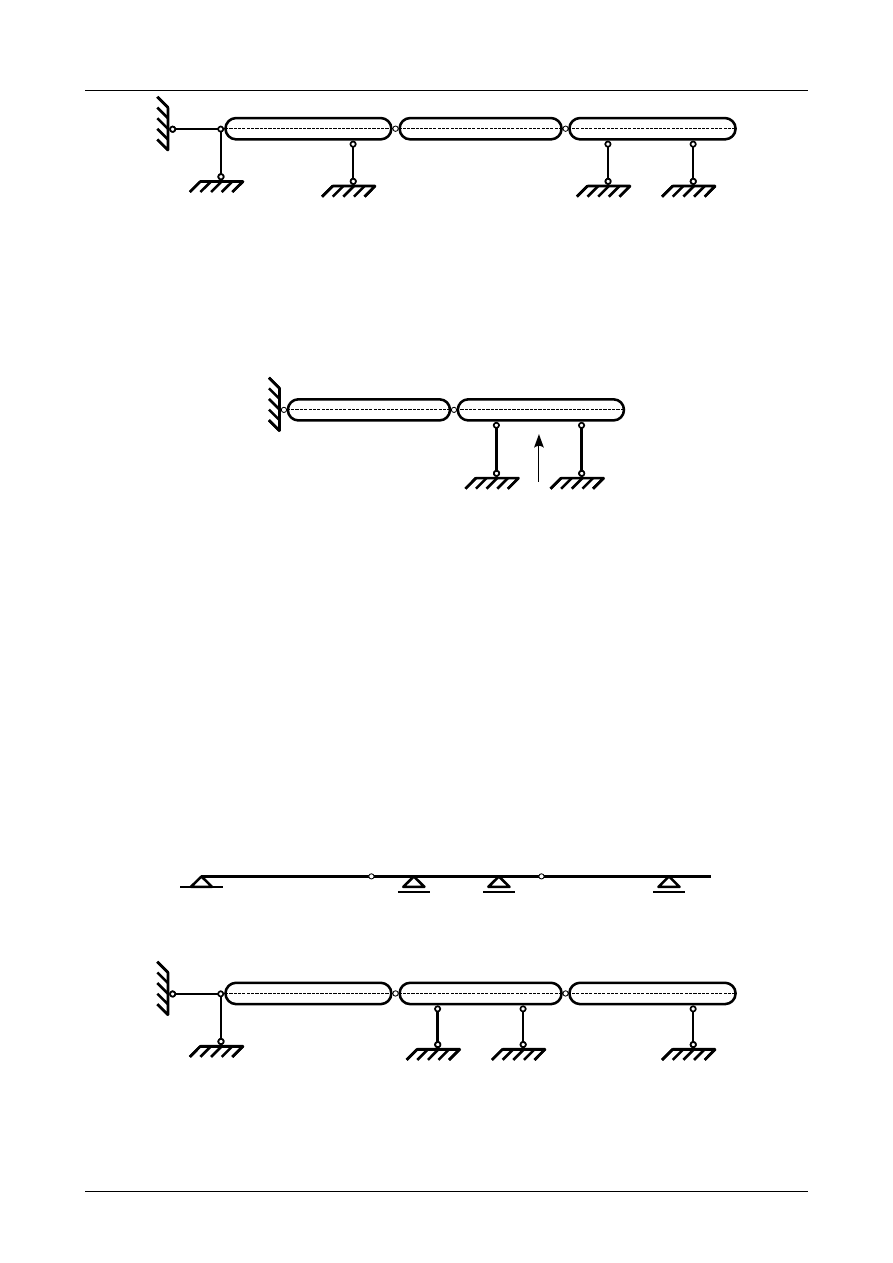
Z2/2.4. Belka złożona numer 4
Sprawdzić czy belka złożona przedstawiona na rysunku Z2/2.12 jest układem geometrycznie nie-
zmiennym.
Rys. Z2/2.12. Belka złożona
W pierwszej kolejności musimy pręty belki zamienić na tarcze sztywne a podpory na układ prętów
podporowych. Przedstawia to rysunek Z2/2.13.
Jak widać na rysunku Z2/2.13 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅3=5⋅12⋅2
.
(Z2/2.4)
Warunek konieczny geometrycznej niezmienności został spełniony. Belka może być układem geometrycznie
niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić warunki dosta-
teczne geometrycznej niezmienności.
Dr inż. Janusz Dębiński
WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
5
4
5
1
2
3
A
B
I
II
III
Rys. Z2/2.13. Zastępczy układ tarcz sztywnych
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/2.14.
4
5
A
B
II
III
C
∞
Rys. Z2/2.14. Zastępczy układ tarcz sztywnych
Tarcze numer II i III tworzą układ trójprzegubowy z przegubami rzeczywistymi A i B oraz przegubem
niewłaściwym C utworzonym z prętów podporowych numer 4 i 5. Wszystkie przeguby nie leżą na jednaj
prostej. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz sztywnych.
Wobec tego są one geometrycznie niezmienne.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
belka złożona jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
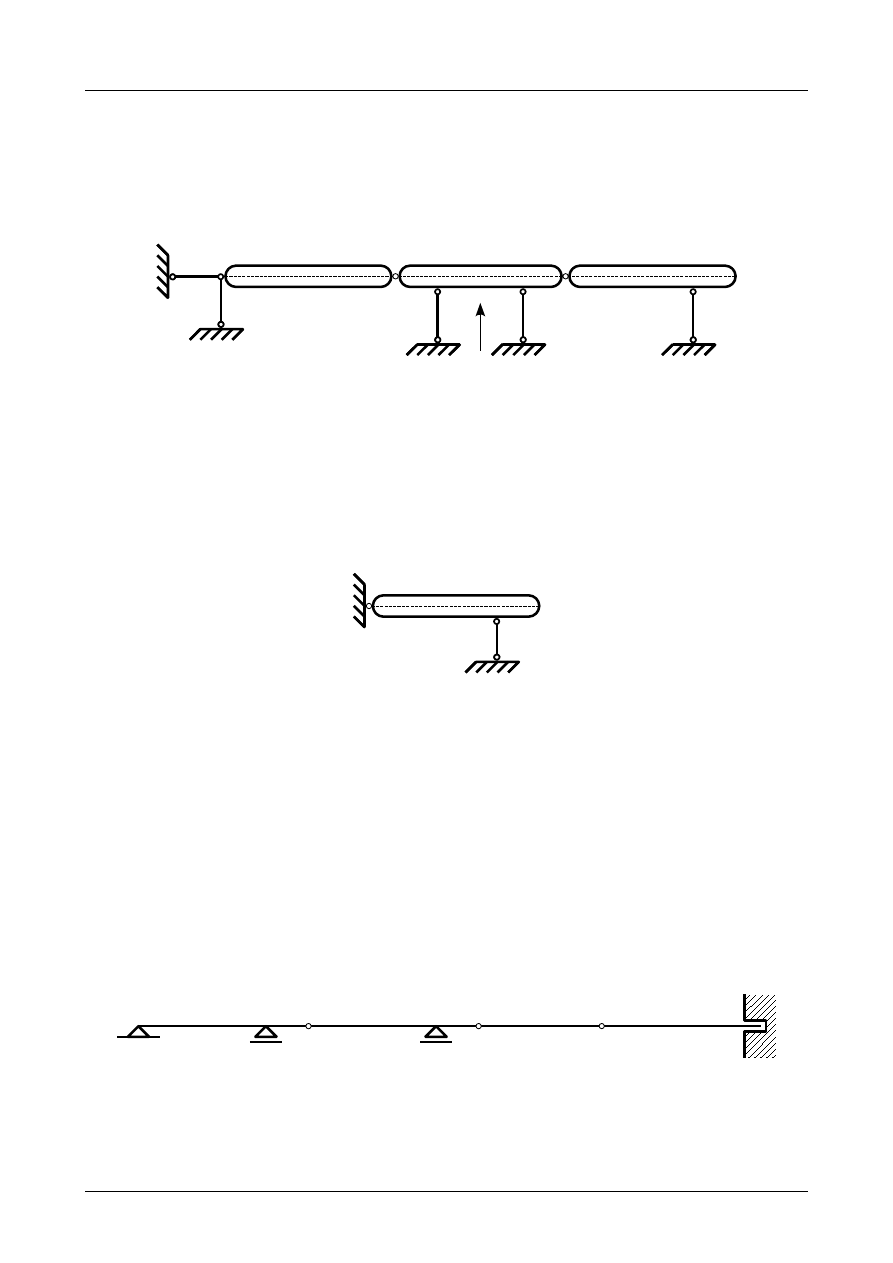
Z2/2.5. Belka złożona numer 5
Sprawdzić czy belka złożona przedstawiona na rysunku Z2/2.15 jest układem geometrycznie nie-
zmiennym.
W pierwszej kolejności musimy pręty belki zamienić na tarcze sztywne a podpory na układ prętów
podporowych. Przedstawia to rysunek Z2/2.16.
Rys. Z2/2.15. Belka złożona
4
5
1
2
3
B
D
I
II
III
Rys. Z2/2.16. Zastępczy układ tarcz sztywnych
Jak widać na rysunku Z2/2.16 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
Dr inż. Janusz Dębiński
WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
6
3⋅3=5⋅12⋅2
.
(Z2/2.5)
Warunek konieczny geometrycznej niezmienności został spełniony. Belka może być układem geometrycznie
niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić warunki dosta-
teczne geometrycznej niezmienności.
4
5
1
2
3
B
D
I
II
III
C
∞
A
Rys. Z2/2.17. Zastępczy układ tarcz sztywnych
Zgodnie z rysunkiem Z2/2.17 tarcze numer I i II tworzą układ trójprzegubowy z przegubem fikcyjnym
A utworzonym z prętów podporowych numer 1 i 2, przegubem rzeczywistym B oraz przegubem
niewłaściwym C z prętów podporowych numer 3 i 4. Wszystkie przeguby nie leżą na jednaj prostej. Został
więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz sztywnych. Wobec tego są
one geometrycznie niezmienne i mogą stanowić podłoże dla tarczy numer III. Przedstawia to rysunek
Z2/2.18.
5
D
III
Rys. Z2/2.18. Zastępcza tarcza sztywna
Tarcza numer III jest podparta przegubem rzeczywistym D oraz prętem podporowym numer 5. Prze-
gub D nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
belka złożona jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
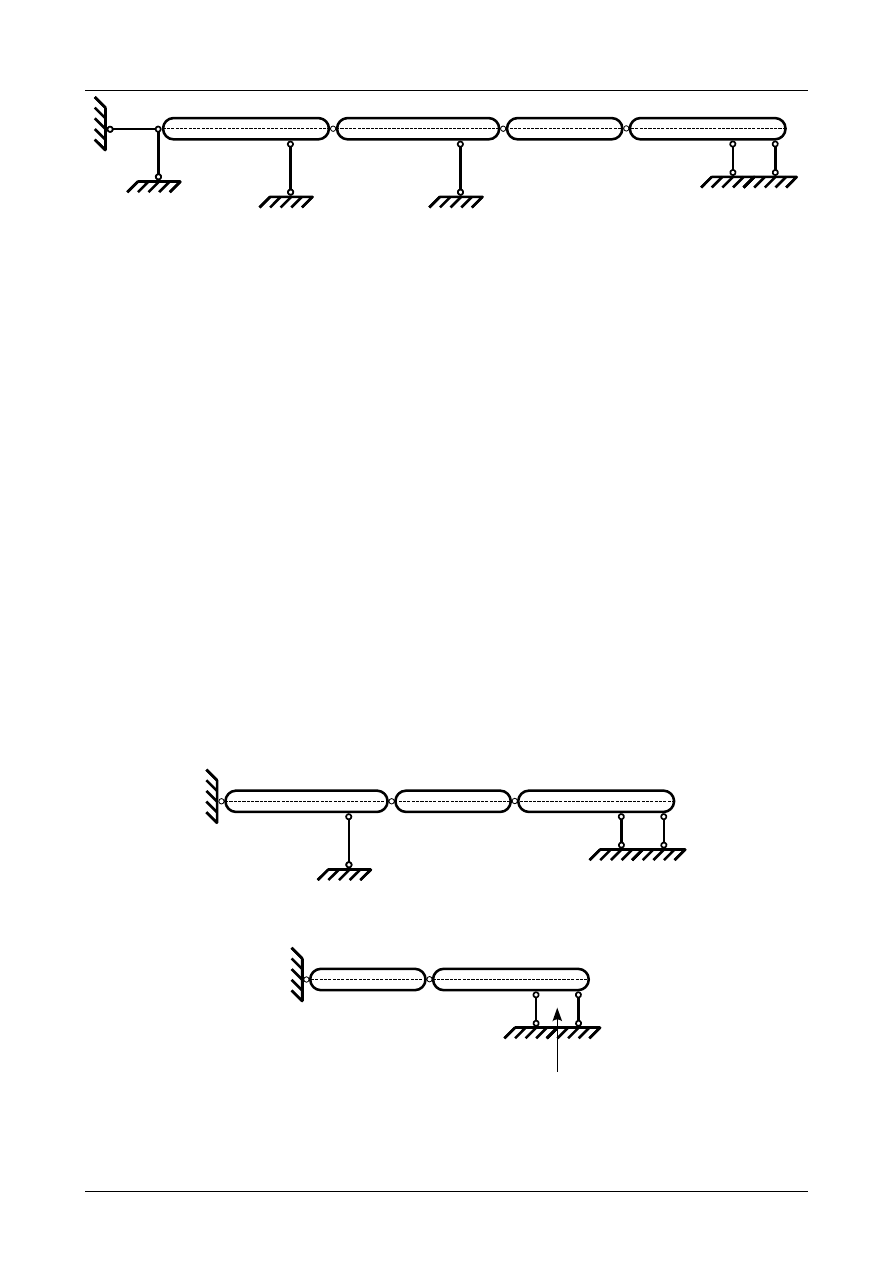
Z2/2.6. Belka złożona numer 6
Sprawdzić czy belka złożona przedstawiona na rysunku Z2/2.19 jest układem geometrycznie nie-
zmiennym.
Rys. Z2/2.19. Belka złożona
W pierwszej kolejności musimy pręty belki zamienić na tarcze sztywne a podpory na układ prętów
podporowych. Przedstawia to rysunek Z2/2.20.
Dr inż. Janusz Dębiński
WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
7
3
4
A
B
I
II
5
6
1
2
III
IV
C
Rys. Z2/2.20. Zastępczy układ tarcz sztywnych
Jak widać na rysunku Z2/2.20 liczba tarcz wynosi 4, liczba prętów podporowych wynosi 6 natomiast
liczba przegubów rzeczywistych wynosi 3. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅4=6⋅13⋅2
.
(Z2/2.6)
Warunek konieczny geometrycznej niezmienności został spełniony. Belka może być układem geometrycznie
niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić warunki
dostateczne geometrycznej niezmienności.
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/2.21.
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić
podłoże dla pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/2.22.
Tarcze numer III i IV tworzą układ trójprzegubowy z przegubami rzeczywistymi B i C oraz
przegubem niewłaściwym D utworzonym z prętów podporowych numer 5 i 6. Wszystkie przeguby nie leżą
na jednaj prostej. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz
sztywnych. Wobec tego są one geometrycznie niezmienne.
4
A
B
II
5
6
III
IV
C
Rys. Z2/2.21. Zastępczy układ tarcz sztywnych
B
5
6
III
IV
C
D
∞
Rys. Z2/2.22. Zastępczy układ tarcz sztywnych
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
belka złożona jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Dr inż. Janusz Dębiński
WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
8
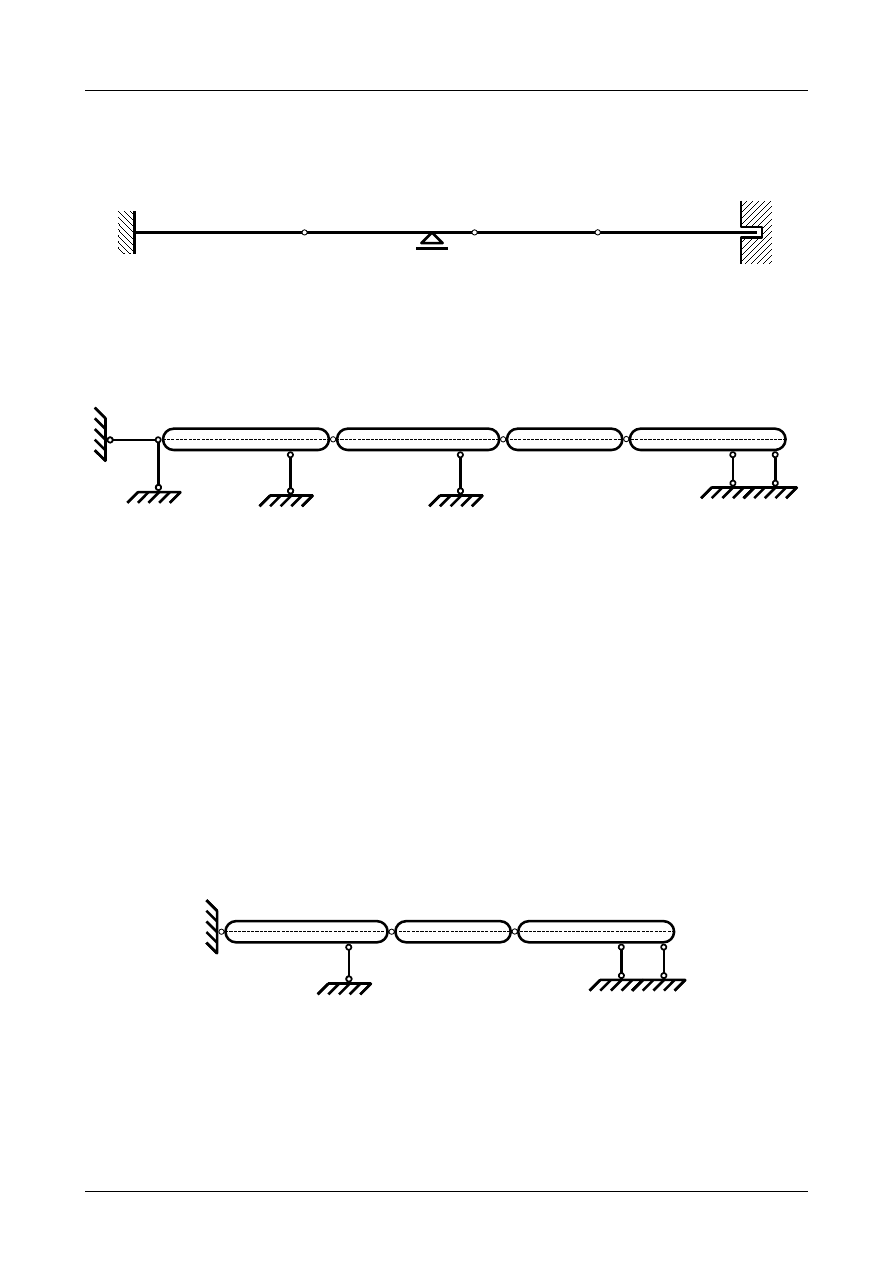
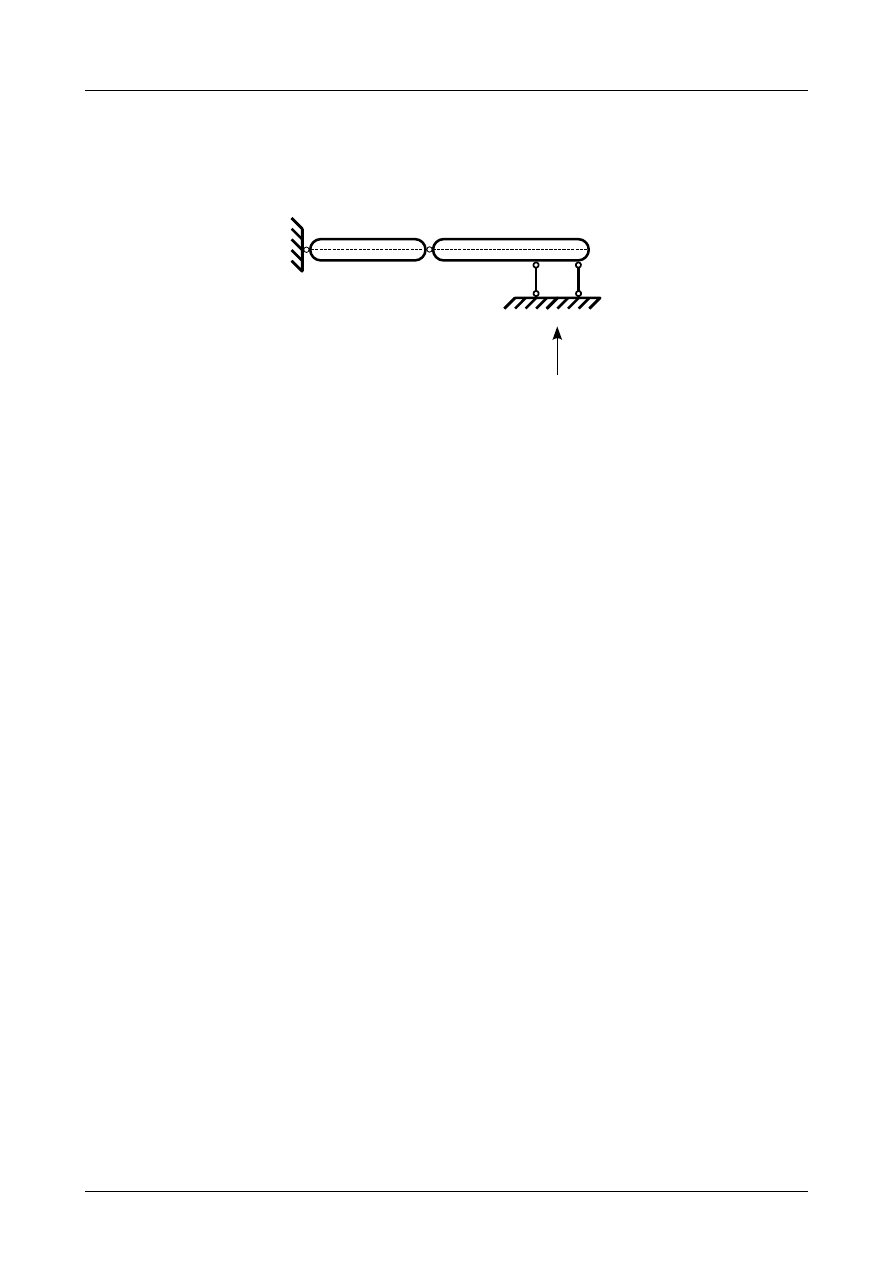
Z2/2.7. Belka złożona numer 7
Sprawdzić czy belka złożona przedstawiona na rysunku Z2/2.23 jest układem geometrycznie nie-
zmiennym.
Rys. Z2/2.23. Belka złożona
W pierwszej kolejności musimy pręty belki zamienić na tarcze sztywne a podpory na układ prętów
podporowych. Przedstawia to rysunek Z2/2.24.
3
4
A
B
I
II
5
6
1
2
III
IV
C
Rys. Z2/2.24. Zastępczy układ tarcz sztywnych
Jak widać na rysunku Z2/2.24 liczba tarcz wynosi 4, liczba prętów podporowych wynosi 6 natomiast
liczba przegubów rzeczywistych wynosi 3. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅4=6⋅13⋅2
.
(Z2/2.7)
Warunek konieczny geometrycznej niezmienności został spełniony. Belka może być układem geometrycznie
niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić warunki
dostateczne geometrycznej niezmienności.
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/2.25.
4
A
B
II
5
6
III
IV
C
Rys. Z2/2.25. Zastępczy układ tarcz sztywnych
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić
podłoże dla pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/2.26
Tarcze numer III i IV tworzą układ trójprzegubowy z przegubami rzeczywistymi B i C oraz
przegubem niewłaściwym D utworzonym z prętów podporowych numer 5 i 6. Wszystkie przeguby nie leżą
Dr inż. Janusz Dębiński
WM
Z2/2. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 2
9
na jednaj prostej. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz
sztywnych. Wobec tego są one geometrycznie niezmienne.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
belka złożona jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
B
5
6
III
IV
C
D
∞
Rys. Z2/2.26. Zastępczy układ tarcz sztywnych
Dr inż. Janusz Dębiński
Document Outline