WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
1
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
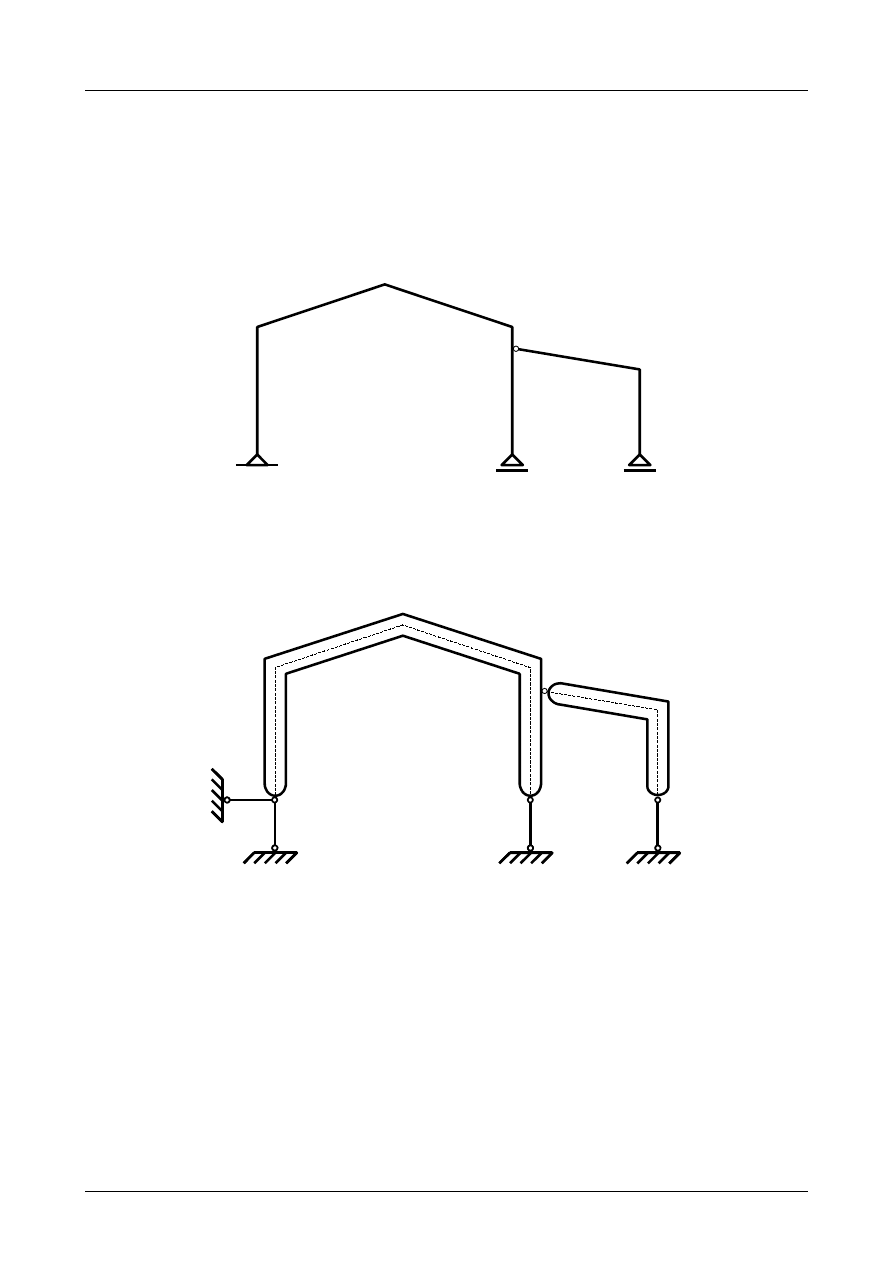
Z2/3.1. Rama płaska numer 1
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.1 jest układem geometrycznie niezmien-
nym.
Rys. Z2/3.1. Rama płaska
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne a podpory na układ
prętów podporowych. Przedstawia to rysunek Z2/3.2.
2
4
1
3
A
I
II
Rys. Z2/3.2. Zastępczy układ tarcz sztywnych
Jak widać na rysunku Z2/3.2 liczba tarcz wynosi 2, liczba prętów podporowych wynosi 4 natomiast
liczba przegubów rzeczywistych wynosi 1. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅2=4⋅11⋅2
.
(Z2/3.1)
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem
geometrycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić
warunki dostateczne geometrycznej niezmienności.
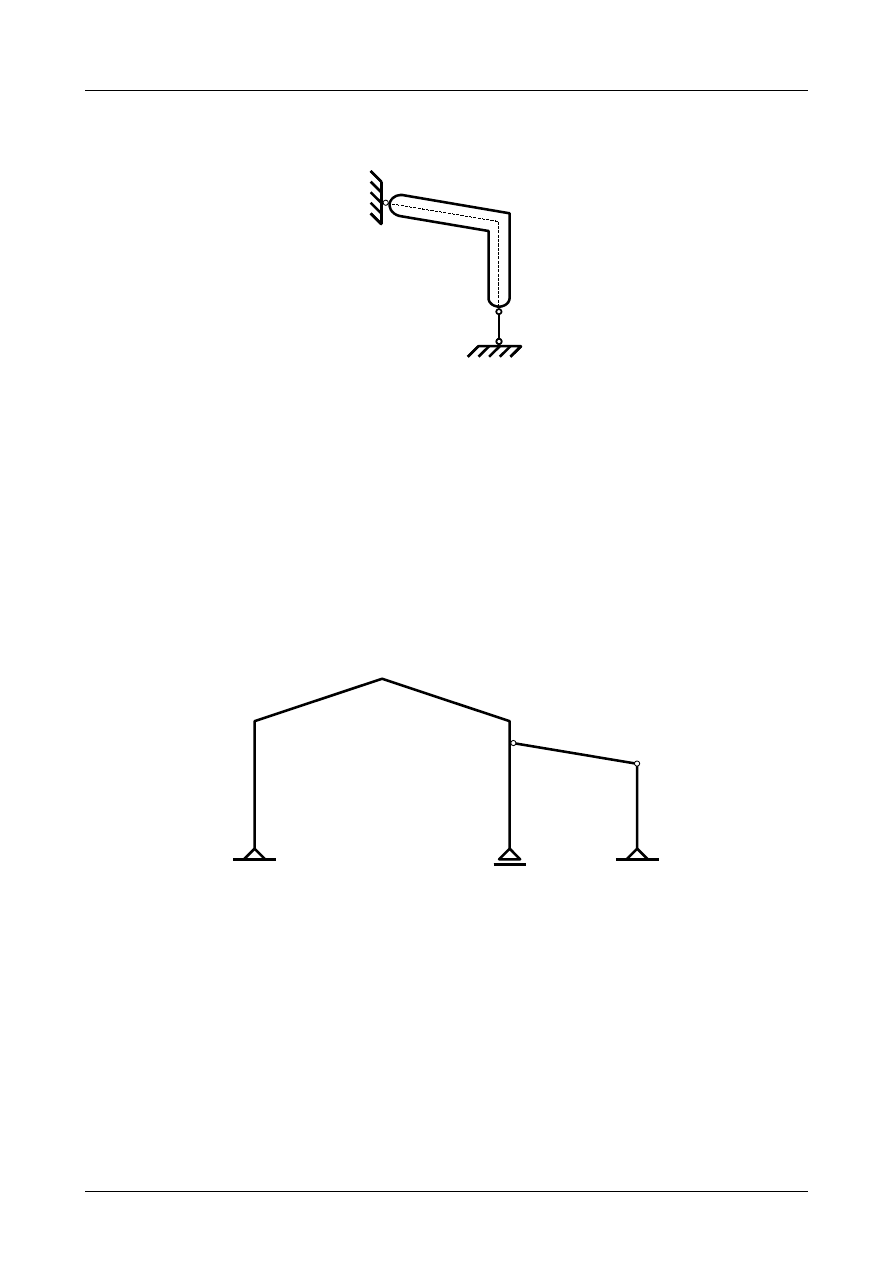
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
2
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałej tarczy sztywnej. Przedstawia to rysunek Z2/3.3.
4
A
II
Rys. Z2/3.3. Zastępcza tarcza sztywna
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
rama płaska jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
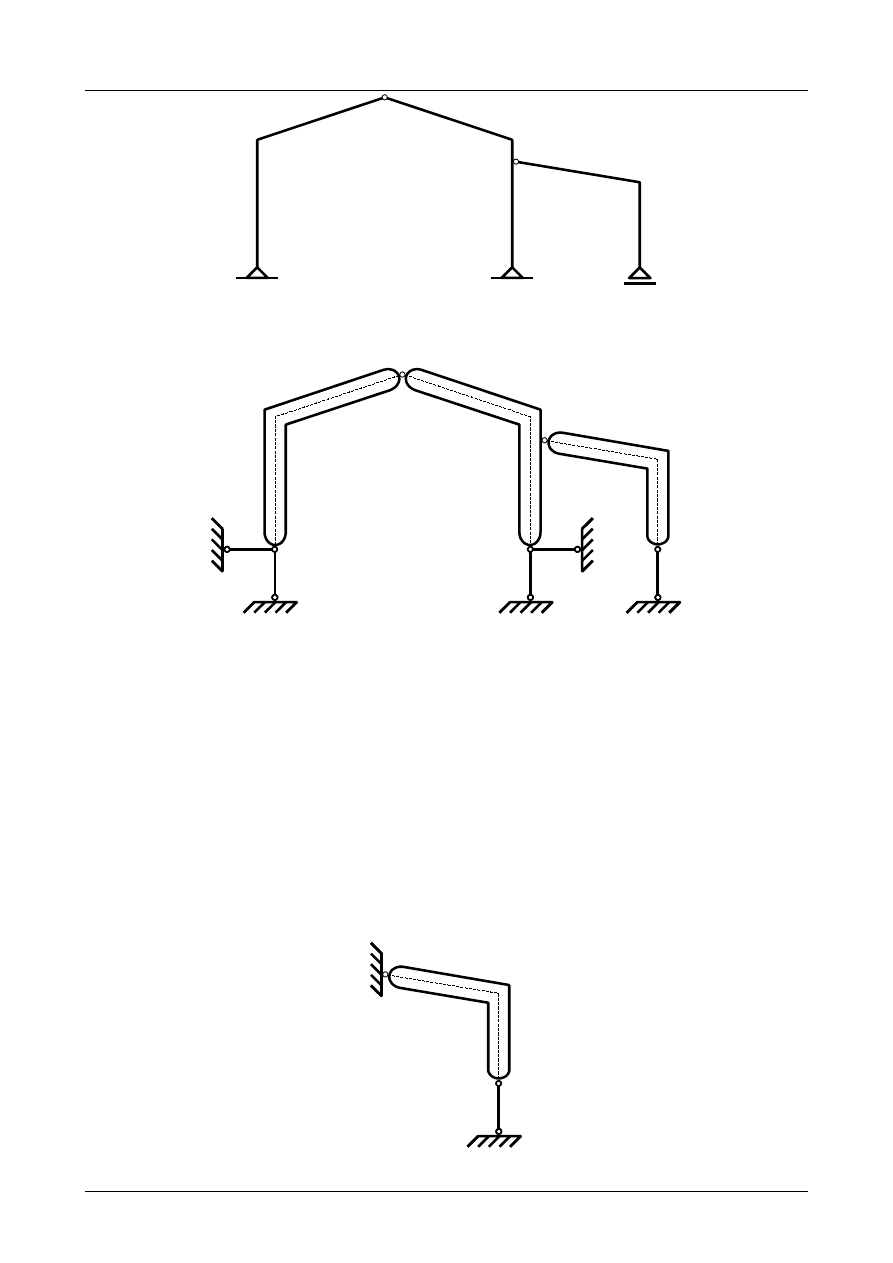
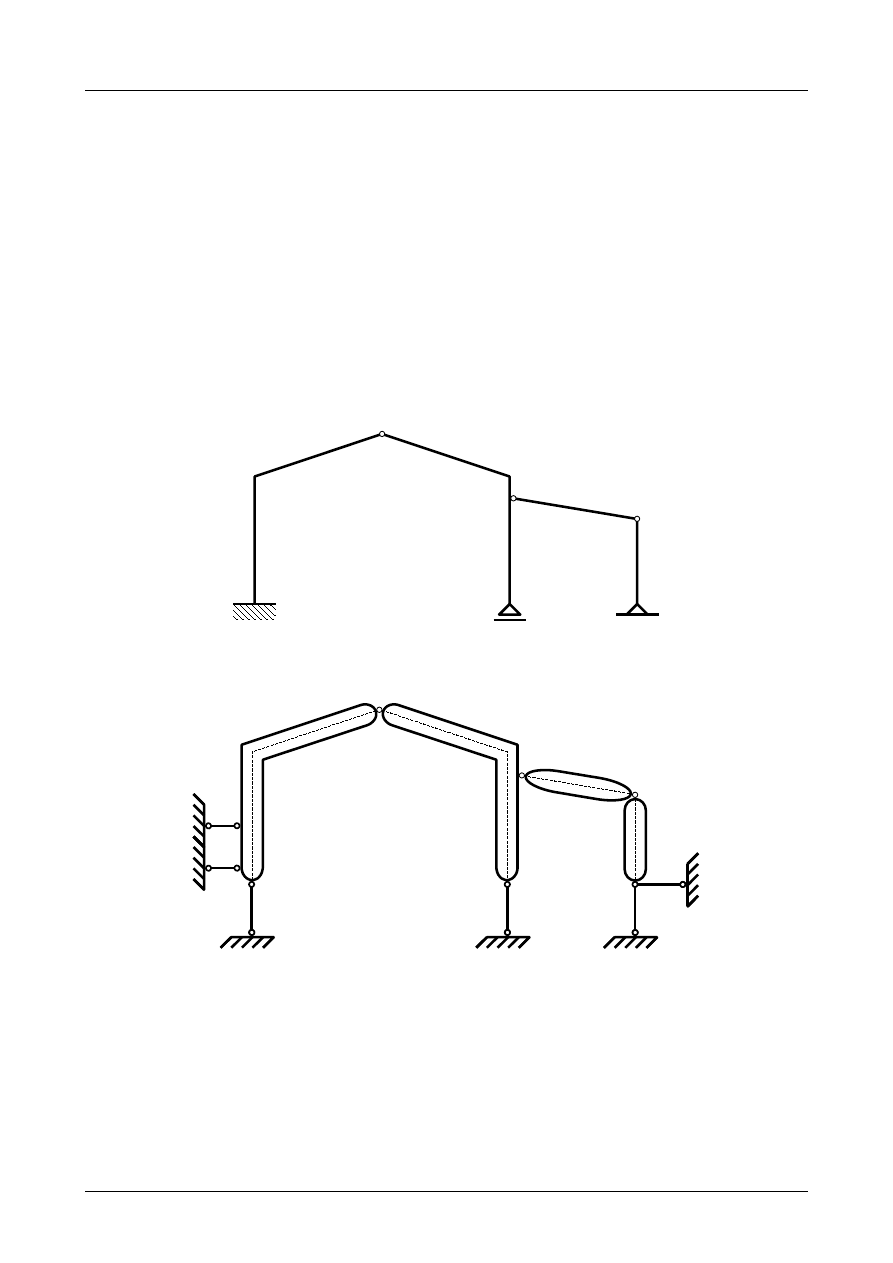
Z2/3.2. Rama płaska numer 2
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.4 jest układem geometrycznie niezmien-
nym.
Rys. Z2/3.4. Rama płaska
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne. Przedstawia to
rysunek Z2/3.5.
Jak widać na rysunku Z2/3.5 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅3=5⋅12⋅2
.
(Z2/3.2)
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem
geometrycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić
warunki dostateczne geometrycznej niezmienności.
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
3
2
4
1
3
A
B
5
I
II
III
C
Rys. Z2/3.5. Zastępczy układ tarcz sztywnych
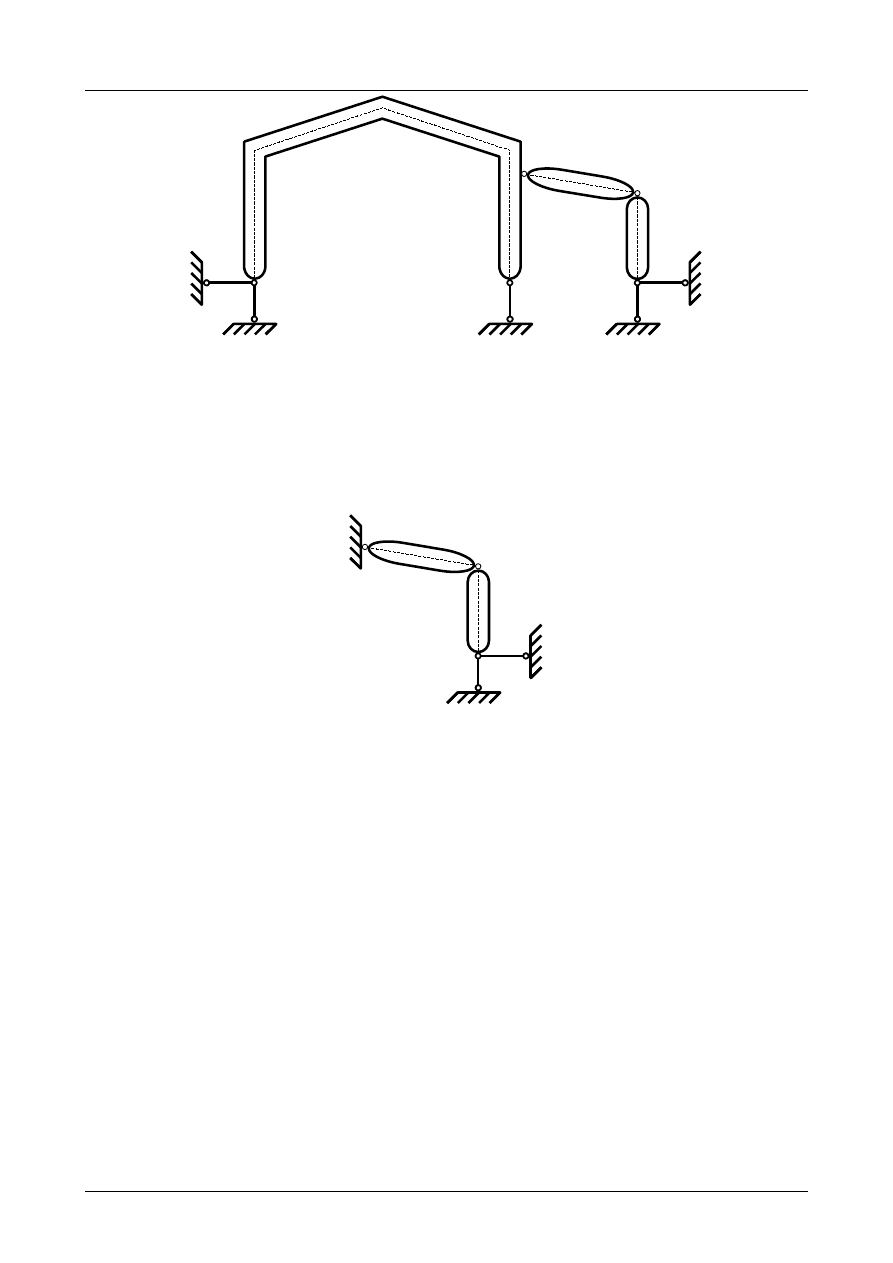
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/3.6.
4
A
B
5
II
III
C
Rys. Z2/3.6. Zastępczy układ tarcz sztywnych
Tarcze numer II i III tworzą układ trójprzegubowy z przegubami rzeczywistymi A i B oraz przegubem
fikcyjnym C utworzonym z prętów podporowych numer 4 i 5. Wszystkie przeguby nie leżą na jednaj prostej.
Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz sztywnych. Wobec
tego są one geometrycznie niezmienne.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
rama płaska jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Z2/3.3. Rama płaska numer 3
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.7 jest układem geometrycznie niezmien-
nym.
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne. Przedstawia to
rysunek Z2/3.8.
Jak widać na rysunku Z2/3.8 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅3=5⋅12⋅2
.
(Z2/3.3)
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
4
Rys. Z2/3.7. Rama płaska
2
5
1
3
D
I
III
II
B
4
A
C
Rys. Z2/3.8. Zastępczy układ tarcz sztywnych
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem geo-
metrycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić
warunki dostateczne geometrycznej niezmienności.
Tarcze sztywne numer I i II tworzą układ trójprzegubowy z przegubem fikcyjnym A utworzonym
z prętów podporowych numer 1 i 2, przegubem rzeczywistym B oraz przegubem fikcyjnym C, który tworzą
pręty podporowe numer 3 i 4. Wszystkie przeguby nie leżą na jednaj prostej. Został więc spełniony warunek
dostateczny geometrycznej niezmienności dla tych tarcz sztywnych. Wobec tego są one geometrycznie
niezmienne i mogą stanowić podłoże dla pozostałej tarczy sztywnej. Przedstawia to rysunek Z2/3.9.
Tarcza numer III jest podparta przegubem rzeczywistym D oraz prętem podporowym numer 5. Prze-
gub D nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna.
5
D
III
Rys. Z2/3.9. Zastępcza tarcza sztywna
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
5
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
rama płaska jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
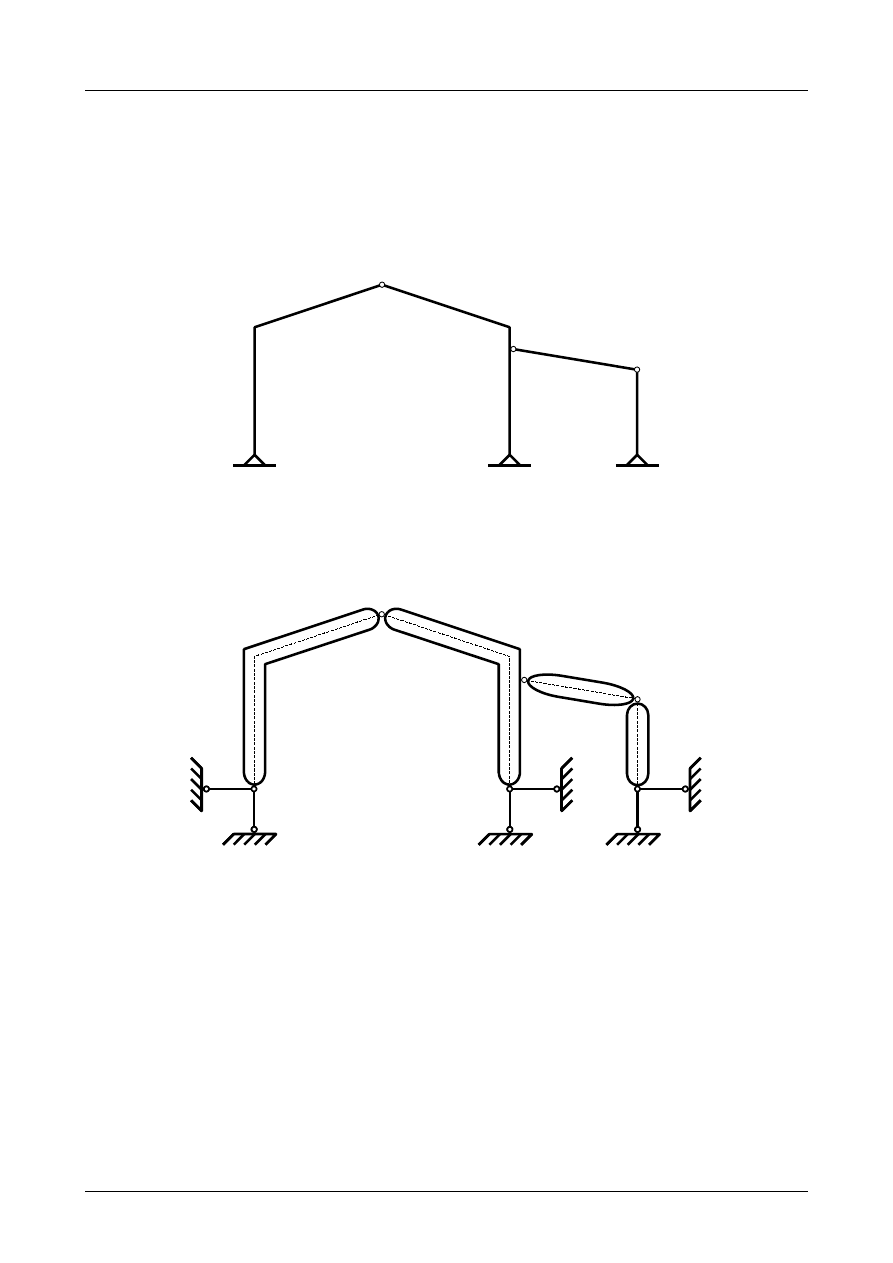
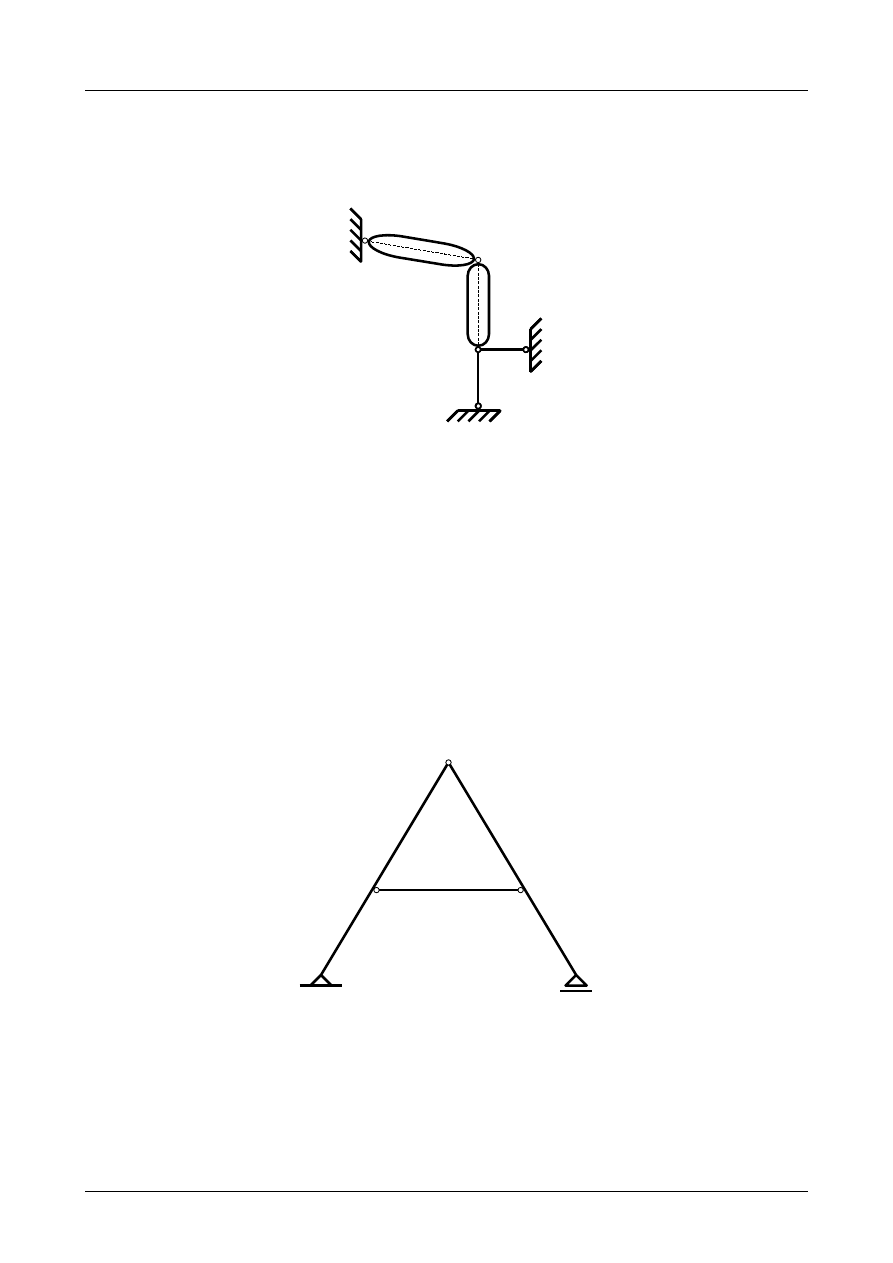
Z2/3.4. Rama płaska numer 4
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.10 jest układem geometrycznie niezmien-
nym.
Rys. Z2/3.10. Rama płaska
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne a podpory na układ
prętów podporowych. Przedstawia to rysunek Z2/3.11.
2
1
3
I
IV
II
A
4
5
B
C
6
III
D
E
F
Rys. Z2/3.11. Zastępczy układ tarcz sztywnych
Jak widać na rysunku Z2/3.11 liczba tarcz wynosi 4, liczba prętów podporowych wynosi 6 natomiast
liczba przegubów rzeczywistych wynosi 3. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅4=6⋅13⋅2
.
(Z2/3.4)
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem
geometrycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić
warunki dostateczne geometrycznej niezmienności.
Tarcze sztywne numer I i II tworzą układ trójprzegubowy z przegubem fikcyjnym A utworzonym
z prętów podporowych numer 1 i 2, przegubem rzeczywistym B oraz przegubem fikcyjnym C, który tworzą
pręty podporowe numer 3 i 4. Wszystkie przeguby nie leżą na jednaj prostej. Został więc spełniony warunek
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
6
dostateczny geometrycznej niezmienności dla tych tarcz sztywnych. Wobec tego są one geometrycznie
niezmienne i mogą stanowić podłoże dla pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/3.12.
IV
5
6
III
D
E
F
Rys. Z2/3.12. Zastępczy układ tarcz sztywnych
Tarcze numer III i IV tworzą układ trójprzegubowy z przegubami rzeczywistymi D i E oraz
przegubem fikcyjnym F utworzonym z prętów podporowych numer 5 i 6. Wszystkie przeguby nie leżą na
jednaj prostej. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz
sztywnych. Wobec tego są one geometrycznie niezmienne.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
rama płaska jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
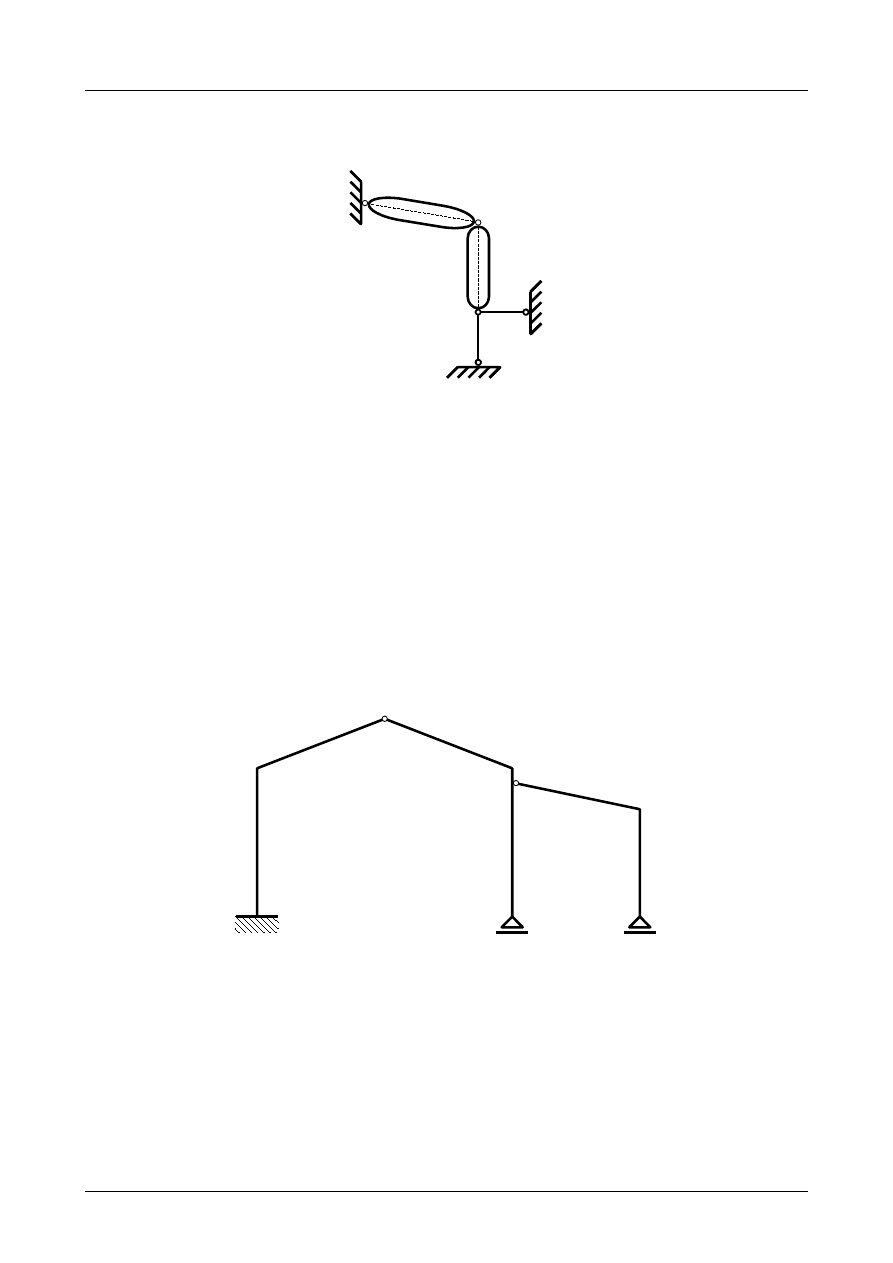
Z2/3.5. Rama płaska numer 5
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.13 jest układem geometrycznie niezmien-
nym.
Rys. Z2/3.13. Rama płaska
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne a podpory na układ
prętów podporowych. Przedstawia to rysunek Z2/3.14.
Jak widać na rysunku Z2/3.14 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅3=5⋅12⋅2
.
(Z2/3.5)
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
7
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem
geometrycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić
warunki dostateczne geometrycznej niezmienności.
1
5
B
I
III
II
A
4
2
3
Rys. Z2/3.14. Zastępczy układ tarcz sztywnych
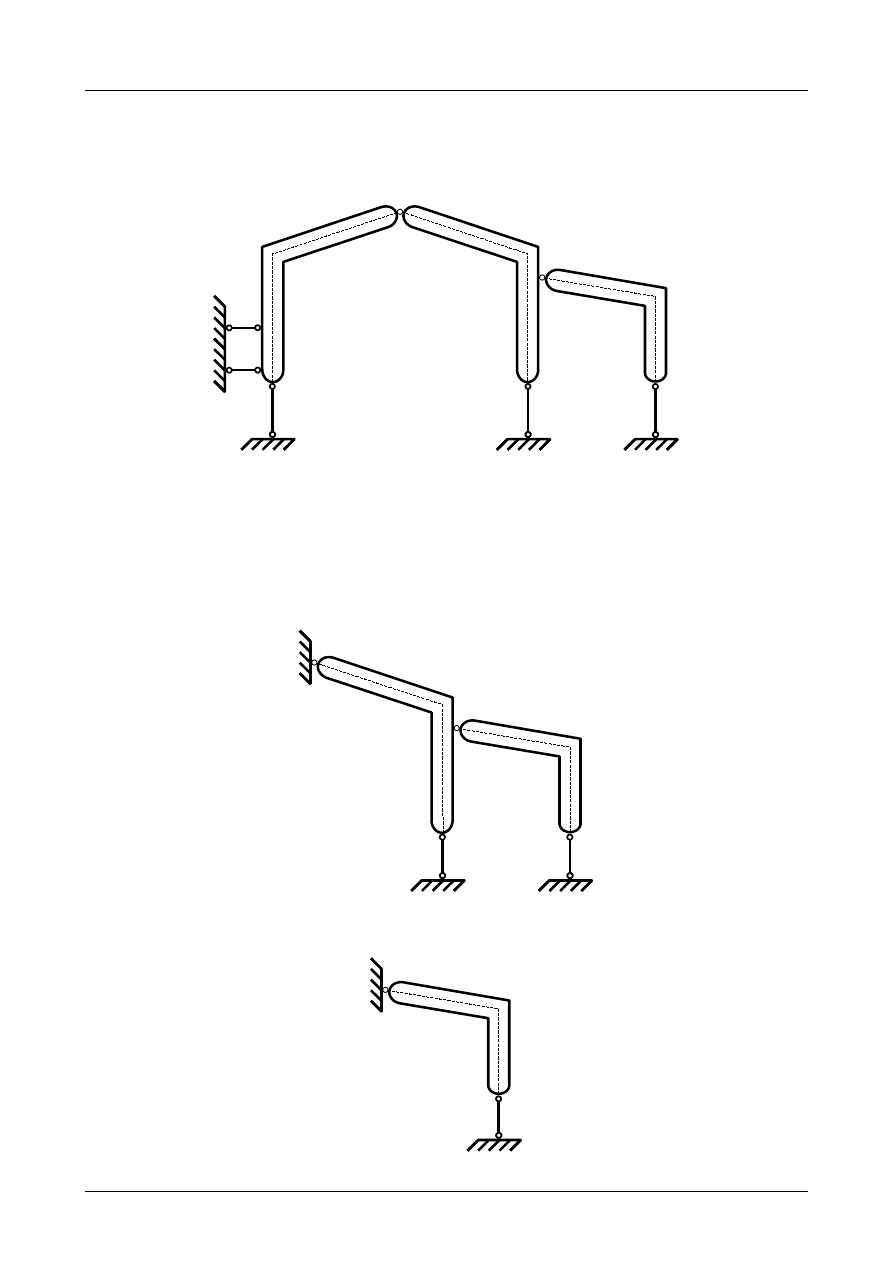
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla pozos-
tałych tarcz sztywnych. Przedstawia to rysunek Z2/3.15.
5
B
III
II
A
4
Rys. Z2/3.15. Zastępczy układ tarcz sztywnych
5
B
III
Rys. Z2/3.16. Zastępcza tarcza sztywna
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
8
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić
podłoże dla pozostałej tarczy sztywnej. Przedstawia to rysunek Z2/3.16.
Tarcza numer III jest podparta przegubem rzeczywistym B oraz prętem podporowym numer 5. Prze-
gub B nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
rama płaska jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
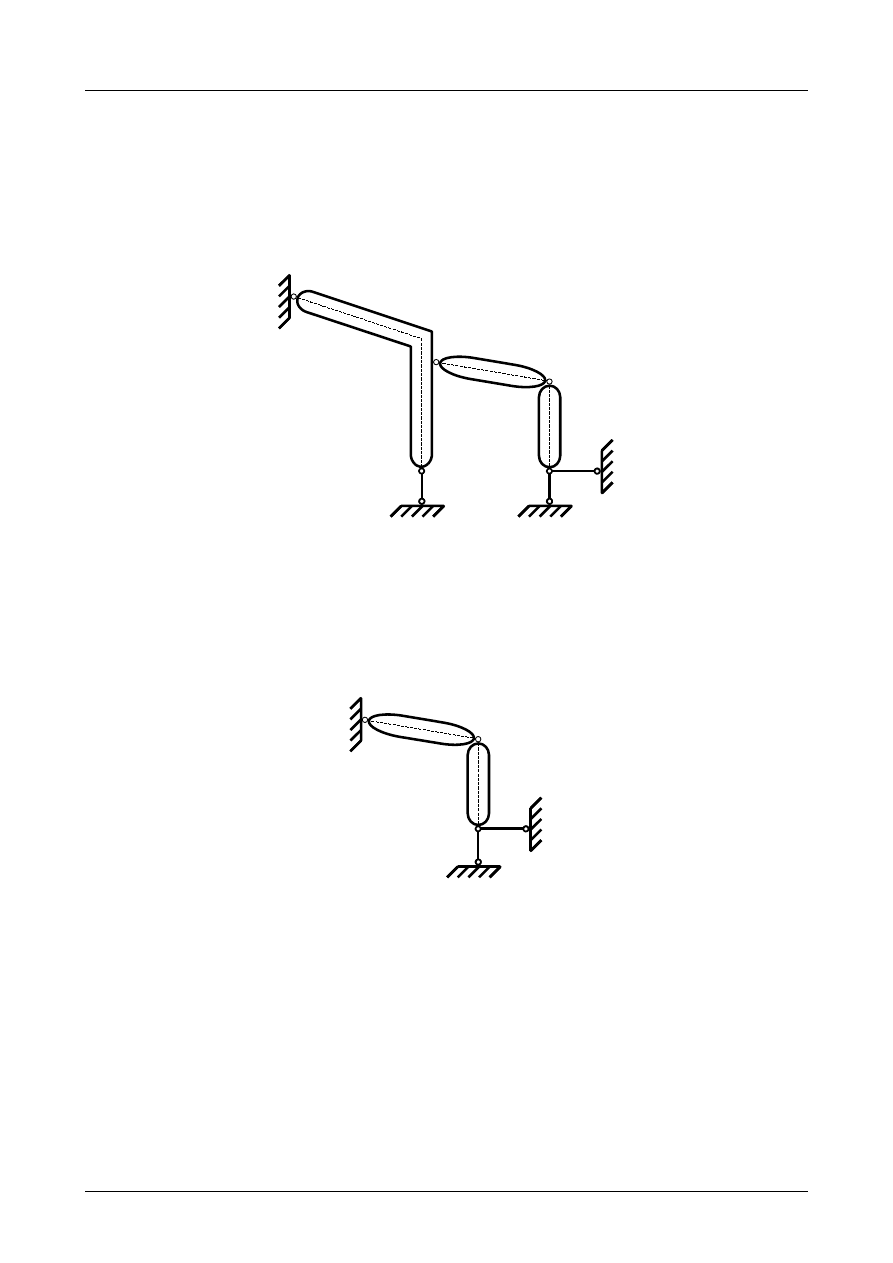
Z2/3.6. Rama płaska numer 6
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.17 jest układem geometrycznie niezmien-
nym.
Rys. Z2/3.17. Rama płaska
I
IV
II
4
5
A
6
III
B
C
D
1
2
3
Rys. Z2/3.18. Zastępczy układ tarcz sztywnych
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne a podpory na układ
prętów podporowych. Przedstawia to rysunek Z2/3.18.
Jak widać na rysunku Z2/3.18 liczba tarcz wynosi 4, liczba prętów podporowych wynosi 6 natomiast
liczba przegubów rzeczywistych wynosi 3. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅4=6⋅13⋅2
.
(Z2/3.6)
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
9
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem
geometrycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić
warunki dostateczne geometrycznej niezmienności.
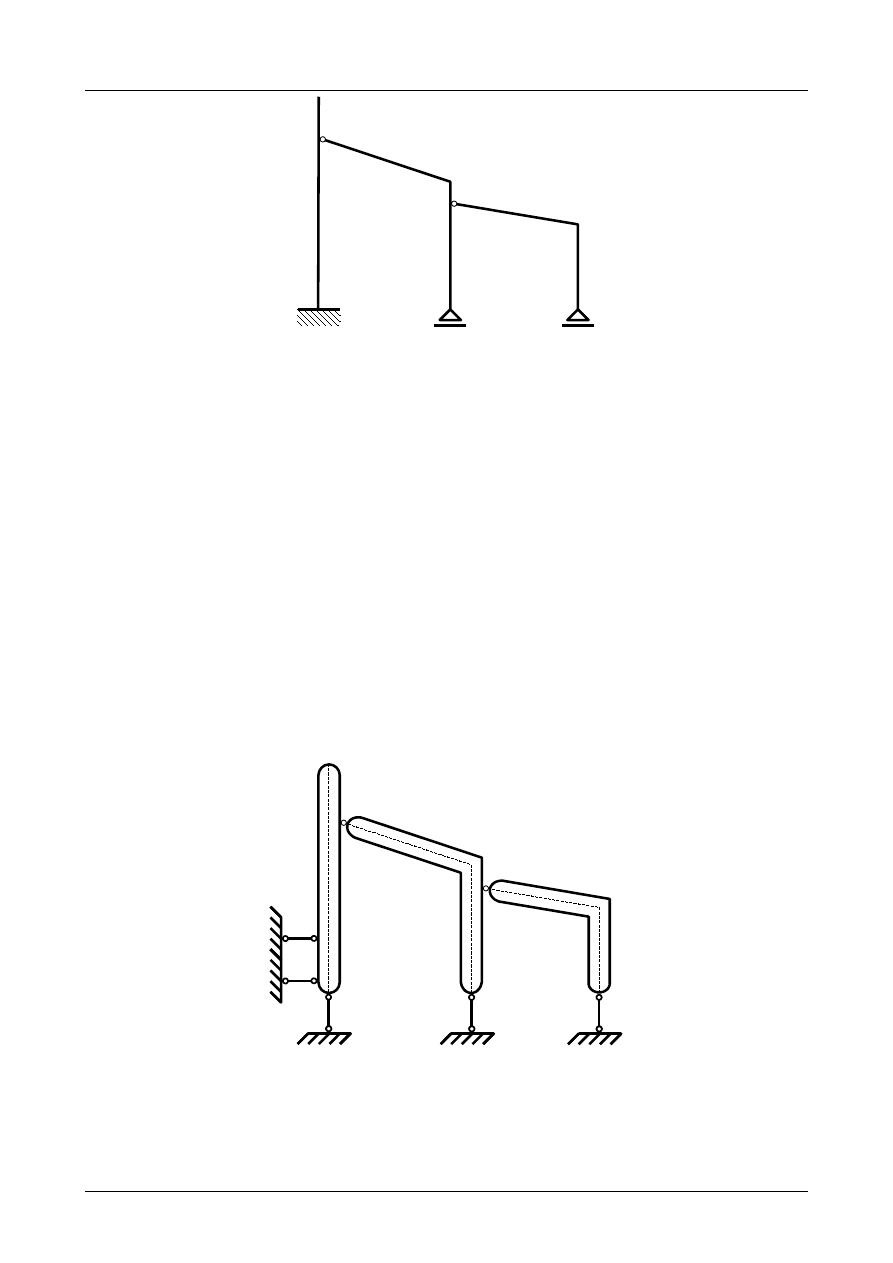
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/3.19.
IV
II
4
5
A
6
III
B
C
D
Rys. Z2/3.19. Zastępczy układ tarcz sztywnych
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić
podłoże dla pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/3.20.
IV
5
6
III
B
C
D
Rys. Z2/3.20. Zastępczy układ tarcz sztywnych
Tarcze numer III i IV tworzą układ trójprzegubowy z przegubami rzeczywistymi B i C oraz
przegubem fikcyjnym D utworzonym z prętów podporowych numer 5 i 6. Wszystkie przeguby nie leżą na
jednaj prostej. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz
sztywnych. Wobec tego są one geometrycznie niezmienne.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
rama płaska jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
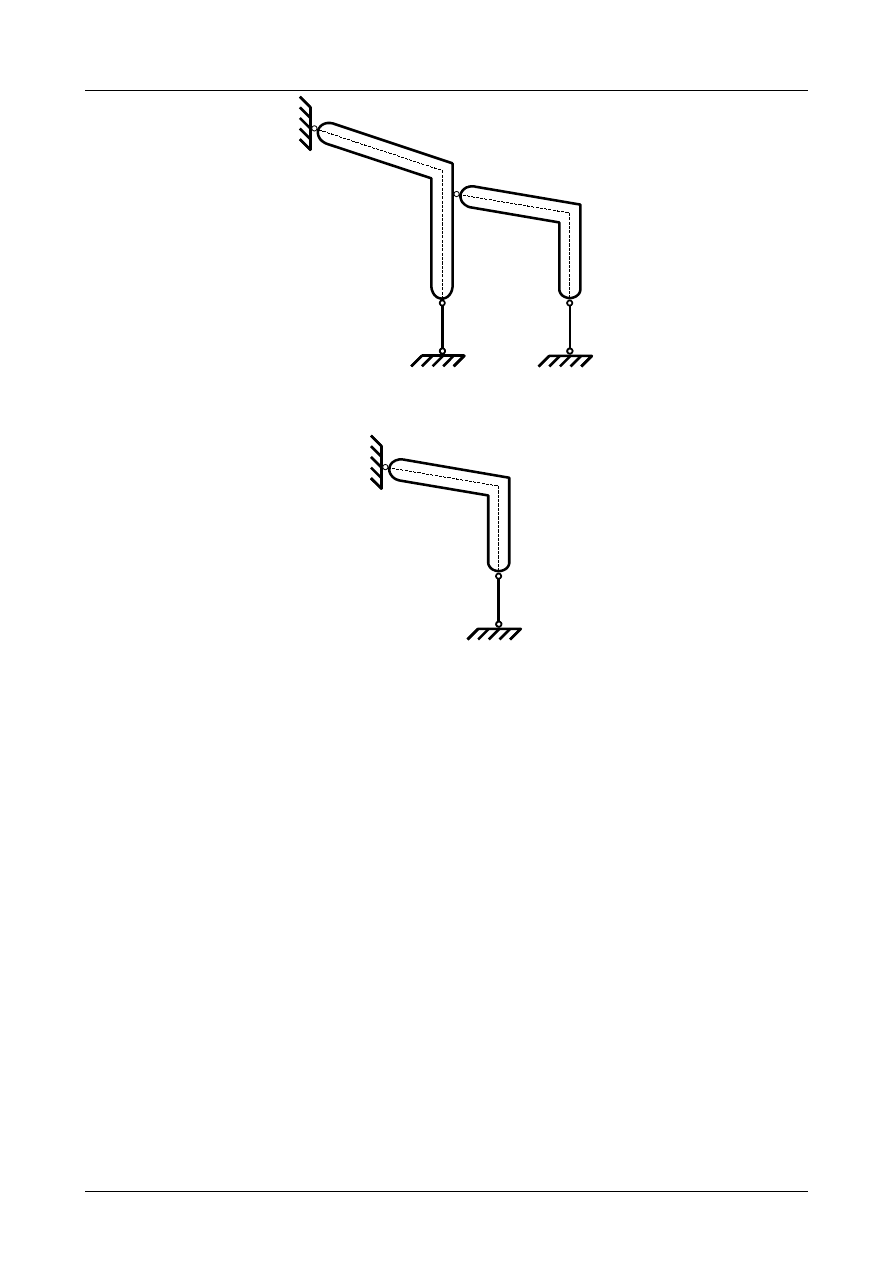
Z2/3.7. Rama płaska numer 7
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.21 jest układem geometrycznie niezmien-
nym.
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
10
Rys. Z2/3.21. Rama płaska
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne a podpory na układ
prętów podporowych. Przedstawia to rysunek Z2/3.22.
Jak widać na rysunku Z2/3.22 liczba tarcz wynosi 3, liczba prętów podporowych wynosi 5 natomiast
liczba przegubów rzeczywistych wynosi 2. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅3=5⋅12⋅2
.
(Z2/3.7)
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem
geometrycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić
warunki dostateczne geometrycznej niezmienności.
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla
pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/3.23.
1
5
B
I
III
II
4
2
3
A
Rys. Z2/3.22. Zastępczy układ tarcz sztywnych
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić
podłoże dla pozostałej tarczy sztywnej. Przedstawia to rysunek Z2/3.24.
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
11
5
B
III
II
4
A
Rys. Z2/3.23. Zastępczy układ tarcz sztywnych
5
B
III
Rys. Z2/3.24. Zastępcza tarcza sztywna
Tarcza numer III jest podparta przegubem rzeczywistym B oraz prętem podporowym numer 5. Prze-
gub B nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
rama płaska jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
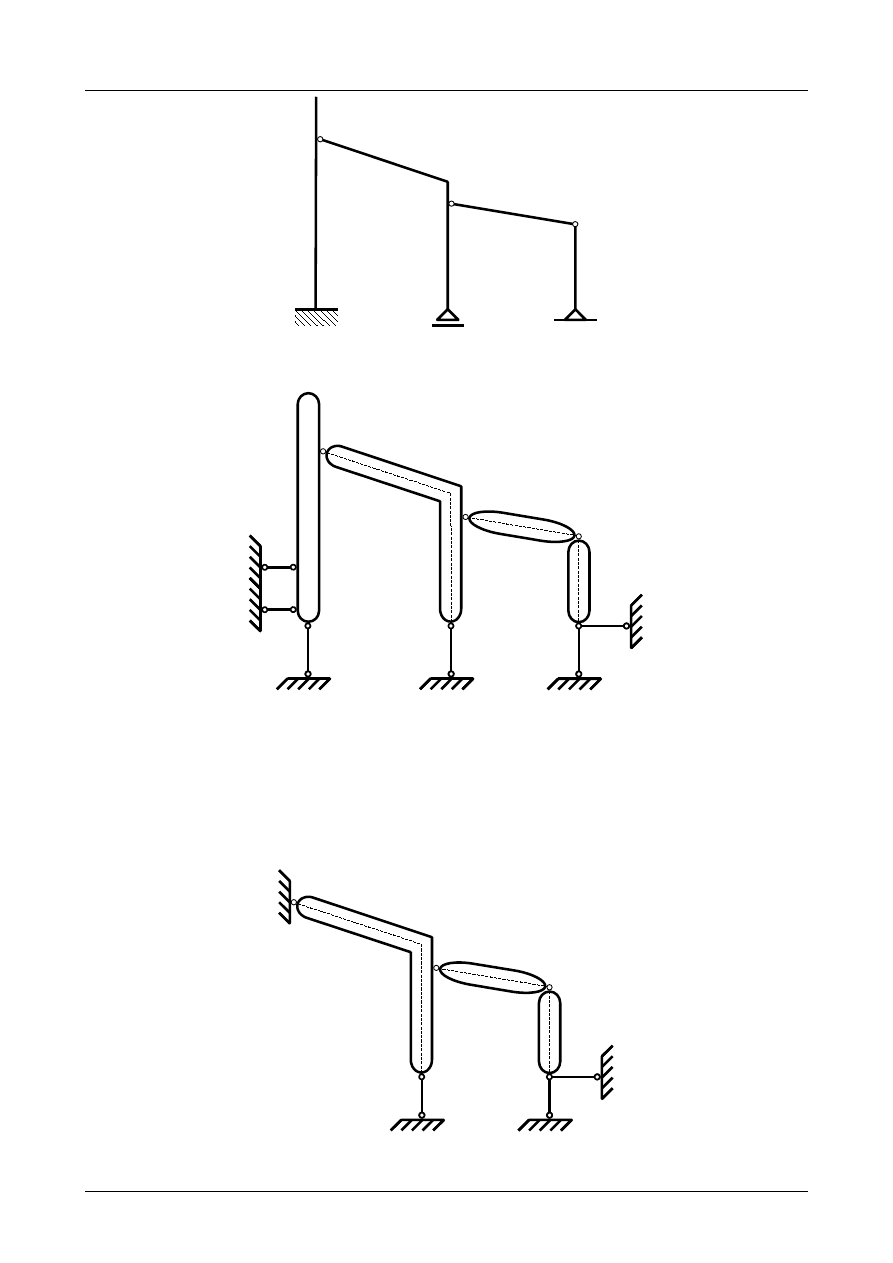
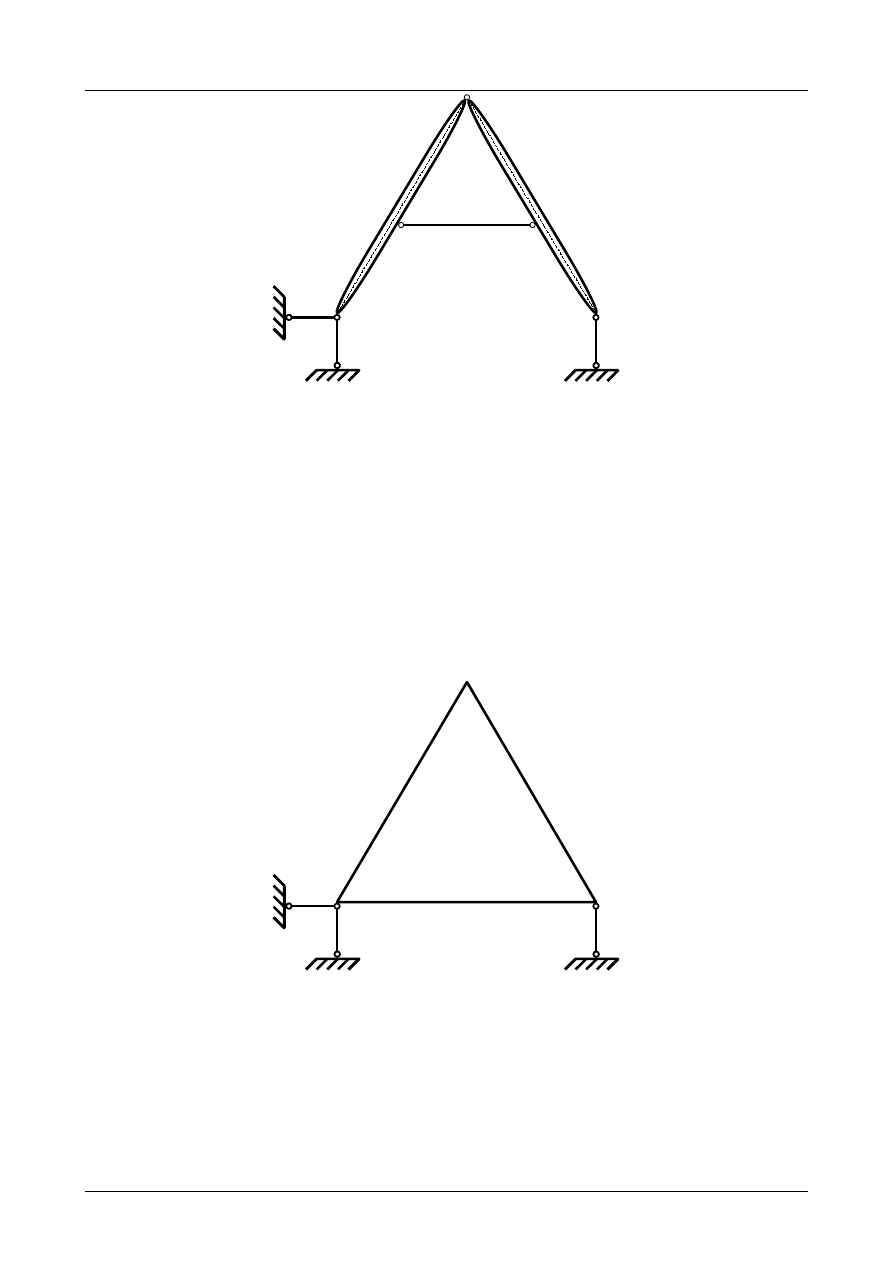
Z2/3.8. Rama płaska numer 8
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.25 jest układem geometrycznie niezmien-
nym.
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne a podpory na układ
prętów podporowych. Przedstawia to rysunek Z2/3.26.
Jak widać na rysunku Z2/3.22 liczba tarcz wynosi 4, liczba prętów podporowych wynosi 6 natomiast
liczba przegubów rzeczywistych wynosi 3. Warunek konieczny geometrycznej niezmienności ma więc
postać
3⋅4=6⋅13⋅2
.
(Z2/3.8)
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem geomet-
rycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić warunki
dostateczne geometrycznej niezmienności.
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
12
Rys. Z2/3.25. Rama płaska
I
IV
II
4
5
A
6
III
B
C
D
1
2
3
Rys. Z2/3.26. Zastępczy układ tarcz sztywnych
Tarcza numer I jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki nie prze-
cinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla
tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić podłoże dla pozosta-
łych tarcz sztywnych. Przedstawia to rysunek Z2/3.27.
IV
II
4
5
6
III
B
C
D
A
Rys. Z2/3.27. Zastępczy układ tarcz sztywnych
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
13
Tarcza numer II jest podparta przegubem rzeczywistym A oraz prętem podporowym numer 4. Przegub
A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny geometrycznej
niezmienności dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna i może stanowić
podłoże dla pozostałych tarcz sztywnych. Przedstawia to rysunek Z2/3.28.
IV
5
6
III
B
C
D
Rys. Z2/3.28. Zastępczy układ tarcz sztywnych
Tarcze numer III i IV tworzą układ trójprzegubowy z przegubami rzeczywistymi B i C oraz
przegubem fikcyjnym D utworzonym z prętów podporowych numer 5 i 6. Wszystkie przeguby nie leżą na
jednaj prostej. Został więc spełniony warunek dostateczny geometrycznej niezmienności dla tych tarcz
sztywnych. Wobec tego są one geometrycznie niezmienne.
Jak więc widać wszystkie tarcze sztywne są geometrycznie niezmienne. Możemy więc stwierdzić, że
rama płaska jest układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Z2/3.9. Rama płaska numer 9
Sprawdzić czy rama płaska przedstawiona na rysunku Z2/3.29 jest układem geometrycznie niezmien-
nym.
Rys. Z2/3.29. Rama płaska
W pierwszej kolejności musimy pręty ramy płaskiej zamienić na tarcze sztywne a podpory na układ
prętów podporowych. Przedstawia to rysunek Z2/3.30.
Jak widać na rysunku Z2/3.30 liczba tarcz wynosi 2, liczba prętów podporowych wynosi 4 natomiast
liczba przegubów rzeczywistych wynosi 1. Warunek konieczny geometrycznej niezmienności ma więc
postać
Dr inż. Janusz Dębiński
WM
Z2/3. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 3
14
2
4
1
3
A
I
II
Rys. Z2/3.30. Zastępczy układ tarcz sztywnych
3⋅2=4⋅11⋅2
.
(Z2/3.9)
Warunek konieczny geometrycznej niezmienności został spełniony. Rama płaska może być układem
geometrycznie niezmiennym i statycznie wyznaczalnym. W dalszej kolejności musimy jeszcze sprawdzić
warunki dostateczne geometrycznej niezmienności.
Tarcze numer I i II są połączone między sobą przegubem rzeczywistym A i prętem podporowym 3.
Pręt podporowy numer 3 nazywany jest ściągiem. Przegub A nie leży na kierunku tego pręta. Został więc
spełniony warunek dostateczny geometrycznej niezmienności. Tarcze numer I i II tworzą więc jedną tarczę
sztywną numer I+II. Przedstawia to rysunek Z2/3.31.
2
4
1
I+II
Rys. Z2/3.31. Tarcza sztywna I+II
Tarcza numer I+II jest podparta trzema prętami podporowymi numer 1, 2 i 4, których kierunki nie
przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmienności
dla tej tarczy sztywnej. Wobec tego jest ona geometrycznie niezmienna.
Ostatecznie możemy więc stwierdzić, że rama płaska jest układem geometrycznie niezmiennym
i statycznie wyznaczalnym.
Dr inż. Janusz Dębiński
Document Outline