WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
1
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
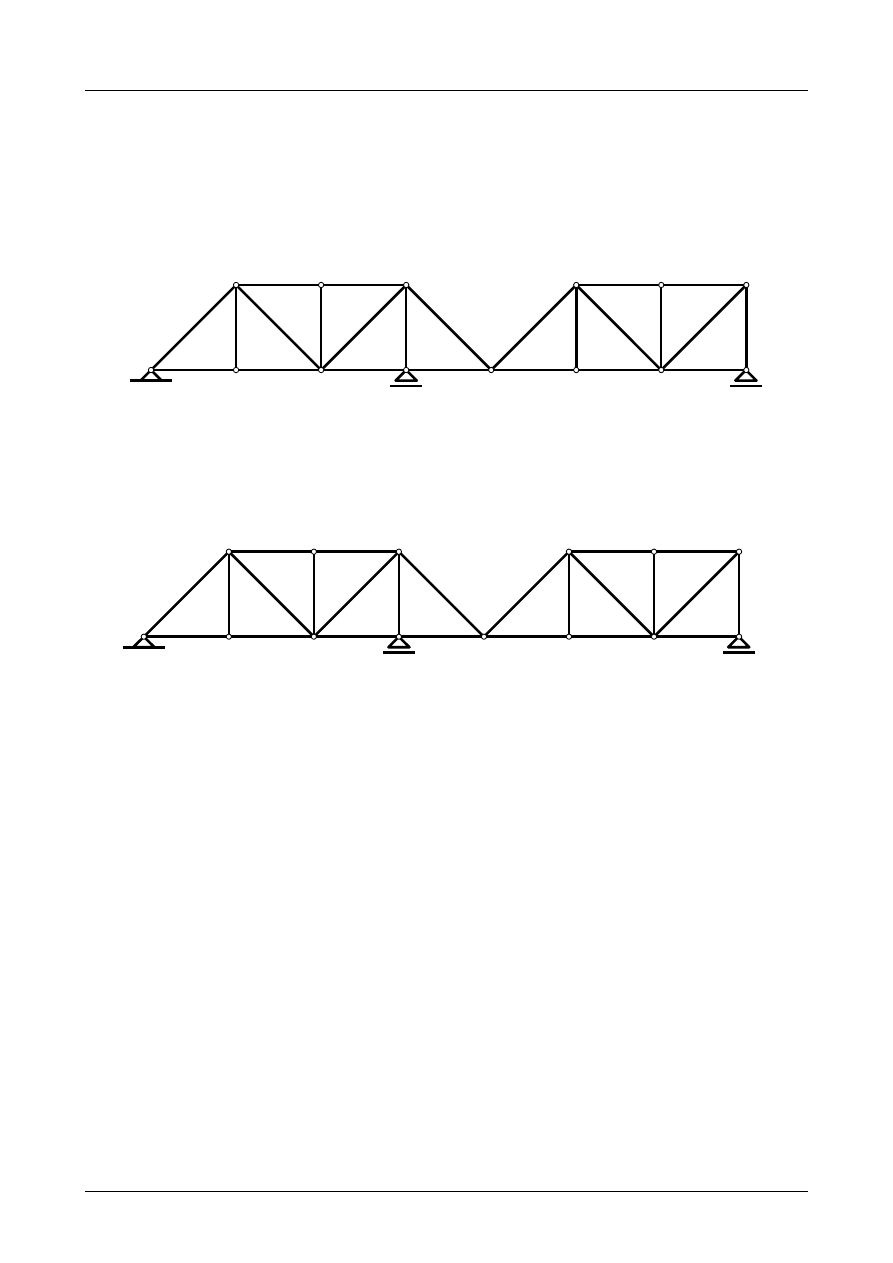
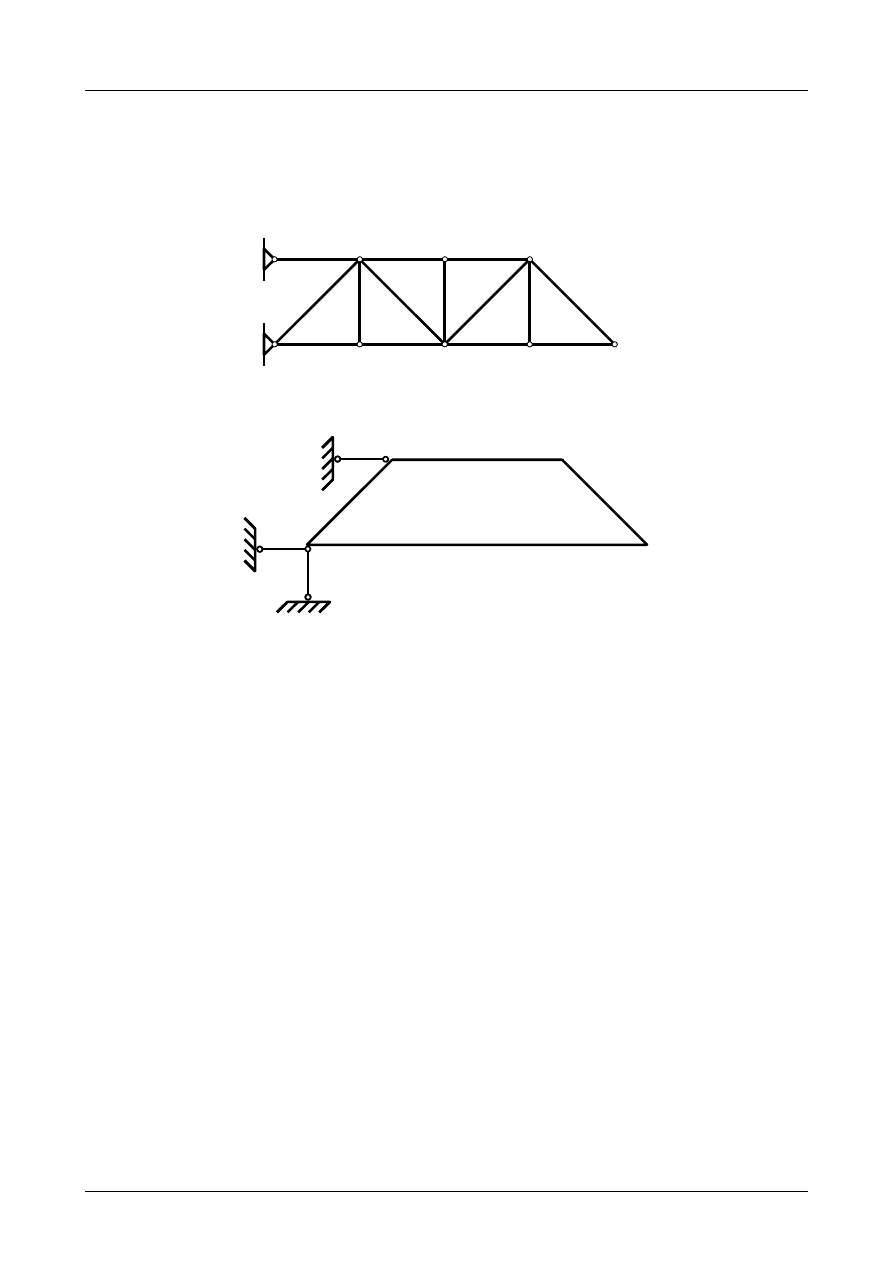
Z2/1.1. Kratownica numer 1
Sprawdzić czy kratownica płaska przedstawiona na rysunku Z2/1.1 jest układem geometrycznie nie-
zmiennym.
Rys. Z2/1.1. Kratownica płaska
W pierwszej kolejności ponumerujmy wszystkie pręty i węzły kratownicy. Przedstawia to rysunek
Z2/1.2.
1
2
3
4
5
6
8
7
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
1
2
3
4
5
6
7
8
9
11
10
12
13
14
Rys. Z2/1.2. Ponumerowane pręty i węzły kratownicy płaskiej
Jak widać liczba prętów kratownicy wynosi 24, liczba węzłów kratownicy wynosi 14. Podpora
przegubowo-nieprzesuwna odbiera dwa stopnie swobody. Dwie podpory przegubowo-przesuwne odbierają
razem także dwa stopnie swobody. Warunek konieczny geometrycznej niezmienności ma postać
2
⋅
14
=
24
2
1
1
.
(Z2/1.1)
Warunek konieczny geometrycznej niezmienności dla kratownicy płaskiej został więc spełniony.
Kratownica może więc być układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Jak widać na rysunkach Z2/1.1 i Z2/1.2 kratownica jest zbudowana z trójkątów i jest kratownicą
o strukturze prostej. Możemy więc zastąpić ją dwiema tarczami sztywnymi. Rysunek Z2/1.3 przedstawia
zastępczy układ tarcz sztywnych. Układ ten składa się z dwóch tarcz połączonych między sobą przegubem.
Jest to przegub numer 8 na rysunku Z2/1.2. Na rysunku Z2/1.3 oznaczymy go jako A. Tarcze sztywne są
podparte 4 prętami podporowymi i 1 przegubem rzeczywistym. Warunek konieczny geometrycznej
niezmienności dla zastępczego układu tarcz sztywnych ma postać
3⋅2=4⋅11⋅2
.
(Z2/1.2)
Jak widać warunek konieczny geometrycznej niezmienności został spełniony. Zastępczy układ tarcz
sztywnych może być geometrycznie niezmienny i statycznie wyznaczalny.
Dr inż. Janusz Dębiński
WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
2
1
A
I
II
2
3
4
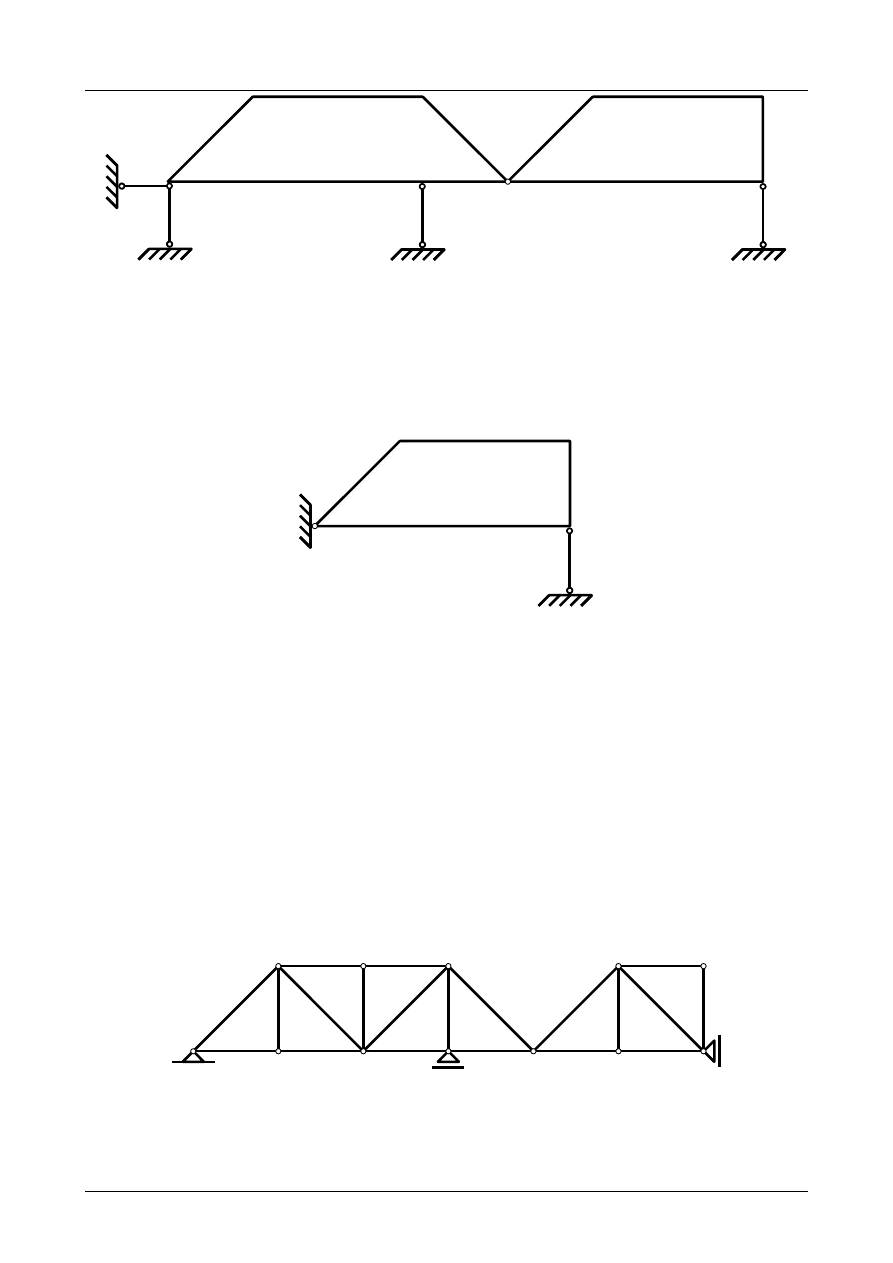
Rys. Z2/1.3. Zastępczy układ tarcz sztywnych
Tarcza numer I jest podparta do podłoża trzema prętami podporowymi numer 1, 2 i 3, których
kierunki nie przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej
niezmienności. Tarcza numer I jest więc geometrycznie niezmienna i może stanowić podłoże dla tarczy
numer II. Przedstawia to rysunek Z2/1.4.
A
II
4
Rys. Z2/1.4. Zastępcza tarcza sztywna numer II
Tarcza sztywna numer II podparta jest do podłoża przegubem rzeczywistym A i prętem podporowym
numer 4. Przegub A nie leży na kierunku pręta podporowego. Został więc spełniony warunek dostateczny
geometrycznej niezmienności. Tarcza numer II jest więc także geometrycznie niezmienna.
Możemy więc stwierdzić, że zastępczy układ tarcz sztywnych jest układem geometrycznie nie-
zmiennym. Został więc spełniony także warunek dostateczny geometrycznej niezmienności dla kratownicy
płaskiej. Kratownica ta jest więc ostatecznie układem geometrycznie niezmiennym i statycznie wyzna-
czalnym.
Z2/1.2. Kratownica numer 2
Sprawdzić czy kratownica płaska przedstawiona na rysunku Z2/1.5 jest układem geometrycznie nie-
zmiennym.
Rys. Z2/1.5. Kratownica płaska
W pierwszej kolejności ponumerujmy wszystkie pręty i węzły kratownicy. Przedstawia to rysunek
Z2/1.6.
Dr inż. Janusz Dębiński
WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
3
1
2
3
4
5
6
8
7
9
10
11
12
13
14
15
16
17
18
19
20
1
2
3
4
5
6
7
8
9
11
10
12
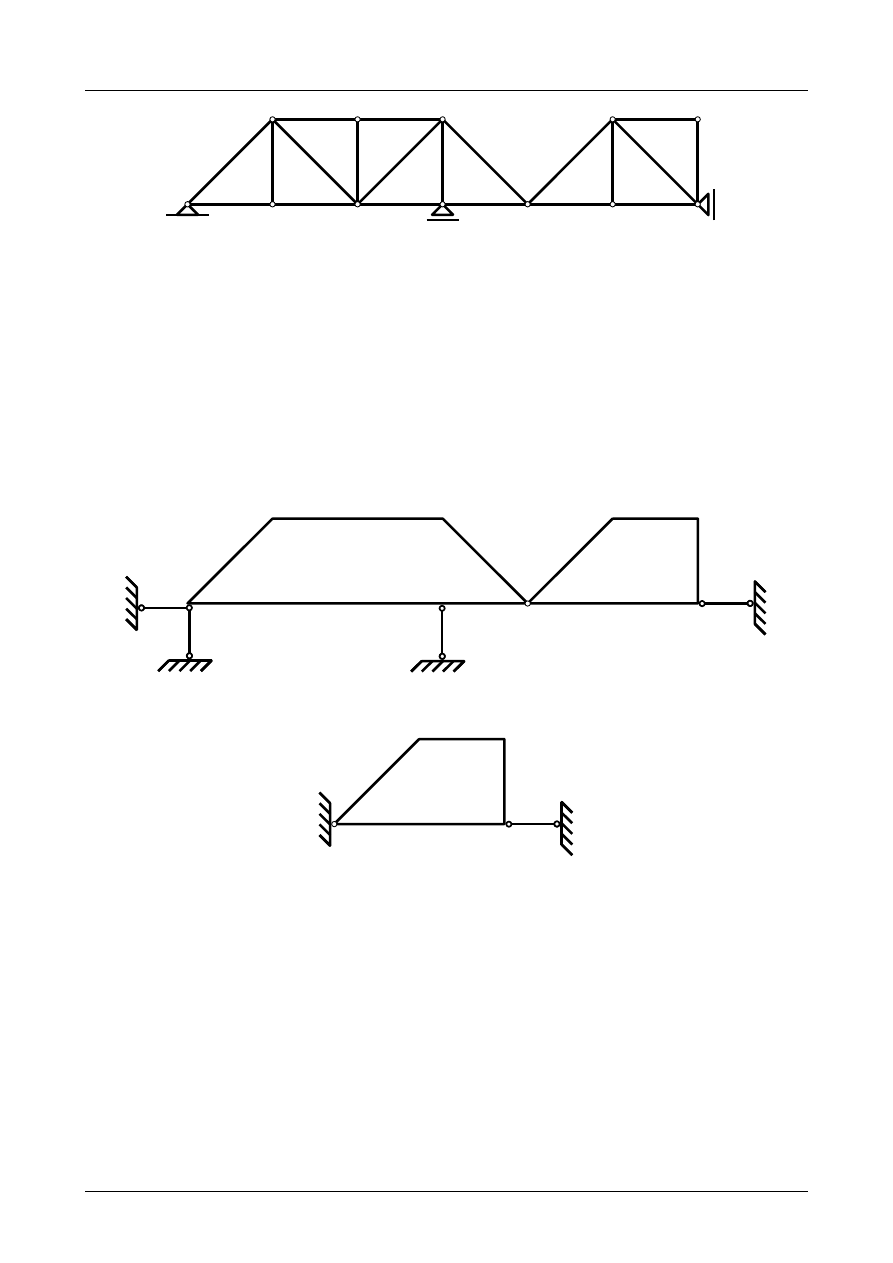
Rys. Z2/1.6. Ponumerowane pręty i węzły kratownicy płaskiej
Jak widać liczba prętów kratownicy wynosi 20, liczba węzłów kratownicy wynosi 12. Podpora
przegubowo-nieprzesuwna odbiera dwa stopnie swobody. Dwie podpory przegubowo-przesuwne odbierają
razem także dwa stopnie swobody. Warunek konieczny geometrycznej niezmienności ma postać
2⋅12=20211
.
(Z2/1.3)
Warunek konieczny geometrycznej niezmienności dla kratownicy płaskiej został więc spełniony.
Kratownica może więc być układem geometrycznie niezmiennym i statycznie wyznaczalnym.
1
A
I
II
2
3
4
Rys. Z2/1.7. Zastępczy układ tarcz sztywnych
A
II
4
Rys. Z2/1.8. Zastępcza tarcza sztywna numer II
Jak widać na rysunkach Z2/1.5 i Z2/1.6 kratownica jest zbudowana z trójkątów i jest kratownicą
o strukturze prostej. Możemy więc zastąpić ją dwiema tarczami sztywnymi. Rysunek Z2/1.7 przedstawia
zastępczy układ tarcz sztywnych. Układ ten składa się z dwóch tarcz połączonych między sobą przegubem.
Jest to przegub numer 8 na rysunku Z2/1.6. Na rysunku Z2/1.7 oznaczymy go jako A. Tarcze sztywne są
podparte 4 prętami podporowymi i 1 przegubem rzeczywistym. Warunek konieczny geometrycznej nie-
zmienności dla zastępczego układu tarcz sztywnych ma postać
3⋅2=4⋅11⋅2
.
(Z2/1.4)
Jak widać warunek konieczny geometrycznej niezmienności został spełniony. Zastępczy układ tarcz
sztywnych może być geometrycznie niezmienny i statycznie wyznaczalny.
Dr inż. Janusz Dębiński
WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
4
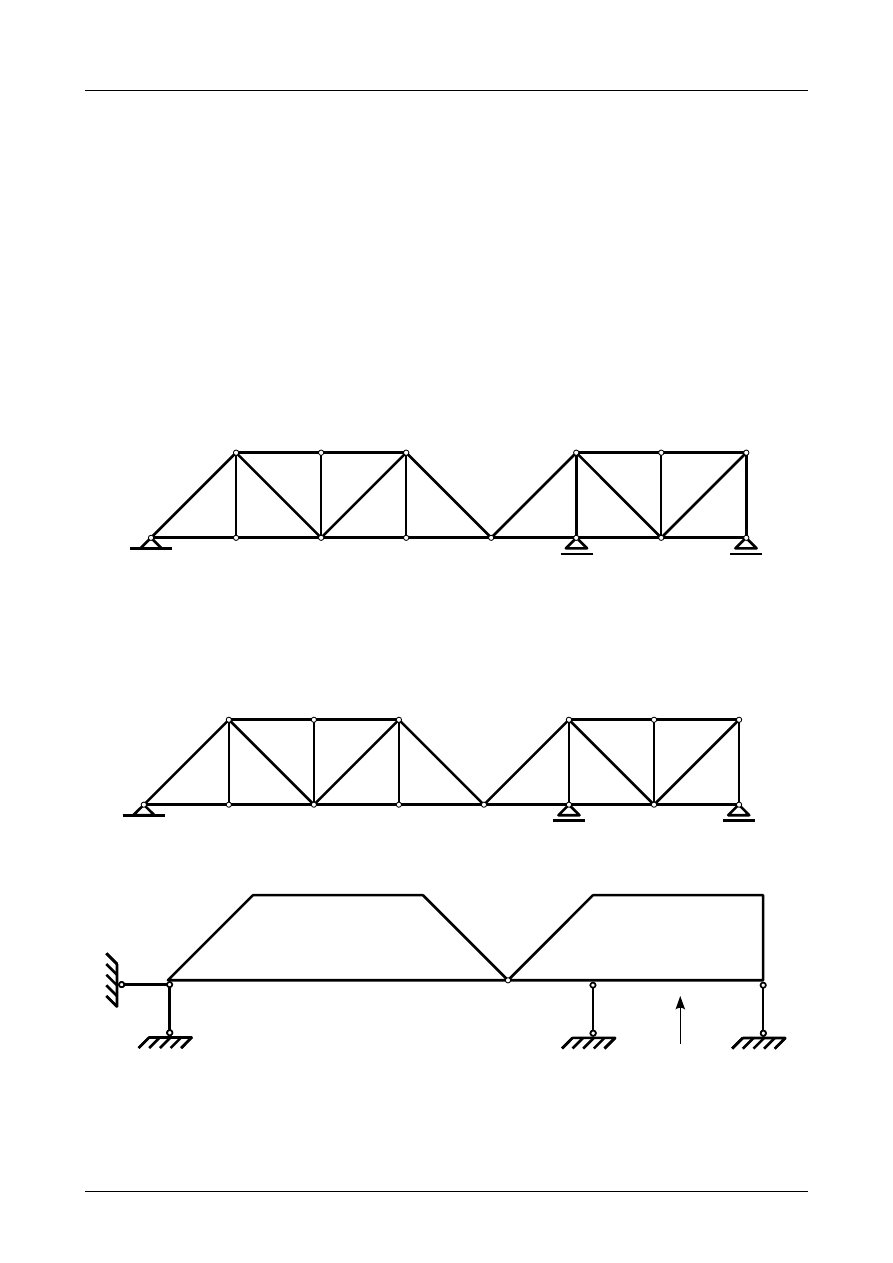
Tarcza numer I jest podparta do podłoża trzema prętami podporowymi numer 1, 2 i 3, których
kierunki nie przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej
niezmienności. Tarcza numer I jest więc geometrycznie niezmienna i może stanowić podłoże dla tarczy
numer II. Przedstawia to rysunek Z2/1.8.
Tarcza sztywna numer II podparta jest do podłoża przegubem rzeczywistym A i prętem podporowym
numer 4. Przegub A leży jednak na kierunku pręta podporowego. Nie został więc spełniony warunek
dostateczny geometrycznej niezmienności. Tarcza numer II jest więc geometrycznie zmienna.
Możemy więc stwierdzić, że zastępczy układ tarcz sztywnych jest układem geometrycznie zmiennym.
Nie został więc spełniony warunek dostateczny geometrycznej niezmienności dla kratownicy płaskiej.
Kratownica ta jest więc układem geometrycznie zmiennym.
Z2/1.3. Kratownica numer 3
Sprawdzić czy kratownica płaska przedstawiona na rysunku Z2/1.9 jest układem geometrycznie nie-
zmiennym.
Rys. Z2/1.9. Kratownica płaska
W pierwszej kolejności ponumerujmy wszystkie pręty i węzły kratownicy. Przedstawia to rysunek
Z2/1.10.
1
2
3
4
5
6
8
7
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
1
2
3
4
5
7
8
9
11
10
12
13
14
6
Rys. Z2/1.10. Ponumerowane pręty i węzły kratownicy płaskiej
1
B
I
II
2
3
4
A
C
∞
Rys. Z2/1.11. Zastępczy układ tarcz sztywnych
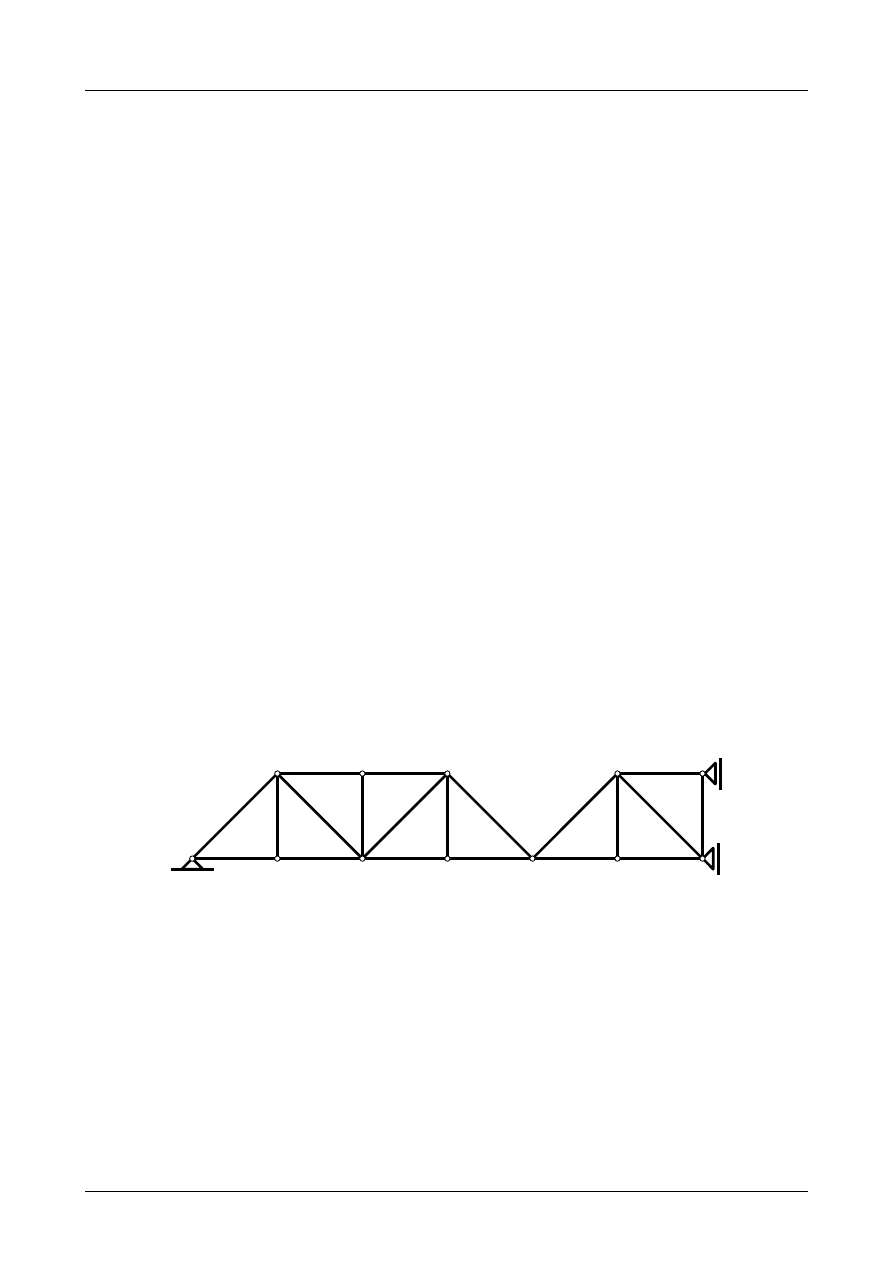
Jak widać liczba prętów kratownicy wynosi 24, liczba węzłów 14. Podpora przegubowo-nieprze-
suwna odbiera dwa stopnie swobody. Dwie podpory przegubowo-przesuwne odbierają razem także dwa
stopnie swobody. Warunek konieczny geometrycznej niezmienności dla tej kratownicy płaskiej ma postać
Dr inż. Janusz Dębiński
WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
5
2⋅14=24211
.
(Z2/1.5)
Warunek konieczny geometrycznej niezmienności dla kratownicy płaskiej został więc spełniony. Kra-
townica może więc być układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Jak widać na rysunkach Z2/1.9 i Z2/1.10 kratownica jest zbudowana z trójkątów i jest kratownicą
o strukturze prostej. Możemy więc zastąpić ją dwiema tarczami sztywnymi. Rysunek Z2/1.11 przedstawia
zastępczy układ tarcz sztywnych. Układ ten składa się z dwóch tarcz połączonych między sobą przegubem.
Jest to przegub numer 8 na rysunku Z2/1.10. Na rysunku Z2/1.11 oznaczymy go jako B. Tarcze sztywne są
podparte 4 prętami podporowymi i 1 przegubem rzeczywistym. Warunek konieczny geometrycznej nie-
zmienności dla zastępczego układu tarcz sztywnych ma postać
3⋅2=4⋅11⋅2
.
(Z2/1.6)
Jak widać warunek konieczny geometrycznej niezmienności został spełniony. Zastępczy układ tarcz sztyw-
nych może być geometrycznie niezmienny i statycznie wyznaczalny.
Zastępczy układ tarcz sztywnych tworzy układ trójprzegubowy z przegubem fikcyjnym A powstałym
z prętów podporowych numer 1 i 2, przegubem rzeczywistym B, przegubem niewłaściwym C powstałym
z prętów podporowych numer 3 i 4. Wszystkie te trzy przeguby nie leżą na jednej prostej. Został więc
spełniony warunek dostateczny geometrycznej niezmienności. Zastępczy układ tarcz sztywnych jest więc
geometrycznie niezmienny.
Został więc spełniony także warunek dostateczny geometrycznej niezmienności dla kratownicy
płaskiej. Kratownica ta jest więc ostatecznie układem geometrycznie niezmiennym i statycznie wyzna-
czalnym.
Z2/1.4. Kratownica numer 4
Sprawdzić czy kratownica płaska przedstawiona na rysunku Z2/1.12 jest układem geometrycznie nie-
zmiennym.
Rys. Z2/1.12. Kratownica płaska
W pierwszej kolejności ponumerujmy wszystkie pręty i węzły kratownicy. Przedstawia to rysunek
Z2/1.13.
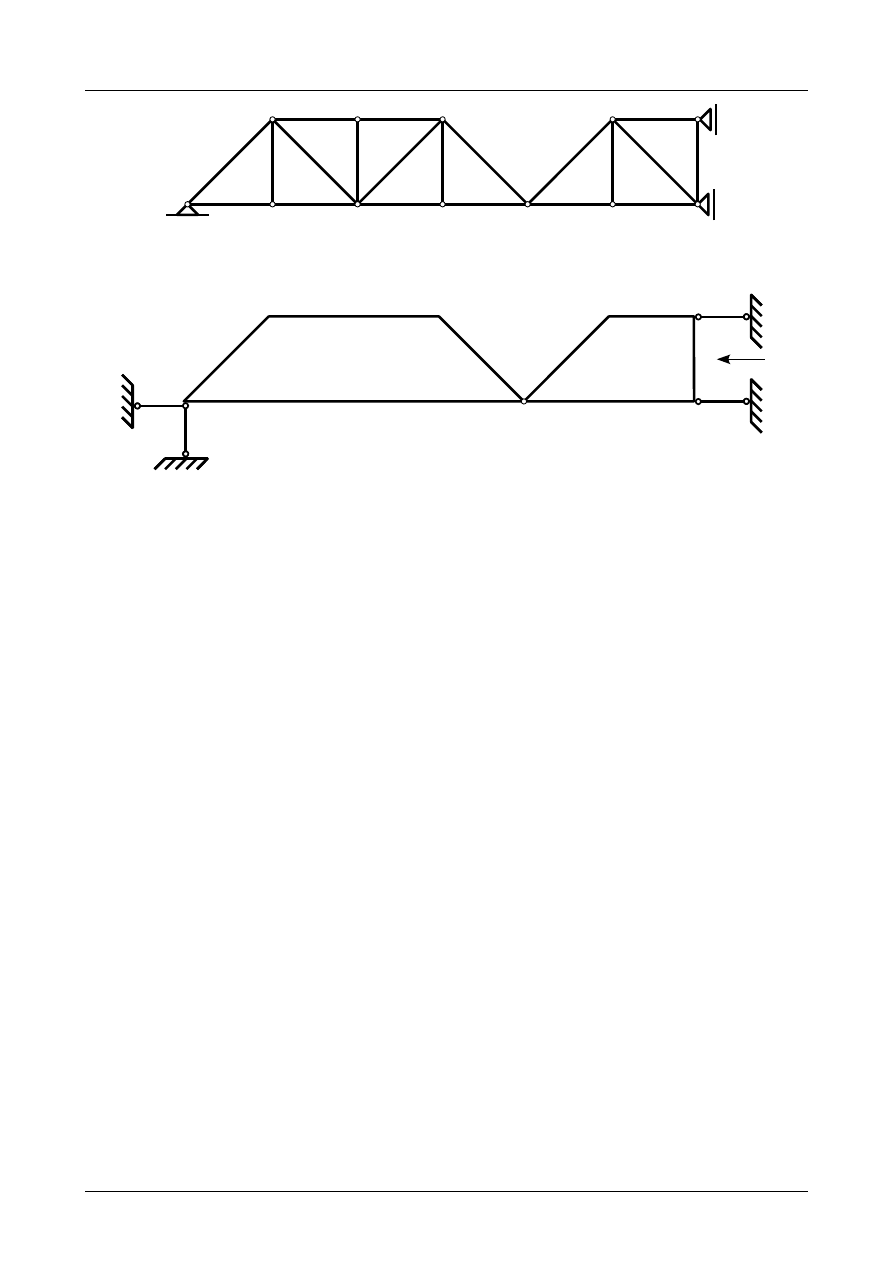
Jak widać liczba prętów kratownicy wynosi 20, liczba węzłów 12. Podpora przegubowo-nieprze-
suwna odbiera dwa stopnie swobody. Dwie podpory przegubowo-przesuwne odbierają razem także dwa
stopnie swobody. Warunek konieczny geometrycznej niezmienności ma postać
2⋅12=20211
.
(Z2/1.7)
Warunek konieczny geometrycznej niezmienności dla kratownicy płaskiej został więc spełniony. Kratow-
nica może więc być układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Dr inż. Janusz Dębiński
WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
6
1
2
3
4
5
6
8
7
9
10
11
12
13
14
15
16
17
18
19
20
1
2
3
4
5
7
8
9
11
10
12
6
Rys. Z2/1.13. Ponumerowane pręty i węzły kratownicy płaskiej
1
B
I
II
2
3
4
C
∞
A
Rys. Z2/1.14. Zastępczy układ tarcz sztywnych
Jak widać na rysunkach Z2/1.12 i Z2/1.13 kratownica jest zbudowana z trójkątów i jest kratownicą
o strukturze prostej. Możemy więc zastąpić ją dwiema tarczami sztywnymi. Rysunek Z2/1.14 przedstawia
zastępczy układ tarcz sztywnych. Układ ten składa się z dwóch tarcz połączonych między sobą przegubem.
Jest to przegub numer 8 na rysunku Z2/1.13. Na rysunku Z2/1.14 oznaczymy go jako B. Tarcze sztywne są
podparte czterema prętami podporowymi i jednym przegubem rzeczywistym. Warunek konieczny geomet-
rycznej niezmienności dla zastępczego układu tarcz sztywnych ma postać
3⋅2=4⋅11⋅2
.
(Z2/1.8)
Jak widać warunek konieczny geometrycznej niezmienności został spełniony. Zastępczy układ tarcz
sztywnych może być geometrycznie niezmienny i statycznie wyznaczalny.
Zastępczy układ tarcz sztywnych tworzy układ trójprzegubowy z przegubem fikcyjnym A powstałym
z prętów podporowych numer 1 i 2, przegubem rzeczywistym B, przegubem niewłaściwym C powstałym
z prętów podporowych numer 3 i 4. Wszystkie te trzy przeguby jednak leżą na jednej prostej. Nie został
spełniony warunek dostateczny geometrycznej niezmienności. Zastępczy układ tarcz sztywnych jest więc
geometrycznie zmienny.
Nie został więc spełniony także warunek dostateczny geometrycznej niezmienności dla kratownicy
płaskiej. Kratownica ta jest więc układem geometrycznie zmiennym.
Z2/1.5. Kratownica numer 5
Sprawdzić czy kratownica płaska przedstawiona na rysunku Z2/1.15 jest układem geometrycznie nie-
zmiennym.
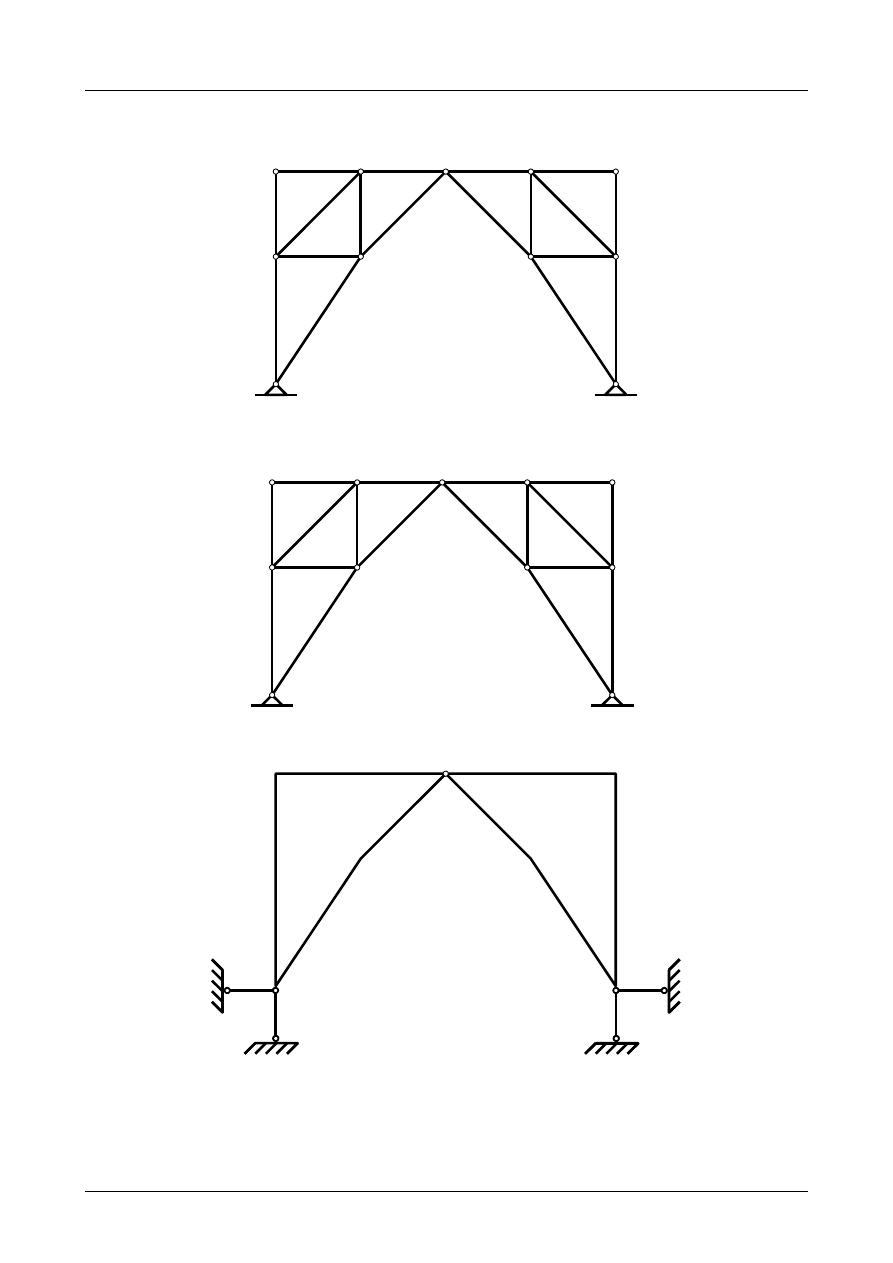
W pierwszej kolejności ponumerujmy wszystkie pręty i węzły kratownicy. Przedstawia to rysunek
Z2/1.16. Liczba prętów kratownicy wynosi 18, liczba węzłów 11. Dwie podpory przegubowo-nieprzesuwne
odbierają po dwa stopnie swobody każda. Warunek konieczny geometrycznej niezmienności ma postać
2⋅11=182⋅2
.
(Z2/1.9)
Dr inż. Janusz Dębiński
WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
7
Warunek konieczny geometrycznej niezmienności dla kratownicy płaskiej został więc spełniony.
Kratownica może więc być układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Rys. Z2/1.15. Kratownica płaska
1
2
3
4
5
7
8
9
11
10
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Rys. Z2/1.16. Ponumerowane pręty i węzły kratownicy płaskiej
2
3
1
4
A
B
C
I
II
Rys. Z2/1.17. Zastępczy układ tarcz sztywnych
Jak widać na rysunkach Z2/1.15 i Z2/1.16 kratownica jest zbudowana z trójkątów i jest kratownicą
o strukturze prostej. Możemy więc zastąpić ją dwiema tarczami sztywnymi. Rysunek Z2/1.17 przedstawia
zastępczy układ tarcz sztywnych. Układ ten składa się z dwóch tarcz połączonych między sobą przegubem.
Dr inż. Janusz Dębiński
WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
8
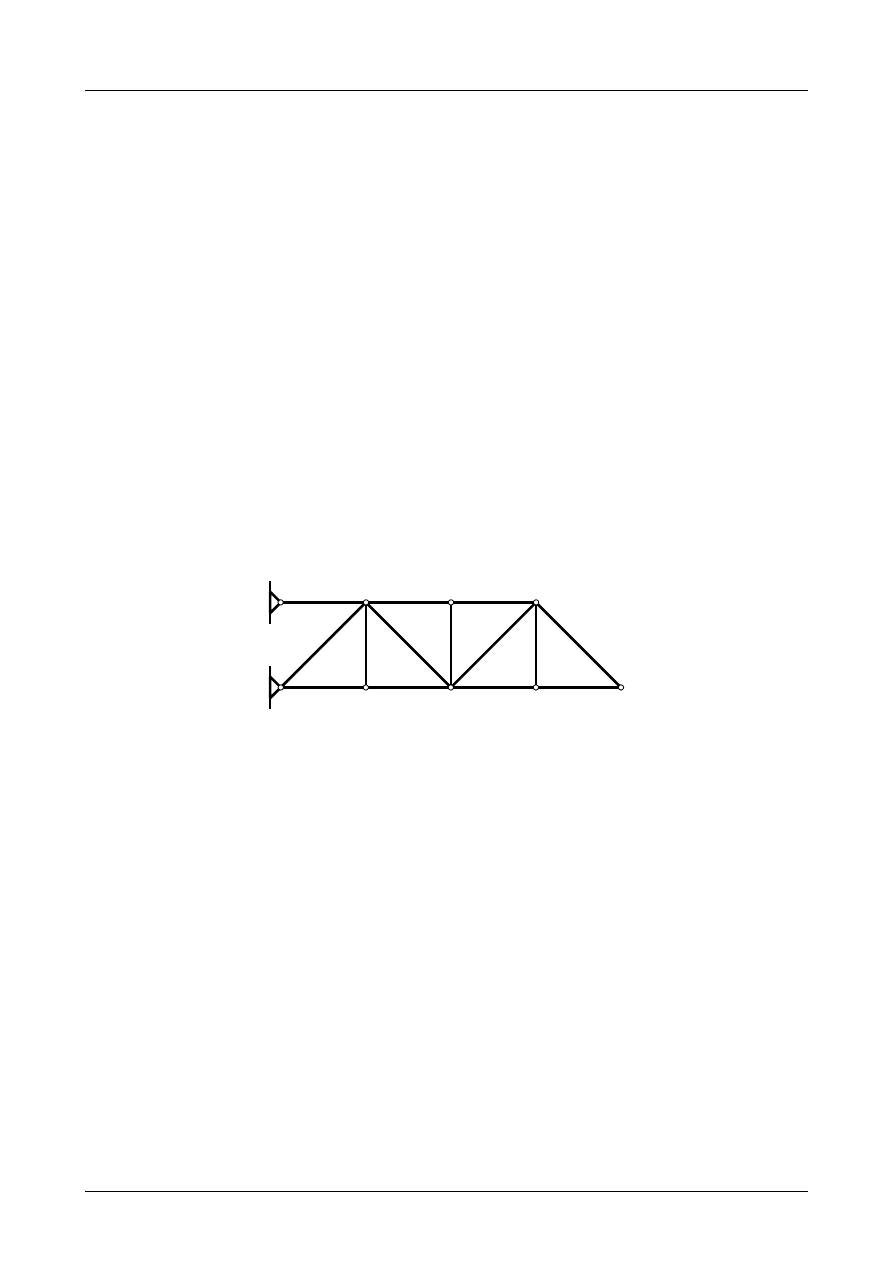
Jest to przegub numer 6 na rysunku Z2/1.16. Na rysunku Z2/1.17 oznaczymy go jako B. Tarcze sztywne są
podparte 4 prętami podporowymi i 1 przegubem rzeczywistym. Warunek konieczny geometrycznej nie-
zmienności dla zastępczego układu tarcz sztywnych ma postać
3⋅2=4⋅11⋅2
.
(Z2/1.10)
Jak widać warunek konieczny geometrycznej niezmienności został spełniony. Zastępczy układ tarcz
sztywnych może być geometrycznie niezmienny i statycznie wyznaczalny.
Zastępczy układ tarcz sztywnych tworzy układ trójprzegubowy z przegubem fikcyjnym A powstałym
z prętów podporowych numer 1 i 2, przegubem rzeczywistym B, przegubem fikcyjnym C powstałym
z prętów podporowych numer 3 i 4. Wszystkie te trzy przeguby nie leżą na jednej prostej. Został więc
spełniony warunek dostateczny geometrycznej niezmienności. Zastępczy układ tarcz sztywnych jest więc
geometrycznie niezmienny.
Został więc spełniony także warunek dostateczny geometrycznej niezmienności dla kratownicy
płaskiej. Kratownica ta jest więc układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Z2/1.6. Kratownica numer 6
Sprawdzić czy kratownica płaska przedstawiona na rysunku Z2/1.18 jest układem geometrycznie nie-
zmiennym.
Rys. Z2/1.18. Kratownica płaska
W pierwszej kolejności ponumerujmy wszystkie pręty i węzły kratownicy. Przedstawia to rysunek
Z2/1.19.
Jak widać liczba prętów kratownicy wynosi 14, liczba węzłów kratownicy wynosi 9. Podpory
przegubowo-nieprzesuwne odbierają po dwa stopnie swobody każda. Warunek konieczny geometrycznej
niezmienności ma postać
2⋅9=142⋅2
.
(Z2/1.11)
Warunek konieczny geometrycznej niezmienności dla kratownicy płaskiej został więc spełniony. Kratow-
nica może więc być układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Jak widać na rysunkach Z2/1.18 i Z2/1.19 kratownica jest zbudowana z trójkątów i jest kratownicą
o strukturze prostej. Jednak nie cała kratownica tworzy tarczę sztywną. Pręt kratownicy numer 1 musimy
traktować jako pręt podporowy numer 1. Rysunek Z2/1.20 przedstawia zastępczą tarczę sztywną. Tarcza
sztywna jest podparta trzema prętami podporowymi. Warunek konieczny geometrycznej niezmienności ma
postać
3⋅1=3⋅1
.
(Z2/1.12)
Dr inż. Janusz Dębiński
WM
Z2/1. ANALIZA KINEMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH
ZADANIE 1
9
Jak widać warunek konieczny geometrycznej niezmienności został spełniony. Zastępcza tarcza sztywna
może być geometrycznie niezmienna i statycznie wyznaczalna.
Zastępcza tarcza sztywna jest podparta trzema prętami podporowymi numer 1, 2 i 3, których kierunki
nie przecinają się w jednym punkcie. Został więc spełniony warunek dostateczny geometrycznej niezmien-
ności. Zastępcza tarcza sztywna jest więc geometrycznie niezmienna.
1
3
2
5
4
6
9
7
8
1
2
3
4
7
5
6
8
9
10
11
12
13
14
Rys. Z2/1.19. Ponumerowane pręty i węzły kratownicy płaskiej
1
2
3
I
Rys. Z2/1.20. Zastępcza tarcza sztywna
Został więc spełniony także warunek dostateczny geometrycznej niezmienności dla kratownicy
płaskiej. Kratownica ta jest więc układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Dr inż. Janusz Dębiński
Document Outline