MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

1

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

1.1. Płaskie układy tarcz sztywnych

Analiza kinematyczna służy nam do określenia czy dany układ spełnia wszystkie warunki aby być

konstrukcją budowlaną.

Podstawowym pojęciem stosowanym w analizie kinematycznej belek i ram płaskich jest tarcza

sztywna. Jest to uogólnienie znanej z kursu fizyki bryły sztywnej czyli ciała, którego odkształcanie w
warunkach danego zagadnienia jest zaniedbywalnie małe a odległość pomiędzy dwoma dowolnymi
punktami bryły sztywnej jest stała niezależnie od wielkości działających sił. Tarczę sztywną możemy sobie
wyobrazić jako bardzo cienką, płaską bryłę sztywną w kształcie plastra. Tarcza sztywna wraz z obciążeniem
na nią działającym znajdują się na jednej płaszczyźnie.

Przyjęcie tarczy sztywnej jako modelu rzeczywistej konstrukcji jest uzasadnione tym, że deformacje

mierzone w rzeczywistych konstrukcjach są bardzo małe w porównaniu z jej wymiarami. Można więc
przyjąć, że analizujemy konstrukcję niezdeformowaną czyli tak zwaną konfigurację pierwotną
konstrukcji. Inaczej powyższą zasadę nazywa się zasadą zesztywnienia.

Następnym bardzo ważnym pojęciem przy analizie kinematycznej jest stopień swobody. Jest to

niezależny parametr, za pomocą którego opisujemy położenie tarczy sztywnej na płaszczyźnie. Ich liczba
określa nam liczbę stopni swobody tarczy sztywnej. Aby znać dokładne położenie tarczy sztywnej na
płaszczyźnie wystarczy znać położenie dowolnego odcinka AB. Położenie tego odcinka może być opisane za
pomocą dwóch współrzędnych punktu A (x

A

i y

A

) i kąta

α

, który jest kątem nachylenia odcinka AB.

Przedstawia to rysunek 1.1. Można więc stwierdzić, że pojedyncza tarcza sztywna posiada na
płaszczyźnie trzy stopnie swobody.

X

Y

A

B

x

A

y

A

α

Rys. 1.1. Stopnie swobody tarczy sztywnej na płaszczyźnie

Od konstrukcji budowlanej wymagamy aby nie była ona mechanizmem i pozostała nieruchoma

pod wpływem obciążenia. Aby tak było należy odebrać jej wszystkie stopnie swobody. Robi się to
przymocowując tarcze sztywne do nieruchomej tarczy podporowej za pomocą więzów. Tarczą podporową
w przypadku rzeczywistych konstrukcji jest na przykład podłoże gruntowe.

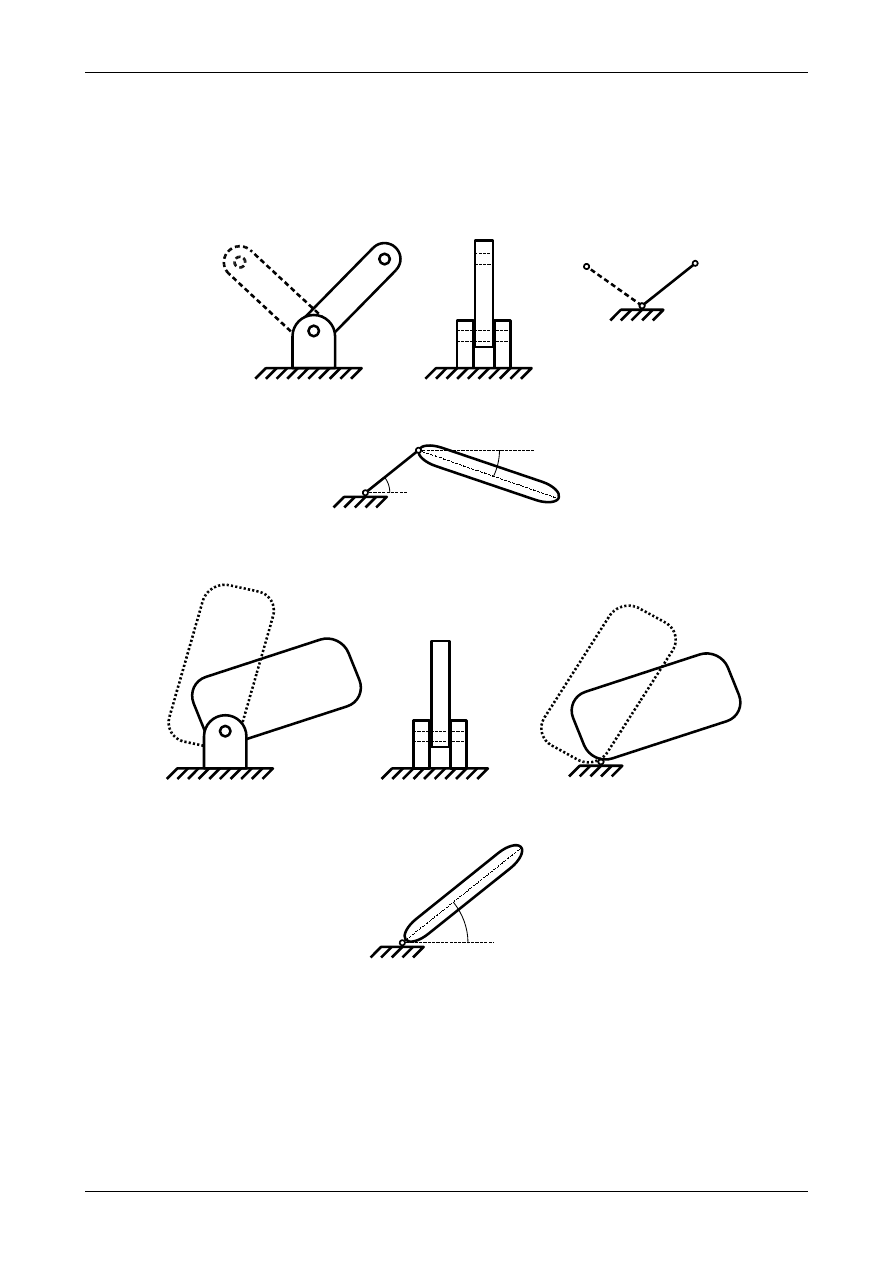
Pierwszym rodzajem więzu jest pręt podporowy. Został on przedstawiony na rysunku 1.2 a i b.

Schemat pręta podporowego przedstawia rysunek 1.2 c.

Jak widać na rysunku 1.2 pręt podporowy ma możliwość obrotu względem sworznia (a w zasadzie

punktu) A. Tarczę sztywną podpartą prętem podporowym przedstawia rysunek 1.3. Do opisu położenia
tarczy sztywnej połączonej z podłożem jednym prętem podporowym potrzebne są dwa niezależne parametry
(kąty

α

oraz

β

). Czyli tarcza sztywna utraciła jeden stopień swobody. Można więc ostatecznie stwierdzić, że

pręt podporowy odbiera tarczy sztywnej jeden stopień swobody.

Drugim rodzajem więzu jest przegub. Przedstawia go rysunek 1.4. Tarcza sztywna ma możliwość

obrotu względem takiego przegubu.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

2

Przegub przedstawiony na rysunku 1.4 nazywa się przegubem rzeczywistym. Do opisu położenia

tarczy sztywnej połączonej z podłożem przegubem rzeczywistym potrzebny jest jeden niezależny parametr
(kąt nachylenia tarczy sztywnej do poziomu). Przedstawia to rysunek 1.5. Tarcza sztywna utraciła więc dwa
stopnie swobody. Można więc ostatecznie stwierdzić, że przegub rzeczywisty odbiera tarczy sztywnej
dwa stopnie swobody.

A

A

a)

b)

c)

A

Rys. 1.2. Pręt podporowy

A

α

β

Rys. 1.3. Stopnie swobody tarczy sztywnej popartej prętem podporowym

A

A

a)

b)

c)

A

Rys. 1.4. Przegub

A

α

Rys. 1.5. Stopnień swobody tarczy sztywnej podpartej przegubem rzeczywistym

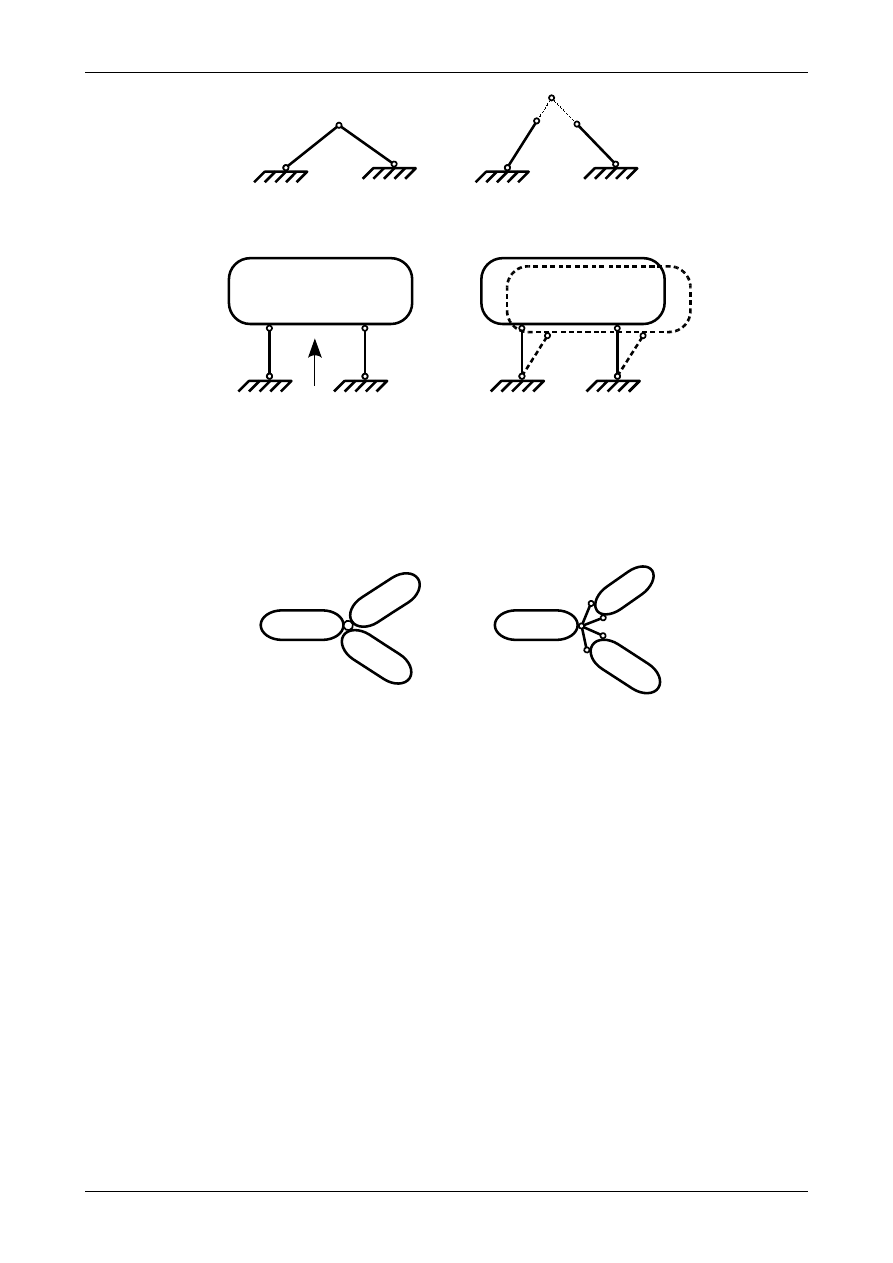
Przegub może być także utworzony z dwóch prętów podporowych. Mówimy wtedy o przegubie

fikcyjnym. Punkt przegubu znajduje się na przecięciu kierunków obu prętów podporowych. Przedstawia to
rysunek 1.6. Może się zdarzyć taka sytuacja, że oba pręty podporowe tworzące przegub fikcyjny będą do
siebie równoległe. Wtedy przegub fikcyjny znajduje się w nieskończoności i taki przegub nazywa się
przegubem niewłaściwym. Tarczę sztywną podpartą dwoma równoległymi prętami podporowymi
przedstawia rysunek 1.7 a. Rysunek 1.7 b przedstawia ruch tarczy sztywnej, która przesunęła się w kierunku
prostopadłym do kierunku obu prętów podporowych.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

3

A

A

Rys. 1.6. Przegub fikcyjny

A

∞

a)

b)

Rys. 1.7. Tarcza sztywna podparta przegubem niewłaściwym w nieskończoności

Możliwe jest także połączenie więcej niż dwóch tarcz sztywnych przegubem. Przegub taki nazywa się

przegubem wielokrotnym. Rysunek 1.8 a przedstawia trzy tarcze sztywne połączone przegubem
wielokrotnym.

I

II

I

II

III

A

A

a)

b)

III

Rys. 1.8. Przegub wielokrotny

Jak widać przegub wielokrotny A łączący trzy tarcze sztywne odpowiada czterem prętom

podporowym. Ogólnie jeżeli przegub wielokrotny łączy t tarcz sztywnych to odpowiada on

2

⋅



t

−1



(1.1)

prętom podporowym.

Pojedyncza tarcza sztywna posiada na płaszczyźnie trzy stopnie swobody. Jeżeli tych tarcz będzie t to

będą one posiadały

3

⋅t

(1.2)

stopni swobody. Warunkiem koniecznym geometrycznej niezmienności układu tarcz sztywnych jest
zależność

3

⋅t p

,

(1.3)

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

4

w której t oznacza liczbę tarcz natomiast p oznacza liczbę stopni swobody odbieranych przez więzy.
Nierówność (1.3) oznacza, że liczba stopni swobody odbieranych przez więzy jest większa lub równa liczbie
stopni swobody wszystkich tarcz sztywnych stanowiących układ tarcz sztywnych. Układy, w których
zastosowano większą niż minimalna liczba więzów nazywa się układami geometrycznie niezmiennymi
statycznie niewyznaczalnymi. Układy tego typu nie będą tutaj rozpatrywane ze względu na to, że do
rozwiązania ich konieczne będą dodatkowe równania niż tylko rozpatrywane w dalszej części równania
równowagi.

Układy, w których zastosowano minimalną liczbę więzów nazywa się układami geometrycznie

niezmiennymi statycznie wyznaczalnymi. Spełniają one warunek

3

⋅t= p

.

(1.4)

Układy tarcz sztywnych, które nie spełniają warunku (1.3) nazywa się układami geometrycznie

zmiennymi.

Równanie (1.4) jest warunkiem koniecznym ale niewystarczającym geometrycznej niezmienności.

Możliwe są układy, które spełniają równanie (1.4) jednak będące układami geometrycznie zmiennymi.
Układ tarcz sztywnych musi spełniać także warunki dostateczne geometrycznej niezmienności. Dopiero
spełnienie warunku koniecznego oraz warunków dostatecznych geometrycznej niezmienności stanowi o
tym, że układ tarcz sztywnych jest geometrycznie niezmienny.

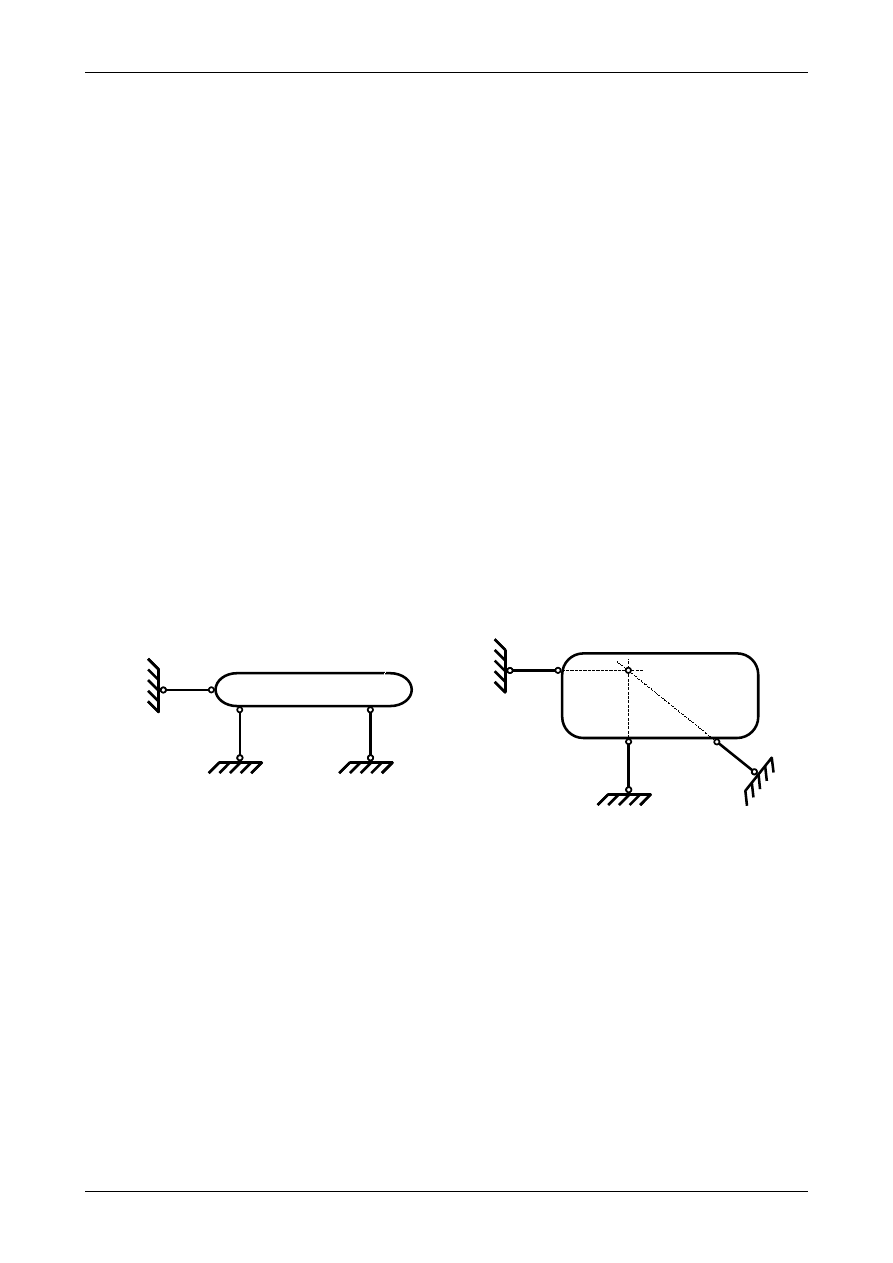
Dla pojedynczej tarczy sztywnej podpartej trzema prętami podporowymi warunkiem dostatecznym

geometrycznej niezmienności jest to, że kierunki wszystkich trzech prętów podporowych nie mogą
przecinać się w jednym punkcie. Rysunek 1.9 a przedstawia tarczę sztywną geometrycznie niezmienną
natomiast rysunek 1.9 b przedstawia tarczę sztywną geometrycznie zmienną.

a)

b)

Rys. 1.9. Tarcza sztywna: a)geometrycznie niezmienna, b) geometrycznie zmienna

Dla pojedynczej tarczy sztywnej podpartej przegubem rzeczywistym i prętem podporowym

warunkiem dostatecznym geometrycznej niezmienności jest to, aby przegub rzeczywisty nie znajdował się
na kierunku pręta podporowego. Rysunek 1.10 a przedstawia tarczę sztywną geometrycznie niezmienną
natomiast rysunek 1.10 b przedstawia tarczę sztywną geometrycznie zmienną.

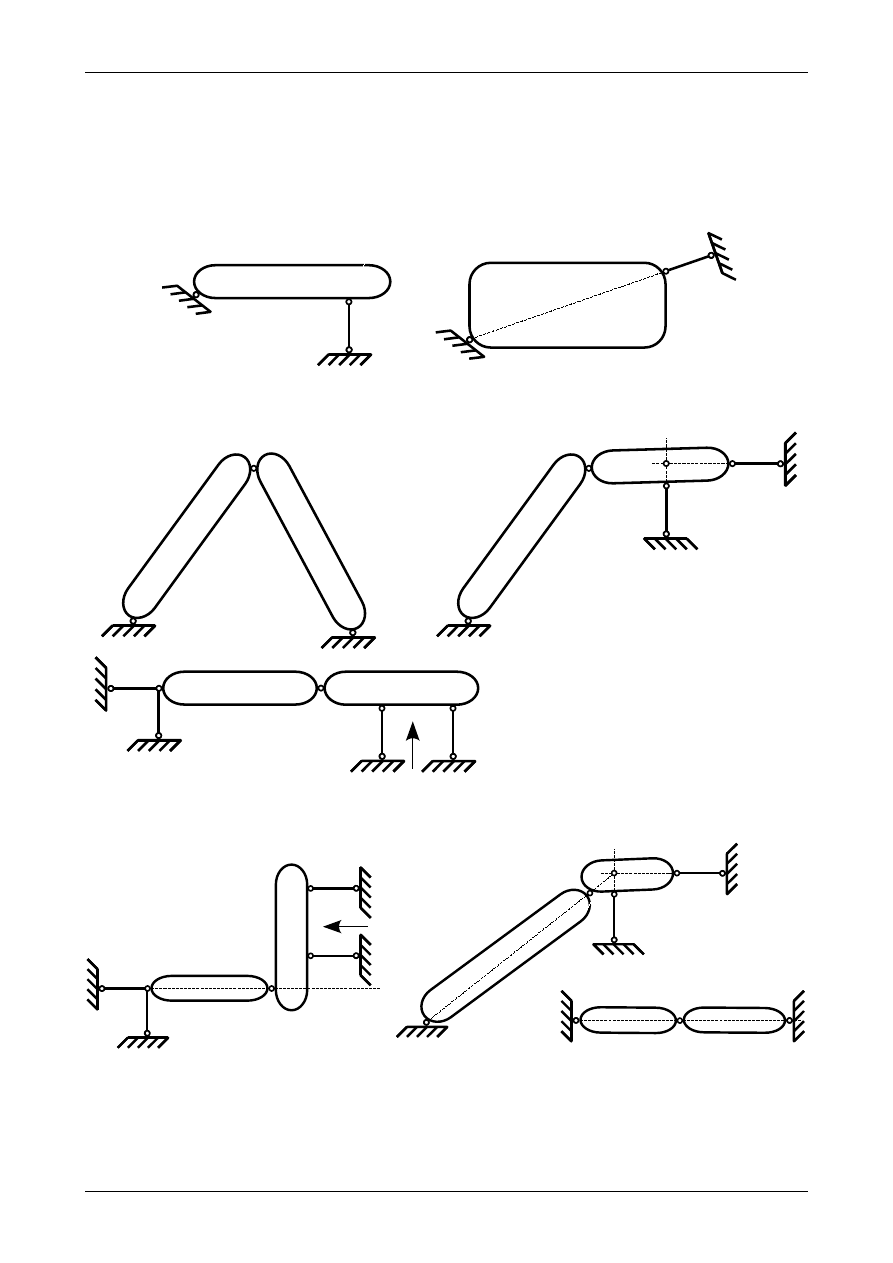
Często wykorzystywanym układem tarcz sztywnych jest układ trzech tarcz (z których jedna może być

tarczą podporową) połączonych między sobą przegubami (rzeczywistym, fikcyjnym lub niewłaściwym).
Układ taki nazywamy układem trójprzegubowym. Dla takiego układu tarcz sztywnych warunkiem
dostatecznym geometrycznej niezmienności jest fakt, że trzy przeguby nie znajdują się na jednej prostej.
Rysunek 1.11 przedstawia układy trójprzegubowe geometrycznie niezmienne natomiast rysunek 1.12
przedstawia układy trójprzegubowe geometrycznie zmienne.

Korzystając z trzech powyższych warunków dostatecznych geometrycznej niezmienności można

udowodnić, geometryczną niezmienność większości przypadków układów tarcz sztywnych. Analizę
kinematyczną zaczyna się od tej tarczy sztywnej lub układu trójprzegubowego, które spełniają jeden z
powyższych warunków dostatecznych. Taką tarczę lub układ trójprzegubowy można więc teraz uznać jako

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

5

tarczę podporową dla pozostałych tarcz sztywnych. Analizę pozostałych tarcz sztywnych przeprowadza się
podobnie jak na początku analizy kinematycznej. Istnieją układy tarcz sztywnych, dla których nie da się
udowodnić geometrycznej niezmienności w sposób opisany powyżej. Dla takich układów analizę
kinematyczną przeprowadza się metodą nazywaną planem biegunów (metoda ta nie będzie tutaj
rozpatrywana) lub przy wykorzystaniu równań równowagi, co zostanie opisane w dalszej części.

a)

b)

Rys. 1.10. Tarcza sztywna: a)geometrycznie niezmienna, b) geometrycznie zmienna

A

B

C

A

B

C

A

B

C

∞

Rys. 1.11. Geometrycznie niezmienne układy trójprzegubowe

A

B

C

A

B

C

A

B

C

∞

Rys. 1.12. Geometrycznie zmienne układy trójprzegubowe

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

6

1.2. Układy prętowe

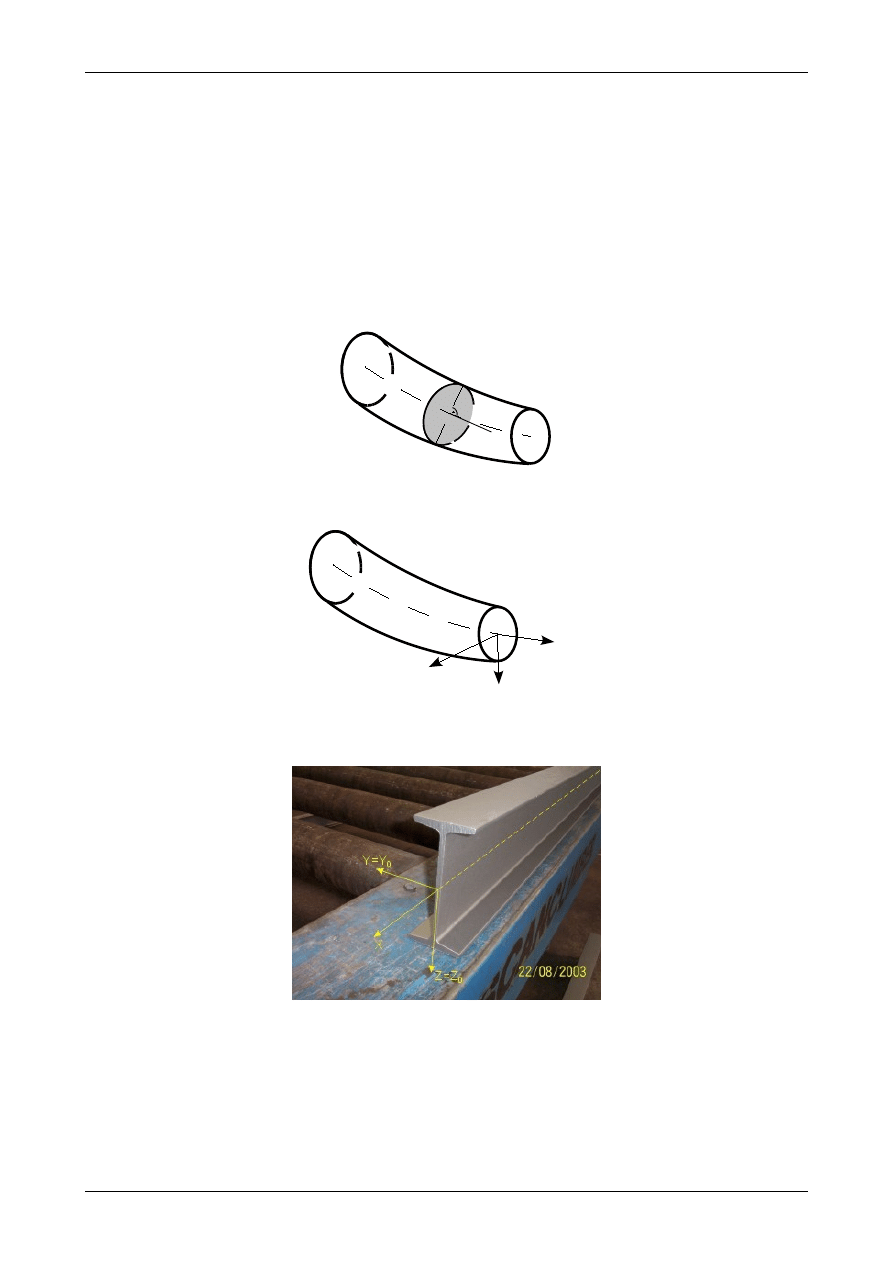
Podstawowym elementem konstrukcyjnym jest pręt. Pręt powstaje wtedy, gdy po linii regularnej AB

przemieszcza się środek ciężkości figury płaskiej (jeżeli wykonamy figurę z cienkiej blachy i podeprzemy
go dokładnie w środku ciężkości na szpilce to będzie on leżał stabilnie) w taki sposób aby płaszczyzna
figury była zawsze prostopadła do linii AB. Kontur figury opisuje bryłę geometryczną, która wypełniona
materiałem tworzy pręt. Przedstawia to rysunek 1.13. Figurę tworzącą pręt nazywamy przekrojem pręta
natomiast linię AB nazywamy osią pręta. Z przekrojem pręta będzie związany układ współrzędnych XYZ.
Początek tego układu znajduje się w środku ciężkości przekroju (punkt A). Oś X jest styczna do osi pręta.
Położenie pozostałych osi przedstawia rysunek 1.14. Przykłady rzeczywistych prętów znajdują się na
rysunkach 1.15 i 1.16.

A

B

Rys. 1.13. Pręt

A

B

X

Y=Y

0

Z=Z

0

B

Rys. 1.14. Układ współrzędnych związany z przekrojem pręta

Rys. 1.15. Pręt

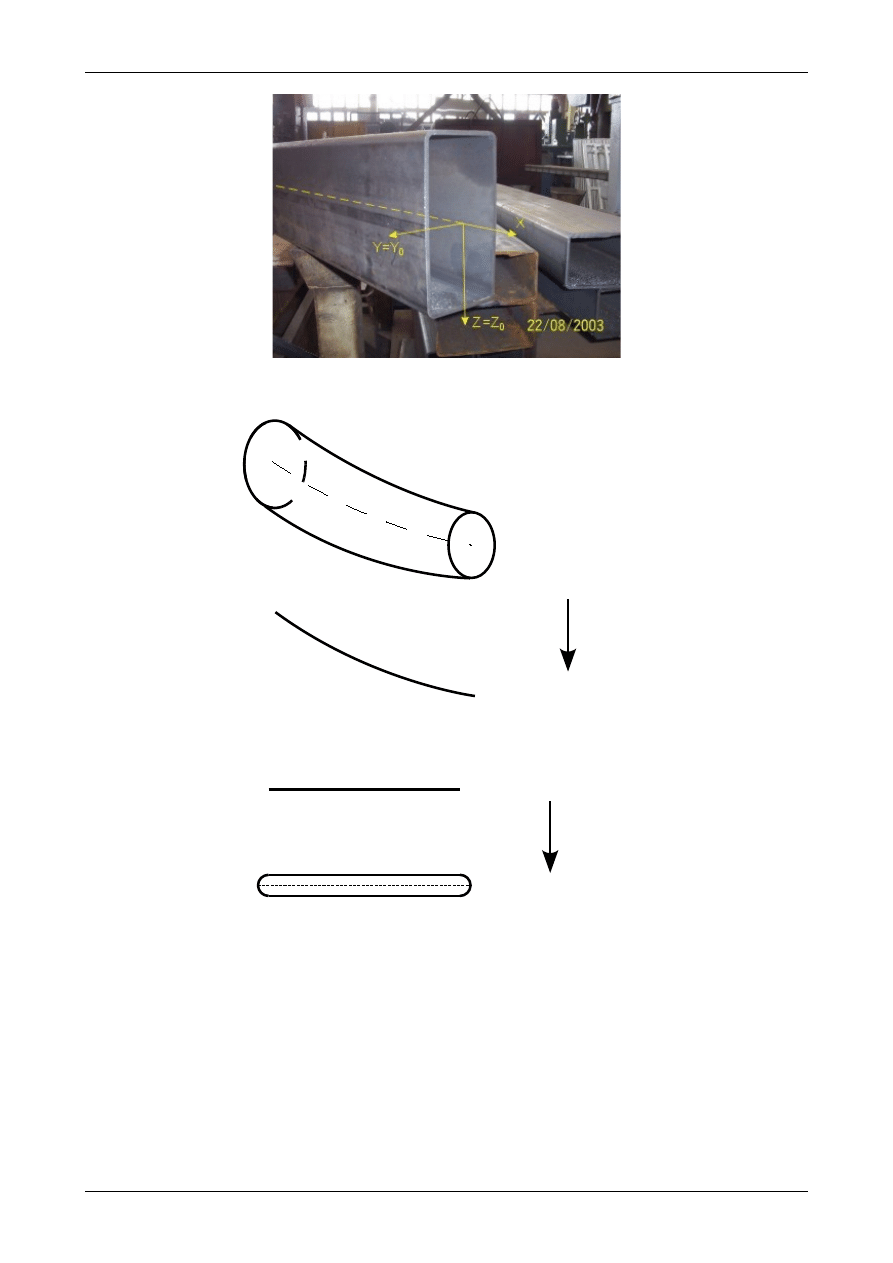
Jeżeli przekrój pręta jest stały to pręt jest prętem pryzmatycznym. Większość rzeczywistych prętów

jest właśnie prętami pryzmatycznymi. Modelem matematycznym pręta jest jest jego oś. Przedstawia to
rysunek 1.17. W zagadnieniach przedstawionych w niniejszym rozdziale osie wszystkich prętów będą
znajdowały się na jednej płaszczyźnie. Na potrzeby analizy kinematycznej płaskich układów prętowych
możemy pręt traktować jako bardzo wydłużoną tarczę sztywną. Przedstawia to rysunek 1.18.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

7

Rys. 1.16. Pręt

A

B

A

B

Rzeczywisty obiekt

Model matematyczny

Rys. 1.17. Model matematyczny pręta

Tarcza sztywna

Model matematyczny

Rys. 1.18. Pręt jako tarcza sztywna

W przypadku płaskich układów prętowych więzy odbierające prętowi stopnie swobody nazywane są

podporami. Mamy kilka ich rodzajów. Pierwszym z nich jest podpora przegubowo-przesuwna,
odpowiadająca jednemu prętowi podporowemu. Odbiera ona więc jeden stopień swobody. Podporę taką
przedstawia rysunek 1.19. Podporę przegubowo-przesuwną w rzeczywistych konstrukcjach budowlanych
przedstawiają rysunki od 1.20 do 1.26.

Drugim rodzajem podpory jest podpora przegubowo-nieprzesuwna, odpowiadająca dwóm

nierównoległym prętom podporowym. Odbiera ona więc dwa stopnie swobody. Podporę taką przedstawia
rysunek 1.27. Podporę przegubowo-nieprzesuwną w rzeczywistych konstrukcjach budowlanych
przedstawiają rysunki od 1.28 do 1.30.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

8

Rys. 1.19. Podpora przegubowo-przesuwna

Rys. 1.20. Rzeczywista podpora przegubowo-przesuwna

Rys. 1.21. Rzeczywista podpora przegubowo-przesuwna

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

9

Rys. 1.22. Rzeczywista podpora przegubowo-przesuwna (trasa PST w Poznaniu)

Rys. 1.23. Rzeczywista podpora przegubowo-przesuwna (trasa PST w Poznaniu)

Rys. 1.24. Rzeczywista podpora przegubowo-przesuwna (trasa PST w Poznaniu)

Rys. 1.25. Rzeczywista podpora przegubowo-przesuwna (trasa PST w Poznaniu)

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

10

Rys. 1.26. Rzeczywista podpora przegubowo-przesuwna (trasa PST w Poznaniu)

Rys. 1.27. Podpora przegubowo-nieprzesuwna

Rys. 1.28. Rzeczywista podpora przegubowo-nieprzesuwna

Rys. 1.29. Rzeczywista podpora przegubowo-nieprzesuwna

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

11

Rys. 1.30. Rzeczywista podpora przegubowo-nieprzesuwna (trasa PST w Poznaniu)

Trzecim rodzajem podpory jest przegub, łączący ze sobą dwa pręty i odpowiadający przegubowi

rzeczywistemu. Odbiera on więc dwa stopnie swobody. Podporę taką przedstawia rysunek 1.31. Przegub
w rzeczywistej konstrukcji budowlanej przedstawia rysunek 1.32.

A

A

Rys. 1.31. Przegub

Rys. 1.32. Przegub w rzeczywistej konstrukcji prętowej

Czwartym rodzajem podpory jest podpora teleskopowa, która odpowiada dwóm równoległym do

siebie prętom podporowym. Odbiera ona więc dwa stopnie swobody. Podporę taką przedstawia rysunek
1.33.

Rys. 1.33. Podpora teleskopowa

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

12

Czwartym rodzajem podpory jest utwierdzenie, które odpowiada trzem prętom podporowym, których

kierunki nie przecinają się w jednym punkcie. Odbiera ono więc trzy stopnie swobody. Podporę taką
przedstawia rysunek 1.34. Rysunek 1.35 przedstawia rzeczywisty pręt, do którego przymocowana jest
prostokątna blacha z otworami na śruby fundamentowe. Śruby te łączą pręt z betonowym blokiem
fundamentowym w kształcie prostopadłościanu, który traktujemy jako tarczę sztywną dla tego pręta. Za
pomocą tych czterech śrub zrealizowane jest utwierdzenie. Utwierdzenie takie jest przedstawione na
rysunku 1.36 i 1.37.

Rys. 1.34. Utwierdzenie

Rys. 1.35. Rzeczywiste utwierdzenie

Rys. 1.36. Rzeczywiste utwierdzenie

Rys. 1.37. Rzeczywiste utwierdzenie

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

13

1.3. Kratownice płaskie

Kratownicą płaską nazywamy układ prętów prostych leżących na jednej płaszczyźnie, które są

połączone między sobą przegubami. Przeguby nazywa się węzłami kratownicy. Kratownica następnie jest
podparta do podłoża za pomocą podpór przegubowo-przesuwnej i przegubowo-nieprzesuwnej. Rysunek 1.38
przedstawia przykładową kratownicę.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

Rys. 1.38. Kratownica

Poszczególne pręty kratownicy mają swoje charakterystyczne nazwy. Opierając się na oznaczeniach

prętów przedstawionych na rysunku 1.38 pręty kratownicy możemy podzielić na:

•

pręty pasa dolnego – od numeru 1 do 4

•

pręty pasa górnego – od numeru 5 do 8

•

słupki – od numeru 9 do 13

•

krzyżulce – od numeru 14 do 17.

Rysunki od 1.39 do 1.42 przedstawiają rzeczywiste kratownice wraz z zaznaczonymi modelami

matematycznymi tych kratownic.

Rys. 1.39. Rzeczywista kratownica

W modelu matematycznym przyjmujemy, że węzeł kratownicy jest przegubem. Jednak w

rzeczywistych obiektach najczęściej nie da się wykonstruować przegubu. Rzeczywiste węzły kratownic
przedstawiają rysunki od 1.43 do 1.46.

Kratownica może być częścią innej konstrukcji. Na rysunkach 1.47 i 1.48 przedstawione są

kratownice będące pomostem mostu wiszącego.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

14

Rys. 1.40. Rzeczywista kratownica

Rys. 1.41. Rzeczywista kratownica

Rys. 1.42. Rzeczywista kratownica

Rys. 1.43. Rzeczywisty węzeł kratownicy

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

15

Rys. 1.44. Rzeczywisty węzeł kratownicy

Rys. 1.45. Rzeczywisty węzeł kratownicy

Rys. 1.46. Rzeczywisty węzeł kratownicy

Oprócz kratownic płaskich spotykane są kratownice przestrzenne, które składają się z kilku kratownic

płaskich leżących na różnych płaszczyznach. Kratownice takie przedstawiają rysunki od 1.49, 1.50 i 1.51.

Dotychczas przedstawione kratownice wykonane były ze stali. Jednak nie jest to jedyny materiał, z

którego wykonuje się kratownice. Rysunek 1.52 przedstawia kratownicę wykonaną z żelbetu, który składa
się z betonu z zatopionymi wewnątrz prętami stalowymi.

Kratownica może być także wykonana z drewna. Kratownice tego typu są przedstawione na rysunku

1.53.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

16

Rys. 1.47. Kratownica będąca pomostem mostu wiszącego

Rys. 1.48. Kratownica będąca pomostem mostu wiszącego (Golden Gate Bridge)

Rys. 1.49. Kratownice przestrzenne

Analiza kinematyczna kratownic przebiega w nieco inny sposób niż w przypadku innych typów

konstrukcji prętowych. Rysunek 1.54 przedstawia dowolny punkt, który reprezentuje nam węzeł kratownicy
w płaskim układzie współrzędnych. Jak widać do opisu jego położenia potrzebujemy dwóch parametrów,
którymi są współrzędne x

A

i y

A

. Możemy więc stwierdzić, że punkt posiada dwa stopnie swobody.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

17

Rys. 1.50. Kratownice przestrzenne

Rys. 1.51. Kratownice przestrzenne

Rys. 1.52. Kratownica żelbetowa

Jeżeli dana kratownica składa się z w węzłów to posiadają one

2

⋅

w

(1.5)

stopni swobody.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

18

Rys. 1.53. Kratownice drewniane

X

Y

A

x

A

y

A

Rys. 1.54. Stopnie swobody punktu na płaszczyźnie

Wszystkie stopnie swobody muszą zostać odebrane węzłom przez pręty kratownicy oraz podpory.

Warunkiem koniecznym geometrycznej niezmienności będzie więc warunek

2

⋅

w

≤

p



r

,

(1.6)

w którym w oznacza liczbę węzłów kratownicy, p oznacza liczbę prętów kratownicy natomiast r oznacza
liczbę stopni swobody odbieranych przez podpory.

Kratownice, w których pręty oraz podpory odbierają więcej stopni swobody niż posiadają je węzły

nazywa się kratownicami geometrycznie niezmiennymi statycznie niewyznaczalnymi. Układy tego typu
nie będą tutaj rozpatrywane ze względu na to, że do rozwiązania ich konieczne będą dodatkowe równania
niż tylko rozpatrywane w dalszej części równania równowagi.

Układy, w których pręty oraz podpory odbierają dokładnie tyle stopni swobody ile posiadają ich

węzły nazywa się układami geometrycznie niezmiennymi statycznie wyznaczalnymi. Spełniają one
warunek

2

⋅w= pr

.

(1.7)

Kratownice, które nie spełniają warunku (1.6) nazywamy kratownicami geometrycznie zmiennymi.

Nie mogą one być konstrukcjami budowlanymi.

Podobnie jak w przypadku płaskiego układu tarcz sztywnych kratownice muszą oprócz warunku

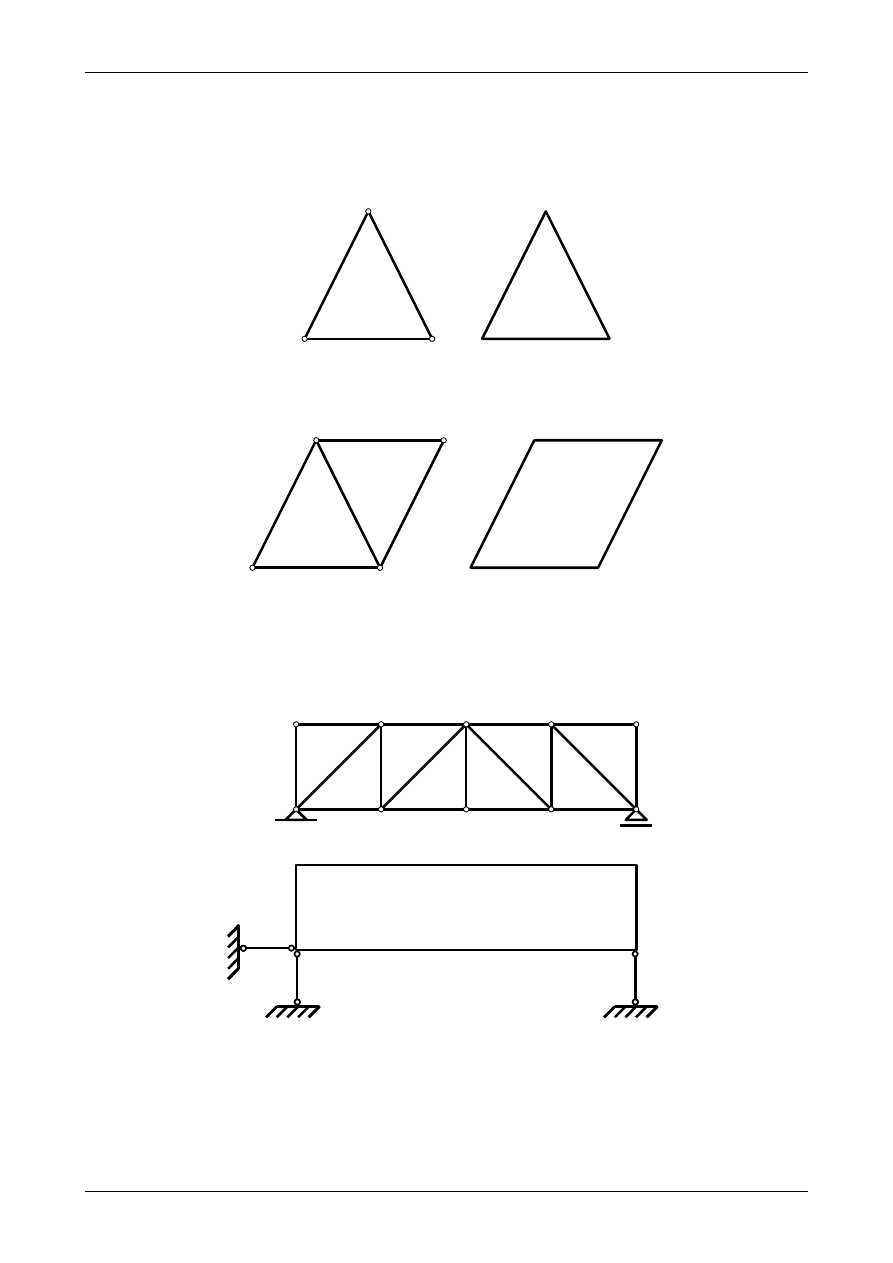
koniecznego spełnić także warunki dostateczne geometrycznej niezmienności. Kratownica pokazana na
rysunku 1.55 jest geometrycznie niezmienna, ponieważ nie można zmienić położenia dowolnego węzła bez
zmiany długości prętów kratownicy. Stanowi ona więc tarczę sztywną. Dokładając do niej następny węzeł za
pomocą dwóch prętów, jak to jest przedstawione na rysunku 1.56, kratownica taka pozostaje nadal
geometrycznie niezmienna. Ogólnie możemy więc powiedzieć, że kratownica składająca się z trójkątów
jest tarczą sztywną. Kratownicę taką nazywamy kratownicą o strukturze prostej. Jeżeli więc mamy do

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

19

czynienia z kratownicą o strukturze prostej to w analizie kinematycznej możemy ją traktować jako tarczę
sztywną i dalej będziemy mogli stosować do niej warunki dostateczne geometrycznej niezmienności jak dla
płaskiego układu tarcz sztywnych.

1

2

3

1

2

3

=

Rys. 1.55. Kratownica będąca tarczą sztywną

1

2

3

1

2

3

=

4

4

5

Rys. 1.56. Kratownica będąca tarczą sztywną

Rysunek 1.57 przedstawia kratownicę o strukturze prostej traktowaną w analizie kinematycznej jako

tarczę sztywną podpartą trzema prętami podporowymi.

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

=

Rys. 1.57. Kratownica będąca tarczą sztywną podpartą trzema prętami podporowymi

1.4. Belki

Belką nazywamy układ prętowy, który składa się z prętów leżących na jednej prostej. Podporami

belek są wszystkie przedstawione wcześniej typy podpór.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

20

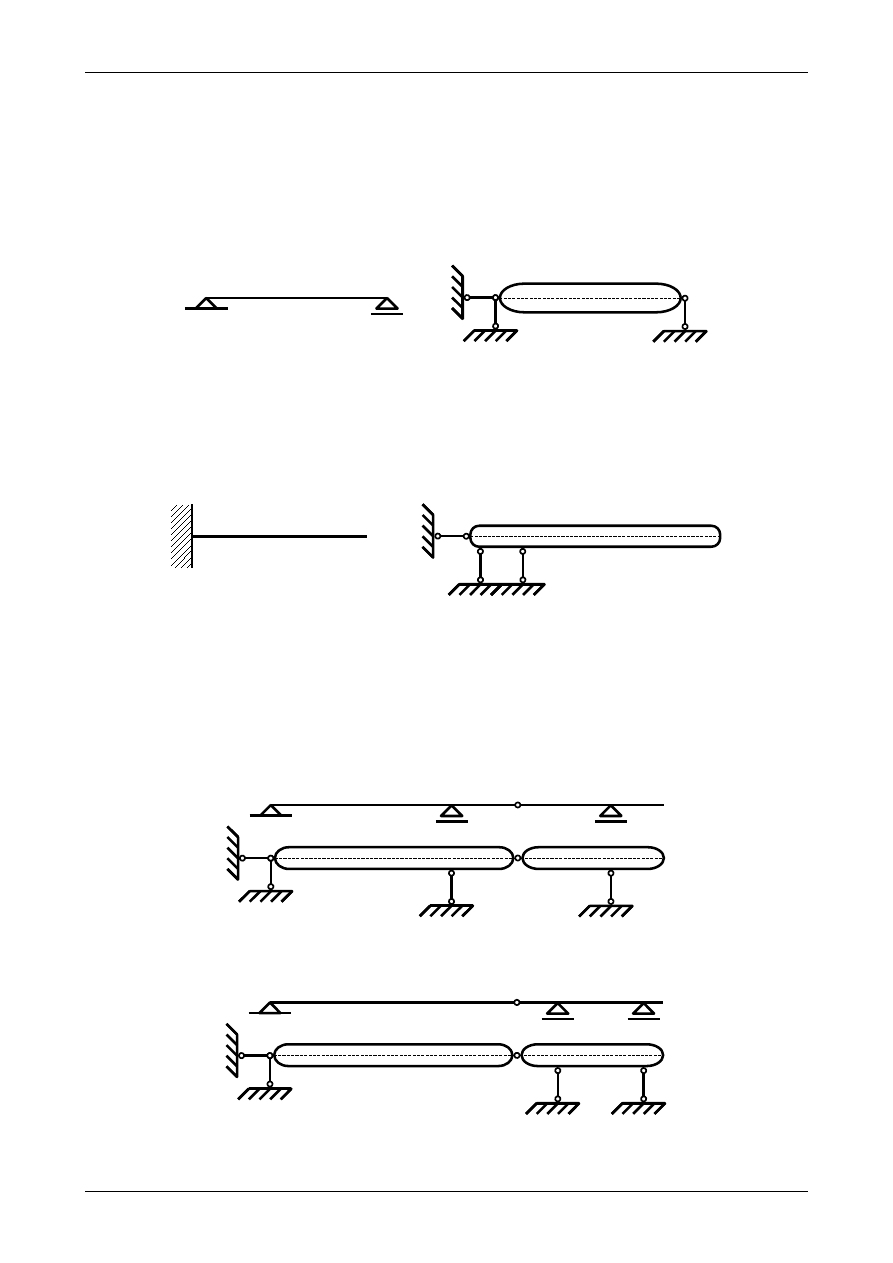
Jeżeli belka składa się z jednego tylko pręta to belkę taką nazywamy belką prostą. Istnieją dwa typy

belek prostych. Pierwszym z nich jest belka swobodnie podparta. Przedstawia ją rysunek 1.58. Podporami
tej belki są podpora przegubowo-przesuwna i przegubowo-nieprzesuwna. Stanowią one układ trzech prętów
podporowych. Dzięki ich liczbie spełniony jest warunek konieczny geometrycznej niezmienności. Kierunki
tych trzech prętów podporowych nie przecinają się w jednym punkcie, przez co spełniony jest także
warunek dostateczny geometrycznej niezmienności. Belka ta jest więc układem geometrycznie niezmiennym
i statycznie wyznaczalnym.

Rys. 1.58. Belka swobodnie podparta

Drugim rodzajem belki prostej jest belka wspornikowa. Belka ta jest przedstawiona na rysunku 1.59.

Podporą tej belki jest utwierdzenie. Przez to belka ta jest układem geometrycznie niezmiennym i statycznie
wyznaczalnym.

Rys. 1.59. Belka wspornikowa

Jeżeli belka składa się z przynajmniej dwóch prętów to nazywamy ją belką złożoną. Rysunki od 1.60

do 1.63 przedstawiają przykłady belek złożonych.

Do analizy kinematycznej belek stosujemy zasady jak dla płaskich układów tarcz sztywnych. Belki

przedstawione na poniższych rysunkach są układami geometrycznie niezmiennymi i statycznie
wyznaczalnymi.

Rys. 1.60. Belka złożona

Rys. 1.61. Belka złożona

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

21

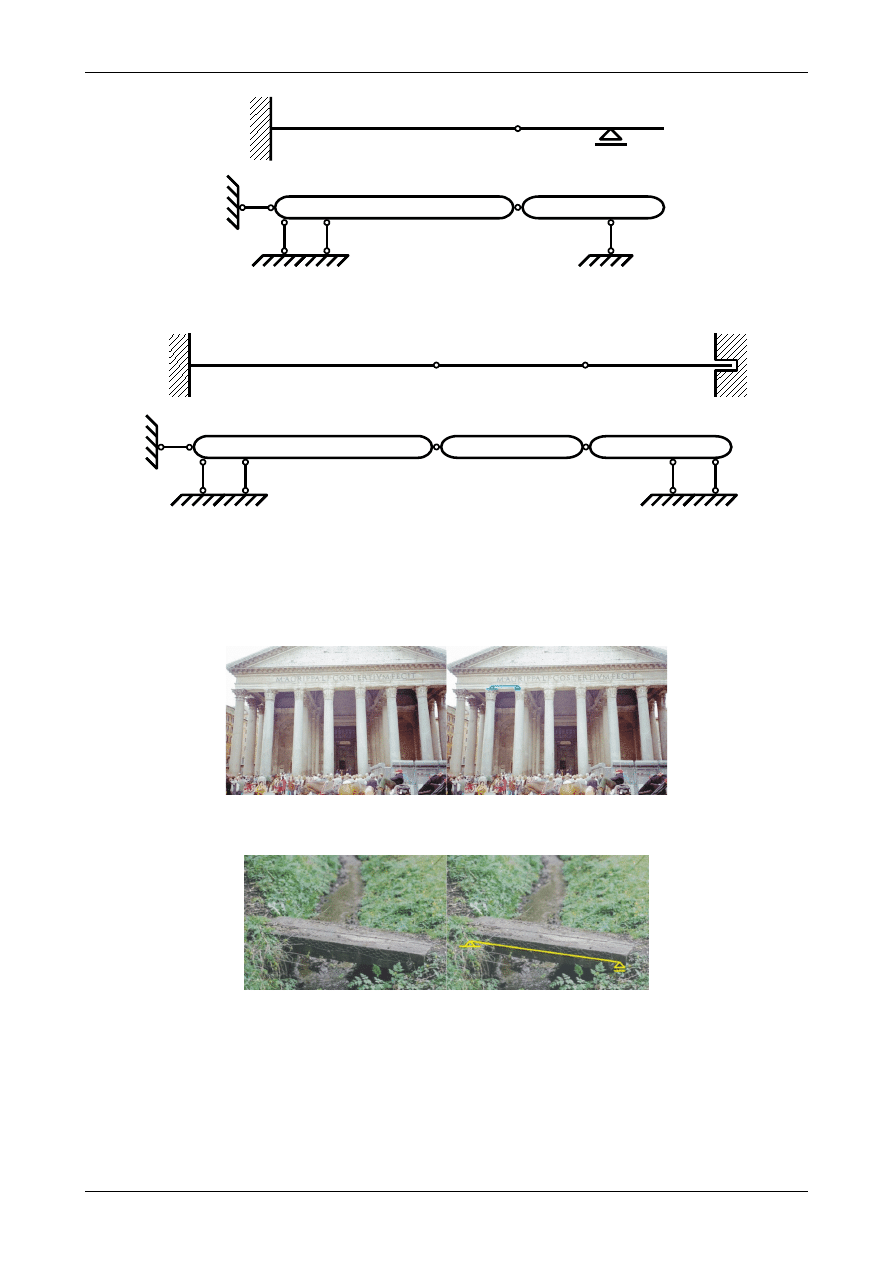
Rys. 1.62. Belka złożona

Rys. 1.63. Belka złożona

Rysunki od 1.64 do 1.68 przedstawiają rzeczywiste belki swobodnie podparte. Rysunki 1.69 i 1.70

przedstawiają tak zwane belki ciągłe, które to są belkami statycznie niewyznaczalnanymi.

Rys. 1.64. Rzeczywista belka swobodnie podparta

Rys. 1.65. Rzeczywista belka swobodnie podparta

1.5. Ramy płaskie

Ramą płaską nazywamy układ prętowy, w którym pręty nie leżą na jednej prostej. Poszczególne

pręty ramy płaskiej mogą się łączyć między sobą za pomocą przegubów lub połączeń sztywnych.
Połączenie sztywne to takie połączenie, które nie pozwala na obrót poszczególnych prętów ramy względem
siebie wokół miejsca połączenia. Miejsce sztywnego połączenia prętów w ramie płaskiej nazywamy węzłem

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

22

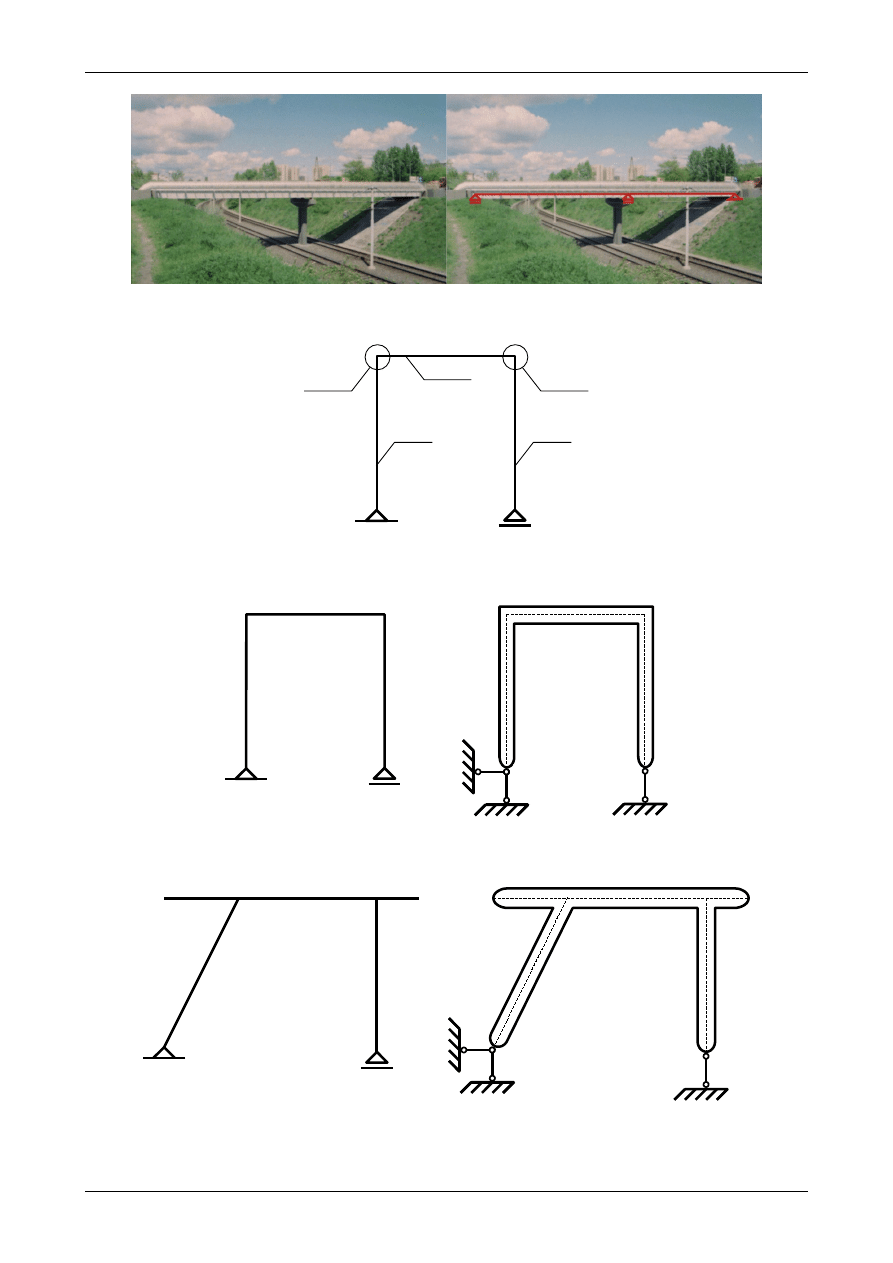
ramy. Pionowe pręty w ramie płaskiej nazywamy słupami natomiast poziome pręty nazywamy ryglami.
Jeżeli wszystkie pręty w ramie płaskiej są do siebie prostopadłe to taką ramę nazywamy ramą ortogonalną.
Rysunek 1.71 przedstawia ramę ortogonalną z zaznaczonymi węzłami, słupami i ryglem.

Rys. 1.66. Rzeczywista belka swobodnie podparta (Stonehenge)

Rys. 1.67. Rzeczywista belka swobodnie podparta

Rys. 1.68. Rzeczywista belka swobodnie podparta (trasa PST w Poznaniu)

Rys. 1.69. Rzeczywista belka ciągła

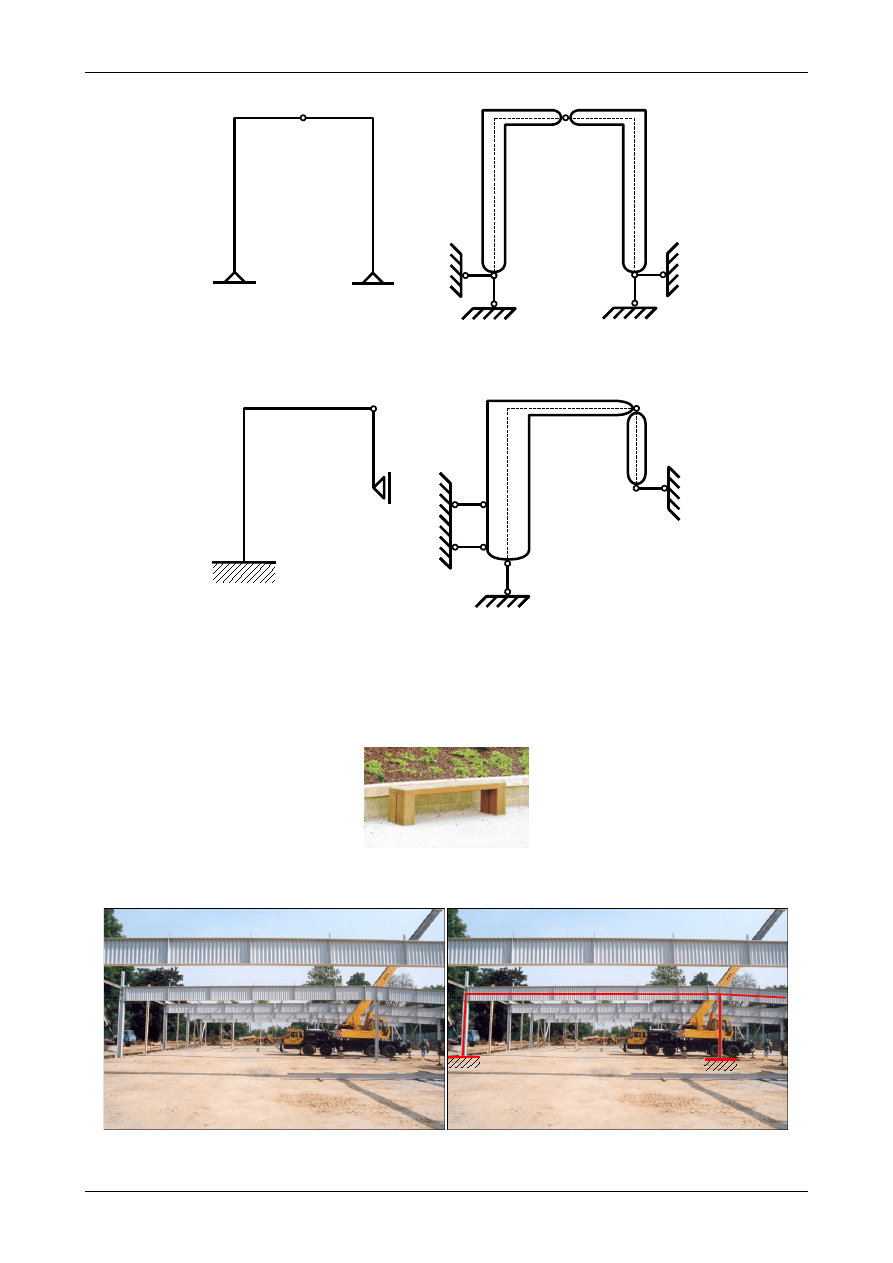
Rysunki od 1.72 do 1.75 przedstawiają przykładowe ramy płaskie. Do analizy kinematycznej ram

płaskich stosujemy zasady jak dla płaskich układów tarcz sztywnych. Ramy płaskie przedstawione na
poniższych rysunkach są układami geometrycznie niezmiennymi i statycznie wyznaczalnymi.

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

23

Rys. 1.70. Rzeczywista belka ciągła (trasa PST w Poznaniu)

Słup

Słup

Rygiel

Węzeł

Węzeł

Rys. 1.71. Ortogonalna rama płaska

Rys. 1.72. Rama płaska

Rys. 1.73. Rama płaska

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

24

Rys. 1.74. Rama płaska

Rys. 1.75. Rama płaska

Rzeczywiste ramy płaskie przedstawiają rysunki od 1.76 do 1.83. Rysunki od 1.84 do 1.89

przedstawiają rzeczywiste węzły sztywne w ramach płaskich.

Rys. 1.76. Rzeczywista rama płaska

Rys. 1.77. Rzeczywista rama płaska

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

25

Rys. 1.78. Rzeczywista rama płaska

Rys. 1.79. Rzeczywista rama płaska

Rys. 1.80. Rzeczywista rama płaska

Rys. 1.81. Rzeczywista rama płaska

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

26

Rys. 1.82. Rzeczywista rama płaska

Rys. 1.83. Rzeczywista rama płaska

Rys. 1.84. Sztywny węzeł ramy płaskiej

Rys. 1.85. Sztywny węzeł ramy płaskiej

Dr inż. Janusz Dębiński

Zaoczni

MO

1. ANALIZA KINAMATYCZNA PŁASKICH UKŁADÓW PRĘTOWYCH

27

Rys. 1.86. Sztywny węzeł ramy płaskiej

Rys. 1.87. Sztywny węzeł ramy płaskiej

Rys. 1.88. Sztywny węzeł ramy płaskiej

Rys. 1.89. Sztywny węzeł ramy płaskiej

Dr inż. Janusz Dębiński

Zaoczni