EKSTREMA WARUNKOWE

Rozważmy zbiór A rozwiązań układu równań

Definicja

Funkacja f ma

ekstremum warunkowe

w punkcie przy warunkach

jeśli funkcja zawężona ma ekstremum lokalne w punkcie .

Przykład

Zbadać ekstremum funkcji
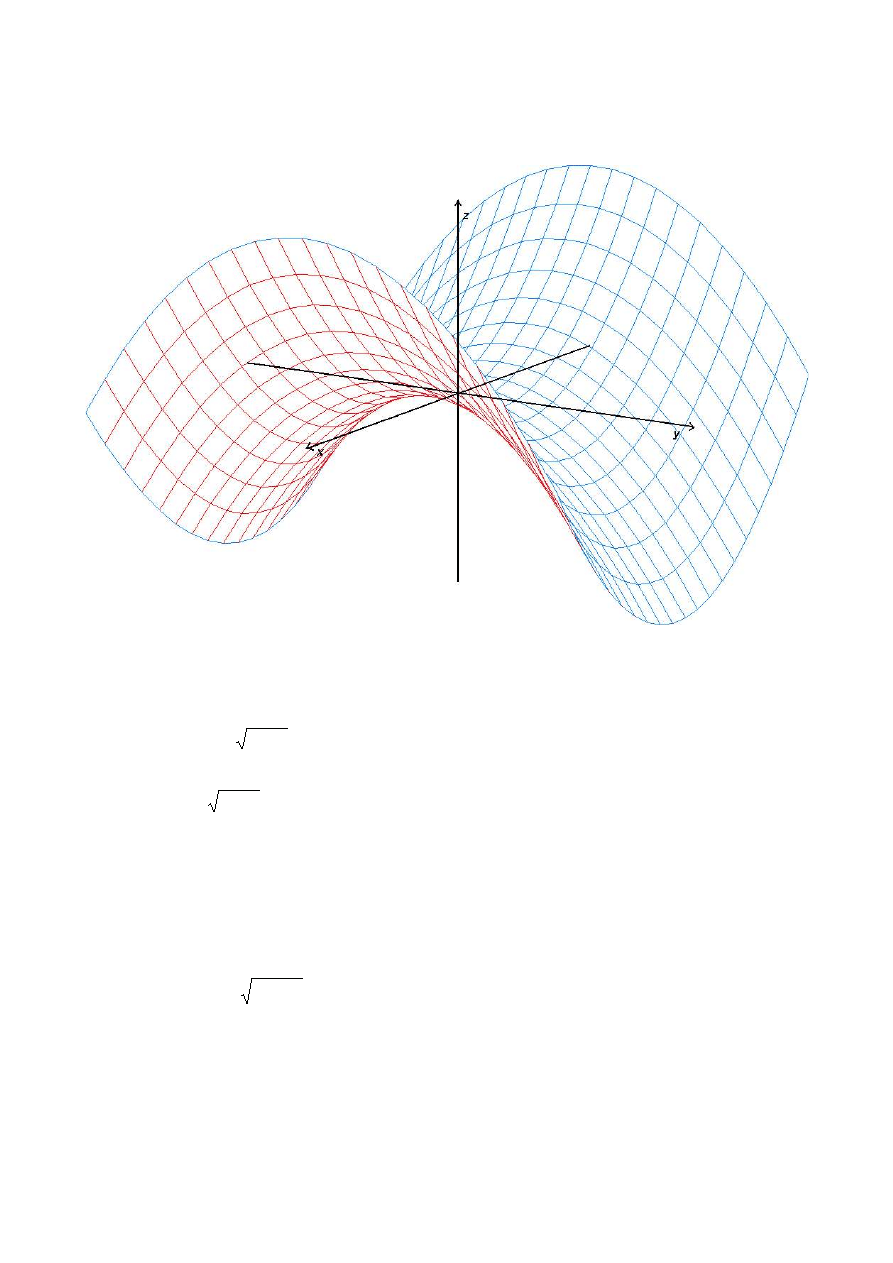
Wyznaczmy wykres funkcji f.

przekrój wykresu płaszczyzną jest parabolą

przekrój wykresu płaszczyzną jest parabolą

przekrój wykresu płaszczyzną jest parabolą

przekrój wykresu płaszczyzną jest hiperbolą

1

,

:

,

Top

otwarty),

i

spójny

(zbiór

-

Niech

R

R

obszar





U

f

U

U

n

.

,...,

1

,

:

s

j

U

g

j



 R

 



 

  

0

...

:

2

1













x

g

x

g

x

g

U

x

A

s

A

x



0



















,

0

0

0

2

1

s

g

g

g



A

f

 

.

1

ku

przy warun

,

2

2

2

2









y

x

y

x

y

x

f

 

 

 



















,

0

0

0

2

1

x

g

x

g

x

g

s



0

x

 

2

2

0

0

,

x

z

y

x

x

f





















2

2

2

2

1

1

,

x

k

z

kx

y

x

k

kx

x

f













 

const

const

const

,

2

2













z

y

x

y

x

f

 

2

2

0

,

0

y

z

x

y

y

f













Obliczmy wartość funkcji f dla punktów należących do wykresów krzywych

i zbadajmy funkcję w przedziale (-1,1).

stąd

2





 

.

1

,

0

1

,

0

punkcie

w

warunkowe

minimum

ma

funkcja

,

0

punkcie

w

lokalne

minimum

ma

funkcja

Zatem

2

min

1

min

1







x

P

f

x

f

 









 

 

,

1

,

1

dla

1

,

,

1

.

i

.

1

,

1

dla

1

y

otrzymujem

1

warunku

Z

1

2

1

2

1

2

2

,

1

2

2



























x

x

f

x

x

f

y

x

f

y

y

x

x

y

y

x

 





 

 

0

0

4

''

0

0

4

'

1

2

1

min

1

1

2

2

2

1

1



























x

x

f

x

x

x

f

x

x

x

x

f

f

i zbadajmy funkcję w przedziale (-1,1).

stąd

Jednakże jeśli z równania wyznaczymy x, to

Podobnie jak wcześniej obliczmy wartości funkcji f dla punktów należących do wykresów

i zbadajmy funkcję w przedziale (-1,1).

stąd

i zbadajmy funkcję w przedziale (-1,1).

stąd

3

 

.

1

,

1

dla

1

1

2

2

,

1

2

2















y

y

x

y

x





 

 

 





.

0

go

poprzednie

do

ie

analogiczn

i

1

2

1

,

1

,

1

dla

1

,

,

2

min

2

2

2

2

2

2

2

2







































x

x

x

x

x

f

f

x

x

f

x

x

f

y

x

f









 

 

 

 

 

0

0

4

''

~

0

0

4

'

~

2

1

1

~

~

1

,

1

dla

~

,

1

,

1

max

1

1

2

2

2

1

1

1

2

1











































y

y

f

y

y

y

f

y

y

y

y

f

f

y

y

f

y

y

f

y

x

f





 









 

 

,

1

,

1

dla

~

,

1

,

2

.

0

,

1

0

,

1

punkcie

w

we

warunko

maksimum

ma

funkcja

,

0

punkcie

w

lokalne

maksimum

ma

~

funkcja

Zatem

2

2

2

2

max

3

max

1





















y

y

f

y

y

f

y

x

f

y

P

f

y

f

 

.

0

go

poprzednie

do

ie

analogiczn

i

2

1

1

~

~

max

2

2

2

2

2













y

y

y

y

y

f

f









.

0

,

1

0

,

1

punkcie

w

warunkowe

maksimum

ma

funkcja

,

0

punkcie

w

lokalne

maksimum

ma

~

funkcja

Zatem

2

max

4

max

2











y

P

f

y

f









.

1

,

0

1

,

0

punkcie

w

warunkowe

minimum

ma

funkcja

,

0

punkcie

w

lokalne

minimum

ma

funkcja

Zatem

2

min

2

min

1











x

P

f

x

f

.

i

krzywych

2

1

x

x

Metoda współczynników nieoznaczonych Lagrange'a (mnożników Lagrange'a)

Dla funkcji f i warunków

zdefiniujmy

funkcję Lagrange'a:

Ponieważ prawdziwa jest implikacja

więc warunkiem koniecznym istnienia ekstremum warunkowego w punkcie

jest:

czyli układ n+s równań

WK

Twierdzenie

(

WW istnienia ekstremum warunkowego

)

Zał:

funkcja Lagrange'a

liniowo niezależne

zbiór wektorów, dla których zerują się różniczki

Teza: Jeśli
to funkcja f ma

minimum warunkowe

w punkcie

Jeśli
to funkcja f ma

maksimum warunkowe

w punkcie

4

 

 

 





.

,...,

,

,...,

gdzie

,

:

1

1

1

R















s

n

s

j

j

j

U

x

x

x

x

g

x

f

x









 

 

















R

s

j

s

j

x

g

x







,...,

,

,...,

1

gdzie

,

0

,

0

1

0

0

'

 

 























s

j

x

g

n

i

x

x

j

i

,...,

1

,

0

,...,

1

,

0

0

0



.

,...,

,

,...,

ch

niewiadomy

o

1

0

0

1

s

n

x

x

s

n







   

 

 

     

 

niech

oraz

-

...,

,

,

2

0

0

0

1

niech

Ponadto

0

0

2

0

1

0

0

1

0

'

'

'

'

x

g

x

g

x

g

x

g

x

g

x

s

s













 

,

i

0

dla

0

1

2

0

H

h

h

h

d

x











.

0

...

kach

przy warun

2

1

0









s

g

g

g

x

 

,

i

0

dla

0

2

2

0

H

h

h

h

d

x











.

0

...

kach

przy warun

2

1

0









s

g

g

g

x

0

...

1







s

g

g

0

punkcie

w

funkcji

x

g

j

 















s

j

h

g

d

h

H

j

x

n

,...,

1

dla

0

:

:

0

R

 

 

x

f

x

A

x













0

0

2

0

1

0

,...,

,

n

x

x

x

x



 

















s

j

j

j

j

s

s

n

g

f

U

g

g

f

U

g

g

f

U

1

2

1

1

,

:

,

,...,

,

,

:

,...,

,

,

obszar w

-

Niech

R

C

R

R







Przykład cd.

Utwórzmy funkcję Lagrange'a

Zbadamy WK. Ponieważ

zatem wystarczy rozwiązać układ

i stąd rozwiązania układu równań w każdym z przypadków:

Zatem otrzymaliśmy dwa punkty stacjonarne

Wyznaczmy teraz macierz drugiej różniczki

i stąd

5

 





1

,

0

1

,

0

2

1



P

P

 





0

,

1

0

,

1

4

3



P

P

 









































0

0

0

4

2

2

0

2

2

2

2

2

2

2

2

1













P

d

y

y

x

x





 

 

,

dowolne)

i

(

1

2

albo

1

i

0

1

albo

:

y

otrzymujem

0

1

równania

pierwszego

Z

















x

x

x







  



1

dla

1

,

0

,

1

,

0

2

1







P

P

  



.

1

dla

0

,

1

,

0

,

1

e

stacjonarn

punkty

dwa

oraz

4

3









P

P

  



.

1

przy

1

,

0

punkcie

w

1

2







P

d

 

 

.

1

,

warunku

i

,

funkcji

dla

2

2

2

2











y

x

y

x

g

y

x

y

x

f



































1

0

1

0

1

czyli

2

2

y

x

y

x





 

 

1

1

0

1

1

1

1

0

2

1

























































y

x

y

x

 

























































1

0

2

2

0

2

2

2

2

2

2

.

1

,

2

2

2

2

2

2

y

x

y

y

x

x

y

y

y

x

x

x

y

x

y

x

y

x

















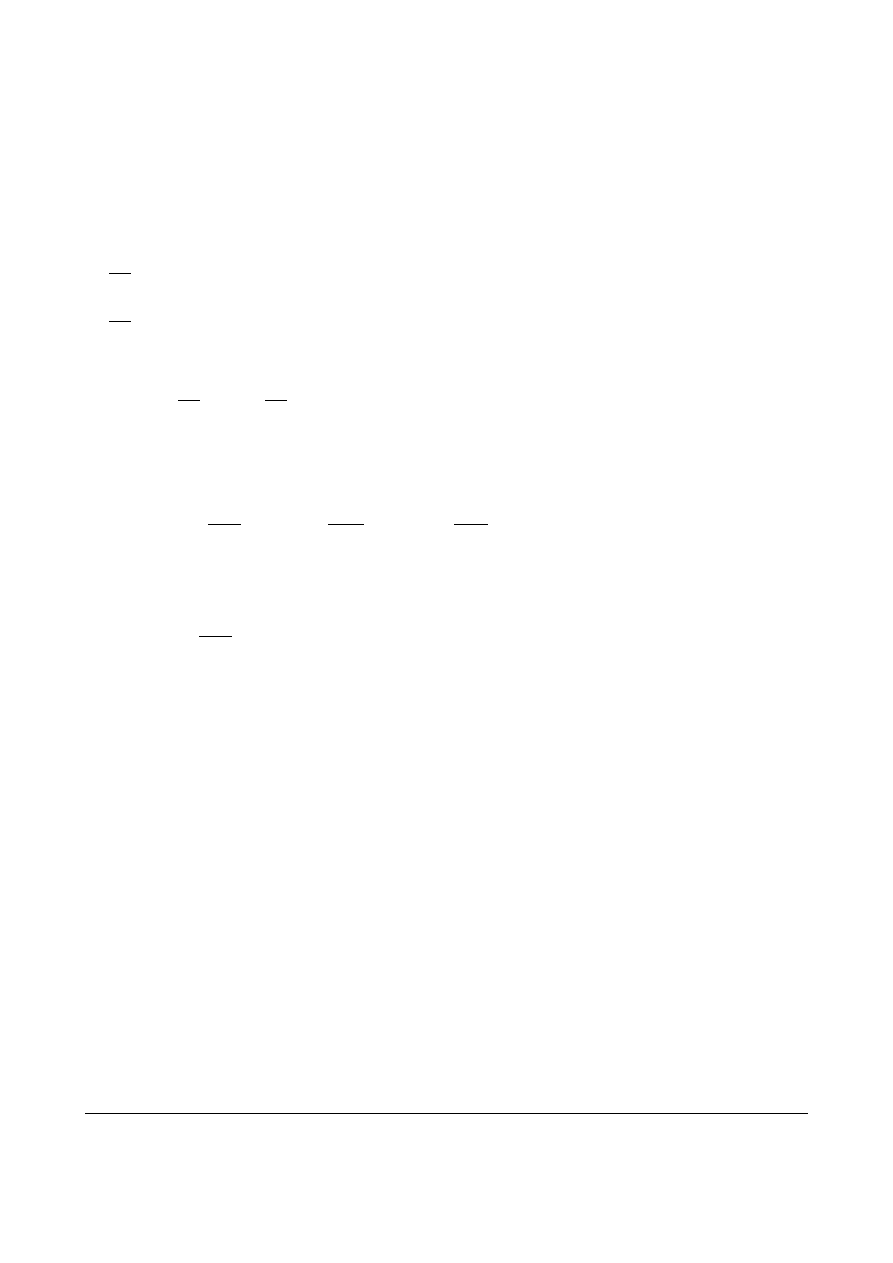
jest formą półokreśloną dodatnio (bo ).

Wyznaczmy teraz zbiór tych wektorów h, dla których zeruje się pierwsza różniczka funkcji g w

Ponieważ

więc

Zbadajmy teraz określoność formy

więc funkcja f ma w

Dla pozostałych punktów postępowanie jest analogiczne jak w przypadku punktu .

opracował Marcin Uszko

6

0

,

4

2

1



 d

d



2

1

Czyli

P

d

.

punkcie

1

P

.

1

ku

przy warun

warunkowe

minimum

2

2

1



 y

x

P

1

P





 

 

 

 

 

 

0

4

0

,

y

Otrzymujem

.

0

gdzie

0

,

dla

czyli

,

0

dla

2

,

2

1

2

1

1

2

2

1

2

1

1

2

2

1

2

2

2

1

1

2

2

1

1

2

2

2

1

2

1

1





















































h

h

P

x

h

d

h

h

h

H

h

h

h

P

y

h

h

P

y

x

h

P

x

h

h

d

P

P













 

 

 

 





.

,

0

,

zatem

0

0

2

0

2

2

1

1

2

2

1

2

1

1

1

1

R















































h

h

H

h

h

h

h

P

y

g

h

P

x

g

h

g

d

y

y

g

x

x

g

P