Ekstrema
warunkowe

dr Tomasz Kowalski

Wykład 28

Slajd nr 2 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Ekstrema warunkowe funkcji wielu
zmiennych

Niech f będzie funkcją określoną w pewnym
zbiorze D

f

wzorem z = f(x

1

, x

2

, x

3

, …, x

n

).

minimum warunkowe , jeżeli spełniony jest
warunek

0

0

0

1

2

1

2

( , ,..., )

( , ,..., )

n

n

f x x

x

f x x

x

>

Funkcja f posiada w punkcie
zbioru D

P x x

x

n

0

1

0

2

0

0

( , ,..., )

dla wszystkich punktów P(x

1

, x

2

, x

3

, …, x

n

) z pewnego

sąsiedztwa S punktu , leżących
równocześnie w zbiorze D.

0

0

0

0

1

2

( , ,..., )

n

P x x

x

Niech D oznacza zbiór złożony z tych punktów
zbioru D

f

, które spełniają układ warunków

(ograniczeń):



















.

0

)

...,

,

,

(

........

..........

..........

,

0

)

...,

,

,

(

,

0

)

...,

,

,

(

2

1

2

1

2

2

1

1

n

m

n

n

x

x

x

g

x

x

x

g

x

x

x

g

Slajd nr 3 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Ekstrema warunkowe funkcji wielu
zmiennych

maksimum
warunkowe.

Podobnie , jeżeli spełniony jest warunek

0

0

0

1

2

1

2

( , ,..., )

( , ,..., )

n

n

f x x

x

f x x

x

<

to funkcja ta posiada w punkcie

P x x

x

n

0

1

0

2

0

0

( , ,..., )

dla wszystkich punktów P(x

1

, x

2

, x

3

, …, x

n

) z pewnego

sąsiedztwa S punktu należących
równocześnie do D,

0

0

0

0

1

2

( , ,..., ),

n

P x x

x

Minima i maksima warunkowe nazywamy ekstremami
warunkowymi.

Slajd nr 4 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

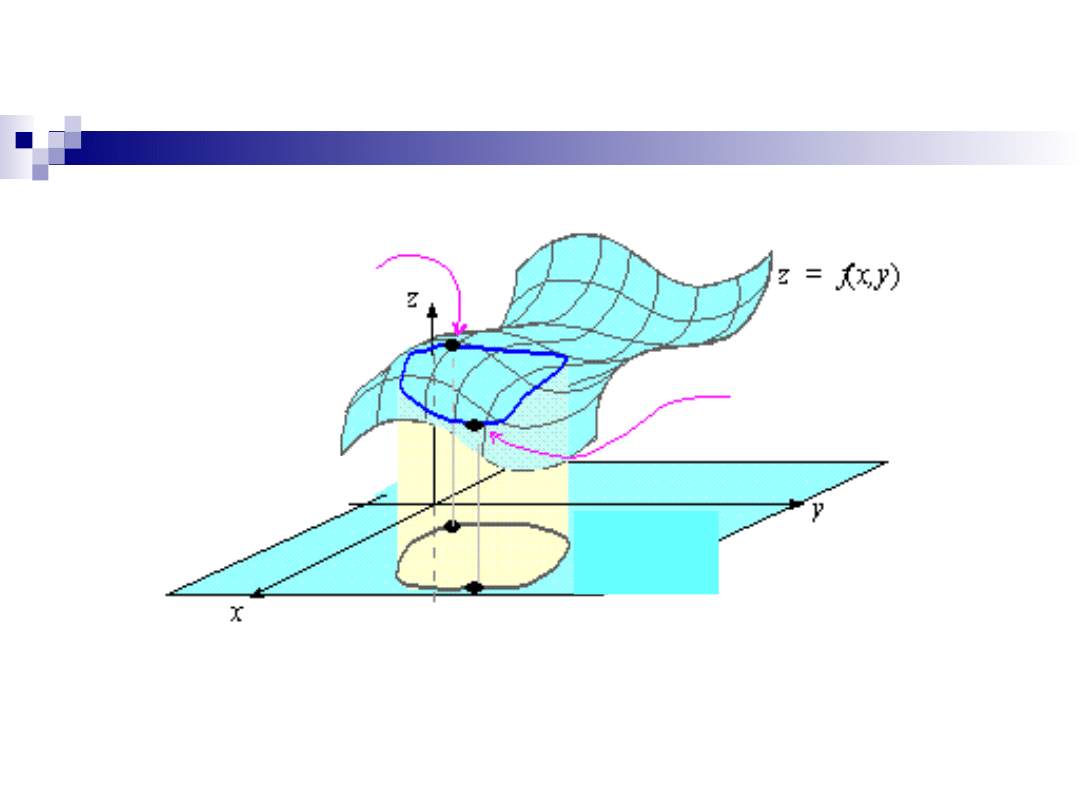
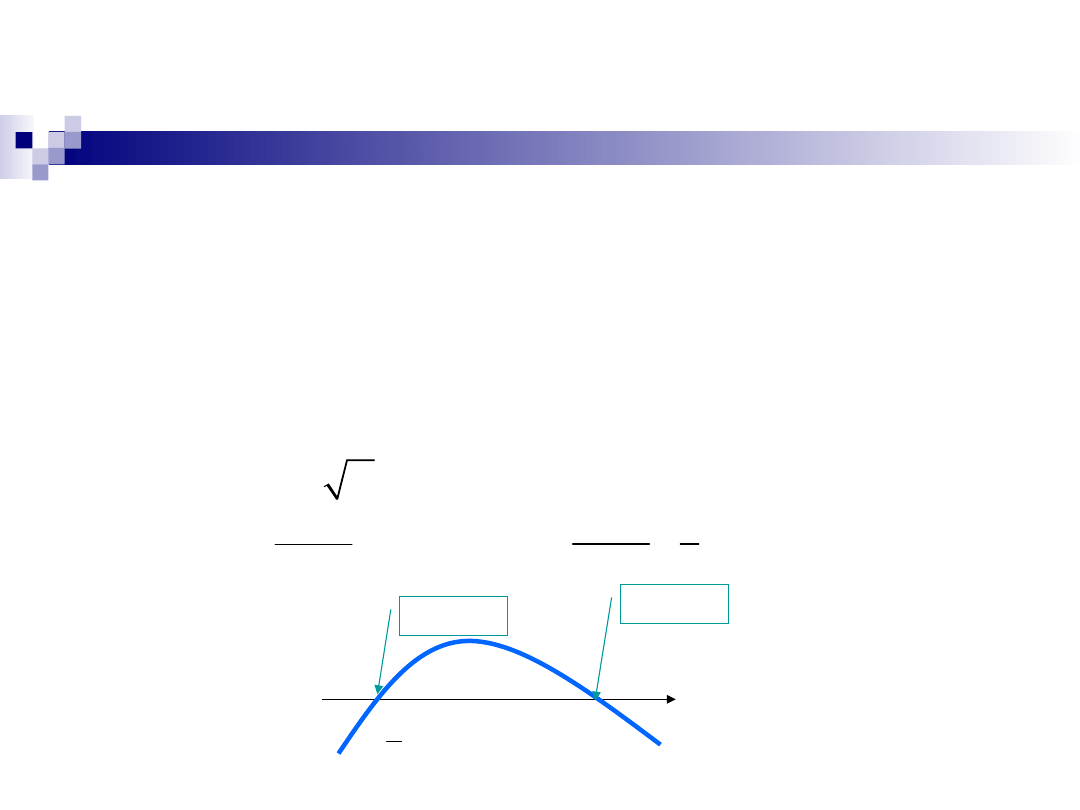
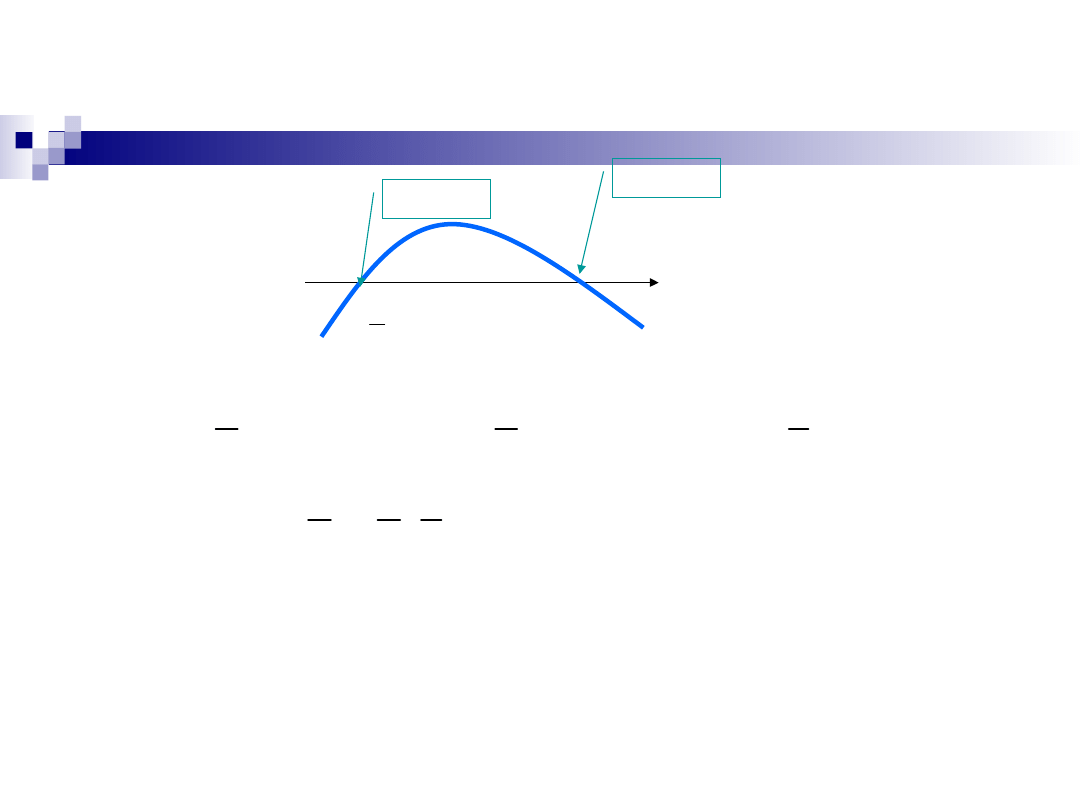
Interpretacja ekstremów

warunkowych funkcji dwóch

zmiennych

g(x,y) =
0

minimum
warunkowe

maksimum
warunkowe

Slajd nr 5 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Ekstrema warunkowe -
metody

Ekstrema warunkowe funkcji wielu zmiennych
poszukiwać można:

1. metodą eliminacji
zmiennych,

2. metodą mnożników
Lagrange'a.

Slajd nr 6 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Metoda eliminacji

Metoda eliminacji zmiennych polega na
wyznaczeniu m zmiennych z układu złożonego z m
ograniczeń i wstawieniu tych zmiennych do wzoru
badanej funkcji.

Szukanie ekstremów warunkowych sprowadza się
wówczas do szukania "zwykłych "ekstremów funkcji
n – m niewiadomych.

Slajd nr 7 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 1

2

2

( , )

2

f x y

x

y

= +

Wyznaczyć ekstrema warunkowe funkcji:

przy warunku:

3 0.

x y

+ - =

Wyznaczając zmienną y z podanego warunku
mamy y = 3 – x.

Podstawiając tę wielkość do wzoru funkcji
otrzymujemy

2

2

( ,3

)

2(3

)

f x

x

x

x

-

= +

-

Jest to funkcja jednej zmiennej, którą oznaczymy
przez F(x) i która po uporządkowaniu zapisu
przyjmie postać:

2

2

2(9 6

)

x

x x

= +

-

+

2

( ) 3

12

18.

F x

x

x

=

-

+

Slajd nr 8 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 1

2

( ) 3

12

18.

F x

x

x

=

-

+

F jest trójmianem kwadratowym, który osiąga
minimum

w punkcie wierzchołkowym

2.

2

w

b

x

a

=-

=

Ponieważ dla x = 2 mamy y = 3 – x = 1, to badana
funkcja dwóch zmiennych posiada minimum
warunkowe w punkcie P(2,1).

Slajd nr 9 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 2

3

( , )

3

f x y

x

y

= -

Wyznaczyć ekstrema warunkowe funkcji:

przy warunku:

2

0.

y x

-

=

Wyznaczając zmienną y z podanego warunku
mamy y = x

2

.

Podstawiając tę wielkość do wzoru funkcji
otrzymujemy

2

3

2

( , )

3 .

f x x

x

x

= -

Jest to funkcja jednej zmiennej, którą oznaczymy
przez F(x).

3

2

( )

3 .

F x

x

x

= -

Slajd nr 10 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 2

3

2

( )

3 .

F x

x

x

= -

/

2

( ) 3

6

F x

x

x

=

-

Gdy x = 0 oraz y = 0, to badana funkcja dwóch
zmiennych posiada maksimum warunkowe, gdy x = 2 i
y = 4 - minimum warunkowe.

3 (

2)

x x

=

-

0

2

+

_

+

max

min

2

y x

=

Slajd nr 11 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 3

2

2

( , , )

3

f x y z

x

xy y

z

= + + +

Wyznaczyć ekstrema warunkowe funkcji:

przy warunku:

3.

x y z

+ + =

Wyznaczając zmienną z z podanego warunku mamy
z = 3 – x – y.

Podstawiając tę wielkość do wzoru funkcji
otrzymujemy

2

2

( , ,3

)

9 3

3

f x y

x y

x

xy y

x

y

- -

= + + + -

-

Jest to funkcja dwóch zmiennych, którą oznaczymy
przez F(x, y).

2

2

( , )

9 3

3 .

F x y

x

xy y

x

y

= + + + -

-

Zbadamy zwykłe ekstrema funkcji F.

Slajd nr 12 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 3

2

2

( , )

9 3

3 .

F x y

x

xy y

x

y

= + + + -

-

Pochodne cząstkowe funkcji są równe:

/

( , ) 2

3,

x

F x y

x y

= + -

/

( , )

2

3.

y

F x y

x

y

= +

-

Szukamy najpierw punktów stacjonarnych – „kandydatów
na ekstrema”:

2

3 0,

2

3 0.

x y

x

y

+ - =

�

�

+

- =

�

3 2

y

x

= -

3

3

x

-

=-

2(3 2 ) 3 0

x

x

+

-

- =

1

x=

1

y =

Jedynym punktem stacjonarnym jest
P

0

(1, 1).

Slajd nr 13 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 3

/

( , ) 2

3,

x

F x y

x y

= + -

/

( , )

2

3.

y

F x y

x

y

= +

-

Hess ( , )

F x y

�

�

=�

�

�

�

2

1

1

2

=Hess (1,1)

F

2

3 0.

M = >

1

2 0,

M = >

W punkcie (1,1) pomocnicza funkcja F osiąga
minimum lokalne.

Oznacza to, że badana funkcja trzech zmiennych
w punkcie (1, 1, 1) ma minimum warunkowe.

Dla x = 1 i y = 1 z warunku ograniczającego z = 3 –
x – y =1.

Slajd nr 14 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 4

( , , )

f x y z

xyz

=

Wyznaczyć ekstrema warunkowe funkcji:

przy warunkach:

2, 3

6.

x y z

x y z

+ + =

- + =

Rozwiązując układ warunków ze względu na y i z
kolejno mamy:

2,

3

6

x y z

x y z

+ + =

�

�

- + =

�

2

,

6 3

y z

x

y z

x

+ = -

�

�

- + = -

�

Stąd po dodaniu stronami

2

8 4

z

x

= -

4 2

z

x

= -

a po odjęciu stronami

2

4 2

y

x

=- +

2

y

x

=- +

Pozwala to wyeliminować zmienną y i z ze wzoru
danej funkcji.

Slajd nr 15 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 4

1

8 4 2

6

3

x

- +

=

=

-

( ,

2,4 2 )

(

2)(4 2 )

f x x

x

x x

x

-

-

=

-

-

=

2

(4

2

8 4 )

x x

x

x

=

-

- +

=

3

2

2

8

8

x

x

x

=-

+

-

Otrzymaliśmy funkcję jednej zmiennej, którą
oznaczymy przez F(x).

3

2

( )

2

8

8

F x

x

x

x

=-

+

-

/

2

2

( )

6

16

8 2( 3

8

4)

F x

x

x

x

x

=-

+

- = -

+ -

64 48 16,

4

D= -

=

D =

2

+

_

min

max

2

( 2

8

8)

x

x

x

-

+ -

=

1

8 4

2

6

x

- -

=

=

-

_

2
3

Slajd nr 16 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 4

Gdy

3

2



x

, to

3

4

2 





x

y

oraz

3

8

2

4







x

z

2

+

_

min

max

_

2
3

W punkcie mamy do czynienia z
minimum

warunkowym wyjściowej funkcji.

)

3

8

,

3

4

,

3

2

(

1



P

Gdy

2



x

, to

0

2



x

y

oraz

0

2

4







x

z

.

W punkcie P

2

(2, 0, 0) badana funkcja posiada

maksimum warunkowe.

.

Slajd nr 17 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Metoda mnożników
Lagrange’a

Metoda mnożników Lagrange’a stosowana
jest w przypadku, gdy eliminacja zmiennych jest
niemożliwa bądź prowadzi do skomplikowanych
obliczeń.

W dalszej części zostanie zademonstrowana metoda
w przypadku poszukiwania ekstremum funkcji
dwóch zmiennych z = f(x,y) przy warunku g(x,y) =
0.

Slajd nr 18 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Metoda mnożników
Lagrange’a

Poszukiwanie ekstremów sprowadza się w tej
metodzie do badania pomocniczej funkcji
(tzw. funkcji Lagrange’a):

( , )

( , )

( , ),

L x y

f x y

g x y

l

=

+ �

gdzie



oznacza pewną stałą.

Slajd nr 19 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Załóżmy, że w pewnym zbiorze D funkcje f i g
posiadają ciągłe pochodne cząstkowe rzędu
pierwszego.

W punkcie P(x

0

,y

0

) tego zbioru może wystąpić

ekstremum warunkowe jedynie wtedy, gdy istnieje
liczba



, która wraz ze współrzędnymi tego

punktu spełnia układ równań:

Metoda mnożników
Lagrange’a



















.

0

)

,

(

,

0

)

,

(

,

0

)

,

(

0

0

0

0

/

0

0

/

y

x

g

y

x

L

y

x

L

y

x

Slajd nr 20 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Mnożniki Lagrange’a – warunek
konieczny

Z poprzedniego faktu wynika, że aby wyznaczyć
„kandydatów na ekstrema warunkowe” należy:

1. obliczyć pochodne cząstkowe funkcji Lagrange’a i
przyrównać do zera,

2. dopisać warunek ograniczający,

3. rozwiązać otrzymamy układ równań.

Slajd nr 21 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Hesjan obramowany funkcji
Lagrange’a

Hesjanem obramowanym funkcji Lagrange’a
nazywać będziemy macierz postaci:

/

/

/

//

//

/

//

//

0

x

y

x

xx

yx

y

xy

yy

g

g

g

L

L

g

L

L

�

�

�

�

�

�

�

�

�

�

�

�

Macierz ta po podstawieniach: x = x

0

, y = y

0

,



=



0

, jest macierzą liczbową, która podobnie

jak w przypadku „zwykłych ekstremów”, pozwala
rozstrzygnąć, czy w danym punkcie występuje
ekstremum warunkowe.

Slajd nr 22 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Mnożniki Lagrange’a – warunek
wystarczający

Załóżmy, że w pewnym zbiorze D funkcje f i g
posiadają ciągłe pochodne cząstkowe rzędu
drugiego oraz trójka liczb

została wyłoniona w procesie poszukiwania
kandydatów na ekstrema.

0

0

0

( , , )

x y l

Niech

/

/

/

//

//

O

0

0

/

//

//

0

Hess ( , )

x

y

x

xx

yx

y

xy

yy

g

g

L x y

g

L

L

g

L

L

�

�

�

�

D=

=�

�

�

�

�

�

�

�

będzie hesjanem obramowanym funkcji L obliczonym dla
tej trójki liczb.

Jeżeli det > 0, to w punkcie (x

0

, y

0

) funkcja z = f(x,y)

posiada maksimum przy warunku g(x,y) = 0.
Jeżeli det < 0, to w punkcie (x

0

, y

0

) funkcja z = f(x,y)

posiada minimum przy warunku g(x,y) = 0.

Slajd nr 23 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 5

3

3

( , )

f x y

x

y

= +

Wyznaczyć ekstrema funkcji

przy warunku:

2 0.

x y

+ - =

3

3

( , )

(

2)

L x y

x

y

x y

l

= + +

+ -

Tworzymy funkcję Lagrange’a

Pochodne cząstkowe funkcji są równe:

/

2

3

,

x

L

x

l

=

+

/

2

3

,

y

L

y

l

=

+

Szukamy „kandydatów na ekstrema warunkowe”
rozwiązując układ:

2

2

3

0,

3

0,

2 0

x

y

x y

l

l

� + =

�

�

+ =

�

� + - =

�

�

2

3y

l =-

2

2

3

3

x

y

-

=-

2

3x

l =-

2

2

x

y

=

lub

y x

y

x

=

=-

2

2 0

x- =

1

x =

1

y =

3

l =-

2 0

x x

- - =

sprzeczno
ść

Rozwiązaniem układu jest
trójka liczb:

0

0

0

1,

1,

3

x

y

l

=

=

=-

Slajd nr 24 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 5

/

2

3

,

x

L

x

l

=

+

/

2

3

.

y

L

y

l

=

+

O

Hess ( , )

.

L x y

�

�

�

�

D=

=�

�

�

�

�

�

6y

6x

( , )

2

g x y

x y

= + -

0

1

1

1

1

0

0

Dla trójki

0

0

0

1,

1,

3:

x

y

l

=

=

=-

0 1 1

det

1 6 0

12 0

1 0 6

D=

=-

<

W punkcie P(1, 1) występuje minimum
warunkowe.

/

/

/

//

//

/

//

//

0

x

y

x

xx

yx

y

xy

yy

g

g

g

L

L

g

L

L

�

�

�

�

�

�

�

�

�

�

�

�

Slajd nr 25 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 6

( , ) 31 4

3

f x y

x

y

= -

-

Wyznaczyć ekstrema funkcji

przy warunku:

2

2

25 0.

x

y

+ -

=

2

2

( , ) 31 4

3

(

1)

L x y

x

y

x

y

l

= -

-

+

+ -

Tworzymy funkcję Lagrange’a

Pochodne cząstkowe funkcji są równe:

/

4 2 ,

x

L

x

l

=- +

/

3 2 ,

y

L

y

l

=- +

Szukamy „kandydatów na ekstrema warunkowe”
rozwiązując układ:

2

2

4 2

0,

3 2

0,

25 0

x

y

x

y

l

l

�- +

=

�

- +

=

�

� + - =

�

3

2

y

l

=

2

2

16

9

25

4

4

l

l

+

=

4

2

x

l

=

2

25

25

4l

=

2

4

1

l =

Slajd nr 26 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 6

Rozwiązaniem układu są powyższe dwie
trójki liczb.

3

2

y

l

=

2

1

2

l =

4

2

x

l

=

1

4

x =-

2

4

1

l =

2

1

4

l =

1

1

2

l =-

1

3

y =-

2

4

x =

2

3

y =

Slajd nr 27 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 6

/

4 2 ,

x

L

x

l

=- +

/

3 2 ,

y

L

y

l

=- +

O

Hess ( , )

.

L x y

�

�

�

�

D=

=�

�

�

�

�

�

2l

2l

25

)

,

(

2

2







y

x

y

x

g

0

2x

2y

2x

2y

0

0

Przypadek 1.

Przypadek 2.

2

2

2

1

4,

3,

.

2

x

y

l

=

=

=

1

1

1

1

4,

3,

2

x

y

l

=-

=-

=-

1

0

8

6

det

8

1 0

100 0

6

0

1

-

-

D = -

-

=

>

-

-

W punkcie P

1

(-4,-3)

występuje maksimum
warunkowe.

2

0 8 6

det

8 1 0

100 0

6 0 1

D =

=-

<

W punkcie P

2

(4,3)

występuje minimum
warunkowe.

/

/

/

//

//

/

//

//

0

x

y

x

xx

yx

y

xy

yy

g

g

g

L

L

g

L

L

�

�

�

�

�

�

�

�

�

�

�

�

Slajd nr 28 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Wartości optymalne funkcji

Dowodzi się że funkcja dwóch zmiennych z =
f(x,y) ciągła na zbiorze domkniętym przyjmuje
w tym zbiorze wartość największą M
i  najmniejszą m.

Podobnie jak w przypadku funkcji jednej zmiennej
wartości optymalne funkcja może osiągnąć w
punktach wewnętrz zbioru lub na jego brzegu.

W przypadku, gdy wartość największa lub najmniejsza
osiągnięta jest w punkcie wewnętrznym zbioru, to w
punkcie występuje ekstremum lokalne, w
szczególności jest więc to punkt stacjonarny.

Jeżeli wartość największa lub najmniejsza
osiągnięta jest na brzegu, to w punkcie tym
występuje ekstremum warunkowe.

Slajd nr 29 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przypadek – brzeg obszaru złożony z
kilku linii

Aby wyznaczyć wartość największą M lub
najmniejszą m funkcji z = f(x,y) określonej
i różniczkowalnej na zbiorze domkniętym
ograniczonym D należy:

Znaleźć wszystkie punkty stacjonarne funkcji
leżące wewnątrz obszaru

Podzielić brzeg obszaru na części dające się
opisać równaniami y = p(x) lub x = r(y), gdzie x
lub y przebiega pewien przedział. Ze wzoru
funkcji z = f(x,y) wyrugować jedną zmienną
wykorzystując równanie fragmentu brzegu.

Wyznaczyć punkty stacjonarne otrzymanych
funkcji wewnątrz odpowiednich przedziałów.

Slajd nr 30 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Wyznaczyć punkty stanowiące końce rozważanych
fragmentów brzegu (zwykle są to wierzchołki).

Obliczyć wartości funkcji z = f(x,y) we wszystkich
wyznaczonych punktach.

Wybrać największą i najmniejszą wartość spośród
wszystkich otrzymanych; największa wartość to
szukana wartość M, najmniejsza - to m.

Przypadek – brzeg obszaru złożony z
kilku linii

Slajd nr 31 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 7

2

2

( , )

6

6

14

f x y

xy x

x y

y

= + -

+ -

+

Wyznaczyć największą i najmniejszą wartość
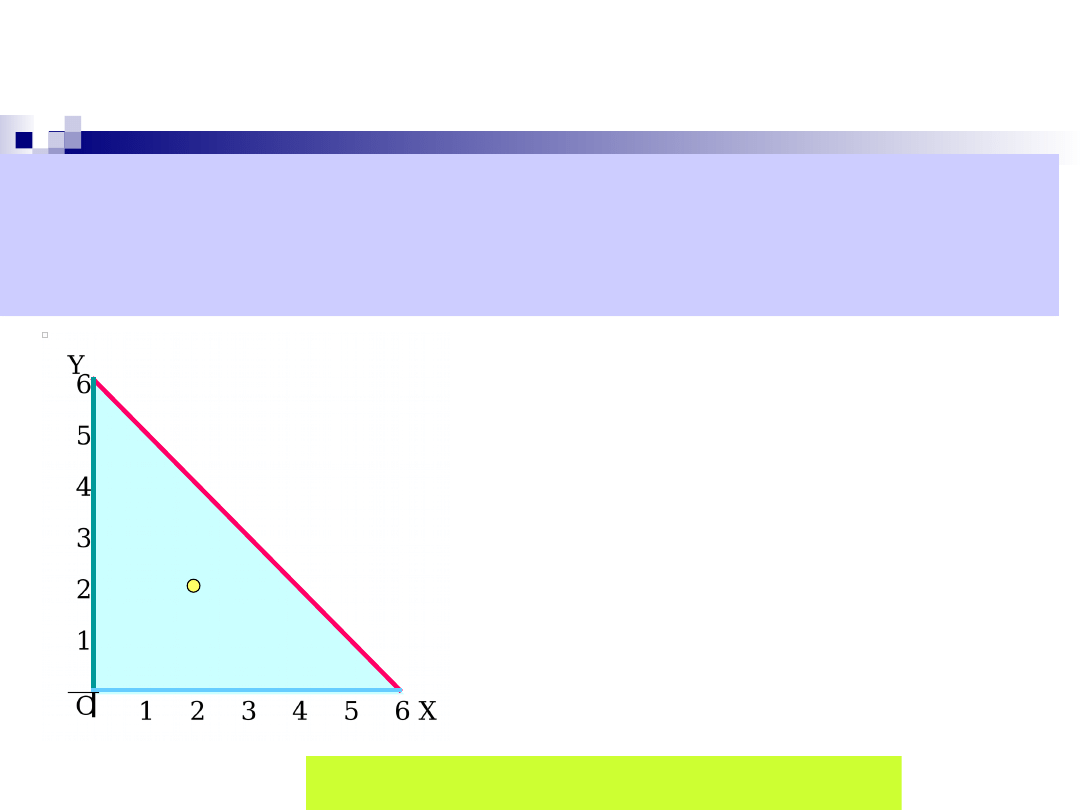
funkcji

w trójkącie D wyznaczonym przez osie układu i prostą x
+ y = 6.

A

B

C

Znajdujemy najpierw punkty
stacjonarne leżące wewnątrz
obszaru D.

/

2

6,

x

f

y

x

= + -

/

2

6.

y

f

x

y

= +

-

2

6 0,

2

6 0

y

x

x

y

+ - =

�

�

+

- =

�

6 2

y

x

= -

2(6 2 ) 6

x

x

+

-

=

3

6

x

-

=-

2

x=

6 4 2

y = - =

P

1

(2,2)

Punkt P

1

(2,2) leży wewnątrz

obszaru.

Slajd nr 32 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 7

A

B

C

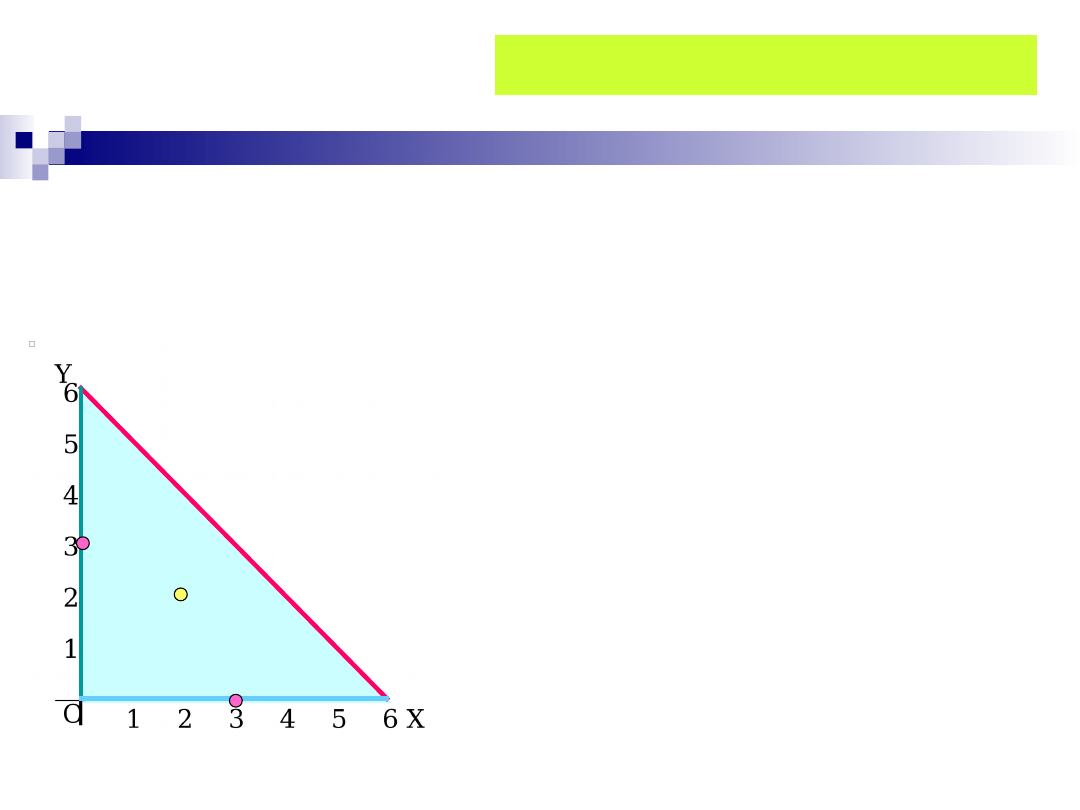
Na (niebieskim) odcinku AB
mamy:

0, 0

6

y

x

=

� �

2

( )

( ,0)

6

14

m x

f x

x

x

=

= -

+

/

( ) 2

6

m x

x

= -

2

6 0

x- =

3

x =

0

y =

P

1

(2,2)

Punkt P

2

(3,0) leży wewnątrz odcinka.

P

2

(3,0)

Na (zielonym) odcinku AC mamy:

0, 0

6

x

y

=

� �

2

( )

(0, )

6

14

n y

f

y

y

y

=

=

-

+

/

( ) 2

6

n y

y

=

-

2

6 0

y- =

3

y =

0

x=

Zbadamy teraz funkcję
na odcinkach AB, AC,
BC.

P

3

(0,3)

Punkt P

3

(0,3) leży wewnątrz odcinka.

2

2

( , )

6

6

14

f x y

xy x

x y

y

= + -

+ -

+

Slajd nr 33 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 7

A

B

C

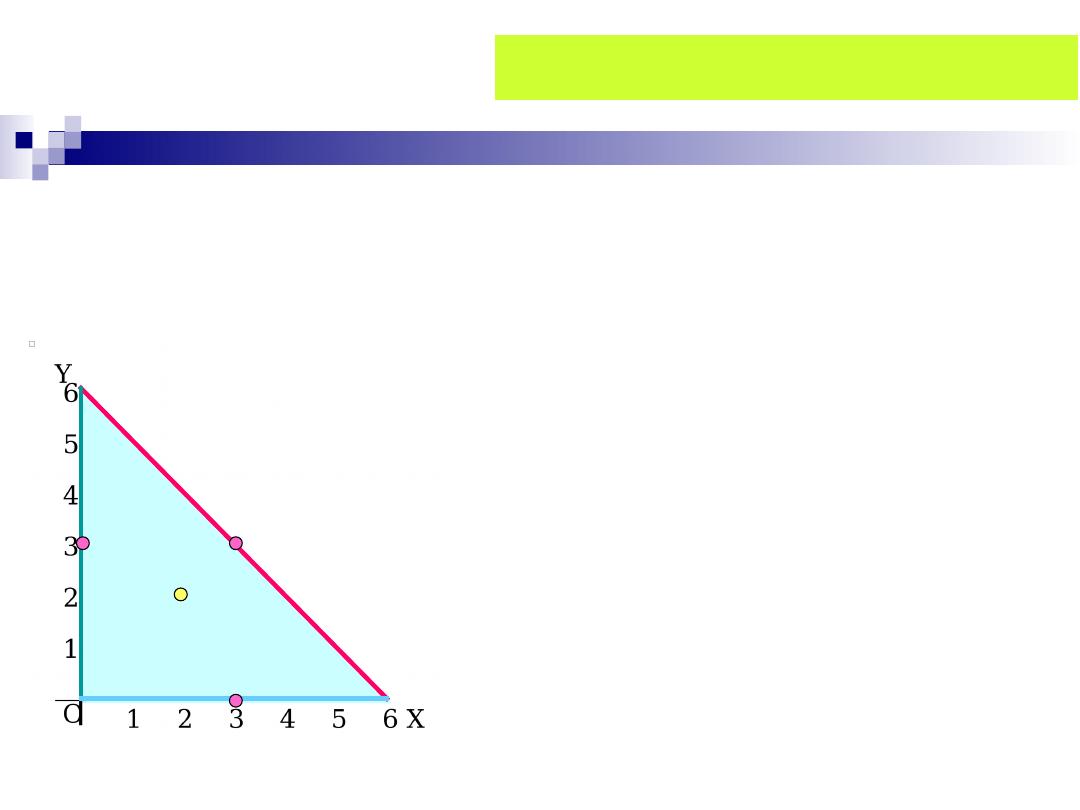
Na (czerwonym) odcinku BC
mamy:

6

, 0

6

y

x

x

= -

� �

2

2

( )

( ,6

)

(6

)

6

(6

)

6(6

) 14

p x

f x

x

x

x

x

x

x

x

=

-

=

-

+ -

+ -

-

-

+

2

2

2

( ) 6

6

36 12

36 6

14

p x

x x

x

x

x x

x

= -

+ -

+ -

+ -

+ +

2

( )

6

14

p x

x

x

= -

+

P

1

(2,2)

P

2

(3,0)

/

( ) 2

6

p x

x

= -

2

6 0

x- =

3

x=

6 3 3

y = - =

P

3

(0,3)

Punkt P

4

(3,3) leży wewnątrz odcinka.

2

2

( , )

6

6

14

f x y

xy x

x y

y

= + -

+ -

+

P

4

(3,3)

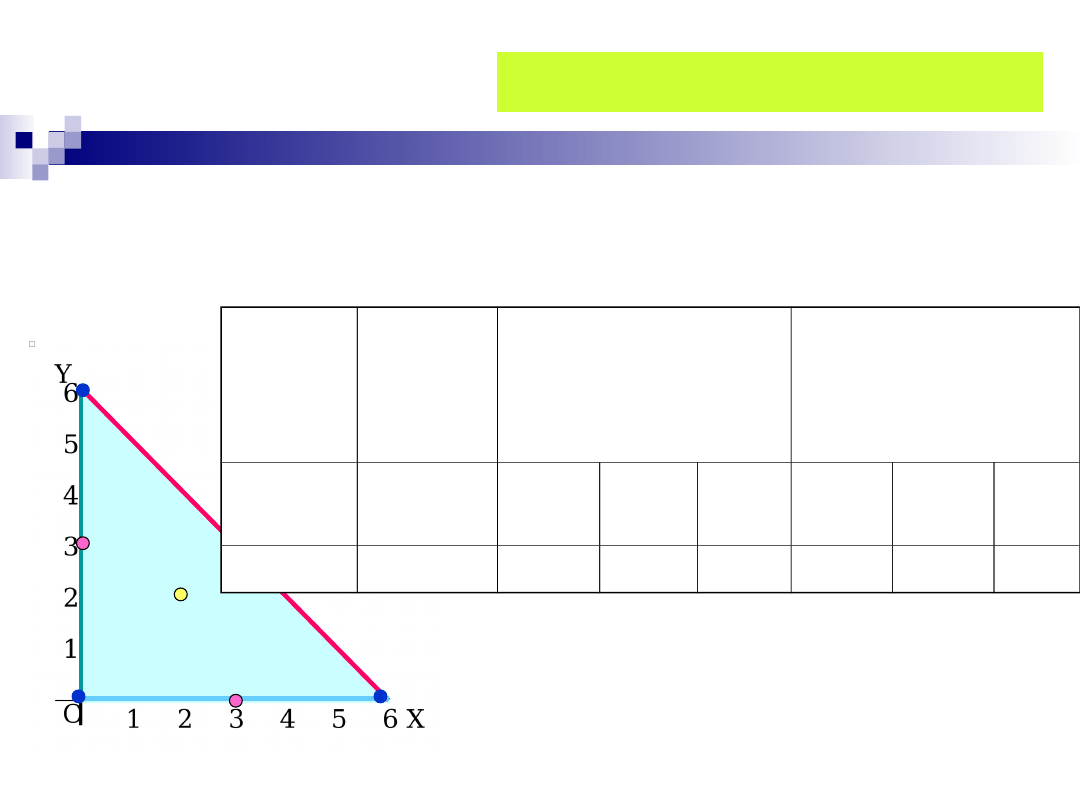
Slajd nr 34 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 7

A

B

C

P

1

(2,2)

P

2

(3,0)

P

3

(0,3)

W rozważaniach należy jeszcze uwzględnić
wierzchołki obszaru, będące końcami
odpowiednich odcinków.

P

4

(3,3)

P

5

(0,0)

P

6

(6,0)

P

7

(0,6)

Pkt.we

w.

obszar

u

Pkty stacjonarne

na brzegu

Wierzchołki

Współr

z.

(2,2)

(3,0) (0,3) (3,3) (0,0) (6,0) (0,6

)

f(x,y) =

2

2

( , )

6

6

14

f x y

xy y

x y

y

= + -

+ -

+

2

5

5

5

14

14 14

Wartość najmniejszą m = 2
funkcja osiąga w punkcie (2,
2).

Wartość największą M = 14
funkcja osiąga w punktach (0,
0), (6,0), (0,6).

Slajd nr 35 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Slajd nr 36 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

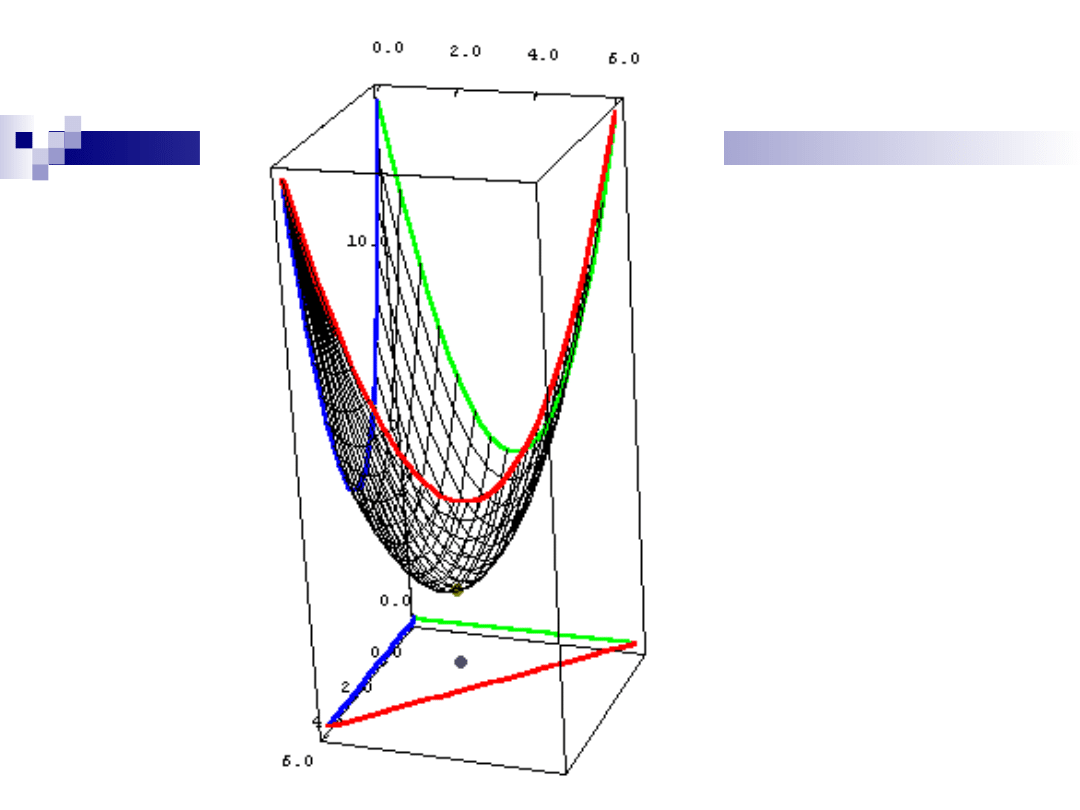
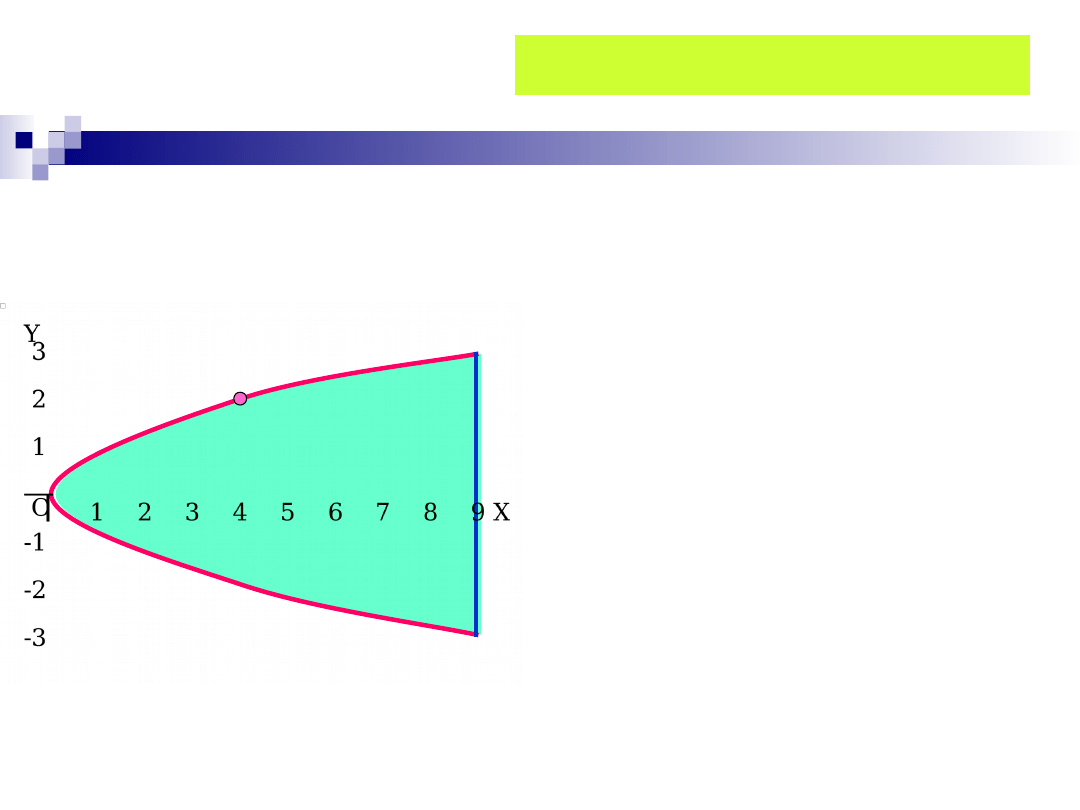
Przykład 8

2

2

( , )

2

2

32

60

f x y

x

x

y

y

= -

+

-

+

Wyznaczyć największą i najmniejszą wartość
funkcji

w zbiorze D ograniczonym parabolą x = y

2

i prostą

x = 9.

A

B

Znajdujemy najpierw
punkty stacjonarne
leżące wewnątrz obszaru
D.

/

2

2,

x

f

x

= -

/

4

32.

y

f

y

=

-

2

2 0,

4

32 0

x

y

- =

�

�

-

=

�

1

x=

8

y =

Punkt P(1,8) leży poza
obszarem.

Slajd nr 37 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 8

Zbadamy teraz funkcję na łuku AB paraboli i
odcinku AB.

A

B

Punkt P(8,9) leży poza
odcinkiem.

Na (niebieskim) odcinku AB
mamy:

9,

3

3

x

y

=

- � �

2

( )

(9, ) 81 18 2

32

60

m y

f

y

y

y

=

= -

+

-

+

2

( ) 2

32 123

m y

y

y

=

-

+

/

( ) 4

32

m y

y

= -

8

y =

4

32 0

y-

=

9

x=

2

2

( , )

2

2

32

60

f x y

x

x

y

y

= -

+

-

+

Slajd nr 38 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

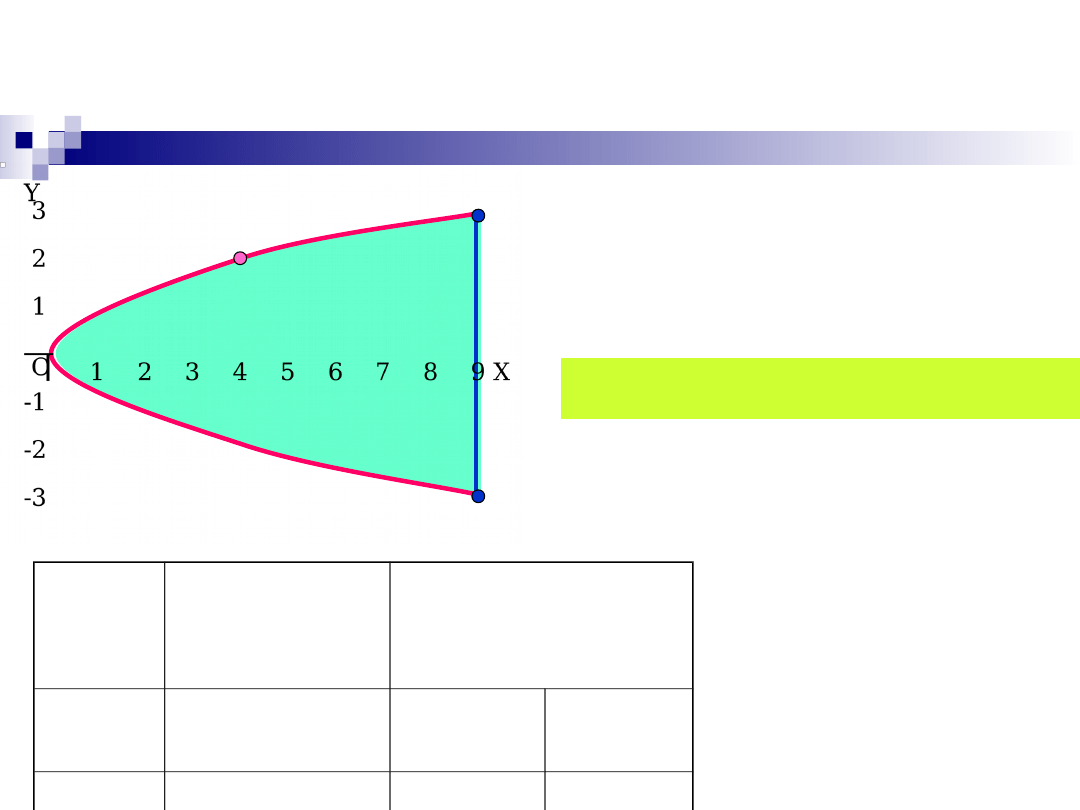
Przykład 8

A

B

Punkt P

1

(4,2) leży

wewnątrz łuku.

Na (czerwonym) łuku AB
mamy:

2

,

3

3

x y

y

=

- � �

2

4

2

2

( )

( , )

2

2

32

60

n y

f y y

y

y

y

y

=

= -

+

-

+

4

( )

32

60

n y

y

y

= -

+

/

3

( ) 4

32

n y

y

=

-

3

8

y =

3

4

32 0

y -

=

2

y =

4

x =

P

1

(4,2)

2

2

( , )

2

2

32

60

f x y

x

x

y

y

= -

+

-

+

Slajd nr 39 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

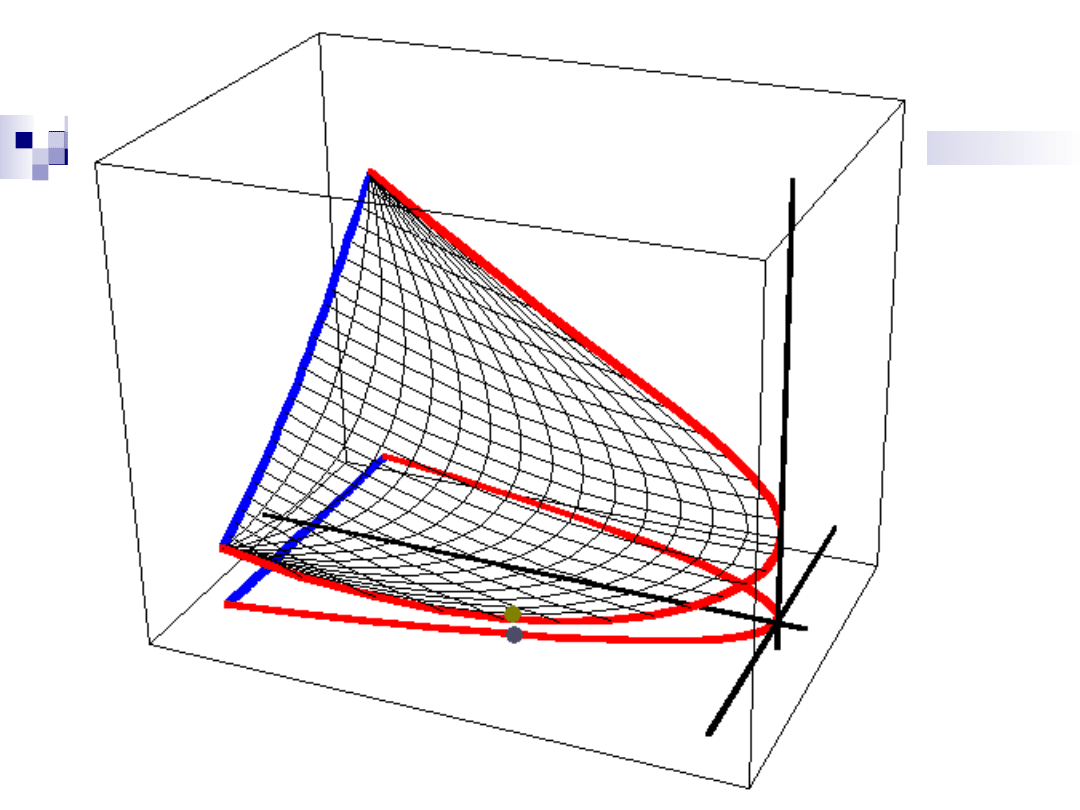
Przykład 8

W rozważaniach musimy
jeszcze uwzględnić
wierzchołki.

A

B

P

1

(4,2)

P

2

(9,-

3)

P

3

(9,3)

Pkty

stacjonarne

na brzegu

Wierzchołki

Współr
z.

(4,2)

(9,-3)

(9,3)

f(x,y)

=

12

23
7

45

2

2

( , )

2

2

32

60

f x y

x

x

y

y

= -

+

-

+

Wartość
najmniejszą m
= 12 funkcja
osiąga w punkcie
(4, 2).

Wartość
największą M =
237 funkcja osiąga
w punkcie (9, -3).

Slajd nr 40 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Slajd nr 41 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przypadek – brzeg obszaru złożony z
jednej linii

Aby wyznaczyć wartość największą M lub
najmniejszą m funkcji z = f(x,y) określonej
i różniczkowalnej na zbiorze domkniętym
ograniczonym D należy:

Znaleźć wszystkie punkty stacjonarne funkcji
leżące wewnątrz obszaru.

Utworzyć funkcję Lagrange’a i znaleźć jej punkty
stacjonarne.

Obliczyć wartości funkcji z = f(x,y) we wszystkich
wyznaczonych punktach.

Wybrać największą i najmniejszą wartość spośród
wszystkich otrzymanych; największa wartość to
szukana wartość M, najmniejsza - to m.

Slajd nr 42 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 9

2

2

( , )

4

3

z f x y

x

y

x

y

=

= + -

-

Wyznaczyć największą i najmniejszą wartość
funkcji

w kole D wyznaczonym przez nierówność x

2

+ y

2

 25:

Znajdujemy najpierw punkty
stacjonarne leżące wewnątrz
obszaru D.

/

2

4,

x

f

x

= -

/

2

3.

y

f

y

=

-

2

4 0,

2

3 0

x

y

- =

�

�

- =

�

2

x=

3
2

y =

3
2

(2, )

P

Punkt leży wewnątrz
obszaru.

3
2

(2, )

P

Slajd nr 43 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 9

Badanie funkcji na brzegu sprowadza się do
wyznaczenia ekstremów funkcji

przy warunku:

2

2

25 0

x

y

+ -

=

2

2

2

2

( , )

4

3

(

25).

L x y

x

y

x

y

x

y

l

= + -

-

+

+ -

Przeprowadzimy je metodą mnożników
Lagrange’a:

Pochodne cząstkowe funkcji są równe:

/

2

4 2 ,

x

L

x

x

l

= - +

/

2

3 2 .

y

L

y

y

l

=

- +

Szukamy punktów stacjonarnych
rozwiązując układ:

2

2

2

4 2

0,

2

3 2

0,

25 0

x

x

y

y

x

y

l
l

� - +

=

�

- +

=

�

� + - =

�

3

2 2

y

l

=

+

2

2

4

3

(

)

(

)

25

2 2

2 2

l

l

+

=

+

+

4

2 2

x

l

=

+

2

2

( , )

4

3

z f x y

x

y

x

y

=

= + -

-

Slajd nr 44 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 9

3

2 2

y

l

=

+

2

2

4

3

(

)

(

)

25

2 2

2 2

l

l

+

=

+

+

4

2 2

x

l

=

+

2

2

16

9

25

(2 2 )

(2 2 )

l

l

+

=

+

+

2

25

25

(2 2 )

l

=

+

2

(2 2 )

1

l

+

=

1

1

2

l =-

2

3
2

l =-

1

4

x =

2 2

1 lub 2 2

1

l

l

+

=

+

=-

Punktami, które należy uwzględnić w
badaniu są:

1

2

(4,3) i

( 4, 3).

P

P - -

1

3

y =

2

4

x =-

2

3

y =-

Slajd nr 45 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe

Przykład 9

Pkty

stacjonarne

wewn.

obszaru

Pkty stacjonarne

funkcji

Lagrange’a

Współr
z.
f(x,y)

=

0

(4, 3)

50

2

2

( , )

4

3

z f x y

x

y

x

y

=

= + -

-

Wartość największą M = 50 funkcja osiąga w
punkcie (-4, -3).

3

(2, )

2

(-4,

-3)

25

4

-

Wartość najmniejszą funkcja osiąga w
punkcie .

3

(2, )

2

25

4

m=-

Slajd nr 46 / 46

Tomasz Kowalski. Matematyka. Wykład 28: Ekstrema warunkowe