IX Ekstrema lokalne, warunek konieczny i warunki dostateczne istnienia ekstremów lokalnych.
Definicja
Niech ![]()
oraz funkcja ![]()
. Punkt ![]()
nazywać będziemy:
a). minimum lokalnym (max) funkcji f, gdy
![]()
b). właściwym minimum lokalnym (max) funkcji f, gdy
![]()
e). punktem stacjonarnym (krytycznym) funkcji f, gdy istnieją pochodne cząstkowe funkcji f w punkcie x* i spełniony jest warunek:
![]()
.
Twierdzenie (w-k konieczny dla jednej zmiennej)
Jeżeli ![]()
klasy ![]()
osiąga ekstremum w punkcie ![]()
, to ![]()
.
Twierdzenie (w-k dostateczny)
Jeśli ![]()
klasy ![]()
spełnia następujące warunki:
1). ![]()
2). ![]()
zmienia znak w otoczeniu punktu ![]()
wtedy f ma w ![]()
ekstremum lokalne właściwe.
( z - na + to jest minimum lokalne, a z + na - maximum lokalne).
Twierdzenie (II w-k dostateczny )
Jeżeli ![]()
klasy ![]()
spełnia następujące warunki:
1). ![]()
2). ![]()
to funkcja f ma ekstremum lokalne właściwe w ![]()
( jeżeli ![]()
- min, a jeśli ![]()
- max)
(jeżeli kolejna pochodna jest parzysta i jest różna od zera to jest ekstremum, a jak jest nieparzysta to mamy punkt przegięcia)
Twierdzenie (w-k konieczny dla wielu zmiennych)
Niech ![]()
oraz ![]()
. Jeżeli ![]()
jest punktem w którym funkcja f osiąga ekstremum lokalne, to f posiada pochodną cząstkową w punkcie x*
![]()
.
Twierdzenie (w-k wystarczający dla wielu zmiennych)
Załóżmy, że ![]()
ma wszystkie pochodne cząstkowe rzędu drugiego, ciągła w punkcie ![]()
oraz, że ![]()
. Wówczas
1). Jeśli ![]()
dla ![]()
, to f ma w punkcie a minimum lokalne właściwe
2). Jeśli ![]()
dla ![]()
, to f ma w punkcie maksimum lokalne właściwe.
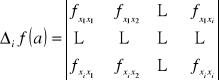
Wyszukiwarka
Podobne podstrony:
zagadnienia, punkt 8, VIII Warunek konieczny różniczkowalności
zagadnienia, punkt 14, XIV Twierdzenie o lokalnej odwracalności odwzorowań klasy C1
zagadnienia, punkt 19, XIX Macierze, działania, rząd macierzy
zagadnienia, punkt 5, V Punkt skupienia zbioru
zagadnienia, punkt 18, XVIII Przestrzenie liniowe
zagadnienia, punkt 2, II Przestrzenie metryczne zupełne
zagadnienia, punkt 6, VI Własności funkcji ciągłych na zbiorach zwartych (tw
zagadnienia, punkt 22, XXII Działania wewnętrzne, działania przemienne, działania łączne, element ne
zagadnienia, punkt 7, VII Pojęcie pochodnej w punkcie funkcji jednej zmiennej - interpretacja fizycz
zagadnienia, punkt 24, XXIV Centralne twierdzenie graniczne Lindeberga-Levy'ego
zagadnienia, punkt 24, XXIV Centralne twierdzenie graniczne Lindeberga-Levy'ego
zagadnienia, punkt 15, XV Ciała i sigma-ciała zbiorów
zagadnienia, punkt 20, XX Przekształcenia liniowe i podstawowe ich własności
Warunki konieczne, Warunki konieczne
zagadnienia, punkt 12, XII Ciągi i szeregi funkcyjne - zbieżność punktowa i jednostajna
zagadnienia, punkt 13, XIII Pochodna kierunkowa, pochodne cząstkowe, pochodna mocna
zagadnienia, punkt 21, XXI Przekształcenia liniowe przestrzeni skończenie wymiarowych
zagadnienia, punkt 11, XI Całka oznaczona funkcji ograniczonej na [a,b]
Zagadnienia wymagane na teście z Lokalnych Sieci Komputerowych
więcej podobnych podstron