XII Ciągi i szeregi funkcyjne - zbieżność punktowa i jednostajna. Kryterium jednostajnej zbieżności szeregów funkcyjnych. Ciągłość, różniczkowalność i całkowalność granicy ciągu funkcyjnego i sumy szeregu funkcyjnego. Szeregi potęgowe - definicja, przykłady.

Definicja

Niech E będzie ustalonym zbiorem. Ciąg
funkcji
,
, nazywamy ciągiem funkcyjnym. Jeśli

(*)
dla

to ciąg funkcyjny
nazywamy szeregiem funkcyjnym o wyrazie ogólnym f_n i oznaczamy przez
.

Definicja

Niech
,
oraz

a). mówimy, że ciąg funkcyjny (f_n) jest punktowo zbieżny na zbiorze E do funkcji f, gdy warunek
zachodzi dla każdego
, tzn. gdy

Zapisujemy
. Funkcję f nazywamy granicą punktową ciągu f_n.

b). mówimy, że ciąg funkcyjny (f_n) jest jednostajnie zbieżny na zbiorze E do funkcji f, gdy

Zapisujemy
. Funkcję f nazywamy granicą jednostajną.

c). mówimy, że szereg funkcyjny
jest punktowo (jednostajnie) zbieżny na E, gdy ciąg funkcyjny
dany wzorem (*) jest punktowo (jednostajnie) zbieżny na E. Granicę ciągu (s_n) oznaczamy przez
i nazywamy suma danego szeregu.

Twierdzenie

Ciąg funkcyjny
,
jest zbieżny do funkcji

gdy ciąg liczbowy
dany wzorem
jest zbieżny do zera.

Twierdzenie (Cauchy'ego - jednostajny w-k)

Niech
,
. Ciąg (f_n) jest zbieżny jednostajnie na E
spełnia on jednostajny w-k Cauchy'ego :

.

Twierdzenie Weierstrassa

Niech
,
. Załóżmy, że
przy czym szereg liczbowy
jest zbieżny. Wtedy szereg funkcyjny
jest zbieżny na E.

Przykład

zatem
więc szereg jest zbieżny jako szereg harmoniczny więc szereg
z kryterium Weierstrassa jest zbieżny.

Twierdzenie Diniego

Niech E będzie p-nią metryczną zwartą i niech
będzie ciągiem funkcji ciągłych
,
zbieżnym punktowo i monotonicznie na E do funkcji ciągłej
.

Wtedy ciąg
jest jednostajnie zbieżny do f na E.

Twierdzenie

Załóżmy, że funkcje
,
są całkowalne w sensie Riemanna na [a,b] oraz ciąg (f_n) jest jednostajnie zbieżny na [a,b] do funkcji
. Wtedy funkcja f jest całkowalna w sensie Riemanna na [a,b], ciąg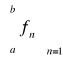
jest zbieżny oraz

.

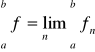
Twierdzenie

Niech (f_n) będzie ciągiem funkcji rzeczywistych różniczkowalnych na [a,b]. Załóżmy, że

1). Ciąg liczbowy
jest zbieżny dla pewnego punktu

2). Ciąg funkcyjny
jest jednostajnie zbieżny na [a,b]

Wtedy ciąg (f_n) jest jednostajnie zbieżny na [a,b] do pewnej funkcji
, która jest różniczkowalna na [a,b] i spełnia równość

.

Wniosek (różniczkowanie szeregu wyraz po wyrazie)

Niech dany będzie szereg funkcyjny
, gdzie funkcja
są różniczkowalne na
. Załóżmy, że szereg liczbowy
jest zbieżny do pewnego punktu
i szereg liczbowy
jest jednostajnie zbieżny na
.

Wtedy szereg
jest jednostajnie zbieżny na
oraz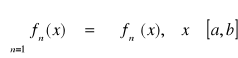
.

Definicja

Niech
oraz niech dany będzie ciąg liczbowy
Szereg funkcyjny postaci
nazywamy szeregiem potęgowym. Liczby a_n,
nazywamy współczynnikami danego szeregu.

Lemat Abela

Jeżeli szereg potęgowy
jest zbieżny w punkcie
, to

a). jest bezwzględnie zbieżny dla

b). jest jednostajnie zbieżny na każdym przedziale (-p,p), gdzie p jest dowolną liczbą spełniającą w-k
.

Twierdzenie Cauchy'ego-Hadamarda

Niech dany będzie szereg potęgowy
. Przyjmijmy
oraz

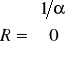
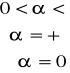
. Wtedy szereg
jest bezwzględnie zbieżny dla
oraz rozbieżny dla
.

Twierdzenie d'Alemberta

Niech dany będzie szereg potęgowy
, gdzie
dla n=1,2,…Załóżmy, że istnieje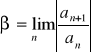
. Niech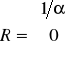

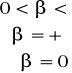
. Wtedy szereg
jest bezwzględnie zbieżny dla
oraz rozbieżny dla
.

Definicja

a). liczbę R>0 taka, że szereg potęgowy
jest zbieżny w przedziale (-R,R), zaś rozbieżny w zbiorze
nazywamy promieniem zbieżności.

b). przedział (-R,R) nazywa się przedziałem zbieżności danego szeregu. Jeżeli szereg jest zbieżny tylko w punkcie 0 to przyjmujemy R=0, zaś jeżeli szereg jest zbieżny na całym zbiorze R to przyjmujemy
.

Twierdzenie (o jednostajnej zbieżności szeregu)

Załóżmy, że (-R,R) jest przedziałem zbieżności szeregu potęgowego
. Wtedy dla każdej liczby
dany szereg jest jednostajnie zbieżny na przedziale [-r,r]. Ponadto suma szeregu
jest funkcją różniczkowalną (więc także ciągłą) na (-R,R) oraz

.

---