XI Całka oznaczona funkcji ograniczonej na [a,b]. Własności funkcji całkowalnych w sensie Riemanna. Twierdzenie o funkcji górnej granicy całkowania. Twierdzenie o wartości średniej dla całek.
Niech dany będzie przedział [a,b] oraz ![]()
. Rozważmy punkty ![]()
takie, że
![]()
.
![]()
- podział przedziału [a,b]
![]()
![]()
![]()
- średnica
![]()
- i-ty punkt pośredni
Definicja
Niech f będzie funkcją ograniczoną na [a,b]. Całkę oznaczoną Riemanna funkcji f na [a,b] definiujemy następująco:
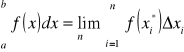
.
Twierdzenie (liniowość całki)
Niech ![]()
oraz ![]()
. Jeśli f,g są całkowalne na [a,b], to
a). 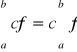
b). 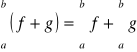
.
Twierdzenie (monotoniczność całki)
Jeśli funkcje rzeczywiste ![]()
są całkowalne w sensie Riemanna na [a,b] oraz ![]()
dla każdego ![]()
, to 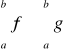
.
Twierdzenie (addytywność względem przedziału)
Niech ![]()
i ![]()
. Jeżeli f jest całkowalna na [a,b], to
(*) 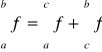
.
Twierdzenie
Niech ![]()
jest całkowalna na [a,b], to 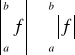
.
Twierdzenie (o równości całek)
Jeżeli ![]()
jest całkowalna na [a,b] oraz funkcja g różni się tylko od funkcji f w skończonej liczbie punktów tego przedziału, to funkcja g jest całkowalna na [a,b] oraz
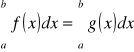
.
Twierdzenie (Newtona-Leibniza)
Jeżeli f jest całkowalna na [a,b] oraz f jest funkcją pierwotną f na [a,b], to
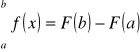
.
Twierdzenie (o funkcji górnej granicy całkowania)
Niech ![]()
całkowalna na [a,b]. Określmy funkcję górnej granicy całkowania wzorem
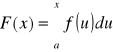
dla ![]()
Wówczas
a). funkcja F spełnia warunek Lipschitza na [a,b](zatem jest jednostajnie ciągła na [a,b]).
b). jeśli funkcja f jest ciągła w punkcie ![]()
to funkja F jest różniczkowalna w x0 oraz ![]()
.
Warunek Lipschitza
Niech ![]()
. Mówimy, że funkcja f spełnia w-k Lipschitza ze stałą C>0, gdy
![]()
.
Twierdzenie (o wartości średniej dla całek)
Załóżmy, że ![]()
jest funkcją ciągłą, zaś funkcja g jest całkowalna w sensie Riemanna na [a,b] oraz nieujemna na [a,b] lub niedodatnia na [a,b]. Wówczas
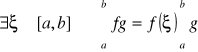
.
Wyszukiwarka
Podobne podstrony:
zagadnienia, punkt 7, VII Pojęcie pochodnej w punkcie funkcji jednej zmiennej - interpretacja fizycz
18 rachunek calkowy 5 5 calka riemanna funkcji ograniczonej
10 11 wyklad calka oznaczonaid Nieznany (2)
zagadnienia, punkt 10, X Funkcja pierwotna, całka nieoznaczona
zagadnienia, punkt 6, VI Własności funkcji ciągłych na zbiorach zwartych (tw
matma, CAŁKA OZNACZONA = liczba, CAŁKA NIEOZNACZONA = funkcja
Calka oznaczona
RACHUNEK CAŁKOWY. CAŁKA OZNACZONA I JEJ ZASTOSOWANIA, SZKOŁA, Matematyka, Matematyka
Przed maturą Zestaw XI Ciągłość i pochodna funkcji
calka oznaczona Wronicz id 1079 Nieznany
Calka oznaczona zadania
Zestaw 9 Całka oznaczona, pole obszaru, całka niewłaściwa
całka oznaczona
public relations, public reletions (11 str), PUBLIC RELATIONS- funkcja zarządzania, która nawiązuje
zagadnienia, punkt 19, XIX Macierze, działania, rząd macierzy
zagadnienia, punkt 5, V Punkt skupienia zbioru
więcej podobnych podstron