
Matematyka
sem. II
Całka Riemanna funkcji
jednej zmiennej.
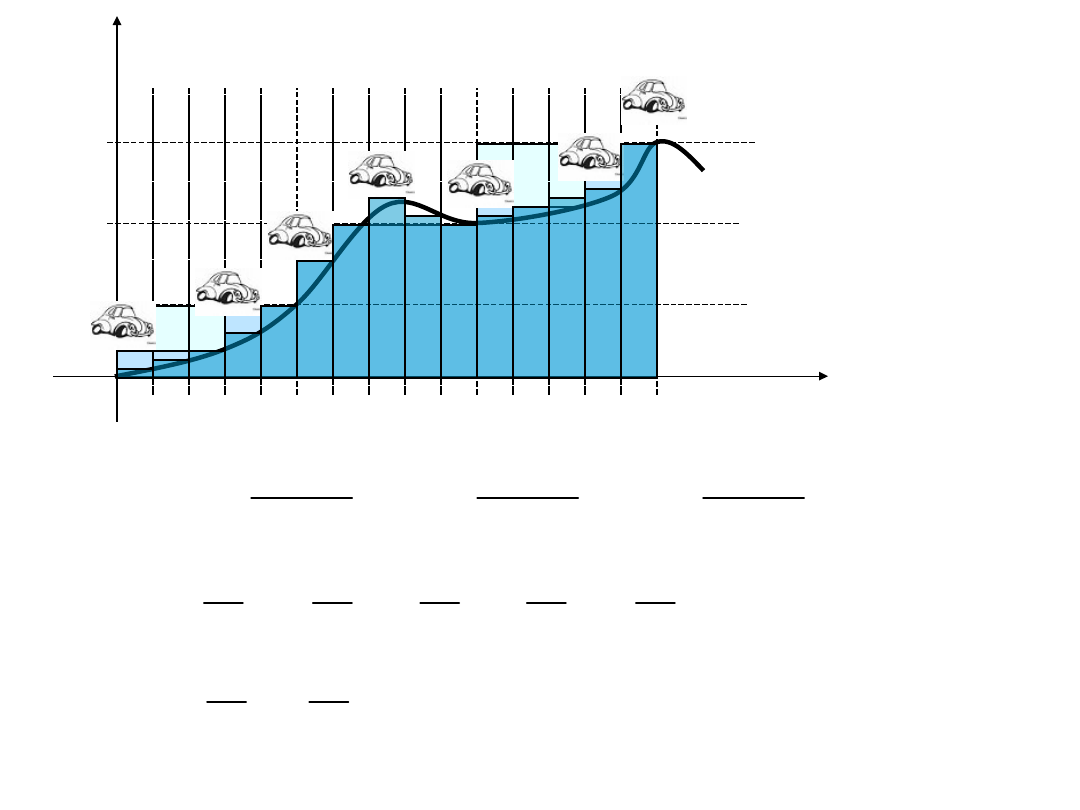
t
1
5
10
15
30
60
90
v
km
15
min
60
km
90
min
5
min
60
km
60
min
5
min
60
km
30
min
5
1
s
km
13
60
90
2
60
70
3
60
60
5
60
30
2
60
10
3
2
s
?
...
1
60
10
1
60
5
1
3
s
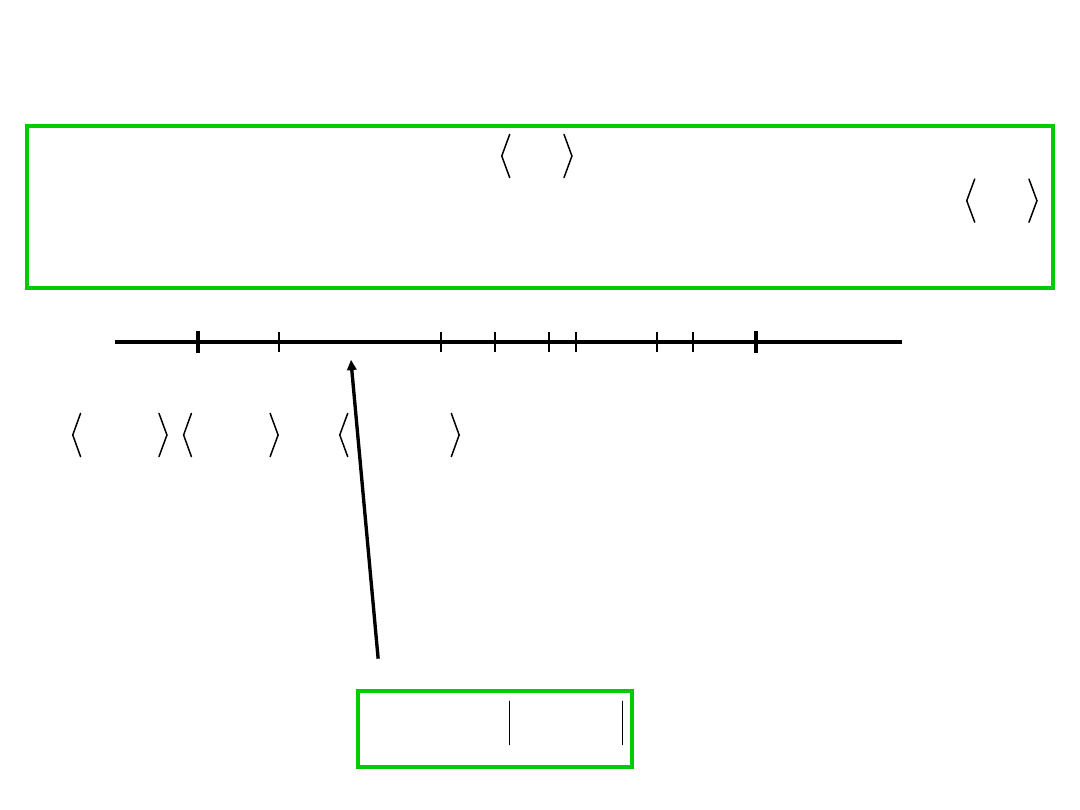
1. Podstawowe definicje
b
a,
}
,...,
,
{
1
0
n
x
x
x
X
b
x
x
x
x
x
a
n
n
1
2
1
0
...
a
b
=x
0
x
1
x
2
x
n-1
=x
n
n
n
x
x
x
x
x
x
,
,....,
,
,
,
1
2
1
1
0
przedziały częściowe
Można wykonać wiele podziałów odcinka <a,b> na
n podziałów częściowych.
W każdym podziale można znaleźć przedział
częściowy o największej długości. Długość tego
przedziału nazywamy
średnicą
podziału:
1
,...,
2
,
1
max
i
i
n
i
x
x
d
Niech dany będzie przedział . Mówimy, że zbiór
punktów wynacza
podział
przedziału jeżeli:
b
a,
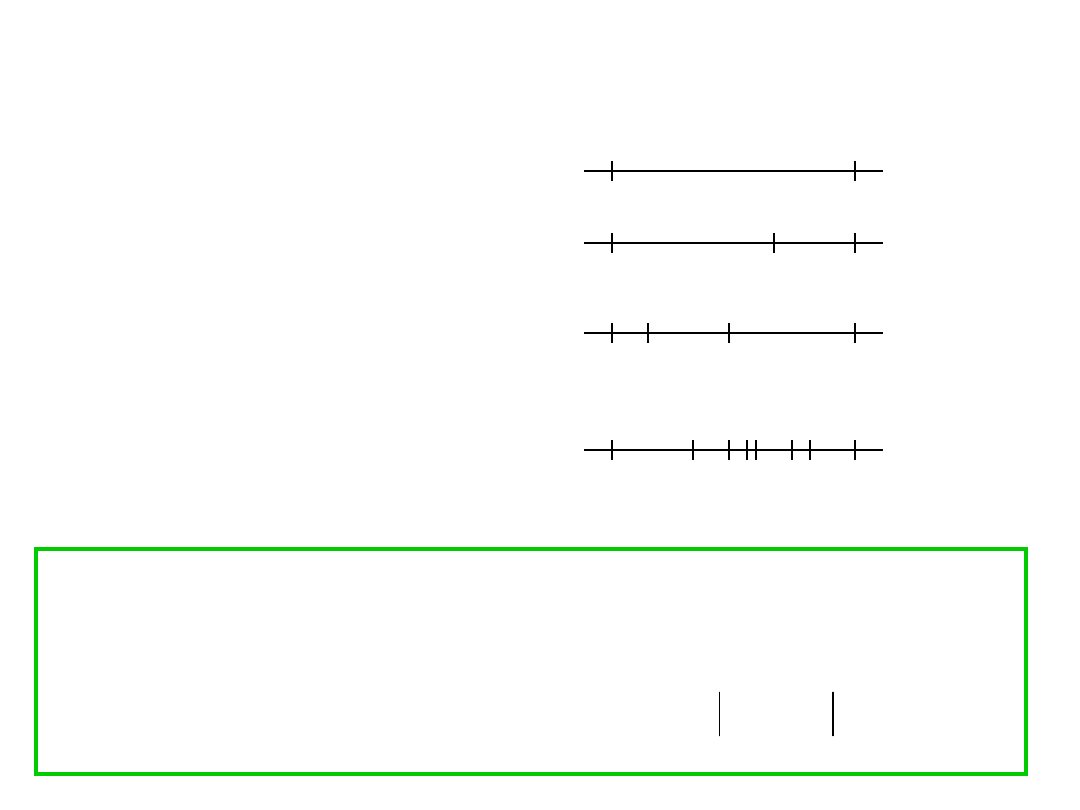
Można utworzyć ciągi podziałów, w których
elementami będą podziały na coraz większą liczbę
przedziałów częściowych.
a
b=x
1
x
1
a
b=x
2
x
2
a
b=x
3
x
1
x
n-1
a
b=x
n
x
1
x
2
.................................... .......
...........
}
,
{
1
0
1
b
x
a
x
X
}
,
,
{
2
1
0
2
b
x
x
a
x
X
}
,
,
,
{
3
2
1
0
3
b
x
x
x
a
x
X
}
,
,...,
,
,
{
1
2
1
0
b
x
x
x
x
a
x
X
n
n
n
.................................... .......
...........
Ciąg podziałów X
n
przedziału <a,b> nazywamy
normalnym
ciągiem podziałów, jeżeli średnice
kolejnych podziałów maleją do zera, czyli
1
,...,
2
,
1
max
gdzie
0
lim
i
i
n
i
n
n
n
x
x
d
d
x
0
=
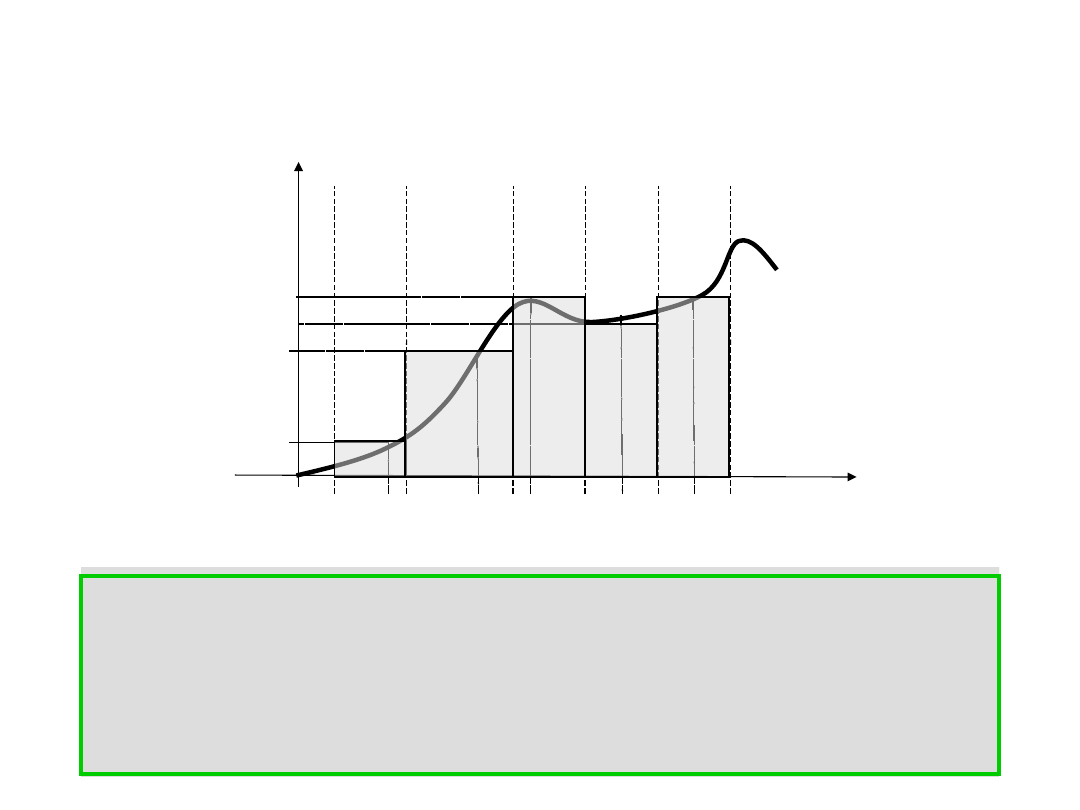
2. Sumy całkowe.
Niech dana będzie funkcja f(x) określona i ograniczona
na <a,b>.
x
a
b
y=f(
x)
y
Rozważmy podział X
n
przedziału <a,b> na n
przedziałów częściowych.
x
1
=x
n
x
2
x
i-1
x
i
W każdym przedziale częściowym można wybrać
punkt pośredni
i
i
i
x
x ,
1
1
2
3
i
)
(
1
f
)
(
2
f
)
(
i
f
Można utworzyć iloczyny:
)
)(
(
0
1
1
x
x
f
)
)(
(
1
2
2
x
x
f
)
)(
(
1
i
i
i
x
x
f
...
...
a następnie sumę :
n
i
i
i
i
n
n
n
n
x
x
f
x
x
f
x
x
f
x
x
f
S
1
1
1
1
2
2
0
1
1
)
)(
(
)
)(
(
...
)
)(
(
)
)(
(
-
sumę całkową
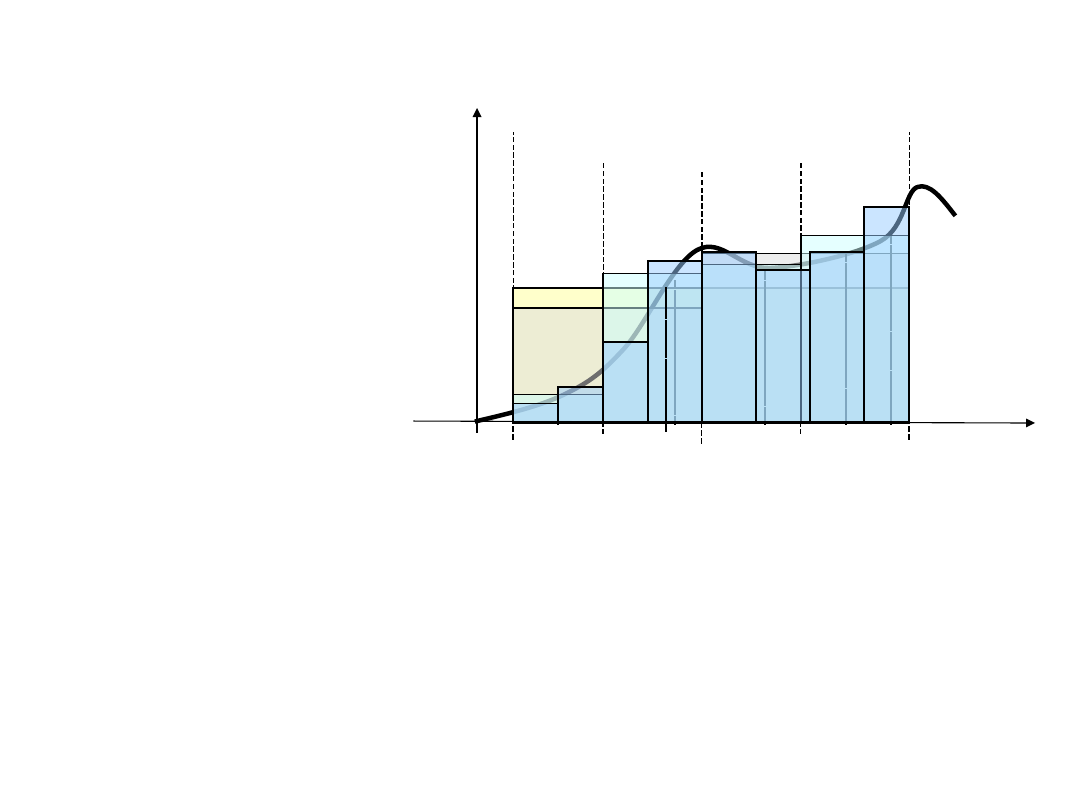
Opisane postępowanie przeprowadzić można dla każdego
podziału z ciągu (X
n
) podziałów.
x
a
b
y=f(
x)
y
Otrzymując ciąg
sum całkowych:
n
i
i
i
i
n
n
n
n
x
x
f
x
x
f
x
x
f
x
x
f
S
1
1
1
1
2
2
0
1
1
)
)(
(
)
)(
(
...
)
)(
(
)
)(
(
)
)(
(
)
)(
(
1
2
2
0
1
1
2
x
x
f
x
x
f
S
)
)(
(
0
1
1
1
x
x
f
S
1

3. Całka oznaczona.
Definicja:
Niech funkcja będzie funkcją
ograniczoną. Funkcję f nazywamy
całkowalną
w sensie Riemanna
w przedziale <a,b> , jeżeli
dla dowolnego normalnego ciągu (X
n
) podziałów
przedziału <a,b> istnieje granica ciągu
sum całkowych (S
n
) niezależna od wyboru
punktów pośrednich .
Granicę tą nazywamy
całką Riemanna (całką
oznaczoną)
funkcji f w przedziale <a,b> i
oznaczamy:
R
b
a
f
,
:
n
n
S
lim
b
a
dx
x
f )
(
Ponadto przyjmiemy oznaczenia:
a
b
b
a
dx
x
f
dx
x
f
)
(
)
(
0
)
(
a
a
dx
x
f
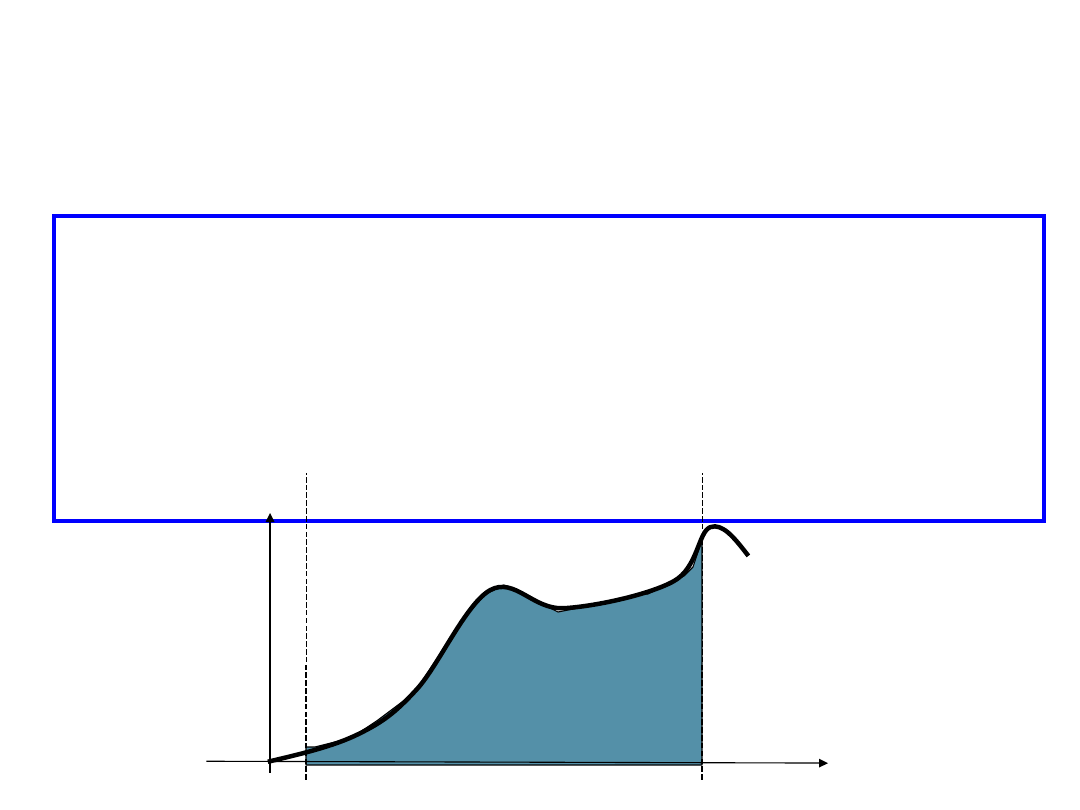
Wprost z definicji całki Riemanna wynika, że dla
funkcji
nieujemnej całkę możemy
interpretować jako
pole pod wykresem funkcji f na przedziale <a,b>.
b
a
dx
x
f )
(
x
a
b
y=f(
x)
y

4. Warunki istnienia całki Riemanna.
Tw.1. [Warunek konieczny]
Jeżeli f(x) jest całkowalna na <a,b> to
jest na tym przedziale ograniczona.
Wnioski
1. Jeżeli f(x) nie jest ograniczona na <a,b> to
nie może być na tym przedziale całkowalna
(w sensie Riemanna).
2. Jeżeli f(x) jest ograniczona na <a,b> to
może być na tym przedziale całkowalna, ale
nie musi.

Tw.2 [Funkcje całkowalne w sensie
Riemanna]
Niech będzie funkcją
ograniczona.
1. Jeżeli f jest ciągła to jest całkowalna w
sensie Riemanna.
2. Jeżeli f ma skończoną ilość punktów
nieciągłości, to jest całkowalna w sensie
Riemanna.
3. Jeżeli f jest monotoniczna, to jest
całkowalna w sensie Riemanna.
R
b
a
f
,
:

5. Własności całki oznaczonej.
R
b
a
g
f
,
:
,
Tw.1. [Liniowość całki]
Jeżeli są funkcjami
całkowalnymi w sensie Riemanna, a<b,
to:
Funkcje k
f , f+g , f-g , f
g, f/g (o ile g(x)
0 dla
x z (a,b)) są całkowalne w sensie Riemanna oraz:
b
a
b
a
dx
x
f
k
dx
x
kf
)
(
)
(
b
a
b
a
b
a
dx
x
g
dx
x
f
dx
x
g
x
f
)
(
)
(
)
(
)
(
R
k
Tw.2.
Jeżeli jest całkowalna w sensie
Riemanna, a<b, to funkcja |f(x)| jest całkowalna
w sensie Riemanna oraz:
b
a
b
a
dx
x
f
dx
x
f
)
(
)
(
R
b
a
f
,
:
Tw.3.
Jeżeli jest całkowalna w sensie
Riemanna, a<b, c
(a,b) to prawdziwa jest
zależność:
b
c
c
a
b
a
dx
x
f
dx
x
f
dx
x
f
)
(
)
(
)
(
R
b
a
f
,
:
Tw. 4. [Monotoniczność całki]
Jeżeli są funkcjami
całkowalnymi w sensie Riemanna, f
g to:
R
b
a
g
f
,
:
,
b
a
b
a
dx
x
g
dx
x
f
)
(
)
(
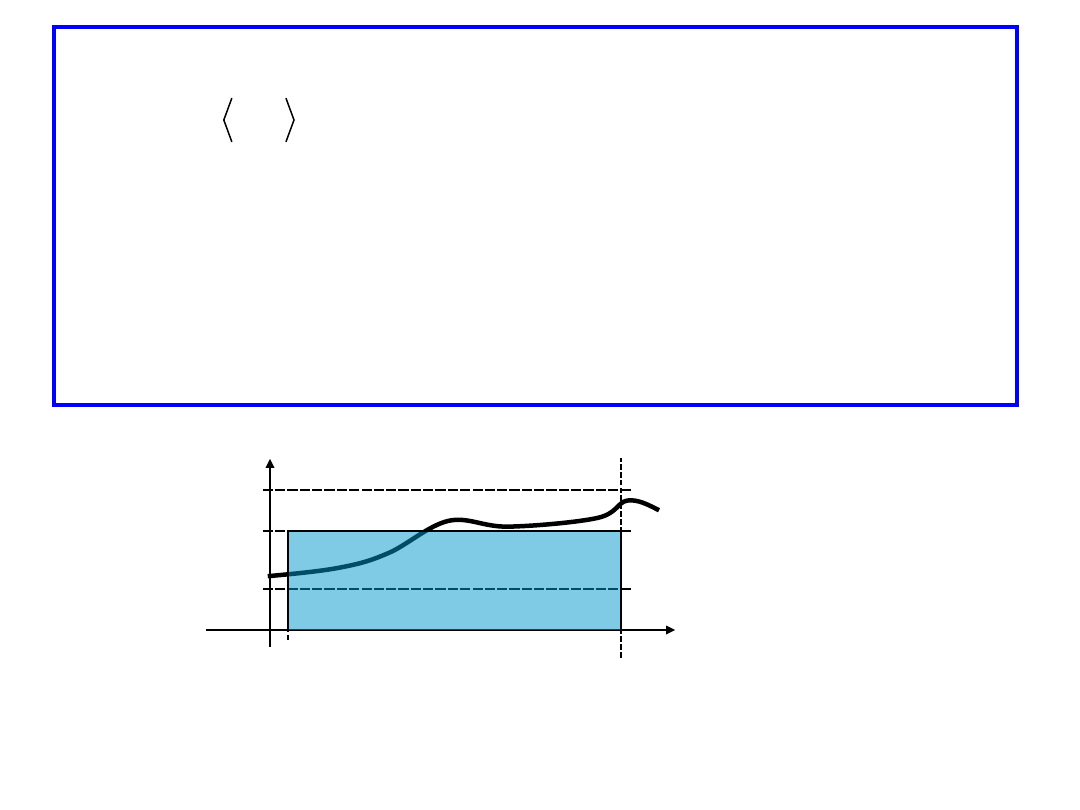
Tw.5. [Twierdzenie całkowe o wartości
średniej]
Jeżeli jest całkowalna w sensie
Riemanna oraz
to
R
b
a
f
,
:
M
x
f
m
b
a
x
R
M
m
)
(
,
,
)
(
)
(
)
(
a
b
M
dx
x
f
a
b
m
b
a
x
a
b
M
m
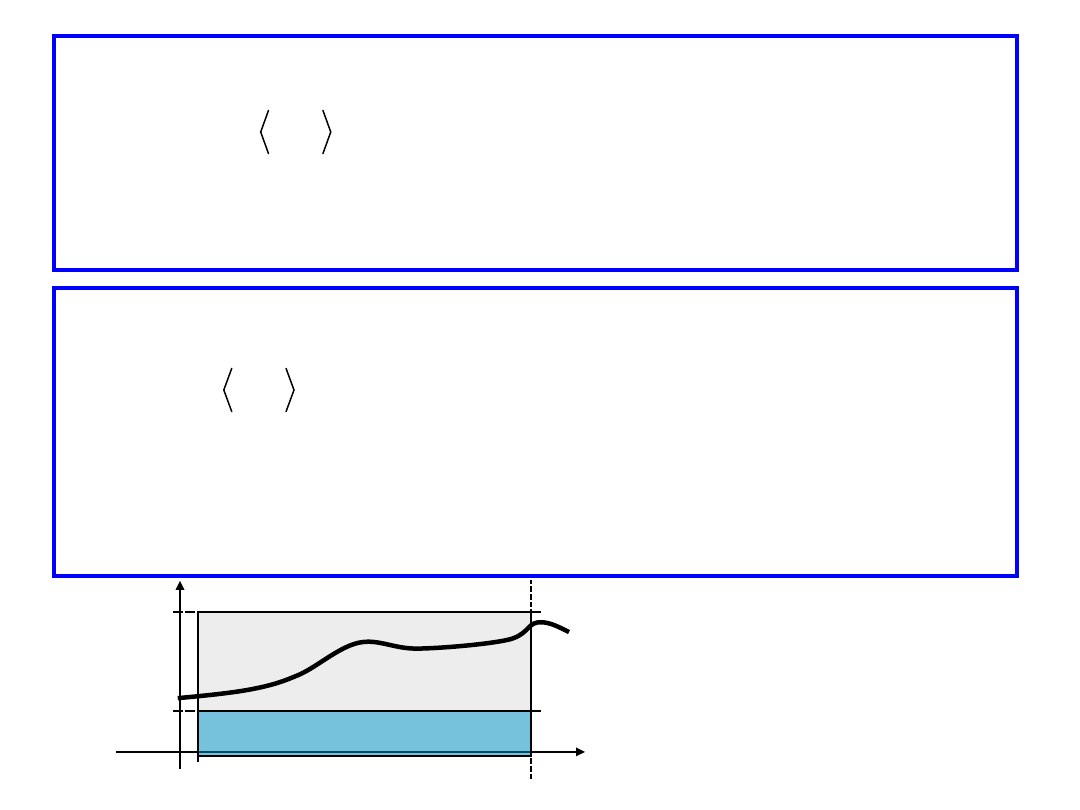
Tw.6. [Twierdzenie całkowe o wartości
średniej]
Jeżeli jest całkowalna w sensie
Riemanna oraz
to
R
b
a
f
,
:
M
x
f
m
b
a
x
R
M
m
)
(
,
,
)
(
)
(
,
a
b
dx
x
f
b
a
M
m
a
b
M
m

Tw.7.
Jeżeli jest nieparzysta i
całkowalna w sensie Riemanna na <-a,a> to
0
)
(
a
a
dx
x
f
R
a
a
f
,
:
Tw.8.
Jeżeli jest parzysta i całkowalna
w sensie Riemanna na <-a,a> to
a
a
a
dx
x
f
dx
x
f
0
)
(
2
)
(
R
a
a
f
,
:
6. Podstawowe twierdzenie rachunku
całkowego.
Tw.[ Newtona-Laibniza]
Jeżeli jest funkcją ciągłą , F jest
funkcją pierwotną funkcji f, to:
Oznaczenia:
R
b
a
f
,
:
)
(
)
(
)
(
a
F
b
F
dx
x
f
b
a
)
(
)
(
)
(
a
F
b
F
x
F
b
a

Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
Wyszukiwarka
Podobne podstrony:
RACHUNEK CAŁKOWY. CAŁKA OZNACZONA I JEJ ZASTOSOWANIA, SZKOŁA, Matematyka, Matematyka
calka oznaczona Wronicz id 1079 Nieznany
Calka oznaczona zadania
Zestaw 9 Całka oznaczona, pole obszaru, całka niewłaściwa
całka oznaczona
5 Całka oznaczona 3 przykładowe rozwiązania
Calka oznaczona teoria
całka oznaczona
sem2 ZJAZD 6 CALKA OZNACZONA wer 2
mat, fiz, pnom, Pole-pod-krzywa-a-calka-oznaczona[2], POLE POD KRZYWĄ A CAŁKA OZNACZONA
2 Całka oznaczona
07 energ całka oznaczona
5 4 Całka oznaczona Riemanna
1 Całka oznaczona
matma, CAŁKA OZNACZONA = liczba, CAŁKA NIEOZNACZONA = funkcja
zagadnienia, punkt 11, XI Całka oznaczona funkcji ograniczonej na [a,b]
Całka oznaczona
więcej podobnych podstron