5.4. Całka oznaczona Riemanna

Całka oznaczona Riemanna jest uogólnieniem całki oznaczonej w sensie Newtona -

Leibniza; dla funkcji ciągłej w przedziale domkniętym [a, b] obie całki są równe, o czym

mówi twierdzenie podane w tym paragrafie.

Normalny ciąg podziału przedziału

Niech f będzie funkcją określoną w przedziale [a, b] . Przyporządkujemy każdej

liczbie naturalnej n ciąg podziałów przedziału [a, b] na podprzedziały, wyznaczony przez

punkty pośrednie a = c

0

< c

1

< c

2

< … < c

n

= b .

Rysunek przedstawia podział przedziału [a, b] na 5 podprzedziałów punktami

c

0

, c

1

, c

2

, c

3

, c

4

, c

5

:

Definicja

Ciąg podziałów przedziału [a, b] dowolnie wybranymi punktami nazywamy ciągiem

normalnym podziałów, gdy średnica najdłuższego z tych podprzedziałów, zmierza do

zera, gdy liczba punktów podziału rośnie nieograniczenie.

Sumy całkowe Riemanna

Niech f będzie funkcją określoną w przedziale [a, b] . Dzielimy punktami pośrednimi

a = c

0

< c

1

< c

2

< … < c

n

= b przedział [a, b] na podprzedziały.

Wybieramy dowolnie w każdym z podprzedziałów [c

k

, c

k+1

] liczbę x

k

, tzw. punkt

pośredni. Następnie obliczamy wartość f(x

k

) w tym punkcie i tworzymy sumę

∑

=

+

−

n

k

k

k

k

c

c

x

f

1

1

)

)(

(

zwaną sumą całkową Riemana funkcji f w przedziale [a, b].

a =c

0

b=c

5

c

1

c

2

c

3

c

4

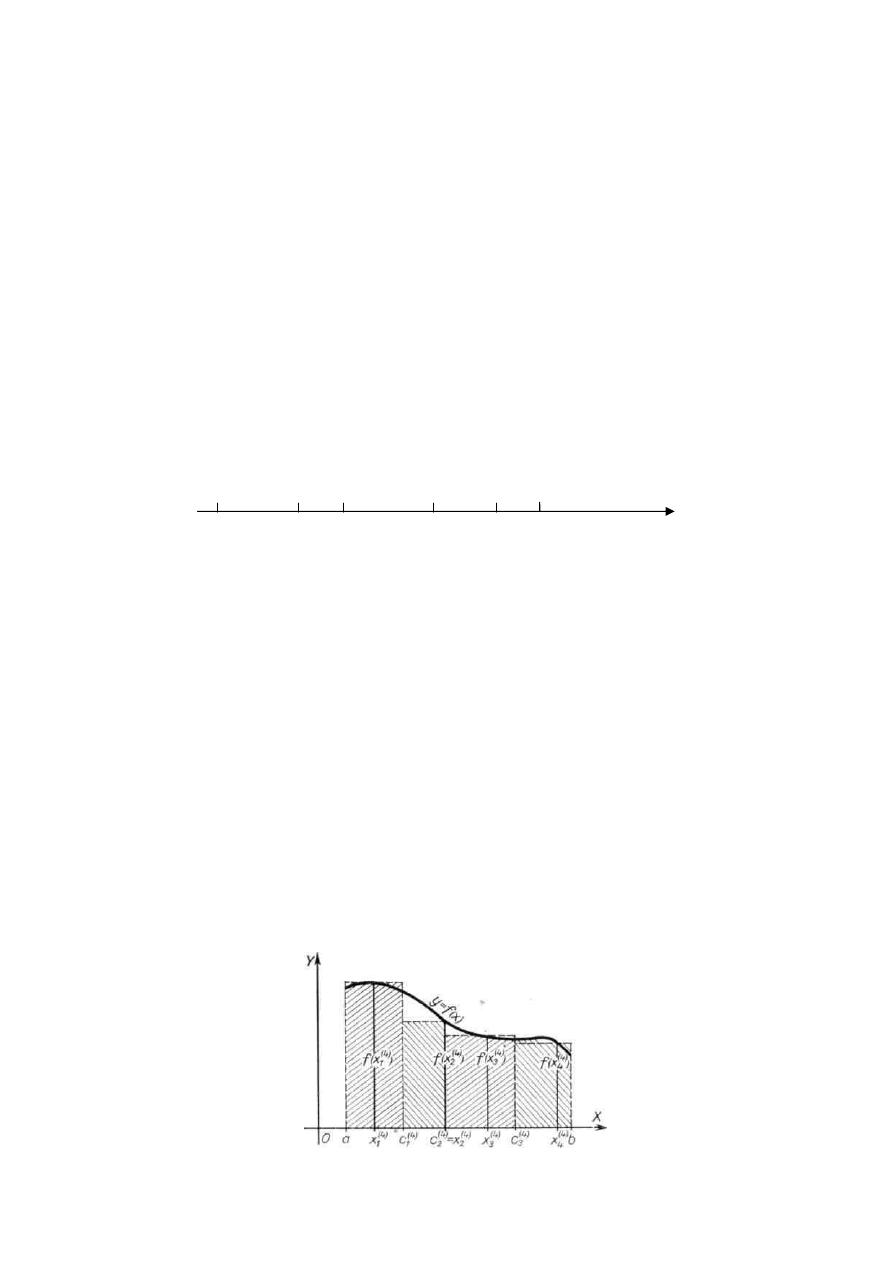
Rysunek przedstawia interpretację geometryczną sumy całkowej w przypadku podziału

przedziału [a, b] na cztery podprzedziały punktami a = c

0

, c

1

, c

2

, c

3,

c

4

= b. Suma ta to nic

innego jak suma pól prostokątów.

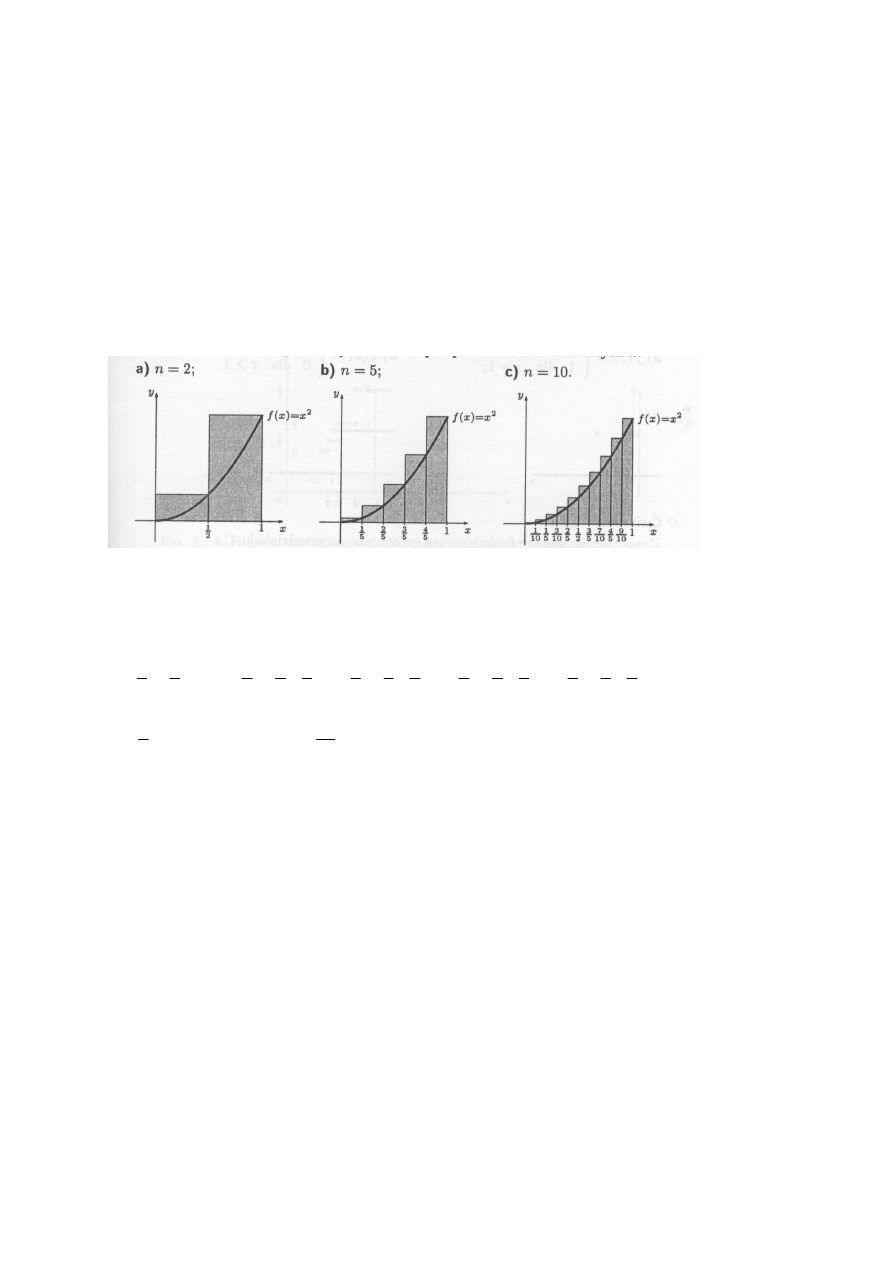
Przykład

Rysunek poniżej przedstawia sumy całkowe funkcji f(x) = x

2

na odcinku [0, 1], w przypadku

gdy ten odcinek podzielono na n równych części ( n = 2, n= 5, n = 10 oraz punkty pośrednie są

prawymi końcami odcinka, do którego należą.

Obliczmy sumę całkową Riemana w przypadku n = 5:

∑

=

+

−

5

1

1

)

)(

(

k

k

k

k

c

c

x

f

=

=

)

0

5

1

(

5

1

2

−













+

)

5

1

5

2

(

5

2

2

−













+

)

5

2

5

3

(

5

3

2

−













+

)

5

3

5

4

(

5

4

2

−













+

)

5

4

5

5

(

5

5

2

−













=

=

)

25

16

9

4

1

(

5

1

3

+

+

+

+













=

25

11

.

Całka Riemana

Definicja

Jeżeli dla każdego ciągu normalnego podziałów przedziału [a, b] ciąg sum całkowych

∑

=

+

−

n

k

k

k

k

c

c

x

f

1

1

)

)(

(

jest zbieżny do tej samej granicy właściwej (czyli będącej liczbą) niezależnej

od wyboru punktów x

k

to granicę tę nazywamy całką Riemanna funkcji f w przedziale [a, b] i

oznaczamy symbolem

∫

b

a

dx

x

f

R

)

(

)

(

.

Definicje

Przedział [a, b] nazywamy, podobnie jak w przypadku całki oznaczonej, przedziałem

całkowania, a — dolną granicą całkowania, b — górną granicą całkowania, f zaś — funkcją

podcałkową.

Jeżeli granica

∑

=

+

−

n

k

k

k

k

c

c

x

f

1

1

)

)(

(

istnieje, to mówimy, że funkcja f jest całkowalna w sensie

Riemanna w przedziale [a, b].

Twierdzenie (o całkowalności w sensie Riemanna funkcji ciągłej).

Jeżeli funkcja f jest ciągła w przedziale domkniętym [a, b], to jest całkowalna w sensie

Riemanna w tym przedziale.

Funkcje całkowalne w sensie Riemanna stanowią szerszą klasę niż funkcje ciągłe. W

szczególności są to funkcje określone i monotoniczne na przedziale [ a, b].

Uwaga

1. Całka Riemanna ma wszystkie podstawowe własności całki oznaczonej, o których była

mowa w poprzednich paragrafach.

2. Funkcja nieograniczona na [a, b] nie jest całkowalna na tym przedziale.

Okazuje się, że w przypadku funkcji ciągłej całka oznaczona w sensie Newtona - Leibniza

jest identyczna z całką Riemanna; mówi o tym:

Twierdzenie

Jeżeli funkcja f jest ciągła w przedziale [a, b], to

∫

b

a

dx

x

f

R

)

(

)

(

=

∫

b

a

dx

x

f

)

(

.

Praktyczne reguły

1.

Aby obliczyć całkę Riemanna w przypadku funkcji ciągłej wystarczy obliczyć całkę

nieoznaczoną Newtona - Leibniza (czyli rodzinę F funkcji pierwotnych) i wykorzystać

wzór:

∫

b

a

dx

x

f

)

(

= F(b) – F(a).

2.

Jeśli f jest funkcją ciągłą i nieujemną w przedziale [a, b], to jak wynika z rozumowania

prowadzącego do określenia całki Riemanna, całka

∫

b

a

dx

x

f

)

(

jest polem obszaru D

stanowiącego zbiór punktów P = (x, y) płaszczyzny , których współrzędne spełniają

warunki a

≤

x

≤

b, 0

≤

y

≤

f(x), czyli

pole D =

∫

b

a

dx

x

f

)

(

, gdzie D = { (x, y) : a

≤

x

≤

b, 0

≤

y

≤

f(x)}.

3.

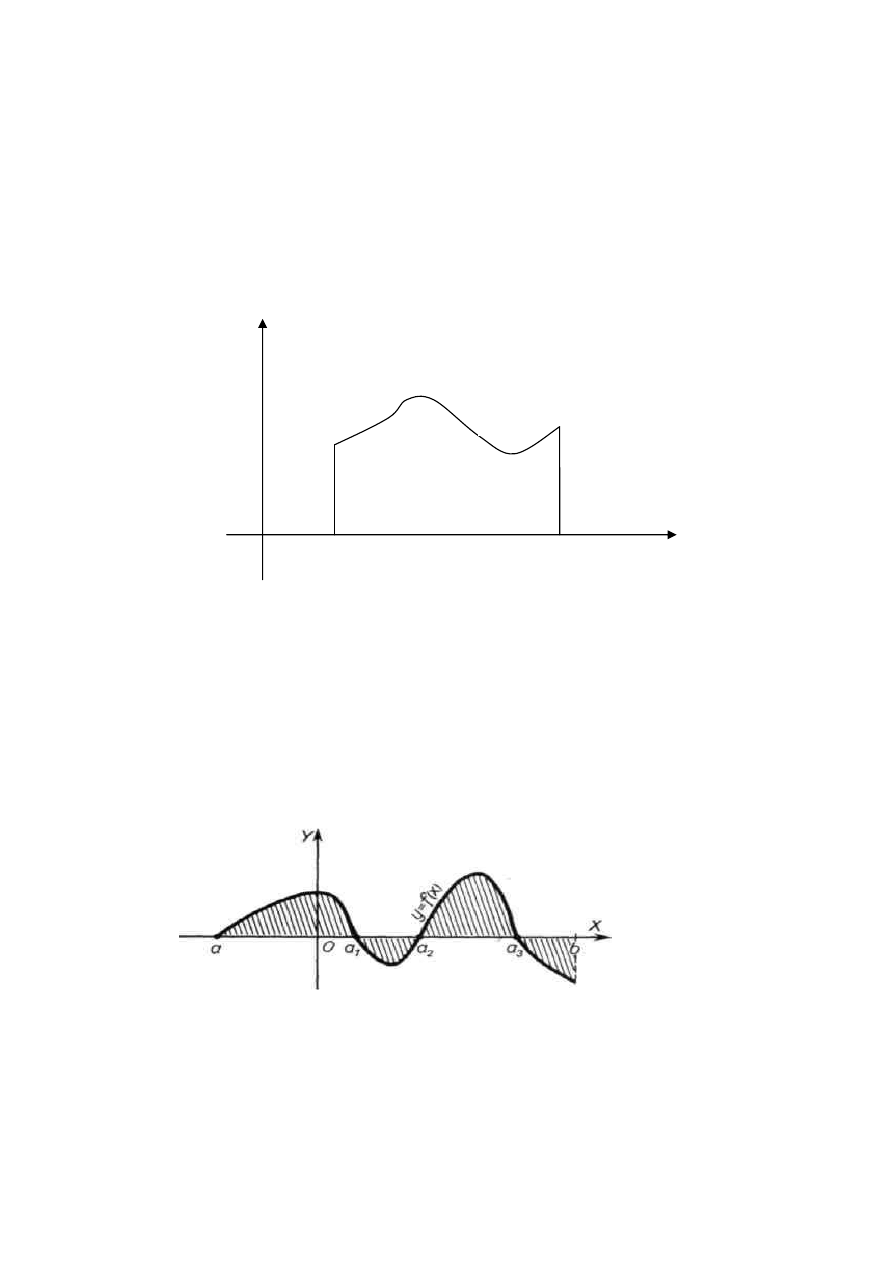
Jeśli więc chcemy obliczyć pole P obszaru ograniczonego łukiem krzywej y = f(x),

odcinkiem osi 0X oraz prostymi x = a i x = b, przy czym o funkcji f wiemy, że w

przedziale [a, b] przyjmuje wartości zarówno dodatnie jak i ujemne, to dzielimy [a, b] na

podprzedziały tak, by w każdym z nich z osobna funkcja f była stale bądź nieujemna,

bądź niedodatnia. Szukane pole jest wtedy sumą pól wyznaczonych przez łuki krzywej w

poszczególnych podprzedziałach przedziału [a, b] (zob. rys.).

Widać stąd, że zawsze pole P określonego wyżej obszaru można wyrazić całką

oznaczoną:

Pole P =

∫

b

a

dx

x

f

|

)

(

|

.

D

a

b

y=f(x)