1

W 5

Pracownia Fizyczna CMF

Absorpcja elektronów

pochodzących z rozpadu

β

1. Pochłanianie elektronów w ośrodku materialnym i źródła elektronów

1.1 Oddziaływanie elektronów z materią.

Elektrony, ze względu na swoją małą masę i fakt posiadania ładunku elektrycznego, łatwo

oddziaływują z materią. Przechodząc przez próbkę substancji są pochłaniane i rozpraszane na kilka
sposobów:

− Sprężyste zderzenia z elektronami związanymi z atomem. Następuje wówczas zmiana

kierunku ruchu elektronu i zmniejsza się jego energia.

− Niesprężyste zderzenia z elektronem walencyjnym. Następuje wówczas jonizacja atomu.

Strata energii jest w tym przypadku znaczna.

− Sprężyste zderzenie z jądrem atomowym. Następuje tylko zmiana kierunku ruchu elektronu.

Strata energii jest zaniedbywalnie mała.

− Hamowanie w polu elektrycznym atomu. Elektron traci energię emitując falę elektro-

magnetyczną

1.2 Źródła elektronów

Źródłem strumienia elektronów mogą być procesy naturalne, jak na przykład:

− rozpad jądrowy

β

,

− promieniowanie kosmiczne.

Wiązkę elektronów można wytworzyć również w akceleratorze liniowym, bądź w cyklotronie.
W rozpadzie

β

mogą powstawać nie tylko elektrony, ale także ich antycząstki – pozytony.

Cząstki te mają taką samą masę jak elektron, ale ładunek dodatni. W związku z tym rozpad

β

możemy podzielić na :

− rozpad

−

β

− rozpad

+

β

i dodatkowo jeszcze

− wychwyt elektronu

Elektrony promieniowania kosmicznego powstają w tak zwanej kaskadzie elektromagnetycznej

w wyniku kreacji par elektron-pozyton.. Elektrony pochodzące z tego źródła są stale obecne
w naszym otoczeniu, ale ich ilość, energia i kierunek ruchu podlegają dużym wahaniom.

Strumień elektronów wytwarzany w akceleratorach różni się od wiązki uzyskiwanej

z naturalnych źródeł. Elektrony z akceleratorów mają dość ściśle określoną energię i energia ta
może osiągać znaczne wartości – są to z reguły elektrony relatywistyczne.

Rozpad

−

β

W rozpadzie

−

β

neutron zawarty w jądrze promieniotwórczego izotopu rozpada się na proton,

elektron i antyneutrino elektronowe

e

e

p

n

ν

+

+

→

−

2

Na przykład w przypadku izotopu strontu w wyniku rozpadu powstaje izotop itru

e

e

Y

Sr

ν

+

+

→

−

90

39

90

38

W ćwiczeniu, jako źródło promieniowania

−

β

użyto właśnie izotopu strontu

90

Sr. Kanał rozpadu

pokazany w powyższym równaniu jest jedynym możliwym dla tego radioizotopu. Powstający
izotop itru nie jest trwały i ulega dalszemu rozpadowi. Prawie w 100 procentach jest to znów
rozpad

β

−

w którym powstaje trwały izotop cyrkonu

90

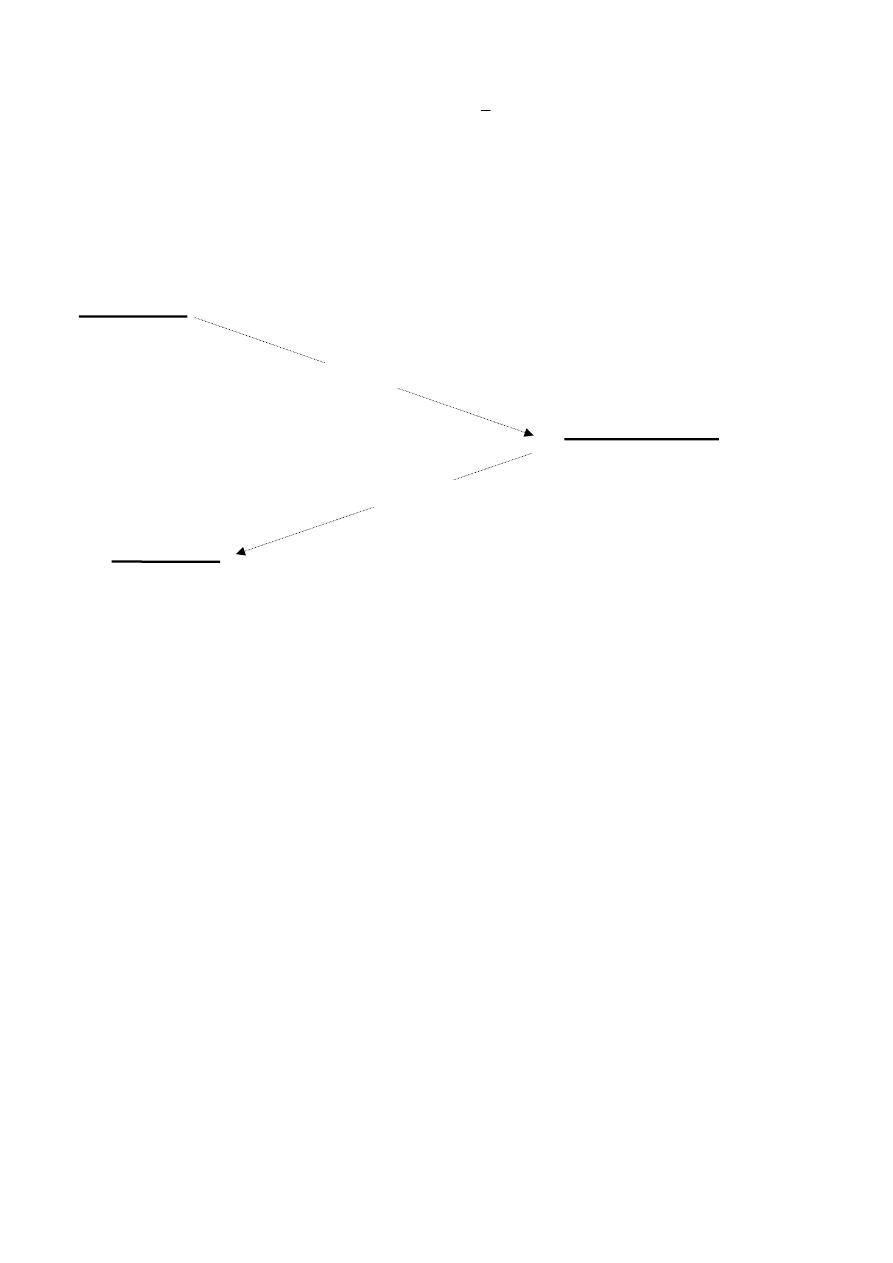
Zr. Cały szereg przemian jądrowych

zachodzących w próbce

90

Sr ilustruje poniższy diagram. Liczby podane w nawiasie przy każdym

izotopie oznaczają czas połowicznego zaniku a liczby przy

−

β

to energia rozpadu.

Jak widać z powyższego diagramu energia uwalniana podczas rozpadu jest różna dla różnych

izotopów.

Rozpad

+

β

W rozpadzie

+

β

liczba atomowa pierwiastka X zmniejsza się o jeden i postaje izotop

pierwiastka Y o takiej samej liczbie masowej:

e

A

Z

A

Z

e

Y

X

ν

+

+

→

+

−1

gdzie e

+

oznacza pozyton. Rozpadowi temu towarzyszy powstanie neutrina elektronowego.

Przykładem rozpadu

+

β

może być reakcja rozpadu izotopu węgla C

11

6

:

e

e

B

C

ν

+

+

→

+

11

5

11

6

Wychwyt elektronu
Trzecią przemianą

β

jest tzw. wychwyt elektronu. Przemiana ta nie jest źródłem elektronów ani

pozytonów, ponieważ nie polega na emisji tych cząstek a na przechwyceniu przez jądro jednego
z elektronów związanych w atomie. W wyniku takiej przemiany, podobnie jak w przemianie

+

β

,

liczba atomowa jądra zmniejsza się a jego liczba masowa pozostaje stała:

e

A

Z

A

Z

Y

e

X

ν

+

→

+

−

−

1

Jedyną emitowaną cząsteczką w tej przemianie jest neutrino elektronowe. Przykładem reakcji

wychwytu elektronu może być przemiana izotopu niklu:

e

Co

e

Ni

ν

+

→

+

−

59

27

59

28

90

Sr (28,5 roku)

90

Y (64,1 godziny)

90

Zr (trwały)

−

β

(0,546 MeV)

−

β (2,274 MeV)

3

1.3 Rozkład energii w promieniowaniu

β

W czasie rozpadu

β

uwalnia się znaczna ilość energii, która unoszona jest przez elektron

i neutrino.

Jeżeli w wyniku rozpadu powstają dwa produkty, wówczas ich energia jest ściśle określona

zasadą zachowania pędu i energii. Zakładając, że początkowo dysponowaliśmy nieruchomym
jądrem o masie M, z którego powstały dwa produkty o masach m

1

i m

2

, możemy zapisać:

2

2

1

1

0

V

m

V

m

−

=

2

2

2

2

2

2

1

1

V

m

V

m

W

−

=

gdzie W jest energią wydzieloną w reakcji. Znając tę energię i masy, możemy wyznaczyć
jednoznacznie prędkości a więc i energie obu produktów. W przypadku trzech produktów rozpadu
energie te nie są jednoznacznie określone, ponieważ prędkości poszczególnych produktów mogą
mieć różne kierunki na płaszczyźnie, zatem zasada zachowania pędu przyjmie następującą postać:

X

X

X

V

m

V

m

V

m

3

3

2

2

1

1

0

+

+

=

Y

Y

Y

V

m

V

m

V

m

3

3

2

2

1

1

0

+

+

=

Jeżeli nawet uwzględnimy jeszcze zasadę zachowania energii, to mamy tylko trzy równania

i sześć niewiadomych (składowe prędkości). Wynika stąd, że cząsteczki w takim rozpadzie mogą
mieć różne energie.

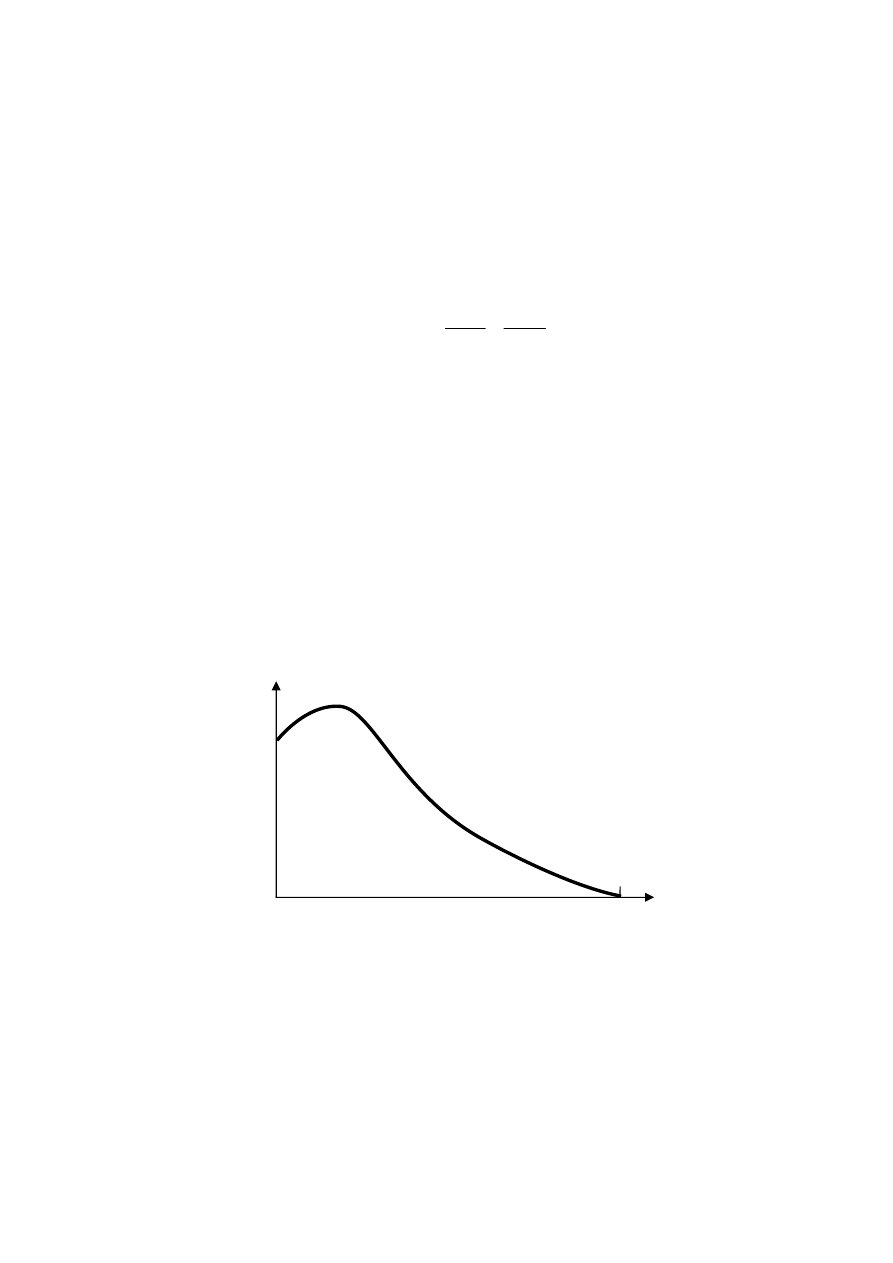
Dlatego elektrony powstające w rozpadzie

β

mają widmo ciągłe (ciągły rozkład energii), który

jest zilustrowany na wykresie:

Istnieje pewna maksymalna energia, którą może posiadać elektron promieniowania

β

. Jest to

energia rozpadu W, wówczas elektron przejmuje prawie całą energię rozpadu.

1.4 Krzywa pochłaniania

Jeżeli wiązka elektronów przechodzi przez próbkę substancji, część elektronów wytraca energię

na skutek wymienionych wyżej procesów do tego stopnia, że mówimy o nich, iż zostały
pochłonięte. Ponieważ elektron traci energię w oddziaływaniu z atomem, jest oczywiste, że ilość
traconych elektronów powinna być proporcjonalna do rozmiarów atomów i ich gęstości
powierzchniowej, tzn. ilości atomów przypadających na jednostkę powierzchni próbki.

energia elektronu

liczba elektronów

rys.1

E

max

4

Gęstość powierzchniowa jest z kolei tym większa im większa jest grubość próbki, ponieważ jest

to gęstość zrzutowana z całej objętości próbki. Dla bardzo cienkiej warstwy próbki można więc
przyjąć, że liczba elektronów, które zostały pochłonięte dN, jest proporcjonalna do grubości próbki
dx. Jest ona również proporcjonalna do ilości elektronów padających na próbkę N:

Ndx

dN

μ

−

=

( 1)

gdzie

μ jest współczynnikiem proporcjonalności. Prawa strona równania jest ujemna, ponieważ dN

jest ubytkiem a nie przyrostem ilości elektronów w wiązce.

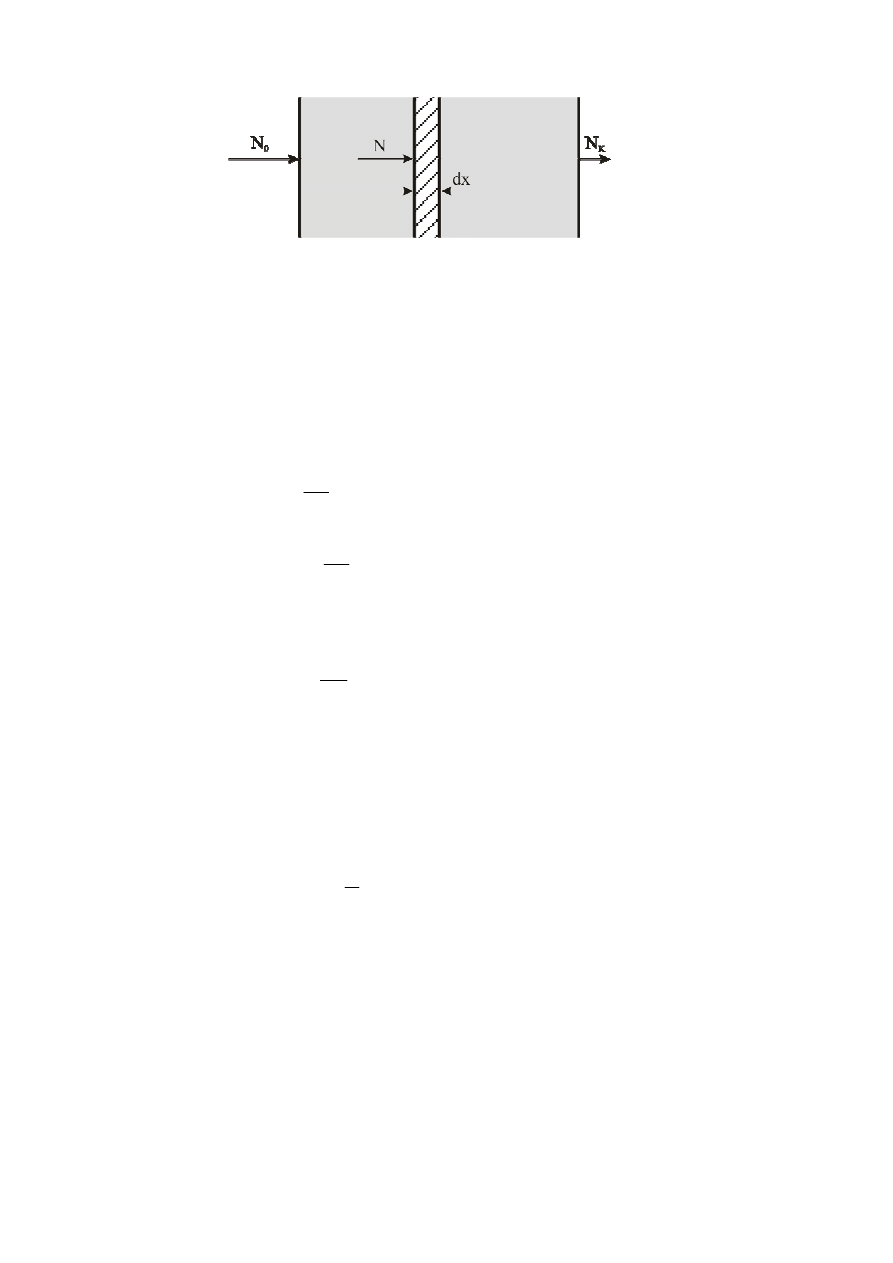
Jeżeli chcemy policzyć liczbę elektronów przechodzących przez dowolnie grubą próbkę, należy

wysumować liczby elektronów traconych na wszystkich cienkich warstwach próbki (rys.2), czyli
wycałkować równanie (1)

dx

N

dN

μ

−

=

( 2)

∫

∫

−

=

0

0

0

x

N

N

dx

N

dN

K

μ

( 3)

gdzie x

0

jest grubością płytki. Po wykonaniu całkowania otrzymujemy

0

0

ln

x

N

N

K

μ

−

=

( 4)

0

0

x

K

e

N

N

μ

−

=

( 5)

Współczynnik

μ nazywamy współczynnikiem absorpcji elektronów. Ma on stałą wartość dla

określonego rodzaju substancji. Istnieje również bardziej uniwersalna stała, która nie zależy od
rodzaju materiału próbki, chociaż zależy od rodzaju źródła elektronów. Ta stała to masowy
współczynnik absorpcji

μ

*

definiowany wzorem

ρ

μ

μ

=

*

( 6)

gdzie

ρ jest gęstością substancji. Liczbę cząsteczek przenikających przez próbkę można zatem

zapisać

0

*

0

x

K

e

N

N

ρμ

−

=

( 7)

Powyższe rozważanie jest uproszczone, ponieważ nie uwzględnia złożoności oddziaływania

elektronów z materią, np. faktu, że liczba elektronów w wiązce może rosnąć na skutek jonizacji.
Jednak okazuje się, że dla elektronów promieniowania

β

opisany wyżej model pochłaniania

okazuje się słuszny. Niejednorodność oddziaływań promieniowania

β

z materią jest kompensowa-

na niejednorodnością rozkładu energetycznego elektronów.

rys. 2

5

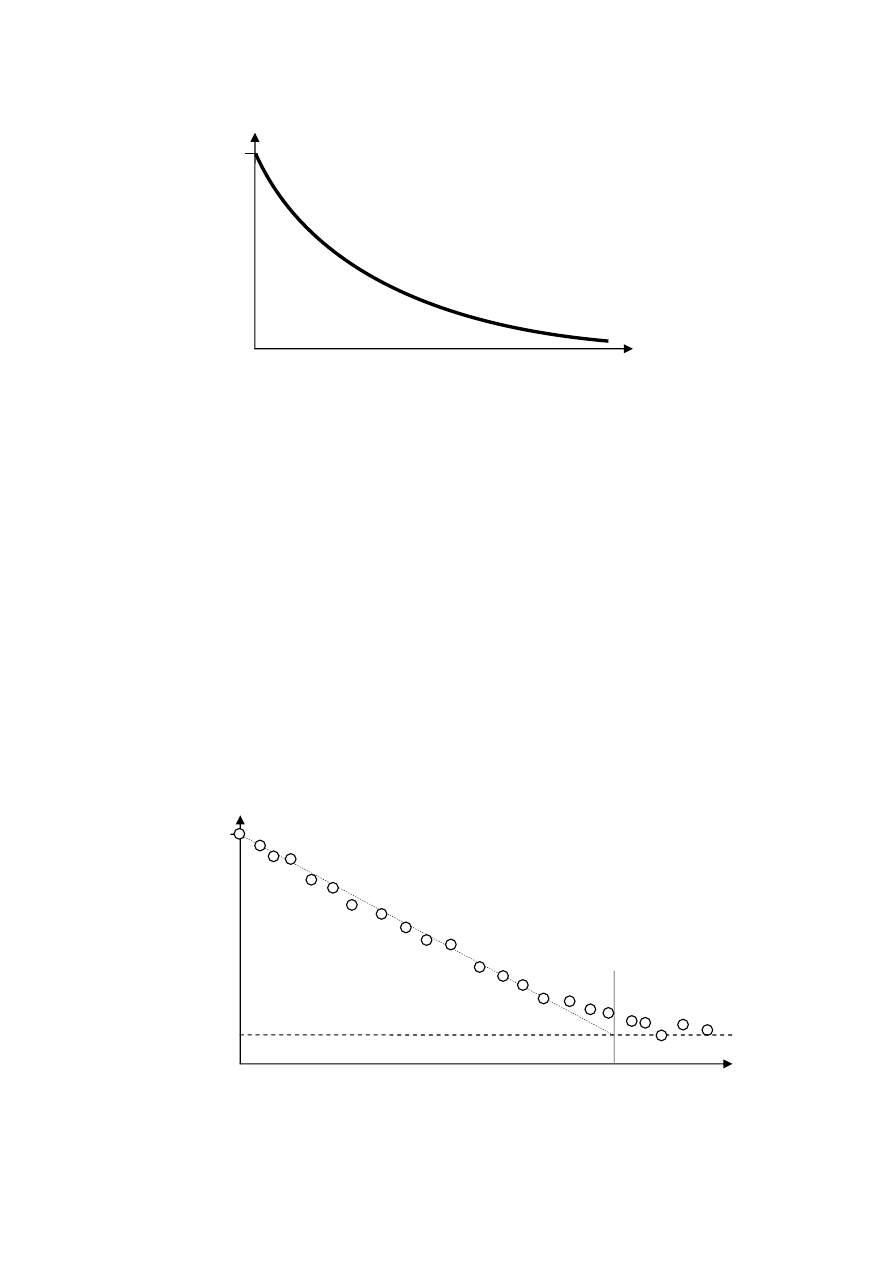
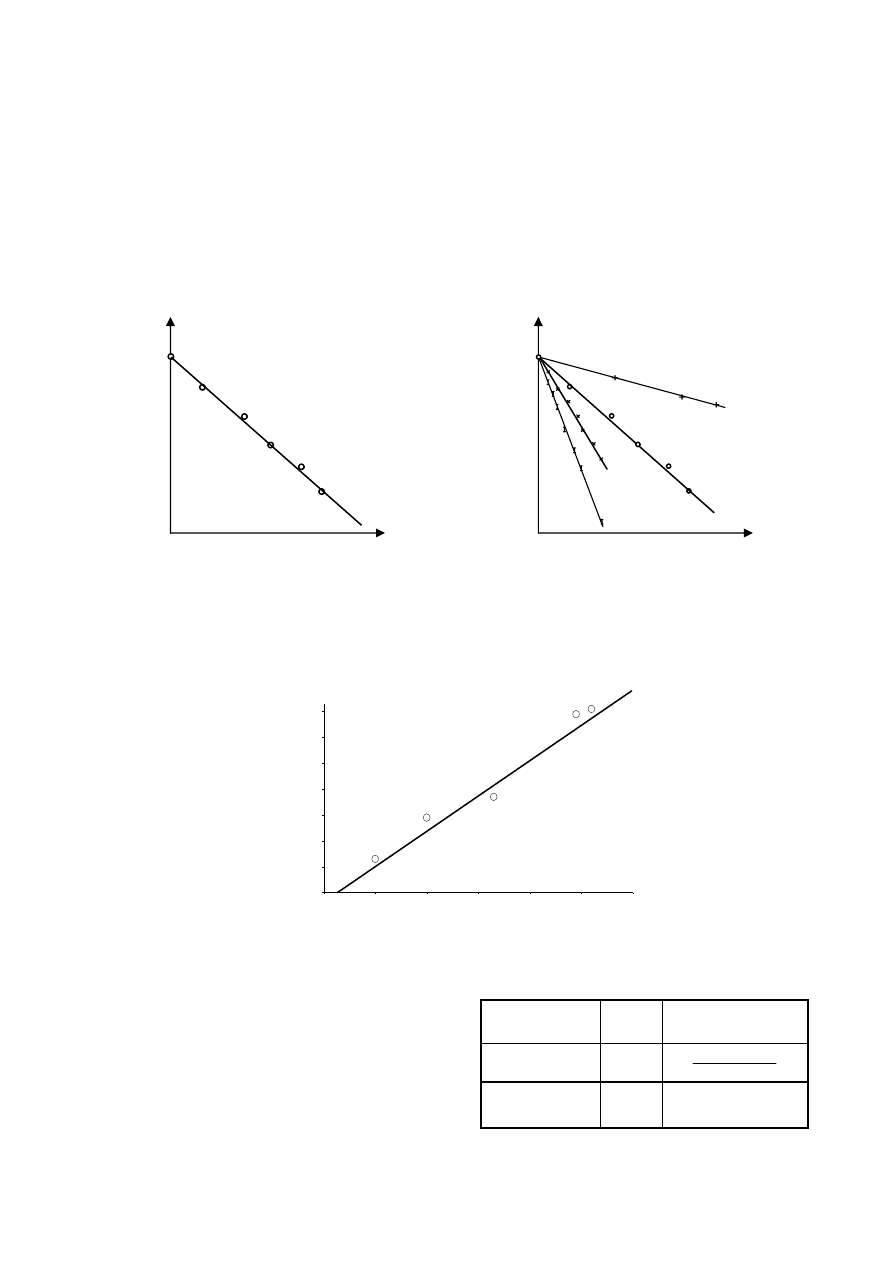
Zatem dla elektronów o takim rozkładzie energii krzywa pochłaniania ma postać wykładniczą, jak
zostało to pokazane we wzorze (5) (rys.3). Dla wiązki elektronów monoenergetycznych
(o określonej jednej energii) z akceleratora krzywa pochłaniania jest bardziej skomplikowana. Jest
to skutkiem złożonych procesów towarzyszących przechodzeniu elektronów przez materię,
o których była mowa na początku. Kształt krzywej pochłaniania zależeć też może od energii
elektronów (różne procesy oddziaływania dominują przy różnych energiach) a także od rodzaju
absorbenta.

1.5 Zasięg promieniowania

β

Wykres przedstawiony na rys.3 jest prawdziwy dla promieniowania

β

przy braku innego,

dodatkowego promieniowania. W rzeczywistości, na skutek promieniotwórczości naturalnej
i promieniowania kosmicznego, w otoczeniu pojawia się pewne słabe promieniowanie jonizujące
nazywane promieniowaniem tła. Aby wzór (5) był ściśle poprawny, powinniśmy zamiast
N wstawić do niego N – N

t

. Jednak dla dużych wartości N promieniowanie tła można zaniedbać

i rozbieżność pojawia się dopiero dla N bliskich poziomu tła W skali logarytmicznej wykres
doświadczalny powinien być linią prostą dla dużych N (rys.4). Dla małych wartości N wykres
wygina się w kierunku poziomu tła. Przedłużając prostoliniową część wykresu w kierunku linii
promieniowania tła możemy odczytać zasięg promieniowania

β

.

Zasięg promieniowania

β

zależy od rodzaju materiału pochłaniającego i częściowo też od

energii elektronów i jej rozkładu, a więc od rodzaju źródła

rys.3

N

x

N

0

rys.4

ln(N)

x

ln(N

0

)

N

t

R

max

6

2. Cel ćwiczenia

W doświadczeniu wyznaczymy współczynniki pochłaniania elektronów w różnych materiałach,

poprzez zbadanie ilości elektronów przechodzących przez próbkę, w zależności od jej grubości.
Następnie obliczymy masowy współczynnik pochłaniania.

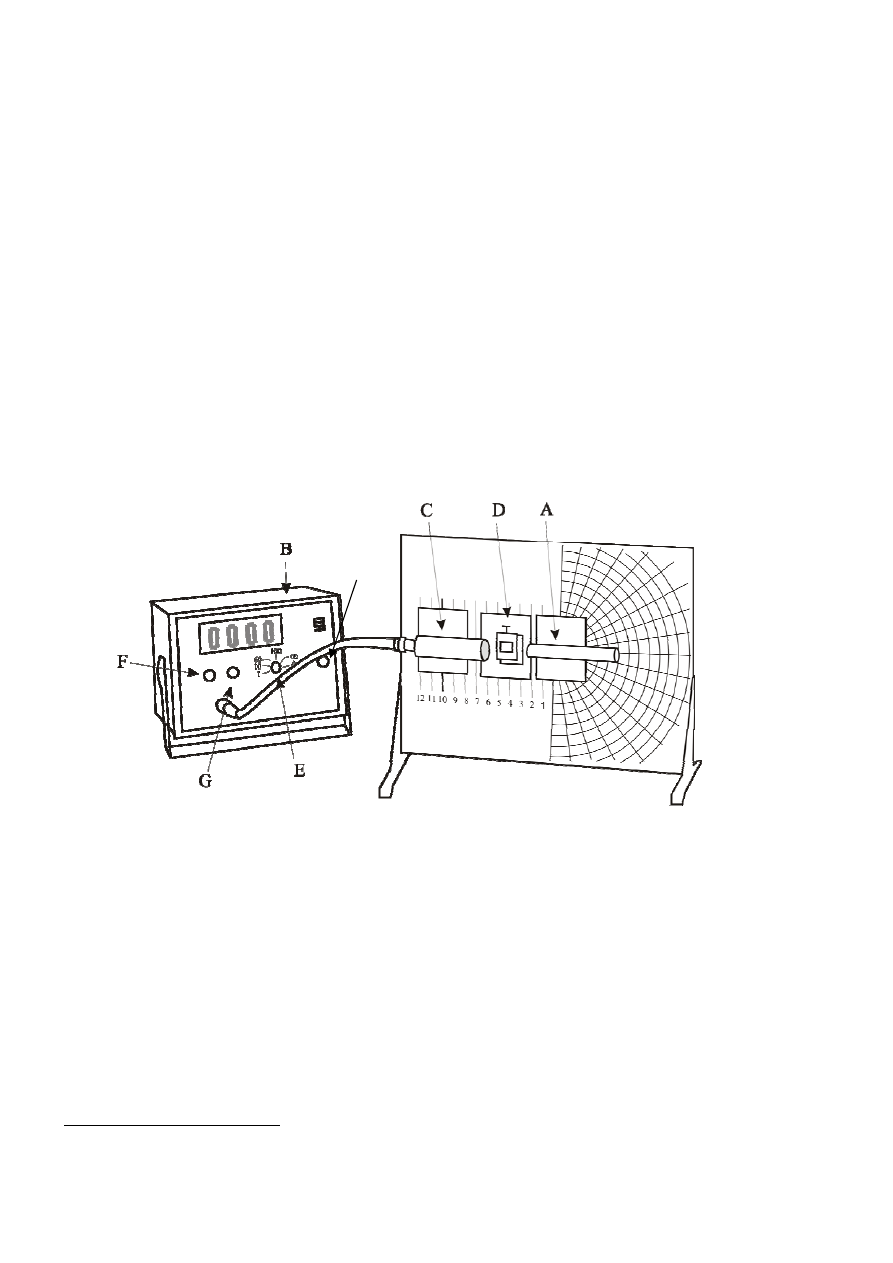
3. Aparatura pomiarowa i metoda pomiaru

Zasadniczym składnikiem aparatury pomiarowej jest źródło promieniotwórczego (A). Źródło to

zawiera radioaktywny izotop strontu

90

Sr o aktywności 74 kBq

*

. Do zliczania ilości elektronów

służy licznik Geigera-Müllera (B) połączony ekranowanym kablem z rurką pomiarową (C).
Pomiędzy źródłem promieniowania a rurką pomiarową licznika umieszcza się płytki badanej
substancji. Do ich mocowania służy specjalna śruba (D). Licznik Geigera-Müllera wyposażony jest
w nastawę czasową umożliwiającą zliczanie impulsów w zadanym czasie(E). Licznik można także
włączyć na dowolny okres, posługując się przyciskiem START/STOP (F). Zerowanie licznika
można przeprowadzić wciskając przycisk RESET (G). Przycisk H służy do włączania podsłuchu
zliczeń licznika.

W uchwycie na próbki można mocować badane płytki o różnej grubości. Ponieważ, zgodnie ze

wzorem (4), logarytm ilości rejestrowanych elektronów jest proporcjonalny do grubości absorbentu
(x), można sporządzić wykres zależności

( )

x

N

x

N

μ

−

=

0

ln

ln

(

8)

Z postaci tego równania widać, że wykres powinien być linią prostą o współczynniku nachylenia

-

μ (rys.6).

Najwyższy punkt na tym wykresie będzie odpowiadał ilości zliczeń licznika Geigera-Müllera

przy braku absorbenta. Wszystkie wartości N, przed naniesieniem na wykres i wykorzystaniem ich

*

Aktywność 1 Bq (beqerel) oznacza 1 rozpad

β na sekundę. Dla porównania – aktywność 1 g radu wynosi 3,7⋅10

10

Bq,

czyli jest około pół miliona razy większa.

rys.5

H

7

do obliczeń, powinny zostać pomniejszone o ilość zliczeń dla elektronów tła N

T

. Źródłem tych

elektronów jest promieniotwórczość naturalna otoczenia oraz promieniowanie kosmiczne.

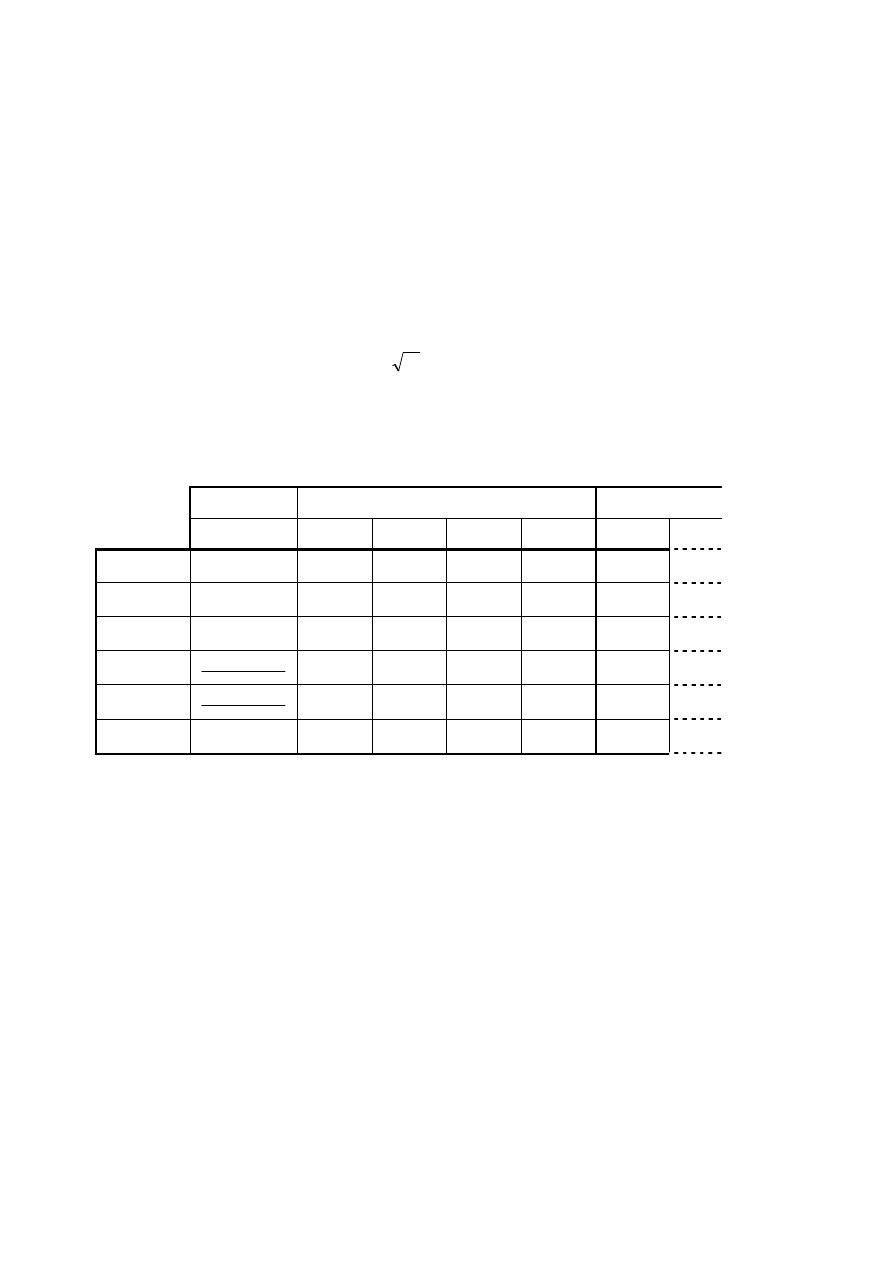
Dla innych substancji pochłaniających wykresy lnN(x) wyglądają podobnie, tzn. są liniowe,

wychodzą z punktu lnN

0

(0) a różnią się tylko stopniem nachylenia (rys.7). Z nachylenia wykresów

można obliczyć współczynniki pochłaniania poszczególnych substancji

μ. Znając gęstości

badanych absorbentów, można sporządzić wykres współczynnika absorpcji od gęstości

μ(ρ). Ze

wzoru (6) mamy:

ρ

μ

μ

*

=

(

9)

gdzie

μ

*

jest masowym współczynnikiem absorpcji.

Jak stąd widać zależność

μ(ρ) też jest zależnością liniową (rys.8), w której współczynnikiem

proporcjonalności jest masowy współczynnik absorpcji.

4. Przebieg pomiaru

4.1

Zmontować zestaw według rysunku 5,

bez źródła promieniotwórczego.
Uwaga: Nie wolno usuwać osłony z tuby
pomiarowej – grozi uszkodzeniem licznika!!!

4.2

Zmierzyć przez 10 minut poziom promie-

niowania tła n

T

. Pomiar można przeprowadzić

jednorazowo, można również zrobić dziesięć pomiarów po minucie, aby zaobserwować zmienność
czasową promieniowania tła. Wynik zapisać w tabeli.

n

T

t

T

N

T

liczba zliczeń min

min

zliczeń

liczba

lnN

x

rys. 6

lnN

x

rys. 7

μ

ρ

rys. 8

8

4.3

Zainstalować źródło promieniowania β, tak aby jego odległość od końca rurki licznika

wynosiła około 2,5 cm i przeprowadzić pomiar (n

0

) bez absorbentu, przez ustalony czas (np. 10 s).

4.4

Pomiędzy źródłem promieniowania β a rurką licznika Geigera-Müllera umieścić próbkę

badanego materiału i przeprowadzić pomiar ilości zliczeń w ciągu ustalonego czasu (np. 10s, 60s,
100s lub więcej).

UWAGA:
W przypadku pomiaru w czasie powyżej 100s należy posłużyć się stoperem, lub przeprowadzić

pomiar wielokrotny – w zależności od sugestii prowadzącego, lub własnej oceny. Podstawowym
kryterium w doborze czasu powinna być pewna minimalna ilość rejestrowanych zliczeń. Można na
przykład przyjąć taką zasadę postępowania: Jeżeli liczna zliczeń spada poniżej 100, wówczas
wydłużamy czas pojedynczego pomiaru. Zasada ta wynika z faktu, że liczna zliczeń N podlega
rozkładowi Poissona, w którym błąd wynosi N . Zatem błąd względny rośnie bardzo szybko wraz
ze zmniejszaniem się liczby pomiarów.

4.5

Powtórzyć ostatni pomiar dla różnych grubości badanego absorbentu.

4.6

Powtórzyć czynności opisane w punktach 4.3 - 4.4 dla innych absorbentów. Wyniki

pomiarów zapisać w tabeli:

absorbent:

szkło organiczne (polimetakrylan...)

aluminium

jednostka

1 2 3 4 1

2

x

grubość

mm

0

n

liczba zliczeń

n

0

t

min

N

min

zliczeń

liczba

N-N

T

min

zliczeń

liczba

ln(N-N

T

)

Dla każdego z absorbentów należy sporządzić podobną tabelę. W zależności od sugestii

prowadzącego i dostępności próbek liczba rubryk w tabeli może być większa.

5. Opracowanie wyników pomiaru

5.1

Sporządzić wykres ln(N-N

T

) w funkcji grubości próbki x; wykres ten umożliwi wizualną

ocenę liniowości tej zależności.

5.2

Metodą najmniejszych kwadratów obliczyć współczynnik absorpcji

μ oraz jego błąd.

5.3

Powtórzyć kroki 5.2 – 5.1 dla pozostałych absorbentów. Wykresy mogą być zebrane na

jednym rysunku jak na rys.7.

9

5.4

Posługując się gęstościami badanych próbek, sporządzić wykres

μ(ρ). Można skorzystać

z danych zawartych w tabeli.

5.5

Metodą najmniejszych kwadratów obliczyć masowy

współczynnik absorpcji

μ

*

wraz z błędem.

UWAGA:

Masowy współczynnik absorpcji

μ

*

zależy od energii

elektronów a więc również od rodzaju źródła promieniowa-
nia

β

. Dlatego przy ocenie wyników obliczeń i ewentualnym

porównywaniu ich z danymi zaczerpniętymi z literatury,
należy mieć ten fakt na uwadze.

5.6

Zapisać ostateczne wyniki wszystkich obliczeń z uwzględnieniem zasad zaokrąglania

błędów. Można wyniki zebrać w tabeli.

5.7

Na podstawie znajomości masowego współczynnika absorpcji obliczyć współczynnik

pochłaniania dla substancji wskazanej przez prowadzącego, np. dla wody.

5.8

W zależności od sugestii prowadzącego, można też wyznaczyć zasięg promieniowania

β

.

5.9

Podać wnioski wynikające z przeprowadzonego doświadczenia i uzyskanych rezultatów.

Przy opracowaniu wniosków można kierować się zasugerowaną poniżej tematyką

− Ocenić stopień oddziaływania elektronów z materią.

− Jakie czynniki mają wpływ na wielkość absorpcji elektronów.

− Jaka jest skuteczność ochrony radiologicznej przed promieniowaniem β.

− Jakie czynniki mogą mieć wpływ na dokładność uzyskanych w doświadczeniu rezultatów,

co można zmienić w procedurze pomiarów, aby wyniki obarczone były mniejszym błędem.

6. Źródła informacji

6.1

D. Halliday, R. Resnick, J. Walker, Podstawy Fizyki t.5, (PWN 2003).

6.2

A. Strzałkowski, Wstęp do fizyki jądra atomowego (PWN 1978).

6.3

E. Skrzypczak, Z. Szefliński - Wstęp do fizyki jądra atomowego i cząstek elementarnych,

(PWN 1995).

ρ

[g/cm

3

]

papier maszynowy

0,852

bakelit 1,39

szkło 2,37

aluminium 2,70

polimetakrylan metylu

1,18