Bartosz Góra, Kamil Jakubczak

Projekt cz. 2 - metoda Sztywnych Elementów Skoñczonych SES

Dane liczbowe

In[1]:=

dane

=

9

a

®

1.1, b

®

1.4, F

®

40 000, q

®

2000, EE

®

2.1

*

10 ^ 11, ro

®

7850,

Jz

®

bp

*

hp

3

12

, bp

®

0.047, hp

®

3

2

bp, Ap

®

bp

*

hp, kt

®

1.2, GG

®

0.8

*

10 ^ 11

=

;

Podzia³ ramy na elementy

In[2]:=

N1

=

15;

N2

=

21;

N3

=

17;

N4

=

14;

Ne

=

N1

+

N2

+

N3

+

N4

+

1

Out[6]=

68

In[7]:=

Nss

=

3

*

Ne

Out[7]=

204

In[8]:=

D

L1

=

a

N1

;

D

L2

=

0.5

*

a

N2

;

D

L3

=

0.5

*

a

N3

;

D

L4

=

b

N4

;

Wektor przemieszczeñ uogólnionych i pomocniczy wektor numeracji

In[12]:=

Do

@8

wq

@

3

*

k

-

2

D =

qx

@

k

D

,

wq

@

3

*

k

-

1

D =

qy

@

k

D

,

wq

@

3

*

k

D = j@

k

D

<

,

8

k, 1, Ne

<D

In[13]:=

Do

@8

num

@

k

D =

k

<

,

8

k, 1, Nss

<D

In[14]:=

wq

@

1

D

Out[14]=

qx

@

1

D

In[15]:=

wq

@

2

D

Out[15]=

qy

@

1

D

In[16]:=

WQ

=

Array

@

wq, Nss

D

;

In[17]:=

NUM

=

Array

@

num, Nss

D

;

In[18]:=

MatrixForm

@

Transpose

@8

NUM, WQ

<DD

;

Wektor bezw³adnoœci

In[19]:=

k

=

1;

wA

@

3

*

k

-

2

D =

m1k;

wA

@

3

*

k

-

1

D =

m1k;

wA

@

3

*

k

D =

J1k;

Do

@8

wA

@

3

*

k

-

2

D =

m1;

wA

@

3

*

k

-

1

D =

m1;

wA

@

3

*

k

D =

J1;

<

,

8

k, 2, N1

<D

;

k

=

N1

+

1;

wA

@

3

*

k

-

2

D =

m12;

wA

@

3

*

k

-

1

D =

m12;

wA

@

3

*

k

D =

J12;

Do

@8

wA

@

3

*

k

-

2

D =

m2;

wA

@

3

*

k

-

1

D =

m2;

wA

@

3

*

k

D =

J2;

<

,

8

k, N1

+

2, N1

+

N2

<D

;

k

=

N1

+

N2

+

1;

wA

@

3

*

k

-

2

D =

m23;

wA

@

3

*

k

-

1

D =

m23;

wA

@

3

*

k

D =

J23;

Do

@8

wA

@

3

*

k

-

2

D =

m3;

wA

@

3

*

k

-

1

D =

m3;

wA

@

3

*

k

D =

J3;

<

,

8

k, N1

+

N2

+

2, N1

+

N2

+

N3

<D

;

k

=

N1

+

N2

+

N3

+

1;

wA

@

3

*

k

-

2

D =

m34;

wA

@

3

*

k

-

1

D =

m34;

wA

@

3

*

k

D =

J34;

Do

@8

wA

@

3

*

k

-

2

D =

m4;

wA

@

3

*

k

-

1

D =

m4;

wA

@

3

*

k

D =

J4;

<

,

8

k, N1

+

N2

+

N3

+

2, Ne

-

1

<D

;

k

=

Ne;

wA

@

3

*

k

-

2

D =

m4k;

wA

@

3

*

k

-

1

D =

m4k;

wA

@

3

*

k

D =

J4k;

In[43]:=

WA

=

Array

@

wA, Nss

D

;

MatrixForm

@

Transpose

@8

NUM, WA

<DD

;

Energia potencjalna sprê¿ystoœci

2

proj_SES_moj.nb

In[45]:=

Ep

=

1

2

*

â

k

=

1

N1

I

CN1

*

H

xA

@

k

+

1

D -

xB

@

k

DL

2

+

CT1

*

H

yA

@

k

+

1

D -

yB

@

k

DL

2

+

CG1

*

Hj@

k

+

1

D - j@

k

DL

2

M +

â

k

=

N1

+

2

N1

+

N2

I

CN2

*

H

xA

@

k

+

1

D -

xB

@

k

DL

2

+

CT2

*

H

yA

@

k

+

1

D -

yB

@

k

DL

2

+

CG2

*

Hj@

k

+

1

D - j@

k

DL

2

M +

â

k

=

N1

+

N2

+

1

N1

+

N2

+

N3

-

1

I

CN3

*

H

xA

@

k

+

1

D -

xB

@

k

DL

2

+

CT3

*

H

yA

@

k

+

1

D -

yB

@

k

DL

2

+

CG3

*

Hj@

k

+

1

D - j@

k

DL

2

M +

â

k

=

N1

+

N2

+

N3

+

1

N1

+

N2

+

N3

+

N4

I

CN4

*

H

xA

@

k

+

1

D -

xB

@

k

DL

2

+

CT4

*

H

yA

@

k

+

1

D -

yB

@

k

DL

2

+

CG4

*

Hj@

k

+

1

D - j@

k

DL

2

M +

I

CN2

*

H

xA

@

N1

+

2

D -

yB

@

N1

+

1

DL

2

+

CT2

*

H

yA

@

N1

+

2

D +

xB

@

N1

+

1

DL

2

+

CG2

*

Hj@

N1

+

2

D - j@

N1

+

1

DL

2

M +

I

CN4

*

H

yA

@

N1

+

N2

+

N3

+

1

D -

xB

@

N1

+

N2

+

N3

DL

2

+

CT4

*

H

xA

@

N1

+

N2

+

N3

+

1

D +

yB

@

N1

+

N2

+

N3

DL

2

+

CG4

*

Hj@

N1

+

N2

+

N3

+

1

D - j@

N1

+

N2

+

N3

DL

2

M +

I

CN1u

*

xA

@

1

D

2

+

CT1u

*

yA

@

1

D

2

+

CG1u

* j

@

1

D

2

M +

I

CN4p

*

xB

@

Ne

D

2

+

CT4p

*

yB

@

Ne

D

2

+

CG4p

* j

@

Ne

D

2

M

;

Przemieszczenia punktów zamocowania ES

In[46]:=

k

=

1;

xA

@

k

D =

qx

@

k

D

;

xB

@

k

D =

qx

@

k

D

;

yA

@

k

D =

qy

@

k

D -

D

L1

4

* j

@

k

D

;

yB

@

k

D =

qy

@

k

D +

D

L1

4

* j

@

k

D

;

Do

A9

xA

@

k

D =

qx

@

k

D

;

xB

@

k

D =

qx

@

k

D

;

yA

@

k

D =

qy

@

k

D -

D

L1

2

* j

@

k

D

;

yB

@

k

D =

qy

@

k

D +

D

L1

2

* j

@

k

D

;

=

,

8

k, 2, N1

<E

;

k

=

N1

+

1;

pA1

=

8

qx

@

k

D

, qy

@

k

D

, 0

< + 8

0, 0,

j

@

k

D<‰9

a

-

D

L1

2

-

xC12,

-

yC12, 0

=

;

pB1

=

8

qx

@

k

D

, qy

@

k

D

, 0

< + 8

0, 0,

j

@

k

D<‰9

a

-

xC12,

D

L2

2

-

yC12, 0

=

;

pD1

=

8

qx

@

k

D

, qy

@

k

D

, 0

< + 8

0, 0,

j

@

k

D<‰8

a

-

xC12,

-

yC12, 0

<

;

xA

@

k

D =

pA1

@@

1

DD

;

yA

@

k

D =

pA1

@@

2

DD

;

xB

@

k

D =

pB1

@@

1

DD

;

yB

@

k

D =

pB1

@@

2

DD

;

xD

@

k

D =

pD1

@@

1

DD

;

yD

@

k

D =

pD1

@@

2

DD

;

Do

A9

xA

@

k

D =

qx

@

k

D

;

xB

@

k

D =

qx

@

k

D

;

yA

@

k

D =

qy

@

k

D -

D

L2

2

* j

@

k

D

;

;

proj_SES_moj.nb

3

In[46]:=

yB

@

k

D =

qy

@

k

D +

D

L2

2

* j

@

k

D

;

=

,

8

k, N1

+

2, N1

+

N2

<E

;

k

=

N1

+

N2

+

1;

D

L23

=

D

L2

+ D

L3

2

;

xA

@

k

D =

qx

@

k

D

;

xB

@

k

D =

qx

@

k

D

;

yA

@

k

D =

qy

@

k

D -

D

L23

2

* j

@

k

D

;

yB

@

k

D =

qy

@

k

D +

D

L23

2

* j

@

k

D

;

Do

A9

xA

@

k

D =

qx

@

k

D

;

xB

@

k

D =

qx

@

k

D

;

yA

@

k

D =

qy

@

k

D -

D

L3

2

* j

@

k

D

;

yB

@

k

D =

qy

@

k

D +

D

L3

2

* j

@

k

D

;

=

,

8

k, N1

+

N2

+

2, N1

+

N2

+

N3

<E

;

k

=

N1

+

N2

+

N3

+

1;

pA2

=

8

qx

@

k

D

, qy

@

k

D

, 0

< + 8

0, 0,

j

@

k

D<‰9

a

-

xC34, a

-

D

L3

2

-

yC34, 0

=

;

pB2

=

8

qx

@

k

D

, qy

@

k

D

, 0

< + 8

0, 0,

j

@

k

D<‰9

a

+

D

L4

2

-

xC34, a

-

yC34, 0

=

;

pD2

=

8

qx

@

k

D

, qy

@

k

D

, 0

< + 8

0, 0,

j

@

k

D<‰8

a

-

xC34, a

-

yC34, 0

<

;

xA

@

k

D =

pA2

@@

1

DD

;

yA

@

k

D =

pA2

@@

2

DD

;

xB

@

k

D =

pB2

@@

1

DD

;

yB

@

k

D =

pB2

@@

2

DD

;

xD

@

k

D =

pD2

@@

1

DD

;

yD

@

k

D =

pD2

@@

2

DD

;

Do

A9

xA

@

k

D =

qx

@

k

D

;

xB

@

k

D =

qx

@

k

D

;

yA

@

k

D =

qy

@

k

D -

D

L4

2

* j

@

k

D

;

yB

@

k

D =

qy

@

k

D +

D

L4

2

* j

@

k

D

;

=

,

8

k, N1

+

N2

+

N3

+

2, N1

+

N2

+

N3

+

N4

<E

;

k

=

Ne;

xA

@

k

D =

qx

@

k

D

;

xB

@

k

D =

qx

@

k

D

;

yA

@

k

D =

qy

@

k

D -

D

L4

4

* j

@

k

D

;

yB

@

k

D =

qy

@

k

D +

D

L4

4

* j

@

k

D

;

Macierz sztywnoœci

In[86]:=

pEp

= ¶

8

WQ

<

Ep;

4

proj_SES_moj.nb

In[87]:=

Do

@8

Do

@8

mC

@

kw, kk

D =

Coefficient

@

pEp

@@

kw

DD

, WQ

@@

kk

DDD

<

,

8

kk, 1, Nss

<D

<

,

8

kw, 1, Nss

<D

In[88]:=

MC

=

Array

@

mC,

8

Nss, Nss

<D

;

MatrixForm

@

MC

D

;

Wspó³czynniki sztywnoœci

In[90]:=

CN1

=

EE

*

Ap

D

L1

;

CT1

=

GG

*

Ap

kt

* D

L1

;

CG1

=

EE

*

Jz

D

L1

;

CN2

=

EE

*

Ap

D

L2

;

CT2

=

GG

*

Ap

kt

* D

L2

;

CG2

=

EE

*

Jz

D

L2

;

CN3

=

EE

*

Ap

D

L3

;

CT3

=

GG

*

Ap

kt

* D

L3

;

CG3

=

EE

*

Jz

D

L3

;

CN4

=

EE

*

Ap

D

L4

;

CT4

=

GG

*

Ap

kt

* D

L4

;

CG4

=

EE

*

Jz

D

L4

;

In[102]:=

CN1u

=

5

*

CN1;

CT1u

=

5

*

CT1;

CG1u

=

5

*

CG1;

In[105]:=

CN4p

=

5

*

CN4;

CT4p

=

5

*

CT4;

CG4p

=

0;

Œrodki mas elementów “nieregularnych”

proj_SES_moj.nb

5

In[108]:=

xC1

=

a

-

D

L1

4

;

yC1

=

0;

A1

=

D

L1

2

*

hp;

xC2

=

a;

yC2

=

D

L2

4

;

A2

=

D

L2

2

*

hp;

A12

=

A1

+

A2;

xC12

=

xC1

*

A1

+

xC2

*

A2

A12

;

yC12

=

yC1

*

A1

+

yC2

*

A2

A12

;

xC23

=

a;

yC23

=

a



2

-

D

L2

2

+

D

L23

2

;

xC3

=

a;

yC3

=

a

-

D

L3

4

;

A3

=

D

L3

2

*

hp;

xC4

=

a

+

D

L4

4

;

yC4

=

a;

A4

=

D

L4

2

*

hp;

A34

=

A3

+

A4;

xC34

=

xC3

*

A3

+

xC4

*

A4

A34

;

yC34

=

yC3

*

A3

+

yC4

*

A4

A34

;

8

xC12, yC12

< 

. dane

8

a, 0

< 

. dane

8

xC23, yC23

< 

. dane

8

a, a



2

< 

. dane

8

xC34, yC34

< 

. dane

8

a, a

< 

. dane

Out[128]=

8

1.08649, 0.00172306

<

Out[129]=

8

1.1, 0

<

Out[130]=

8

1.1, 0.551541

<

Out[131]=

8

1.1, 0.55

<

Out[132]=

8

1.11889, 1.09802

<

Out[133]=

8

1.1, 1.1

<

Numeryczna wersja macierzy sztywnoœci

6

proj_SES_moj.nb

In[134]:=

numMC

=

MC



. dane;

MatrixForm

@

numMC

D

;

Masa i masowe momenty bezw³adnoœci

In[136]:=

m1

=

Ap

* D

L1

*

ro;

m2

=

Ap

* D

L2

*

ro;

m3

=

Ap

* D

L3

*

ro;

m4

=

Ap

* D

L4

*

ro;

m1k

=

m1



2;

m2k

=

m2



2;

m3k

=

m3



2;

m4k

=

m4



2;

m12

=

m1

+

m2

2

;

m23

=

m2

+

m3

2

;

m34

=

m3

+

m4

2

;

J1

=

m1

12

*

ID

L1

2

+

hp

2

M

;

J2

=

m2

12

*

ID

L2

2

+

hp

2

M

;

J3

=

m3

12

*

ID

L3

2

+

hp

2

M

;

J4

=

m4

12

*

ID

L4

2

+

hp

2

M

;

J1k

=

m1k

12

*

D

L1

2

2

+

hp

2

;

J2k

=

m2k

12

*

D

L2

2

2

+

hp

2

;

J3k

=

m3k

12

*

D

L3

2

2

+

hp

2

;

J4k

=

m4k

12

*

D

L4

2

2

+

hp

2

;

J12

=

J1k

+

m1k

*

IH

xC1

-

xC12

L

2

+

H

yC1

-

yC12

L

2

M +

J2k

+

m2k

*

IH

xC2

-

xC12

L

2

+

H

yC2

-

yC12

L

2

M

;

J23

=

m23

12

*

ID

L23

2

+

hp

2

M

;

J34

=

J3k

+

m3k

*

IH

xC3

-

xC34

L

2

+

H

yC3

-

yC34

L

2

M +

J4k

+

m4k

*

IH

xC4

-

xC34

L

2

+

H

yC4

-

yC34

L

2

M

;

In[158]:=

MatrixForm

@

WA

D

;

Zmodyfikowana macierz sztywnoœci

In[159]:=

Do

@8

Do

@8

zmC

@

kw, kk

D =

mC

@

kw, kk

D 

wA

@

kw

D

<

,

8

kk, 1, Nss

<D

<

,

8

kw, 1, Nss

<D

In[160]:=

ZMC

=

Array

@

zmC,

8

Nss, Nss

<D

;

MatrixForm

@

ZMC

D

;

proj_SES_moj.nb

7

In[162]:=

numZMC

=

ZMC



. dane;

MatrixForm

@

numZMC

D

;

Wyznaczanie czêstoœci i postaci drgañ w³asnych ramy

In[164]:=

rozw

=

Eigensystem

@

numZMC

D

;

Kwadraty czêstoœci w³asnych

In[165]:=

KCW

=

rozw

@@

1

DD

;

In[166]:=

CW

=

KCW ;

Analiza pierwszej postaci drgañ w³asnych ramy

In[167]:=

nr

=

1;

nr2

=

Nss

-

nr

+

1;

In[169]:=

Ω =

CW

@@

nr2

DD

Out[169]=

168.526

In[170]:=

pos

=

rozw

@@

2, nr2

DD

;

In[171]:=

Do

@8

qx

@

k

D =

pos

@@

3

*

k

-

2

DD

,

qy

@

k

D =

pos

@@

3

*

k

-

1

DD

,

j

@

k

D =

pos

@@

3

*

k

DD

<

,

8

k, 1, Ne

<D

8

proj_SES_moj.nb

In[172]:=

k

=

1;

rama

@

k

D =

Line

@88

xA

@

k

D

, yA

@

k

D<

,

8D

L1



2

+

xB

@

k

D

, yB

@

k

D<<D

;

Do

@8

j

=

k

-

1;

sx

=

H

j

-

1

L * D

L1

+ D

L1



2;

rama

@

k

D =

Line

@88

sx

+

xA

@

k

D

, yA

@

k

D<

,

8

sx

+ D

L1

+

xB

@

k

D

, yB

@

k

D<<D

<

,

8

k, 2, N1

<D

;

k

=

N1

+

1;

rama

@

k

D =

Line

B::

a

-

D

L1

2

+

xA

@

k

D

, yA

@

k

D>

,

8

a

+

xD

@

k

D

, yD

@

k

D<

,

:

a

+

xB

@

k

D

,

D

L2

2

+

yB

@

k

D>>F

;

Do

@8

j

=

k

-

H

N1

+

1

L

;

sy

=

H

j

-

1

L * D

L2

+ D

L2



2;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, sy

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, sy

+ D

L2

+

xB

@

k

D<<D

<

,

8

k, N1

+

2, N1

+

N2

<D

;

k

=

N1

+

N2

+

1;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, a



2

- D

L2



2

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, a



2

+ D

L3



2

+

xB

@

k

D<<D

;

Do

@8

j

=

k

-

H

N1

+

N2

+

1

L

;

sy

=

a



2

+

H

j

-

1

L * D

L3

+ D

L3



2;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, sy

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, sy

+ D

L3

+

xB

@

k

D<<D

<

,

8

k, N1

+

N2

+

2, N1

+

N2

+

N3

<D

;

k

=

N1

+

N2

+

N3

+

1;

rama

@

k

D =

Line

B::

a

+

xA

@

k

D

, a

-

D

L3

2

+

yA

@

k

D>

,

8

a

+

xD

@

k

D

, a

+

yD

@

k

D<

,

:

a

+

D

L4

2

+

xB

@

k

D

, a

+

yB

@

k

D>>F

;

Do

@8

j

=

k

-

H

N1

+

N2

+

N3

+

1

L

;

sx

=

a

+

H

j

-

1

L * D

L4

+ D

L4



2;

rama

@

k

D =

Line

@88

sx

+

xA

@

k

D

, a

+

yA

@

k

D<

,

8

sx

+ D

L4

+

xB

@

k

D

, a

+

yB

@

k

D<<D

<

,

8

k, N1

+

N2

+

N3

+

2, Ne

<D

;

k

=

Ne

+

1;

rama

@

k

D =

Line

@88

a

+

b

+

xA

@

k

D

, a

+

yA

@

k

D<

,

8

a

+

b

+

xB

@

k

D

, a

+

yB

@

k

D<<D

;

In[186]:=

RAMA1

=

Array

@

rama, Ne

D 

. dane;

wr1

=

Graphics

@8

Green, RAMA1

<D

;

Analiza drugiej postaci drgañ w³asnych ramy

In[188]:=

nr

=

2;

nr2

=

Nss

-

nr

+

1;

proj_SES_moj.nb

9

In[190]:=

Ω =

CW

@@

nr2

DD

Out[190]=

679.389

In[191]:=

pos

=

rozw

@@

2, nr2

DD

;

In[192]:=

Do

@8

qx

@

k

D =

pos

@@

3

*

k

-

2

DD

,

qy

@

k

D =

pos

@@

3

*

k

-

1

DD

,

j

@

k

D =

pos

@@

3

*

k

DD

<

,

8

k, 1, Ne

<D

10

proj_SES_moj.nb

In[193]:=

k

=

1;

rama

@

k

D =

Line

@88

xA

@

k

D

, yA

@

k

D<

,

8D

L1



2

+

xB

@

k

D

, yB

@

k

D<<D

;

Do

@8

j

=

k

-

1;

sx

=

H

j

-

1

L * D

L1

+ D

L1



2;

rama

@

k

D =

Line

@88

sx

+

xA

@

k

D

, yA

@

k

D<

,

8

sx

+ D

L1

+

xB

@

k

D

, yB

@

k

D<<D

<

,

8

k, 2, N1

<D

;

k

=

N1

+

1;

rama

@

k

D =

Line

B::

a

-

D

L1

2

+

xA

@

k

D

, yA

@

k

D>

,

8

a

+

xD

@

k

D

, yD

@

k

D<

,

:

a

+

xB

@

k

D

,

D

L2

2

+

yB

@

k

D>>F

;

Do

@8

j

=

k

-

H

N1

+

1

L

;

sy

=

H

j

-

1

L * D

L2

+ D

L2



2;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, sy

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, sy

+ D

L2

+

xB

@

k

D<<D

<

,

8

k, N1

+

2, N1

+

N2

<D

;

k

=

N1

+

N2

+

1;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, a



2

- D

L2



2

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, a



2

+ D

L3



2

+

xB

@

k

D<<D

;

Do

@8

j

=

k

-

H

N1

+

N2

+

1

L

;

sy

=

a



2

+

H

j

-

1

L * D

L3

+ D

L3



2;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, sy

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, sy

+ D

L3

+

xB

@

k

D<<D

<

,

8

k, N1

+

N2

+

2, N1

+

N2

+

N3

<D

;

k

=

N1

+

N2

+

N3

+

1;

rama

@

k

D =

Line

B::

a

+

xA

@

k

D

, a

-

D

L3

2

+

yA

@

k

D>

,

8

a

+

xD

@

k

D

, a

+

yD

@

k

D<

,

:

a

+

D

L4

2

+

xB

@

k

D

, a

+

yB

@

k

D>>F

;

Do

@8

j

=

k

-

H

N1

+

N2

+

N3

+

1

L

;

sx

=

a

+

H

j

-

1

L * D

L4

+ D

L4



2;

rama

@

k

D =

Line

@88

sx

+

xA

@

k

D

, a

+

yA

@

k

D<

,

8

sx

+ D

L4

+

xB

@

k

D

, a

+

yB

@

k

D<<D

<

,

8

k, N1

+

N2

+

N3

+

2, Ne

<D

;

k

=

Ne

+

1;

rama

@

k

D =

Line

@88

a

+

b

+

xA

@

k

D

, a

+

yA

@

k

D<

,

8

a

+

b

+

xB

@

k

D

, a

+

yB

@

k

D<<D

;

In[207]:=

RAMA2

=

Array

@

rama, Ne

D 

. dane;

wr2

=

Graphics

@8

Red, RAMA2

<D

;

Analiza trzeciej postaci drgañ w³asnych ramy

In[209]:=

nr

=

3;

nr2

=

Nss

-

nr

+

1;

proj_SES_moj.nb

11

In[211]:=

Ω =

CW

@@

nr2

DD

Out[211]=

1154.11

In[212]:=

pos

=

rozw

@@

2, nr2

DD

;

In[213]:=

Do

@8

qx

@

k

D =

pos

@@

3

*

k

-

2

DD

,

qy

@

k

D =

pos

@@

3

*

k

-

1

DD

,

j

@

k

D =

pos

@@

3

*

k

DD

<

,

8

k, 1, Ne

<D

12

proj_SES_moj.nb

In[214]:=

k

=

1;

rama

@

k

D =

Line

@88

xA

@

k

D

, yA

@

k

D<

,

8D

L1



2

+

xB

@

k

D

, yB

@

k

D<<D

;

Do

@8

j

=

k

-

1;

sx

=

H

j

-

1

L * D

L1

+ D

L1



2;

rama

@

k

D =

Line

@88

sx

+

xA

@

k

D

, yA

@

k

D<

,

8

sx

+ D

L1

+

xB

@

k

D

, yB

@

k

D<<D

<

,

8

k, 2, N1

<D

;

k

=

N1

+

1;

rama

@

k

D =

Line

B::

a

-

D

L1

2

+

xA

@

k

D

, yA

@

k

D>

,

8

a

+

xD

@

k

D

, yD

@

k

D<

,

:

a

+

xB

@

k

D

,

D

L2

2

+

yB

@

k

D>>F

;

Do

@8

j

=

k

-

H

N1

+

1

L

;

sy

=

H

j

-

1

L * D

L2

+ D

L2



2;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, sy

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, sy

+ D

L2

+

xB

@

k

D<<D

<

,

8

k, N1

+

2, N1

+

N2

<D

;

k

=

N1

+

N2

+

1;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, a



2

- D

L2



2

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, a



2

+ D

L3



2

+

xB

@

k

D<<D

;

Do

@8

j

=

k

-

H

N1

+

N2

+

1

L

;

sy

=

a



2

+

H

j

-

1

L * D

L3

+ D

L3



2;

rama

@

k

D =

Line

@88

a

-

yA

@

k

D

, sy

+

xA

@

k

D<

,

8

a

-

yB

@

k

D

, sy

+ D

L3

+

xB

@

k

D<<D

<

,

8

k, N1

+

N2

+

2, N1

+

N2

+

N3

<D

;

k

=

N1

+

N2

+

N3

+

1;

rama

@

k

D =

Line

B::

a

+

xA

@

k

D

, a

-

D

L3

2

+

yA

@

k

D>

,

8

a

+

xD

@

k

D

, a

+

yD

@

k

D<

,

:

a

+

D

L4

2

+

xB

@

k

D

, a

+

yB

@

k

D>>F

;

Do

@8

j

=

k

-

H

N1

+

N2

+

N3

+

1

L

;

sx

=

a

+

H

j

-

1

L * D

L4

+ D

L4



2;

rama

@

k

D =

Line

@88

sx

+

xA

@

k

D

, a

+

yA

@

k

D<

,

8

sx

+ D

L4

+

xB

@

k

D

, a

+

yB

@

k

D<<D

<

,

8

k, N1

+

N2

+

N3

+

2, Ne

<D

;

k

=

Ne

+

1;

rama

@

k

D =

Line

@88

a

+

b

+

xA

@

k

D

, a

+

yA

@

k

D<

,

8

a

+

b

+

xB

@

k

D

, a

+

yB

@

k

D<<D

;

In[228]:=

RAMA3

=

Array

@

rama, Ne

D 

. dane;

wr3

=

Graphics

@8

Blue, RAMA3

<D

;

In[230]:=

belka0

=

Graphics

@8

Black, Line

@88

0, 0

<

,

8

a, 0

<

,

8

a, a

<

,

8

a

+

b, a

<<D

<D 

. dane;

proj_SES_moj.nb

13

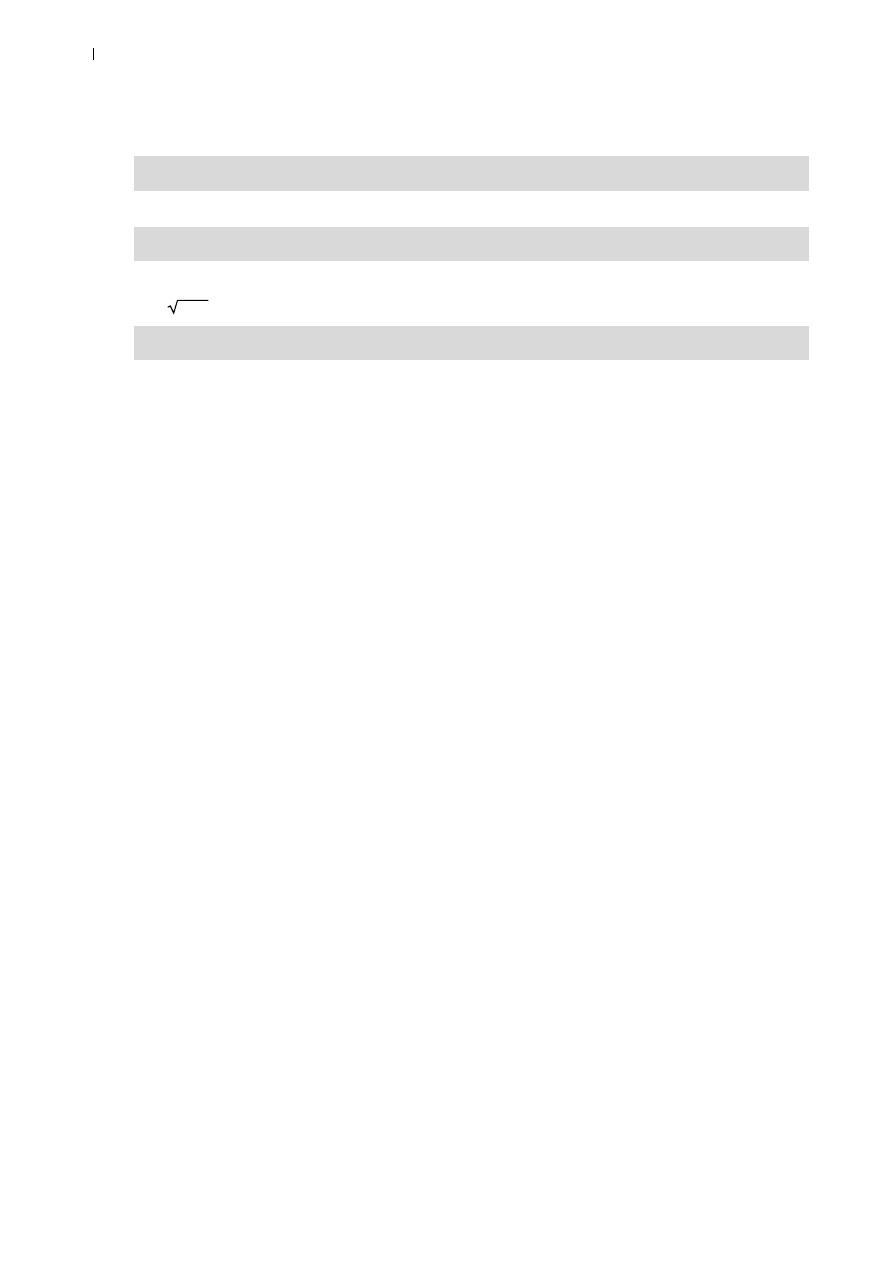
In[231]:=

Show

@8

belka0, wr1, wr2, wr3

<

, Frame

®

True

D

Out[231]=

0.0

0.5

1.0

1.5

0.0

0.2

0.4

0.6

0.8

1.0

1.2

Ugiêcie statyczne

In[232]:=

Do

@8

wp

@

3

*

k

-

2

D =

fx

@

k

D

,

wp

@

3

*

k

-

1

D =

fy

@

k

D

,

wp

@

3

*

k

D =

m

j

@

k

D

<

,

8

k, 1, Ne

<D

In[233]:=

WP

=

Array

@

wp, Nss

D

;

MatrixForm

@

Transpose

@8

NUM, WP

<DD

;

14

proj_SES_moj.nb

In[235]:=

Do

@8

fx

@

k

D =

0;

fy

@

k

D =

0;

m

j

@

k

D =

0;

<

,

8

k, 1, Ne

<D

fy

@

1

D = -

q

*

D

L1

2

;

Do

@8

fy

@

k

D = -

q

* D

L1;

<

,

8

k, 2, N1

<D

;

fy

@

N1

+

1

D = -

q

*

D

L1

2

;

fy

@

N1

+

N2

+

1

D = -

F;

fy

@

N1

+

N2

+

N3

+

1

D = -

q

*

D

L4

2

;

Do

@8

fy

@

k

D = -

q

* D

L4;

<

,

8

k, N1

+

N2

+

N3

+

2, Ne

<D

;

fy

@

Ne

+

1

D = -

q

*

D

L4

2

;

In[243]:=

MatrixForm

@

Transpose

@8

NUM, WP

<DD

;

Numeryczna postaæ wektora si³ uogólnionych

In[244]:=

numWP

=

WP



. dane;

MatrixForm

@

numWP

D

;

Wyznaczenie statycznego ugiêcia ramy

In[246]:=

WQs

=

LinearSolve

@

numMC, numWP

D

;

In[247]:=

Do

@8

qx

@

k

D =

WQs

@@

3

*

k

-

2

DD

,

qy

@

k

D =

WQs

@@

3

*

k

-

1

DD

,

j

@

k

D =

WQs

@@

3

*

k

DD

<

,

8

k, 1, Ne

<D

In[248]:=

sk

=

10;

proj_SES_moj.nb

15

In[249]:=

k

=

1;

rama4

@

k

D =

Line

@88

sk

*

xA

@

k

D

, sk

*

yA

@

k

D<

,

8D

L1



2

+

sk

*

xB

@

k

D

, sk

*

yB

@

k

D<<D

;

Do

@8

j

=

k

-

1;

sx

=

H

j

-

1

L * D

L1

+ D

L1



2;

rama4

@

k

D =

Line

@88

sx

+

sk

*

xA

@

k

D

, sk

*

yA

@

k

D<

,

8

sx

+ D

L1

+

sk

*

xB

@

k

D

, sk

*

yB

@

k

D<<D

<

,

8

k, 2, N1

<D

;

k

=

N1

+

1;

rama4

@

k

D =

Line

B::

a

-

D

L1

2

+

sk

*

xA

@

k

D

, sk

*

yA

@

k

D>

,

8

a

+

sk

*

xD

@

k

D

, sk

*

yD

@

k

D<

,

:

a

+

sk

*

xB

@

k

D

,

D

L2

2

+

sk

*

yB

@

k

D>>F

;

Do

@8

j

=

k

-

H

N1

+

1

L

;

sy

=

H

j

-

1

L * D

L2

+ D

L2



2;

rama4

@

k

D =

Line

@88

a

-

sk

*

yA

@

k

D

, sy

+

sk

*

xA

@

k

D<

,

8

a

-

sk

*

yB

@

k

D

, sy

+ D

L2

+

sk

*

xB

@

k

D<<D

<

,

8

k, N1

+

2, N1

+

N2

<D

;

k

=

N1

+

N2

+

1;

rama4

@

k

D =

Line

@88

a

-

sk

*

yA

@

k

D

, a



2

- D

L2



2

+

sk

*

xA

@

k

D<

,

8

a

-

sk

*

yB

@

k

D

, a



2

+ D

L3



2

+

sk

*

xB

@

k

D<<D

;

Do

@8

j

=

k

-

H

N1

+

N2

+

1

L

;

sy

=

a



2

+

H

j

-

1

L * D

L3

+ D

L3



2;

rama4

@

k

D =

Line

@88

a

-

sk

*

yA

@

k

D

, sy

+

sk

*

xA

@

k

D<

,

8

a

-

sk

*

yB

@

k

D

, sy

+ D

L3

+

sk

*

xB

@

k

D<<D

<

,

8

k, N1

+

N2

+

2, N1

+

N2

+

N3

<D

;

k

=

N1

+

N2

+

N3

+

1;

rama4

@

k

D =

Line

B::

a

+

sk

*

xA

@

k

D

, a

-

D

L3

2

+

sk

*

yA

@

k

D>

,

8

a

+

sk

*

xD

@

k

D

, a

+

sk

*

yD

@

k

D<

,

:

a

+

D

L4

2

+

sk

*

xB

@

k

D

, a

+

sk

*

yB

@

k

D>>F

;

Do

@8

j

=

k

-

H

N1

+

N2

+

N3

+

1

L

;

sx

=

a

+

H

j

-

1

L * D

L4

+ D

L4



2;

rama4

@

k

D =

Line

@88

sx

+

sk

*

xA

@

k

D

, a

+

sk

*

yA

@

k

D<

,

8

sx

+ D

L4

+

sk

*

xB

@

k

D

, a

+

sk

*

yB

@

k

D<<D

<

,

8

k, N1

+

N2

+

N3

+

2, Ne

<D

;

k

=

Ne

+

1;

rama4

@

k

D =

Line

@88

a

+

b

+

sk

*

xA

@

k

D

, a

+

sk

*

yA

@

k

D<

,

8

a

+

b

+

sk

*

xB

@

k

D

, a

+

sk

*

yB

@

k

D<<D

;

In[263]:=

RAMA4

=

Array

@

rama4, Ne

D 

. dane;

16

proj_SES_moj.nb

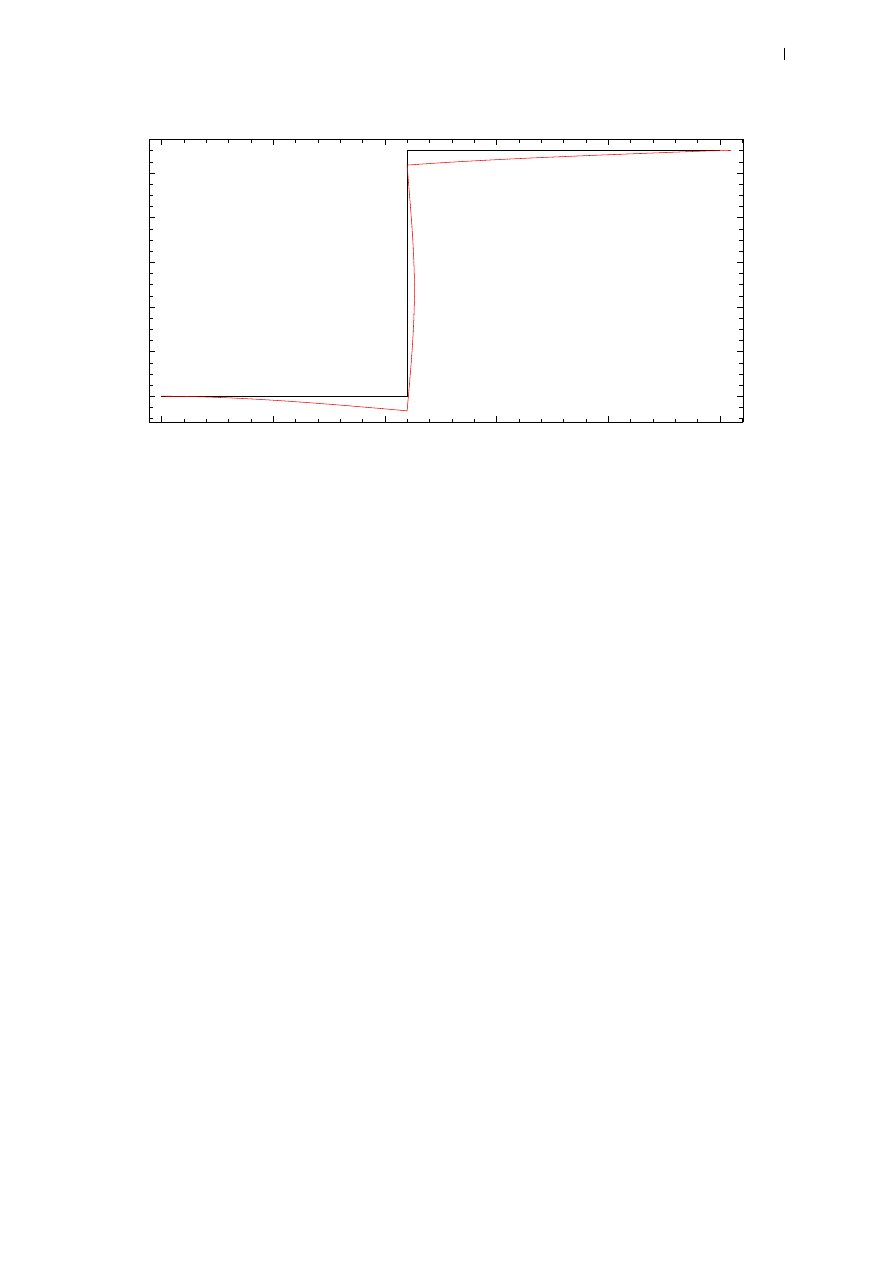
In[264]:=

Show

@

belka0, Graphics

@8

Red, RAMA4

<D

, Frame

®

True

D

Out[264]=

0.0

0.5

1.0

1.5

2.0

2.5

0.0

0.2

0.4

0.6

0.8

1.0

proj_SES_moj.nb

17