KOD

ZDAJĄCEGO

Miejsce na identyfikację szkoły

LISTOPAD

2011

Za rozwiązanie

wszystkich zadań

można otrzymać

łącznie 50 punktów.

PESEL ZDAJĄCEGO

Wpisuje zdajàcy przed rozpocz´ciem pracy

ARKUSZ PRÓBNEJ MATURY

Z OPERONEM

MATEMATYKA

POZIOM PODSTAWOWY

Czas pracy: 170 minut

In struk cja dla zda ją ce go

1.

Sprawdź, czy ar kusz eg za mi na cyj ny za wie ra 15 stron
(za da nia 1–34). Ewen tu al ny brak zgłoś prze wod ni czą -
ce mu ze spo łu nad zo ru ją ce go eg za min.

2.

Roz wią za nia zadań i od po wie dzi za pisz w miej scu
na to prze zna czo nym.

3.

W roz wią za niach za dań ra chun ko wych przed staw tok
ro zu mo wa nia pro wa dzą cy do osta tecz ne go wy ni ku.

4.

Pisz czy tel nie. Uży waj dłu go pi su/pió ra tyl ko z czar nym
tu szem/atra men tem.

5.

Nie uży waj ko rek to ra, a błęd ne za pi sy wy raź nie prze -
kreśl.

6.

Za pi sy w brud no pi sie nie będą oce niane.

7.

Obok nu me ru każ de go za da nia po da na jest mak sy -
mal na licz ba punk tów moż li wych do uzy ska nia.

8. Możesz ko rzy stać z zestawu wzorów matematycznych,

cyrkla i li nij ki oraz kal ku la to ra.

Życzymy powodzenia

!

Arkusz opracowany przez Wydawnictwo Pedagogiczne OPERON.

Kopiowanie w całości lub we fragmentach bez zgody wydawcy zabronione. Wydawca zezwala na kopiowanie zadań

przez dyrektorów szkół biorących udział w programie Próbna Matura z OPERONEM.

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

ZA DA NIA ZA MKNIĘ TE

W zadaniach od 1. do 25. wybierz i zaznacz jedną poprawną odpowiedź.

Zadanie 1. (1 pkt)

Największa liczba naturalna

spełniająca nierówność

to

A. 3

B.

C.

D.

Zadanie 2. (1 pkt)

Liczba jest

równa

A. B. C. D.

Zadanie 3. (1 pkt)

Liczba jest

równa

A. B. C. D.

Zadanie 4. (1 pkt)

pewnej liczby jest o

mniejsze od tej liczby. Tą liczbą jest

A. B. C. D.

Zadanie 5. (1 pkt)

Rozwiązaniem równania

jest liczba

A. B. C. D.

Zadanie 6. (1 pkt)

Większa z liczb spełniających równanie

to

A. B. C. D.

Zadanie 7. (1 pkt)

Przedział zaznaczony na osi liczbowej

jest zbiorem rozwiązań nierówności
A. B. C. D.

n

n

2

1

< r -

5

6

0

7

2

16

3

8

3

1

4

3

+

-

b l

1

-

49

4

2

4

1

-

1

6

log

2

3

log

log

$

log

log

2

12

2

3

log

log

+

2

3

log

log

-

16

%

20

32

20

2

-

20

-

2

x

x

2

1

- =

+

-

1

-

1

3

5

0

6

8

0

x

x

2

+

+

=

2

4

2

-

4

-

X

2

1

0

|

|

x

1

1

G

-

|

|

x

1

1

H

-

|

1 |

2

x

H

+

|

|

x

1

1

G

+

2

BRUD NO PIS

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

3

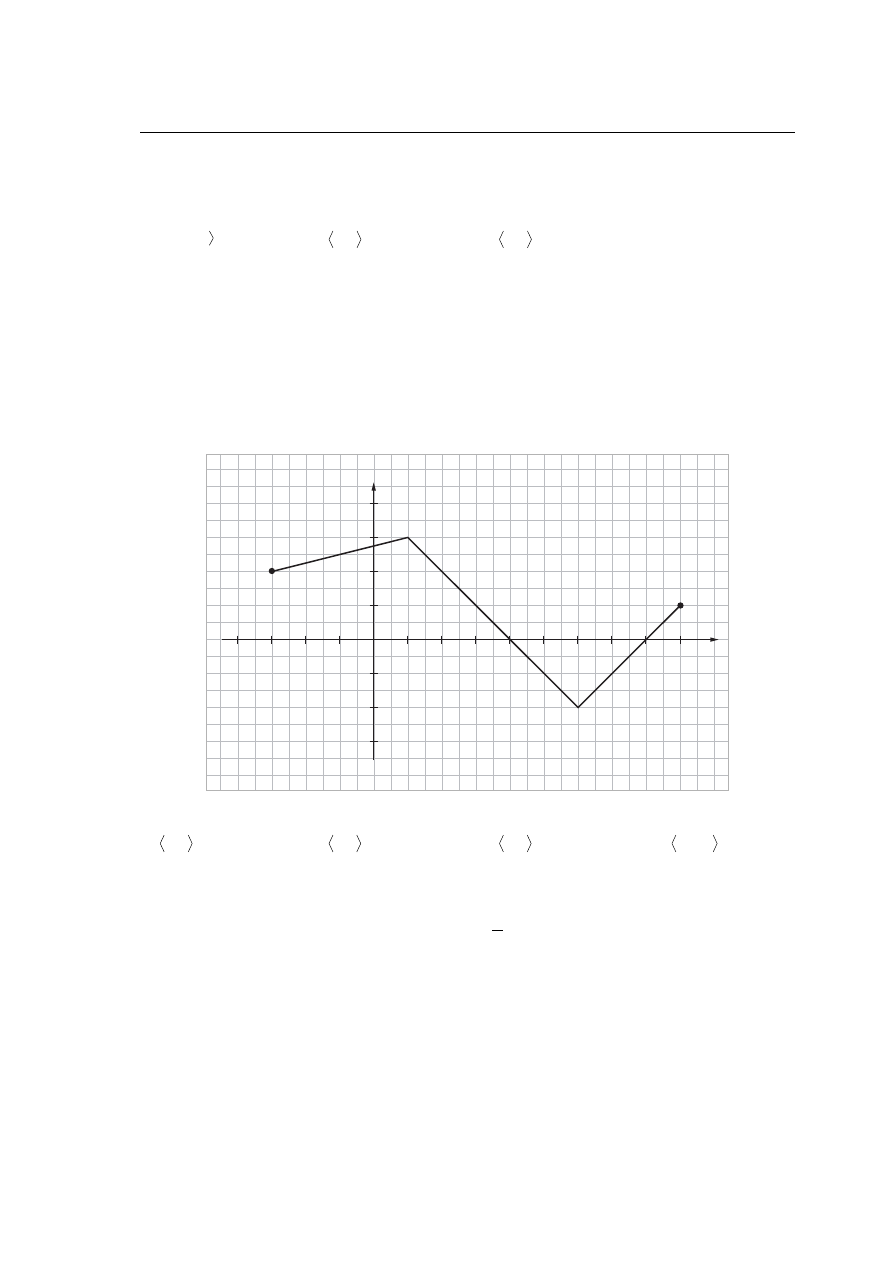
Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Zadanie 8. (1 pkt)

Dziedziną funkcji

jest zbiór

A. B. C. D.

Zadanie 9. (1 pkt)

Funkcja liniowa

jest rosnąca, gdy

A. B. C. D.

Zadanie 10. (1 pkt)

Rysunek przedstawia wykres funkcji

.

Funkcja jest malejąca w przedziale

A. B. C. D.

Zadanie 11. (1 pkt)

Punkt

należy do wykresu funkcji

. Liczba

jest równa

A. B. C. D.

Zadanie 12. (1 pkt)

Do zbioru rozwiązań nierówności

należy liczba

A. B. C. D.

2

3

-

0

2

-

( )

,

,

1

1

4

f x

x

x

x

x

2

1 gdy

gdy

<

G

G

=

-

+

-

*

, 1

3

-

]

g

,

0 4

,

1 4

(

, 4

3

-

( )

(

2)

2

f x

m

x

m

=

+

+

4

m > -

2

m > -

2

m <

2

m < -

y

f x

=

^ h

X

Y

1

– 3

– 2

– 1

0

2

3

4

– 4

– 3

– 2

– 1

2

1

3

4

5

6

7

8

9

2, 4

-

0, 6

1, 6

0, 4

a

( )

f x

x

4

=

,

P

a

1 2

=

+

]

g

1

2

1

-

0

x

9

2

G

4

BRUD NO PIS

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

5

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Zadanie 13. (1 pkt)

Wybierz i zaznacz równanie opisujące prostą prostopadłą do prostej o równaniu

.

A. B. C. D.

Zadanie 14. (1 pkt)

Liczby , ,

są w podanej kolejności drugim, trzecim i czwartym wyrazem ciągu arytmetycznego.

Wówczas liczba

jest równa

A. B. C. D.

Zadanie 15. (1 pkt)

W ciągu geometrycznym

są dane:

,

. Suma czterech kolejnych początkowych

wyrazów tego ciągu jest równa
A. B. C. D.

Zadanie 16. (1 pkt)

Kąt

jest ostry i

. Wówczas

A. B. C. D.

Zadanie 17. (1 pkt)

Dane są wielomiany

oraz

. Stopień wielomianu

jest równy

A. B. C. D.

Zadanie 18. (1 pkt)

Mediana

danych: , , , , jest

równa

A. B. C. D.

Zadanie 19. (1 pkt)

Liczba punktów wspólnych okręgu o równaniu

z prostą o równaniu

jest równa

A. B. C.

D.

Zadanie 20. (1 pkt)

Punkty

i

są wierzchołkami trójkąta równobocznego

. Wysokość tego

trójkąta jest równa

A. B. C. D.

1

y

x

2

1

=

+

2

1

y

x

=

-

1

y

x

2

1

= -

+

0,5

1

y

x

=

-

2

1

y

x

= -

+

2

x +

4

x

x

1

6

3

2

2

q = -

1

a

2

= -

a

n

^ h

7,5

2,5

-

7,5

-

2,5

sin

5

2

a =

a

cos

sin

1

a

a

=

-

cos

sin

<

a

a

cos

sin

>

a

a

cos

sin

a

a

=

( )

( )

W x

V x

+

( )

1

V x

x

4

=

+

( )

1

W x

x

4

=

-

0

16

8

4

1

0

6

2

4

-

1

2,5

0

6

1

y = -

4

y

2

2

x

1 +

=

-

]

g

3

2

1

0

ABC

,

B

2 2

=

]

g

,

A

2

1

= -

-

]

g

2,5 3

5 3

2 3

2,5

6

BRUD NO PIS

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

7

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Zadanie 21. (1 pkt)

Dany jest okrąg o środku w punkcie . Miara kąta

jest równa

.

Suma miar kątów

i

jest równa

A. B. C. D.

Zadanie 22. (1 pkt)

Trapez jest prostokątny. Trójkąty podobne

i

są równoramienne.

Obwód trapezu jest równy

A. B. C. D.

Zadanie 23. (1 pkt)

Graniastosłup ma

wierzchołków. Liczba wszystkich krawędzi tego graniastosłupa jest równa

A. B. C. D.

Zadanie 24. (1 pkt)

Tworząca stożka jest o

dłuższa od promienia podstawy. Pole powierzchni bocznej tego stożka jest

równe

. Tworząca stożka ma zatem długość

A. B. C. D.

Zadanie 25. (1 pkt)

Cztery dziewczynki i sześciu chłopców siedzą na tym samym pniu zwalonego dębu. Dziewczynki siedzą
obok siebie i chłopcy również siedzą obok siebie. Wszystkich możliwych sposobów posadzenia dzieci
w ten sposób jest
A. B.

C. D.

°

70

a

S

S

a

b

c

c

b

140°

70°

210°

°

180

CBD

ABD

A

B

C

D

2

4

4

2

+

2 2

4

2 2

+

2

6

n +

3

9

n +

6

18

n +

4

8

n +

3

n +

2

15r

15

3

5

1

2 4 1 2 3 4 5 6

$

$

$

$

$

$

$

4 6

$

1 2 3 4 6 5 4 3 2 1 2

$

$

$

$

$

$

$

$

$

$

1 2 3 4 6 5 4 3 2 1

$

$

$

$

$

$

$

$

$

8

BRUD NO PIS

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

9

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

ZADANIA OTWARTE

Rozwiązania zadań o numerach od 26. do 34. należy zapisać w wyznaczonych miejscach pod treścią

zadania.

Zadanie 26. (2 pkt)

Napisz równanie prostej równoległej do prostej o równaniu

i przechodzącej przez

punkt .

Odpowiedź: .......................................................................................................................................................

Zadanie 27. (2 pkt)

W trójkącie prostokątnym jedna z przyprostokątnych ma długość . Kąt ostry przy tym boku ma miarę .

Wykaż, że

.

3

4

0

x

y

-

+ -

=

,

P

1

4

= -

-

]

g

a

sin

cos

1

>

a

a

+

a

10

Zadanie 28. (2 pkt)

Wykaż, że przekątna prostopadłościanu o krawędziach długości , , ma długość

.

Zadanie 29. (2 pkt)

Rozwiąż nierówność

.

Odpowiedź: .......................................................................................................................................................

a

b

c

2

2

2

+

+

c

b

a

x

x

5

6

2

G

+

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

11

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Zadanie 30. (2 pkt)

Wiadomo, że

i

są takimi zdarzeniami losowymi zawartymi w

, że

,

i .

Oblicz

.

Odpowiedź: .......................................................................................................................................................

Zadanie 31. (2 pkt)

Przekątna równoległoboku ma długość

cm i tworzy z krótszym bokiem kąt prosty, a z dłuższym

bokiem kąt

. Oblicz długość krótszego boku tego równoległoboku.

Odpowiedź: .......................................................................................................................................................

10

°

30

( )

0,6

P B =

( )

,

P A

0 7

=

X

B

A

(

)

P A

B

+

(

)

,

P A

B

0 8

,

=

12

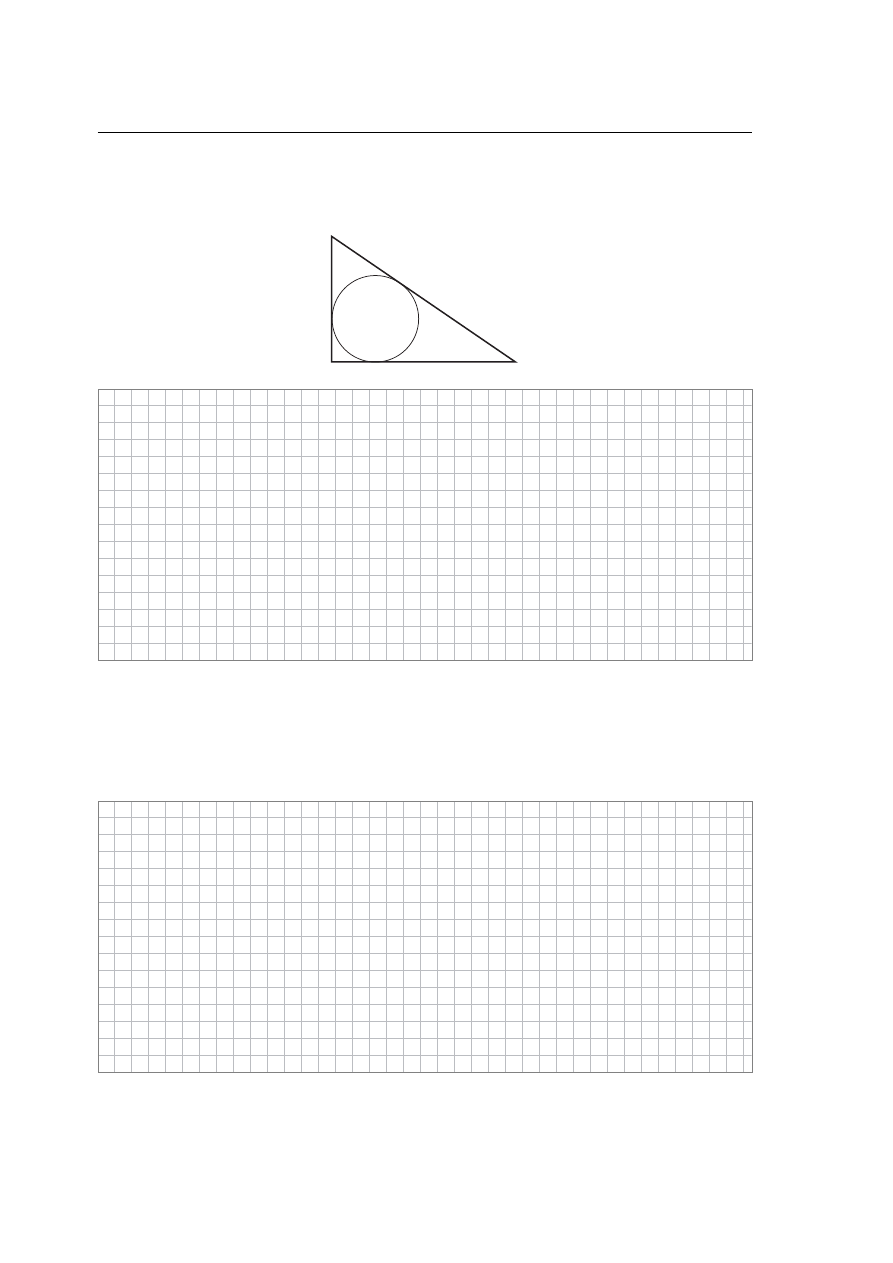
Zadanie 32. (4 pkt)

Okrąg wpisany w trójkąt prostokątny

jest styczny do przeciwprostokątnej

w punkcie

.

Wiadomo, że

i

. Oblicz promień tego okręgu.

Odpowiedź: .......................................................................................................................................................

Zadanie 33. (4 pkt)

Rzucamy dwukrotnie kostką do gry. Jakie jest prawdopodobieństwo tego, że liczba oczek otrzymana
w pierwszym rzucie jest większa od liczby oczek otrzymanej w drugim rzucie?

Odpowiedź: .......................................................................................................................................................

K

AB

ABC

|

|

KB

6

=

|

|

AK

4

=

A

B

K

C

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

13

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

Zadanie 34. (5 pkt)

Piramida ma kształt ostrosłupa prawidłowego czworokątnego, którego wysokość jest równa , a długość

krawędzi bocznej jest równa

. Oblicz miarę kąta nachylenia ściany bocznej piramidy do podstawy.

Odpowiedź: .......................................................................................................................................................

6

2 15

14

BRUD NO PIS (nie pod le ga oce nie)

Matematyka. Poziom podstawowy

Próbna Matura z OPERONEM i „Gazetą Wyborczą”

15