Marek Pęczkowski

Excel

Podstawy

MP, Warszawa 2004

2

Spis treści

Wstęp ......................................................................................................... 3
1. Podstawowe elementy programu ............................................................ 4
2. Poruszanie się po arkuszu ....................................................................... 9
3. Wprowadzanie danych ............................................................................11
4. Zaznaczanie obszarów .............................................................................16
5. Formatowanie komórek.......................................................................... 20
6. Kopiowanie, przenoszenie i usuwanie komórek arkusza..................... 26
7. Automatyczne wypełnianie obszarów.................................................... 30
8. Wprowadzanie wzorów........................................................................... 33
9. Nazwy komórek i obszarów.................................................................... 44
10. Adresy komórek we wzorach.................................................................. 49

Literatura................................................................................................. 59

3

Wstęp

Program Microsoft Excel umożliwia sporządzanie kosztorysów, analiz finansowych i
statystycznych, tworzenie wykresów i profesjonalną prezentację informacji. Pozwala
porównywać różne warianty planów, tworzyć listę płac, rozwiązywać problemy
matematyczne, fizyczne i inżynierskie, przeprowadzać eksperymenty symulacyjne, zarządzać
nieskomplikowaną bazą danych. Program pozwala na tworzenie własnych makropoleceń w
języku Visual Basic dla Aplikacji (VBA). Ze względu na łatwość obsługi i powszechną
dostępność jest szeroko wykorzystywany w biurach, małych firmach, szkołach i na
komputerach domowych. Nauczyciele często przechowują w arkuszu listy i oceny swoich
uczniów, pracownicy biur spisy kontrahentów lub listy stanów magazynowych, cenniki i inne
dane handlowe a naukowcy - wyniki pomiarów doświadczalnych i przeprowadzanych
eksperymentów symulacyjnych.

Silną stroną programu jest naturalny i przyjazny sposób zarządzania danymi oraz
natychmiastowa aktualizacja wyników obliczeń i wykresów przy zmianie parametrów
problemu. Ze względu na łatwość wprowadzania danych i korekty błędów często
wykorzystuje się arkusz jako pierwszy etap przygotowania zbiorów danych do
specjalistycznych analiz statystycznych. Wyniki obliczeń są zapisywane w plikach
rozpoznawanych przez większość programów statystycznych i ekonometrycznych. Ponadto
wiele z tych programów posiada edytory danych wzorowane z koncepcji arkusza
kalkulacyjnego.

Oczywiście, jak każdy program, posiada swoje ograniczenia i w wielu dziedzinach ustępuje
programom specjalistycznym (np. tworzenie map, analizy ekonometryczne, duże bazy
danych, grafika komputerowa, modelowanie procesów gospodarczych). Można mieć też
wiele zastrzeżeń do stosowanej terminologii nie zawsze zgodnej z przyjętą w matematyce,
statystyce i finansach. Zdarzają się też błędy ortograficzne w komunikatach wyświetlanych w
oknach dialogowych.

W tym opracowaniu poruszamy tematy wprowadzania danych do arkusza, formatowania,
wykonywania obliczeń z wykorzystaniem wzorów, funkcji standardowych i nazw komórek.
Nie poruszamy tematów związanych z tworzeniem wykresów, pracy z bazą danych,
drukowania i wykorzystania Excela do rozwiązywania bardziej zaawansowanych problemów
matematycznych, statystycznych i finansowych.

4

1. Podstawowe elementy programu

Excel uruchamia się korzystając z dowolnej metody uruchamiania aplikacji Windows, na
przykład przez kliknięcie przycisku Start i wybranie polecenia Programy | Microsoft Excel
z rozwijanego menu albo przez dwukrotne kliknięcie na ikonie skrótu programu na pulpicie.

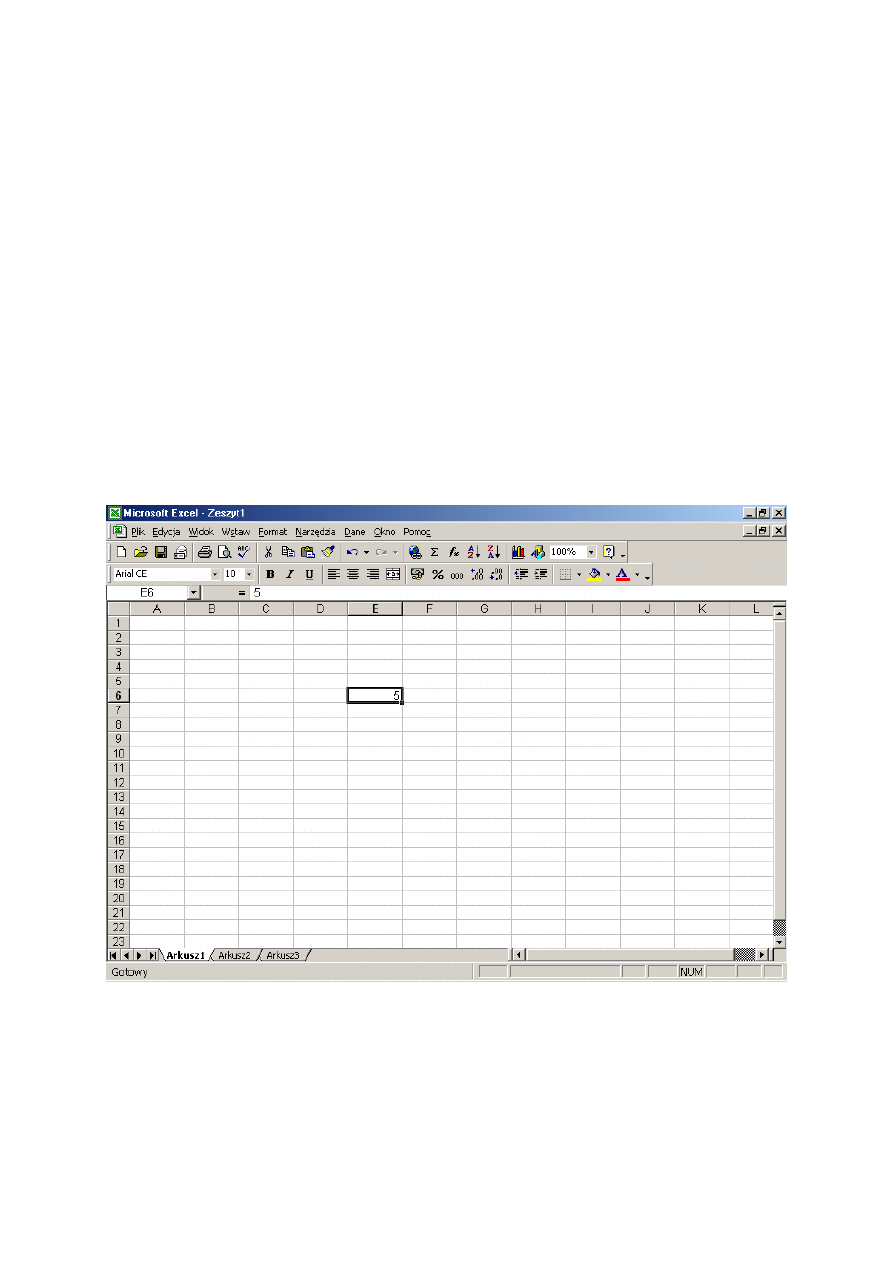
Po uruchomieniu Excela wygląd ekranu jest podobny do przedstawionego na rys. 1.1. Mogą
wystąpić pewne różnice, ponieważ niektóre elementy dają się konfigurować przez
użytkownika. Najwięcej miejsca zajmuje obszar roboczy arkusza. Tu wprowadza się dane i
wykonuje obliczenia.

Arkusz jest prostokątną tablicą składającą się z wierszy i kolumn. Wiersze są oznaczone
kolejnymi liczbami 1, 2, 3,..., a kolumny są oznaczone literami alfabetu łacińskiego A, B, C,...
Na ekranie widzimy tylko niewielką część arkusza (na rysunku 1.1 widać wiersze 1-23 i
kolumny A-L), jednak cały arkusz ma 65536 wierszy (

16

2 ) i 256 kolumn (

8

2 ). Pierwszych 26

kolumn ma oznaczenia jednoliterowe A,...,Z, następne kolumny mają oznaczenia dwuliterowe
AA, AB,....,AZ, BA, BB,...., BZ, CA,. CB,... Ostatnią kolumną jest IV.

Rys. 1.1 Arkusz kalkulacyjny

Kolumny i wiersze są podzielone pionowymi i poziomymi liniami siatki. Zatem arkusz
przypomina ogromną kartkę papieru w kratkę. Na przecięciu wiersza i kolumny znajduje się
komórka, będąca odpowiednikiem kratki w zeszycie. Do komórek arkusza można wpisywać
dane: liczby, daty, teksty i wzory. Adres komórki jest określany za pomocą współrzędnych
kolumny i wiersza, w których znajduje się komórka. Najpierw podajemy symbol (etykietę)
kolumny a później numer (etykietę) wiersza. Adresem komórki znajdującej się na przecięciu

5

czwartego wiersza i trzeciej kolumny (C) jest C4. Adresem komórki znajdującej w prawym
dolnym rogu arkusza jest IV65536.

Jedna komórka jest wyróżniona pogrubionym obramowaniem (na rysunku jest to komórka
E6). Nazywamy ją komórką bieżącą lub komórką aktywną. Jest to komórka, do której w danej
chwili można wpisać dane. Adres komórki bieżącej jest widoczny w polu nazwy znajdującym
się po lewej stronie nad arkuszem. Etykiety wiersza i kolumny komórki bieżącej są
wyróżnione uwypukleniem.

Większość elementów widocznych na ekranie jest typowych dla programów pracujących w
środowisku Windows. Są to:

1. Pasek tytułu

Jest widoczny na samej górze ekranu. Zawiera nazwę programu Microsoft Excel oraz
nazwę dokumentu. Domyślną nazwą pierwszego otwieranego dokumentu jest Zeszyt1.
Nazwa ta obowiązuje do czasu nadania dokumentowi nowej nazwy w momencie
zapisywania go do pliku dyskowego.

2. Pasek menu

Główne menu programu zawiera pozycje: Plik, Edycja, Widok, Wstaw, Format,
Narzędzia, Dane, Okno, Pomoc. Niektóre z nich znane są z innych programów
pracujących w Windows, niektóre są charakterystyczne dla Excela. Pozycje głównego
menu mogą zmieniać się w zależności od wykonywanych operacji (np. podczas pracy z
wykresami pojawia się pozycja Wykres). Każda pozycja menu jest rozwijana, co pozwala
wybierać różne polecenia. Najczęściej wybieramy pozycje z menu za pomocą myszy, ale
można je wybierać korzystając z klawiatury. Każda pozycja ma w nazwie podkreśloną
jedną literę. Jednoczesne naciśnięcie klawiszy [lewy Alt]+[wyróżniona litera] pozwala
wybrać daną pozycję z menu np. [Alt]+[e] wybiera pozycję Edycja.

3. Paski narzędzi

Wiele poleceń wybieranych z menu można wykonać w szybciej korzystając z pasków
narzędzi. Domyślnie aktywne są dwa paski: Standardowy i Formatowanie. Pasek
Standardowy zawiera polecenia czytania, zapisywania i drukowania dokumentów,
kopiowania obiektów, sortowania i inne często używane polecenia. Pasek Formatowanie
zawiera polecenia dotyczące zmiany wyglądu arkuszy i wykresów. Pozostałe paski
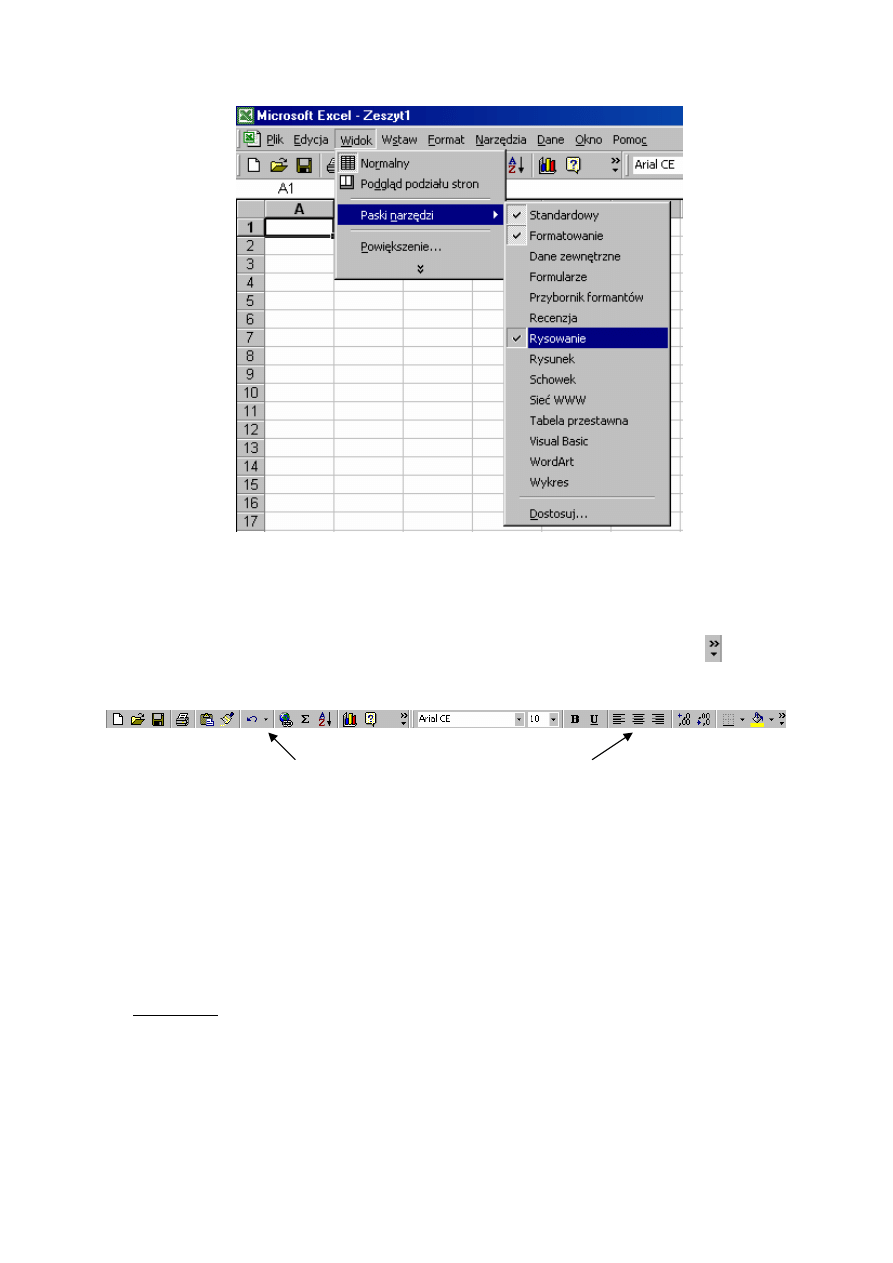
narzędzi można przywołać za pomocą polecenia Widok | Paski narzędzi. Przykładowo,
chcąc uaktywnić pasek Rysowanie, służący do wstawiania i edytowania rysunków, należy
w rozwijanym menu zaznaczyć tę pozycję.

6

Rys. 1.2. Aktywacja paska narzędzi

Pasek Rysowanie zwykle pojawia się na dole ekranu poniżej arkusza. Jeżeli ustawimy
wskaźnik myszy na którymś z przycisków paska narzędzi, uzyskamy wyjaśnienie (na
żółtym tle), do czego dany przycisk służy. Nie wszystkie dostępne przyciski paska są
wyświetlone. Na końcu każdego z pasków narzędzi znajduje się mały przycisk , którego
należy użyć do aktywacji pozostałych przycisków.

Rys. 1.3. Paski narzędzi Standardowy i Formatowanie

W programie Excel 2000 paski narzędzi Standardowy i Formatowanie są umieszczone w
tym samym wierszu poniżej menu, żeby zaoszczędzić miejsca na ekranie. Użytkownik
Excela może przesuwać pasek narzędzi w inne miejsce za pomocą uchwytu znajdującego
się po jego lewej stronie. Jeżeli chcemy ustawić paski Standardowy i Formatowanie w
dwóch wierszach, to należy za pomocą polecenia Narzędzia | Dostosuj | Opcje wyłączyć
ustawienie Paski narzędzi Standardowy i Formatowanie w jednym wierszu.

4. Pasek stanu

Jest to pasek widoczny w dolnej części ekranu. Są na nim wyświetlane informacje o stanie
arkusza (na rys. 1.1 jest to stan Gotowy) oraz o aktywności niektórych klawiszy (np. czy
włączony jest klawisz [NumLock], [CapsLock], [ScrollLock]). Na rys. 1.1 widzimy, że
włączony jest klawisz [NumLock], o czym informuje wskaźnik [NUM]. Należy zwrócić
uwagę, że niektóre operacje mogą być niedostępne, jeżeli arkusz nie znajduje się w stanie
Gotowy np. podczas wprowadzania danych do komórki (arkusz przechodzi wtedy do

Standardowy

Formatowanie

7

stanu Wprowadź) nie jest dostępna większość poleceń formatowania. Jedno z pól paska
stanu zostało zarezerwowane na wyświetlenie wyniku wybranej operacji (np. sumy,
średniej, minimum, maksimum) na wyróżnionych komórkach arkusza. Pasek stanu można
ukryć za pomocą polecenia Widok | Pasek stanu.

5. Paski przewijania pionowego i poziomego

Służą one do szybkiej nawigacji po arkuszu.

Wyjaśnienia wymaga linia znajdująca się nad obszarem arkusza.

Zawiera ona:
− pole nazwy, w którym jest wyświetlany adres bieżącej komórki lub wielkość zaznaczonej

grupy komórek

,

− przyciski Anuluj

i Wpis

pojawiające się w momencie wprowadzania danych,

służące do odwołania lub zatwierdzenia wprowadzanych zmian za pomocą myszy,

− przycisk edycji formuły , przydatny podczas wprowadzania wzorów,

− pole formuły (zwany też polem edycji), w którym jest wyświetlana zawartość bieżącej

komórki. Ustawiając kursor w tym polu możemy edytować zawartość bieżącej komórki.

Począwszy od wersji 5 Excel jest trójwymiarowy. W jednym pliku można zapisać wiele
arkuszy (maksymalnie 256), które tworzą skoroszyt (podobnie jak spięte kartki papieru
tworzą zeszyt). Domyślnie są dostępne 3 arkusze (zakładki z nazwami arkuszy: Arkusz1,
Arkusz2, Arkusz3 są widoczne w dolnej części ekranu). Na rys. 1.1 zakładka jednego z
arkuszy (Arkusz1) jest zaznaczona na białym tle. Jest to arkusz bieżący. Kliknięcie na daną
zakładkę pozwala uaktywnić wybrany arkusz. Aby wstawić nowy arkusz, należy wybrać
polecenie Wstaw | Arkusz. Aby usunąć bieżący arkusz, należy wybrać polecenie Edycja |
Usuń arkusz. Można zmienić nazwę arkusza klikając dwukrotnie na jego zakładce i wpisując
nową nazwę. Nazwa arkusza może mieć do 31 znaków. Niedopuszczalne są znaki : \ / ? * [ ].
Małe i duże litery w nazwach arkuszy są utożsamiane. Można też zmieniać kolejność arkuszy
przeciągając za pomocą myszy odpowiednie zakładki. Po lewej stronie zakładek arkuszy
znajdują się przyciski przewijania arkuszy

. Umożliwiają one dostęp do zakładek

niewidocznych w danej chwili. Pomiędzy zakładkami arkuszy a poziomym paskiem
przewijania znajduje się pole podziału zakładek. Po wskazaniu myszą tego pola kursor
przyjmuje kształt w||x. Przeciągając to pole w lewo wydłużamy pasek przewijania
poziomego, a przeciągając w prawo możemy zwiększyć liczbę wyświetlanych zakładek.

pole podziału
zakładek

Adres komórki (np. C4) odnosi się do komórki bieżącego arkusza. Jeżeli chcemy odwołać się
do komórki z innego arkusza, to należy podać dokładniejszą specyfikację adresu np.
Arkusz3!C4.

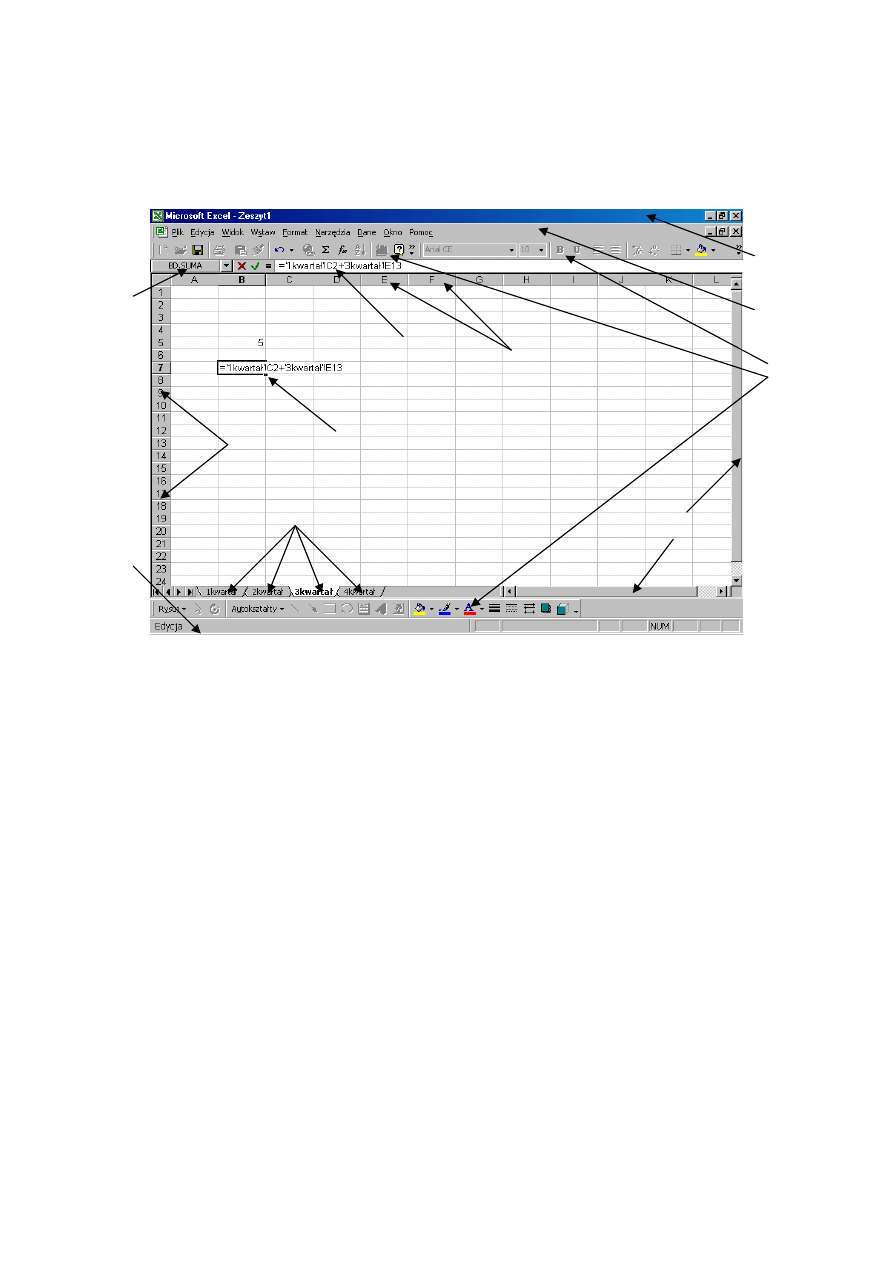
Na rys. 1.4 widzimy 4 arkusze o nazwach 1kwartał, 2kwartał, 3kwartał, 4kwartał. Bieżącym
arkuszem jest arkusz 3kwartał. W polu formuły znajduje się wzór pozwalający dodać dwie

8

komórki (komórkę C2 z arkusza 1kwartał i komórkę E13 z bieżącego arkusza 3kwartał).
Ponieważ jesteśmy w trakcie wprowadzania lub edytowania danych, w pasku stanu widzimy
napis Edycja (lub Wprowadź, Wskaż). Zaznaczyliśmy też, gdzie znajdują się poszczególne
elementy widoczne w oknie na ekranie.

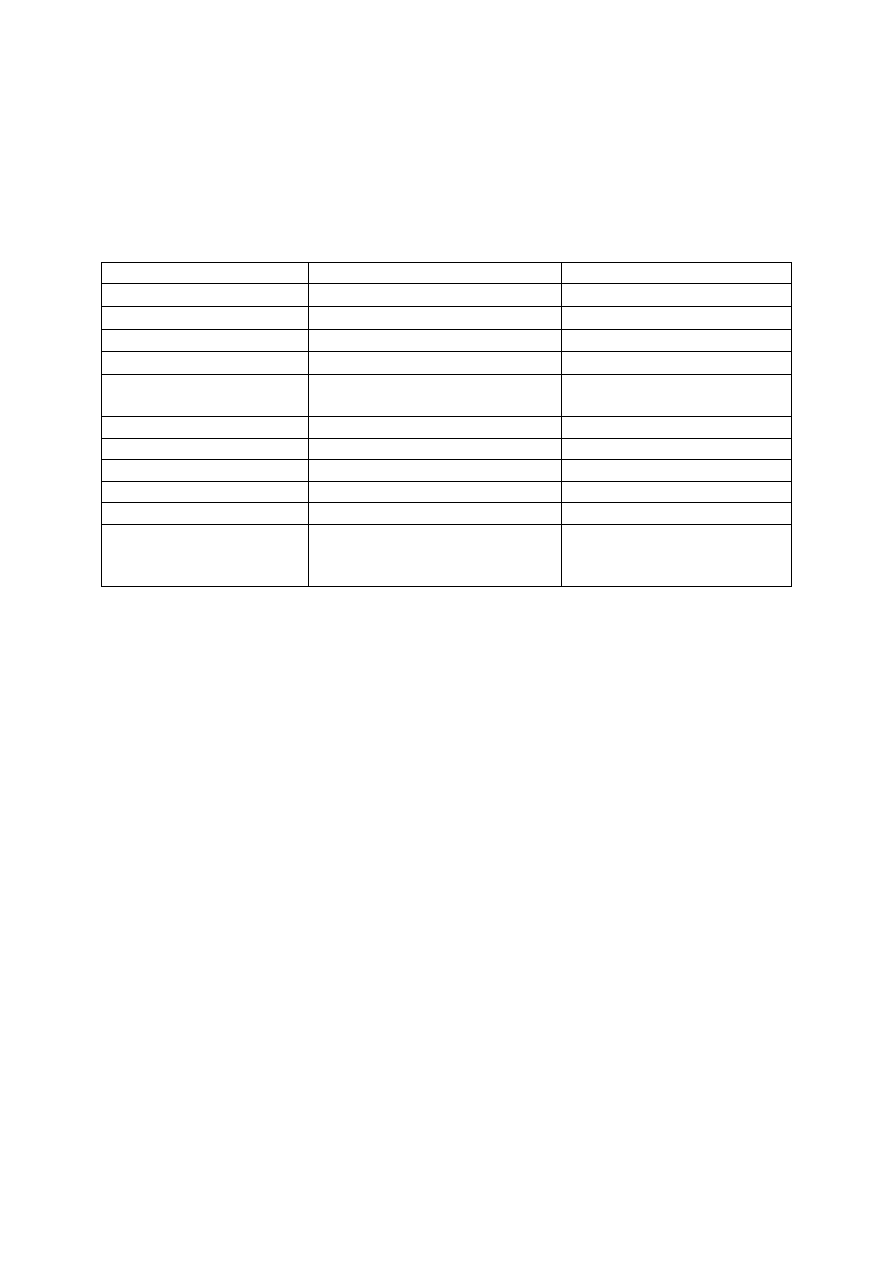
Rys. 1.4. Elementy okna

Przed przystąpieniem do wykonywania praktycznych zadań objaśnimy, jak poruszać się po
arkuszu (wybierać komórkę bieżącą), jak zaznaczać fragmenty arkusza i jak wprowadzać
dane do komórek arkusza. Podczas pracy z Excelem możemy posługiwać się klawiaturą i
myszą. Większość operacji można wykonać kilkoma sposobami: za pomocą klawiatury lub
myszy, w sposób bardziej prosty lub bardziej pracochłonny.

Posługiwanie się myszą

Podczas pracy należy zwracać uwagę na kształt wskaźnika myszy. Zmienia się on w
zależności od tego, jaki element pokazuje mysz.

¾

Biały krzyż

- mysz pokazuje komórkę arkusza. Przeciągając mysz przy
wciśniętym lewym przycisku możemy zaznaczać fragmenty arkusza

¾

Biała strzałka - mysz pokazuje element okna programu lub przycisk z paska

narzędzi. Wciśnięcie lewego przycisku myszy pozwala wybrać
pozycję z menu lub przenieść dane (obiekt) w inne miejsce

¾

I

- mysz wskazuje tekst, liczbę lub wzór w trybie edycji komórki.
Można zaznaczyć lub zmienić wpis umieszczony w komórce

¾

+

- w prawym dolnym rogu komórki znajduje się uchwyt wypełnienia.
Umieszczając tu kursor myszy i przy wciśniętym lewym przycisku
przeciągając mysz możemy kopiować dane do sąsiednich komórek

Pole
nazwy

Pole
formuły

Komórka
bieżąca

Nagłówki
kolumn

Nagłówki
wierszy

Pasek
tytułu

Pasek
menu

Paski
przewijania

Pasek
stanu

Nazwane arkusze wchodzące
w skład otwartego skoroszytu

Obszar danych

Pasek
narzędzi

9

2. Poruszanie się po arkuszu

Spójrzmy na arkusz przedstawiony na rys. 1.1. Bieżącą komórką jest komórka Y56. Aby
zmienić położenie bieżącej komórki należy wykonać jedną z poniższych operacji.

Tab. 2.1. Klawisze sterujące

Operacja

Znaczenie

Nowa komórka bieżąca

[

↓] lub [Enter]

przejście o 1 komórkę w dół Y57

[

↑]

przejście o 1 komórkę w górę Y55

[

←] lub [Shift]+[Tab]

przejście o 1 komórkę w lewo

X6

[

→] lub [Tab]

przejście o 1 komórkę w prawo

Z6

[Home]

przejście do lewej skrajnej
kolumny w tym samym wierszu

A56

[Ctrl]+[Home] przejście na początek arkusza

A1

[PageUp] przejście o 1 ekran w górę tu:

Y21

[PageDown] przejście o 1 ekran w dół tu:

Y91

[Alt]+[PageUp] przejście o 1 ekran w lewo

tu: J56

[Alt]+[PageDown] przejście o 1 ekran w prawo

tu: AN56

[Ctrl]+[Backspace] wyświetlenie obszaru arkusza, w

którym znajduje się komórka
bieżąca

Gdy włączony jest klawisz [ScrollLock], to klawisze nawigacyjne ([

↓], [↑], [←], [→])

przewijają ekran o jeden wiersz (jedną kolumnę) w kierunku strzałki, podczas gdy komórka
bieżąca nie ulega zmianie.

ƒ

Aby wskazać komórkę widoczną na ekranie (np. J23) wystarczy kliknąć na niej myszą,

ƒ

Do każdej komórki arkusza można dojść korzystając z pasków przewijania,

ƒ

Po wpisania adresu komórki ( np. AB188) w polu nazwy i naciśnięciu [Enter] dana

komórka staje się komórką bieżącą,

ƒ

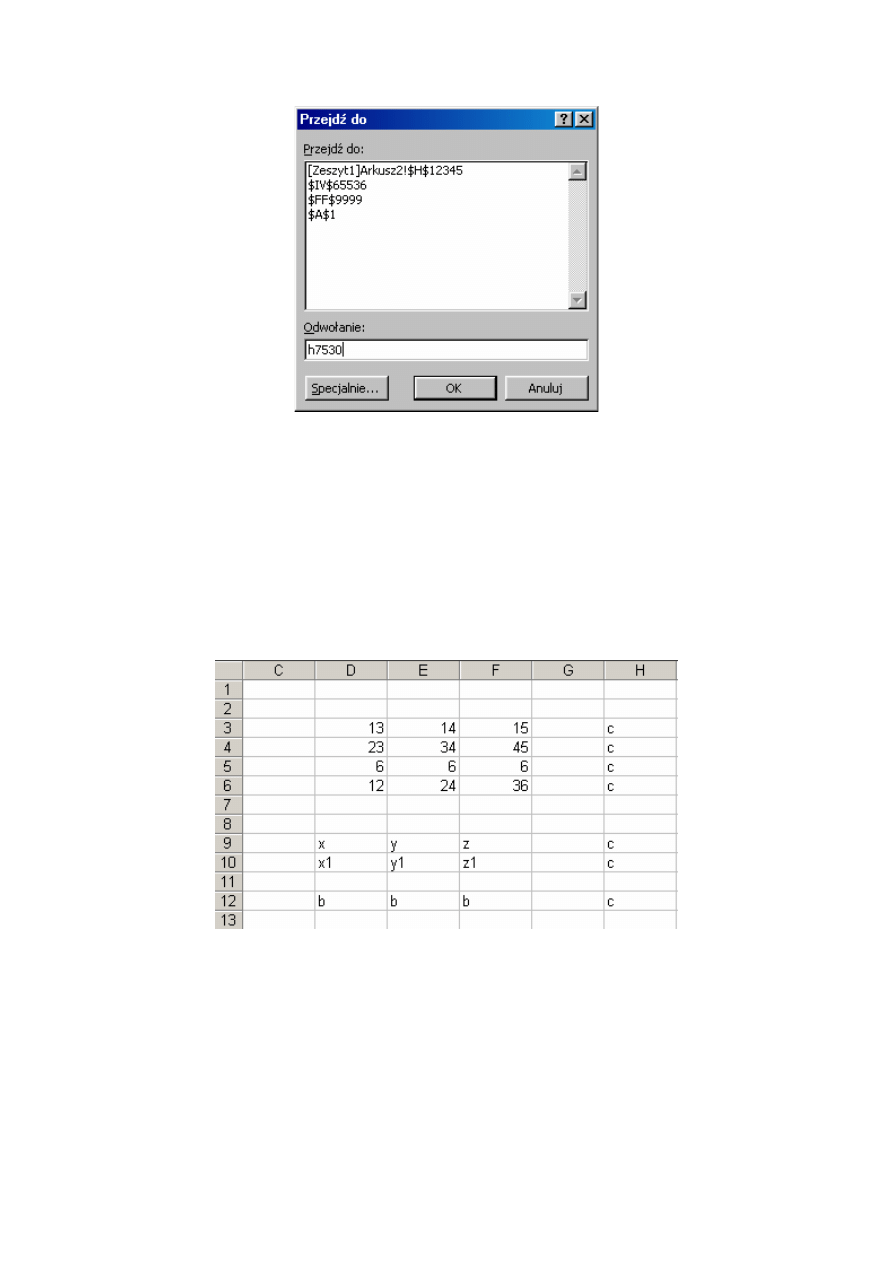
Innym sposobem przejścia do wybranej komórki jest wciśnięcie klawisza funkcyjnego

[F5] i wpisanie adresu komórki w polu Odwołanie: okna dialogowego Przejdź do. Jako
ćwiczenie polecamy sprawdzić to dla adresów: FF9999, IV65536, Arkusz2!H12345).

10

Rys. 2.1. Okno dialogowe Przejdź do

W rozdz. 9 poznamy też sposób ustalania komórki bieżącej polegający na wykorzystaniu
nazw komórek.

Powyższe metody działają nawet na pustym arkuszu. Czasami zachodzi potrzeba przejścia do
ostatniej (pierwszej) zapisanej (niepustej) komórki jakiegoś obszaru. Można używać wówczas
sekwencji [End] i strzałki. Np. kolejne wciśnięcie klawiszy [End] i [

↓] pozwala przejść w dół

do ostatniej niepustej komórki obszaru (np. z D4 do D6 na rys. 2.2) lub pierwszej niepustej
komórki następnego obszaru (np. z F6 do F9 lub z H7 do H9 na rys. 2,2). Jeżeli nie ma takich
komórek do przechodzimy do skrajnej komórki danej wiersza/kolumny.

Rys. 2.2. Fragment danych w arkuszu

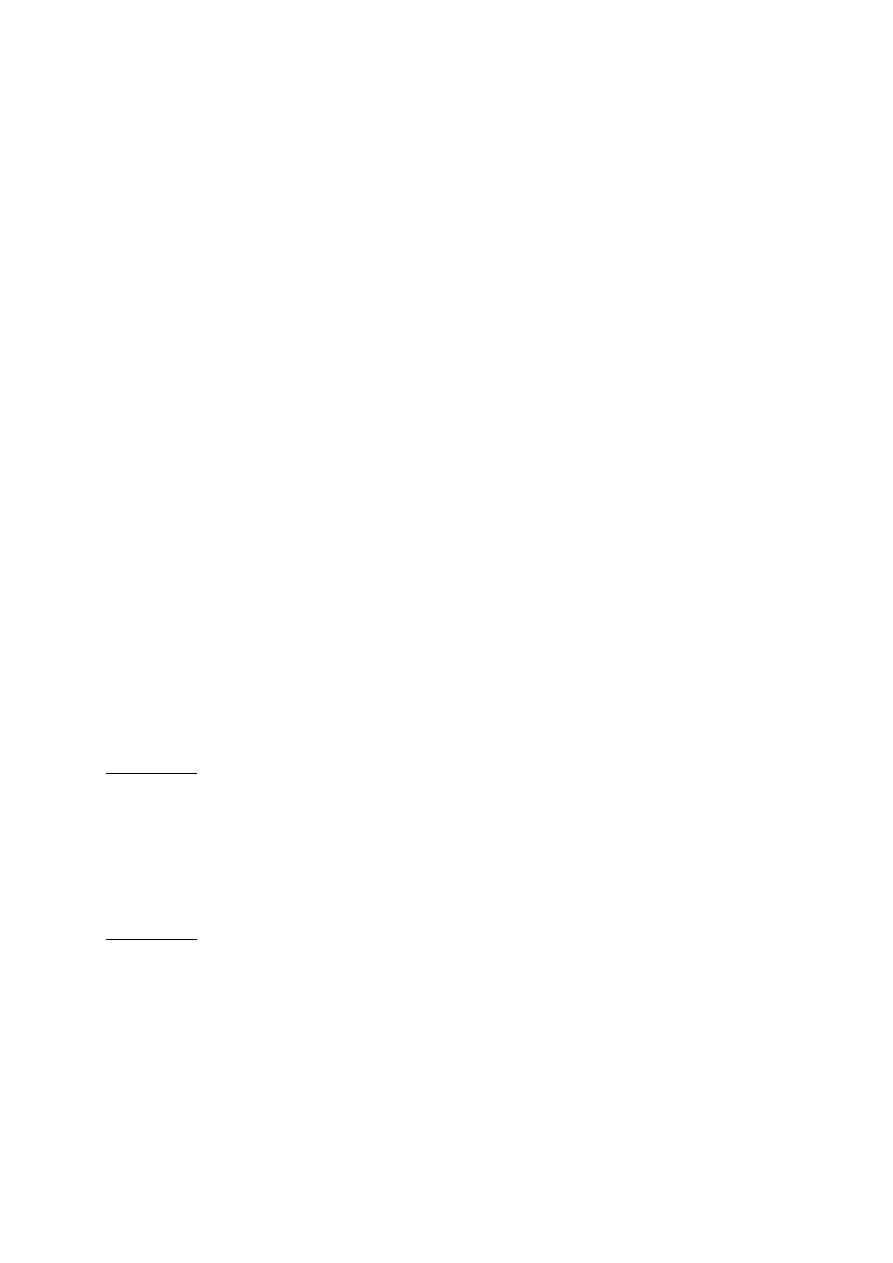
11

3. Wprowadzanie danych

W wyniku uruchomienia programu zostaje otwarty nowy skoroszyt i możemy przystąpić do
wprowadzenia danych. Jeżeli tego nie widać lub jeżeli chcemy wprowadzać dane do innego
skoroszytu, należy wybrać z głównego menu polecenie Plik | Nowy. Polecenie Plik | Otwórz
pozwala wczytać istniejący skoroszyt.

Aby wprowadzić z klawiatury dane do komórki arkusza, należy ustawić ją jako komórkę
bieżącą. Umieszczenie danych w komórce następuje po kliknięciu przycisku Wpis lub
wciśnięciu klawisza [Enter] (albo innego klawisza sterującego np. [

→]) lub kliknięciu na inną

komórkę arkusza. Przed wpisaniem danych do komórki możemy w razie pomyłki użyć
klawisza [Backspace]. Nowy wpis usuwa poprzedni, jeżeli bieżąca komórka nie była pusta.
Kliknięcie przycisku Anuluj lub wciśnięcie klawisza [Esc] oznacza rezygnację z zapisu
danych do komórki.

Do komórek arkusza można wprowadzać:
− liczby: 8,2

− teksty: Data

zakupu

− daty:

2003-11-12

− wzory
(czyli formuły obliczeniowe): =f5*g5

Program automatycznie rozpoznaje, czy do komórki jest wprowadzana liczba czy tekst.
Wprowadzając wzory (formuły) musimy rozpoczynać je od znaku równości (=). Daty są
traktowane w Excelu jako liczby zapisane w formacie Data. Na przykład data 12.11.2003
odpowiada liczbie 37937, będącej numerem dnia licząc od 01.01.1900. Niektóre wartości
wpisywane do komórek Excel domyślnie traktuje jako datę (nie zawsze zgodnie z naszym
zamiarem) np. wpis 3-4 może zostać potraktowany jako dzień 4 marca. Aby dowolna wartość
liczbowa była potraktowana jako tekst, należy poprzedzić ją znakiem ' (apostrof)

Przykład 3.1

'15

- to nie jest traktowane jako liczba 15, ale tekst 15

'=30

- to nie jest traktowane jako wzór, ale tekst =30

'2003-11-12

- to nie jest traktowane jako data, ale tekst 2003-11-12

''t Jong

- to jest tekst 't Jong (należało użyć dwóch apostrofów)

Przykład 3.2
Do komórek D5,...,H5 zostały wprowadzone dane. Komórka D5 zawiera datę. Komórka E5
zawiera tekst. Komórki F5 i G5 zawierają liczby, przy czym pierwsza z nich jest wyświetlana
w formacie walutowym (ze znakiem waluty). Komórka H5 zawiera wzór wiążący
wyświetlaną wartość z wartościami znajdującymi się w komórkach F5 i G5.

12

Rys. 3.2. Przykład danych

Wzór jest wyświetlony w polu formuły, gdyż H5 jest komórką bieżącą, natomiast napis
wyświetlony w tej komórce pokazuje aktualną wartość wyrażenia. Należy odróżniać
zawartość komórki, czyli wpis umieszczony w komórce i wyświetlany w polu formuły (w
przykładzie jest to =F5+G5) od napisu wyświetlonego w komórce (w przykładzie jest to
wartość 49,20 zł). Podobnie napis widoczny w komórce F5 to 8,20 zł, mimo że do komórki
została wprowadzona liczba 8,2. Napis widoczny w komórce jest to reprezentacja wpisu i
zależy ona od przyjętego formatu komórki i od szerokości danej kolumny.

W Polsce, w przeciwieństwie do wielu innych krajów, znakiem oddzielającym część
całkowitą i część dziesiętną liczby jest przecinek. Wprowadzenie kropki (np. 8.2) spowoduje,
że zapis nie będzie potraktowany przez Excel jako liczba lecz jako tekst. W celu uniknięcia
tego błędu zaleca się do wpisywania wartości liczbowych używać klawiszy numerycznych,
znajdujących się po prawej stronie klawiatury. Jeżeli korzystamy z polskiej wersji systemu
operacyjnego, to naciśnięcie przycisku z kropką na klawiaturze numerycznej powoduje
wpisanie przecinka.


3.1. Przykłady liczb wprowadzanych do komórki arkusza

Dane liczbowe możemy wprowadzać do arkusza w różny sposób. Oto kilka przykładów.

Tab. 3.1. Sposoby wprowadzania liczb

-225,1 liczba

dziesiętna ujemna

,6 liczba

dziesiętna o wartości 0,6

7,30 zł

liczba ze znakiem waluty

71,5%

liczba w postaci procentu (0,715)

1,3e6

liczba w postaci wykładniczej (1300000)

+28

liczba poprzedzona znakiem + (28)

(28) liczba

ujęta w nawiasy okrągłe, interpretowana jako

liczba ujemna (-28)

3.2. Wyświetlanie wartości liczbowych w komórkach arkusza

Domyślnie w komórce ukazują się liczby w takiej postaci, w jakiej są wprowadzone z
klawiatury z tym, że:
1. EXCEL pomija nieznaczące zera i znak "+" przed liczbą (+000,75000 wyświetla jako

0,75).

2. Jeżeli komórka zawiera wzór, to jest wyświetlana wartość liczbowa wzoru, np. komórka

H5 na rys. 3.2.

13

3. Sposób wyświetlania liczby zależy od szerokości komórki. Jeżeli liczba nie mieści się w

określonym formacie, to w komórka jest wypełniana znakami #########, ale do obliczeń
są brane poprawne wartości.

4. Jeżeli wartość liczbowa wzoru nie może zostać obliczona (np. =7/0, =ln(0),

=pierwiastek(-1) ), to w komórce jest wyświetlany odpowiedni komunikat diagnostyczny
np. #DZIEL/0!, #LICZBA!.

Zmiana formatu komórki powoduje zmianę sposobu wyświetlania liczby.


3.3. Zmiana sposobu wyświetlania liczb w komórkach arkusza

Przykład 3.3
Niech komórka A5 zawiera liczbę 256,7947. Wyświetlimy zawartość komórki A5 w różny
sposób (np. z dokładnością do jednego miejsca dziesiętnego, w procentach, w notacji
wykładniczej). Najogólniejszym sposobem jest skorzystanie z polecenia Format | Komórki.

1. Wybieramy polecenie: Format | Komórki
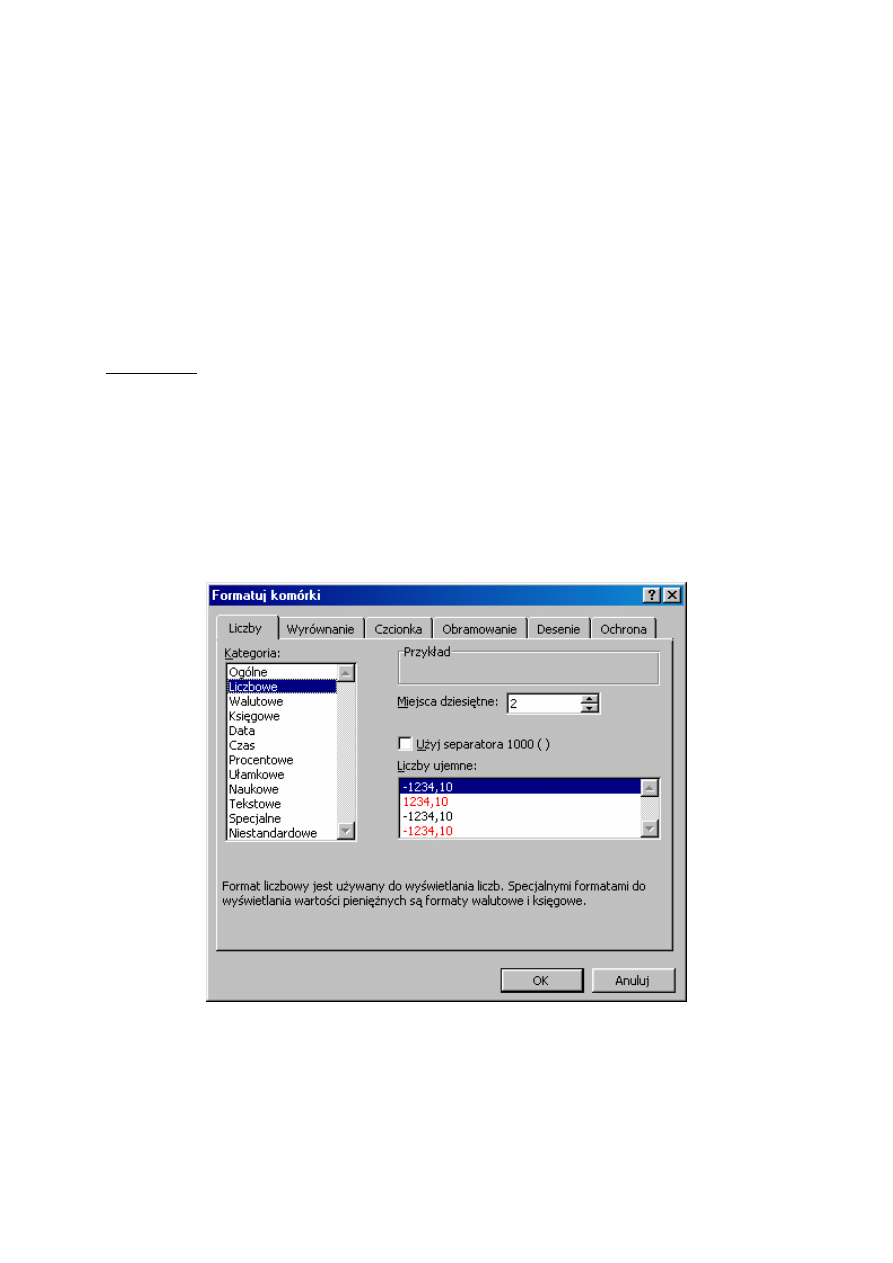
2. Pojawi się okno dialogowe Formatuj komórki. Możemy dokonać w nim następujących

ustaleń: Liczby, Wyrównanie, Czcionka, Obramowanie, Desenie, Ochrona. Aby
ustalić format wyświetlania liczb, należy wybrać zakładkę Liczby. Na ogół jest ona już
wybrana.

Rys. 3.3. Okno Formatuj komórki

Teraz w polu Kategoria należy zaznaczyć wybrany typ formatu i ustalić jego parametry.

14

Przykłady kategorii formatów:
− Ogólne

- format jest ustalany na podstawie sposobu wpisania liczby np. jeżeli

wpiszemy 10%, to będzie wybrany format procentowy, jeżeli
wpiszemy 4-3, Excel potraktuje to jako datę 3 kwietnia.

− Liczbowe

- format stały z określoną liczba miejsc dziesiętnych np. 15,2500,

− Walutowe

- ze znakiem waluty (np. zł po liczbie),

− Księgowe

-

ze znakiem waluty i wyrównaniem przecinka dziesiętnego,

− Procentowe

- format procentowy np. 45,40% ,

− Ułamkowe

- liczba jest wyświetlana w postaci ułamka zwykłego np. 5/8,

− Naukowe

- liczba jest wyświetlana w notacji wykładniczej np. 3,7E-9,

− Tekstowe

- liczby są wyświetlane jako tekst,

− Specjalne

- zapis liczbowy może być traktowany jako: kod pocztowy, numer
telefonu, numer PESEL, numer NIP i odpowiednio formatowany np.
po wpisaniu liczby 2435 widzimy napis 02-435 (kod pocztowy),

− Niestandardowe -

jeżeli żaden z formatów liczbowych oferowanych przez program nie

odpowiada naszym potrzebom, to możemy definiować własny format
liczbowy.

Najczęściej zmienia się format komórek za pomocą przycisków z paska narzędzi. Dla danych
numerycznych są to przyciski:
− Dodaj pozycję dziesiętną

,

− Zmniejsz miejsce dziesiętne

,

− Zapis procentowy

,

− Zapis walutowy

,

− Zapis dziesiętny

.

Jeżeli chcemy zmienić format dla obszaru komórek np. A5:C10, należy najpierw zaznaczyć
ten obszar. O obszarach i zaznaczaniu ich będzie mowa w następnym rozdziale.

Na rys. 3.4 przedstawiamy wygląd wprowadzonej liczby 256,7947 w różnych formatach.

Rys. 3.4. Liczba 256,7947 w różnych formatach

15

3.4. Wyświetlanie tekstów w komórkach arkusza

Domyślnie liczby są wyrównywane do prawej strony, a teksty są wyrównywane do lewej

strony. Można zmienić te ustalenia za pomocą przycisków z paska narzędzi

albo

za pomocą polecenia Format | Komórki | Wyrównanie. Jeżeli napis nie mieści się w
szerokości komórki, to jest wyświetlany w sąsiednich komórkach (po prawej stronie), o ile są
one puste. Jeżeli sąsiednie komórki nie są puste, to wyświetla się tylko część napisu. Aby
widzieć cały napis musimy wybrać jeden ze sposobów:
− zmienić szerokość kolumny (Format | Kolumna | Szerokość albo Format | Kolumna |

Autodopasowanie obszaru),

− zmniejszyć czcionkę napisu (Format | Komórki | Czcionka),
− zawinąć tekst (Format | Komórki | Wyrównanie z zaznaczeniem pola Zawijaj tekst).

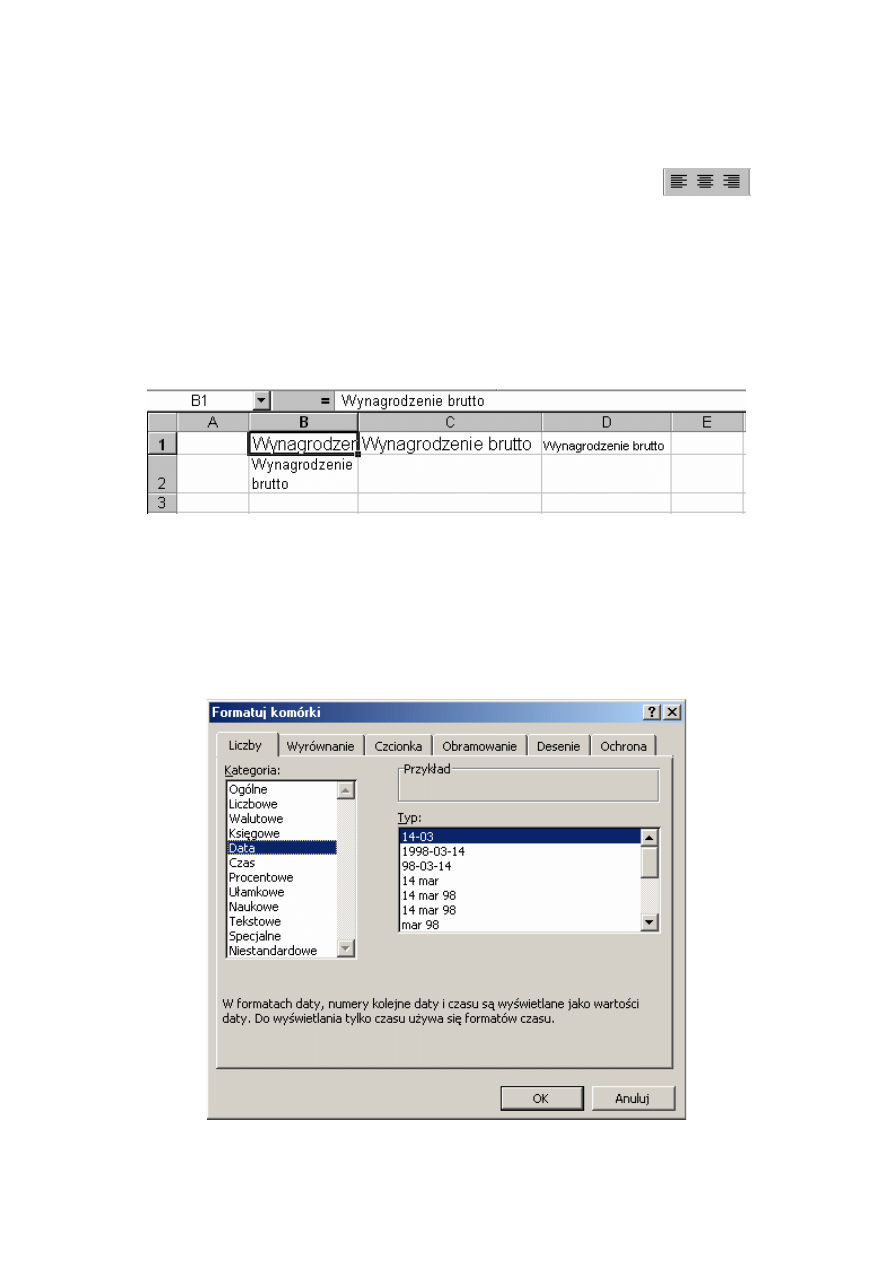
Rys. 3.5. Różne formaty tekstu

Tekst Wynagrodzenie brutto nie mieści się w komórce B1 arkusza. Sąsiednia komórka (C1)
została rozszerzona, w komórce D1 zmniejszyliśmy rozmiar czcionki (8 pikseli zamiast 10), a
tekst w komórce C2 jest zawinięty. Ponieważ Komórka B1 jest komórką bieżącą, w polu
formuły widzimy całą zawartość komórki.

3.5. Wprowadzanie i wyświetlanie dat i czasu

Rys. 3.6. Okno dialogowe pozwalające wybrać format daty

16

Sposób wprowadzania daty do komórek arkusza zależy od ustawień. systemu operacyjnego.
Ta sama data może być wyświetlana w różny sposób, w zależności od wyboru opcji Typ w
oknie dialogowym Formatuj komórki w kategorii Data. Podobne ustalenia dotyczą kategorii
Czas.

Przykład 3.4
W kolejnych komórkach arkusza wyświetliliśmy w różnych formatach tę samą datę i czas: 29
lutego 2004 godzina 18.45. Odpowiada jej liczba 38046,78125 (ponieważ o godzinie 18.45
mija 0,78125 doby).

Rys. 3.7. Różne formaty daty i czasu

Aby sprawdzić, jak należy wprowadzać daty, należy wybrać z menu Start polecenie
Ustawienia | Panel sterowania | Opcje regionalne i po kliknięciu na zakładki Data
zobaczyć, jak została podana data. Domyślnym formatem jest rrrr-mm-dd tzn. np. dzień 29
lutego 2004 należy wprowadzić jako 2004-02-29. Wybierając odpowiednie opcje w oknie
dialogowym Data (ewentualnie Godzina) możemy zmienić domyślny sposób wprowadzania
daty i czasu.

Bieżącą datę i czas możemy wstawić do arkusza używając zapisu =dziś() oraz =teraz(). Jest
to przykład użycia funkcji standardowych Excela.

Aby szybko wstawić do komórki arkusza bieżącą datę, wystarczy ustawić kursor w danej
komórce i wcisnąć klawisze [Ctrl]+[;]. Żeby stawić bieżącą godzinę i minutę , należy wcisnąć
klawisze [Shift]+[Ctrl]+[;].

17

4. Zaznaczanie obszarów

Excel pracuje w danej chwili tylko z jedną komórką - komórką bieżącą. Jednak powtarzanie
takich operacji jak formatowanie, kopiowanie, usuwanie kolejno dla wielu komórek byłoby
uciążliwe. Wygodniej jest wykonywać te operacje jednocześnie na wyróżnionych grupach
komórek. Należy jedynie określić, które komórki mają być uwzględniane w danej operacji.
Prowadzi to do pojęcia bloku komórek, czyli obszaru.

Obszar jest to prostokątna część arkusza. Na rysunku 4.1. jest zaznaczony obszar składający
się z 12 komórek należących do wierszy 3, 4, 5, 6 i kolumn D, E, F. Adres obszaru podajemy
specyfikując dwa jego przeciwległe narożniki, oddzielone dwukropkiem (D3:F6).

Szczególnymi przykładami obszarów są:
− obszar zawierający jeden wiersz i kilka kolumn np. B9:H9,

− obszar zawierający jedną kolumnę i kilka wierszy np. K2:K8,

− obszar składający się tylko z jednej komórki np. A2:A2.


4.1. Zaznaczanie obszarów prostokątnych

Rys. 4.1. Zaznaczanie obszaru

Sposoby zaznaczania obszarów prostokątnych.
1. Przeciągnąć myszą przy wciśniętym lewym przycisku.
2. Trzymać wciśnięty klawisz [Shift] i korzystać z klawiszy kierunkowych (strzałek). Ten

sposób jest dobry przy zaznaczaniu obszarów, których rozmiar przekracza fragment
arkusza widoczny na ekranie.

3. Ustawić komórkę bieżącą w jednym z narożników zaznaczanego obszaru. Trzymając

wciśnięty klawisz [Shift] kliknąć na komórce przeciwległego narożnika. W ten sposób
można zaznaczać obszary trójwymiarowe, jeżeli drugi narożnik zostanie wybrany w
innym arkuszu.

Rzadziej korzysta się z obszarów trójwymiarowych. Obszar Arkusz1:Arkusz3!C4:D6 składa
się z komórek znajdujących się w kolumnie C i D, wierszach 4, 5, 6 i arkuszach Arkusz1,
Arkusz2, Arkusz3. Razem jest to 18 komórek.

W momencie zaznaczania obszaru w miejscu, gdzie zwykle jest wyświetlony adres komórki,
pojawia się napis postaci 6Wx5K. Wskazuje on, że w danym momencie zaznaczyliśmy
obszar o rozmiarach 6 wierszy i 5 kolumn. W zaznaczonym obszarze komórką bieżącą jest ta,

18

od której rozpoczęliśmy operację zaznaczania. Po zaznaczeniu obszaru wszystkie komórki
należące do niego, z wyjątkiem komórki bieżącej, mają szaroniebieskie tło.

W dalszych rozdziałach poznamy sposób zaznaczania nazwanych obszarów.


4.2. Zaznaczanie całych wierszy lub kolumn

Aby zaznaczyć cały wiersz, należy kliknąć myszą na nagłówku wiersza. Podobnie, aby
zaznaczyć całą kolumnę, należy kliknąć myszą na nagłówku kolumny. Przeciągając myszą
kilka sąsiednich wierszy lub kolumn można je zaznaczyć jednocześnie. Kolumnę zawierającą
komórkę bieżącą można zaznaczyć wciskając klawisze [Ctrl]+[Space], a wiersz z komórką
bieżącą - wciskając [Shift]+[Space].


4.3. Zaznaczanie całego arkusza

Aby zaznaczyć cały arkusz, należy kliknąć myszą na pustym polu znajdującym się na
nagłówkiem pierwszego wiersza i po lewej stronie nagłówka kolumny A. Innym sposobem
zaznaczenia całego arkusza jest wciśnięcie klawiszy [Shift]+[Ctrl]+[Space].


4.4. Zaznaczanie kilku obszarów

Można zaznaczać kilka obszarów na raz. Trzeba zaznaczyć pierwszy z nich, a potem
trzymając wciśnięty klawisz [Ctrl] zaznaczać pozostałe.

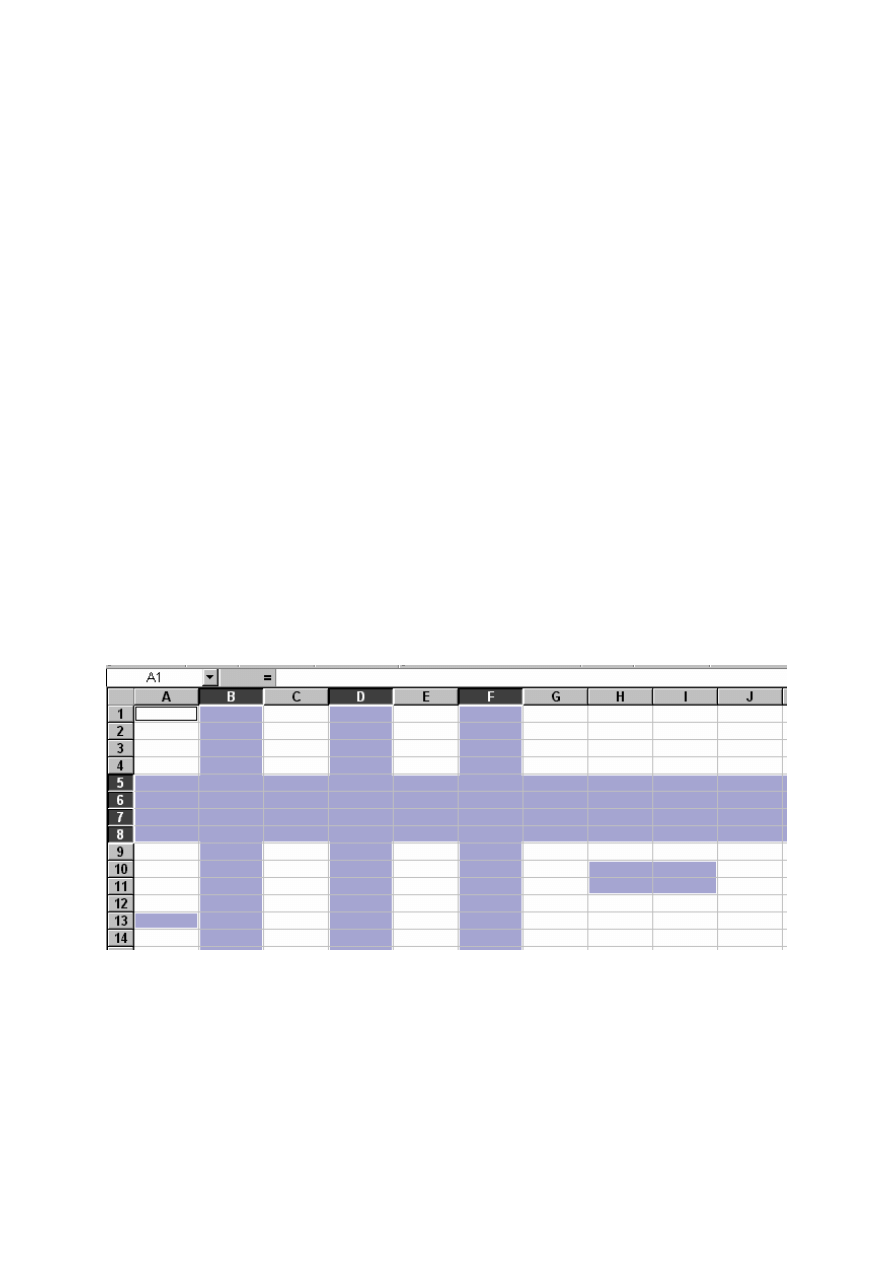
Rys. 4.2. Zaznaczanie kilku obszarów

Na rys. 4.2 zaznaczone są: komórka A13, obszar H10:I11, kolumny B, D, E, wiersze od 5 do
8 oraz komórka bieżąca A1.

19

Na zaznaczonych obszarach (nazywanych zakresem) można wykonywać operacje edycyjne
np.
− usunąć zawartość komórek z obszaru,

− skopiować lub przenieść zawartość komórek w inne miejsce,

− zmienić format komórek.

Wciskając klawisz [Tab] w zaznaczonych obszarach poruszamy się poziomo w obrębie tych
obszarów (od lewej do prawej strony), a wciskając [Enter] - pionowo wzdłuż kolejnych
kolumn.

Niektóre z tych operacji są dozwolone tylko dla jednego zaznaczonego obszaru, a nie dla
kilku obszarów jednocześnie.

Również można wykorzystywać obszary jako argumenty funkcji i innych operacji
obliczeniowych.

20

5. Formatowanie komórek

Formatowanie ma na celu nadanie arkuszowi estetycznej i czytelnej formy graficznej.

Uwagi dotyczące formatowania liczb przedstawiliśmy w pkt. 3.3. Tutaj opiszemy możliwości
programu w zakresie rozmieszczenia napisów w komórce, rodzaju stosowanej czcionki,
obramowania tabel i postaci tła w komórkach.

Przykład 5.1
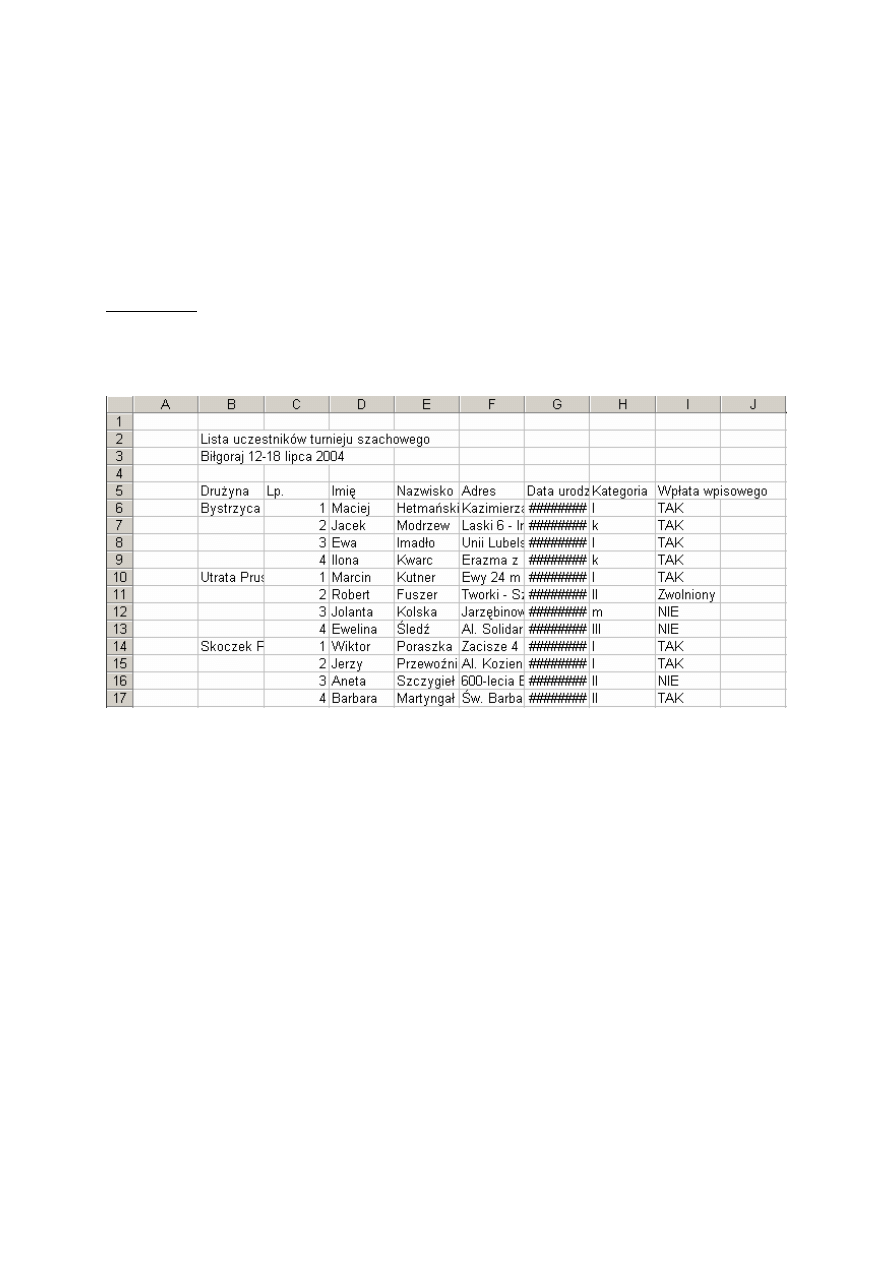
Utworzymy listę uczestników drużynowego turnieju szachowego odbywającego się w
Biłgoraju. Fragment tabeli jest pokazany na rys. 5.1. Sformatujemy tabelę. Jej ostateczna
postać jest pokazana na rys. 5.7.

Rys. 5.1. Dane niesformatowane

5.1. Rozmieszczenie napisów

21

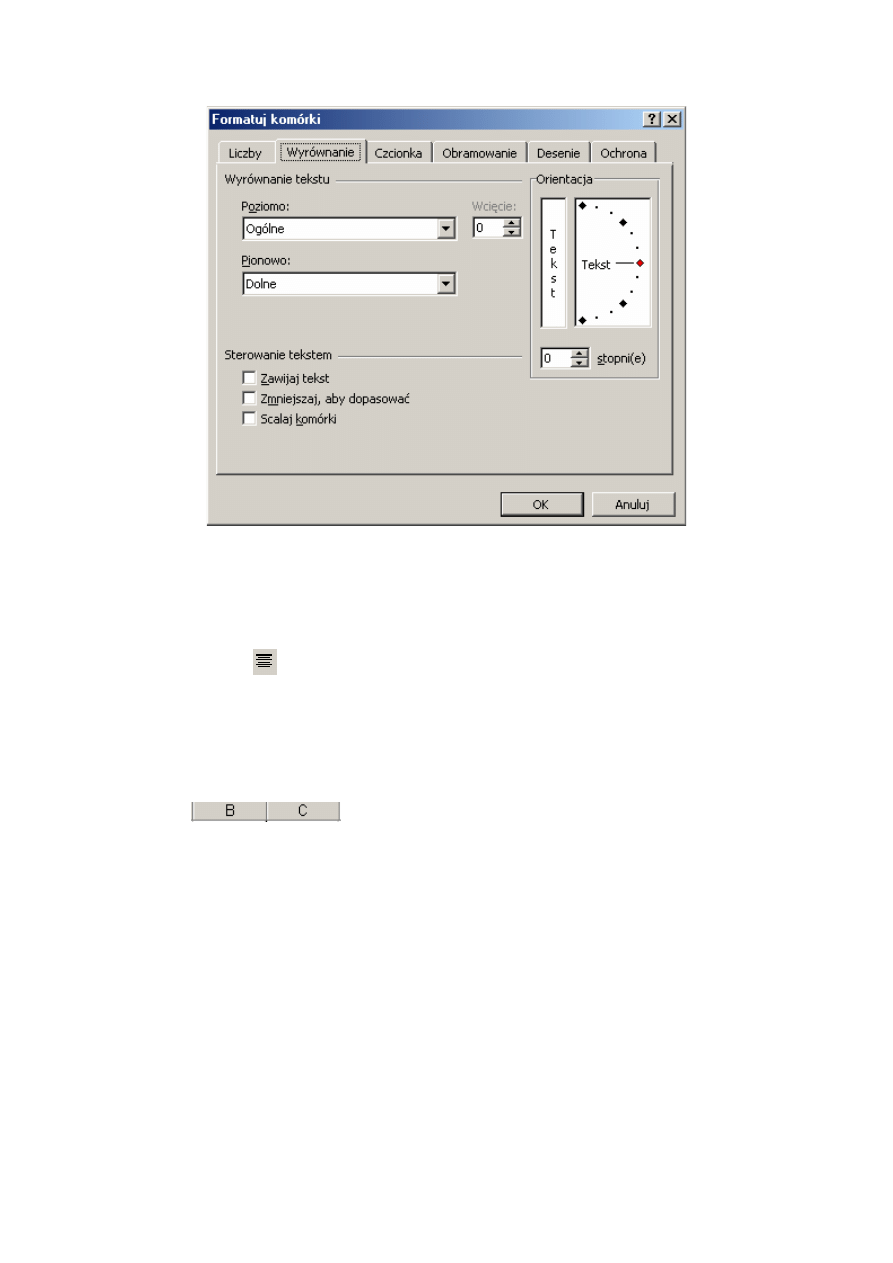
Rys. 5.2. Okno dialogowe Formatuj komórki - Wyrównanie

Wyrównanie tekstu

Standardowo teksty są wyrównywane do lewej krawędzi komórki, a liczby i daty do prawej
krawędzi. Aby ustawić na środku nagłówki kolumn, należy zaznaczyć obszar B5:I5 i kliknąć
przycisk Wyśrodkuj

. Ustawimy na środku również dane wpisane w kolumnach C i H.

Szerokość kolumny, wysokość wiersza

Kolumny B, E i F zawierają dane nie mieszczące się w szerokości komórek. Ponieważ
sąsiednie komórki są zajęte, część napisów nie jest widoczna. Możemy rozszerzyć te kolumny
dopasowując je do szerokości najdłuższego wpisu. Dla kolumny B należy kliknąć dwukrotnie
w miejscu

. Podobnie trzeba postąpić dla kolumn E i F. Kolumna G

zawiera daty urodzenia zawodników. Znaki ######## informują, że wartości w komórkach są
zbyt długie, aby mogły być wyświetlone.

W podobny sposób jak szerokość kolumn można zmieniać wysokość wierszy.

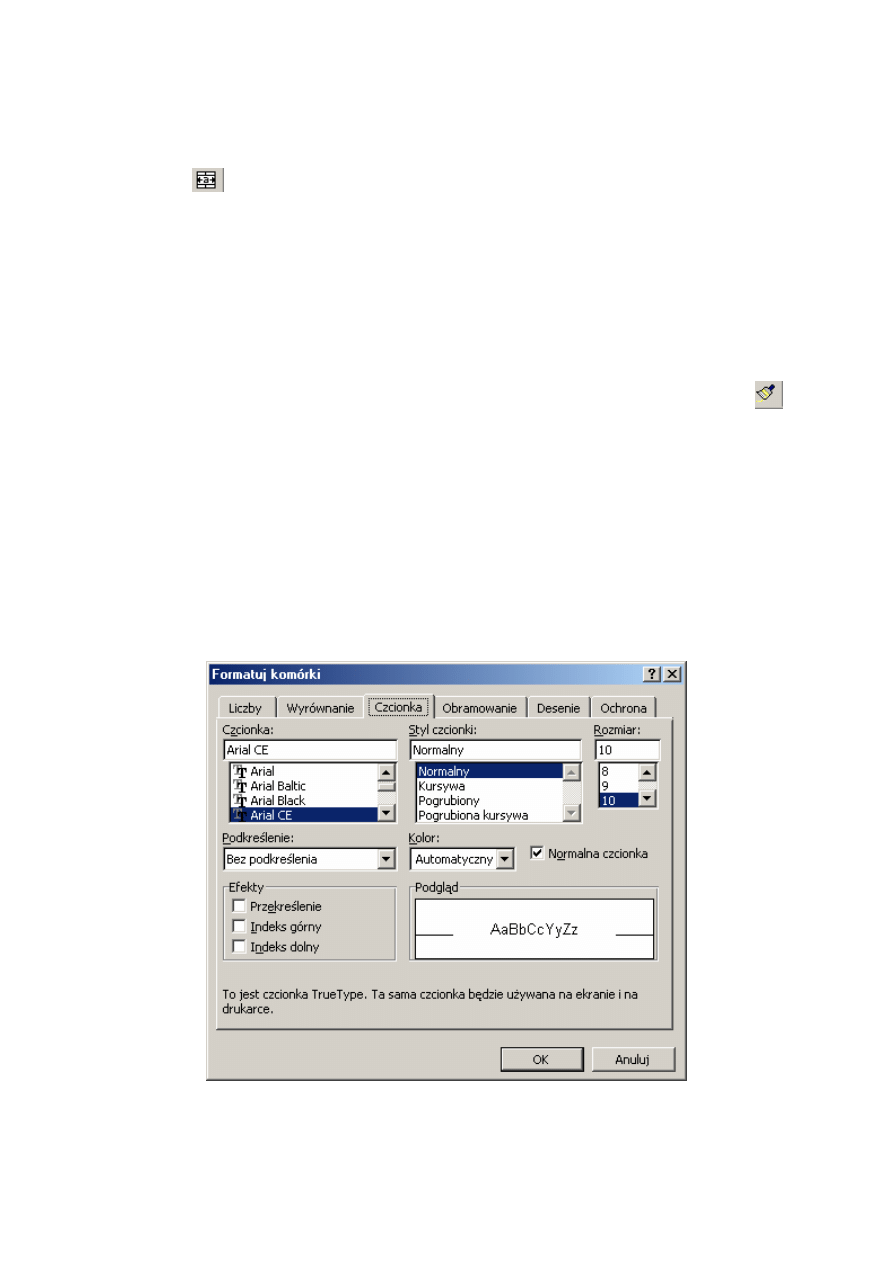
Zawijanie tekstu

Kolumna I zawiera dosyć krótkie teksty, jednak ma długi nagłówek. Można zapisać jej
nagłówek w dwóch liniach używając opcji Zawijaj tekst. Wówczas wiersz 5 zwiększy swoją
wysokość, a wszystkie nagłówki zostaną wyrównane w pionie do dołu wiersza. Jest to opcja
domyślna (Wyrównanie tekstu Pionowo: Dolne). Zmienimy to wyrównanie na Pionowo:
Środek.

22

Scalanie komórek

Tytuł tabeli wyśrodkujemy w zakresie wszystkich kolumn używając przycisku Scal i
wyśrodkuj

. Należy przedtem zaznaczyć obszar B2:I3.

Orientacja

Tekst może być umieszczony pionowo. Zrobimy to dla nazw drużyn. Należy zaznaczyć
komórki B6:B9 i wybrać polecenie Scalaj komórki, a następnie zaznaczyć orientację tekstu
90 stopni. Również wybieramy opcję Zawijaj tekst.

Malarz formatów

Format komórki można przekopiować za pomocą przycisku Malarz formatów

.

Kliknijmy na pionowy napis w komórce B6, a następnie na przycisk Malarz formatów i na
komórkę B10. Format komórki zostanie przekopiowany. Jeżeli chcemy skopiować format w
kilka miejsc, klikamy dwukrotnie na przycisk Malarz formatów, a następnie na komórki
docelowe. Jeżeli Malarz formatów został wywołany dla pojedynczego użycia, to wyłącza się
automatycznie. W przeciwnym razie musimy jeszcze kliknąć na przycisk, aby go wyłączyć.


5.2. Czcionka

Tekst jest pisany domyślnym rodzajem czcionki (np. Arial CE), stylem normalnym o
domyślnym rozmiarze (np. 10 pikseli).

Rys. 5.3. Okno dialogowe Formatuj komórki - Czcionka

23

Rodzaj i rozmiar czcionki możemy łatwo skorygować wybierając odpowiednie opcje z paska
narzędzi Formatowanie

. Obok znajdują się przyciski

Pogrubienie

, Kursywa

i Podkreślenie

. Te właściwości czcionki można ustawić

też w oknie dialogowym Formatuj komórki (Czcionka) w polach Styl czcionki oraz
Podkreślenie. Korzystają z przycisku Kolor czcionki

na pasku narzędzie Formatowanie

albo zmieniając ustawienia pola Kolor można z palety wybrać kolor czcionki tekstu. W
naszym przykładzie zaznaczymy pogrubioną czcionką tytuł tabeli oraz nazwy drużyn.
Zwiększymy rozmiar czcionki tytułu tabeli do 16 pikseli. Kolorem czerwonym zaznaczymy
imiona i nazwiska kapitanów drużyn.

Aby zmienić czcionkę w całym arkuszu należy najpierw zaznaczyć arkusz klikając puste pole
nad etykietą pierwszego wiersza z lewej strony etykiety kolumny A. Następnie wybieramy
odpowiedni rodzaj czcionki np. Times New Roman.

Przekreślenie i indeksy

Przykłady tekstów tak sformatowanych są pokazane na rys. 5.4. Najwygodniej jest napisać
tekst zwykła czcionką, a potem zaznaczyć fragment tekstu i wybrać odpowiednie pole w
grupie Efekty.

Rys. 5.4. Przekreślenie, indeks górny i indeks dolny

5.3. Obramowanie

Linie siatki pełnią funkcję pomocniczą i można je usunąć z arkusza za pomocą polecenia
Narzędzia | Opcje | Widok z usunięciem zaznaczenia Linie siatki w oknie dialogowym.
Różne formy obramowania tabel możemy uzyskać korzystając z przycisku Obramowanie

albo okna dialogowego pokazanego na rys. 5.5.

24

Rys. 5.5. Okno dialogowe Formatuj komórki - Obramowanie

W naszej tabeli zastosujemy gruby podwójny kontur całej tabel, oddzielimy grubszą linią
poszczególne drużyny i zlikwidujemy linię pomiędzy imionami a nazwiskami zawodników.


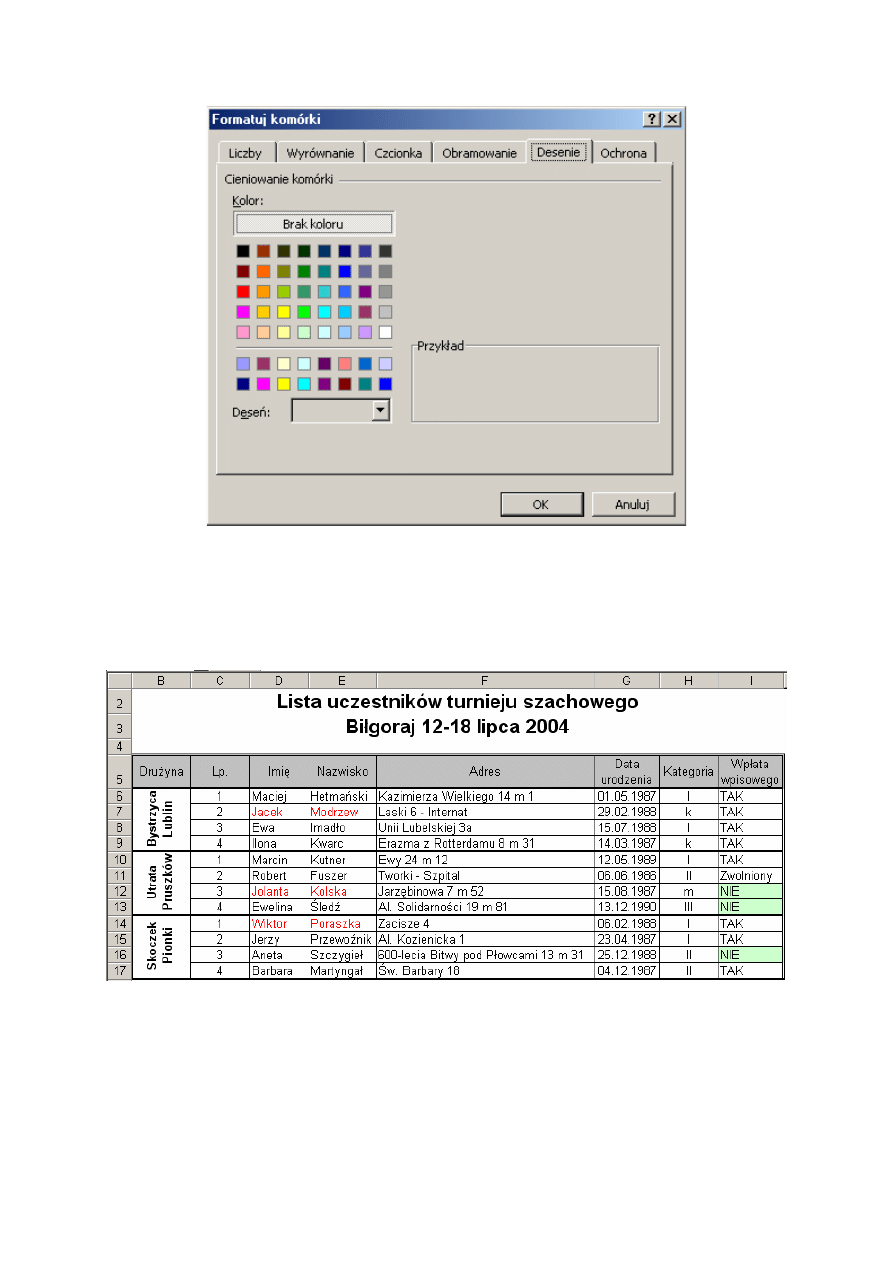
5.4. Desenie

Przycisk

paska narzędzi Formatowanie albo polecenie Format | Komórki | Desenie

pozwala określić kolor tła i sposób cieniowania komórek. Można też pokryć tło komórki
deseniem, np. kratką, kropkami, ukośnymi kreskami . Określamy to w polu Deseń.

25

Rys. 5.6. Okno dialogowe Formatuj komórki - Desenie

W naszym przykładzie zacieniujemy nagłówki kolumn tabeli i zaznaczymy zielonym tłem
brak opłaty wpisowego (komórki I12, I13, I16).

Po sformatowaniu tabela 5.1 ma postać 5.7.

Rys. 5.7. Dane sformatowane

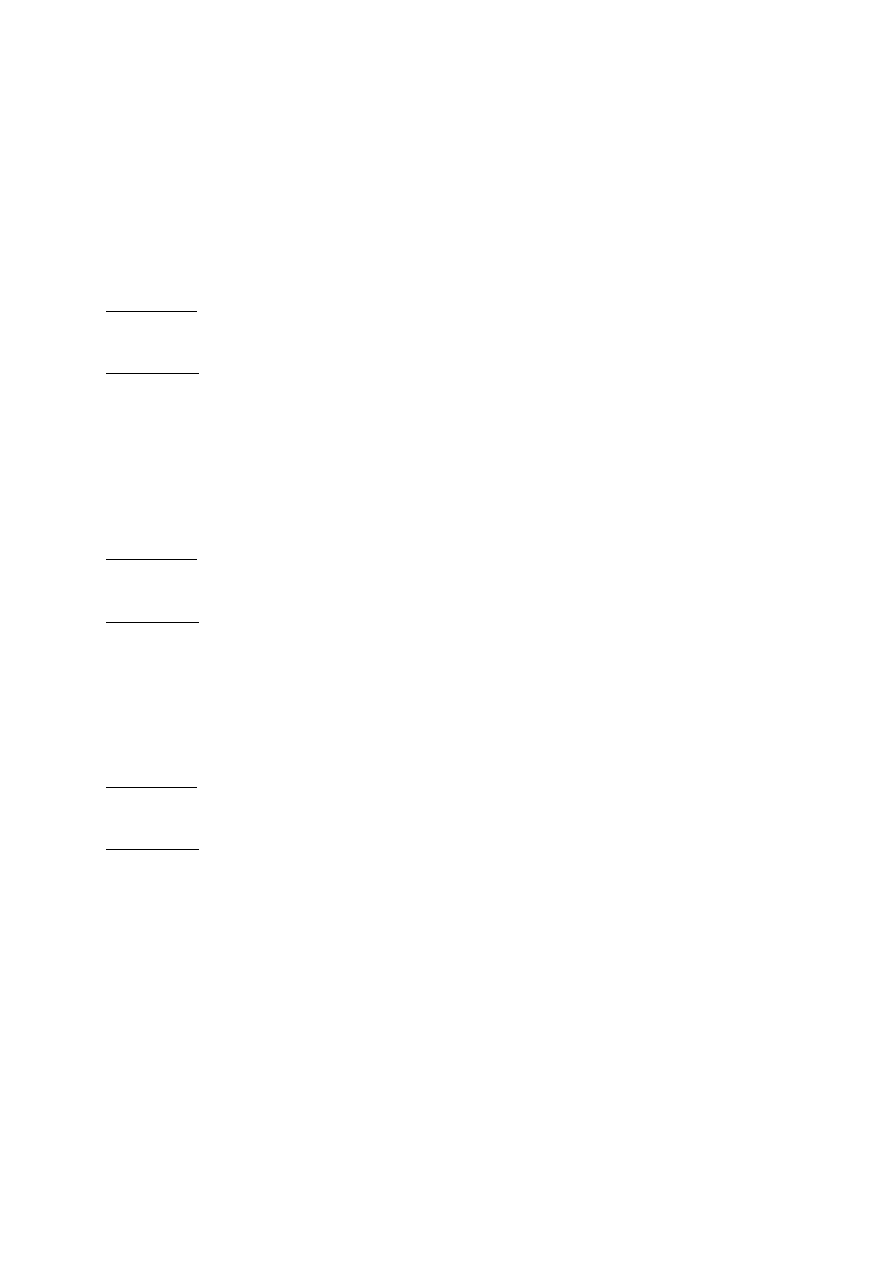
26

6. Kopiowanie, przenoszenie i usuwanie komórek arkusza


6.1. Kopiowanie i przenoszenie

Mamy kilka sposobów kopiowania i przenoszenia komórek lub całych obszarów. Zaczniemy
od przykładów. Niech w komórkach obszaru A1:E4 będą wpisane dane.

Przykład 6.1
Należy skopiować obszar A1:E4 w obszar rozpoczynający się od komórki D17

Rozwiązanie
1. Zaznaczamy dany obszar.
2. Wybieramy polecenie Edycja | Kopiuj (lub ikonę Kopiuj z paska narzędzi

Standardowy).

3. Ustawiamy wskaźnik bieżącej komórki w D17.
4. Wybieramy polecenie Edycja | Wklej (lub ikonę Wklej z paska narzędzi Standardowy).
Komórka A1 zostanie skopiowana do D17, natomiast kopia całego obszaru A1:E4 zajmie
obszar D17:H20.

Przykład 6.2
Należy przenieść obszar A1:E4 w obszar rozpoczynający się od komórki B8

Rozwiązanie
1. Zaznaczamy dany obszar.
2. Wybieramy polecenie Edycja | Wytnij (lub ikonę Wytnij z paska narzędzi

Standardowy).

3. Ustawiamy wskaźnik bieżącej komórki w B8.
4. Wybieramy polecenie Edycja | Wklej (lub ikonę Wklej z paska narzędzi Standardowy).
Obszar A1:E4 zostanie przeniesiony do B8:F11, (oryginał zniknie).

Przykład 6.3
Należy skopiować komórkę B10 do komórek obszaru G1:H6

Rozwiązanie
Zadanie wykonujemy analogicznie jak w przykładzie 1. Przed wyborem polecenia Edycja |
Kopiuj ustawiamy wskaźnik bieżącej komórki w B10. Przed wyborem polecenia Edycja |
Wklej zaznaczamy obszar docelowy G1:H6.

Widzimy, że możliwe jest kopiowanie (przenoszenie):
− jednej komórki w inne miejsce,

− obszaru komórek w inne miejsce (zaznaczamy wtedy tylko lewy górny róg obszaru

docelowego),

− jednej komórki do obszaru komórek (zawartość komórki powiela się we wszystkich

komórkach obszaru docelowego).

W powyższy sposób kopiuje się (przenosi się) zawartość komórki łącznie z formatem
komórki. Jeżeli komórka zawiera wzory, to kopiowanie przebiega w inny sposób. Wzór
wpisany do komórki może zmienić się.

27

Kopiowanie lub przenoszenie polega na:
− zapisaniu obiektu źródłowego w schowku (operacja Kopiuj nie narusza oryginału, a

operacja Wytnij usuwa oryginał),

− pobraniu obiektu zapisanego w schowku (operacja Wklej).

Inne sposoby kopiowania i przenoszenia polegają na użyciu przycisków paska narzędzi
Standardowy, podręcznego menu dostępnego po wciśnięciu prawego przycisku myszy oraz
kombinacji klawiszy.

Zapisanie do schowka

Zapisanie do schowka z usuwaniem Pobranie ze schowka

Edycja | Kopiuj

Edycja | Wytnij

Edycja | Wklej

Ikona

Kopiuj

Ikona

Wytnij

Ikona

Wklej

Prawy

przycisk

Kopiuj Prawy

przycisk

Kopiuj

Prawy przycisk Wklej

[Ctrl]+[C]

[Ctrl]+[X] [Ctrl]+[V]

W ten sposób możemy kopiować lub przenosić komórki (obszary) do innych arkuszy, a nawet
do innych dokumentów Excela lub innych programów (np. do dokumentów Word). Można
też kopiować całe wiersze, całe kolumny lub całe arkusze. Trzeba je wcześniej zaznaczyć.

Przykład 6.4
Należy skopiować Arkusz1 do Arkusza2.

Rozwiązanie
1. Zaznaczamy cały arkusz klikając na pustym polu nad nagłówkiem pierwszego wiersza.
2. Wybieramy operację kopiowania.
3. Klikamy na zakładce drugiego arkusza.
4. Ustawiamy komórkę A1 jako bieżącą komórkę tego arkusza.
5. Wybieramy operację wklejania.
Jeżeli komórką bieżącą arkusza docelowego będzie inny komórka niż A1, to wystąpi błąd.

Jeżeli chcemy skopiować lub przenieść komórki w tym samym arkuszu na bliską odległość
(np. jeden lub kilka wierszy poniżej), to najprostszym sposobem jest zaznaczenie
odpowiedniego obszaru i przeciągnięcie go myszą.

Przykład 6.5
Należy przenieść obszar B8:F11 do C11:E14.

Rozwiązanie
1. Zaznaczamy dany obszar.
2. Ustawiamy wskaźnik myszy (w dolnej części obszaru), aby zmienił on kształt na strzałkę.
3. Wciskamy lewy przycisk myszy i przeciągamy obszar w miejsce docelowe, a następnie

zwalniamy przycisk myszy.

Kopiowanie odbywa się w ten sam sposób, z tą różnicą, że po ustawieniu wskaźnika myszy
(pkt. 2 przykładu 6.5) wciskamy klawisz [Ctrl] i nie zwalniamy go podczas całej operacji
przeciągania (pkt. 3 przykładu 6.5).

28

6.2. Usuwanie

Aby usunąć zawartość bieżącej komórki, wystarczy wcisnąć klawisz [Delete]. Aby usunąć
zawartość jednego lub kilku obszarów, należy je zaznaczyć. Usuwana jest tylko zawartość
komórki ale nie zmieniają się formaty komórek. Po usunięciu zawartości i ponownym
wpisaniu danych format przypisany komórce jest nadal ważny. Aby usunąć zawartość łącznie
z formatem albo tylko format, należy wybrać polecenie Edycja | Wyczyść | Wszystko albo
Edycja | Wyczyść | Formaty.


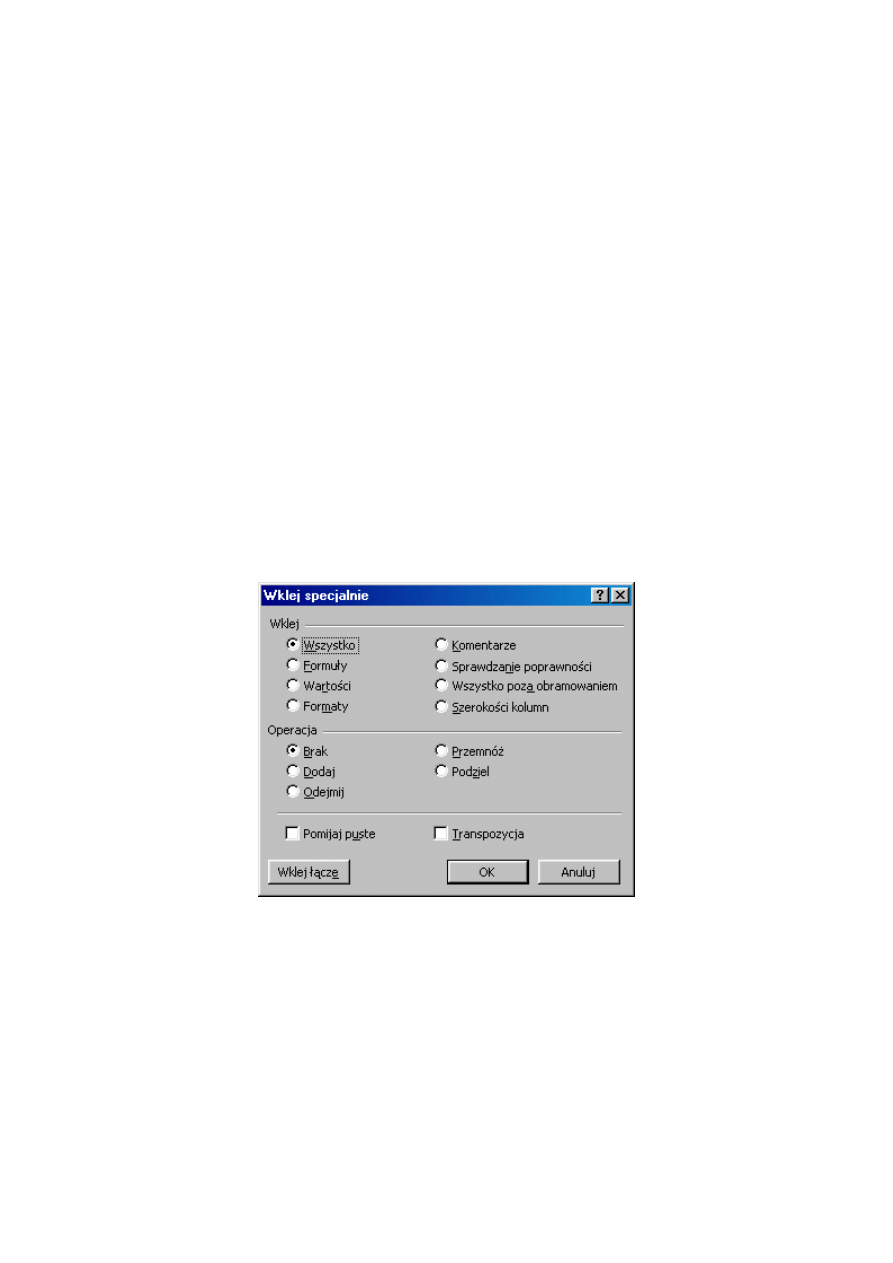
6.3. Wklejanie specjalne

Niekiedy chcemy przenieść lub skopiować zawartość komórek, ale nie zmieniać formatu
komórek docelowych. Możemy też kopiować sam format komórek bez zmiany zawartości
obszaru docelowego. Te i podobne operację wykonujemy korzystając z polecenia Edycja |
Wklej specjalnie. Po skopiowaniu danych komórek do schowka wybieramy miejsce
docelowe i polecenia wklejania specjalnego (można skorzystać z prawego przycisku myszy).
Pojawia się okno dialogowe Wklej specjalnie, w którym zaznaczamy, jakie elementy chcemy
uwzględnić w kopiowaniu (np. Wartości lub Formaty). Polecenie wklejania specjalnego
pozwala też dokonać transpozycji (zamiany wierszy z kolumnami) komórek w obszarze
docelowym.

Rys. 6.1. Okno dialogowe Wklej specjalnie

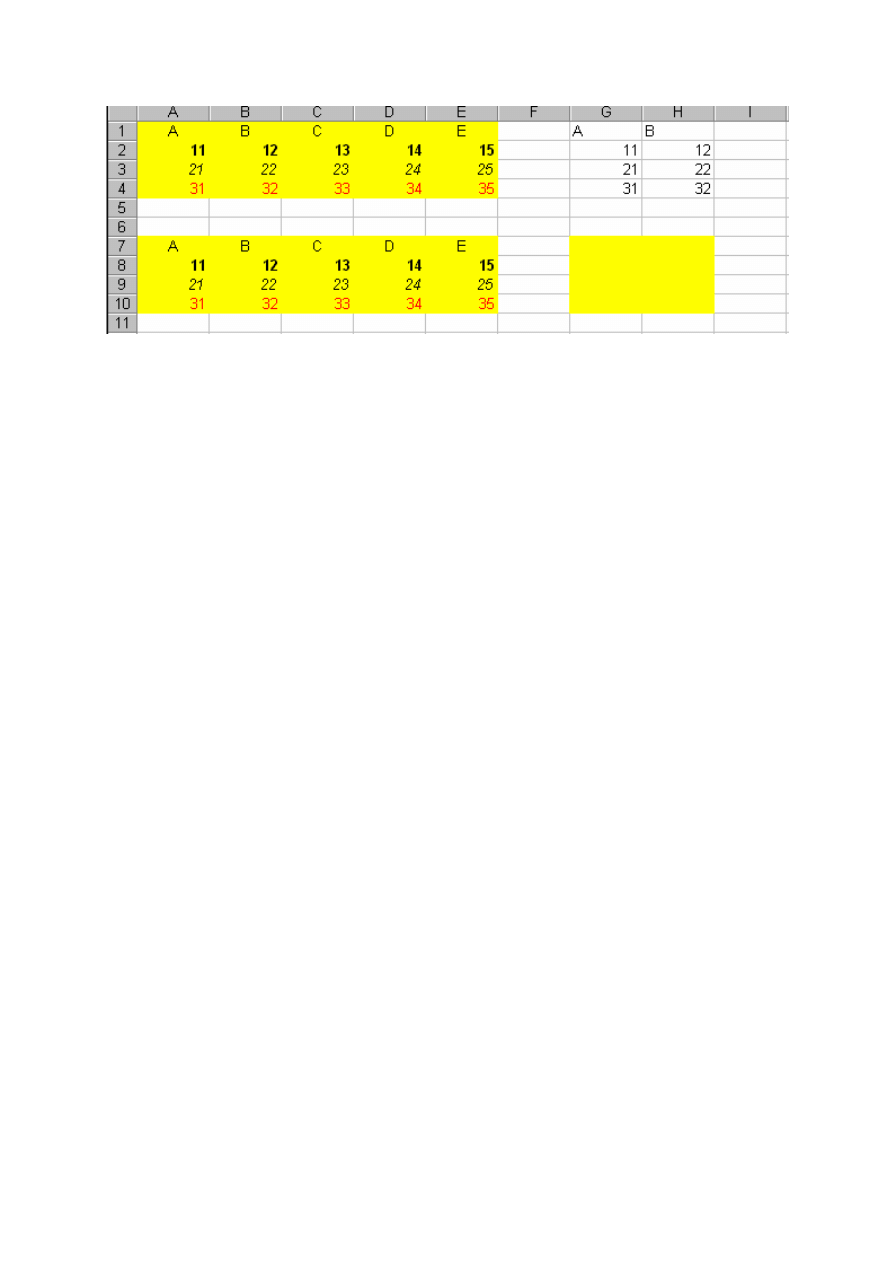
W przykładzie skopiowaliśmy komórki obszaru A1:E4 w zwykły sposób do obszaru A7:E10.
Następnie obszar A1:B4 skopiowaliśmy specjalnie do G1:H4 (Wklej Wartości) oraz do
G7:H10 (Wklej Formaty).

29

Rys. 6.2. Przykłady wklejania specjalnego

30

7. Automatyczne wypełnianie obszarów

Często zdarza się, że musimy wypełnić komórki arkusza kolejnymi liczbami naturalnymi (np.
przygotowując formularz listy obecności) albo kolejnymi nazwami miesięcy (przygotowując
sprawozdanie roczne). Możemy uprościć sobie pracę.

Do powielania liczb lub dat z zadanym krokiem wykorzystuje się tzw. uchwyt wypełnienia.
Jest to mały kwadracik, który znajduje się w prawym dolnym rogu komórki bieżącej lub
zaznaczonego obszaru komórek. Jeżeli ustawimy wskaźnik myszy na uchwycie wypełnienia,
duży krzyż zostaje zastąpiony małym czarnym krzyżykiem. Po wciśnięciu lewego przycisku
myszy i przeciągnięciu myszy w dół lub w prawo Excel automatycznie wypełni komórki.
Zasadę wypełniania ilustrują poniższe przykłady.

Przykład 7.1
Wpiszmy do komórek A8 i A9 liczby 1 i 2, a następnie zaznaczmy obszar A8:A9 i
przeciągnijmy uchwyt wypełnienia do kilku komórek poniżej. Komórki te zostaną
wypełnione liczbami 3, 4, 5,.... Podczas przeciągania należy obserwować pojawiający się z
prawej strony kwadrat na żółtym tle. Wyświetlane są w nim kolejne liczby.

Przykład 7.2
Wpiszmy do komórek B8 i B9 liczby 1980 i 1985 i postępujmy tak jak w przykładzie 1.Teraz
w kolejnych komórkach pojawią się liczby 1990, 1995, 2000, 2005,....Excel wypełnia
komórki kolejnymi wyrazami ciągu arytmetycznego, którego dwa pierwsze wyrazy znajdują
się w komórkach B8 i B9. Ciąg arytmetyczny jest jednoznacznie określony, jeżeli podamy
dwa pierwsze jego wyrazy. Zasadę tę możemy sprawdzić jeszcze raz wpisując do komórek
C8 i C9 liczby 0,6 i 0,4. Wówczas przyrost wynosi -0,2 i ten sam przyrost jest zachowany
przy wypełnianiu następnych komórek. Otrzymujemy ciąg: 0,2 0, -0,2, -0,4 itd.

Przykład 7.3
Podobna zasada odnosi się do dat. Jeżeli do komórek D8 i D9 wpiszemy daty 2003-06-25 i
2003-06-27, to kolejne komórki zostaną wypełnione datami 2003-06-29, 2003-07-01, 2003-
07-03,.... Przyrost dat wynosi 2 dni. Format daty zostaje zachowany. Podobnie zostają
tworzone ciągi czasu. Niech komórki E8 i E9 zawiera dane: 11:45 i 11:55 (format czasu).
Następnymi wartościami będą 12:05, 12:15, 12:25 (przyrost wynosi 10 minut).

Automatyczne wypełnianie można zastosować do nazw miesięcy i dni tygodnia. Wówczas
wystarczy zaznaczyć tylko jedną komórkę.

Przykład 7.4
Wpiszmy do komórki A3 tekst Styczeń i przeciągnijmy uchwyt wypełnienia do komórek
znajdujących się na prawo. W miarę zaznaczania w komórkach pojawią się nazwy kolejnych
miesięcy. Po nazwie Grudzień znów zostaje wpisana nazwa Styczeń. W podobny sposób
możemy wypełniać komórki nazwami kolejnych dni tygodnia. Nazwy miesięcy i dni tygodnia
można podawać na dwa sposoby: styczeń, luty,... albo sty, lut,... oraz poniedziałek,

+

Uchwyt
wypełnienia

31

wtorek,... albo pn, wt,.... Jeżeli chcemy wypełniać komórki nie kolejnymi miesiącami, ale np.
co trzy miesiące, to należy zaznaczyć dwa początkowe wyrazy ciągu (np. styczeń i
kwiecień).

Przykład 7.5
Można sprawdzić, że Excel pozwala tworzyć ciągi postaci a1, a2, a3,... albo krok 11, krok 12,
krok 13,.... Należy wówczas zaznaczyć dwa pierwsze wyrazy ciągu.

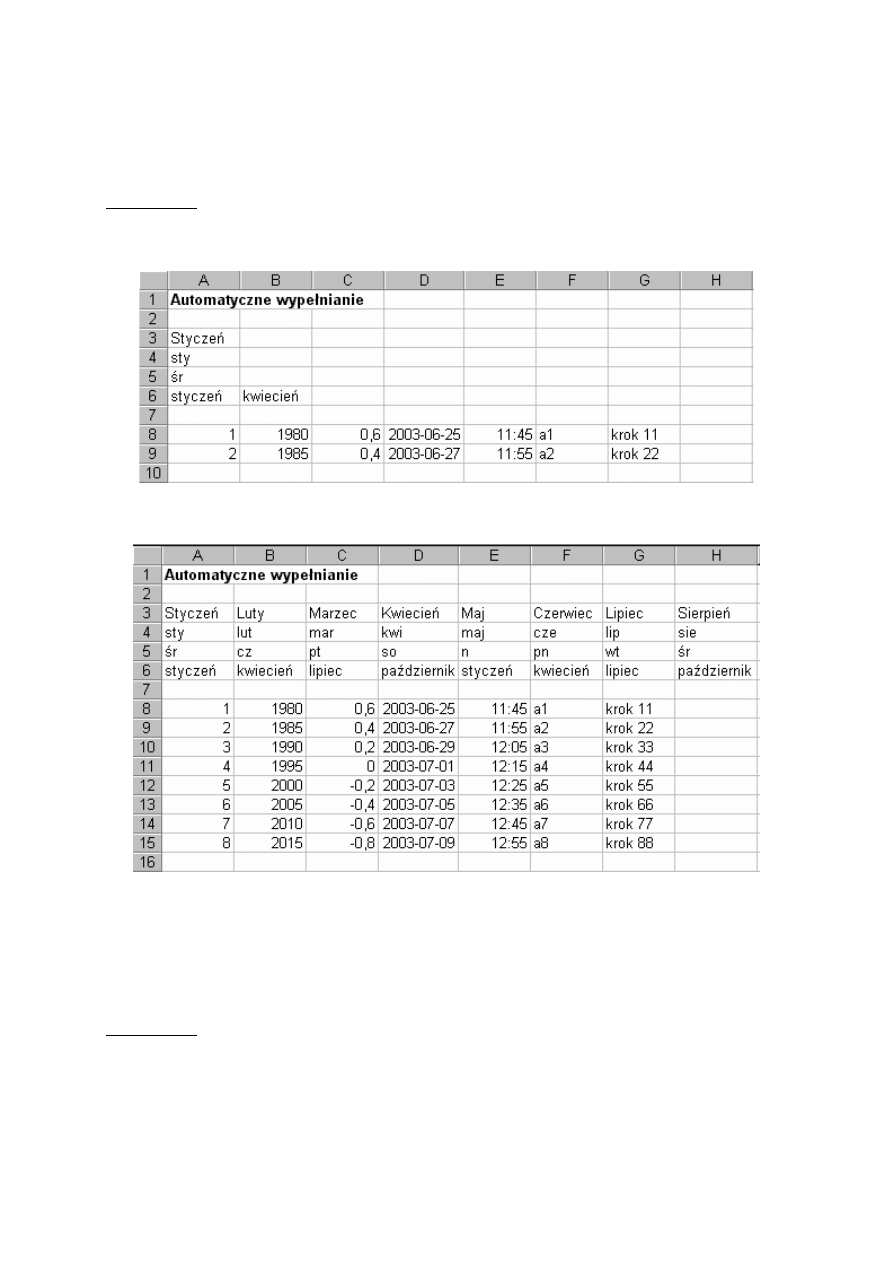
Rys. 7.1. Dane przed automatycznym wypełnieniem (przykłady 7.1-7.5)

Rys. 7.2. Dane po automatycznym wypełnieniu (przykłady 7.1-7.5)

Dalsze możliwości automatycznego wypełniania daje polecenie Edycja | Wypełnij | Serie
danych.... Otwiera się okno dialogowe Serie. Możemy zdefiniować nie tylko ciąg
arytmetyczny i ciąg dat, ale także ciąg geometryczny.

Przykład 7.6
Chcemy wypełnić kolejne komórki kolumny B począwszy od komórki B5 wyrazami 6, 12,
24, 48, 96,.... Liczby te tworzą ciąg geometryczny postaci

n

2

6

⋅ (gdzie n = 0,1,2,...).

Pierwszym wyrazem ciągu jest liczba 6, a stosunek dwóch sąsiednich wyrazów wynosi 2.
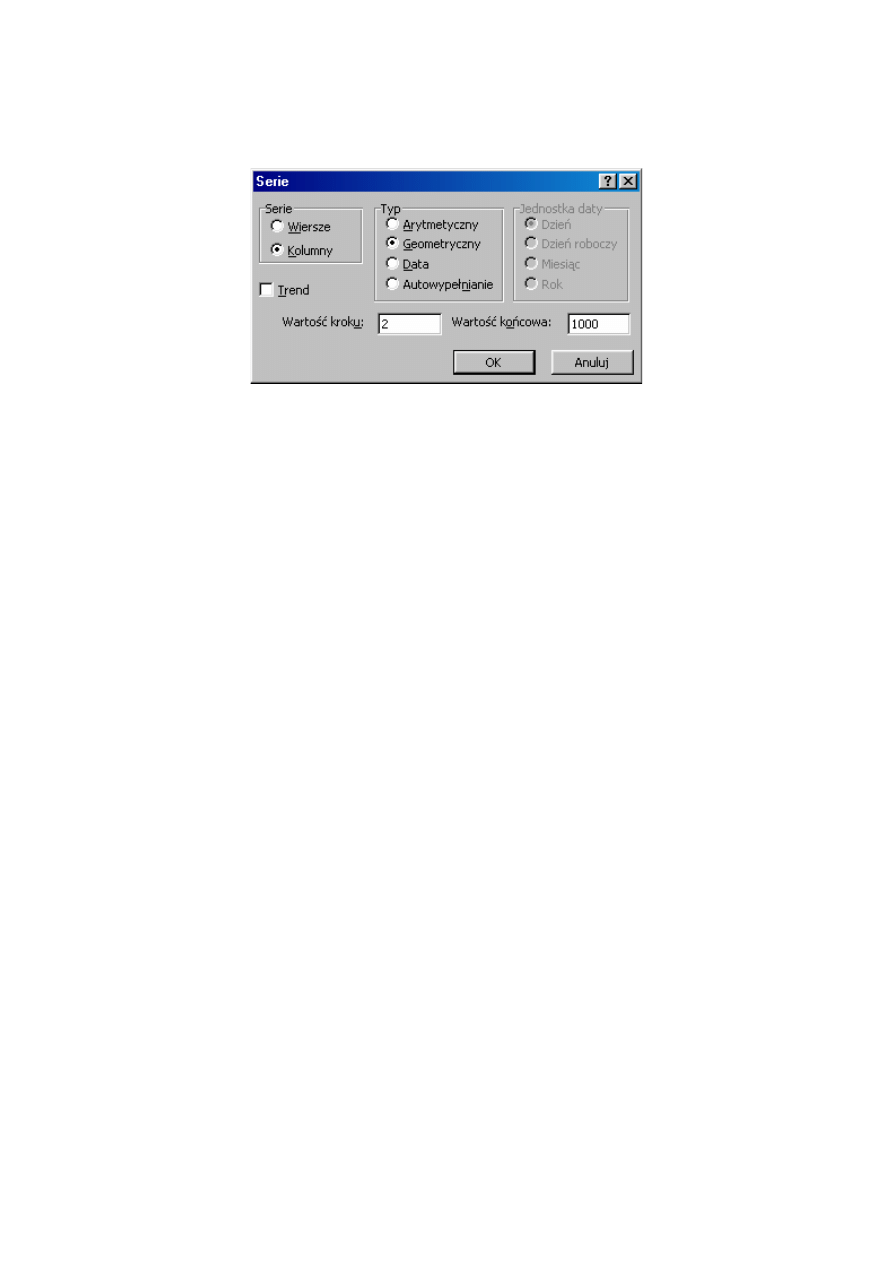
Załóżmy, że ostatnia liczba ciągu nie może przekroczyć 1000. Wówczas należy wpisać liczbę

32

6

(pierwszy wyraz ciągu) do komórki B5, otworzyć okno Serie i wypełnić pola, jak pokazano

na rys. 7.3.

Rys. 7.3. Okno dialogowe Serie - ciąg geometryczny

Zostaną wypełnione tylko komórki do B12 (liczby 6, 12, 24, 48, 96, 192, 384, 768), ponieważ
następny wyraz ciągu przekracza już 1000. Gdybyśmy przed wykonaniem polecenia
zaznaczyli kilka komórek (np. obszar B5:B9), to tylko komórki w zaznaczonym obszarze
byłyby wypełniane. Wówczas można nie podawać wartości końcowej ciągu.

33

8. Wprowadzanie wzorów

8.1. Wyrażenia arytmetyczne

W najprostszym zastosowaniu można wykorzystać Excel jako kalkulator. Jeżeli
wprowadzimy do komórki zapis postaci: =2+3, to Excel potraktuje go jako wyrażenie
arytmetyczne, którego wartość trzeba obliczyć i wyświetli wynik w danej komórce. Sposób
wyświetlania liczby zależy od przyjętego formatu komórki. Jeżeli wprowadzimy zapis 2+3,
Excel potraktuje to jako tekst i wyświetli w komórce napis 2+3. Aby zapis był traktowany
jako wyrażenie do obliczenia, musi zaczynać się od znaku równości (=) a dalej zawierać
„sensowną treść”. Jaką, najlepiej wyjaśnić to na przykładach.

Tabl. 8.1.

Wyrażenie

Zapis w Excelu

Wartość Uwagi

2

4

3

2

⋅

+

=2+3*4^2

50

Używamy innych oznaczeń dla
operatorów arytmetycznych.(np.*-
mnożenie, / - dzielenie, ^ -
potęgowanie Kolejność działań
jest podobna jak w matematyce

2

]

4

)

3

2

[(

⋅

+

=((2+3)*4)^2

400

Aby zmienić kolejność działań
należy używać nawiasów. Tylko
nawiasy okrągłe są dozwolone, ale
można je zagnieżdżać

2

=pierwiastek(2) 1,4142...

W programie jest wbudowanych
wiele funkcji matematycznych i
innych. Argumenty funkcji
umieszczamy w nawiasach
okrągłych

{

}

4

2

3

2

4

3

,

,

max

=max(3^3;4^2;2^4)

27

Funkcja może mieć wiele
argumentów. Oddzielamy je
wtedy średnikiem. Argumentem
funkcji może być inne wyrażenie

π

=pi() 3,14...

Liczba

π jest traktowana jako

funkcja zeroargumentowa o
nazwie pi. Brak argumentów
funkcji zaznaczamy jako pusty
tekst umieszczony w nawiasach

)

ln(sin

o

45

2

= ln(sin(radiany(45))^2)

lub

=ln(sin(pi()/4)^2

-0,693...

Można używać funkcji złożonych,
których argumentami są wyrażenia
zawierające funkcje. Argumenty
funkcji trygonometrycznych
należy podawać w mierze
łukowej. Funkcja radiany(kąt)
przelicza stopnie na radiany
(np.

4

45

/

o

π

=

)

5

2

5

12

,

%

,

⋅

)%

5

,

1

06

,

0

(

⋅

=12,5%*2,5

=(0,06*1,5)%

0,3125
0,0009

Liczby we wzorach mogą być
zapisane w różnych formatach (np.
procentowym, wykładniczym,
walutowym)

34

8.2. Wyrażenia zawierające adresy komórek

Przykład 8.1
1. Aby obliczyć objętość walca o promieniu podstawy 5 i wysokości 10, wystarczy wpisać do
pewnej komórki wzór =pi()*5^2*10. Aby obliczyć pole powierzchni całkowitej tego walca,
należy wpisać wzór =2*pi()*5*(5+10). Jeżeli chcemy obliczać pole i objętość innych
walców, to powyższe wzory wymagają gruntownej korekty.
2. Można postąpić inaczej, wykorzystując bardzo ważną własność Excela, polegającą na
automatycznym przeliczaniu wzorów. Objętość i pole walca zależą od dwóch parametrów:
promienia podstawy (r) i wysokości (h). Wybierzmy dwie komórki, do których wpiszemy te
dane. Niech będą to komórki B1 i B2.

Rys. 8.1. Obliczenia

Do komórki B3 wpiszemy wyrażenie zawierające wzór na obliczanie objętości walca.
Do komórki B4 wpiszemy wyrażenie zawierające wzór na obliczanie pola powierzchni walca.

Wtedy w komórkach B3 i B4 otrzymamy wyniki: odpowiednio liczby 785,3982 i 471,2389.
Jeżeli zmienimy zawartość komórki B1 lub B2, to Excel na nowo przeliczy wzory i wyświetli
nowe wyniki. W ten sposób możemy łatwo obliczać objętość i pole powierzchni dowolnego
walca.

Uwagi
1. Komórki B1 i B2 powinny zawierać wartości liczbowe. Mogą to być liczby (w różnych

formatach) lub dowolne wzory dające w wyniku liczby. W ten sposób możemy obliczyć
np. objętość walca o promieniu 5 i wysokości

π

2

.

2. Jeżeli komórka B1 lub B2 jest pusta, Excel potraktuje jej wartość liczbową jako zero.

Jeżeli komórka B1 lub B2 zawiera napis (np. abc), to zamiast wyniku otrzymamy
komunikat błędu: #ARG!

3. Excel nie sprawdza, czy dane problemu są sensowne pod względem geometrycznym,

ekonomicznym lub zdroworozsądkowym. Jeżeli wpiszemy liczbę -1 do komórki B1 i
liczbę -3 do komórki B2, to też otrzymamy wynik (-9,42478) w komórce B3. Excel po
prostu oblicza wartość wyrażenia dla ustalonych parametrów.

4. W przedstawionych obliczeniach napisy w kolumnie A są traktowane jako komentarze

pomagające nam odczytywać zapis w arkuszu. Nie mają one znaczenia dla obliczeń.
Zauważmy jednak, że bez takich napisów duże problemy stają się trudne do identyfikacji.

Istnieje prosty sposób wprowadzania adresów komórek do wzoru, co pokazuje poniższy
przykład. Wpiszmy do komórek C1 i C2 jakieś liczby. Naszym celem jest wpisanie do
komórki C5 wzoru =C1*C2.



Przykład 8.2

35

1. Ustawmy kursor w komórce C5 i wpiszmy znak = (lub kliknijmy myszą na przycisku

Edytuj formułę

(

).

2. Kliknijmy myszą w komórce C1 Jej adres wstawi się do tworzonego wzoru.
3. Wprowadźmy z klawiatury znak * i kliknijmy myszą w komórce C2.
4. Kliknijmy myszą na przycisku wpisu

znajdującym się po lewej stronie pola formuły.

W komórce C5 uzyskamy sumę zawartości dwóch komórek.

Ten sposób wprowadzania wzorów jest o tyle wygodny, że nie musimy zwracać uwagi na
adresy komórek, lecz bardziej koncentrować się na ich zawartości. Jest mniejsze
prawdopodobieństwo pomyłki.

Przykład 8.3
Rozwiążemy pewien problem finansowy. Składamy w banku pewną kwotę x (np. 1000 zł) na
oprocentowanym koncie (np. 12% rocznie). Przy rocznej kapitalizacji po roku stan konta
wyniesie

1120

1000

%

12

1000

=

⋅

+

(ogólnie:

)

1

(

p

x

+

+

, gdzie p - jest stopą procentową).

Jeżeli nie wyjmujemy wkładu, to po t latach mamy na koncie kwotę

t

p

x

)

1

(

+

+

. Aby móc

przeprowadzać obliczenia dla różnych kwot początkowych i różnych stóp oprocentowania,
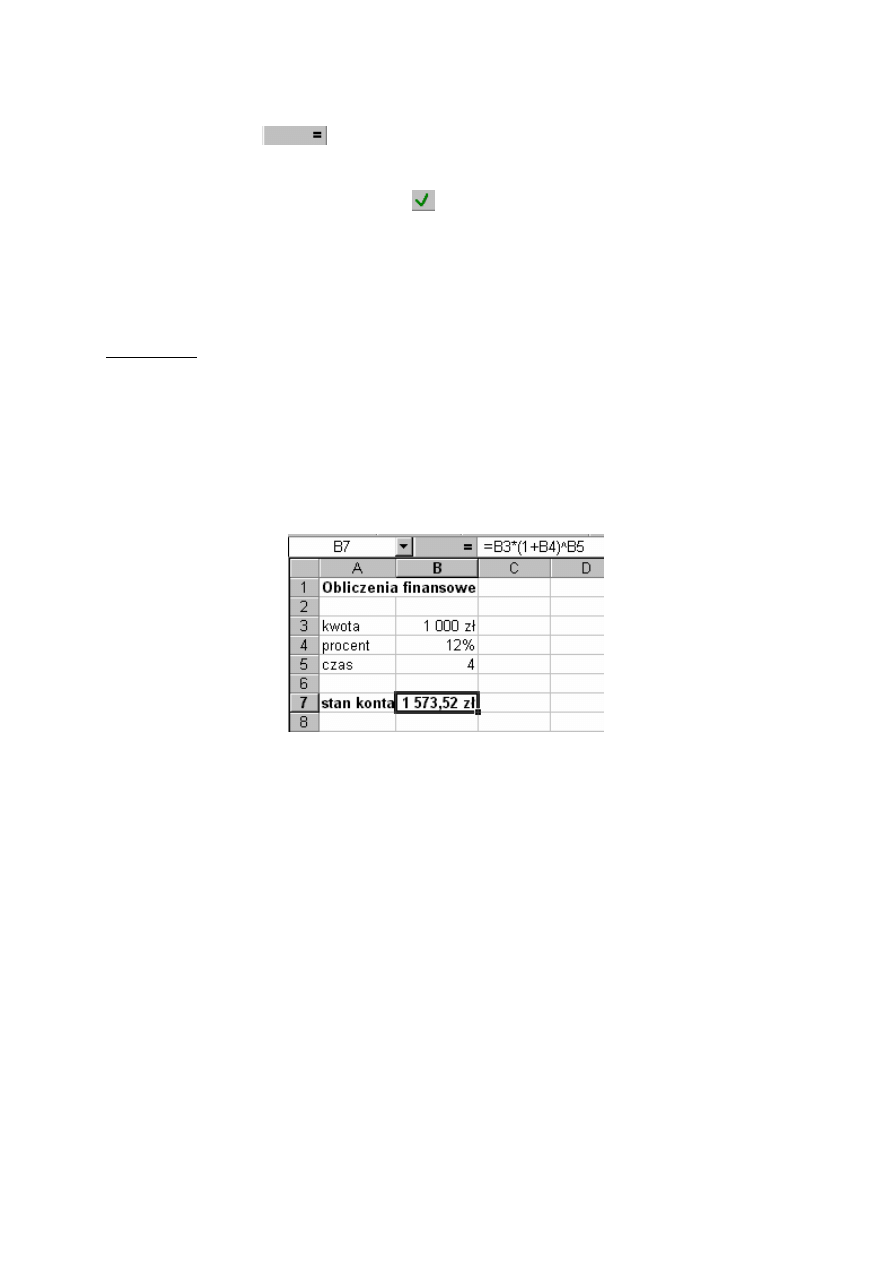
zapiszmy dane zadania w komórkach B3, B4 i B5 arkusza. Komórka B3 zawiera kwotę x, B4
zawiera wartość p, a B5 - czas t.

Rys. 8.2. Obliczenia

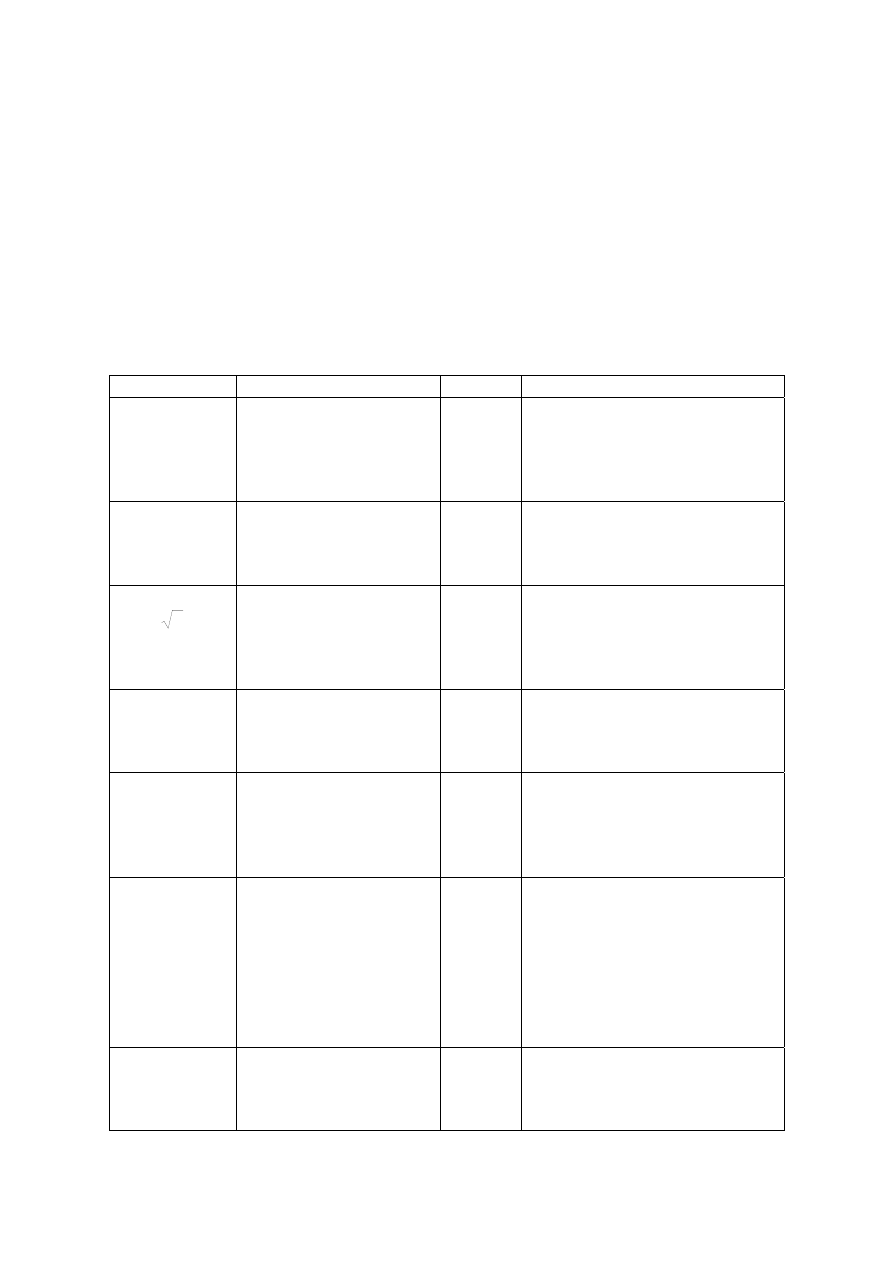
Dla wartości x = 1000zł, p = 12% i t = 4 lata otrzymujemy wynik 1573,52zł. Jeżeli bank
oferuje inną kapitalizację wkładów niż roczna, to musimy zmodyfikować wzór. Wpiszmy do
komórki B6 liczbę m wskazującą, ile razy w ciągu roku następuje kapitalizacja wkładów. Przy
kapitalizacji rocznej m = 1, przy kwartalnej m = 4, a przy miesięcznej m = 12. Wzór
pozwalający obliczyć stan konta po t latach ma postać:

mt

m

p

x

)

/

1

(

+

+

. Musimy przeliczyć

oprocentowanie roczne na kwartalne lub miesięczne (

m

p / ) i ustalić, ile razy odsetki będą

dopisywane do wkładu (

t

m

⋅ ).

Możemy porównać 3 oferty banków:
1. Oprocentowanie 12% i kapitalizacja roczna.
2. Oprocentowanie 11,5% i kapitalizacja kwartalna.
3. Oprocentowanie 11% i kapitalizacja miesięczna.

36

Rys. 8.3. Obliczenia

Druga oferta jest najbardziej atrakcyjna.


8.3. Autosumowanie

Przykład 8.4
Arkusz zawiera dane na temat obrotów dwóch sklepów w kolejnych dniach tygodnia. W
obszarze B4:B9 wpisane są dane dotyczące pierwszego sklepu, a w obszarze C4:C9 -
dotyczące drugiego sklepu. Drugi sklep w środę był zamknięty. Naszym zadaniem jest
obliczyć sumę obrotów sklepów w ciągu całego tygodnia (od poniedziałku do soboty).
Wyniki wpiszemy w wierszu 10. Aby obliczyć obroty pierwszego sklepu można oczywiście
wpisać wzór: =b4+b5+b6+b7+b8+b9, ale jest on dosyć długi, zwłaszcza gdy musimy
zsumować wiele pozycji. Wygodniej skorzystać z funkcji SUMA. Ponieważ operacja
sumowania kolejnych pozycji występuje często w obliczeniach, twórcy Excela udostępnili
przycisk ułatwiający wykonanie podsumowania. Ustawmy kursor w komórce B10
(znajdującej się poniżej komórek zawierającej dzienne obroty i wciśnijmy przycisk
(Autosumowanie)

, znajdujący się na standardowym pasku narzędzi. Excel zaznaczy

obszar, który domyślnie będzie sumowany, a w komórce B10 pojawi się tekst
=SUMA(B4:B9)

. Ponieważ jest to zgodne z naszymi intencjami, potwierdzamy operację

naciskając przycisk

albo wciskając klawisz [Enter]. W komórce pojawi się wartość

235091,11. Jest to suma liczb wyświetlanych w komórkach obszaru B4:B9.

Rys. 8.4. Autosumowanie

W podobny sposób możemy podsumować obroty drugiego sklepu. Tutaj jednak po
ustawieniu kursora w komórce C10 i wybraniu polecenia autosumowania Excel zaznaczy
obszar C7:C9. Dzieje się tak, ponieważ powyżej bieżącej komórki tylko w tym obszarze
znajduje się ciągły zakres wartości liczbowych. Komórka C6 już nie zawiera liczby. Musimy

37

skorygować sumowany zakres zaznaczając obszar C4:C9. Obszar może zawierać wartość
nienumeryczne, ponieważ funkcja SUMA traktuje je jako zera. Otrzymamy wynik 89106,75.

Przykład 8.5
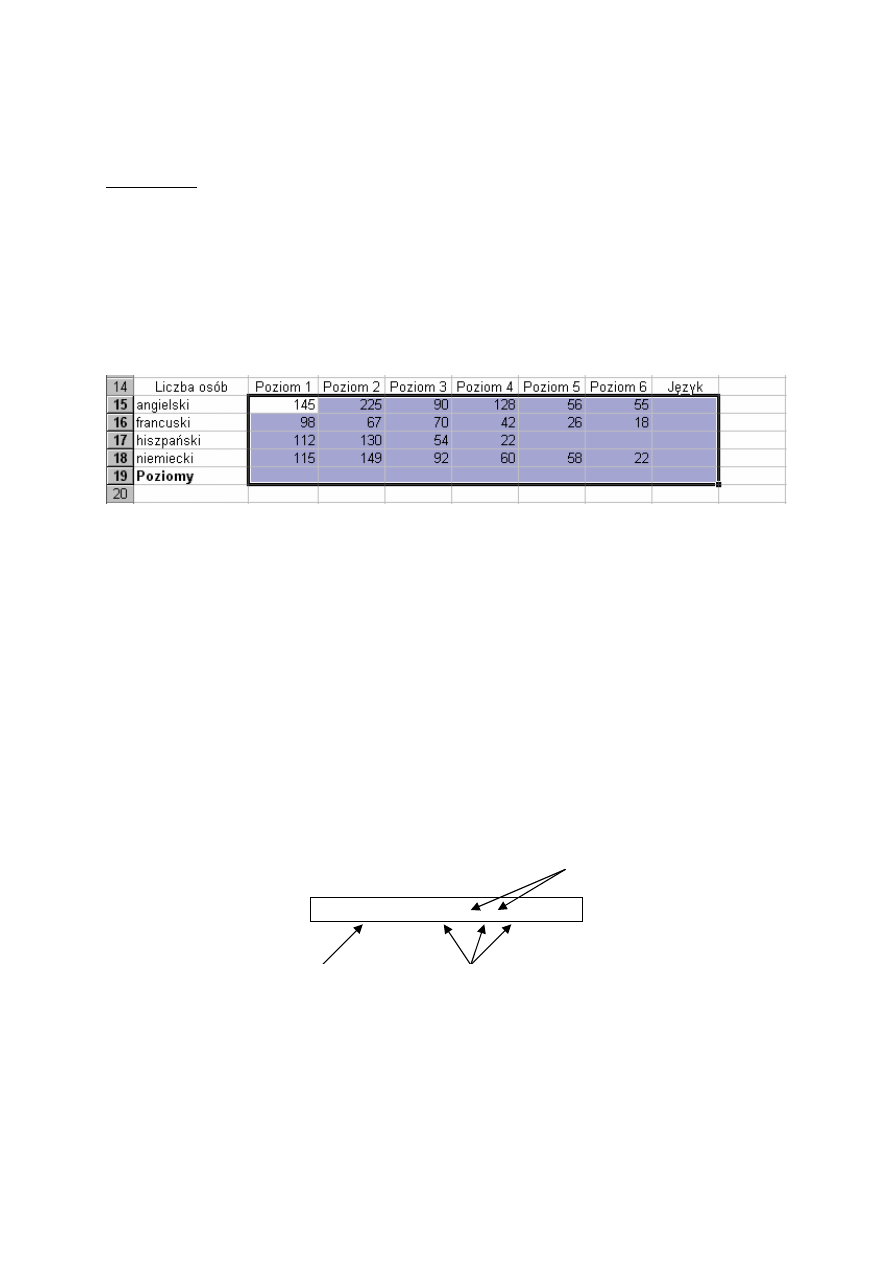
Tabela zawiera liczby uczestników kursów językowych w podziale na języki i poziomy
nauczania. Ponieważ kursy języka hiszpańskiego rozpoczęły się niedawno, nie ma tu osób
uczących się na poziomie 5 i 6. Naszym zadaniem jest obliczyć, ile osób łącznie uczy się
języków na każdym poziomie i ile osób uczy się danego języka, niezależnie od poziomu.
Należy więc podsumować wiersze i kolumny tabeli. Można to zrobić bardzo szybko
zaznaczając obszar zawierający o jeden wiersz i jedną kolumnę więcej niż obszar danych (rys.
8.5) i wciskając przycisk autosumowania. Otrzymamy odpowiednie sumy, a w prawym
dolnym rogu (komórka H19) sumę ogólną (1834).

Rys. 8.5. Autosumowanie

8.4. Sposoby wprowadzania funkcji

SUMA(liczba1;liczba2;...) jest przykładem funkcji. W programie Excel jest dostępnych ponad
300 wbudowanych funkcji. Są one podzielone na 10 grup tematycznych: Finansowe, Daty i
czasu, Matematyczne, Statystyczne, Wyszukiwania i adresu, Bazy danych, Tekstowe,
Logiczne, Informacyjne, Inżynierskie. Użytkownik programu może również definiować swoje
własne funkcje. Każda funkcja jest identyfikowana przez swoją nazwę. Małe i duże litery w
nazwie funkcji są utożsamiane, ale prawidłowe użycie polskich liter jest istotne (Excel nie
rozpozna nazw JEZELI, SREDNIA, MODUL.LICZBY, ZAOKR.W.GORE). Funkcja ma
stałą lub zmienną liczbę argumentów. Argumenty funkcji ujmujemy w nawiasy okrągłe i
oddzielamy od siebie średnikiem. Istnieją też funkcje bez argumentów np. PI(), LOS(),
DZIŚ(), ale trzeba w nich zachować nawiasy po nazwie funkcji. Nazwa funkcji i jej
argumenty nie mogą być oddzielone spacją, pomiędzy argumentami spacje mogą wystąpić).

SUMA(A4:B8; C5; 12)

W ogólności argumentem funkcji może być:

liczba

log(2)

tekst

dł("ekonomia")

adres

komórki

zaokr(a4;c5)

obszar

max(c2:c6)

separator

argumenty

(obszar, komórka, stała)

nazwa

38

wzór

pierwiastek(pi()/6)

nazwa

sin(x),

średnia(pomiary)

Są dwa sposoby wprowadzania funkcji:
1. Wpisujemy bezpośrednio z klawiatury nazwę funkcji i jej argumenty. Nazwy można pisać

małymi literami. Excel zamienia w nazwach funkcji małe litery na duże.

2. Wstawiamy ją za pomocą polecenia Wstaw | Funkcja (lub Kreatora funkcji - przycisku

) widocznego na standardowym pasku narzędzi).

Przykład 8.6
Obliczymy iloczyn skalarny dwóch wektorów, których współrzędne są zapisane w komórkach
A2:A4 i B2:B4.





















−

=

3

7

5

X

i





















−

=

8

4

2

Y

Zamiast wprowadzać wzór =a2*b2+a3*b3+a4*b4 (niewygodny, jeżeli wymiary wektorów są
znacznie większe niż 3) wykorzystamy funkcję SUMA.ILOCZYNÓW.

Rys. 8.6. Zastosowanie funkcji SUMA.ILOCZYNÓW

Postępowanie jest następujące:
1. Wybieramy miejsce w arkuszu, w którym będzie wstawiony wynik (niech będzie to

komórka C2).

2. Wybieramy polecenie Wstaw | Funkcja.

Ukazuje się okno dialogowe Wklej funkcję.

39

Rys. 8.7. Okno dialogowe Wklej funkcję

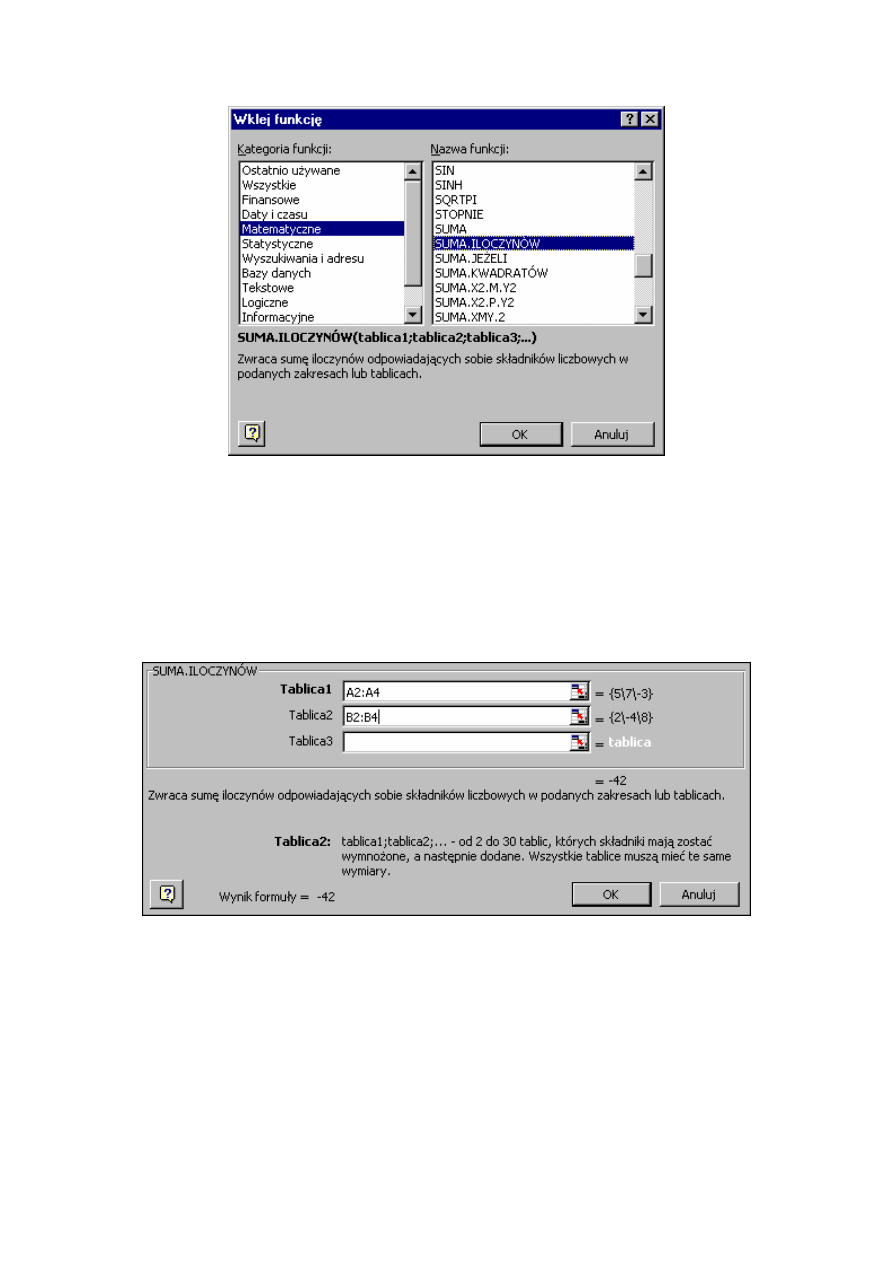
Funkcje są podzielone tematycznie na kategorie. Nasza funkcja należy do kategorii
Matematyczne

. W prawej części okna wyświetla się alfabetyczny wykaz funkcji danej

kategorii. Pod spodem znajduje się objaśnienie na temat zaznaczonej funkcji.

Po wybraniu funkcji SUMA.ILOCZYNÓW klikamy na przycisku OK lub wciskamy
klawisz [Enter]. Ukazuje się okno dialogowe funkcji, w którym określamy argumenty
funkcji.

Rys. 8.8. Definiowanie argumentów funkcji w oknie dialogowym

Należy wstawić adres obszaru zawierającego pierwszy wektor do pola Tablica1 i adres
obszaru zawierającego drugi wektor do pola Tablica2. Funkcja SUMA.ILOCZYNÓW służy

również do obliczania wyrażeń postaci

...

1

i

i

n

i

i

c

b

a

∑

=

, gdzie mamy więcej niż 2 wektory, ale

tutaj nie wykorzystujemy tego. Dlatego pole Tablica3 jest niewypełnione.

Wynikiem jest liczba -42.

40

Uwaga
W tym przypadku obszary tablic muszą mieć te same wymiary. Jeżeli tak nie jest, to w
komórce C2 pojawi się komunikat błędu: #ARG.


8.5. Kilka przykładów funkcji

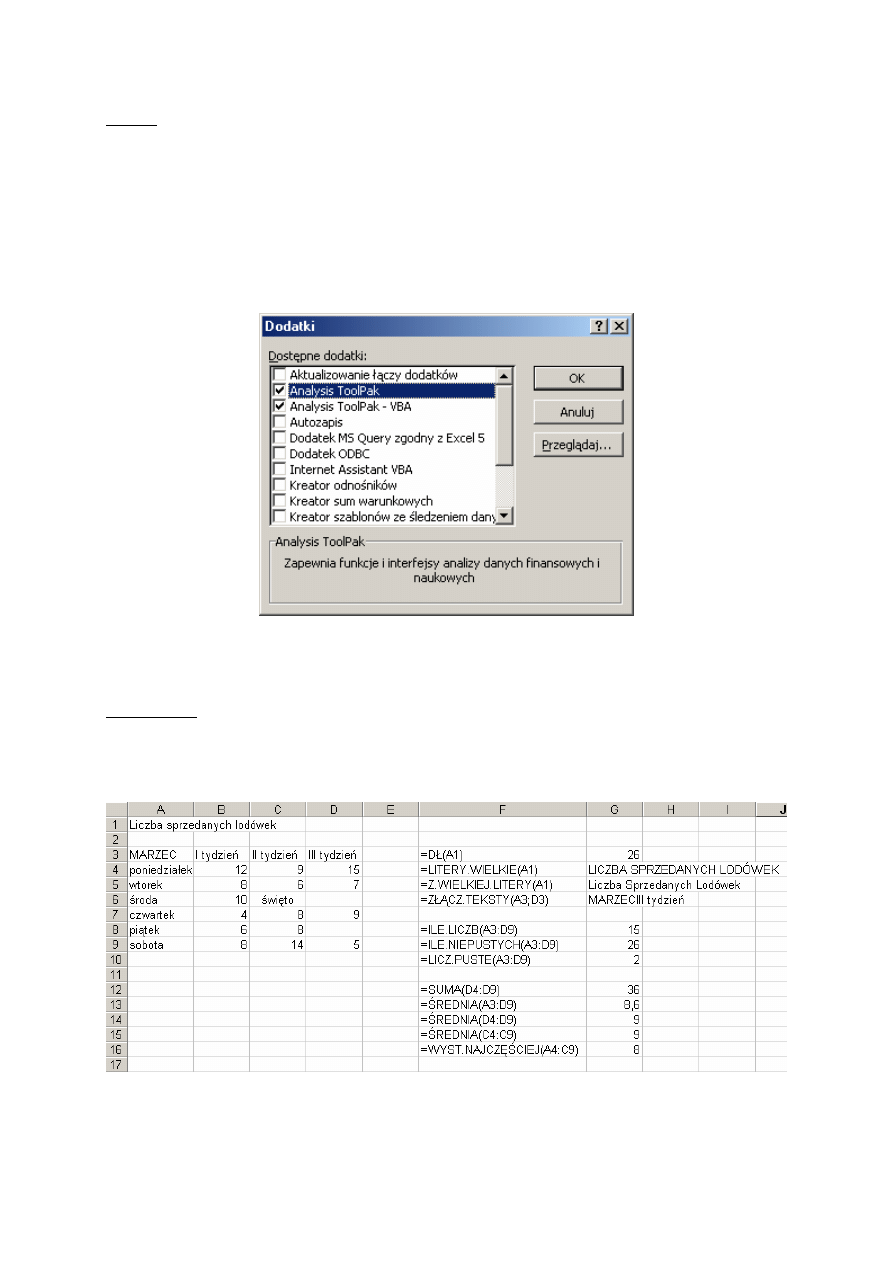
Użycie niektórych funkcji musi być poprzedzone zainstalowaniem dodatkowego modułu za
pomocą polecenie Narzędzia | Dodatki.

Rys. 8.9. Instalowanie modułu zawierającego funkcje finansowe

Tu podamy przykłady zastosowania niektórych funkcji.

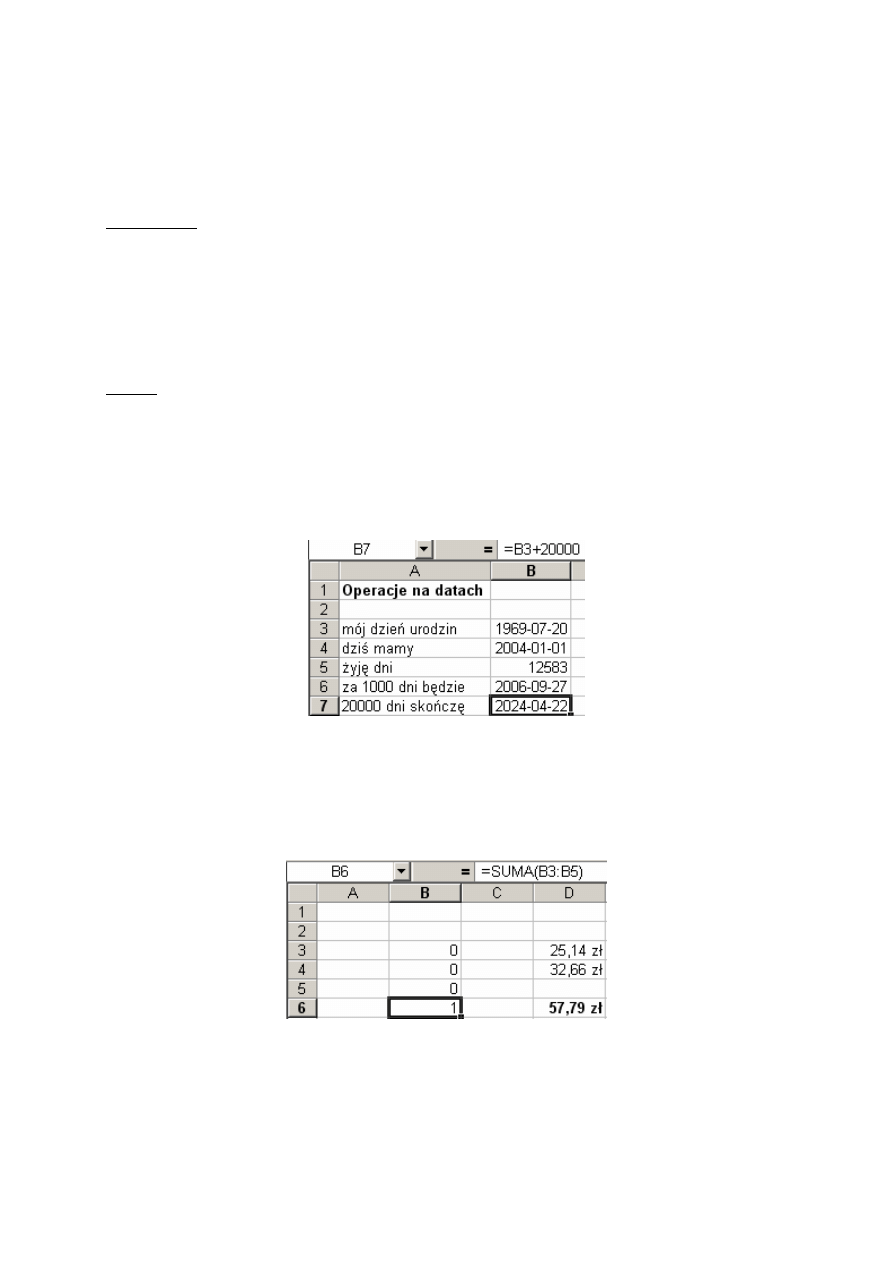
Przykład 8.7
Arkusz zawiera tabelę dotyczącą sprzedanych lodówek w trzech tygodniach marca. Dane
umieszczone są w obszarze B4:D9, przy czym komórka C6 zawiera tekst, a komórki D6 i D8
są puste.

Rys. 8.9. Przykłady funkcji standardowych

W kolumnie F podaliśmy treść formuł, które są wstawione do komórek znajdujących się w
kolumnie G. W tej kolumnie są wyświetlone wartości formuł.

41

DŁ

(tekst)

- oblicza liczbę znaków tekstu znajdującego się w komórce,

LITERY.WIELKIE

(tekst) - zamienia litery w tekście na duże,

Z.WIELKIEJ.LITERY

(tekst) - zamienia tekst na tekst. którym pierwsze litery słów są

duże, a pozostałe małe,

ZŁĄCZ.TEKSTY

(tekst1;tekst2) - łączy dwa lub kilka tekstów w jeden (konkatenacja),

ILE.LICZB

(obszar)

- oblicza, ile komórek w obszarze zawiera wartości liczbowe,

ILE.NIEPUSTYCH

(obszar) - oblicza, ile komórek w obszarze jest niepustych,

LICZ.PUSTE

(obszar)

- oblicza, ile komórek w obszarze jest pustych,

WYST.NAJCZĘSCIEJ

(obszar) - oblicza wartość występującą najczęściej w komórkach

obszaru (czyli dominantę).

Funkcja ŚREDNIA(obszar) oblicza średnią arytmetyczną liczb w podanym obszarze.
Zwróćmy uwagę, że funkcja nie uwzględnia komórek pustych i zawierających tekst.

Przykład 8.8
Na rys.8.10 widzimy przykłady użycia kilku funkcji matematycznych i statystycznych.

Rys. 8.10. Przykłady funkcji standardowych

KOMBINACJE

(n;k) - oblicza na ile sposobów można wybrać k elementów ze zbioru n-

elementowego, czyli współczynnik Newtona













k

n

, np. spośród 13

delegatów można wybrać na 1287 sposobów 5-osobowy zarząd,

SILNIA

(n)

- oblicza n! czyli liczbę permutacji zbioru n-elementowego, np. 13
delegatów mozna uporządkować na 6227020800 sposobów,

ROZKŁAD.DWUM

(k;p;n;c) - oblicza prawdopodobieństwo wystąpienia k sukcesów w n

doświadczeniach schematu Bernoulliego z prawdopodobieństwem p
sukcesu w jednym doświadczeniu (gdy c = 0) lub skumulowane
prawdopodobieństwo nie więcej niż k sukcesów (gdy c = 1), np.
prawdopodobieństwo, że wśród 6 losowo wybranych delegatów jest
dwóch członków 5-osobowego zarządu wynosi 0,318,

MOD

(x;y)

- oblicza resztę z dzielenia x przez y np. gdy 13 delegatów usiądzie
przy stolikach 4-osobowych, to jedna osoba będzie musiała siedzieć
samotnie. Argumenty nie muszą być liczbami całkowitymi np.
MOD(27,8; pi()) = 2,66725877.

42

8.6. Operacje na datach

Korzystając z tego, że Excel traktuje datę jako liczbę dni możemy obliczać, ile dni upływa
między dwiema datami.

Przykład 8.9
Wpiszmy do komórki B3 swoją datę urodzenia (na rys. 8.11 zamiast tego jest wpisana data
lądowania pierwszego człowieka na Księżycu). Do komórki B4 wpiszmy dzisiejszą datę np.
używając formuły =dziś(). Do komórki B5 wpiszmy wzór =b4-b3. Jest to różnica dwóch dat.
Excel niepoprawnie nadaje komórce format daty (i otrzymamy wynik postaci 1934-06-13) Po
skorygowaniu formatu otrzymamy liczbę dni, jaka upłynęła od daty wpisanej w komórce B3
do daty wpisanej w komórce B4.

Uwaga
Różnica pomiędzy użyciem funkcji DZIŚ() a wpisaniem konkretnej stałej daty jest
następująca: jeżeli za tydzień otworzymy arkusz, stała data nie zmieni się (i przestanie być
aktualna), natomiast Excel jako wartość wyrażenia dziś() przyjmie bieżącą datę.

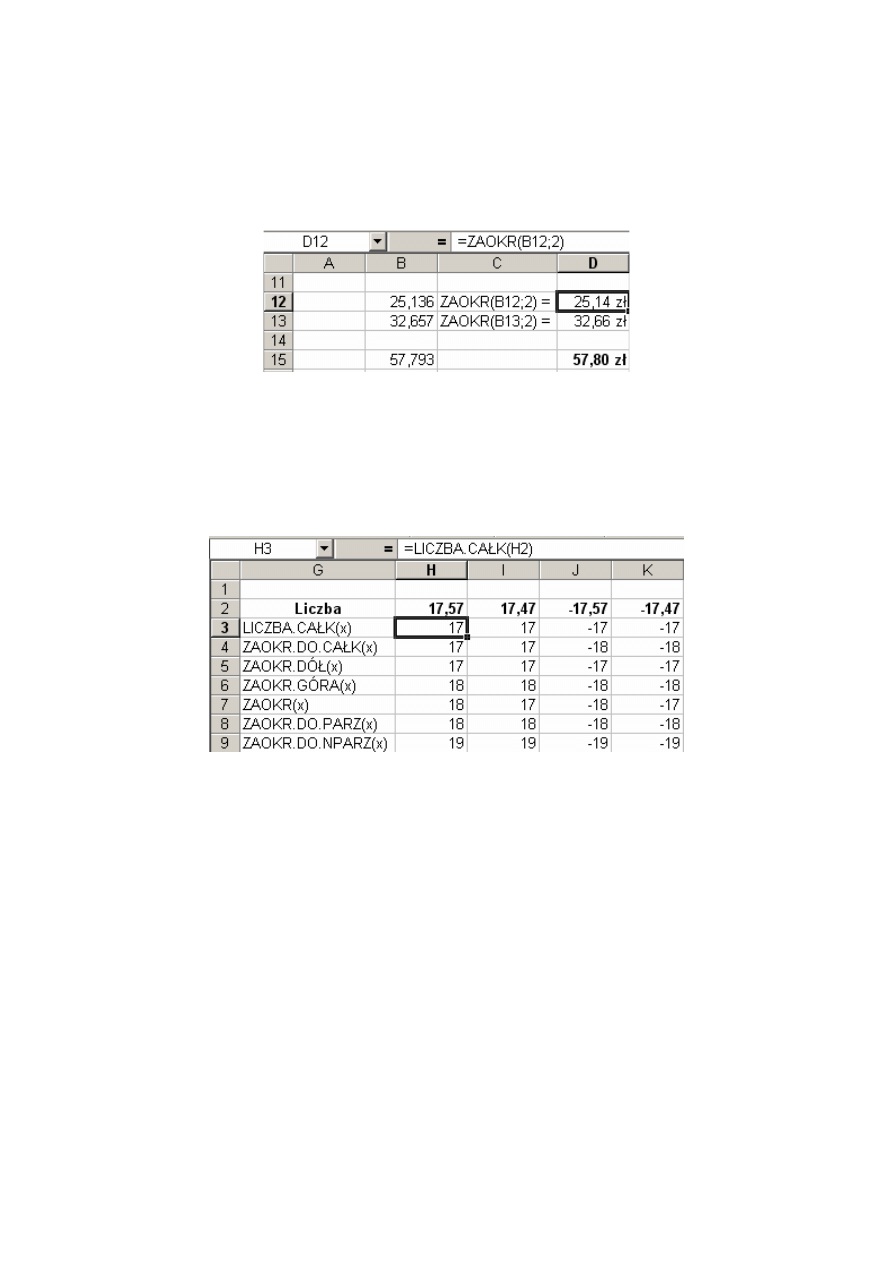
Wpiszmy teraz do komórki B6 wzór =b4+1000. Otrzymamy odpowiedź na pytanie, jaka data
będzie za 1000 dni.

Rys. 8.11. Operacje na datach

8.7. O zaokrągleniach

Zwróćmy uwagę na wygląd arkusza na rys. 8.12.

Rys. 8.12. Zaokrąglenia

W kolumnie B suma zer daje 1, w kolumnie D zginął 1 grosz podczas sumowania. W
rzeczywistości w komórkach B3, B4, B5 są wpisane liczby 0,3, w komórce D3 - 25,136, w
komórce D4 - 32,657. Wartości widoczne w arkuszu wynikają ze sformatowania komórek.
Pierwsza kolumna ma format liczbowy i zero miejsc dziesiętnych. Druga kolumna ma format

43

walutowy z dwoma miejscami dziesiętnymi. Excel bierze do obliczeń dokładne wartości, a
następnie zaokrągla wynik zgodnie z przyjętym formatem.

Jeżeli chcemy, żeby zaokrąglenie liczb następowało przed wykonaniem operacji
arytmetycznej, to należy zastosować jedną z dostępnych funkcji zaokrągleń.

Rys. 8.13. Funkcja zaokrąglania

W Excelu istnieje wiele sposobów zaokrąglania liczb lub obcinania części ułamkowej.
Funkcja ZAOKR(x; n) jest jedną z nich. Zaokrągla ona liczbę x do n miejsc dziesiętnych.
Argument n może być ujemny np. ZAOKR(1453,7;-2) = 1500).

Poniżej widzimy kilka przykładów.

Rys. 8.14. Przykłady działania różnych funkcji zaokrąglania

44

9. Nazwy komórek i obszarów

Zadanie dotyczące obliczania objętości i pola powierzchni walca może być rozwiązane lepiej.
Nie jest łatwo zapamiętywać wzory postaci: =2*pi()*b1*(b1+b2) albo =c17/f23+k9-b2.
Dzięki temu, że komórce lub obszarowi arkusza możemy przypisywać własne nazwy, można
zapisywać wzory w bardziej przejrzysty sposób. Powróćmy do przykładu (rys. 7.1).

Przykład 9.1
Ustawmy komórkę bieżącą B1 i ustawmy wskaźnik myszy w polu nazwy. Zastąpmy napis B1
(adres bieżącej komórki) napisem r i naciśnijmy [Enter]. Oznacza to, że przypisaliśmy
komórce B1 nazwę r (małe i duże litery są utożsamiane). Od tej chwili można odwoływać się
do komórki B1 jako komórki r. W podobny sposób komórkę B2 możemy nazwać h. Teraz
wzory na objętość i pole powierzchni całkowitej walca zapiszemy (w komórkach B3 i B4) w
sposób bardziej naturalny (rys. 9.1).

Rys. 9.1. Obliczenia z użyciem nazw komórek

Uwaga. Przypisanie komórce nazwy nie polega na wpisaniu tej nazwy do komórki. Komórka
B1 w dalszym ciągu zawiera liczbę 5 (a nie tekst r), a komórka B2 zawiera liczbę 10 (a nie
tekst h).

Nazwy komórek mogą być wyrazami np. moglibyśmy nazwać komórkę wysokość lub
promień

lub promień_koła (jeżeli nazwa ma składać się z kilku wyrazów, należy je połączyć

znakiem podkreślenia). W nazwach można używać cyfr (nie na początku). Nie można
definiować nazw komórek będących adresami komórek (np. x1, hp301), a także literami w i
k

. Dwie ostatnie nazwy są odwołaniami do bieżącego wiersza lub bieżącej kolumny.

Nazwy mogą być nadawane nie tylko pojedynczym komórkom, ale także obszarom i zbiorom
obszarów.

Przykład 9.2
Nadamy obszarowi B4:F11 nazwę DANE. Należy zaznaczyć ten obszar, wpisać nazwę
DANE

w polu nazwy i wcisnąć [Enter]. W podobny sposób przypisujemy nazwy do

obszarów B4:B11 (Próbka1), C4:C11 (Próbka2), D4:D11 (Próbka3), E4:E11 (Próbka4),
F4:F11 (Próbka5) . Obszar B4:D11 nazwiemy Trzy_próbki. Nazwy obszarów można
wykorzystywać we wzorach. Przykłady takich wzorów są podane w wierszach 13-16 na rys.
9.2.

Nazwy komórek i obszarów umożliwiają łatwe znalezienie tych obiektów. Wystarczy w polu
nazwy kliknąć na odpowiednią pozycję listy (np. DANE). Żądany obszar zostaje znaleziony i
zaznaczony. Można natychmiast przystąpić do formatowania obszaru lub usunąć jego
zawartość (klawisz [Delete]).

45

Nazwy komórek i obszarów muszą być jednoznaczne. Ten sam obszar może mieć przypisane
dwie różne nazwy, ale dwa obszary (komórki) w skoroszycie nie mogą mieć tej samej nazwy.
Małe i duże litery w nazwach są utożsamiane. Aby usunąć nazwę, musimy skorzystać z
polecenia Wstaw | Nazwa | Definiuj i w oknie dialogowym Definiuj nazwy zaznaczyć
wybraną pozycje listy i kliknąć przycisk Usuń.

Rys. 9.2. Wykorzystanie nazw obszarów

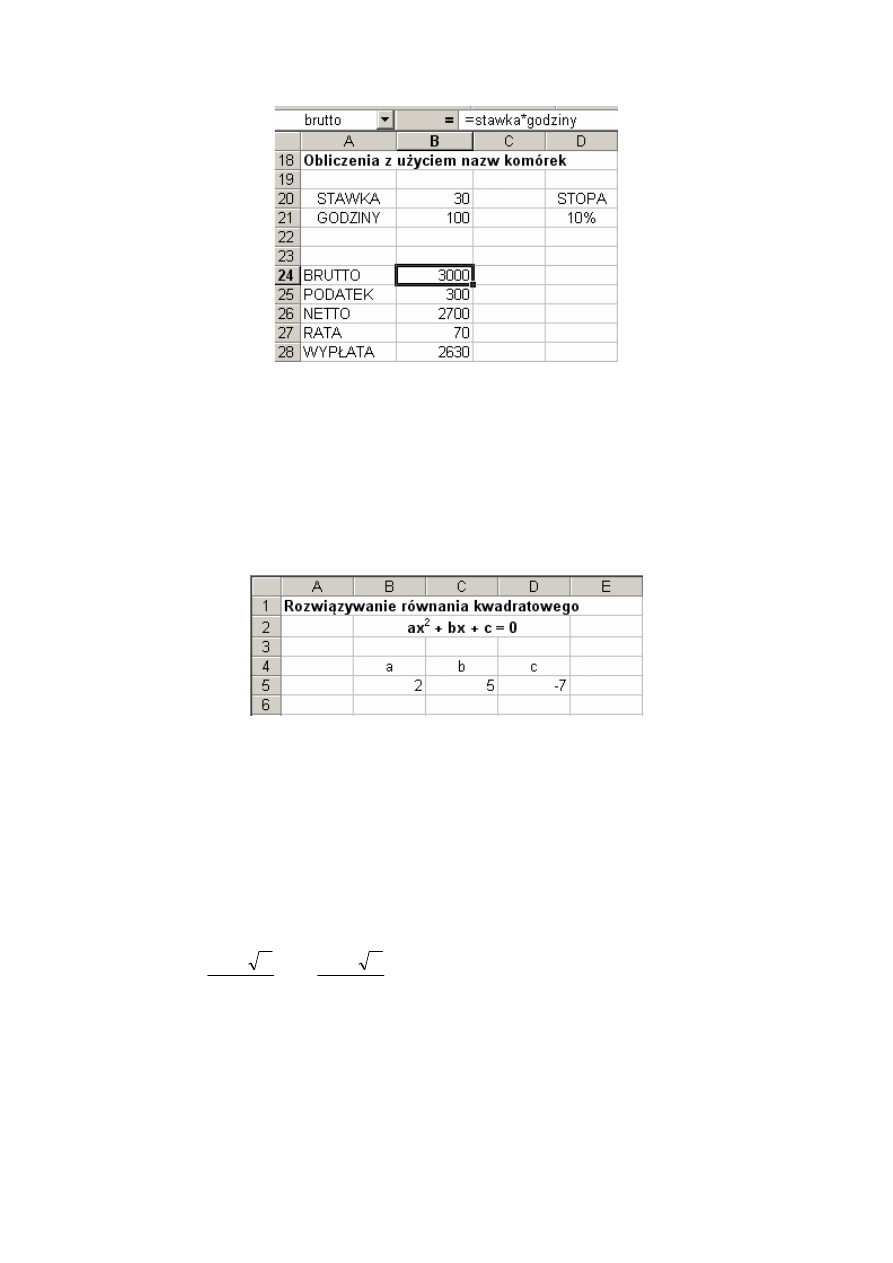
Przykład 9.3
Wynagrodzenie brutto jest obliczane jako iloczyn stawki godzinowej (B20) i liczby
przepracowanych godzin (B21). Podatek jest obliczany jako iloczyn stopy podatkowej (D21) i
wynagrodzenia brutto (B24), a wynagrodzenie netto jako różnica brutto-podatek. Od tego
potrącana jest rata pożyczki i wynik (wypłata) jest umieszczany w komórce B28. Po
przypisaniu odpowiednim komórkom nazw możemy zapisać wzory w obszarze B24:B28 w
bardziej naturalny sposób

Tabl. 9.1. Dane i wzory do rozliczenia finansowego

Komórka Nazwa Zawartość Wynik

B20 stawka 30

30

B21 godziny 100

100

D21 stopa 10% 10%

B24 brutto

=stawka*godziny

3000

B25 podatek

=podatek*brutto

300

B26 netto

=brutto-podatek

3700

B27 rata 70 70
B28 wypłata =netto-rata 2630

46

Rys. 9.3. Obliczenia z użyciem nazw komórek

Rozwiązywanie równania kwadratowego

Chcemy rozwiązać równanie kwadratowe np.

0

7

5

2

2

=

−

+ x

x

. Chcemy rozwiązywać nie

tylko to równanie, ale też inne równania postaci

0

2

=

+

+

c

bx

ax

, gdzie a, b, c są liczbami

rzeczywistymi (

0

≠

a

). Zapiszmy współczynniki równania w trzech komórkach arkusza,

najlepiej obok siebie.

Rys. 9.4. Parametry równania kwadratowego

Wiersz czwarty zawiera nazwy parametrów zadania (niekonieczne dla obliczeń), a wiersz
piąty wartości tych parametrów.

Znamy ze szkoły wzory na obliczanie pierwiastków równania:

ac

b

4

2

−

=

∆

(9.1)

oraz gdy

0

≥

∆

, to

a

b

x

2

1

∆

−

−

=

a

b

x

2

2

∆

+

−

=

(9.2)

Gdy

0

<

∆

, to równania nie ma rozwiązań w liczbach rzeczywistych.

Możemy zapisać w arkuszu wzór (9.1), ale musimy wtedy użyć mało czytelnej formuły
=c5^2-4*b5*d5

(albo podobnej, w zależności od tego, do których komórek wpisaliśmy

dane). Jest to niewygodne. Lepiej przypisać komórkom nazwy, aby móc pisać wzory
podobnie jak w matematyce. Komórkę B5 nazwiemy a, komórkę C5 nazwiemy b, a komórkę

47

D5 nazwiemy c. Będzie nam jeszcze potrzebna komórka E5, którą nazwiemy delta. Możemy
po kolei przypisać nazwy tym czterem komórkom, ale możemy to zrobić jednocześnie.
Wpiszmy do komórki E4 napis delta, a następnie zaznaczmy obszar B4:E5 i wybierzmy z
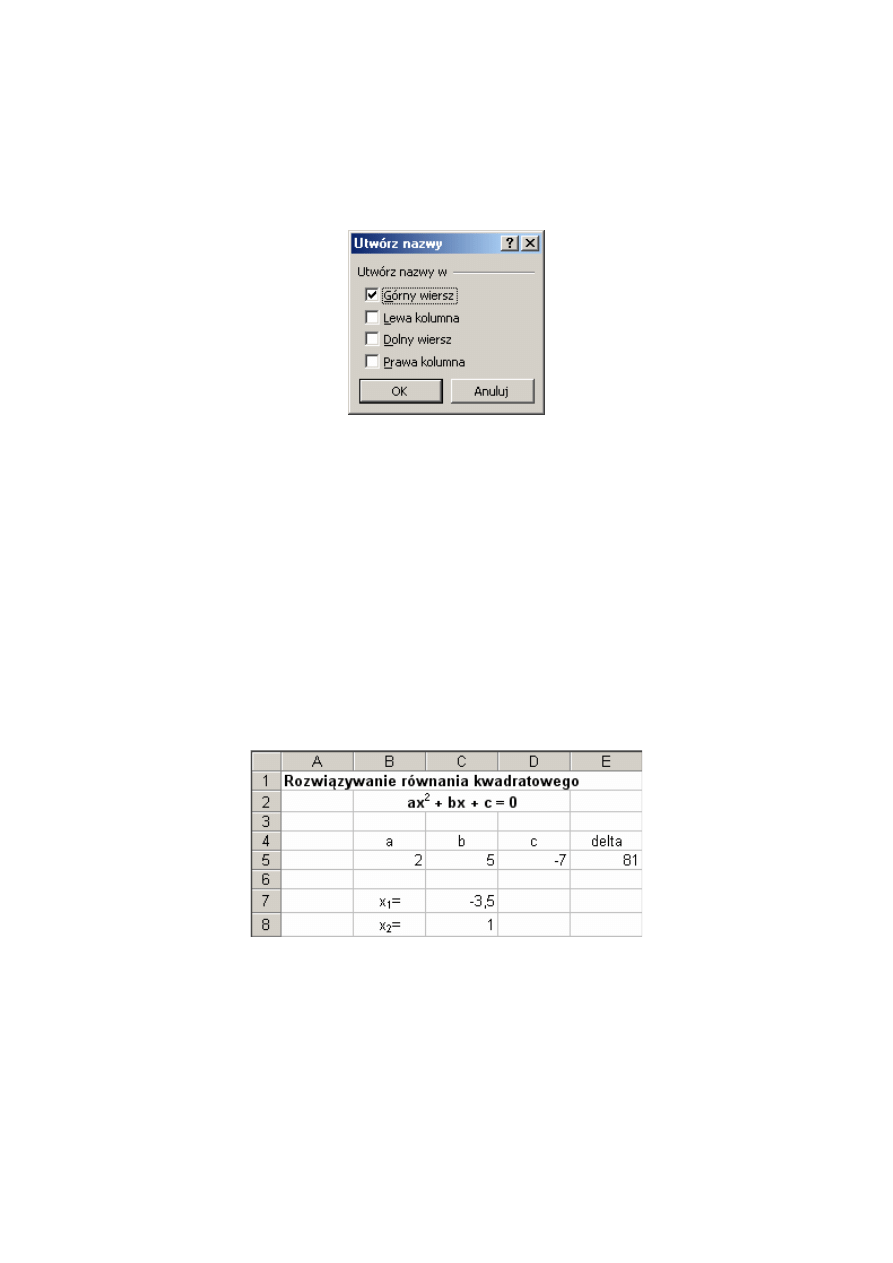
menu programu polecenie Wstaw | Nazwa | Utwórz. Pojawi się okno dialogowe Utwórz
nazwy.

Rys. 9.5. Okno dialogowe Utwórz nazwy

Excel zaznaczył opcję Górny wiersz, co oznacza, że komórki znajdujące się w dolnym
wierszu otrzymają nazwy takie, jak napisy znajdujące się w górnym wierszu. Jeżeli występują
niejednoznaczności, możemy sami zdecydować, który wiersz (lub kolumna) ma być użyty do
nazywania komórek. Po naciśnięciu przypisku OK możemy do komórki E5 wpisać wzór
=b^2-4*a*c

, a do komórek C7 i C8 wzory:

=(-b-pierwiastek(delta)/(2*a)

oraz =(-b+pierwiastek(delta)/(2*a).

Można skopiować pierwszy wzór wpisany do komórki C7 i zmienić w odpowiednim miejscu
znak "-" na znak "+". Przy tworzeniu formuły należy zwrócić uwagę na prawidłowe użycie
nawiasów. Niewłaściwe rozmieszczenie nawiasów prowadzi do błędnego wyniku.

Otrzymujemy rozwiązanie:

81

=

∆

,

5

,

3

1

−

=

x

,

1

2

=

x

.

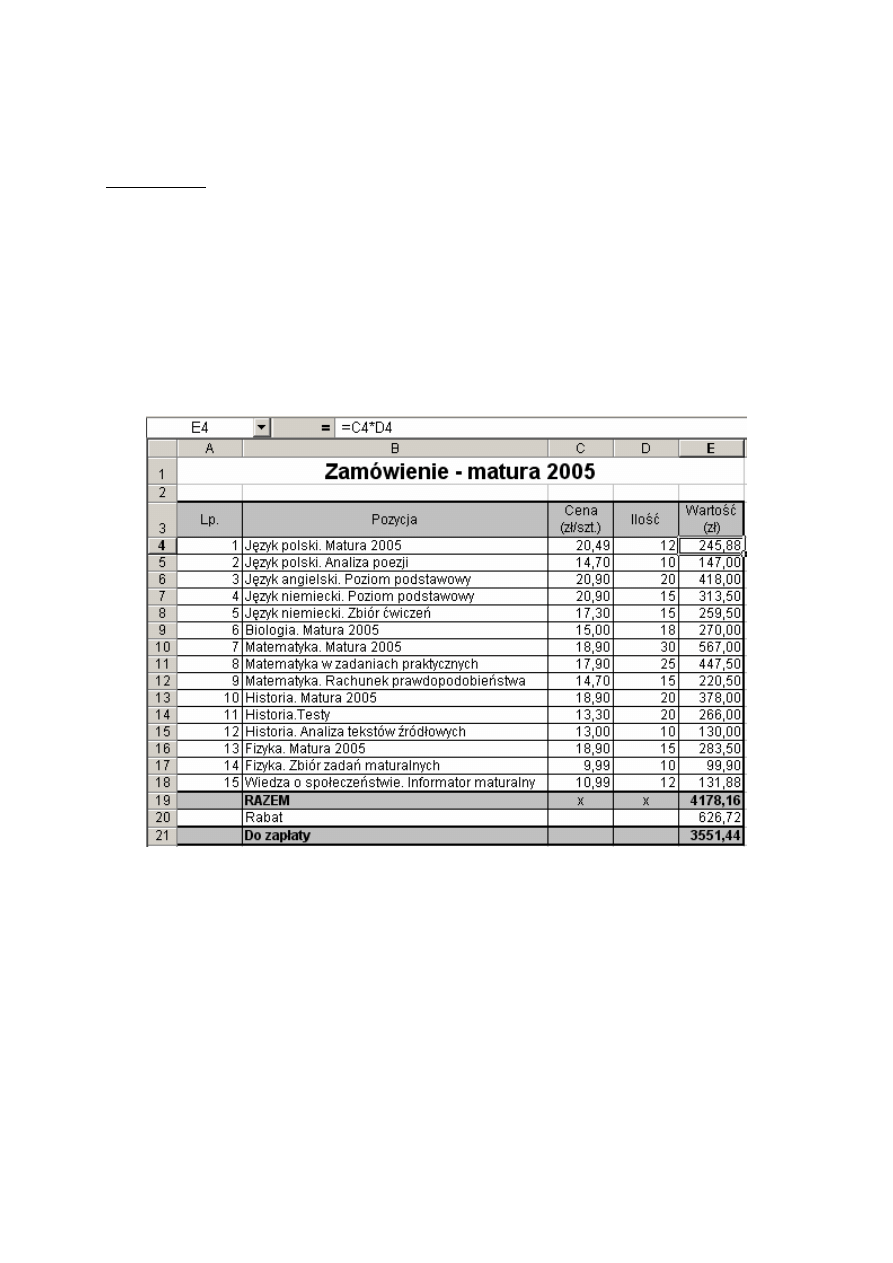
Rys. 9.6. Rozwiązanie równania kwadratowego

Wprowadźmy teraz inne dane do komórek B5:D5. Natychmiast otrzymujemy rozwiązanie
odpowiedniego równania kwadratowego. Mogą jednak pojawić się pewne problemy.
Wprowadźmy na przykład do komórki liczbę 7 (zamiast -7). oznacza to, że nasze równanie
ma postać

0

7

5

2

2

=

+

+ x

x

. Otrzymamy wynik

31

−

=

∆

, a w komórkach C7 i C8 pojawia się

komunikat diagnostyczny #LICZBA! Oznacza to, że Excel nie może obliczyć wyrażenia
(wymaga to obliczania pierwiastka z liczby ujemnej).

48

Można temu zaradzić. Skorzystamy z funkcji JEŻELI. Funkcja standardowa JEŻELI
znajduje się w grupy funkcji logicznych. Ma postać:

=jeżeli(

warunek; gdy_prawda; gdy_fałsz)

Pierwszy argument jest wyrażeniem logicznym, które może przyjmować wartość prawdy lub
fałszu. Gdy warunek jest spełniony, wynikiem jest wartość wyrażenia umieszczonego jako
drugi argument. W przeciwnym razie wynikiem jest wartość wyrażenia umieszczonego jako
trzeci argument.

Zapiszmy w komórce C7 wyrażenie

=jeżeli(delta<0; "Brak rozwiązania";(-b-pierwiastek(delta)/(2*a))

i skopiujmy to do komórki C8 zmieniając w odpowiednim miejscu znak "-" na znak "+".

Rys. 9.7. Rozwiązanie równania kwadratowego (gdy

0

<

∆

)

W podobny sposób można opracować arkusz do rozwiązywania równań trzeciego stopnia
korzystając z wzorów Cardano. Można też rozwiązywać równania kwadratowe w liczbach
zespolonych.

49

10. Adresy komórek we wzorach

Przykład 10.1
Arkusz przedstawiony na rys. 10.1 zawiera specyfikację zakupu podręczników przez firmę
edukacyjną. W poszczególnych kolumnach mamy kolejny numer pozycji, tytuł podręcznika,
cenę jednostkową, ilość zakupionych egzemplarzy i ich wartość. Dane w kolumnach A-D
musimy wprowadzić sami, natomiast wartości oblicza Excel na podstawie wzoru
(cena

×ilość). W każdej komórce kolumny E powinien być inny wzór. W komórce E4 jest to

=C4*D4

, w komórce E5 - =C5*D5, w komórce E6 - =C6*D6 itd. Nie musimy jednak

wprowadzać wzorów do wszystkich komórek (gdyby specyfikacja zawierała 100 pozycji,
byłoby to już uciążliwe). Wystarczy wpisać wzór w komórce E5, a następnie skopiować (np.
przeciągając uchwyt wypełniania) tę komórkę do pozostałych komórek poniżej. Zauważmy,
że Excel zmodyfikował kopiowany wzór zgodnie z naszymi intencjami i wyniki są poprawne.

Rys. 10.1. Specyfikacja zakupów

Wartość w komórce E19 została wpisana za pomocą przycisku autosumowania. Dla zakupów
od 1000 zł przyznawany jest rabat 15%, a dla zakupów poniżej 1000 zł - rabat 7,5%. Zatem w
komórce E20 znajduje się wzór =JEŻELI(E19>=1000; E19*15%; E19*7,5%), a w
komórce E21 wzór =E19-E20.


10.1 Zasada kopiowania wzorów - adresy względne

Umieśćmy w komórce D15 arkusza wzór: =C12+3*SUMA(E7:E10), a następnie skopiujmy
(dowolną metodą) zawartość komórki D15 do komórki G20. Wzór zapisany w komórce G20
ma wtedy postać: =F15+3*SUMA(H12:H15). Widzimy, że podczas kopiowania Excel
zmienił wpisany przez nas wzór.

50

Rys. 10.2. Zmiana adresów podczas kopiowania wzorów

Aby przejść z komórki D15 do G20 musimy przebyć drogę: 5 wierszy w dół i 3 kolumny w
prawo. Wszystkie adresy komórek występujące we wzorze zostaną na tej podstawie
zmodyfikowane. Numery wierszy zwiększą się o 5, a nazwy kolumn o 3 litery alfabetu.
Zauważmy, że wszystkie pozostałe elementy wzoru (stałe liczbowe, operatory arytmetyczne,
nazwy funkcji, nawiasy) nie ulegają zmianie. Jest to adresowanie względne, ponieważ zmiana
adresów zależy od położenia komórki docelowej względem komórki źródłowej. Gdybyśmy
chcieli skopiować komórkę D15 do komórki A20 lub F6, wystąpi błąd:

=#ADR!+3*SUMA(B12:B15)

lub =E3+3*SUMA(#ADR!)

Zgodnie z zasadą zmiany adresu komórek otrzymujemy niepoprawne adresy komórek


10.2. Adresy bezwzględne i mieszane

Przykład 10.2
Adresowanie względne nie zawsze jest wygodne. Na rys. 10.3 widzimy wyniki pięciu
pomiarów zapisane w obszarze B3:F3. Chcemy znormalizować te liczby dzieląc każdą z nich
przez największą. Jeżeli wpiszemy do komórki B4 wzór =b3/max(b3:f3) i będziemy go
kopiować w prawo, to zgodnie z zasadą kopiowania wzorów otrzymamy w komórce C3 wzór
=c3/max(c3:g3)

itd. Chcielibyśmy, żeby adres komórki w liczniku zmieniał się, a w

mianowniku zawsze występował zakres B3:F3. Jest na to rada. Należy zapisać wzór tak jak to
widać w komórce B5 na rys. 10.3 ($b$3 zamiast b3 i $f$3 zamiast f3).
.

5 wierszy

w dół

3 kolumny

w prawo

51

Rys. 10.3. Użycie adresów bezwzględnych

Adresy $B$3 i $F$3 są to adresy bezwzględne. Nie zmieniają się podczas kopiowania
wzorów. Ponadto występują adresy mieszane np. $B3, F$5. W pierwszym przypadku podczas
kopiowania zmienia się tylko numer wiersza, a w drugim przypadku tylko adres kolumny. W
przykładzie z rys. 10.3 moglibyśmy zapisać wzór w komórce B5 jako =b3/max($b3:$f3),
ponieważ dokonujemy kopiowania w obrębie tego samego wiersza (adres wiersza i tak nie
zmieni się).

Różnicę między kopiowaniem adresów względnych, bezwzględnych i mieszanych można
zobaczyć kopiując wzór =C12+$C$12+C$12+$C12 zapisany w komórce F16 do innych
komórek, np. do H19.

Znak dolara ($) można bezpośrednio wpisywać do wzoru z klawiatury, ale można też
wykorzystać klawisz funkcyjny [F4]. Jeżeli ustawimy kursor na adresie komórki w polu
edycji i będziemy naciskać klawisz [F4], to zmienia się sposób adresowania (polecamy
sprawdzić działanie tej operacji).

Przenoszenie (zamiast kopiowania) komórek zawierających adresy nie zmienia zawartości
tych komórek. Natomiast jeżeli przenosimy zawartość jakiejś komórki w inne miejsce, to
wszystkie wzory, w których występuje adres tej komórki zostają odpowiednio
zmodyfikowane. Przenieśmy na przykład komórkę F17 (rys. 10.2) zawierającą liczbę 0,8 do
G12. Wówczas wzór w komórce G20 zamieni się na wzór =G12+3*SUMA(H12:H15).


10.3. Przykłady różnych sposobów użycia adresów we wzorach

Zrozumienie sposobów adresowania jest ważne. Właściwe zapisywanie wzorów może skrócić
czas przygotowania tabel nawet kilkadziesiąt razy. Kolejne przykłady pokazują różne
zastosowania adresów względnych, bezwzględnych i mieszanych.

Przykład 10.3
Tablica zawiera w ujęciu wartościowym stany magazynowe pięciu materiałów (MAT1-
MAT5) w trzech magazynach (M1-M3). Wartości są podane w dolarach amerykańskich. W
komórce G2 jest podany aktualny kurs dolara.

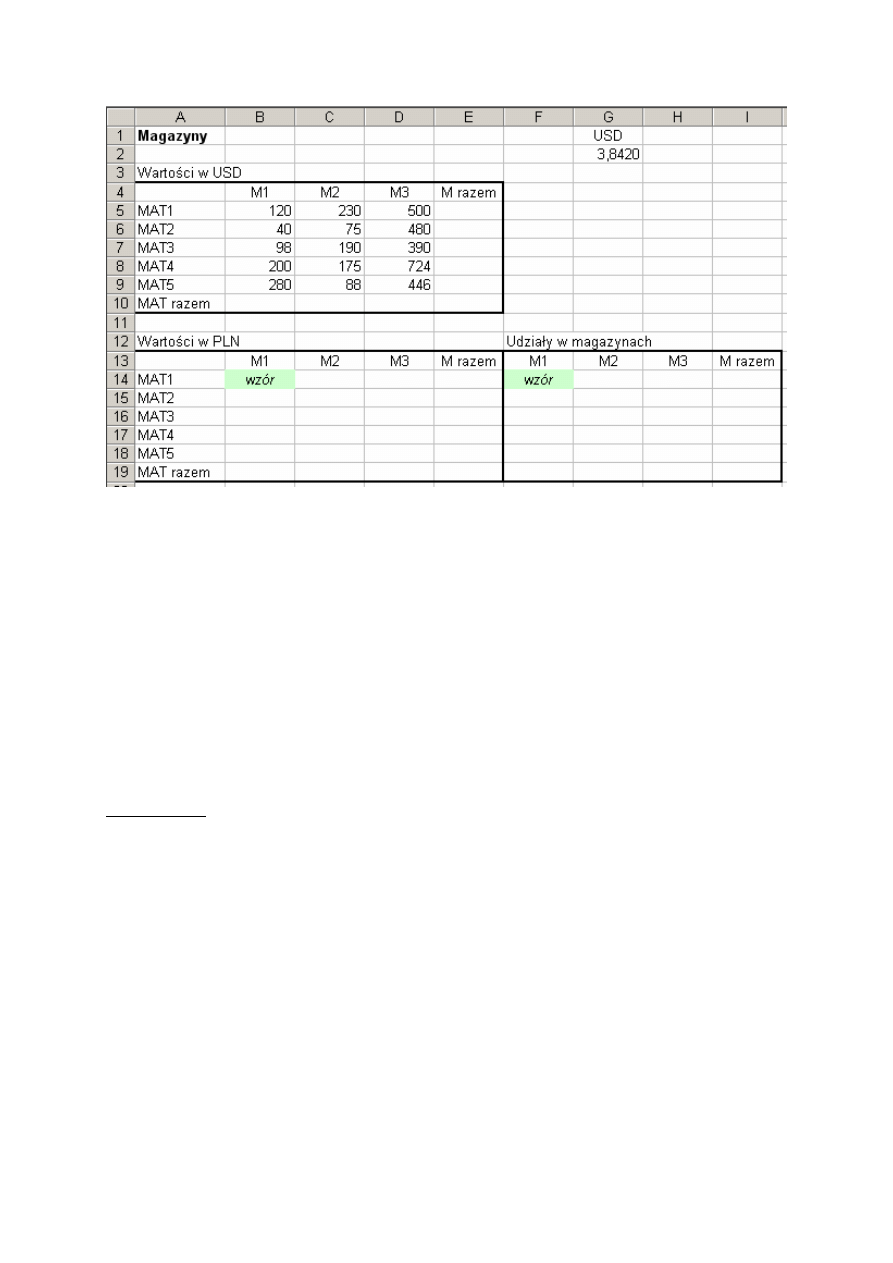
52

Rys. 10.4. Stany magazynowe

a) należy uzupełnić pierwszą tablicę o podsumowania po wierszach i kolumnach (MAT

razem - wartość wszystkich materiałów w poszczególnych magazynach, M razem -
wartość danego materiału we wszystkich magazynach). Wystarczy zaznaczyć obszar
B5:E10 i użyć przycisku autosumowania;

b) w pierwszej części drugiej tablicy podamy stany magazynowe w złotówkach. Należy

wpisać do komórki B14 wzór =b5*$g$2 (konieczne jest użycie adresu bezwzględnego,
gdyż wszystkie wartości mnożymy przez stały przelicznik) i skopiować wzór do obszaru
B13:E19;

c) w drugiej części tej tablicy powinien znaleźć się rozkład wartości materiałów w

poszczególnych magazynach (stosunki wartości materiału do wartości wszystkich
materiałów). Należy do komórki F14 wpisać wzór =b14/b$19 i skopiować go do komórek
obszaru F14:I19. Liczbom w tym obszarze można nadać format procentowy.

Przykład 10.4
Liczba studentów wyższych uczelni w Polsce wyraźnie wzrosła w latach dziewięćdziesiątych
ubiegłego wieku. Tablica na rys. 10.5 pokazuje wartości (w tys. osób) w latach 1990-2002. W
kolumnach D i E zostały obliczone wskaźniki dynamiki:
− indeksy łańcuchowe informujące o zmianach liczby studentów w stosunku do roku

poprzedniego,

− indeksy jednopodstawowe informujące o zmianach liczby studentów w stosunku do roku

1990.

Obliczając wskaźniki w kolumnie D stosujemy adresy względne, natomiast w kolumnie E
należy zastosować adres względny dla licznika wzoru i adres bezwzględny (lub mieszany) dla
mianownika. Wartość w komórce D4 nie może być obliczona na podstawie danych tabeli.
Wzory wpisane do komórek D5 i E4 możemy szybko przekopiować do pozostałych komórek
kolumny.

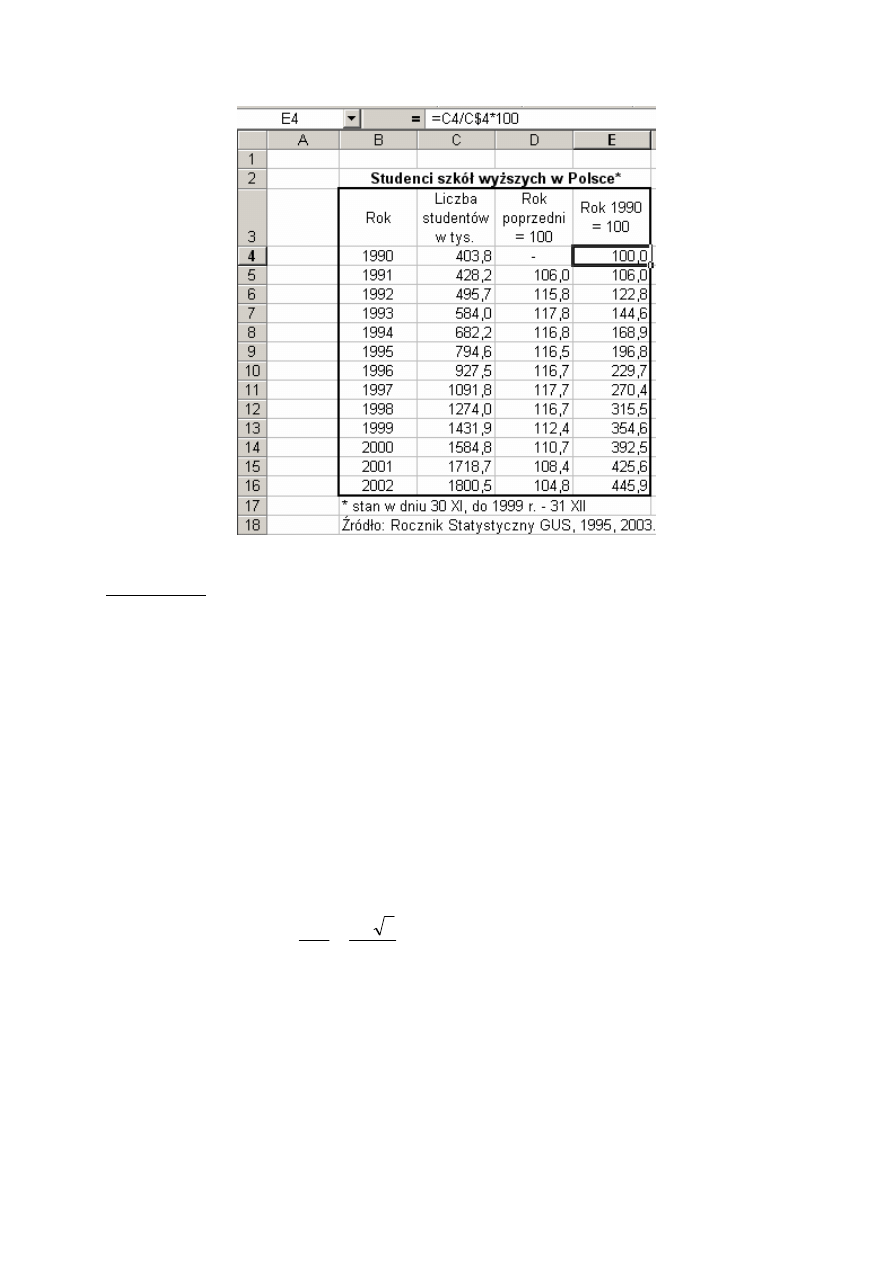
53

Rys. 10.5. Wskaźniki dynamiki

Przykład 10.5
W Excelu bardzo łatwo możemy obliczać kolejne wyrazy ciągów rekurencyjnych. Są to ciągi,
w których definiuje się początkowe wyrazy, a następne wyrazy są określone formułami
zależnymi od wyrazów poprzednich. Przykładem takiego ciągu jest ciąg Fibonacciego (

n

a )

zdefiniowany następująco:

2

dla

1

1

2

1

2

1

>

+

=

=

=

−

−

n

a

a

a

a

a

n

n

n

(10.1)

(kolejny wyraz sumą dwóch wyrazów poprzednich)

Wystarczy wpisać do komórek B4 i B5 liczbę 1, do komórki B5 wzór =b4+b5, a następnie
skopiować komórkę B5 do komórek znajdujących się poniżej. Pierwszych 20 wyrazów ciągu
Fibonacciego widzimy na rys. 10.6. W kolumnie C zapisaliśmy stosunek kolejnych
elementów ciągu. Widać, że ilorazy zbliżają się do liczby równej w przybliżeniu 1,618034.

Można udowodnić, że

...

6180339

,

1

2

5

1

lim

1

=

+

=

−

∞

n

n

n

a

a

54

Rys. 10.6. Liczby Fibonacciego

Przykład 10.6
Trzy oddziały firmy realizują następujący plan wzrostu obrotów.
ƒ

oddział A - przyrost o stałą wartość wpisaną do komórki E5,

ƒ

oddział B - przyrost o stały procent wartości z poprzedniego miesiąca wpisany do

komórki E6,

ƒ

oddział C - przyrost o rosnący procent wartości z poprzedniego miesiąca wpisany do

komórki E7.

Trzy komórki w obszarze E5:E7 zostały odpowiednio nazwane wzrostA, wzrostB i wzrostC.
W komórkach B5:B7 został wpisany wzór =$E$3 (komórka E3 zawiera początkową wartość
obrotów dla oddziałów). Następnie komórka C11 zawiera wzór =B11+wzrostA, komórka C12
zawiera wzór =B12*(1+wzrostB), a komórka C13 zawiera wzór =B13*(1+B9*wzrostC). Po
zaznaczeniu obszaru C11:C13 możemy skopiować zawartość komórek do obszaru
znajdującego się na prawo. Zauważmy, że nazwy komórek występujące we wzorach
zachowują się tak jak adresy bezwzględne.

Rys. 10.7. Plan wzrostu obrotów

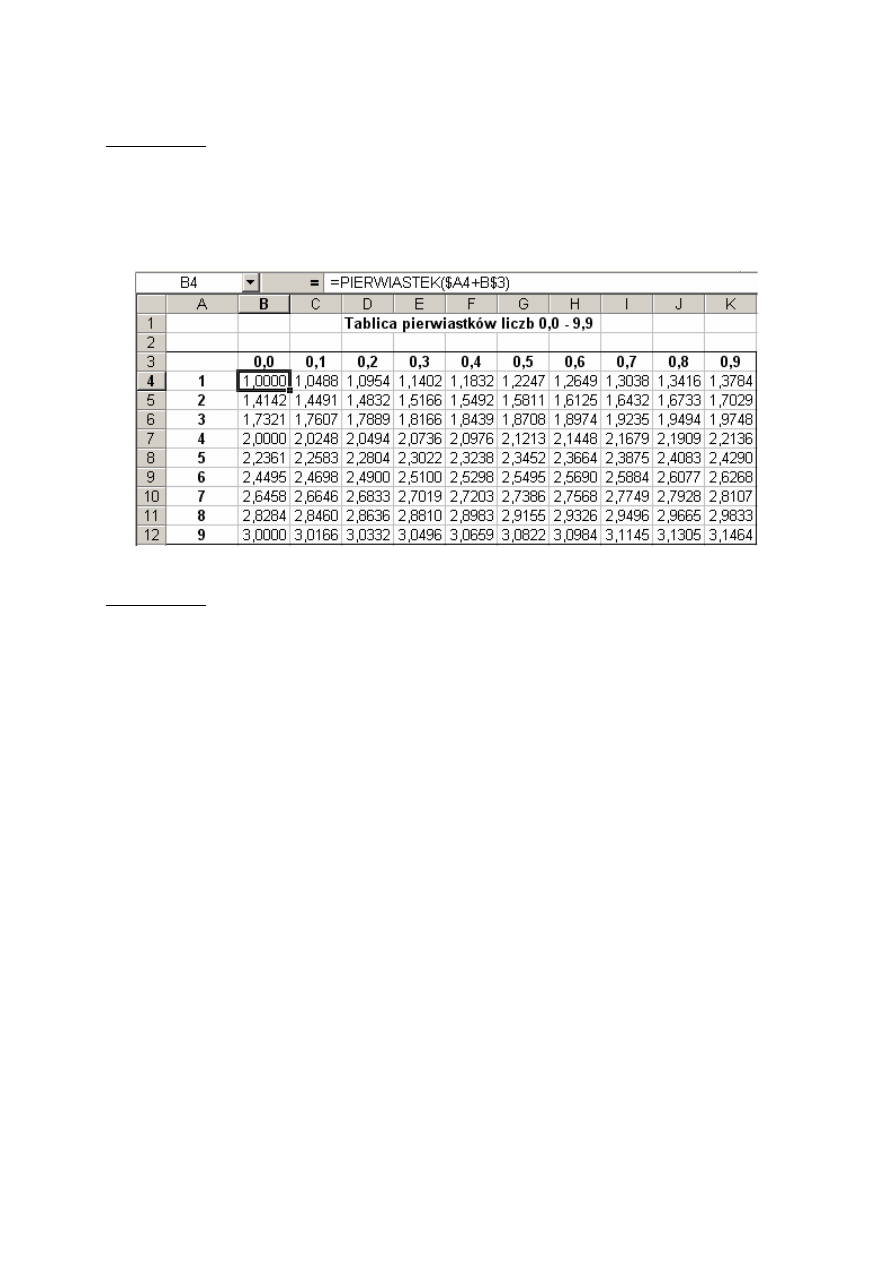
55

Przykład 10.7
Rys. 10.8 pokazuje tablice pierwiastków kwadratowych liczb w przedziale 0,0 -9,9 z krokiem
0,1. Wartość pierwiastka 6,4 odczytujemy w komórce znajdującej się na przecięciu wiersza z
liczbą 6 i kolumny z liczbą 0,4. Aby utworzyć taką tablicę należy do komórki B4 wpisać wzór
używając adresów mieszanych, a następnie przekopiować go do pozostałych komórek
obszaru B4:K12.

Rys. 10.8. Tablica pierwiastków kwadratowych

Przykład 10.8
Przykład jest modyfikacją problemu podanego w książce Tomasza Głuszkowskiego, Arkusze
kalkulacyjne. Przykłady zastosowań, tricki, kruczki, Wydawnictwo "Broker", Łódź 1993 i
dotyczy rozliczenia prowizji grupowej sprzedawców.

Zespól pięciu pracowników zajmuje się sprzedażą następujących wyrobów: płaszcze, kurtki,
kożuchy i futra. Pracownicy zarabiają prowizję dla całego zespołu na każdym sprzedanym
wyrobie. Prowizja zależy od wartości i rodzaju sprzedanego towaru. Wypłata dla każdego ze
sprzedawców składa się ze stałej (jednakowej dla wszystkich) pensji podstawowej oraz premii
proporcjonalnej do wypracowanej prowizji przez danego pracownika. Suma wypłat dla
wszystkich sprzedawców (pensja + premia) jest równa sumie prowizji zarobionej przez cały
zespół.

Zakładamy, że pracownicy sprzedają towar po tych samych cenach jednostkowych, a
prowizja ze sprzedaży każdej sztuki jest stałą częścią ceny danego towaru.

Dane problemu zapisujemy w arkuszu w dwóch tabelach. Pierwsza tabela (A3:E5) zawiera
elementy wspólne dla wszystkich sprzedawców, a więc nazwy, ceny i prowizje. Druga tabela
(A8:E12) zawiera ilościowe zestawienie sprzedaży. Tutaj każdy wiersz tabeli dotyczy innego
pracownika. Identyfikatory pracowników znajdują się w kolumnie A. Ponadto w komórce G4
jest wpisana stała pensja pracowników.

W trzeciej tabeli zamieścimy rozliczenie finansowe wynagrodzeń. Jeden wiersz tabeli opisuje
jednego pracownika, wystąpi również wiersz z podsumowaniami. Najpierw można skopiować
imiona (identyfikatory) sprzedawców z poprzedniej tabeli, potem wypełnimy komórki
odpowiednimi wzorami.

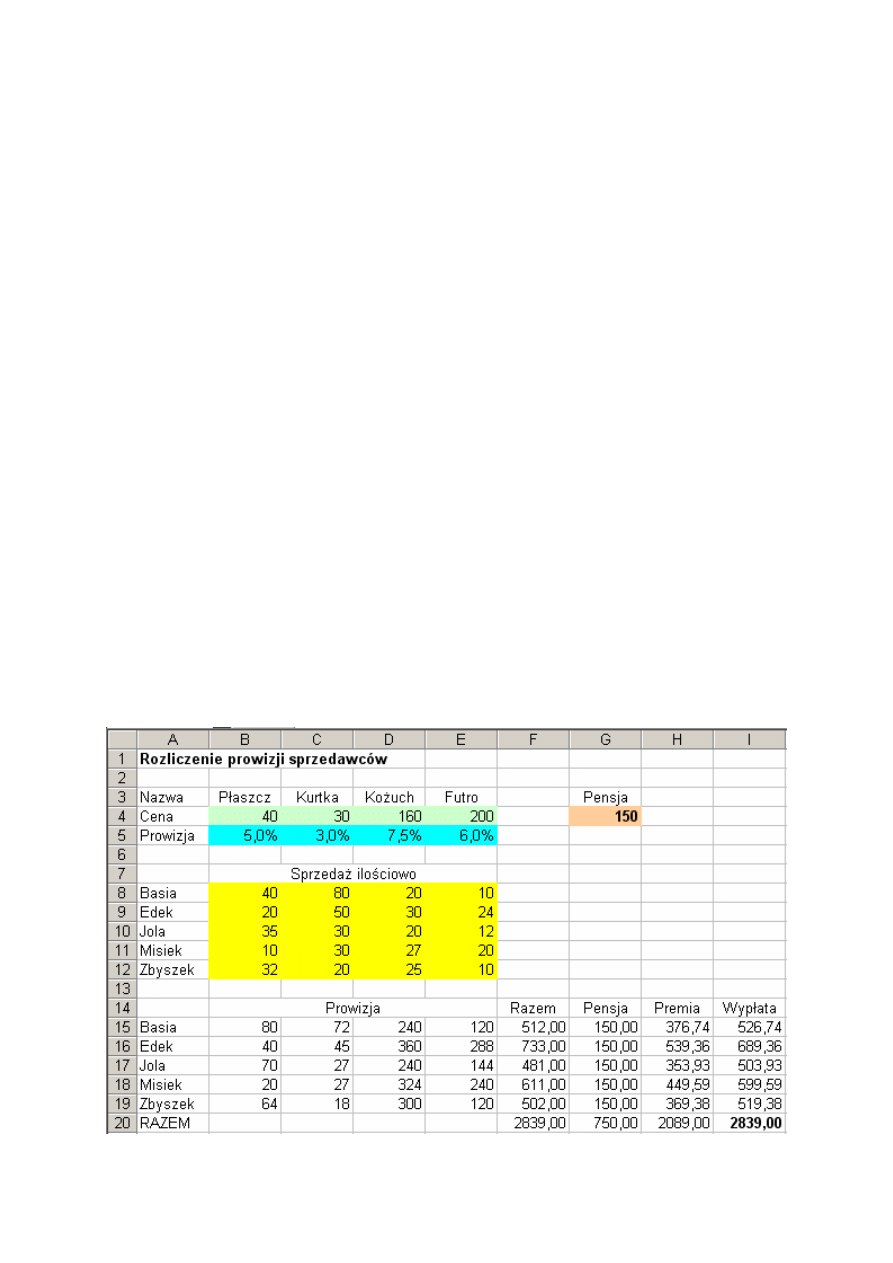
56

W kolumnach B, C, D i E obliczamy prowizję wypracowaną przez każdego pracownika na
sprzedaży poszczególnych towarów. Komórka B15 zawiera wzór =B8*B$4*B$5.
Zastosowaliśmy adresy mieszane B$4 i B$5, ponieważ podczas kopiowania komórki B15 w
dół należy zachować numer wiersza (ceny, procent prowizji), natomiast przy kopiowaniu na
prawo ceny i prowizje procentowe będą zmieniać się wraz ze zmianą towaru. Dzięki takiemu
adresowaniu można natychmiast skopiować komórkę B15 do całego obszaru B15:E19.

Kolumna F zawiera prowizję wypracowaną przez poszczególnych pracowników na
wszystkich towarach (np. komórka F15 zawiera wzór =SUMA(B15:E15), który można
przeciągnąć myszą do czterech komórek poniżej). Komórka F20 zawiera podsumowanie
kolumny i jest suma prowizji wypracowanej przez cały zespół.

Kolumna G zawiera stałą pensję. Wszystkie komórki obszaru G15:G19 zawierają wzór
=$G$4

, a w G20 mamy podsumowanie.

Zanim obliczymy indywidualne premie sprzedawców, musimy obliczyć sumę premii,
ponieważ z założeń zadania wynika, że suma premii i suma pensji musi być równa sumie
zarobionej prowizji. Zatem wartość w komórce H20 jest różnicą prowizji i pensji liczoną
według wzoru =F20-G20. Teraz premię H20 należy rozdzielić na pracowników
proporcjonalnie do wypracowanych przez nich prowizji. Wartości w komórkach w obszarze
H15:H19 powinny być proporcjonalne do wartości w komórkach obszaru F15:F19 i w sumie
dawać wartość H20. Uzyskujemy to wpisując do komórki H15 wzór =F15*$H$20/$F$20 i
kopiując ten wzór do pozostałych czterech komórek.

Dalej już jest łatwo. Wypłaty w kolumnie I są sumą stałej pensji i premii, np. komórka I15
powinna zawierać wzór =G15+H15. Po podsumowaniu wypłat sprawdzamy, że wartości w
komórkach F20 i I20 są takie same (suma wypłat = suma prowizji zespołu).

Rys. 10.9 przedstawia ostateczną wersję projektowanego arkusza.

Rys. 10.9. Rozliczenie prowizji sprzedawców - arkusz po zaprojektowaniu

57

Po zaprojektowaniu arkusza z przykładu 10.8 i wpisaniu danych możemy przestąpić do
eksperymentów symulacyjnych. Będziemy zmieniać dane zadania i oglądać, jak będą
zmieniać się wyniki (najlepiej oglądać to na sporządzonym wykresie). Ponieważ symulację
może przeprowadzać osoba, która nie jest autorem projektu i w dodatku słabo zna Excel,
warto wyraźnie zaznaczyć, które komórki arkusza można zmieniać, a pozostałe zabezpieczyć
przed niepożądaną modyfikacją. Jeżeli zniszczymy wzory w komórkach, to użytkownikowi
arkusza trudno będzie je odtworzyć.

Dokonamy dwóch rzeczy:
− zaznaczymy innym kolorem tła te komórki, których zawartość można zmieniać;

− zabezpieczymy pozostałe komórki przed zmianami.

Wybierzemy następujące kolory dla komórek z danymi:

Ceny

-

bladozielony,

Prowizje -

turkusowy,

Stała pensja - beżowy,
Ilości

- żółty.

10. 4. Zabezpieczanie arkusza

Po zabezpieczeniu arkusza będziemy mogli wprowadzać dane tylko do obszarów B4:E5, G4,
B8:E12. Należy zaznaczyć te komórki (można jednocześnie, używając klawisza [Ctrl]) i
wybrać polecenie Format | Komórki | Ochrona. Trzeba odznaczyć pole Zablokuj
(domyślnie jest ono zaznaczone) i kliknąć przycisk OK.

Rys. 10.10. Okno dialogowe Formatuj komórki - Ochrona

58

Ochrona arkusza działa wtedy, gdy wybierzemy polecenie Narzędzia | Ochrona | Chroń
arkusz

. W oknie dialogowym Chroń arkusz mamy możliwość zabezpieczenia arkusza

hasłem. Wtedy przy próbie odbezpieczenia chronionego arkusza trzeba podać to hasło.

Rys. 10.11. Okno dialogowe Chroń arkusz

Próba wprowadzenia danych do komórki chronionej spowoduje wyświetlenie komunikatu.

Rys. 10.11. Komunikat diagnostyczny dla chronionego arkusza

59

Literatura

[1] Michał Czajkowski, Poznajemy Excela 2000, Wydawnictwo "Edition 2000", Kraków

2000.

[2] Michael B. Karbo, Excel 2000. Samouczek dla każdego, Egmont Polska, Warszawa 2000.
[3] Mirosława Kopertowska, Europejskie Komputerowe Prawo Jazdy. Arkusze kalkulacyjne,

wyd. 2 (rozszerzone), MIKOM, Warszawa 2001.

[4] Grzegorz Kowalczyk, Excel 2000PL. Ćwiczenia praktyczne, Helion, Gliwice 1999.
[5] Kurs podstawowy. Microsoft Excel 2000 wersja polska. Podręcznik studenta,

Wydawnictwo RM, Warszawa 2001.

[6] Witold Sikorski, Mirosława Kopertowska, Funkcje w Excelu, MIKOM, Warszawa 2002.
[7] Iwona Szymacha, Ćwiczenia z Excel 2000 (wersja polska), wyd.2, MIKOM, Warszawa

2000.

[8] Andrzej Tor, Excel 2000. Podstawy, Tortech, Warszawa 2000.
[9] John Walkenbach, Excel 2003. Biblia, Helion, Gliwice 2004.