Z. Kąkol-Notatki do Wykładu z Fizyki

 

Wykład 

36

 

36.  Atomy wieloelektronowe, układ okresowy pierwiastków. 

Fizycy badający strukturę atomów wieloelektronowych starali się odpowiedzieć na 

fundamentalne pytanie, dlaczego wszystkie elektrony w atomie znajdującym się w sta-
nie podstawowym nie są związane na najbardziej wewnętrznej powłoce (orbicie). 
Fizyka klasyczna nie wyjaśnia tego problemu; dopiero mechanika kwantowa przyniosła 
podstawy teoretyczne, na gruncie których można przewidzieć własności pierwiastków. 

36.1 Liczby kwantowe 

Na poprzednich wykładach przedstawione zostało wprowadzenie do świata fizyki 

kwantowej. Poznaliśmy między innymi jak ograniczenie ruchu cząstki do obszaru za-
wartego pomiędzy sztywnymi ściankami wpływa na prawdopodobieństwo jej znalezie-
nia oraz jak wpływa na skwantowanie wartości energii 
 

......

,

2

,

1

,

8

2

2

2

=

=

n

ml

h

n

E

 

 
Podobnie wartości energii elektronu w atomie wodoru zależą tylko od liczby kwanto-
wej n. 
Inaczej jednak jest w przypadku odpowiedniej fali (stojącej) materii. Funkcja falowa 
zależy od 

trzech liczb kwantowych

 co wynika z faktu, że ruch w przestrzeni jest opisany 

przez trzy niezależne zmienne; na każdą współrzędną przestrzenną przypada jedna licz-
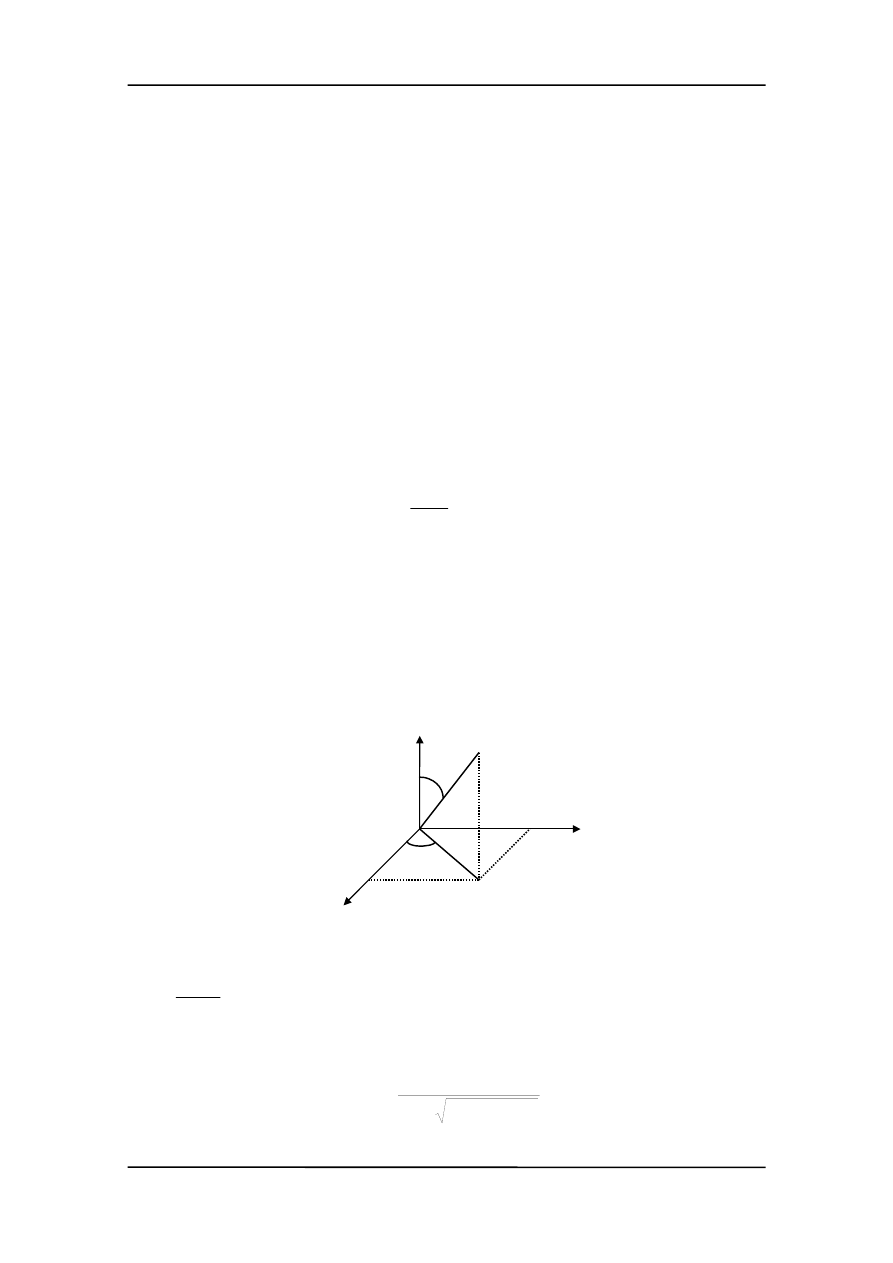
ba. Na rysunku obok pokazane są współrzędne prostokątne (x, y, z) i współrzędne sfe-
ryczne (r, 

θ, ϕ) punktu P. 

x 

y 

z 

x 

y 

z 

P 

r 

θ 

ϕ 

 

Stosowanie współrzędnych sferycznych w zdecydowany sposób ułatwia obliczenia. 
Wynika to z faktu, że energia potencjalna oddziaływania elektronu z jądrem 

r

e

U

0

2

4

πε

−

=

 jest funkcją tylko jednej zmiennej we współrzędnych sferycznych podczas 

gdy we współrzędnych prostokątnych funkcją wszystkich trzech współrzędnych 
 

2

2

2

0

2

4

z

y

x

e

U

+

+

−

=

πε

 

 

 

36-1 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

Trzy liczby kwantowe n, l, m

l

 spełniają następujące warunki 

 

 

l

m

l

l

l

l

l

l

l

m

n

l

n

l

n

l

l

≤

≤

−

−

−

+

−

+

−

−

=

−

≤

≤

−

=

=

lub

,

1

,

2

,

.....

,

2

,

1

,

1

0

lub

1

,

......

,

2

,

1

,

0

.....

,

3

,

2

,

1

 (36.1) 

 
Ze względu na rolę jaką odgrywa liczba 

n

 w określeniu energii całkowitej atomu, jest 

nazywana 

główną liczbą kwantową

. Liczba 

l 

nosi nazwę 

azymutalnej liczby kwantowej

, 

a liczba 

m

l

 nazywana jest 

magnetyczną liczbą kwantową

. Z warunków (36.1) 

widać, że 

dla danej wartości n

 (danej energii) 

istnieje na ogół kilka różnych możliwych wartości l, 

m

l

. 

36.2 Zasada Pauliego 

W 1869 r. Mendelejew jako pierwszy zauważył, że większość własności pierwiast-

ków chemicznych jest okresową funkcją liczby atomowej Z określającej liczbę elektro-
nów w atomie co najlepiej uwidacznia się w odpowiednio skonstruowanym układzie 
okresowym pierwiastków. Właściwości chemiczne i fizyczne pierwiastków powtarzają 
się jeżeli zebrać je w grupy zawierające 2, 8, 8, 18, 18, 32 elementów. 
W 1925 r. Wolfgang Pauli podał prostą zasadę, dzięki której automatycznie są genero-
wane grupy o liczebności 2, 8,18,32. Pauli 

zapostulował,  że na jednej orbicie mogą 

znajdować się nie więcej niż dwa elektrony, czyli tylko dwa elektrony mogą być opisane 
tą samą falą stojącą materii

. 

Zatem na orbicie n = 1 będą dwa elektrony bo mamy tylko jedną falę stojącą, czyli je-
den 

orbital

 

(n, l, m

l

) = (1,0,0) 

Dla n = 2 są cztery orbitale 

(n, l, m

l

) = (2,0,0); 

(2,1,1), (2,1,0), (2,1,–1) 

 
Stąd wynika, że w stanie n = 2 może być 8 elektronów (dwa na orbital). 
Podobnie dla n = 3 mamy 9 orbitali czyli 18 elektronów 
 

(n, l, m

l

) = (3,0,0); 

(3,1,1), (3,1,0), (3,1,–1); 

(3,2,2), (3,2,1), (3,2,0), (3,2,–1), (3,2,–2) 

 
Widać, że okresy 2, 8, 18 są konsekwencja zasady Pauliego i teorii kwantowej, z której 
wynikają warunki (36.1). 
W czasie gdy Pauli podał swoją zasadę była ona zasadą ad hoc, nie można było jej wy-
prowadzić w ramach istniejącej teorii. Pozostawało więc pytanie: dlaczego akurat dwa 
elektrony (a nie inna liczba) mogą być opisane tą samą falą stojącą? 

 

36-2 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

36.2.1 Spin elektronu 

W roku 1926 odkryto, że wszystkie elektrony mają wewnętrzny moment pędu 

L

wew

 = (1/2)(h/2

π), który został nazwany 

spinowym momentem pędu

. 

Elektron zachowuje się tak, jakby był kulką wirującą wokół pewnej osi obrotu (analo-
gicznie jak Ziemia obiegająca Słońce i obracająca się wokół swej osi). 
Wewnętrzny moment pędu elektronu nigdy nie zwiększa się ani też nie maleje. 
Okazało się ponadto, że dla danego stanu orbitalnego są możliwe 

dwa kierunki spinu

. 

Mamy więc inny sposób wyrażenia zasady Pauliego. Oznacza to, że zasada Pauliego nie 
była postulatem wprowadzona ad hoc. 
Znajomość spinu jest niezbędna do opisu stanu elektronu. Kiedy te stany są określone to 
zasada Pauliego, która w pierwotnym brzmieniu stwierdzała, że w danym stanie orbital-
nym nie może być więcej elektronów niż dwa, oznacza teraz, że 

w danym stanie 

(z uwzględnieniem spinu) może znajdować się tylko jeden elektron

. 

36.3  Atomy wieloelektronowe, układ okresowy pierwiastków 

Posługując się zasadą Pauliego można określić jakie stany w atomie będą obsadza-

ne. 
Rozpatrzmy np. jądro neonu Z = 10. Jeżeli w pobliżu jądra umieścimy jeden elektron to 
zajmie on orbital n = 1. Tak samo będzie z drugim elektronem (inny kierunek spinu). Te 
dwa elektrony zapełnią orbitę n = 1. Pozostałe 8 elektronów zapełni orbitę o n = 2, czyli 
cztery orbitale (l, m

l

) = (0,0), (1,1), (1,0), (1,–1). W ten sposób rozpatrzymy przewidy-

waną przez teorię kwantową strukturę niektórych pierwiastków. 
Z = 1, Wodór 
Jedyny elektron znajduje się w stanie n = 1, o energii E = – 13.6 eV. Tak więc 

energia 

wiązania

 czyli 

energia jonizacji

 atomu wodoru wynosi 13.6 eV. Oznacza to, że mini-

malne napięcie potrzebne do zjonizowania atomu wodoru wynosi 13.6 V. To minimalne 
napięcie nazywamy potencjałem jonizacyjnym. 
Z = 2, Hel 
Zacznijmy od jonu helu, He

+

, który składa się z jądra oraz jednego elektronu. 

Mamy układ podobny do wodoru tylko inna jest siła elektrostatyczna działająca na elek-
tron (większa o czynnik Z). Energia jest dana wzorem analogicznym jak w modelu 
Bohra 
 

 

eV

6

.

13

8

2

2

2

2

1

2

2

2

0

4

2

n

Z

n

Z

E

n

h

me

Z

E

−

=

=

−

=

ε

 (36.2) 

 
Ze względu na czynnik Z

2

 energia jonizacji He

+

 wynosi 4·13.6 eV = 54.4 eV. 

Wartość ta zgadza się ze zmierzonym potencjałem jonizacji. 
Jeżeli teraz dodamy drugi elektron na powłokę n = 1 to przez połowę czasu będzie on 
bliżej jądra niż pierwszy i będzie „czuł” ładunek jądra Z, a przez połowę czasu będzie 
dalej więc będzie „widział” jądro o ładunku  Z i 1 elektron czyli „obiekt” o ładunku  
(Z – 1).  Prosta  średnia arytmetyczna tych dwóch wartości daje 

efektywny  ładunek

  

Z

ef

 = 1.5e jaki „czują” elektrony w atomie helu. Możemy teraz uogólnić wzór (36.2) do 

postaci 

 

36-3 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

eV

6

.

13

2

2

n

Z

E

ef

−

=

 (36.3) 

 
Na podstawie tak oszacowanego ładunku efektywnego otrzymujemy potencjał jonizacji 
równy około (1.5)

2

·13.6 V = 30 V. 

W rzeczywistości elektrony nie tylko ekranują ładunek jądra ale też odpychają się na-
wzajem (dodatnia energia potencjalna), więc energia wiązania powinna być mniejsza. 
Wyznaczony doświadczalnie potencjał jonizacyjny helu wynosi 24.6 V i jest najwięk-
szy dla wszystkich pierwiastków. Żadna siła chemiczna nie może dostarczyć takiej 
energii, która jest potrzebna do utworzenia He

+

. 

Gdybyśmy spróbowali utworzyć ujemny jon He

-

 to dodatkowy elektron obsadzi powło-

kę n = 2 o dużo większym promieniu niż n = 1, na której są już dwa elektrony. Ładunek 
efektywny widziany przez ten elektron będzie więc równy zeru, nie działa  żadna siła 
mogąca przytrzymać ten elektron. W rezultacie hel nie tworzy cząsteczek z żadnym 
pierwiastkiem. Hel i inne atomy o całkowicie wypełnionych powłokach  są nazywane 
gazami szlachetnymi. 
Z = 3, Lit 
Dwukrotnie zjonizowany atom litu jest atomem wodoropodobnym przy czym energie 
trzeba pomnożyć przez czynnik Z

2

 = 9. 

Jednokrotnie zjonizowany atom litu ma energie podobne do atomu helu ale  
Z

ef

 

≈ (3 – 1/2) zamiast (2 – 1/2), jak dla helu. 

Trzeci elektron znajduje się na powłoce n = 2. Dla niego ładunek efektywny musi być 
w pobliżu (trochę większy) jedności. Zatem należy oczekiwać,  że potencjał jonizacji 
litu będzie nieco większy niż 13.6/n

2

 = 13.6/2

2

 = 3.4 V. Wartość zmierzona wynosi 5.4 

V co odpowiada Z

ef

 = 1.25e. 

Oderwanie drugiego elektronu wymaga potencjału aż 75.6 V. Zatem w związkach che-
micznych lit powinien zawsze wykazywać wartościowość +1. 
Z = 4, Beryl 
Zgodnie z zasadą Pauliego w stanie n = 2, l = 0 jest miejsce dla dwóch elektronów. Dla 
berylu drugi potencjał jonizacyjny nie jest więc dużo większy od pierwszego i beryl w 
związkach chemicznych ma wartościowość +2. 
Wprowadźmy teraz do opisu konfiguracji następującą konwencję: numer powłoki (n) 
piszemy cyfrą, natomiast podpowłoki:  l = 0, 1, 2, 3 4 oznaczmy literami s,  p,  d,  f. 
Wskaźnik górny przy symbolu podpowłoki określa liczbę znajdujących się w niej elek-
tronów a wskaźnik dolny przy symbolu chemicznym pierwiastka określa wartość Z. 
Tak więc konfiguracje dotychczas omawianych pierwiastków zapiszemy w postaci 
 

1

H :  1s

1

 

2

He :  1s

2

 

3

Li :  1s

2

2s

1

 

4

Be :  1s

2

2s

2

 

 
Od Z = 5 (Boru) do Z = 10 (neonu) 
W tych sześciu pierwiastkach elektrony zapełniają podpowłokę 2p (n = 2, l = 1) 
 

5

B :  1s

2

2s

2

2p

1

 

 

36-4 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

10

Ne :  1s

2

2s

2

2p

6 

 
Wśród tych pierwiastków znajdują się fluor i tlen, którym do zapełnienia orbity p bra-
kuje odpowiednio 1 i 2 elektrony. Pierwiastki te wykazują silną tendencję do przyłącze-
nia dodatkowych elektronów tworząc trwałe jony Fl

–

 i O

– –

. To zjawisko jest zwane 

po-

winowactwem elektronowym

. 

Kontynuując powyższy schemat można napisać konfigurację elektronową dowolnego 
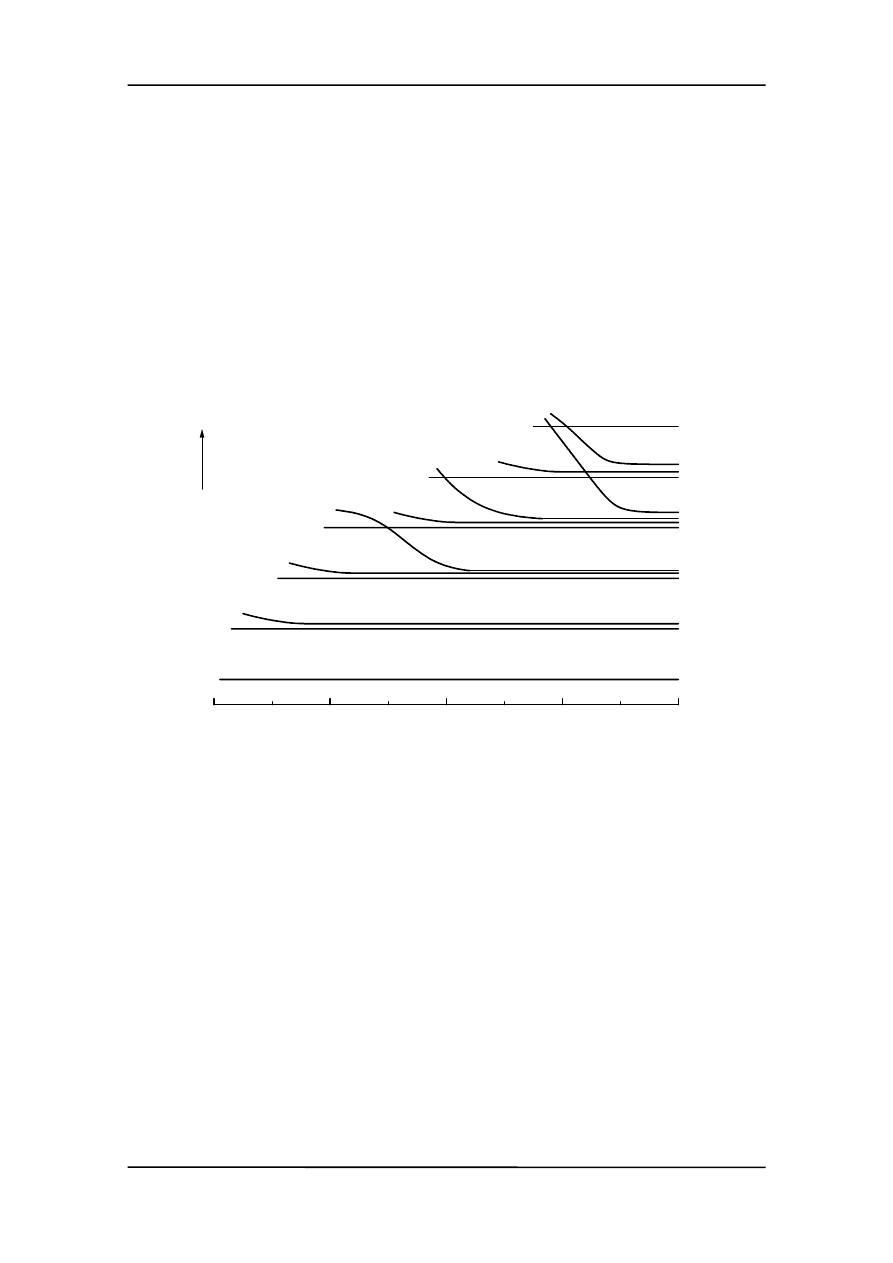
atomu. Okazuje się jednak, że w niektórych przypadkach obserwowane konfiguracje nie 
pokrywają się z obserwowanymi. Wnioskujemy, że różnice energii pomiędzy niektóry-
mi podpowłokami muszą być tak małe, że w pewnych wypadkach może zostać odwró-
cona kolejność ich zapełniania. Można to zobaczyć na rysunku poniżej. Krzywe kończą 
się na Z = 80 (rtęć). Uwaga: skala energii nie jest liniowa. 

0

20

40

60

80

ener

g

ia

5d

4f

6s

5p

4d

5s

4p

3d

4s

3p

3s

2p

2s

1s

Z

 

Zwróćmy też uwagę, że każda podpowłoka p ma wyższą energię od poprzedzającej ją 
powłoki s. Natomiast różnice energii pomiędzy każdą podpowłoką s i poprzedzającą ją 
powłoką  p  są szczególnie duże. W konsekwencji wzbudzenie elektronu w atomach 
pierwiastków, w których zakończyło się  właśnie zapełnianie powłoki  p jest bardzo 
trudne (gazy szlachetne). 
W ten sposób na gruncie mechaniki kwantowej (z uwzględnieniem spinu elektronu) 
można przeanalizować własności wszystkich pierwiastków. 

36.4 Promienie X 

Wielokrotnie mówiliśmy o zastosowaniu promieniowania rentgenowskiego. Teraz 

poznamy więcej szczegółów dotyczących widma tego promieniowania. 
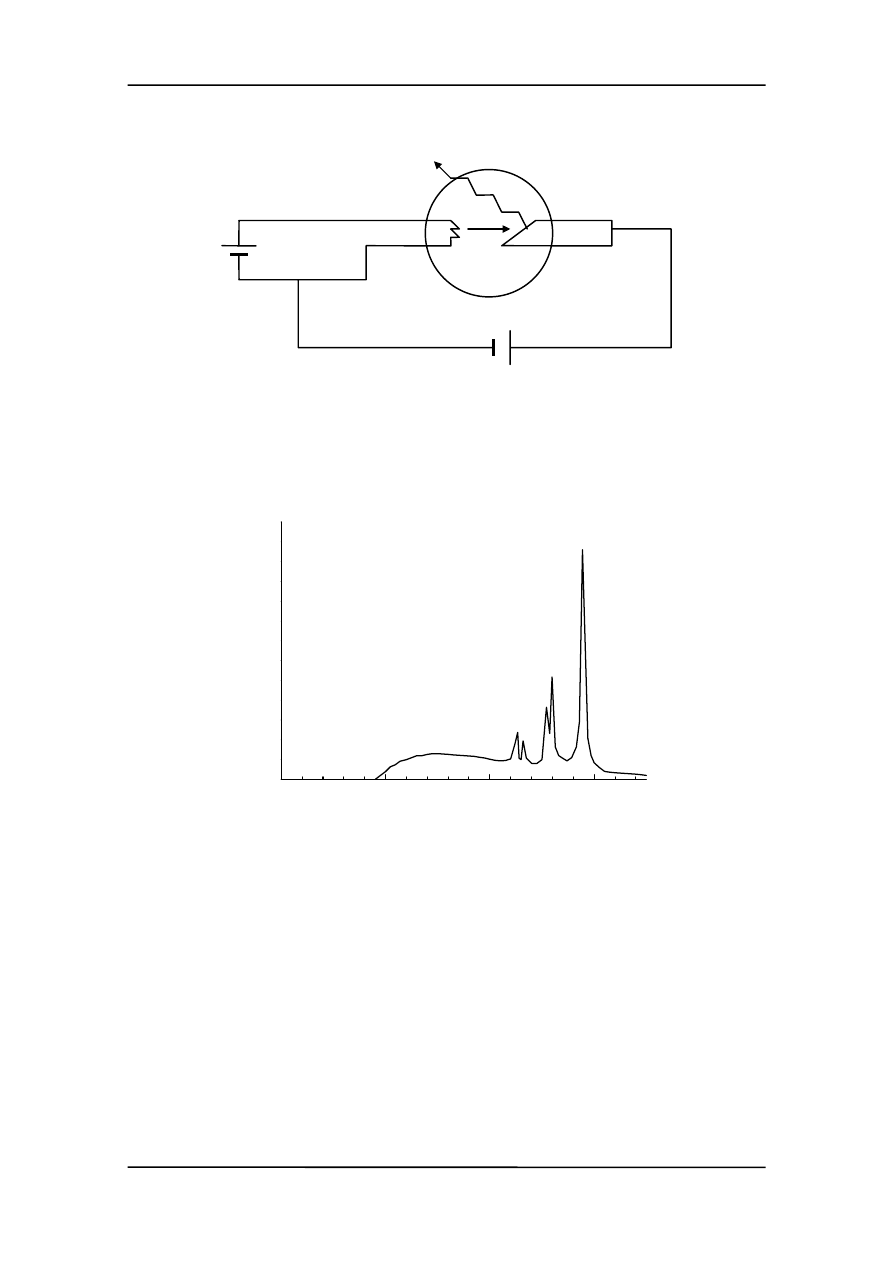
Na rysunku poniżej pokazana jest lampa rentgenowska. 
Elektrony emitowane z katody K są przyspieszane przez napięcie U rzędu 10

4

 V (przy-

łożone pomiędzy katodą i anodą) i wreszcie uderzają w anodę (tarczę). Elektrony są 
hamowane w anodzie, aż do ich całkowitego zatrzymania. 

 

36-5 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 

K 

A 

U 

promieniowanie X 

 

Zgodnie z fizyką klasyczną w wyniku tego hamowania (ładunek doznający przyspiesze-
nia) powinna nastąpić emisja promieniowania elektromagnetycznego o widmie ciągłym

. 

Przykładowy rozkład widmowy rentgenowski otrzymany dla wolframu jest pokazany 
na wykresie poniżej. 

0.00

0.05

0.10

0.15

Nat

ęż

eni

e

λ

 (nm)

 

Najbardziej charakterystycznymi cechami obserwowanych rozkładów widmowych pro-
mieniowania X są: 
•  charakterystyczne linie widmowe tj. maksima natężenia promieniowania występują-

ce dla ściśle określonych długości fal. Zaobserwowano, że 

widmo liniowe

 zależy od 

materiału (pierwiastka) anody. 

•  istnienie dobrze określonej minimalnej długości fali 

λ

min

 

widma ciągłego

. Stwier-

dzono, że wartość 

λ

min

 zależy jedynie od napięcia U i jest taka sama dla wszystkich 

materiałów, z jakich wykonana jest anoda. 

Istnienie krótkofalowej granicy widma ciągłego promieniowania X nie może być wyja-
śnione przez klasyczną teorię elektromagnetyzmu. W świetle tej teorii nie istnieją żadne 
powody, aby z anody nie mogły być wysłane fale o długości mniejszej od jakiejś warto-
ści granicznej. 

 

36-6 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

Jeżeli jednak potraktujemy promieniowanie rentgenowskie jako strumień fotonów to 
wyjaśnienie obserwowanego zjawiska jest proste. 
Elektron o początkowej energii kinetycznej E

k

 (uzyskanej dzięki napięciu U) w wyniku 

oddziaływania z ciężkim jądrem atomu tarczy jest hamowany i energia jaką traci poja-
wia się w formie kwantów (rysunek). 

 

E

k 

E

k

' 

jądro 

foton 

elektron 

 

Energia powstającego fotonu jest dana wzorem: 
 

hv = E

k

 - E

k

' 

 
gdzie E

k

' jest energią elektronu po zderzeniu. Elektron w trakcie zderzenia przekazuje 

jądru pewną energię jednak ze względu na to, że jądra tarczy są bardzo ciężkie (w po-
równaniu do elektronu) możemy ją zaniedbać. 
Długość fali fotonu można obliczyć z relacji 
 

'

k

k

E

E

c

h

−

=

λ

 

 
W wyniku zderzeń elektrony tracą różne ilości energii typowo elektron zostaje zatrzy-
many w wyniku wielu zderzeń z jądrami tarczy - otrzymujemy szereg fotonów o róż-
nych energiach (różnych 

λ). Wobec tego promieniowanie rentgenowskie wytwarzane 

przez wiele elektronów będzie miało 

widmo ciągłe

. 

Powstaje wiele fotonów o długościach od 

λ

min

 do 

λ → ∞, co odpowiada różnym ener-

giom traconym w zderzeniach. 
Foton o najmniejszej długości fali 

λ

min

 (maksymalnej energii) będzie emitowany wtedy 

gdy elektron straci całą energię w jednym procesie zderzenia. Oznacza to, że po tym 
zderzeniu E

k

' = 0 więc 

 

 

k

E

c

h

=

min

λ

 (36.4) 

 
Ponieważ energia kinetyczna jest równa eU (elektron przyspieszony napięciem U) więc 
zachodzi relacja 

eU

c

h

=

min

λ

 

czyli 

 

eU

hc

=

min

λ

 (36.5) 

 

36-7 

Z. Kąkol-Notatki do Wykładu z Fizyki

 

 
Tak więc minimalna długość fali odpowiadająca całkowitej zamianie energii kinetycz-
nej elektronów na promieniowanie zależy jedynie od U, a nie zależy np. od materiału z 
jakiego zrobiono tarczę (anodę). 
Podobnie na gruncie fizyki kwantowej można wyjaśnić powstawanie 

widma liniowego 

(charakterystycznego)

. 

Elektron z wiązki padającej przelatując przez atom anody, niekiedy przechodzi w pobli-
żu elektronu podpowłoki wewnętrznej. W wyniku oddziaływania kulombowskiego 
między tymi elektronami może dojść do wybicia elektronu z podpowłoki poza atom. 
Pozostawia to atom w stanie wysoko wzbudzonym ponieważ ubył elektron o dużej 
energii wiązania. Atom ostatecznie powróci do stanu podstawowego, emitując serię fo-
tonów wysokoenergetycznych. 
Aby to szczegółowo prześledzić rozpatrzmy atom anody, z którego podpowłoki 1s zo-
stał usunięty elektron. W pierwszym kroku powrotu atomu do stanu podstawowego 
elektron z jednej z podpowłok o mniej ujemnej  (wyższej) energii np. elektron 2p, prze-
chodzi na wolne miejsce w podpowłoce 1s. Pozostawia to dziurę w podpowłoce 2p. 
Towarzyszy temu emisja fotonu o energii równej spadkowi energii wzbudzenia tj. róż-
nicy energii atomu z brakującym elektronem 1s i atomu z brakującym elektronem 2p. 
Oczywiście dziura w podpowłoce 2p może być zapełniona przez elektron 3d, a powstała 
dziura w podpowłoce 3d przez elektron 4p itd. 
Zazwyczaj proces powrotu atomu do stanu podstawowego składa się z kilku kroków. 
W każdym kroku dziura przeskakuje do podpowłoki o mniej ujemnej energii, aż przej-
dzie do najbardziej zewnętrznej podpowłoki gdzie zostanie zajęta przez jakiś elektron 
będący w pobliżu. Atom jest znowu w stanie podstawowym i jest obojętny elektrycznie. 
Każdemu przejściu dziury do stanu o mniej ujemnej energii towarzyszy emisja fotonu o 
energii równej spadkowi energii wzbudzenia. W ten sposób powstaje 

widmo liniowe

. 

Ponieważ przejścia odbywają się pomiędzy podpowłokami atomu anody więc wysyłane 
promieniowanie X jest charakterystyczne dla atomów konkretnego pierwiastka anody. 
Liniowe widma rentgenowskie są interesujące praktyczni ze względu na wiele użytecz-
nych zastosowań w nauce i technice. 
 

 

36-8