Model wyboru
międzyokresowego
konsumenta
oraz wybór między
konsumpcją i czasem wolnym
1. Model wyboru konsumpcji w czasie
1.1. Założenia modelu
1.2. Rozwiązanie modelu
1.3. Przykład
2. Wybór między konsumpcją i czasem wolnym
2.1. Założenia modelu
2.2. Rozwiązanie modelu
2.3. Przykład
Bibliografia
2
1. Model wyboru konsumpcji
w czasie
1.1. Założenia modelu
Warunkiem brzegowym dla konsumenta dokonującego alokacji konsumpcji w czasie
jest
międzyokresowa linia ograniczenia budżetowego
. Jest ona zbiorem wszystkich
kombinacji konsumpcji bieżącej i konsumpcji przyszłej, które są osiągalne dla konsumen-
ta przy danych warunkach brzegowych (czyli dochodach bieżących i przyszłych oraz sto-
pie procentowej).
Równanie międzyokresowej linii ograniczenia budżetowego wyprowadzamy przy
następujących założeniach:
1) przedmiotem wyboru konsumenta jest struktura konsumpcji w okresie bieżącym
(będziemy ją oznaczać symbolem C
1
, gdzie: C
1
≥ 0) oraz konsumpcji w okresie przy-
szłym (którą będziemy oznaczać symbolem C
2
,
gdzie: C
2
≥ 0);
2) zakładamy, że konsument „żyje” w dwóch okresach: w okresie bieżącym i w okresie
przyszłym; w każdym z tych okresów dysponuje on dochodem (dla naszej analizy nie
ma znaczenia źródło jego dochodów), który może przeznaczać na konsumpcję; jego
dochód w okresie bieżącym wynosi m
1
> 0, a w okresie przyszłym m
2
> 0;
3) dochody z obu okresów muszą być w całości wydane na konsumpcję w obu okresach
(czyli konsument nic nie przekazuje swoim spadkobiercom);
4) w odróżnieniu od modelu przedstawionego w module 1 przyjmujemy, że konsument
ma dostęp do rynku kredytowego, na którym może zaciągać pożyczki na sfinansowa-
nie swojej bieżącej konsumpcji lub zakładać depozyty w celu sfinansowania swojej
konsumpcji przyszłej.
Przy powyższych założeniach możemy wyprowadzić równanie międzyokresowej li-
nii ograniczenia budżetowego. Oszczędności (S) (przy założeniu, że konsument „żyje”
w dwóch okresach) to różnica między dochodem bieżącym i konsumpcją bieżącą:
S m
C
=
−
1
1
.
(1)
W odróżnieniu od większości wielkości ekonomicznych oszczędności są określone
w zbiorze liczb rzeczywistych. Jeśli S > 0, to konsument ma oszczędności sensu stricto. Je-
śli S < 0, to konsument wydaje więcej w okresie bieżącym niż zarabia, czyli zaciąga kre-
dyt w celu sfinansowania bieżącej konsumpcji. Natomiast S = 0 oznacza, że wartość kon-
sumpcji bieżącej jest równa dochodom bieżącym.
Konsumpcja w okresie przyszłym będzie zatem równa sumie dochodów przyszłych
oraz oszczędności powiększonych o odsetki:
3
C
m
S
r
2
2
1
=
+
+
(
).
(2)
Po podstawieniu równania 1 do równania 2 i przekształceniach otrzymujemy równa-
nie międzyokresowej linii ograniczenia budżetowego:
C
m
m
r
C
r
2
2
1
1
1
1
=
+
+
−
+
(
)
(
).
(3)
A zatem nachylenie międzyokresowej linii ograniczenia budżetowego wynosi:
dC
dC
C C
r
2
1
2
1
1
=
′
= − +
( )
(
).
(4)
Z równania 4 wynika, że międzyokresowa linia ograniczenia budżetowego ma ujem-
ne nachylenie.
Nachylenie międzyokresowej linii ograniczenia budżetowego zależy od wysokości
stopy procentowej. Im wyższa stopa procentowa, tym mniejszy współczynnik nachyle-
nia, a zatem międzyokresowa linia ograniczenia budżetowego będzie bardziej stroma.
Wyrażenie (1 + r) to cena konsumpcji bieżącej. Jeśli konsument wyda jednostkę pie-
niężną w bieżącym okresie, to ponosi również koszt alternatywny w postaci utraconych
odsetek.
Położenie międzyokresowej linii ograniczenia budżetowego zależy od poziomu do-
chodu w okresie bieżącym i w okresie przyszłym. Wzrost (spadek) m
1
lub m
2
powodu-
je przesunięcie międzyokresowej linii ograniczenia budżetowego równolegle w prawo
(w lewo).
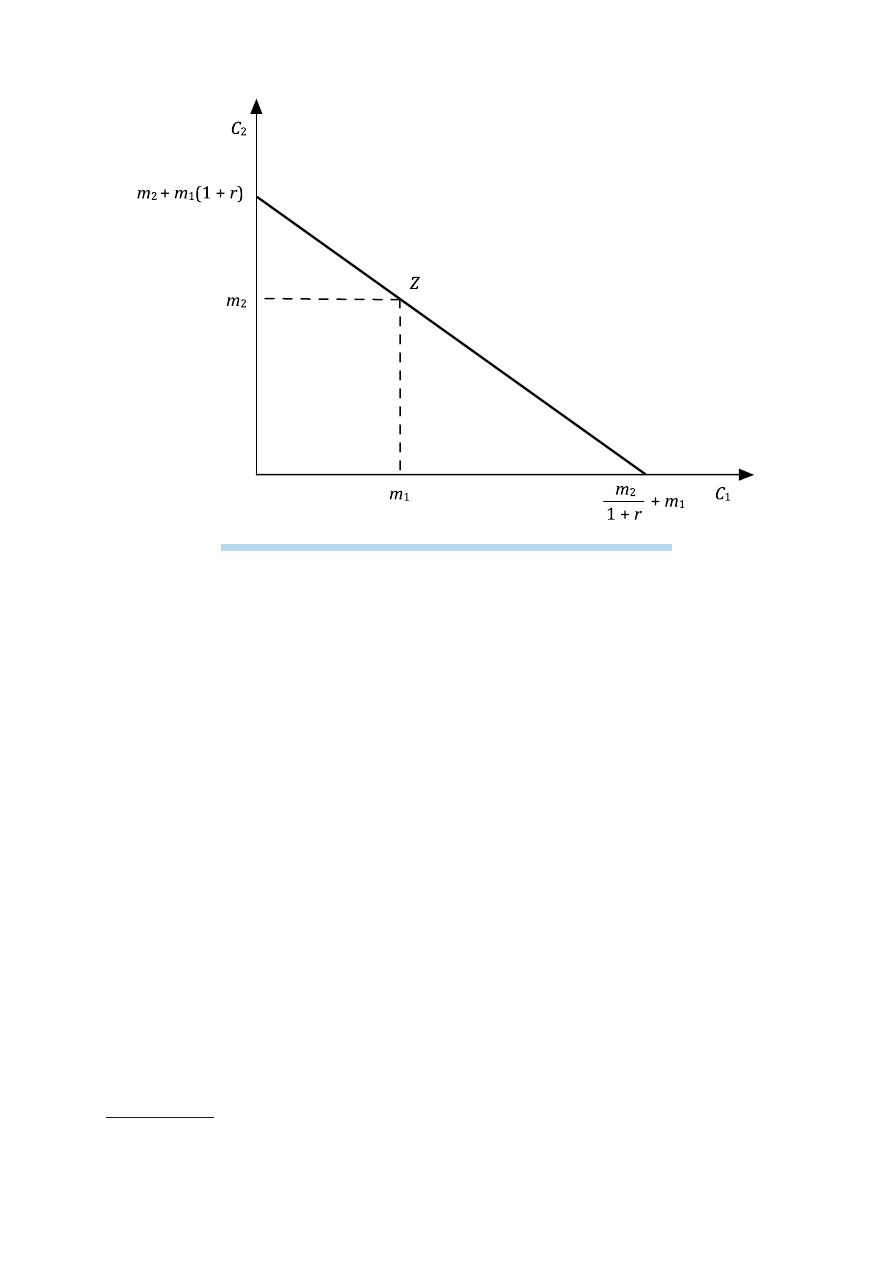
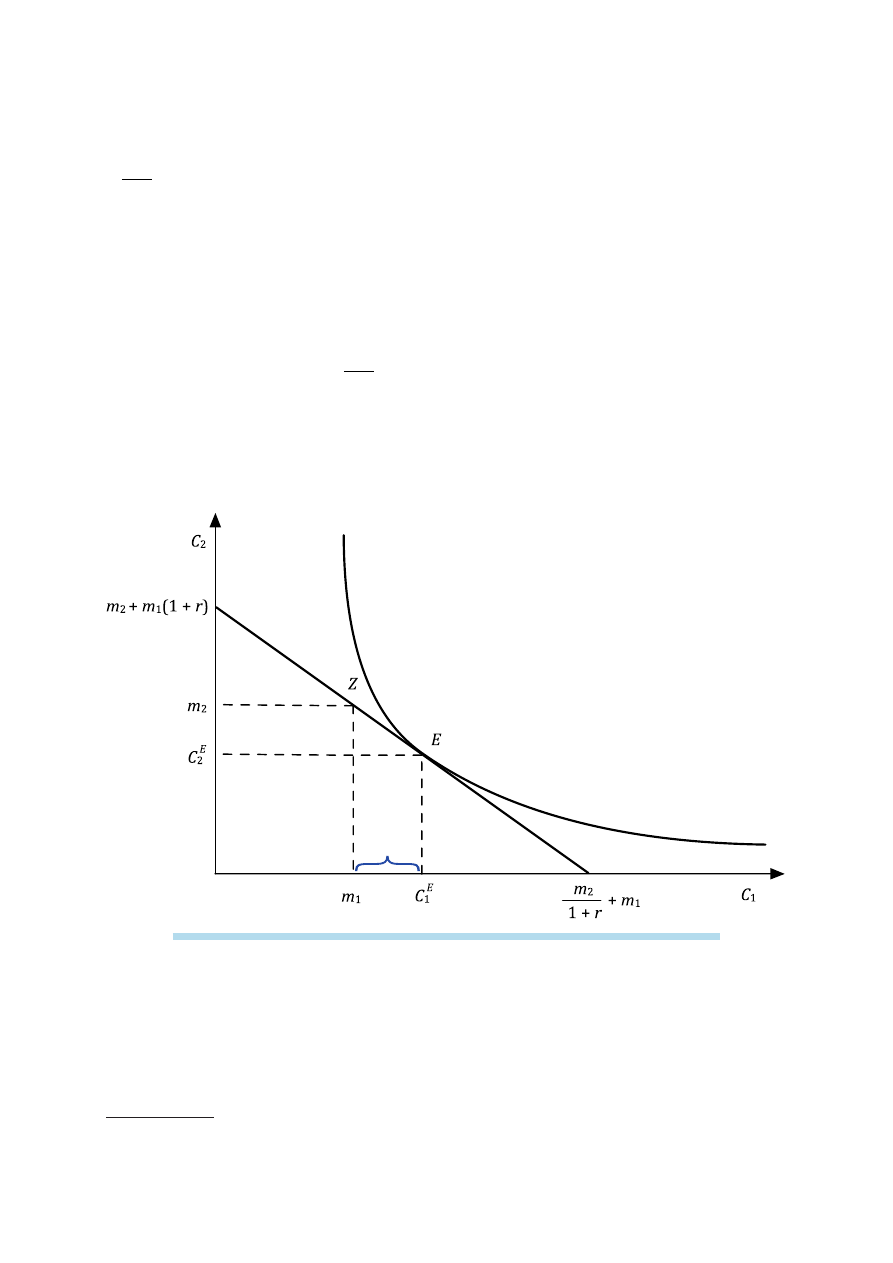
Ilustrację graficzną międzyokresowej linii ograniczenia budżetowego przedstawia
rysunek 1.
Współrzędne punktów brzegowych:
1) m
2
+ m
1
(1 + r) to poziom konsumpcji w okresie przyszłym w sytuacji, gdy C
2
= 0,
2)
m
r
m
2
1
1 +
+
to poziom konsumpcji w okresie bieżącym, gdy C
2
= 0.
Punkt Z o współrzędnych (m
1
, m
2
) to zasób początkowy. W punkcie tym poziom
oszczędności wynosi 0. W każdym punkcie na międzyokresowej linii ograniczenia bu-
dżetowego na prawo od punktu Z konsumpcja w okresie bieżącym przewyższa do-
chód w okresie bieżącym, co oznacza, że konsument jest pożyczkobiorcą (kredytobior-
cą). W każdym punkcie na międzyokresowej linii ograniczenia budżetowego na lewo od
punktu Z konsumpcja w okresie bieżącym jest mniejsza od dochodu w okresie bieżącym,
co oznacza, że konsument jest pożyczkodawcą (kredytodawcą).
4
Rysunek 1. Międzyokresowa linia ograniczenia budżetowego
Celem konsumenta w modelu alokacji konsumpcji w czasie jest maksymalizacja uży-
teczności całkowitej z konsumpcji bieżącej i konsumpcji przyszłej. Tak samo jak w modu-
le 1 zakładamy, że preferencje konsumenta są opisane przez funkcję użyteczności całko-
witej z konsumpcji bieżącej i konsumpcji przyszłej według wzoru:
U C C
( , ).
1
2
(5)
Zakładamy, że funkcja U(C
1
, C
2
) ma te same własności matematyczne co funkcja uży-
teczności całkowitej u(x
1
, x
2
)
1
. Konsument ma zatem dobrze zachowujące się preferencje
dotyczące konsumpcji w okresie bieżącym i przyszłym.
Krzywa obojętności
, będąca ilu-
stracją graficzną preferencji dobrze zachowujących się, jest ujemnie nachylona i wypukła
do początku układu współrzędnych (zob. rys. 2).
Krzywa obojętności
w modelu aloka-
cji konsumpcji w czasie jest zbiorem różnych kombinacji konsumpcji bieżącej i konsump-
cji przyszłej, które zapewniają konsumentowi taki sam poziom użyteczności całkowitej.
1
Chodzi tutaj o warunki 1–4 w module 1, podtemat 1.2.
5
Rysunek 2. Krzywa obojętności w modelu alokacji konsumpcji w czasie
Funkcja użyteczności całkowitej z konsumpcji bieżącej i konsumpcji przyszłej —
U(C
1
, C
2
) — opisuje zależność między poziomem konsumpcji w okresie bieżącym i okre-
sie przyszłym a poziomem użyteczności całkowitej. Użyteczność krańcowa konsumpcji
bieżącej (mu
1
) to stosunek przyrostu użyteczności całkowitej do przyrostu konsumpcji
bieżącej
2
. Użyteczność krańcowa konsumpcji przyszłej (mu
2
) to stosunek przyrostu uży-
teczności całkowitej do przyrostu konsumpcji przyszłej
3
.
1.2. Rozwiązanie modelu
Przyjmujemy, że konsument dokonujący alokacji konsumpcji w czasie postępuje racjo-
nalnie. Dąży on do maksymalizacji użyteczności całkowitej U(C
1
, C
2
) przy danej między-
okresowej linii ograniczenia budżetowego. Wyznaczamy zatem maksimum warunkowe:
U C C
C
( , )
max
1
2
,C
1
→
2
(6)
przy międzyokresowej linii ograniczenia budżetowego:
C
m
m
r
C
r
2
2
1
1
1
1
=
+
+
−
+
(
)
(
).
(7)
2
Jeśli przyrosty konsumpcji bieżącej i użyteczności całkowitej są zbieżne do 0, to
mu
U C , C
C
1
1
=
∂
∂
.
3
Jeśli przyrosty konsumpcji przyszłej i użyteczności całkowitej są zbieżne do 0, to
mu
U C , C
C
2
2
=
∂
∂
.
6
Tak samo jak w module 1, warunki konieczne i dostateczne istnienia maksimum
warunkowego uzyskamy przez wykorzystanie wielomianu Lagrange’a. Wielomian
Lagrange’a jest postaci:
Φ
= ( , )
(
(1
)
(1
)).
1
2
2
1
2
1
U C C
C
C
r
m
m
r
+
+
+
−
−
+
λ
(8)
Parametr λ ∈ ℜ w równaniu 8 to nieoznaczony mnożnik wielomianu Lagrange’a. Nie
nadajemy mu interpretacji ekonomicznej.
Maksymalizacja wielomianu Lagrange’a jest tożsama z maksymalizacją funkcji uży-
teczności U(C
1
, C
2
). Wielomian Lagrange’a będzie osiągał maksimum warunkowe, gdy speł-
nione będą następujące warunki konieczne i dostateczne (zob. Tokarski, 2011: 59–60):
∂
∂
∂
∂
+
+
Φ
C
U C C
C
r
1
1
2
1
=
( , )
(
) = 0
λ
1
(8.1)
∂
∂
∂
∂
+
Φ
C
U C C
C
2
1
2
2
=
( , )
= 0
λ
(8.2)
∂
∂
+
+
−
−
+
=
Φ
λ
=
(1
)
(1
) 0
2
1
2
1
C
C
r
m
m
r
(8.3)
H
C
C C
C
C C
C
C
∧
=
∂
∂
∂
∂ ∂
∂
∂ ∂
∂
∂ ∂
∂
∂
∂
∂ ∂
∂
∂
( )
Φ
Φ
Φ
Φ
Φ
Φ
Φ
Φ
2
1
2
2
1
2
2
1
2
2
1
2
2
2
2
2
2
λ
λ
λλ
λ
λ
∂
∂
∂ ∂
∂
∂
>
C
C
1
2
1
2
2
0
Φ
Φ
(8.4)
Równania 8.1–8.3 to warunki konieczne istnienia maksimum warunkowego, a nie-
równość 8.4 to warunek dostateczny
4
.
Warunek 8.3 jest spełniony dla każdego C
1
, C
2
≥ 0. Z warunku tego wynika, że opty-
malna struktura konsumpcji bieżącej i konsumpcji przyszłej musi znajdować się na mię-
dzyokresowej linii ograniczenia budżetowego.
Po przekształceniu równania 8.1–8.2 przyjmują postać:
mu
r
1
1
+
+
λ
(
) = 0
(8.5a)
mu
2
= 0
+ λ
(8.5b)
4
Warunkiem dostatecznym istnienia maksimum warunkowego jest, aby wyznacznik hesjanu obrze-
żonego
H
∧
( )
Φ
był dodatnio określony w punkcie stacjonarnym, w którym są spełnione warunki koniecz-
ne
(por. Tokarski, 2011: 59–60).
7
Z równań 8.5a i 8.5b otrzymujemy warunek maksymalizacji użyteczności całkowitej
z konsumpcji bieżącej i konsumpcji przyszłej:
−
= − +
mu
mu
r
1
2
1
(
).
(9)
Równanie 8.3 oraz równanie 9 to warunki konieczne maksymalizacji użyteczności
całkowitej z konsumpcji bieżącej i konsumpcji przyszłej. Jak wynika z równania 9, aby
konsument maksymalizował użyteczność całkowitą, stosunek użyteczności krańcowej
konsumpcji bieżącej do użyteczności krańcowej konsumpcji przyszłej musi być równy
stosunkowi ceny konsumpcji bieżącej do ceny konsumpcji przyszłej
5
.
Lewa strona równania 9:
− mu
mu
1
2
to
krańcowa stopa substytucji C
1
i C
2
. Określa ona,
w jakiej relacji konsument będzie skłonny zamieniać konsumpcję przyszłą (C
2
) na kon-
sumpcję bieżącą (C
1
) przy zachowaniu tego samego poziomu użyteczności całkowitej.
W naszym modelu zakładamy, że konsument ma dobrze zachowujące się preferencje,
a zatem krańcowa stopa substytucji ma wartość ujemną.
Rysunek 3. Optimum konsumenta w modelu alokacji konsumpcji w czasie
Prawa strona równania 9 to współczynnik nachylenia międzyokresowej linii ogra-
niczenia budżetowego. Z równania 9 wynika zatem, że konsument maksymalizuje uży-
teczność całkowitą z konsumpcji bieżącej i konsumpcji przyszłej w punkcie, w którym
nachylenie krzywej obojętności jest równe nachyleniu linii ograniczenia budżetowego.
Oznacza to, że punktem optimum jest punkt styczności krzywej obojętności z między-
5
Cena konsumpcji przyszłej wynosi 1.
8
okresową linią ograniczenia budżetowego
6
. Ilustrację graficzną optimum konsumenta
w modelu alokacji konsumpcji w czasie przedstawiono na rysunku 3.
W punkcie E (na rys. 4) konsument maksymalizuje użyteczność całkowitą z konsump-
cji bieżącej i konsumpcji przyszłej. Współrzędne tego punktu —
C C
E
E
1
2
,
(
)
— to optymal-
na struktura konsumpcji bieżącej i konsumpcji przyszłej. Ponieważ punkt optimum znaj-
duje się na prawo od punktu Z, konsument maksymalizuje użyteczność całkowitą, będąc
pożyczkobiorcą (kredytobiorcą). Odcinek zaznaczony na rysunku 3 klamrą (między m
1
a
C
E
1
) to poziom oszczędności (wielkość zaciągniętych pożyczek lub kredytów) w anali-
zowanym przypadku.
Punkt E może znajdować się w dowolnym miejscu na międzyokresowej linii ogra-
niczenia budżetowego (oprócz punktów brzegowych znajdujących się na osiach współ-
rzędnych).
Aby wyznaczyć optymalną strukturę konsumpcji bieżącej i konsumpcji przyszłej, mu-
simy rozwiązać układ równań składający się z warunków koniecznych 8.3 i 9:
−
= − +
+
+
−
−
+
=
mu
mu
r
C
C
r
m
m
r
1
2
1
(
)
(1
)
(1
) 0
2
1
2
1
(10)
Optymalna struktura konsumpcji bieżącej i przyszłej zależy od poziomu stopy pro-
centowej oraz dochodów bieżących i dochodów przyszłych. Zmiana którejkolwiek z tych
wielkości wpłynie na położenie punktu optimum.
1.3. Przykład
Załóżmy, że preferencje konsumenta są opisane przez funkcję użyteczności całkowi-
tej postaci:
U C C
C
C
( , ) = ln( )
ln( ).
1
2
1
2
2
+
Dochód w okresie bieżącym wynosi m
1
> 0, a dochód w okresie przyszłym m
2
> 0. Sto-
pa procentowa wynosi r > 0.
Problem maksymalizacji użyteczności całkowitej możemy zatem opisać w następują-
cy sposób:
U C C
C
C
C C
( , ) ln( ) + 2ln( )
max
1
2
,
1
=
→
1
2
2
(11)
przy danej międzyokresowej linii ograniczenia budżetowego:
C
m
m
r
C
r
2
2
1
1
1
1
=
+
+
−
+
(
)
(
).
(12)
6
Współczynniki nachylenia obu krzywych są sobie równe tylko w punkcie styczności.
9
Wielomian Lagrange’a ma zatem następującą postać:
Φ
= ln( )
ln( )
(
(1
)
(1 )).
2
1
2
1
C
C
C
C
r
m
m
r
1
2
2
+
+
+
+
−
−
+
λ
(13)
Aby równanie 13 osiągało maksimum warunkowe, muszą być spełnione następujące
warunki konieczne
7
:
∂
∂
+
+
Φ
C
C
r
1
=
(
) = 0
1
1
1
λ
(14a)
∂
∂
+
Φ
C
C
2
=
= 0
2
2
λ
(14b)
∂
∂
+
+
−
−
+
=
Φ
λ
=
(1
)
(1
) 0
2
1
2
1
C
C
r
m
m
r
(14c)
Z równań 14a–14b po przekształceniach otrzymujemy:
λ
=
(
)
,
−
+
1
1
1
C
r
(15a)
λ
=
−
2
2
C
.
(15b)
Z porównania stronami równań 15a i 15b otrzymujemy:
1
1
1
C
r
c
(
)
2
2
+
=
.
(16)
Po przekształceniach równanie 16 przyjmuje postać:
2
1
C
r
C
(1
)
0.
2
+
−
=
(17)
Aby wyznaczyć optymalną strukturę konsumpcji bieżącej i konsumpcji przyszłej, mu-
simy rozwiązać następujący układ równań:
2
1
2
C
r
C
C
r
C
m
r
m
(1
)
0
(1
)
(1
)
2
1
2
1
+
−
=
+
+
=
+
+
(18)
Wyznaczniki Cramera dla powyższego układu równań są postaci:
W
r
r
r
r
r
=
+
−
+
=
+
+
+
=
+
>
2 1
1
1
1
2 1
1
3 1
0
(
) ( )
(
)
(
) (
)
(
)
(19a)
7
Przyjmujemy, że spełnienie warunków koniecznych oznacza, że warunek dostateczny jest również
spełniony.
10
W
m
r
m
m
r
m
1
1
2
1
2
0
1
1
1
1
0
=
−
+
+
(
)
=
+
+
>
( )
(
)
(
)
(19b)
W
r
r
m
r
m
m
r
m
r
2
1
2
1
2
2 1
0
1
1
1
1
0
=
+
+
+
+
(
)
=
+
+
(
)
+
(
)
>
(
)
(
)
(
)
2
(
)
(19c)
Wyznacznik W układu równań 19 jest dodatnio określony, a zatem ten układ rów-
nań ma dokładnie jedno rozwiązanie. Rozwiązaniem tego układu równań jest optymalna
struktura konsumpcji bieżącej i przyszłej
8
:
C
W
W
m
r
m
r
m
m
r
E
1
1
1
2
1
2
1
3 1
3
3 1
=
=
+
+
+
=
+
+
(
)
(
)
(
)
(20a)
C
W
W
m
r
m
r
r
m
r
m
E
2
2
1
2
1
2
1
1
3 1
2 1
3
2
3
=
=
+
+
(
)
+
(
)
+
=
+
+
2
(
)
(
)
(
)
(20b)
Ponieważ S = m
1
– C
1
, to w punkcie E poziom oszczędności wyniesie:
S
m
C
m
m
m
r
E
E
=
−
=
−
−
+
1
1
1
1
2
3
3 1
(
)
.
(21)
Poziom oszczędności (a zarazem funkcja oszczędności) jest opisany wzorem:
1
2
2
3
3(1 )
E
m
m
S
.
r
=
−
+
(22)
Z równania 20a wynika, że optymalny poziom konsumpcji bieżącej zależy od m
1
, m
2
oraz r. Aby określić kierunek zależności między konsumpcją bieżącą i poszczególnymi
zmiennymi wpływającymi na konsumpcję bieżącą, musimy zbadać monotoniczność
C
E
1
względem wszystkich zmiennych. Różniczkując
C
E
1
względem m
1
, otrzymujemy:
∂
∂
= >
C
m
E
1
1
1
3
0.
(23a)
A zatem wzrost dochodu bieżącego powoduje (przy założeniu ceteris paribus) wzrost
konsumpcji bieżącej.
Pochodna
C
E
1
względem m
2
wynosi:
∂
∂
=
+
>
C
m
r
E
1
2
1
3 1
0
(
)
.
(23b)
8
Rozwiązanie na wzorach ogólnych pozwala na wyznaczenie zarówno poziomu, jak i funkcji kon-
sumpcji bieżącej i konsumpcji przyszłej.
11
Dodatni znak pochodnej 23b oznacza, że (przy założeniu ceteris paribus) wzrost do-
chodów przyszłych powoduje wzrost konsumpcji bieżącej.
Pochodna
C
E
1
względem stopy procentowej wynosi:
∂
∂
=
−
+
<
C
r
m
r
E
1
2
2
3 1
0
(
)
.
(23c)
Ujemny znak pochodnej 23c oznacza, że (przy założeniu ceteris paribus) wzrost stopy
procentowej powoduje spadek konsumpcji bieżącej.
Z równania 20b wynika, że optymalny poziom konsumpcji przyszłej zależy od m
1
, m
2
oraz r. Wartości pochodnych
C
E
2
względem poszczególnych zmiennych wynoszą odpo-
wiednio:
∂
∂
=
+
>
C
m
r
E
2
1
2 1
3
0
(
)
(24a)
∂
∂
=
>
C
m
E
2
2
2
3
0
(24b)
∂
∂
=
>
C
r
m
E
2
1
2
3
0
(24c)
Dodatnie wartości pochodnych
C
E
2
względem wszystkich zmiennych oznaczają, że
wzrost m
1
lub/i m
2
lub/i r powoduje wzrost konsumpcji w okresie przyszłym (
C
E
2
).
Z równania 22 wynika, że poziom oszczędności S
E
zależy od tego samego zestawu
zmiennych co
C
E
1
oraz
C
E
2
. Wartości pochodnych S
E
względem tych zmiennych wynoszą
odpowiednio:
∂
∂
=
>
S
m
E
1
2
3
0
(25a)
∂
∂
= −
+
<
S
m
r
E
2
1
3 1
0
(
)
(25b)
∂
∂
=
+
>
S
r
m
r
E
2
2
3 1
0
(
)
(25c)
Poziom oszczędności odpowiadający punktowi optimum jest zatem rosnącą funkcją
dochodów bieżących i stopy procentowej oraz malejącą funkcją dochodów przyszłych.
Ponieważ
∂
∂
=
−
+
<
2
2
2
3
2
3 1
0
S
r
m
r
E
(
)
, to wraz ze wzrostem stopy procentowej oszczędno-
ści rosną coraz szybciej.
12
2. Wybór między konsumpcją
i czasem wolnym
2.1. Założenia modelu
Przedmiotem wyboru konsumenta w tym modelu jest konsumpcja i czas wolny. W na-
szej analizie wielkość konsumpcji oznaczać będziemy symbolem C, a czas wolny symbo-
lem R. Przyjmujemy, że w każdym okresie konsument może na pracę i wypoczynek prze-
znaczyć N jednostek czasu (czyli N = R + L, gdzie L — podaż pracy jednostki). Zakładamy
ponadto, że:
1) konsument dysponuje dochodem pozapłacowym M > 0,
2) nominalna stawka płac wynosi w > 0,
3) cena konsumpcji wynosi p > 0,
4) dochody z pracy i dochody pozapłacowe są w całości przeznaczane na konsumpcję.
Przy powyższych założeniach możemy zapisać następujące równanie linii ogranicze-
nia budżetowego w tym modelu:
pC wL M
=
+
.
(26)
Ponieważ przedmiotem wyboru jest czas wolny, z równania 26 musimy wyelimino-
wać czas pracy (L). Wiemy, że N = R + L, a zatem L = N – R. Po podstawieniu do równania
26 i po przekształceniach otrzymujemy postać analityczną linii ograniczenia budżetowe-
go w tym modelu
9
:
C
w
p
R w
p
N
M
p
= −
+
+
,
(27)
gdzie:
w
p
— płaca realna (realna stawka płac),
M
p
— realny dochód pozapłacowy
10
.
Linia ograniczenia budżetowego (będąca wykresem równania 27) jest zbiorem
wszystkich kombinacji konsumpcji i czasu wolnego, które są osiągalne dla konsumen-
ta przy danych warunkach brzegowych, tzn. dochodach pozapłacowych, zasobie czasu
9
Równania 26 i 27 są równoważne.
10
Realny dochód pozapłacowy mierzy siłę nabywczą dochodu pozapłacowego w ujęciu nominalnym.
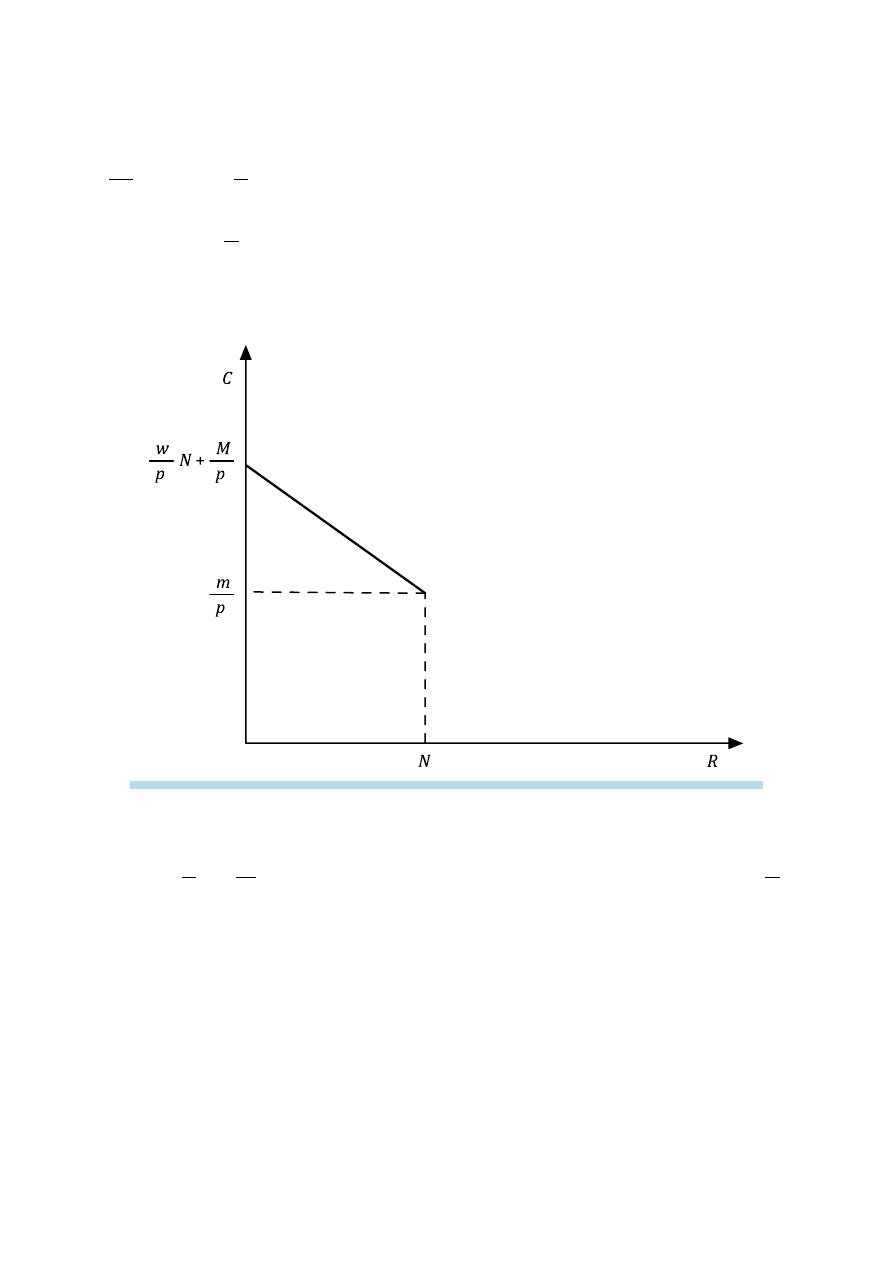
13
przeznaczanego na pracę i wypoczynek (N) oraz nominalnej stawce płac. Z równania 27
wynika, że nachylenie linii ograniczenia budżetowego wynosi:
dC
dR
C R
w
p
=
= −
'
.
( )
(28)
Wyrażenie
w
p
to
płaca realna (realna stawka płac)
. Płaca realna mierzy siłę na-
bywczą płacy nominalnej. Z równania 28 wynika, że wykresem równania 27 jest ujemnie
nachylona linia prosta. Jej ilustrację graficzną przedstawiono na rysunku 4.
Rysunek 4. Linia ograniczenia budżetowego w modelu wyboru między konsumpcją i czasem wolnym
Z równania 27 wynika, że jeśli R = 0, czyli N = L, to maksymalna wartość konsumpcji
wyniesie
w
p
N
M
p
+
. Jeśli natomiast L = 0, czyli R = N, to wartość konsumpcji wyniesie
m
p
.
Jak wynika z równania 27, nachylenie linii ograniczenia budżetowego zależy od nomi-
nalnej i realnej stawki płac. Wzrost (spadek) nominalnej (realnej) stawki płac powoduje
spadek (wzrost) nachylenia linii ograniczenia budżetowego, a linia ograniczenia budże-
towego stanie się bardziej stroma (płaska).
Położenie linii ograniczenia budżetowego zależy od dochodów pozapłacowych oraz
zasobu czasu, który konsument może przeznaczyć na pracę i wypoczynek. Z równania
27 wynika, że wzrost dochodów pozapłacowych przesuwa linię ograniczenia budżeto-
wego równolegle w lewo. Wzrost parametru N powoduje przesunięcie linii ograniczenia
budżetowego równolegle w prawo.
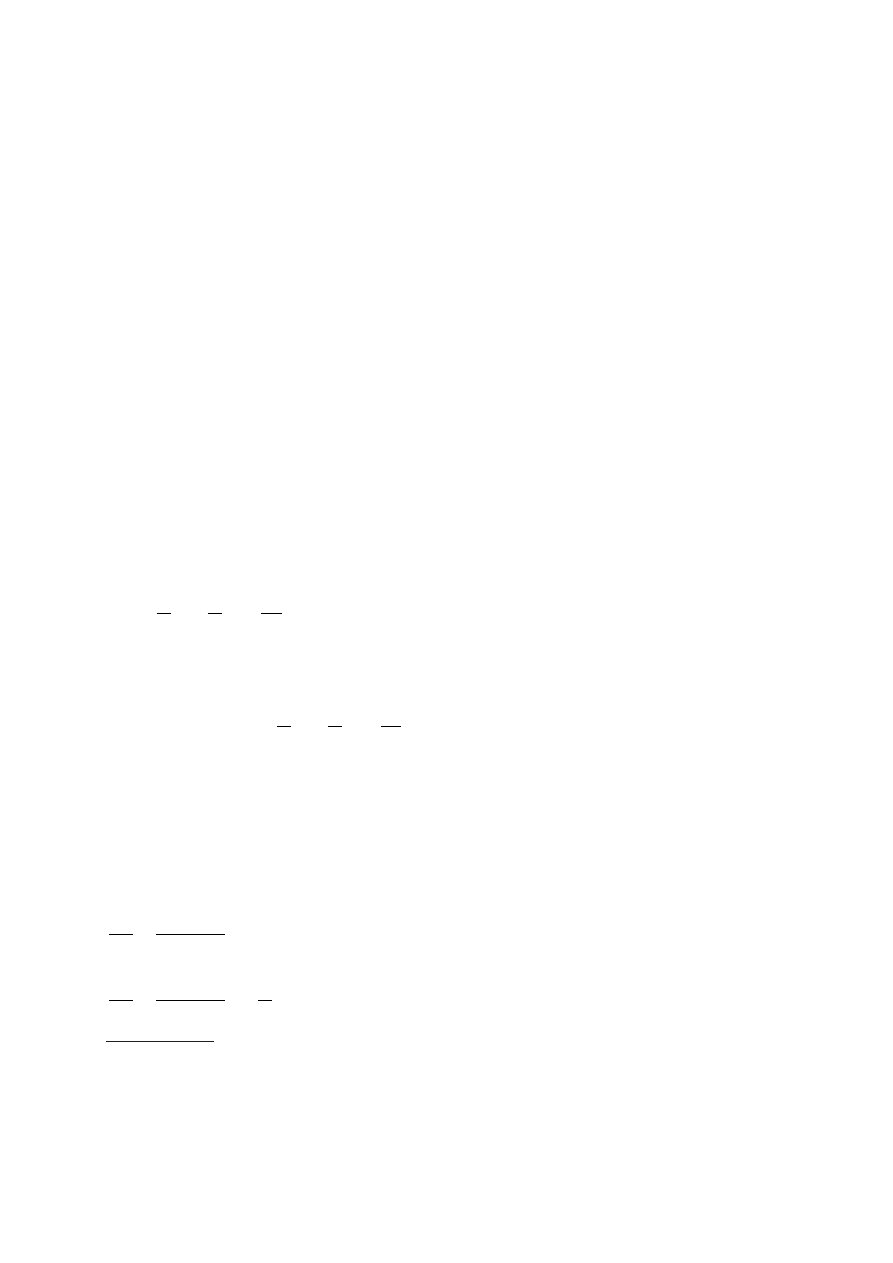
14
Celem konsumenta jest maksymalizacja użyteczności całkowitej z konsumpcji bieżą-
cej i konsumpcji przyszłej. Przyjmujemy, że funkcja użyteczności całkowitej z konsump-
cji i czasu wolnego — U(C, R) — opisuje preferencje dobrze zachowujące się
11
. Krzywa
obojętności będąca jej warstwicą jest zatem ujemnie nachylona i wypukła do początku
układu współrzędnych. Ma ona taki sam kształt jak krzywa obojętności przedstawiona
na rysunku 3.
2.2. Rozwiązanie modelu
Jak wspomniano w podtemacie 2.1, celem konsumenta jest maksymalizacja użytecz-
ności całkowitej z konsumpcji i czasu wolnego. Przy podejmowaniu decyzji dotyczącej
wyboru struktury konsumpcji i czasu wolnego konsument musi brać pod uwagę waru-
nek brzegowy, czyli linię ograniczenia budżetowego. A zatem również w tym modelu szu-
kamy maksimum warunkowego.
Problem wyboru w tym modelu możemy zapisać w następujący sposób:
U C R
C R
( , )
max
,
→
(29)
przy warunku brzegowym:
C
w
p
R w
p
N
M
p
= −
+
+
.
(30)
Wielomian Lagrange’a w prezentowanym modelu ma następującą postać:
Ω
= ( , )
,
U C R
C
w
p
R w
p
N
M
p
+
+
−
−
γ
(31)
gdzie:
γ — mnożnik Lagrange’a określony w zbiorze liczb rzeczywistych (nieposiadający inter-
pretacji ekonomicznej).
Aby wielomian Lagrange’a (31) osiągał maksimum warunkowe, muszą być spełnione
następujące warunki konieczne
12
:
∂
∂
∂
∂
+
Ω
C
U C R
C
=
( , )
= 0
γ
(32a)
∂
∂
∂
∂
+
Ω
R
=
( , )
= 0
U C R
R
w
p
γ
(32b)
11
Oznacza to, że funkcja U(C, R) ma te same własności matematyczne co funkcje użyteczności w oma-
wianych wcześniej modelach. Więcej informacji na temat tego modelu studenci mogą znaleźć w: Tokarski,
2011: 103–111.
12
Przyjmujemy, że spełnienie warunków koniecznych oznacza, że warunek dostateczny jest również
spełniony.
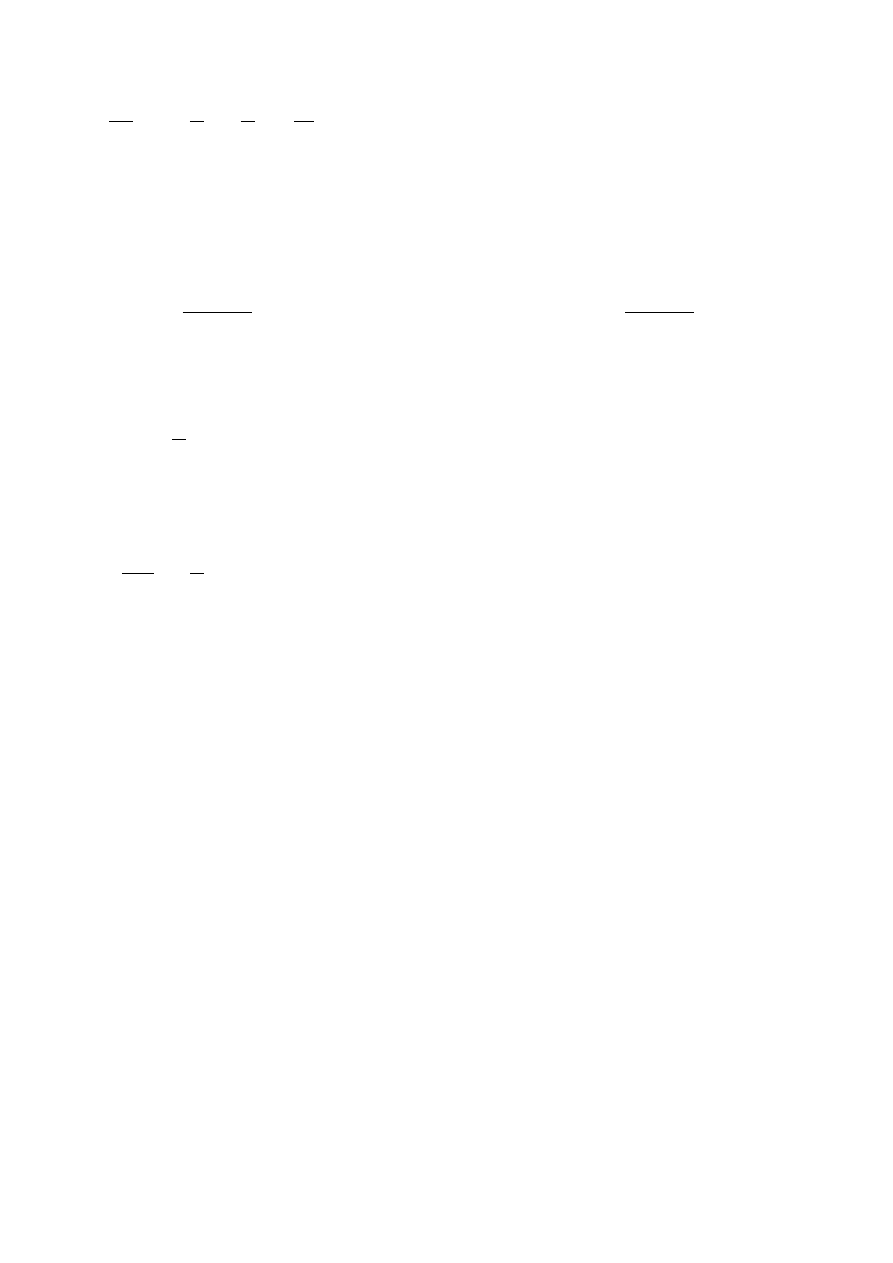
15
∂
∂
+
−
−
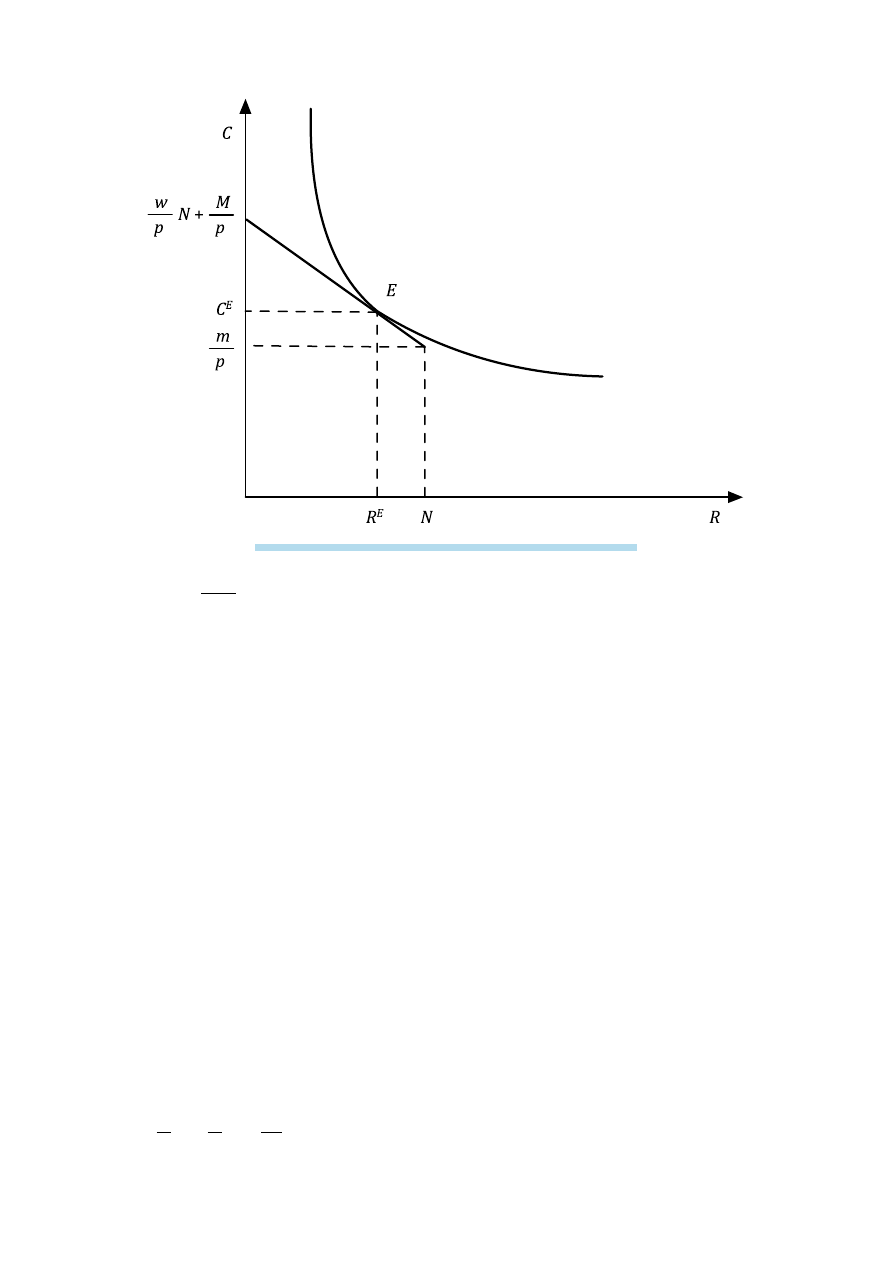
Ω
R
C
w
p
R w
p
N
M
p
=
= 0
(32c)
Warunek konieczny 32c to równanie linii ograniczenia budżetowego. Jest on spełnio-
ny dla każdego C, R ≥ 0. Z tego warunku wynika, że optymalna struktura konsumpcji
i czasu wolnego musi znajdować się na linii ograniczenia budżetowego.
Pochodne cząstkowe funkcji U(C, R) względem C oraz R są równe użytecznoś-
ciom krańcowym konsumpcji i czasu wolnego. Użyteczność krańcowa czasu wolnego
—
mu
U C R
R
R
=
∂
∂
( , )
, a użyteczność krańcowa konsumpcji —
mu
U C R
C
C
=
∂
∂
( , )
. Po podsta-
wieniu do równań 32a–32b otrzymujemy:
mu
C
+ γ
= 0
(33a)
mu
w
p
R
+ γ
= 0
(33b)
Po przekształceniach równań 33a–33b otrzymujemy warunek konieczny maksymali-
zacji użyteczności całkowitej z konsumpcji i czasu wolnego:
−
= −
mu
mu
w
p
R
C
.
(34)
Lewa strona równania 34 to nachylenie krzywej obojętności, czyli krańcowa stopa
substytucji między konsumpcją i czasem wolnym (jest ona miarą nachylenia krzywej
obojętności). Prawa strona to nachylenie linii ograniczenia budżetowego. A zatem opti-
mum konsumenta w tym modelu znajduje się w punkcie styczności obu krzywych.
Oba warunki konieczne maksymalizacji użyteczności całkowitej z konsumpcji i czasu
wolnego (równania 32c i 34
)
są spełnione w punkcie E na rysunku 5. Współrzędne tego
punktu (C
E
, R
E
) to optymalna struktura konsumpcji i czasu wolnego.
16
Rysunek 5. Optymalna struktura konsumpcji i czasu wolnego
Odcinek
R N
E
to wielkość podaży pracy odpowiadająca punktowi E. Optymalna wiel-
kość konsumpcji, czasu wolnego oraz podaży pracy zależy od poziomu nominalnej stawki
płac oraz nominalnego i realnego poziomu dochodów pozapłacowych. Kierunki zależno-
ści zbadamy w przykładowym zadaniu w następnym podtemacie.
2.3. Przykład
Załóżmy, że preferencje konsumenta są opisane przez funkcję użyteczności całkowi-
tej z konsumpcji i czasu wolnego następującej postaci:
U C R
C R
( , ) =
2 3
.
Dochody pozapłacowe konsumenta wynoszą M > 0, stawka płac w > 0, cena konsump-
cji p > 0, a czas przeznaczany na pracę i wypoczynek N > 0 (gdzie: N = L + R).
Konsument dąży do maksymalizacji użyteczności całkowitej z konsumpcji i czasu
wolnego:
U C R
C R
C C
( , )
max
1
,
=
→
2 3
2
(35)
przy danej linii ograniczenia budżetowego:
C
w
p
R w
p
N
M
p
= −
+
+
.
(36)
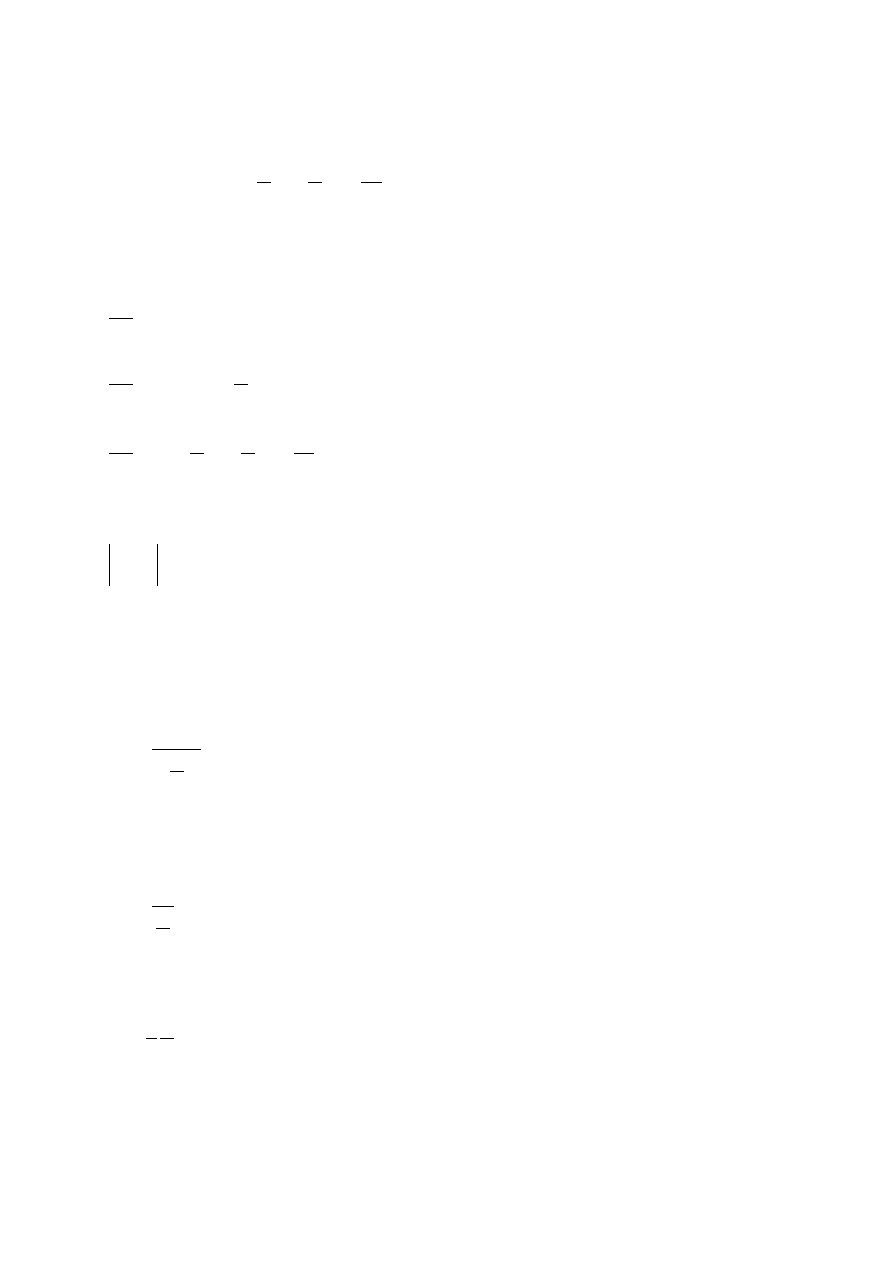
17
Aby wyznaczyć optymalny poziom konsumpcji i czasu wolnego, musimy zbudować
wielomian Lagrange’a. Przy danej funkcji użyteczności ma on następującą postać:
Ω
= C R
C
w
p
R w
p
N
M
p
2 3
+
+
−
−
γ
.
(37)
Aby wielomian Lagrange’a osiągał maksimum warunkowe, muszą być spełnione na-
stępujące warunki konieczne:
∂
∂
+
Ω
C
CR
=
= 0
2
3
γ
(38a)
∂
∂
+
Ω
R
C R
w
p
=
= 0
3
2 2
γ
(38b)
∂
∂
+
−
−
Ω
R
=
= 0
C
w
p
R w
p
N
M
p
(38c)
oraz warunek dostateczny:
H
∧
>
( )
Φ
0.
(39)
Sprawdzenie warunku dostatecznego pomijamy. Z równań 38a–38b po przekształce-
niach otrzymujemy:
γ
= − 2
3
CR
(40a)
γ
= − 3
2 2
C R
w
p
(40b)
Porównując stronami równania 40a–40b oraz dokonując pewnych przekształceń,
otrzymujemy:
2
3
R
C
w
p
=
.
(41)
Ostatecznie równanie 41 przyjmuje postać:
C
w
p
R
= 2
3
.
(42)
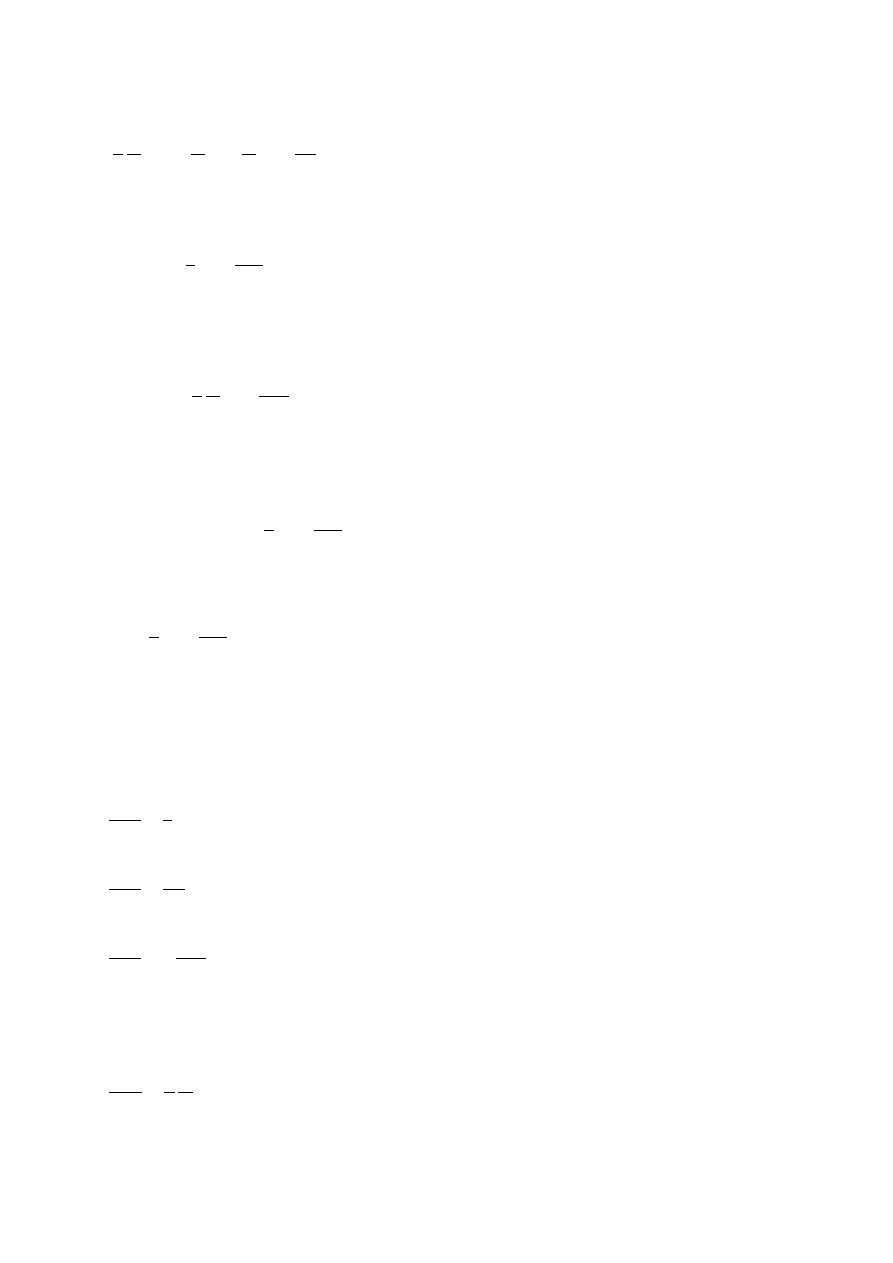
18
Podstawiając równanie 42 do równania 36, otrzymujemy:
2
3
w
p
R
w
p
R w
p
N
M
p
= −
+
+
.
(43)
Po przekształceniach równania 43 otrzymujemy optymalny poziom czasu wolnego:
R R
N
M
w
E
=
=
+
3
5
3
5
.
(44)
Po podstawieniu równania 44 do równania 36 otrzymujemy optymalny poziom kon-
sumpcji:
C C
w
p
N
M
w
E
=
=
+
2
5
2
5
.
(45)
Wiadomo, że N = L + R, a zatem w punkcie optimum również zachodzi ta zależność.
Optymalna wielkość podaży pracy L
E
wynosi zatem:
L
N
R
N
N
M
w
E
E
=
−
=
−
+
3
5
3
5
.
(46)
Po przekształceniach równania 46 otrzymujemy optymalną wielkość podaży pracy:
L
N
M
w
E
=
−
2
5
3
5
.
(46)
Z równania 44 wynika, że optymalna ilość czasu wolnego jest rosnącą funkcją zasobu
czasu N i dochodów pozapłacowych oraz malejącą funkcją stawki płac nominalnych. Po-
twierdzeniem tych zależności są dodatnie wartości pochodnych R
E
względem N i M oraz
ujemna wartość pochodnej R
E
względem w:
∂
∂
= >
R
N
E
3
5
0
(47a)
∂
∂
=
>
R
M
w
E
3
5
0
(47b)
∂
∂
= −
<
R
w
M
w
E
3
5
0
2
(47c)
Z równania 45 wynika, że optymalna wielkość konsumpcji zależy od parametrów N, M
oraz w. Monotoniczność C
E
względem poszczególnych wielkości opisują równania 48a–48c.
∂
∂
=
>
C
N
w
p
E
2
5
0
(48a)
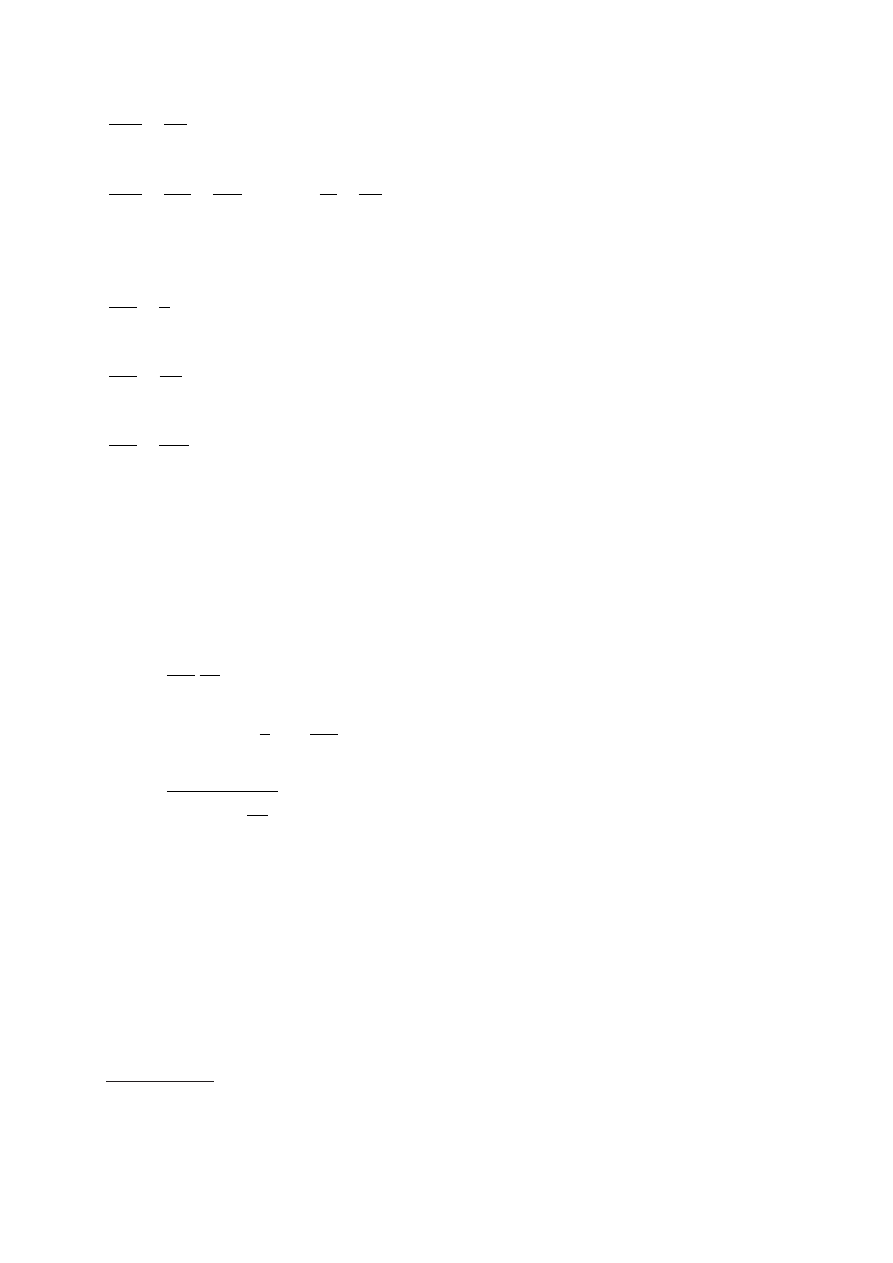
19
∂
∂
=
>
C
M
w
E
2
5
0
(48b)
∂
∂
=
−
>
>
C
w
N
p
M
w
N
p
E
2
5
2
5
0
2
dla
M
w
2
(48c)
Różniczkując równanie 46 względem N, M oraz w otrzymujemy:
∂
∂
=
>
L
N
E
2
5
0
(49a)
∂
∂
=
−
<
L
M
w
E
3
5
0
(49b)
∂
∂
=
>
L
w
M
w
E
3
5
0
2
(49c)
Dodatni znak pochodnej 49a oznacza, że wzrost (spadek) N powoduje wzrost (spadek)
podaży pracy. Ujemny znak pochodnej 49b oznacza z kolei, że wzrost dochodów pozapła-
cowych prowadzi do spadku podaży pracy. Z równania 49c wynika, że podaż pracy jest
rosnącą funkcją stawki płac nominalnych.
Elastyczność funkcji podaży pracy względem stawki płac nominalnych
możemy
obliczyć ze wzoru
13
:
E
L
w
w
L
L w
E
E
E
,
.
=
∂
∂
(50)
Dla funkcji
L
N
M
w
E
=
−
2
5
3
5
elastyczność podaży pracy względem stawki płac wynosi:
E
M
w N
M
w
L w
E
,
0.
=
−
≥
3
2
3
(51)
13
Elastyczność podaży pracy względem stawki płac nominalnych to stosunek procentowej zmiany
podaży pracy do procentowej zmiany płac. Informuje ona, o ile procent wzrośnie podaż pracy, jeśli staw-
ka płac nominalnych wzrośnie np. o 1%.
20
Bibliografia
Tokarski T., 2011, Ekonomia matematyczna. Modele mikroekonomiczne, rozdz. 2 i 3, PTE, Warszawa.