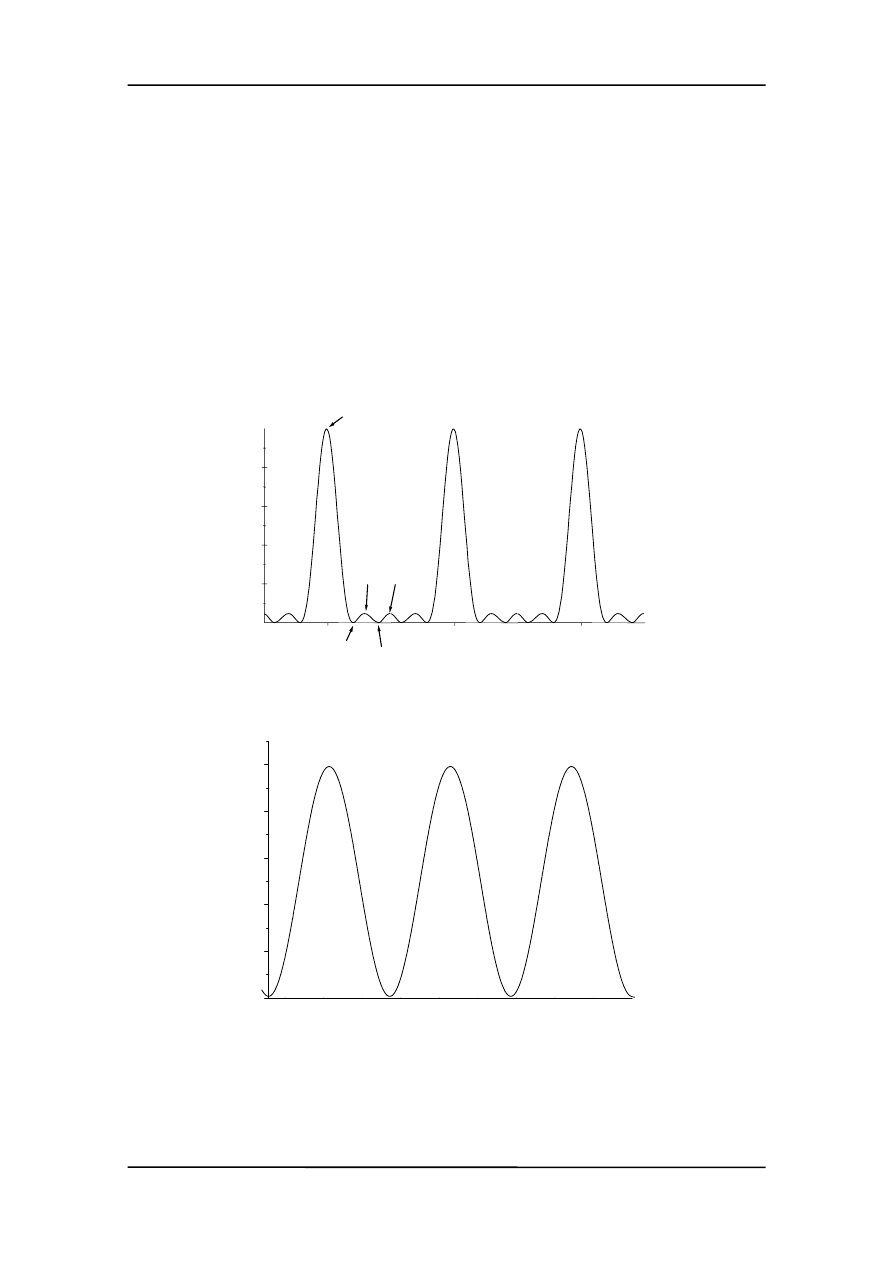
Z. Kąkol-Notatki do Wykładu z Fizyki
Wykład 30
30. Siatki dyfrakcyjne
30.1 Siatki dyfrakcyjne
Rozpatrzymy teraz przypadki gdy liczba centrów rozpraszania jest większa. Tzn.
rozpatrzmy naturalne rozszerzenie doświadczenia Younga poprzez zwiększenie liczby
szczelin od dwu do większej liczby N.
Układ zawierający zespół N równoległych szczelin nazywamy
siatką dyfrakcyjną
(szczelin może być b. dużo np. 10
4
/cm).
Na rysunku poniżej pokazany jest rozkład natężeń dla N = 5 szczelin.
e
d
c
b
a
N = 5
0.2
0.4
0.6
0.8
Dla przypomnienia poniżej pokazano wynik w doświadczeniu Younga.
0.0
0.2
0.4
0.6
0.8
1.0
Z tych rysunków widać, że zwiększenie liczby szczelin
• nie zmienia odległości pomiędzy głównymi maksimami (przy stałych d i
λ)
• nastąpiło natomiast ich zwężenie (wyostrzenie)
• pojawiły się wtórne maksima pomiędzy maksimami bocznymi
Maksima główne wystąpią gdy spełniony jest znany warunek
30-1
Z. Kąkol-Notatki do Wykładu z Fizyki
dsin
θ = mλ, m = 0, 1, 2, (maksima)
(30.1)
gdzie m nazywamy rzędem widma, a d jest odległością między szczelinami (stała siatki
dyfrakcyjnej).
Uwaga: Położenia maksimów głównych nie zależą od N.
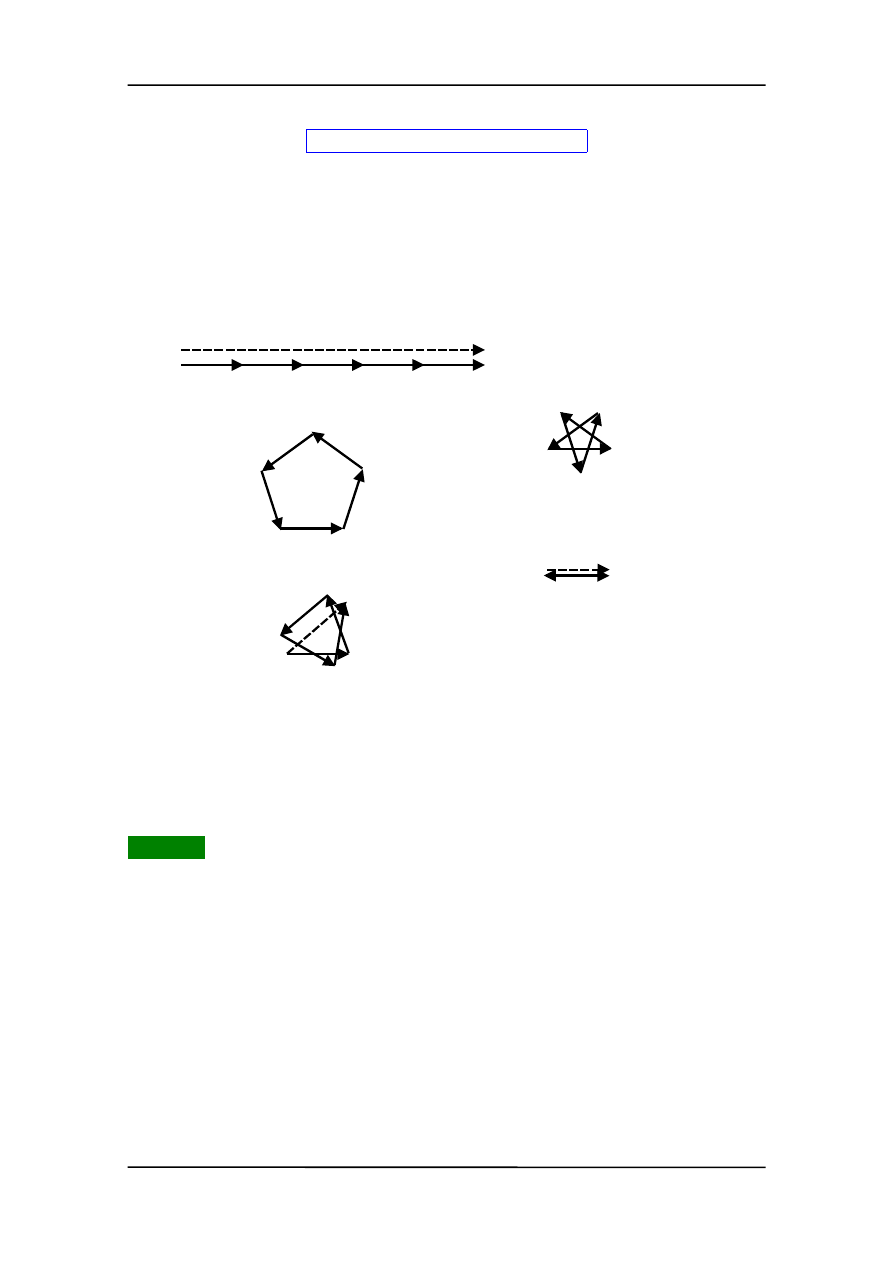
Pochodzenia maksimów wtórnych można wyjaśnić za pomocą metody strzałek fazo-
wych (wskazów).
a)
b)
c)
d)
e)
ϕ = 0
ϕ = 72°
ϕ = 110°
ϕ = 144°
ϕ = 180°
E
θ
E
θ
= 0
E
θ
E
θ
E
θ
= 0
Siatki dyfrakcyjne są często stosowane do
pomiarów długości fali i do badań struktury i
natężenia linii widmowych
.
• Ponieważ stałą siatki dyfrakcyjnej można zmierzyć dokładnie pod mikroskopem to z
warunku na występowanie głównych maksimów możemy wyznaczyć
λ.
• Z tego samego warunku widać, że fale o różnych
λ uginają się pod różnymi kątami
jest więc szansa na ich rozseparowanie.
Przykład 1
Siatka dyfrakcyjna ma 4000 nacięć na 1 cm. Pada na nią prostopadle światło żółte z
lampy sodowej. W świetle tym występują dwie fale o długościach 589.00 i 589.59 nm.
Pod jakim kątem występuje maksimum dla pierwszego rzędu dla 1 z tych linii? Jaka jest
odległość kątowa pomiędzy maksimami pierwszego rzędu dla tych linii?
Maksimum pierwszego rzędu otrzymujemy z warunku
dsin
θ = mλ
dla m = 1
sin
θ = λ/d = 0.236
θ = 13.6°
30-2
Z. Kąkol-Notatki do Wykładu z Fizyki
Najprostszym sposobem znalezienia odległości kątowej jest powtórzenie obliczeń dla
λ = 589.59 i odjęcie obliczonych kątów ale trzeba prowadzić bardzo precyzyjne obli-
czenia tzn. dla wielu liczb znaczących (nie tak jak powyżej).
Powtarzamy obliczenia
dla
λ = 589.00 nm θ = 13.6270°
dla
λ = 589.59 nm θ = 13.6409°
stąd
∆
θ = 0.0139°
Możemy jednak przeprowadzić bezpośrednie obliczenia tej różnicy.
W tym celu zróżniczkujemy nasze równanie
λ
λ
λ
θ
θ
θ
d
d
d
d
d
)
(sin
d
=
d
m
Otrzymujemy wtedy
λ
θ
θ
d
cos
d
m
d
=
Ponieważ długości fal mało się różnią więc możemy zapisać
λ
θ
θ
∆
=
∆
d
m
cos
skąd mamy
θ
λ
θ
cos
∆
=
∆
m
Oczywiście otrzymujemy ten sam wynik ale obliczenia wymagają tylko 2 cyfr znaczą-
cych zamiast 5 (jak
λ).
Wielkość
θ
λ
θ
cos
d
d
d
m
D
=
=
jest nazywana
dyspersją kątową
siatki dyfrakcyjnej i in-
formuje o odległości kątowej (rozdzieleniu) dwóch fal o mało różniących się długo-
ściach.
30.2 Dyfrakcja promieni Roentgena (promieni X)
Promienie X są falami elektromagnetycznymi o długościach fal rzędu 0.1 nm.
(Dla przypomnienia światło żółte z przykładu 1 ma długość równą 589 nm.)
W 1912 r. Max von Laue zauważył, że ciała stałe zawierające regularny układ atomów
mogą stanowić naturalną, trójwymiarową „siatkę dyfrakcyjną” dla promieniowania X.
(Standardowe optyczne siatki dyfrakcyjne są bezużyteczne bo
λ << d.).
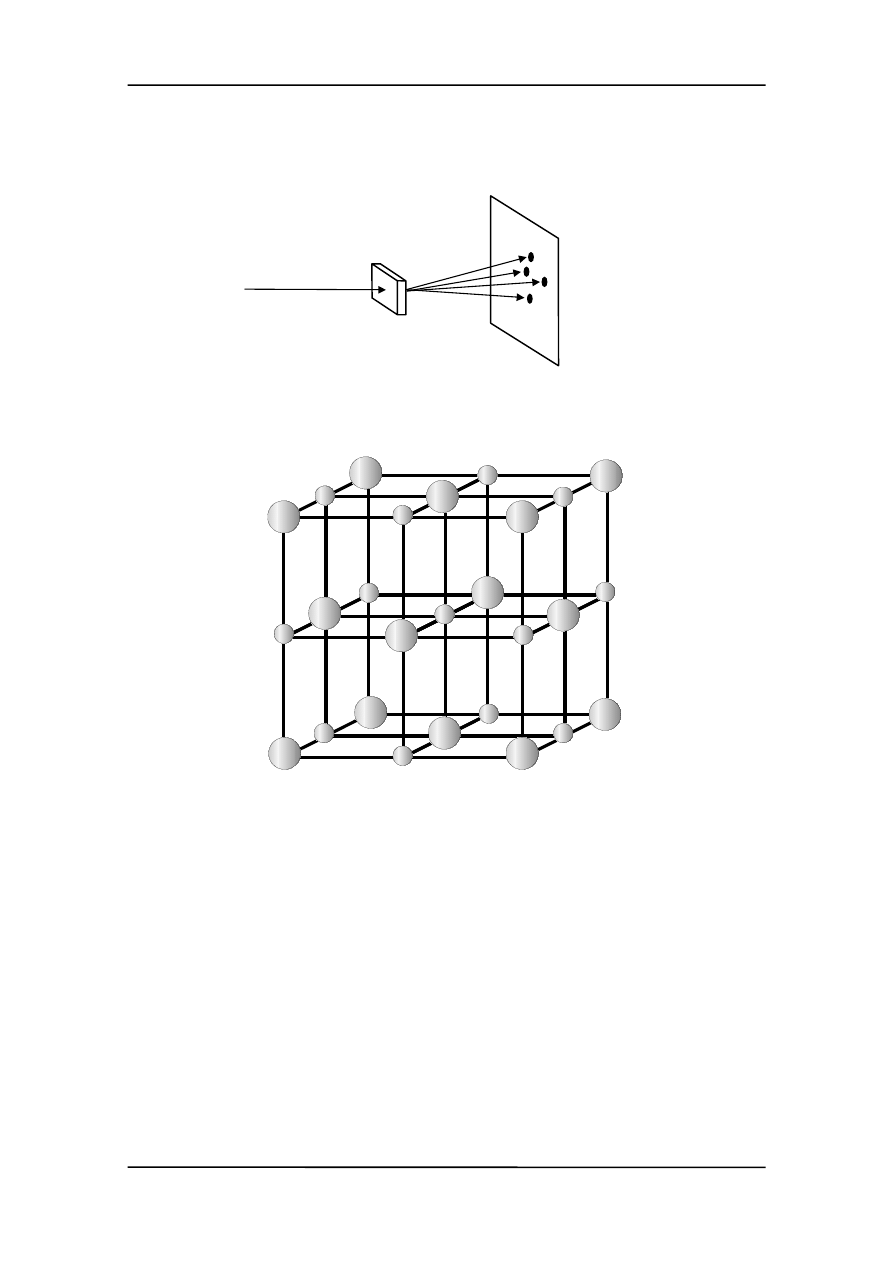
Rysunek
poniżej pokazuje wiązkę promieni X, o widmie ciągłym, padającą na
kryształ. Wiązki promieni powstałe w wyniku interferencji fal ugiętych na atomach pa-
30-3
Z. Kąkol-Notatki do Wykładu z Fizyki
dają na kliszę tworząc na niej charakterystyczny układ punktów zwany
obrazem Lau-
ego
. Analiza położeń i natężeń tych punktów pozwala na określenie struktury kryształu.
wi¹ zka prom. X
kryszta³
wi¹ zki
ugiête
obraz
Lauego
Na kolejnym rysunku pokazana jest komórka elementarna kryształu NaCl.
Małe kule przedstawiają jony sodu, a duże jony chloru.
Jest to najmniejsza jednostka, z której można zbudować kryształ (cegiełka) poprzez do-
dawanie jej (powielanie) w trzech prostopadłych kierunkach.
Każda komórka elementarna NaCl zawiera 4 jony sodu i cztery jony chloru czyli cztery
cząsteczki NaCl (poza jonem w środku, pozostałe należą też do komórek sąsiednich).
Dla NaCl długość boku komórki elementarnej wynosi 0.562737 nm (porównać z długo-
ścią fali promieniowania X).
Natężenia linii siatki dyfrakcyjnej zależą od geometrii pojedynczej szczeliny. W ideal-
nym przypadku zależą od szerokości szczeliny.
Tak samo natężenia wiązek rozproszonych na krysztale zależą od geometrii pojedynczej
rozpraszającej komórki elementarnej.
30-4
Z. Kąkol-Notatki do Wykładu z Fizyki
30.3 Prawo Bragga
Prawo Bragga podaje warunki, w jakich jest możliwa dyfrakcja promieni Roentgena
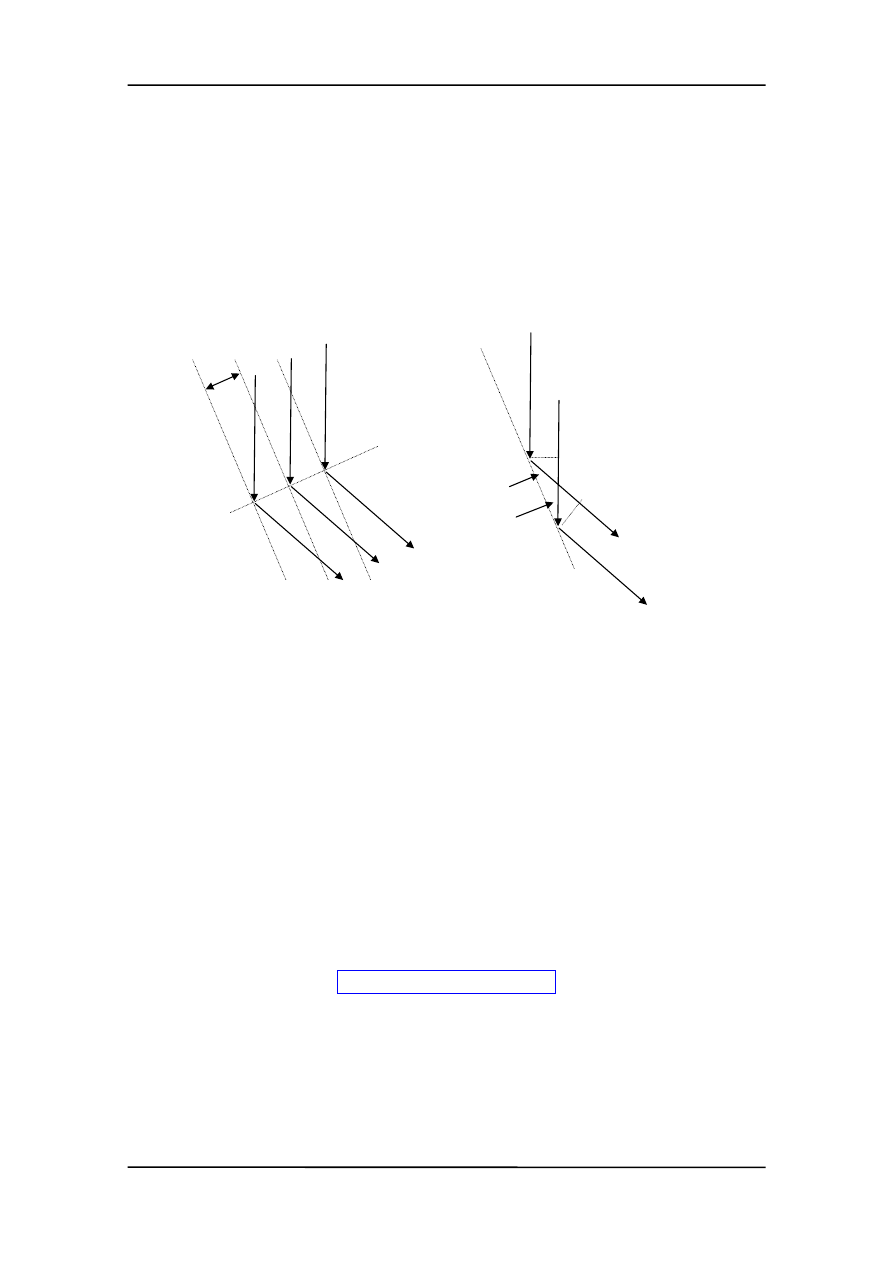
krysztale. Rysunek poniżej pokazuje ugięcie wiązki promieni X na zespole równole-
głych płaszczyzn (linie przerywane). Odległość między płaszczyznami wynosi d.
W krysztale można wybrać wiele różnych rodzin płaszczyzn o różnych odległościach
międzypłaszczyznowych.
Rysunek (a) pokazuje falę oddziałującą z rodziną płaszczyzn, z których jedna jest poka-
zana na rysunku (b).
fala
padająca
fala
padająca
fala
ugięta
fala
ugięta
a
a’
b’
b
β
θ
d
a)
b)
Ugięcie następuje na elementarnych centrach rozpraszania (komórki elementarne - od-
powiednik pojedynczej szczeliny).
Promienie ugięte będą się sumować gdy różnica dróg będzie równa całkowitej wielo-
krotności długości fali.
ab’ – a’b = ab(cos
β − cosθ) = kλ, k = 0, 1, 2,
Dla k = 0 otrzymujemy
β = θ tzn. płaszczyzna wyznaczona przez atomy działa jak
„zwierciadło” odbijające falę padającą (kąt padania = kąt odbicia) tzn. w tym kierunku
jest wzmocnienie promieniowania ugiętego.
Jeżeli chcemy otrzymać wzmocnienie promieniowania odbitego od całej rodziny płasz-
czyzn dla kierunku określonego przez kąt
θ to muszą się wzmacniać promienie odbite
od poszczególnych płaszczyzn. Oznacza to, że różnica dróg dla promieni odbitych od
sąsiednich płaszczyzn musi być równa całkowitej wielokrotności
λ, tak więc
2dsin
θ = mλ, m = 1, 2, 3,....
Zależność ta została podana przez W. L. Bragga i stąd nazwa
prawo Bragga
.
W równaniu tym d oznacza odległość między sąsiednimi płaszczyznami.
Stąd widać, że dyfrakcja promieni X jest metodą doświadczalną w badaniu rozmiesz-
czenia atomów w kryształach.
Aby otrzymać wyniki ilościowe trzeba znać długość fali promieniowania X.
30-5
Wyszukiwarka
Podobne podstrony:
Fizyka Kakol wyklad 17 id 176833
Fizyka Kakol wyklad 13 id 176831
Fizyka Kakol wyklad 14 id 176832
Fizyka Kakol wyklad 24 id 176836
Fizyka Kakol wyklad 37 id 176843
Fizyka Kakol wyklad 22 id 176835
Fizyka Kakol wyklad 26 id 176837
Fizyka Kakol wyklad 8 id 176845
więcej podobnych podstron