Z. Kąkol-Notatki do Wykładu z Fizyki

Wykład 13

13. Ruch drgający

Ruch, który powtarza się w regularnych odstępach czasu, nazywamy

ruchem okre-

sowym

(periodycznym). Przemieszczenie cząstki w ruchu periodycznym można wyrazić

za pomocą funkcji sinus i cosinus. Ruch sinusoidalny jest powszechną formą ruchu ob-
serwowaną w życiu codziennym i dlatego jest ważnym przedmiotem fizyki.

13.1 Siła harmoniczna

Działającą na ciało siłę, która jest proporcjonalna do przesunięcia ciała od początku

układu i która jest skierowana ku początkowi układu, nazywamy

siłą harmoniczną

lub

siłą sprężystości

. Jeżeli obierzemy oś x wzdłuż przesunięcia, to siła harmoniczna jest

wyrażona równaniem

F = – kx

(13.1)

gdzie x jest przesunięciem od położenia równowagi. To równanie opisuje siłę wywiera-
ną przez rozciągniętą sprężynę o ile tylko sprężyna nie została rozciągnięta poza granicę
sprężystości. To jest prawo Hooke'a.

Jeżeli sprężyna zostanie rozciągnięta tak aby masa m (zaczepiona do sprężyny) zna-

lazła się w położeniu x = A, a następnie w chwili t = 0 została zwolniona, to położenie
masy w funkcji czasu będzie dane równaniem

x = Acos

ωt

Sprawdźmy czy to jest dobry opis ruchu. Dla t = 0, x = A tzn. opis zgadza się z założe-
niami. Z drugiej zasady dynamiki Newtona wynika, że

– kx = ma

czyli

– kx = m(d

v

/dt)

wreszcie

–

kx = m(d

2

x/dt

2

)

(13.2)

Równanie takie nazywa się równaniem różniczkowym drugiego rzędu. Staramy się
"odgadnąć" rozwiązanie i następnie sprawdzić nasze przypuszczenia. Zwróćmy uwagę,
że rozwiązaniem jest funkcja x(t), która ma tę właściwość, że jej druga pochodna jest
równa funkcji ale ze znakiem "–". Zgadujemy, że może to być funkcja x = Acos

ωt

i sprawdzamy

dx/dt =

v

= – A

ωsinωt

(13.3)

d

2

x/dt

2

= a = – A

ω

2

cos

ωt

(13.4)

13-1

Z. Kąkol-Notatki do Wykładu z Fizyki

Podstawiamy ten wynik do równania (13.2)

(– kAcos

ωt) = m(– Aω

2

cos

ωt)

i otrzymujemy

ω

2

= k/m

(13.5)

Widzimy, że x = Acos

ωt jest rozwiązaniem równania (13.2) ale tylko gdy

m

k /

=

ω

.

Zwróćmy uwagę, że funkcja x = Asin

ωt jest również rozwiązaniem równania ale nie

spełnia warunku początkowego bo gdy t = 0 to x = 0 (zamiast x = A).
Najogólniejszym rozwiązaniem jest

x = Asin(

ωt + ϕ)

(13.6)

gdzie

ϕ jest dowolną stałą fazową. Stałe A i ϕ są określone przez warunki początkowe.

Wartości maksymalne (amplitudy) odpowiednich wielkości wynoszą:
• dla wychylenia A
• dla prędkości

ωA (występuje gdy x = 0)

• dla przyspieszenia

ω

2

A (występuje gdy x = A)

13.2 Okres

drgań

Funkcja cos

ωt lub sinωt powtarza się po czasie T dla którego ωT = 2π. Ta szczegól-

na wartość czasu jest zdefiniowana jako okres T

T = 2

π/ω

(13.7)

Liczba drgań w czasie t jest równa

n = t/T

Gdy podzielimy obie strony przez t, otrzymamy liczbę drgań w jednostce czasu

T

t

n

1

=

Lewa strona równania jest z definicji częstotliwością drgań f

T

f

1

=

Dla ruchu harmonicznego

ω = k m

/

więc otrzymujemy

k

m

T

π

2

=

(13.8)

13-2

Z. Kąkol-Notatki do Wykładu z Fizyki

Jest to okres drgań masy m przyczepionej do końca sprężyny o stałej sprężystości k.

Przykład 1

Dwie masy, m

1

i m

2

, są przyczepione do przeciwnych końców sprężyny. Jaki będzie

okres drgań, gdy rozciągniemy sprężynę, a następnie zwolnimy obie masy jednocze-
śnie? Stała sprężyny wynosi k.
Niech x

1

będzie przesunięciem masy m

1

od położenia równowagi, a x

2

odpowiednim

przesunięciem masy m

2

. Zauważmy, że środek masy musi pozostawać nieruchomy.

Zatem

m

1

x

1

= – m

2

x

2

, czyli

2

1

2

1

x

m

m

x

−

=

Zastosujmy teraz do wybranej masy np. m

2

równanie F

wypadkowa

= ma. Siłą wypadkową,

działającą na m

2

jest siła F = – k (x

2

– x

1

) gdzie (x

2

– x

1

) jest wypadkowym rozciągnię-

ciem sprężyny.

2

2

2

2

1

2

d

d

)

(

t

x

m

x

x

k

=

−

−

Podstawiamy teraz

2

1

2

1

x

m

m

x

−

=

zamiast x

1

i otrzymujemy

2

2

2

2

2

1

2

2

d

d

t

x

m

x

m

m

x

k

=

























−

−

−

czyli

2

2

1

2

1

2

2

2

)

(

d

d

x

m

m

m

m

k

t

x

+

−

=

więc

2

2

2

2

d

d

x

k

t

x

µ

−

=

gdzie

µ = m

1

m

2

/(m

1

+ m

2

) jest z definicji

masą zredukowaną

. To jest równanie jakie już

rozwiązywaliśmy, w którym zamiast x jest x

2

a zamiast m jest

µ.

Tak więc

µ

ω

/

k

=

czyli

k

T

µ

π

2

=

Zwróćmy uwagę, że

okres drgań harmonicznych T jest niezależny od amplitudy drgań A

(o ile jest spełnione prawo Hooke'a). Tę właściwość drgań harmonicznych prostych za-
uważył Galileusz i wykorzystał ją do skonstruowania zegara wahadłowego.

13-3

Z. Kąkol-Notatki do Wykładu z Fizyki

13.3 Wahadła

13.3.1 Wahadło proste

Wahadło proste jest to wyidealizowane ciało o masie punktowej, zawieszone na

cienkiej, nieważkiej, nierozciągliwej nici. Kiedy ciało wytrącimy z równowagi to za-
czyna się ono wahać w płaszczyźnie poziomej pod wpływem siły ciężkości. Jest to ruch
okresowy. Znajdźmy okres tego ruchu.

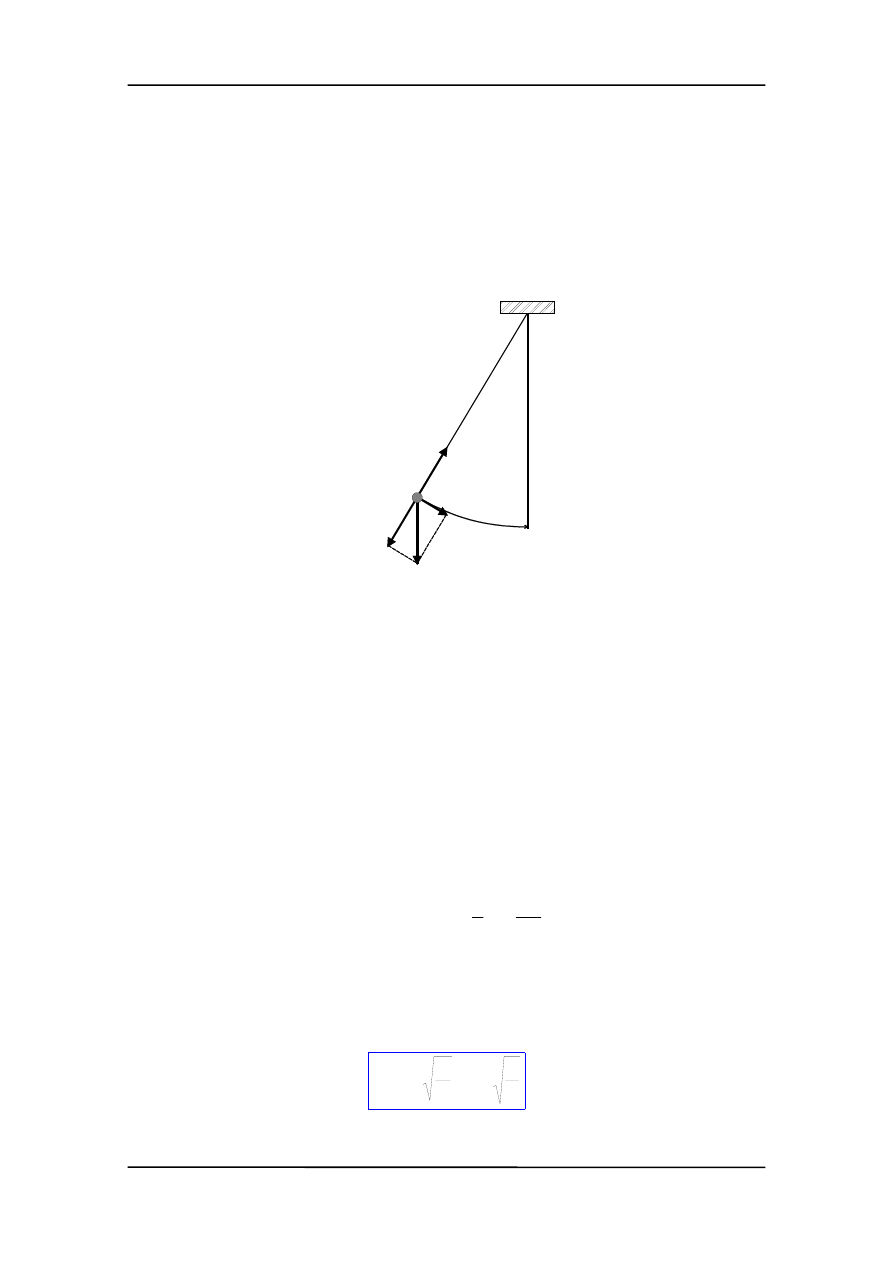
θ

l

N

mg

mgcos

θ

mgsin

θ

x=l

θ

θ

m

Rysunek przedstawia wahadło o długości l i masie m, odchylone o kąt

θ od pionu.

Na masę m działają: siła przyciągania grawitacyjnego mg i naprężenia nici N. Siłę mg
rozkładamy na składową radialną i styczną. Składowa styczna jest siłą przywracającą
równowagę układu i sprowadza masę m do położenia równowagi. Siła ta wynosi

F = mgsin

θ

Podkreślmy, że siła jest proporcjonalna do sin

θ, a nie do θ, więc nie jest to ruch prosty

harmoniczny. Jeżeli jednak kąt

θ jest mały (mniejszy niż 10°) to sinθ jest bardzo bliski

θ (różnica mniejsza niż 0.5%). Przemieszczenie wzdłuż łuku (z miary łukowej kąta)
wynosi x = l

θ. Przyjmując zatem, że sinθ ≅ θ otrzymujemy

x

l

mg

l

x

mg

mg

F

−

=

−

=

−

=

θ

F jest więc proporcjonalna do przemieszczenia (ze znakiem "–"). Jest to kryterium ru-
chu harmonicznego. Stała mg/l określa stałą k w równaniu F = – kx. Przy małej ampli-
tudzie okres wahadła prostego wynosi więc

g

l

k

m

T

π

π

2

2

=

=

(13.9)

Zauważmy, że okres wahadła nie zależy od amplitudy i od masy wahadła.

13-4

Z. Kąkol-Notatki do Wykładu z Fizyki

13.3.2 Wahadło fizyczne

Dowolne ciało sztywne zawieszone tak, że może się wahać wokół pewnej osi prze-

chodzącej przez to ciało nazywamy wahadłem fizycznym.

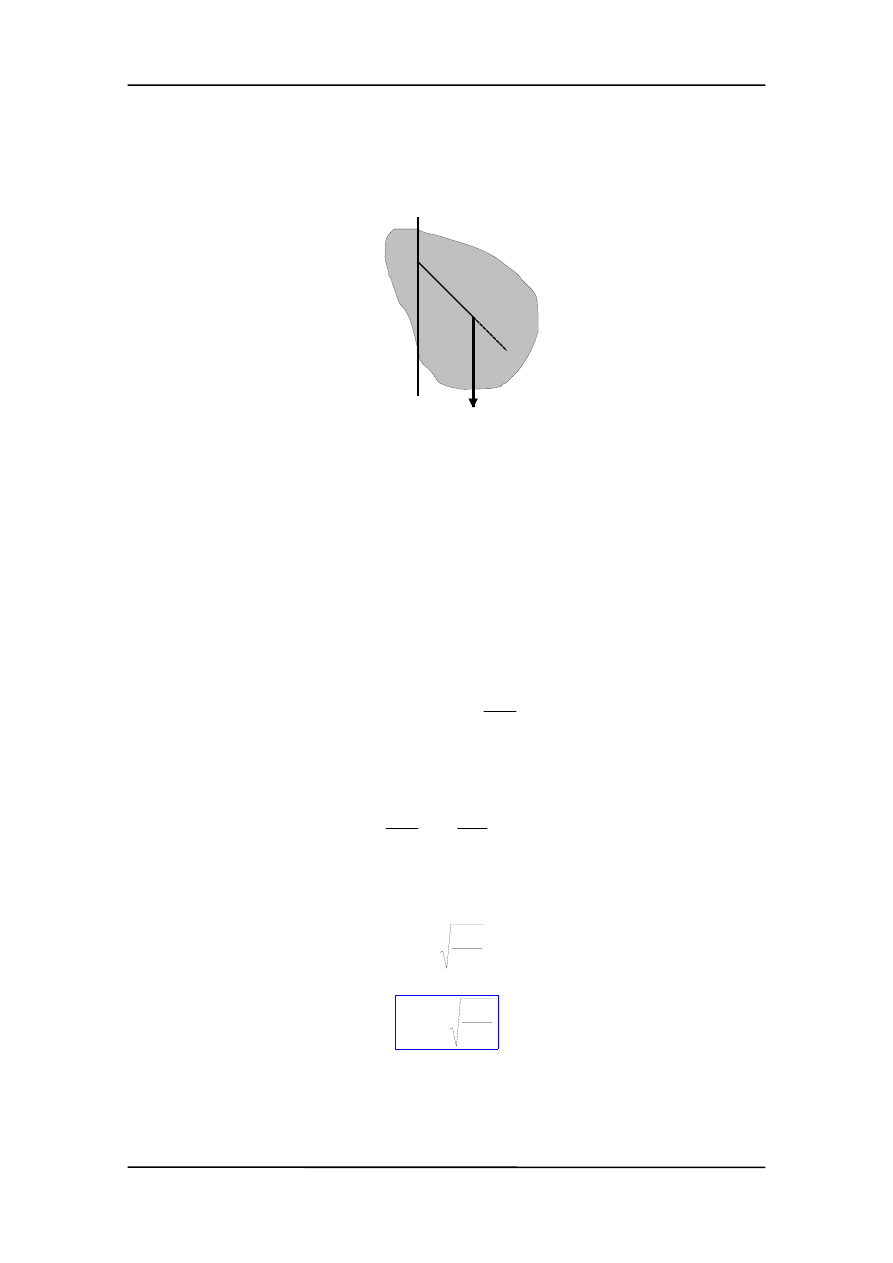
l

mg

P

S

θ

P jest punktem zawieszenia ciała, a punkt S, znajdujący się w odległości l od punkt P,
jest środkiem masy. Moment siły

τ działający na ciało wynosi

τ = – mglsinθ

Korzystając ze związku

τ = Iα =I(d

2

θ /dt

2

)

otrzymujemy

2

2

d

d

sin

t

I

mgl

θ

θ =

−

Dla małych wychyleń, dla których sin

θ ≅ θ dostajemy równanie

θ

θ













−

=

I

mgl

t

2

2

d

d

To równanie ma tę samą postać co równanie dla ruchu harmonicznego więc

I

mgl

=

ω

lub

mgl

I

T

π

2

=

(13.10)

Jako przypadek szczególny rozpatrzmy masę punktową zawieszoną na nici o długości l.
Wówczas I = ml

2

i otrzymujemy znany wzór dla wahadła prostego

13-5

Z. Kąkol-Notatki do Wykładu z Fizyki

g

l

T

π

2

=

Wahadło fizyczne stosuje się do precyzyjnych pomiarów przyspieszenia g.

13.4 Energia ruchu harmonicznego prostego

Energią potencjalną sprężyny zajmowaliśmy się na wykładzie 6 przy okazji dyskusji

o pracy wykonywanej przez siły zmienne. Pokazaliśmy wtedy, że energia potencjalna
(nagromadzona) sprężyny

2

2

kx

E

p

=

(13.11)

Jeżeli masę przymocowaną do sprężyny pociągniemy na odległość x = A to energia

układu (nagromadzona w układzie) jest równa (1/2)kA

2

(E

k

= 0). Jeżeli teraz zwolnimy

sprężynę, to przy założeniu, że nie ma tarcia ani sił oporu, zgodnie z zasadą zachowania
energii w dowolnej chwili suma energii kinetycznej i potencjalnej równa się (1/2)kA

2

2

2

2

2

1

2

1

2

1

kA

kx

m

=

+

v

(13.12)

stąd

(

)

2

2

2

x

A

m

k

−

=

v

Ponieważ k/m =

ω

2

więc

2

2

x

A

−

=

ω

v

Obliczmy teraz wartości średnie czasowe) energii potencjalnej i kinetycznej. (Wartości
średnie oznaczamy kreską umieszczoną ponad symbolem.)

2

2

1

x

k

E

p

=

czyli

t

kA

E

p

ω

2

2

cos

2

1

=

Natomiast

2

2

1

v

m

E

k

=

czyli

t

kA

t

A

k

E

k

ω

ω

ω

ω

2

2

2

2

sin

2

1

)

sin

(

2

1

=

−













=

13-6

Z. Kąkol-Notatki do Wykładu z Fizyki

Wartość średnia

t

ω

2

sin

jest taka sama jak

t

ω

2

cos

i wynosi 1/2. Oba wykresy są takie

same (tylko przesunięte). Poza tym sin

2

ωt + cos

2

ωt = 1 i średnia każdego składnika jest

taka sama. Widać, że

k

p

E

E

=

(Ważne gdy będziemy omawiać ciepło właściwe.)

Przykład 2

Obliczmy jaką część energii całkowitej stanowi energia potencjalna, a jaką energia ki-
netyczna ciała, kiedy znajduje się ono w połowie drogi między położeniem początko-
wym, a położeniem równowagi?

x = A/2

więc

E

p

= kx

2

/2 = kA

2

/8

Ponieważ energia całkowita

E = kA

2

/2

więc

E

p

/E = 1/4

Ponieważ

E = E

p

+ E

k

więc

E

k

/E = 3/4

13.5 Oscylator harmoniczny tłumiony

Dotychczas pomijaliśmy fakt ewentualnego tłumienia oscylatora tzn. strat energii

układu oscylatora.
W przypadku drgań mechanicznych siłą hamującą (tłumiącą) ruch cząstki jest siła oporu
F

op

ośrodka. Siła oporu ma zwrot przeciwny do prędkości i w najprostszej postaci jest

wprost proporcjonalna do prędkości F

op

≈

v

czyli

F

op

=

γ dx/dt

(13.13)

Gdy działa tylko siła tłumienia to

t

x

t

x

M

d

d

d

d

2

2

γ

−

=

lub

13-7

Z. Kąkol-Notatki do Wykładu z Fizyki

v

v

γ

−

=

t

M

d

d

Jeżeli wprowadzimy zmienną (o wymiarze czasu)

τ = M/γ

to otrzymamy równanie

d

v

/dt = – (1/

τ)

v

co można przepisać w postaci

d

v

/

v

= – dt/

τ

Całkujemy to równanie obustronnie

∫

∫

−

=

t

v

v

t

0

d

1

d

0

τ

v

v

Skąd otrzymujemy

ln

v

- ln

v

0

= – (t/

τ)

lub

ln(

v

/

v

0

) = – (t/

τ)

a po przekształceniu

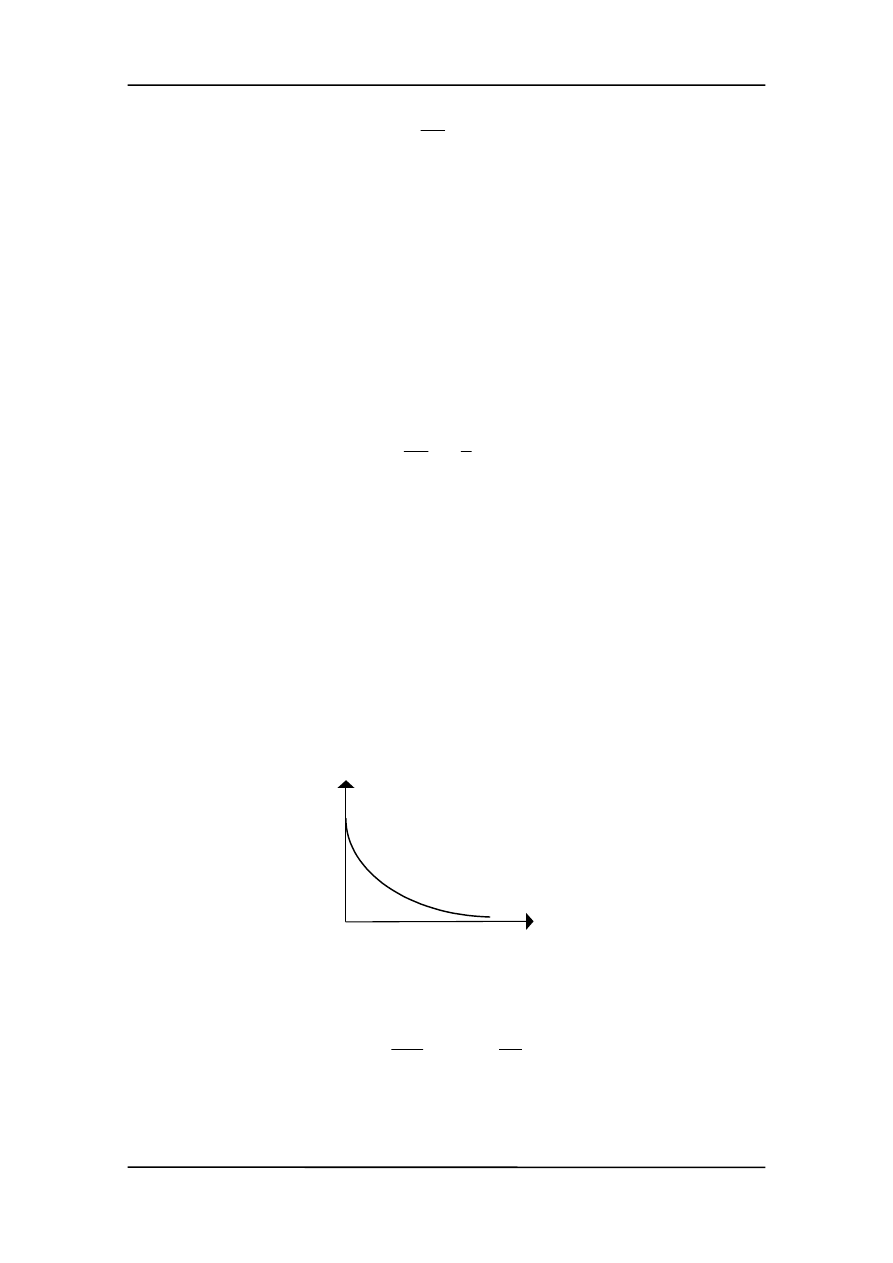
(13.14)

τ

/

0

)

(

t

e

t

−

= v

v

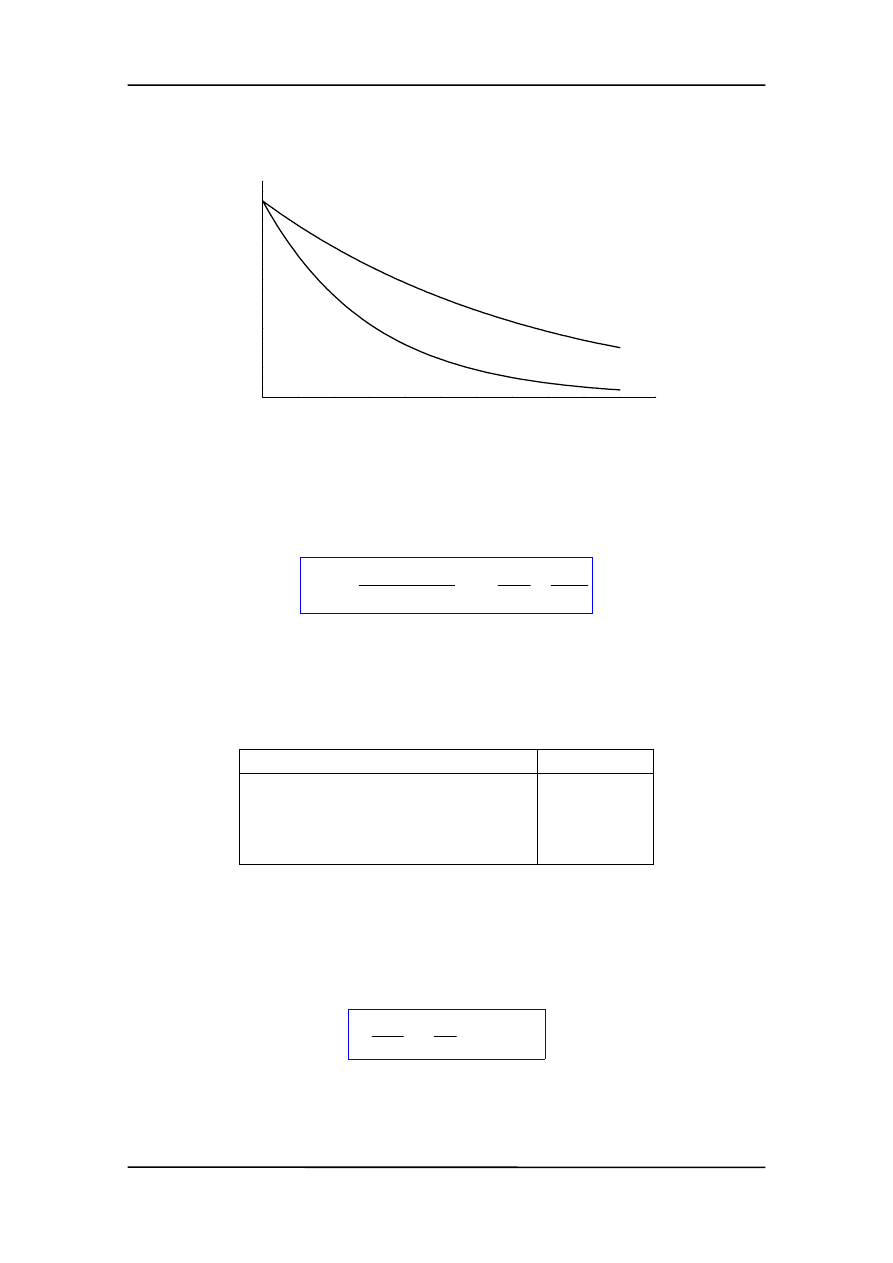
Prędkość maleje wykładniczo z czasem czyli prędkość jest tłumiona ze stałą czasową

τ

(rysunek).

v

t

Jeżeli włączymy siłę hamującą do oscylatora to wówczas równanie ruchu przyjmie po-
stać

t

x

kx

t

x

M

d

d

d

d

2

2

γ

−

−

=

Wprowadzając

τ = M/γ oraz oznaczając częstość drgań nietłumionych ω

0

2

= (k/M)

otrzymujemy

13-8

Z. Kąkol-Notatki do Wykładu z Fizyki

0

d

d

1

d

d

2

0

2

2

=

+

+

x

t

x

t

x

ω

τ

(13.15)

Szukamy rozwiązania w postaci drgań okresowo zmiennych tłumionych np.

t

e

A

x

t

ω

β

cos

−

=

(13.16)

Rozwiązanie zawiera czynnik oscylacyjny (cos

ωt) i tłumiący (exp(-βt)) i jest pokazane

na rysunku poniżej. Współczynnik

β = 1/2τ określający wielkość tłumienia nazywamy

współczynnikiem tłumienia.

Teraz obliczamy odpowiednie pochodne (13.16) i podstawiamy do równania

(13.15). W wyniku rozwiązania dostajemy warunek na częstość drgań tłumionych

2

2

0

β

ω

ω

−

=

(13.17)

Opór zmniejsza więc (oprócz amplitudy) również i częstość

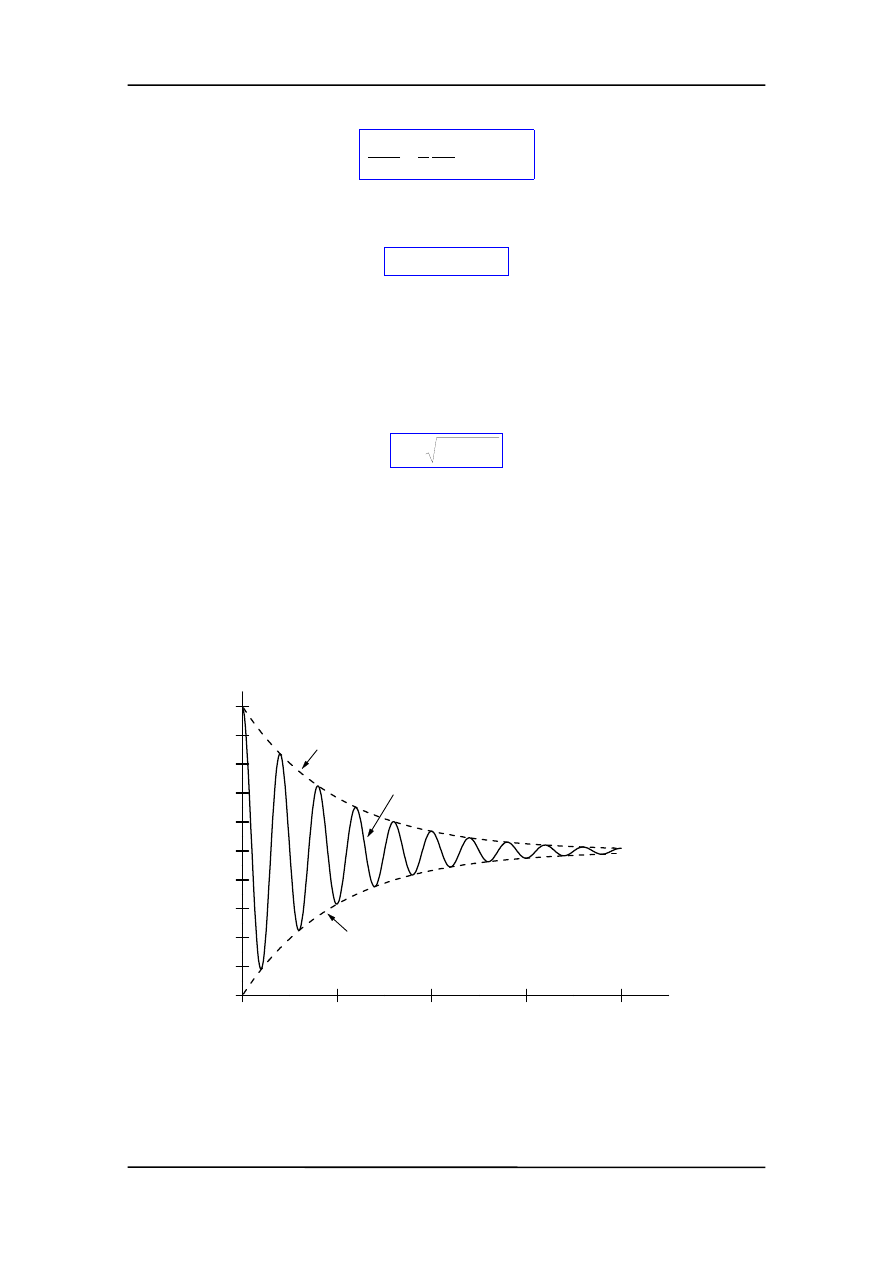
Funkcja (13.16) jest rozwiązaniem równania opisującego ruch harmoniczny tłumio-

ny przy warunku (13.17). Widzimy, że opór zmniejsza zarówno amplitudę jak i częstość
drgań, czyli powoduje spowolnienie ruchu. Wielkość tłumienia określa współczynnik
tłumienia

β (lub stała czasowa τ). Wykres ruchu harmonicznego tłumionego w zależno-

ści od czasu jest pokazany na rysunku

0

-Ae

-

β

t

Ae

-

β

t

Ae

-

β

t

cos

ω

t

-A

A

t

x

Powyższe rozważania dotyczą sytuacji "słabego tłumienia" tj.

β < ω

0

. Gdy tłumienie

wzrośnie powyżej pewnej krytycznej wartości (

β = ω

0

) ruch nie jest ruchem drgającym

ale obserwujemy, że ciało wychylone z położenia równowagi powraca do niego asymp-
totycznie. Takich ruch nazywamy ruchem pełzającym (aperiodycznym). Zależności wy-

13-9

Z. Kąkol-Notatki do Wykładu z Fizyki

chylenia od czasu dla ruchu tłumionego krytycznie (

β = ω

0

) i ruchu pełzającego

(

β > ω

0

) są pokazane na wykresie poniżej.

β

=

ω

0

β

>

ω

0

t

X

13.5.1 Straty mocy, współczynnik dobroci

Współczynnik dobroci Q jest definiowany jako

ω

π

π

/

/

2

2

1

P

E

v

P

E

E

E

Q

okresie

w

stracona

ana

zmagazynow

=

=

=

(13.18)

gdzie P jest średnią stratą mocy, a v częstotliwością.
Dla przypadku słabo tłumionego oscylatora harmonicznego (

β << ω

0

) współczynnik

Q ma w przybliżeniu wartość

ω

0

/2

β.

Kilka typowych wartości Q podano w tabeli

Oscylator Q

Ziemia dla fali sejsmicznej
Struna fortepianu lub skrzypiec
Atom wzbudzony
Jądro wzbudzone

250-400

1000

10

7

10

12

13.6 Drgania wymuszone oscylatora harmonicznego

Jeżeli oprócz tarcia istnieje siła zewnętrzna F(t) (która ma za zadanie podtrzymywać

gasnące drgania) przyłożona do oscylatora to równanie ruchu ma postać

)

(

d

d

d

d

2

2

t

F

kx

t

x

t

x

M

=

+

+

γ

(13.19)

albo po podstawieniu

τ = M/γ oraz ω

0

2

= k/M

13-10

Z. Kąkol-Notatki do Wykładu z Fizyki

otrzymujemy

M

t

F

x

t

x

t

x

)

(

d

d

1

d

d

2

0

2

2

=

+

+

ω

τ

(2.20)

Ponownie

ω

0

jest częstością własną układu, to jest częstością drgań swobodnych gdy

nie działa siła zewnętrzna i nie ma tarcia ani innych sił oporu, a

τ stałą czasową związa-

ną ze współczynnikiem tłumienia

β relacją β = 1/2τ. Zauważmy ponadto, że układ jest

zasilany z częstością

ω różną od częstości własnej ω

0

.

Gdy układ jest

zasilany częstością

ω różną od ω

0

wówczas drgania będą odbywały

się z częstością siły zewnętrznej a nie z częstością własną

. Siłę taką nazywamy

siłą wy-

muszającą

.

Załóżmy, że siła wymuszająca ma postać

t

M

t

F

M

t

F

ω

α

ω

sin

sin

)

(

0

0

=

=

(13.21)

gdzie

α

0

= F

0

/M.

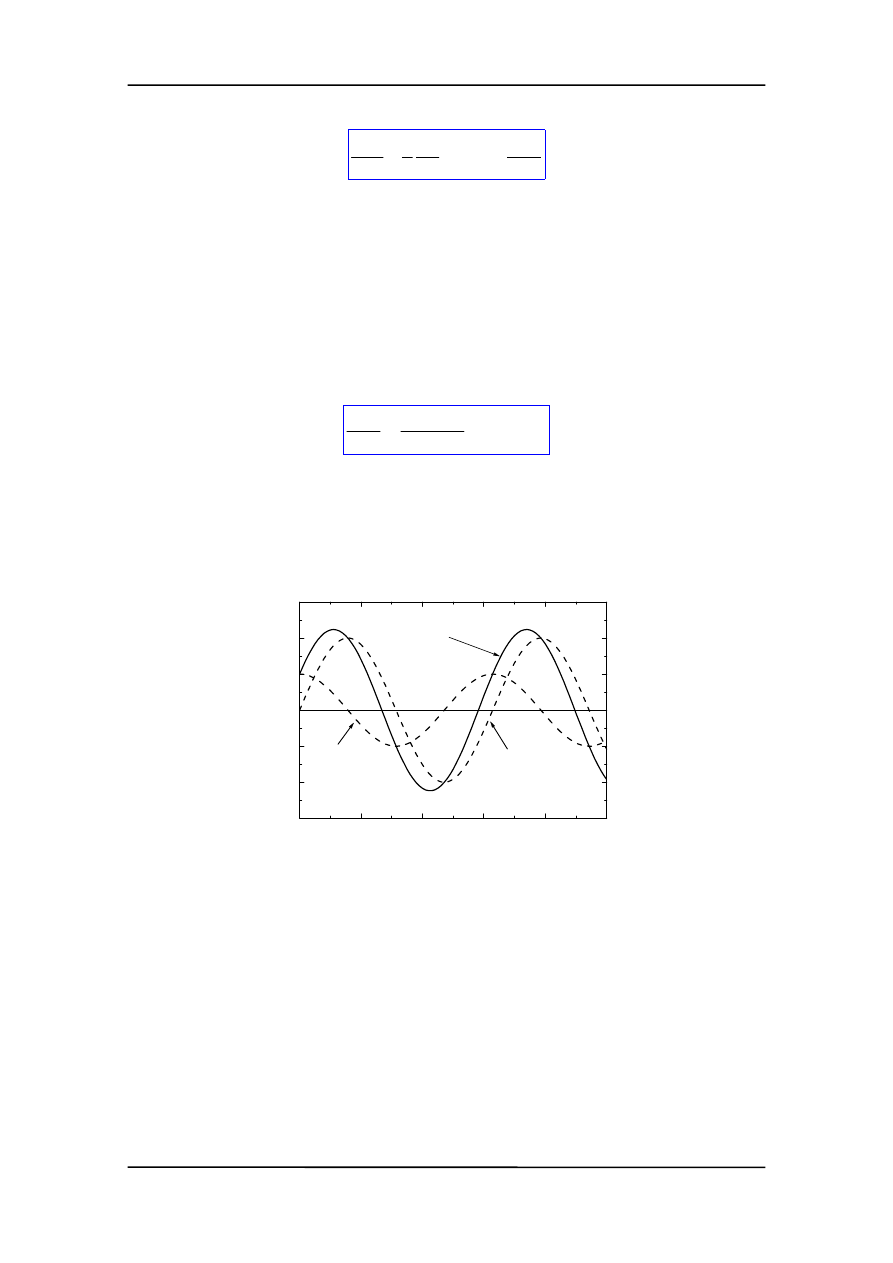
Mamy teraz w równaniu dwie wielkości okresowo zmienne położenie x oraz siłę
wymuszającą F. W najogólniejszym przypadku suma (złożenie) dwóch funkcji okreso-
wych daje w wyniku też funkcję okresową (rysunek).

A

1

cos

ω

t + A

2

sin

ω

t

A

2

sin

ω

t

A

1

cos

ω

t

A

1

cos

ωt + A

2

sin

ωt = Asin(ωt + ϕ)

Szukamy więc rozwiązania postaci Asin(

ωt + ϕ).

Musimy znaleźć amplitudę A oraz przesunięcie fazowe

ϕ.

Najpierw zdefiniujmy jednak

przesunięcie fazowe

ϕ

. Zarówno siła wymuszająca jak

i wychylenie zmieniają się cyklicznie (harmonicznie) tzn. pełny cykl np. od maksimum
do maksimum obejmuje 360

° czyli 2π.

Przesunięcie fazowe

ϕ mówi nam o jaki kąt maksimum przemieszczenia wyprzedza mak-

simum siły

(o ile przesunięte są wykresy x(t) i F(t)).

Np. siła osiąga swoje maksimum gdy przemieszczenie jest równe zeru (i rośnie w kie-
runku dodatnim). Oznacza to, że x opóźnia się względem siły o

π/2.

Poszukiwanie rozwiązania zaczynamy od obliczenia pochodnych

13-11

Z. Kąkol-Notatki do Wykładu z Fizyki

dx/dt=

ωAcos(ωt + ϕ), oraz d

2

x/dt

2

= -

ω

2

Asin(

ωt + ϕ)

Równanie ruchu ma teraz postać

(

ω

0

2

-

ω

2

) Asin(

ωt + ϕ) + (ω/τ)Acos(ωt + ϕ) = α

0

sin

ωt

Równanie to przekształcamy korzystając ze związków

sin(

ωt + ϕ) = sinωt cosϕ + cosωt sinϕ

cos(

ωt + ϕ) = cosωt cosϕ − sinωt sinϕ

Wtedy otrzymujemy

[(

ω

0

2

−

ω

2

)cos

ϕ − (ω/τ)sinϕ] Asinωt + [(ω

0

2

−

ω

2

)sin

ϕ − (ω/τ)cosϕ] Acosωt = α

0

sin

ωt

Równanie to może być tylko spełnione gdy czynniki przy sin

ωt będą sobie równe,

a czynnik przy cos

ωt będzie równy zeru. Ten ostatni warunek można zapisać jako

2

2

0

2

2

0

2

/

cos

sin

ω

ω

βω

ω

ω

τ

ω

ϕ

ϕ

ϕ

−

=

−

=

= tg

(13.22)

Z tego warunku znam już

ϕ. Teraz możemy wyznaczyć amplitudę

2

/

1

2

2

2

2

2

0

0

2

/

1

2

2

2

2

0

0

]

4

)

[(

]

)

/

(

)

[(

ω

β

ω

ω

α

τ

ω

ω

ω

α

+

−

=

+

−

=

A

(13.23)

gdzie już podstawiono za cos

ϕ i sinϕ. Łącząc wzory (13.22) i (13.23) otrzymujemy

rozwiązanie













−

+

+

−

=

2

2

0

2

/

1

2

2

2

2

2

0

0

2

sin

]

4

)

[(

ω

ω

βω

ω

ω

β

ω

ω

α

arctg

t

x

(13.24)

(Wygląda skomplikowanie ale to jest rozwiązanie postaci

x = Asin(

ωt + ϕ)

).

13.6.1 Rezonans
Zauważmy, że chociaż drgania odbywają się z częstością w siły wymuszającej to
amplituda i faza zależą od relacji pomiędzy częstością wymuszającą

ω, a częstością

własną

ω

0

. W szczególności gdy częstość siły wymuszającej osiągnie odpowiednią czę-

stotliwość, to amplituda drgań może wzrosnąć gwałtownie nawet przy niewielkiej war-
tości siły wymuszającej. Zjawisko to nazywamy

rezonansem

.

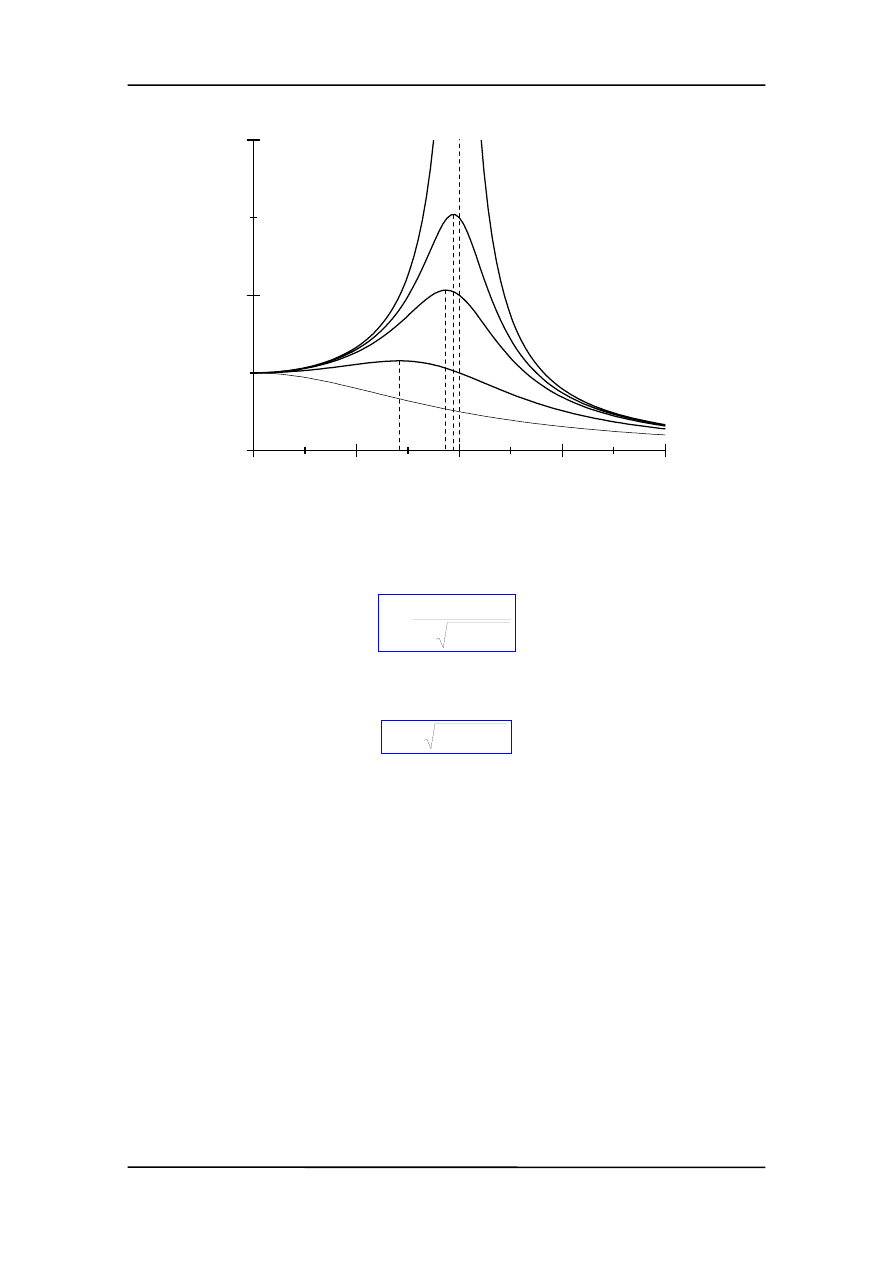
Wykres przedstawiający rezonansowy wzrost amplitudy drgań w funkcji częstości siły
wymuszającej pokazany jest na rysunku poniżej dla różnych wartości współczynnika
tłumienia

β (β

0

<

β

1

<

β

2

<

β

3

<

β

4

).

13-12

Z. Kąkol-Notatki do Wykładu z Fizyki

ω

0

A

ω

β

4

β

3

β

2

β

1

β

0

= 0

Częstość rezonansową

ω

r

i amplitudę rezonansową A

r

możemy obliczyć z warunku na

maksimum amplitudy drgań danej wzorem (13.23). Funkcja A(

ω) osiąga maksimum

2

2

0

0

2

β

ω

β

α

−

=

A

dla częstości rezonansowej

2

2

0

2

β

ω

ω

−

=

r

Widać, że im mniejsze tłumienie

β (dłuższy czas τ) tym większa amplituda A. Jeżeli

tłumienie jest słabe (

β << ω

0

) to wówczas maksymalna amplituda odpowiada częstości

drgań własnych

ω

r

=

ω

0

. Jednocześnie, ten warunek odpowiada przesunięciu fazowemu

ϕ = π/2 pomiędzy siłą a wychyleniem. Siła nie jest zgodna w fazie z wychyleniem. Za-
uważmy jednak, że moc pochłaniana przez oscylator zasilany siłą wymuszającą F zale-
ży od prędkości

P = F

v

Trzeba więc, żeby to prędkość (a nie wychylenie) była zgodna w fazie z siłą, a to ozna-
cza, że siła musi wyprzedzać wychylenie o

π/2. Gdy x = 0 to

v

=

v

max

i wtedy siła też

ma być maksymalna. W punktach zwrotnych, gdzie prędkość zmienia swój kierunek,
siła też musi zmienić swój kierunek (siła działa cały czas to nie są impulsy tak jak np.
przy popychaniu huśtawki).

Skutki rezonansu mogą być zarówno pozytywne jak i negatywne. Z jednej strony

staramy się wyeliminować przenoszenie drgań np. z silnika na elementy nadwozia w
samochodzie, a z drugiej strony działanie odbiorników radiowych i telewizyjnych jest

13-13

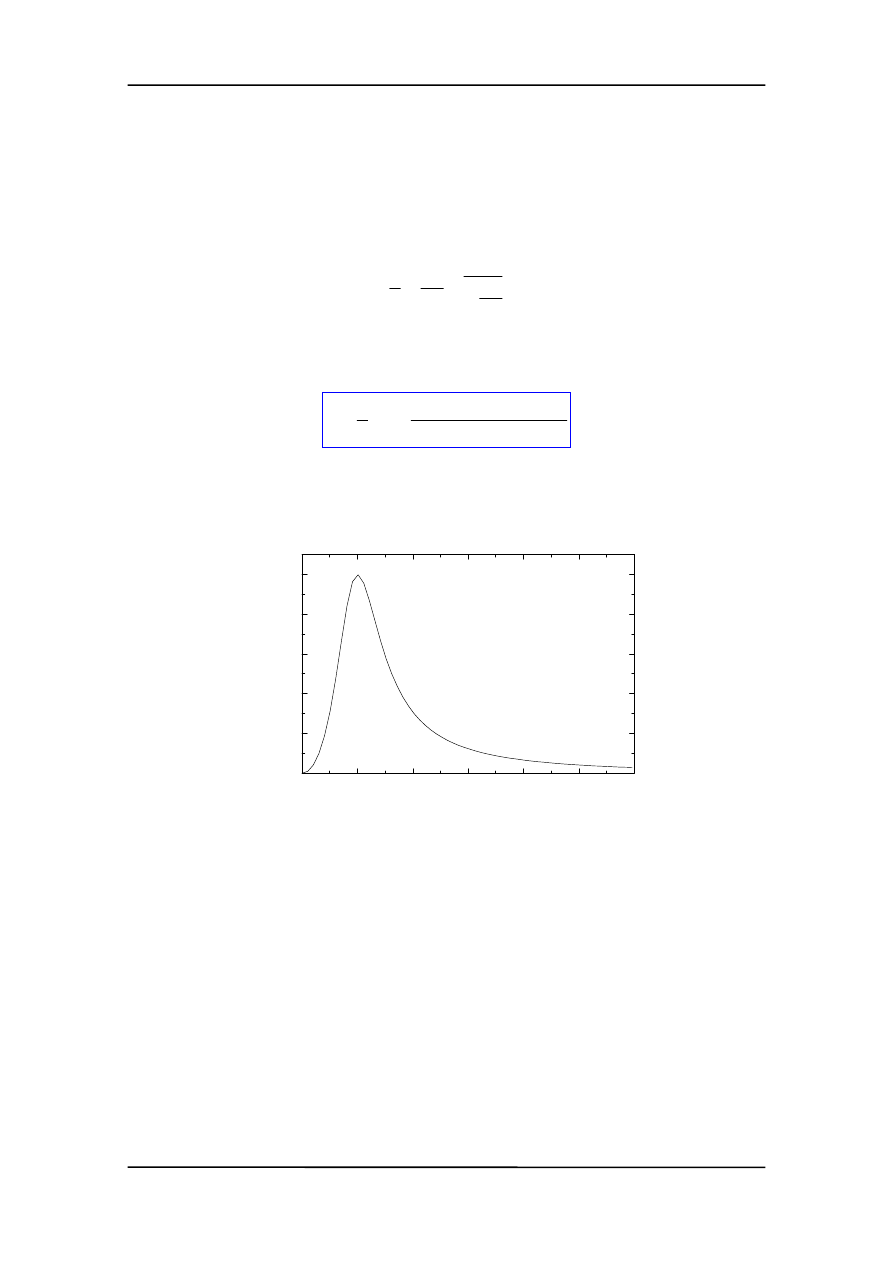
Z. Kąkol-Notatki do Wykładu z Fizyki

możliwe dzięki wykorzystaniu rezonansu elektrycznego. Dostrajając odbiornik do czę-
stości nadajnika spełniamy właśnie warunek rezonansu. Zjawisko rezonansu jest bardzo
rozpowszechnione w przyrodzie.

13.6.2 Moc absorbowana

Średnia moc absorbowana jest dana wyrażeniem

t

x

F

F

P

d

d

v =

=

Korzystając ze wzoru (13.21), (13.22) i (13.24) otrzymujemy

2

2

2

2

0

2

2

0

)

2

(

)

(

2

2

1

βω

ω

ω

βω

α

+

−

= M

P

(13.25)

Zależność mocy absorbowanej od częstości drgań wymuszających jest przedstawiona
na rysunku poniżej.

0

1

2

3

4

5

6

0.0

0.2

0.4

0.6

0.8

1.0

ω

/

ω

0

P/

P

ma

x

Dla rezonansu P = (1/2) M

α

0

2

τ . Natomiast dobroć Q = ω

0

/2

β jest miarą dostrojenia

układu do częstości wymuszającej.

13-14