
Z. Kąkol-Notatki do Wykładu z Fizyki
Wykład 17
17. Kinetyczna teoria gazów i termodynamika II
17.1 Średnia droga swobodna
Średnia droga swobodna to inaczej średnia odległość między miejscami kolejnych
zderzeń
. Zależy od rozmiarów cząsteczek i od ich liczby w jednostce objętości.
Rozpatrujemy cząstkę kulistą o średnicy d. Zderzenie będzie miało miejsce gdy odle-
głość między środkami będzie mniejsza niż d. Inaczej mówiąc cząsteczka jest "tarczą" o
powierzchni
σ = πd
2
Ta powierzchnia nosi nazwę
całkowitego przekroju czynnego
.
W czasie t cząsteczka poruszająca się z prędkością v "przemiata" objętość walca
v
t
σ.
Jeżeli n jest liczbą cząsteczek w jednostce objętości to w tym walcu nasza cząstka napo-
tka (zderzy się z)
n
z
=
v
t
σn
cząstek.
Średnia droga swobodna to średnia odległość pomiędzy punktami kolejnych zderzeń.
Jest ona równa całkowitej odległości przebywanej przez cząstkę podzielonej przez licz-
bę zderzeń
n
d
n
n
t
t
2
1
1
π
σ
σ
λ
=
=
=
v
v
(17.1)
To równanie wyprowadzono w oparciu o założenie, że cząstka zderza się z nierucho-
mymi obiektami. W rzeczywistości cząsteczki uderzają w poruszający się cel. Częstość
zderzeń jest większa, a średnia droga swobodna mniejsza
n
d
2
2
1
π
λ =
(17.2)
Zwróćmy uwagę, że wtedy w równaniu (17.1) dwie występujące tam prędkości są róż-
ne: prędkość w liczniku to prędkość średnia v cząsteczek względem naczynia, a pręd-
kość w mianowniku to średnia prędkość względna
wzgl
v
w stosunku do innych cząste-
czek. Można się przekonać jakościowo, że
wzgl
v
> v
Np. gdy cząstki biegną naprzeciw siebie to
wzgl
v
= 2v , gdy pod kątem prostym to
v
v
2
=
wzgl
, a gdy w tę samą stronę to
wzgl
v
= 0. Uwzględniając rzeczywisty rozkład
prędkości otrzymujemy
v
2
=
wzgl
v
.
Przykład 1
17-1
Z. Kąkol-Notatki do Wykładu z Fizyki
Cząstki powietrza w temperaturze 273 K i pod ciśnieniem 1 atm.
d = 2·10
-8
cm, v = 10
5
cm/s, n = 3·10
19
/cm
3
.
Wówczas średnia droga swobodna jest równa 2·10
-5
cm (około 1000d).
Odpowiednia częstość zderzeń wynosi 5·10
9
/s.
17.2 Rozkład prędkości Maxwella
Na poprzednim wykładzie omawialiśmy prędkość średnią kwadratową cząsteczek
gazu. Jednak każdy gaz ma charakterystyczny rozkład prędkości, który zależy od tem-
peratury (cząstki nie mogą mieć takich samych prędkości bo prędkości zmieniają się w
wyniku zderzeń).
Clerk Maxwell podał prawo rozkładu prędkości cząsteczek, które dla gazu zawierające-
go N cząsteczek ma postać
kT
m
e
kT
m
N
N
2
2
2
3
2
2
4
)
(
v
v
v
−
=
π
π
(17.3)
W równaniu tym N(
v
)d
v
jest liczbą cząstek o prędkościach z przedziału od
v
do
v
+
d
v
. T - temperatura bezwzględna, k - stała Boltzmana, m - masa cząsteczki.
Całkowitą liczbę cząsteczek można zatem obliczyć dodając (całkując) liczby dla po-
szczególnych różniczkowych przedziałów prędkości
∫
∞
=
0
d
)
(
v
v
N
N
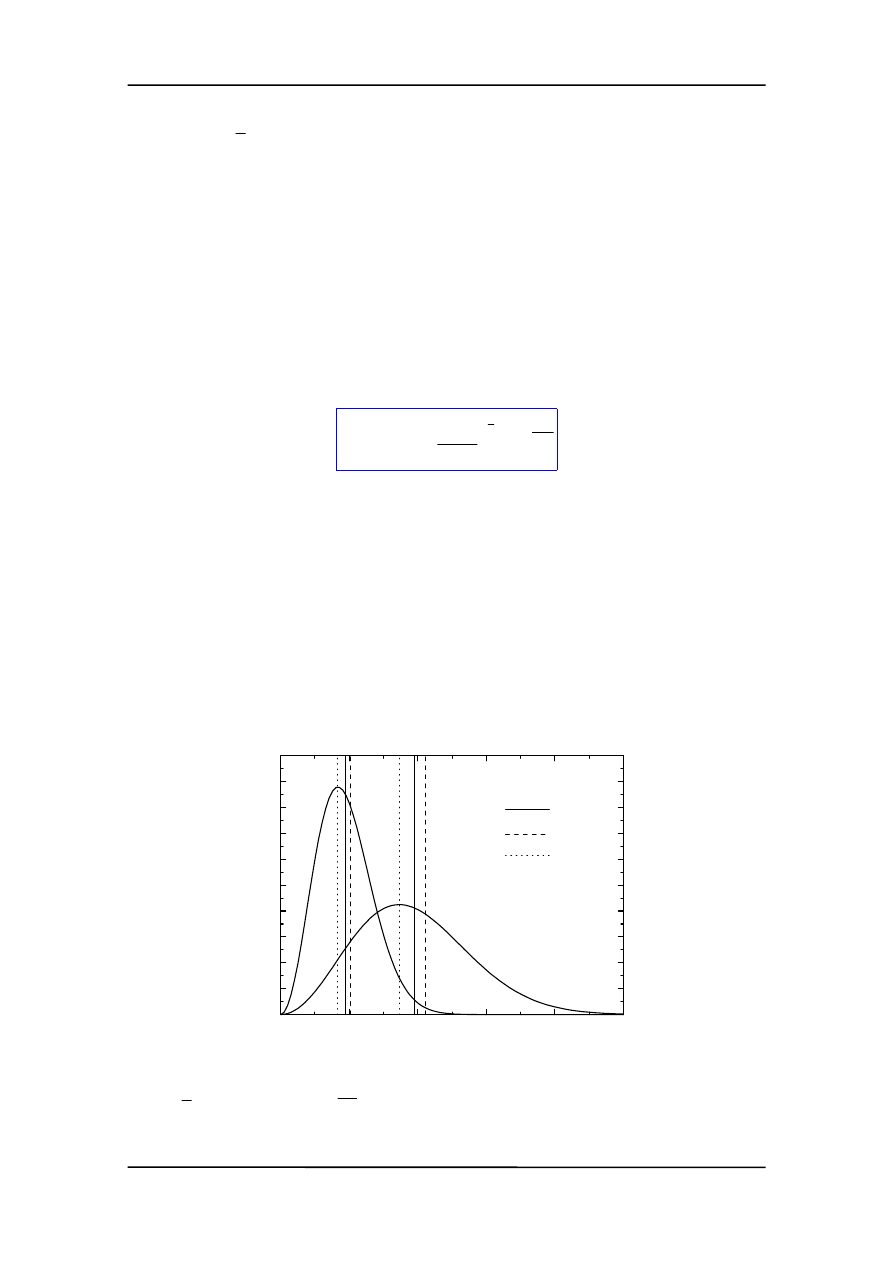
Na rysunku przedstawiony jest rozkład Maxwella dla dwóch różnych temperatur.
0.000
200.000 400.000 600.000 800.000 1000.000
__
_
v
v
2
v
p
v (m/s)
N(
v)
T=300 K
T=70 K
gdzie -v prędkość średnia,
2
v - prędkość średnia kwadratowa,
v
p
– prędkość najbar-
dziej prawdopodobna.
17-2

Z. Kąkol-Notatki do Wykładu z Fizyki
Krzywa nie jest symetryczna bo dolny limit równy jest zeru podczas gdy górny nie-
skończoności. Ze wzrostem temperatury rośnie prędkość średnia kwadratowa. Obszar
prędkości jest teraz większy. Ponieważ liczba cząstek (pole pod krzywą) jest stała więc
rozkład się "rozpłaszcza". Wzrost, wraz z temperaturą, liczby cząstek o prędkościach
większych od danej tłumaczy wiele zjawisk takich jak np. wzrost szybkości reakcji
chemicznych towarzyszących zwiększeniu temperatury. Z równania widać, że rozkład
prędkości zależy od masy cząsteczek. Im mniejsza masa tym więcej szybkich cząste-
czek (w danej temperaturze). Dlatego wodór łatwiej ucieka z górnych warstw atmosfery
niż tlen czy azot.
17.3 Równanie Van der Waalsa
Równanie stanu gazu doskonałego
pV = nRT
dobrze opisuje gazy rzeczywiste ale przy małych gęstościach. Przy większych gęsto-
ściach nie można pominąć faktu, że cząstki zajmują część objętości dostępnej dla gazu
oraz że zasięg sił międzycząsteczkowych może być większy niż odległości międzyczą-
steczkowe.
J.D. Van der Waals wprowadził zmienione równanie stanu gazu, które uwzględnia
te czynniki. Jeżeli cząstki posiadają skończoną objętość to rzeczywista objętość dostęp-
na dla cząstek jest mniejsza od objętości naczynia. "Objętość swobodna" jest mniejsza
od objętości naczynia o "objętość własną" cząsteczek b. Jeżeli oznaczymy przez v obję-
tość przypadającą na jeden mol
v
= V/n to otrzymamy zmodyfikowane równanie stanu
gazu
p(v – b) = RT
Można również prosto uwzględnić efekt sił międzycząsteczkowych. Siły przyciągania
pomiędzy n cząsteczkami (na jednostkę objętości) "po lewej" z n cząsteczkami (na jed-
nostkę objętości) "po prawej" jest proporcjonalna do n
2
czyli proporcjonalna do 1/
v
2
.
Siła przyciągająca znajduje swoje odzwierciedlenie w dodatkowym ciśnieniu, które zo-
stało uwzględnione w równaniu Van der Waalsa
RT
b
a
p
=
−
+
)
(
2
v
v
(17.4)
gdzie stałe a i b wyznaczamy doświadczalnie. (Równanie Van der Waalsa też bywa za-
wodne ale nie jest znana prosta formuła, która stosowałaby się do różnych gazów w
różnych warunkach).
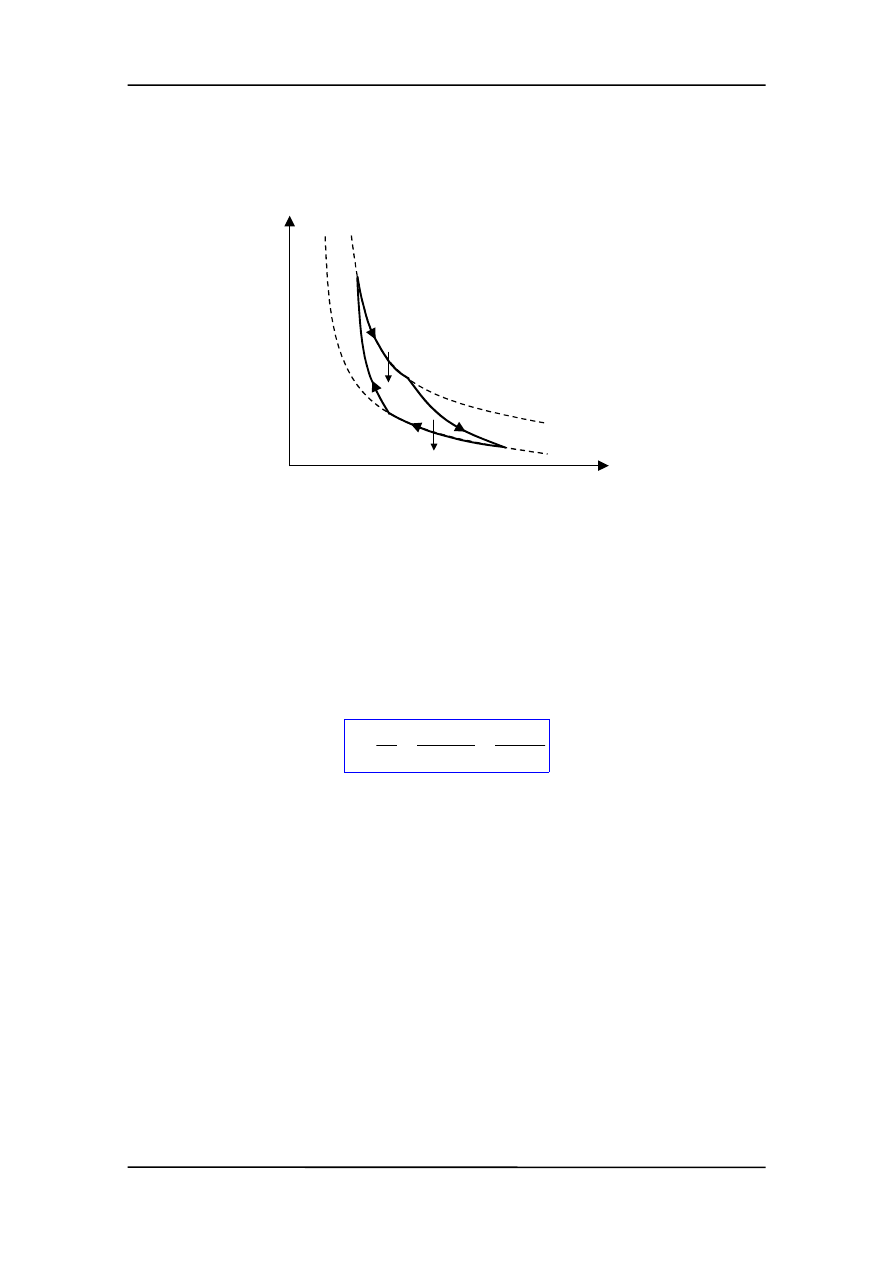
Na rysunku poniżej porównano zachowanie się gazu doskonałego (rysunek po lewej)
w stałej temperaturze z gazem Van der Waalsa (po prawej).
17-3

Z. Kąkol-Notatki do Wykładu z Fizyki
2 0
300
350
400
17.4 Entropia i druga zasada termodynamiki
17.4.1 Procesy odwracalne i nieodwracalne
Rozpatrzmy dwa przypadki izotermicznego sprężanie gazu.
1. Tłok przesuwamy bardzo szybko i czekamy aż ustali się równowaga z otoczeniem.
W czasie takiego procesu ciśnienie i temperatura gazu nie są dobrze określone bo
nie są jednakowe w całej objętości.
2. Tłok przesuwamy bardzo powoli, tak że ciśnienie i temperatura gazu są w każdej
chwili dobrze określone. Ponieważ zmiana jest niewielka to gaz szybko osiąga no-
wy stan równowagi. Możemy złożyć cały proces z ciągu takich małych przesunięć
tłoka i wtedy podczas całego procesu gaz jest bardzo blisko równowagi. Jeżeli bę-
dziemy zmniejszać nasze zmiany to w granicy dojdziemy do procesu idealnego, w
którym wszystkie stany pośrednie (pomiędzy początkowym i końcowym) są stana-
mi równowagi.
Proces typu (1) nazywamy
procesem nieodwracalnym
a proces typu (2)
procesem
odwracalnym
.
Proces nazywamy odwracalnym gdy za pomocą bardzo małej (różniczkowej) zmiany
otoczenia można wywołać proces odwrotny do niego tzn. przebiegający po tej samej
drodze w przeciwnym kierunku
.
17.4.2 Cykl Carnota
Bardzo ważnym cyklem odwracalnym jest cykl Carnota. Cykl ten wyznacza granicę
naszych możliwości zamiany ciepła na pracę.
1) Gaz znajduje się w stanie p
1
, V
1
, T
1
(punkt A). Cylinder stawiamy na zbiorniku ciepła
i pozwalamy, żeby gaz rozprężył się izotermicznie do stanu p
2
, V
2
, T
1
(punkt B). Gaz
pobiera ciepło Q
1
.
2) Cylinder stawiamy na izolującej podstawce i pozwalamy na dalsze rozprężanie adia-
batyczne gazu (np. zmniejszając obciążenie tłoka) do stanu p
3
, V
3
, T
2
(punkt C). Gaz
wykonuje pracę przy podnoszeniu tłoka i jego temperatura spada do T
2
.
17-4
Z. Kąkol-Notatki do Wykładu z Fizyki
3) Cylinder stawiamy na (zimniejszym) zbiorniku (T
2
) i sprężamy gaz izotermicznie do
stanu p
4
, V
4
, T
2
(punkt D). Z gazu do zbiornika przechodzi ciepło Q
2
.
4) Cylinder stawiamy na izolującej podstawce i sprężamy adiabatycznie do stanu p
1
, V
1
,
T
1
(punkt A). Siły zewnętrzne wykonują pracę i temperatura gazu podnosi się do T
1
.
A
B
C
D
Q
1
Q
2
W
T
1
T
2
V
p
Wypadkowa praca W wykonana przez układ w czasie pełnego cyklu jest opisana
przez powierzchnię zawartą wewnątrz krzywej 1,2,3,4. Wypadkowa ilość ciepła pobra-
na przez układ podczas jednego cyklu wynosi Q
1
- Q
2
. Wypadkowa zmiana energii we-
wnętrznej wynosi zero bo stan końcowy pokrywa się z początkowym. Z pierwszej zasa-
dy termodynamiki mamy więc
W = Q
1
– Q
2
Sprawność silnika wynosi
1
2
1
1
2
1
1
T
T
T
Q
Q
Q
Q
W
−
=
−
=
=
η
(17.5)
Cykl Carnota można prowadzić w kierunku przeciwnym (maszyna chłodząca).
17.4.3 Druga zasada termodynamiki
Zwróćmy jeszcze raz uwagę na to, że w trakcie pracy (cyklu) silnika cieplnego
część pobieranego ciepła była oddawana do zbiornika o niższej temperaturze i w konse-
kwencji ta ilość ciepła nie była zamieniana na pracę. Powstaje pytanie, czy można
skonstruować urządzenie, które pobierałoby ciepło i w całości zamieniałoby je na pra-
cę? Moglibyśmy wtedy wykorzystać ogromne (z naszego punktu widzenia nieskończo-
ne) ilości ciepła zgromadzone w oceanach, które byłyby stale uzupełniane poprzez
promieniowanie słoneczne.
Negatywna, niestety, odpowiedź na to pytanie jest zawarta w
drugiej zasadzie ter-
modynamiki
. Poniżej podane zostały równoważne sformułowania tej zasady
1) Nie można zbudować perpetum mobile drugiego rodzaju.
2) Gdy dwa ciała o różnych temperaturach znajdą się w kontakcie termicznym, wów-
czas ciepło będzie przepływało z cieplejszego do chłodniejszego.
17-5
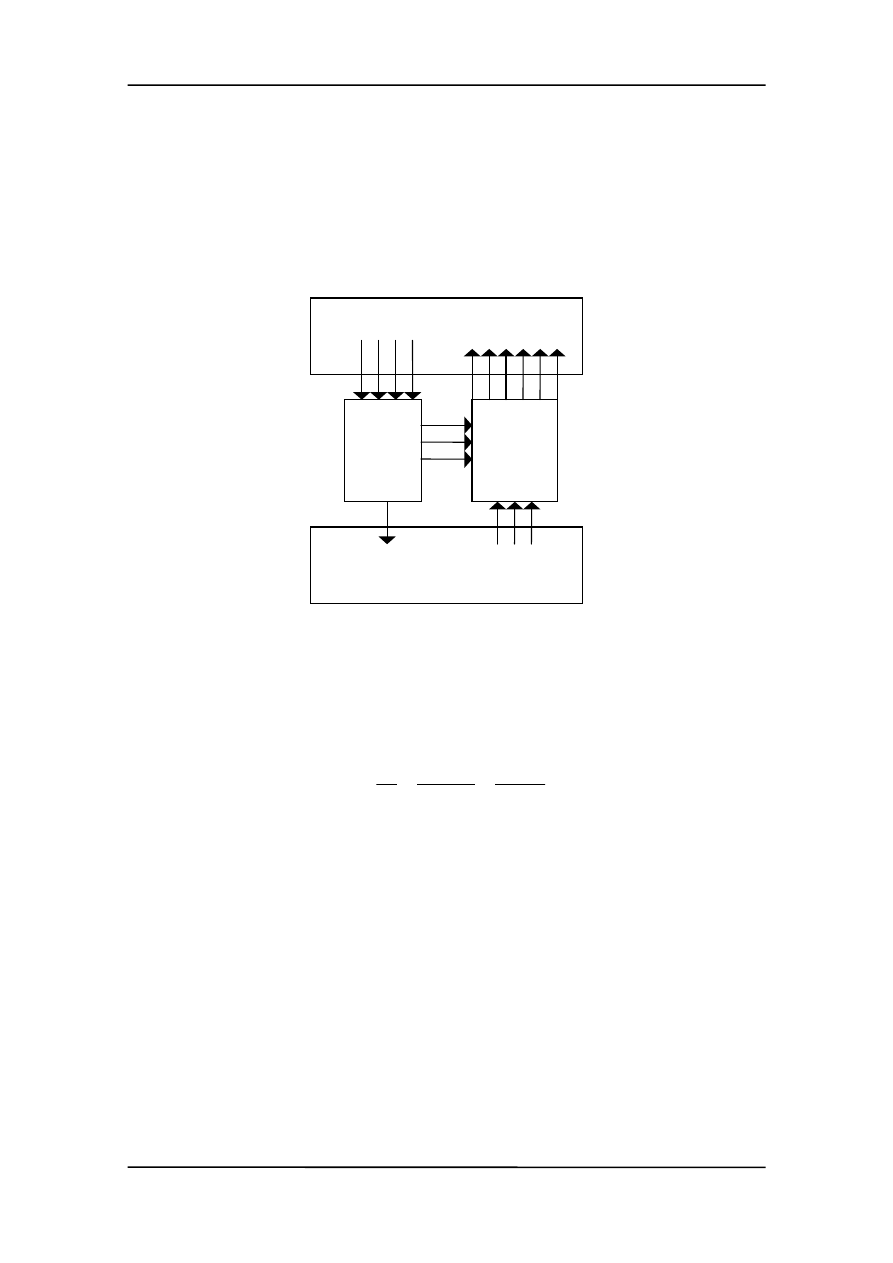
Z. Kąkol-Notatki do Wykładu z Fizyki
3) Żadna cykliczna maszyna cieplna pracująca pomiędzy temperaturami T
1
i T
2
nie mo-
że mieć sprawności większej niż (T
1
- T
2
)/T
1
.
4) W układzie zamkniętym entropia nie może maleć.
Rozpatrzmy następujący schemat (pokazany na rysunku poniżej),w którym super
silnik o sprawności większej od silnika Carnota napędza ten silnik. Efektem końcowym
jest przeniesienie dwóch jednostek ciepła z zimniejszego do cieplejszego zbiornika.
T
1
(gor¹ cy zbiornik)
Q
1
=4
Q
1
'
=6
Silnik
Carnota
η =0.5
Super
silnik
η
S
=0.75
W=3
Q
2
=1 Q
2
'
=3
T
2
(zimny zbiornik)
17.4.4 Termodynamiczna skala temperatur
Pokazaliśmy więc, że sprawność silnika Carnota jest równa
1
2
1
1
2
1
1
T
T
T
Q
Q
Q
Q
W
−
=
−
=
=
η
Wynika stąd, że
T
1
/T
2
= Q
1
/Q
2
Zatem stosunek temperatur dowolnych zbiorników ciepła można wyznaczyć mierząc
przenoszenie ciepła podczas jednego cyklu Carnota. Powyższy wzór stanowi definicję
termodynamicznej skali temperatur
.
17.4.5 Entropia
•
Zerowa zasada termodynamiki wiąże się z pojęciem
temperatury
• Pierwsza zasada termodynamiki wiąże się z pojęciem
energii wewnętrznej
•
Druga zasada termodynamiki wiąże się z pojęciem
entropii
17-6

Z. Kąkol-Notatki do Wykładu z Fizyki
Entropia jest
miarą nieuporządkowania
układu cząstek. Im większy jest stan niepo-
rządku położeń i prędkości w układzie tym większe prawdopodobieństwo, że układ bę-
dzie w tym stanie.
Przykłady sytuacji gdy nieuporządkowanie rośnie bo tracimy część zdolności do klasy-
fikacji cząstek.
• Rozprężanie swobodne
• Przepływ ciepła do wyrównania temperatur
Z definicji entropia S układu jest równa
S = kln
ω
(17.6)
gdzie k - stała Boltzmana,
ω - prawdopodobieństwo, że układ jest w danym stanie
(w odniesieniu do wszystkich pozostałych stanów).
Zgodnie z definicją prawdopodobieństwa układ częściej będzie w stanie o większym
prawdopodobieństwie niż w stanie o mniejszym prawdopodobieństwie. Układ więc
"poszukuje" stanów o większym prawdopodobieństwie, a w miarę wzrostu
ω rośnie
również S. Stąd
∆S ≥ 0
To jest czwarte sformułowanie drugiej zasady termodynamiki. Pokażmy, że pozostałe
sformułowania są mu równoważne.
∆S = S
2
− S
1
= kln
ω
2
− kln
ω
1
∆S = kln(
ω
2
/
ω
1
)
Rozpatrzmy teraz swobodne rozprężanie gazu od objętości V
1
do objętości końcowej
V
2
.
Względne prawdopodobieństwo znalezienia jednej cząstki w V
1
w porównaniu do V
2
jest
2
1
.
1
2
1
V
V
cz
=
ω
ω
Dla N cząstek stosunek prawdopodobieństw
N
Ncz
V
V
=
2
1
.
2
1
ω
ω
Otrzymujemy więc
∆S =Nkln(V
2
/V
1
)
Podzielmy i pomóżmy równanie przez T; otrzymamy wtedy
17-7

Z. Kąkol-Notatki do Wykładu z Fizyki
T
V
V
NkT
S
1
2
ln
=
∆
Wyrażenie w liczniku jest równe ilości ciepła
∆Q dostarczonego do układu aby ten
przeszedł do stanu końcowego w sposób odwracalny (rozprężanie izotermiczne).
T
Q
S
T
Q
S
d
d
d
lub
=
∆
=
∆
(17.7)
więc ostatecznie
∫
=
T
Q
S
d
(17.8)
gdzie dQ jest ciepłem dostarczanym do układu w procesie odwracalnym.
Entropia S jest termodynamiczną funkcją zależną tylko od początkowego i końcowego
stanu układu, a nie od drogi przejścia pomiędzy tymi stanami
(termodynamiczna defini-
cja entropii).
Z tego punktu widzenia szczególnie interesujące są procesy adiabatyczne nie zwią-
zane z przepływem ciepła pomiędzy układem i otoczeniem. W procesie adiabatycznym
dQ = 0, więc dla procesu odwracalnego dS = 0 na podstawie równania (17.8).
Oznacza to, że
entropia układu izolowanego adiabatycznie, w którym zachodzą pro-
cesy odwracalne, jest stała
. Jednocześnie można pokazać, że
dla procesu adiabatyczne-
go nieodwracalnego, entropia układu rośnie
.
Można uogólnić zasadę wzrostu entropii na układy nieizolowane adiabatycznie tzn.
takie, które wymieniają ciepło z otoczeniem. Traktujemy wtedy nasz układ i otoczenie
razem jako jeden "większy" układ ponownie izolowany adiabatycznie. Wtedy
0
d
d
≥
+
o
S
S
gdzie dS
o
jest zmianą entropii otoczenia. Zmienia się więc entropia naszego układu i
otoczenia. Jeżeli proces jest odwracalny to podczas przenoszenia ciepła dQ z otoczenia
do naszego układu entropia otoczenia maleje o dQ/T, a entropia układu rośnie o tę samą
wartość dQ/T, więc całkowita zmiana entropii jest równa zeru.
Zatem posługując się entropią (zgodnie z drugą zasadą termodynamiki) możemy
stwierdzić czy
dany proces może zachodzić w przyrodzie
.
Przykład
Stosując wzór (17.8) można pokazać, np. że ciepło przepływa z ciała gorącego do zim-
nego, a nie odwrotnie. Dwa identyczne ciała o T
1
i T
2
kontaktujemy termicznie. Po
chwili temperatury wynoszą odpowiednio T
1
- dT
1
, T
2
+ dT
2
wskutek przepływu ciepła:
dQ
1
= -mcdT
1
i dQ
2
= mcdT
2
17-8

Z. Kąkol-Notatki do Wykładu z Fizyki
Ponieważ dQ
1
= – dQ
2
więc dT
1
= – dT
2
= dT
Zmiana entropii każdego z ciał jest równa
dS
1
= – mcdT/T
1
i dS
2
= mcdT/T
2
Wypadkowa zmiana entropii wynosi
dS = mcdT(1/T
2
– 1/T
1
)
skąd zmiana temperatury
−
=
2
1
2
1
d
d
T
T
S
mc
T
T
T
dS jest dodatnia więc dT ma taki sam znak jak (T
1
– T
2
). Tak więc jeżeli T
1
> T
2
to cie-
pło przepływa z ciała o T
1
do ciała o T
2
.
Przypuśćmy, że ten strumień ciepła dQ
1
został użyty do napędzania silnika Carnota pra-
cującego pomiędzy T
1
i T
2
. Wówczas zgodnie z wyrażeniem na sprawność
1
2
1
1
d
d
T
T
T
Q
W
−
=
można uzyskać pracę mechaniczną
S
T
T
T
Q
T
W
d
1
1
d
d
2
1
2
1
2
=
−
=
Można pokazać całkiem ogólnie, że jeżeli w układzie zamkniętym zawierającym ciała
o różnych temperaturach następuje wzrost entropii dS to towarzyszy temu strata energii
mechanicznej dW równa iloczynowi dS i temperatury najchłodniejszego ciała.
Uwaga: możliwe jest lokalne zmniejszenie entropii, kiedy jednak bierze się pod uwagę
wszystkie części układu (układ zamknięty) to wypadkowa zmiana entropii będzie równa
zeru lub będzie dodatnia.
17.5 Stan równowagi, zjawiska transportu
17.5.1 Stan równowagi
Stan równowagi układu to taki stan, w którym żaden z parametrów potrzebnych do
makroskopowego opisu układu nie zależy od czasu. Dla układu jednorodnego (np. ga-
zu) w stanie równowagi wystarcza znajomość dwu podstawowych parametrów stanu
np. ciśnienie i objętość.
Opis komplikuje się gdy mamy układ niejednorodny np. ciecz w równowadze z parą.
Dla danej temperatury stan równowagi tego układu jest możliwy przy różnych objęto-
ściach układu (od objętości zależy ilość fazy ciekłej i gazowej). Natomiast temperatura i
17-9
Z. Kąkol-Notatki do Wykładu z Fizyki
ciśnienie przestają być niezależne. W każdej temperaturze równowaga jest możliwa tyl-
ko przy określonym ciśnieniu (pary nasyconej). Przy wyższym istnieje tylko ciecz, przy
niższym para. Podobnie ciecz i ciało stałe mogą istnieć w równowadze tylko w tempera-
turze topnienia, która jest funkcją ciśnienia. Wreszcie ciało stałe współistnieje w rów-
nowadze z parą nasyconą, której ciśnienie jest funkcją temperatury. Krzywe równowagi
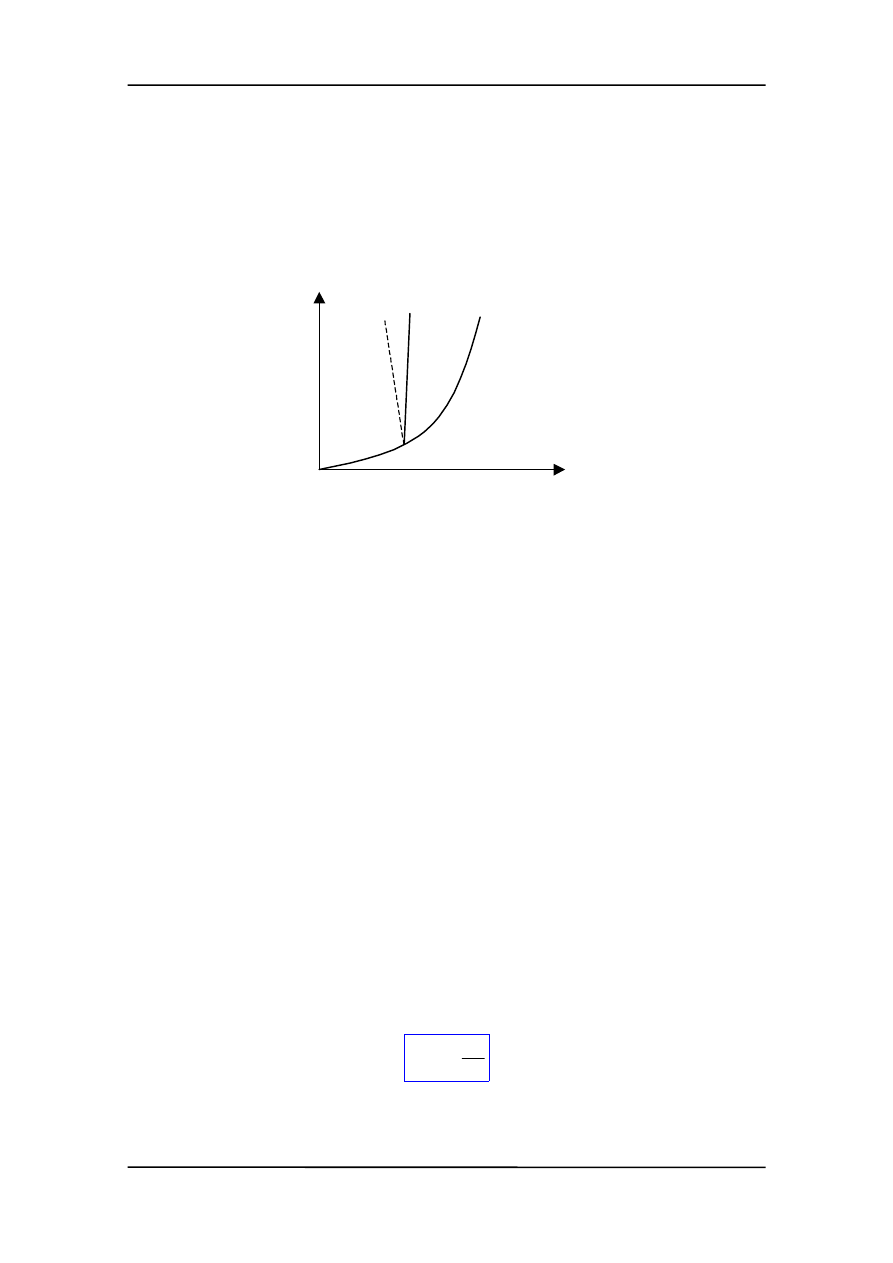
pokazane na rysunku poniżej.
Literą a oznaczona jest krzywa równowagi ciało stałe - ciecz (związek temperatury top-
nienia z ciśnieniem). Krzywa a' przedstawia tę zależność dla kilku nietypowych sub-
stancji, które przy topnieniu zmniejszają objętość np. lód.
p
T
a
a'
b
b'
K
P
I
II
III
Krzywa b + b' pokazuje zależność ciśnienia pary nasyconej od temperatury. Punkt P
nazywamy punktem potrójnym. Odcinek b' to krzywa równowagi ciało stałe – para, a
odcinek b krzywa równowagi ciecz – para. W punkcie potrójnym mogą istnieć wszyst-
kie trzy stany skupienia. Dla wody odpowiada to ciśnieniu p = 4.57 mm Hg, T = 273.16
K (O
°C). Krzywa b kończy się w punkcie krytycznym K powyżej którego nie istnieje
różnica pomiędzy gazem i cieczą. Dlatego żeby skroplić gaz trzeba obniżyć temperaturę
poniżej temperatury krytycznej.
17.5.2 Zjawiska transportu
Dotychczas zajmowaliśmy się właśnie układami w stanie równowagi. Teraz zapo-
znamy się z bardzo uproszczonym opisem zjawisk, które zachodzą gdy układ dąży do
takiego stanu. W zjawiskach tych mamy zawsze do czynienia z przenoszeniem (trans-
portem):
• materii
• energii
• pędu
• ładunku elektrycznego
Wszystkie te zjawiska transportu opisujemy w pierwszym przybliżeniu za pomocą rów-
nania różniczkowego, które
przedstawia propagację pewnej wielkości fizycznej
ϕ mają-
cą na celu osiągnięcie równowagi
x
K
j
∂
∂ϕ
−
=
(17.8)
gdzie j jest gęstością strumienia wielkości
ϕ (gęstość prądu), K jest stałą charakteryzu-
jącą daną sytuację fizyczną. Stałą K wiążemy z właściwościami mikroskopowymi rozpa-
17-10

Z. Kąkol-Notatki do Wykładu z Fizyki
trywanego układu statystycznego, z tzw. współczynnikami transportu. Wiążą się one
z nośnikami np. cząsteczkami gazu, elektronami w metalu.
•
Dyfuzja w gazie
czyli przenoszenie cząstek w kierunku obszarów o mniejszej kon-
centracji n (dążenie do wyrównania koncentracji). Równanie dyfuzji
gradn
D
x
n
D
j
D
−
=
−
=
∂
∂
gdzie j
D
gęstość strumienia cząstek, n - koncentracja cząstek. Równanie to znane jest
pod nazwą prawa Ficka.
Współczynnik dyfuzji (dla rozrzedzonego gazu)
λ
v
3
1
=
D
•
Przewodnictwo cieplne
czyli transport energii, wskutek ruchu cząstek w kierunku
obszaru o niższej T (dążenie do wyrównania temperatury).
Równanie (prawo Fouriera) ma postać
gradT
x
T
j
Q
κ
∂
∂
κ
−
=
−
=
gdzie j
Q
jest gęstością strumienia ciepła,
κ jest współczynnikiem przewodnictwa ciepl-
nego. Dla rozrzedzonego gazu
λ
κ
V
c
nv
3
1
=
•
Lepkość gazu
polegająca na przenoszeniu pędu między warstwami gazu o różnych
prędkościach (dążenie do wyrównania prędkości).
Równanie (prawo Newtona) ma postać
gradu
x
u
j
p
η
∂
∂
η
−
=
−
=
gdzie u jest prędkością (unoszenia) warstwy. Współczynnik lepkości dla rozrzedzonego
gazu wynosi
λ
η
m
nv
3
1
=
•
Przewodnictwo elektryczne
czyli przenoszenie ładunku elektrycznego w wyniku ru-
chu elektronów (dążenie do wyrównania potencjałów elektrycznych). Równanie (prawo
Ohma) ma postać
17-11

Z. Kąkol-Notatki do Wykładu z Fizyki
gradV
σ
ρ
σ
−
=
=
=
E
E
j
1
gdzie przewodność elektryczna
σ jest dana wyrażeniem
v
m
nq
m
nq
λ
τ
σ
2
2
=
=
Uwaga: wszystkie współczynniki transportu zależą od temperatury (poprzez prędkość
średnią, średnią drogę swobodną itd.)
17-12
Wyszukiwarka
Podobne podstrony:
Fizyka Kakol wyklad 13 id 176831
Fizyka Kakol wyklad 14 id 176832
Fizyka Kakol wyklad 30 id 176839
Fizyka Kakol wyklad 24 id 176836
Fizyka Kakol wyklad 37 id 176843
Fizyka Kakol wyklad 22 id 176835
Fizyka Kakol wyklad 26 id 176837
Fizyka Kakol wyklad 8 id 176845
więcej podobnych podstron