Temat: Czas połowicznego rozpadu.

Podczas pracy z niektórymi izotopami promieniotwórczymi okazało się, że proces rozpadu
jest czasami bardzo szybki. Określenie czasu, w którym jądro ulegnie rozpadowi jest
praktycznie niemożliwe, ale gdy jąder jest dużo, to możemy obliczyć, w jaki sposób zmniejsza
się ich liczba. Dla ułatwienia opisu wprowadzono czas połowicznego rozpadu.

Dla każdego izotopu można określić czas T, w ciągu którego rozpadnie się połowa jego jąder.
Czas ten nazywamy czasem połowicznego rozpadu.

Dla przykładu: czas połowicznego rozpadu izotopu azotu

wynosi 10 minut. Jeżeli mamy

początkowo próbkę zawierającą 1 000 000 atomów, to po 10 minutach będzie ich połowa,
czyli 500 000. W ciągu kolejnych 10 minut rozpadnie się połowa z istniejący i pozostanie
250 000. Po kolejnych 10 minutach pozostanie 125 000. Itd.

Podczas tej przemiany azot ulega rozpadowi , czyli liczba atomowa zmniejsza się o jeden. W
efekcie powstaje węgiel.

Przeliczając na masę - jeżeli na początku mieliśmy 1 kg azotu, to po 10 minutach pozostanie
nam 0,5 kg, po kolejnych 10 minutach zostanie 0,25 kg azotu, itd.

Czas połowicznego rozpadu jest inny dla każdego izotopu i może wynosić od trylionowych
części sekundy do miliarda lat.

Przykłady czasu połowicznego rozpadu dla wybranych izotopów różnych pierwiastków.

Izotop

Nazwa pierwiastka

Czas połowicznego rozpadu

bor

0,02 s

azot

0,011 s

azot

0,011 s

fluor

110 min

wodór (tryt)

12 lat

węgiel

5730 lat

potas

1,3 mld lat

radon

3,8 doby

rad

1600 lat

uran

4,5 mld lat

polon

45 s

Zależność ilości jąder danego izotopu promieniotwórczego znajdujących się w substancji
promieniotwórczego od czasu została odkryta przez Ernesta Rutherforda w 1899 roku.

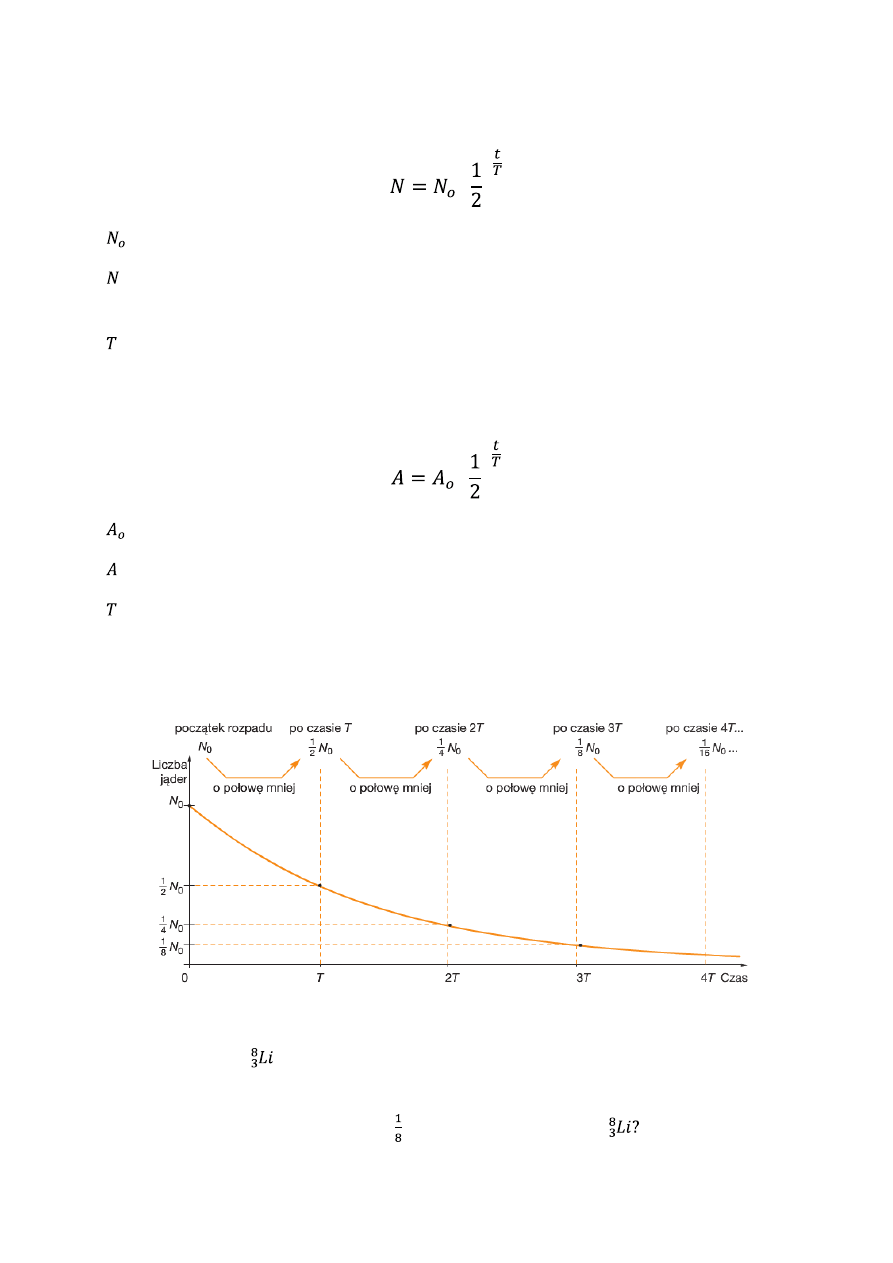
Prawo rozpadu promieniotwórczego

– liczba jąder promieniotwórczych na początku,

– liczba jąder promieniotwórczych, które pozostały w próbce po upływie czasu t od chwili

początkowej,

– czas połowicznego rozpadu, wielkość tabelaryczna.

Tak samo jak liczba substancji promieniotwórczej zmienia się aktywność, którą możemy
zapisać za pomocą wzoru:

– aktywność początkowa,

- aktywność po czasie t,

– czas połowicznego rozpadu, wielkość tabelaryczna.

Za pomocą wykresu prawo rozpadu możemy przedstawić następująco:

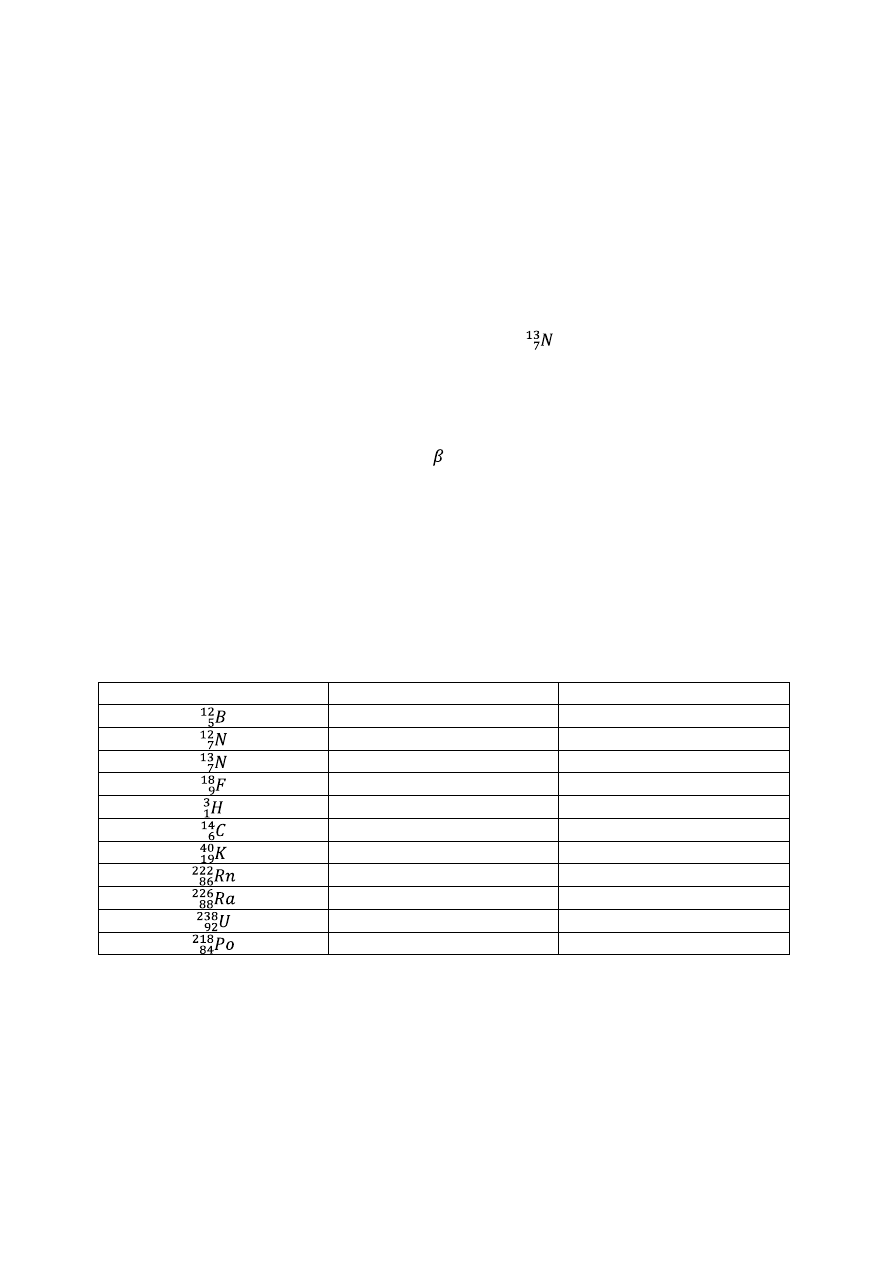
Zadanie 1

Mamy 1 kg izotopu

o czasie połowicznego rozpadu 0,8 s.

a) Ile pozostanie go po upływie 1,6 s?

b) Po jakim czasie pozostanie nam początkowej ilości atomów

c) Szukaną ilość możemy zapisać jako

, czyli na taką ilość musimy poczekać trzy

okresy połowicznego rozpadu. Skoro okres połowicznego rozpadu

wynosi 0,8 s, to

Zadanie 2

Czas T połowicznego rozpadu kobaltu

wynosi 5 lat. Pewna próbka zawiera 0,04 g tego

izotopu. Oblicz jego masę m w próbce po 10 latach.

Rozwiązanie

W czasie pierwszych 5 lat rozpadowi ulegnie połowa liczby jąder, czyli połowa masy próbki.
W czasie następnych 5 lat rozpadnie się połowa z pozostałej ilości, czyli połowa z połowy, co
daje nam czwartą część początkowej ilości jąder, które znajdowały się na początku w próbce.

W konsekwencji po 10 latach pozostanie masy początkowej.

Masa w próbce po 10 latach wynosi:

Odpowiedź: Po 10 latach pozostanie 0,01 g izotopu

.

Zadanie 3

Na skutek awarii reaktora w Czarnobylu do atmosfery dostały się promieniotwórcze izotopy
jodu

o czasie połowicznego rozpadu 8 dni oraz cezu

o czasie połowicznego

rozpadu 30 lat. Dnia 28 kwietnia 1986 roku w Warszawie aktywność jodu przy powierzchni

gruntu wynosiła

. Przed awarią pierwiastek ten był niewykrywalny. Tego samego dnia

aktywność cezu osiągnęła wartość

i była 80 000 razy większa niż przed awarią.

a) Oblicz aktywność jodu w 2013 roku, czyli 26 lat po awarii.
b) Oszacuj czas t, po upływie którego aktywność A cezu wróci do stanu sprzed awarii

.

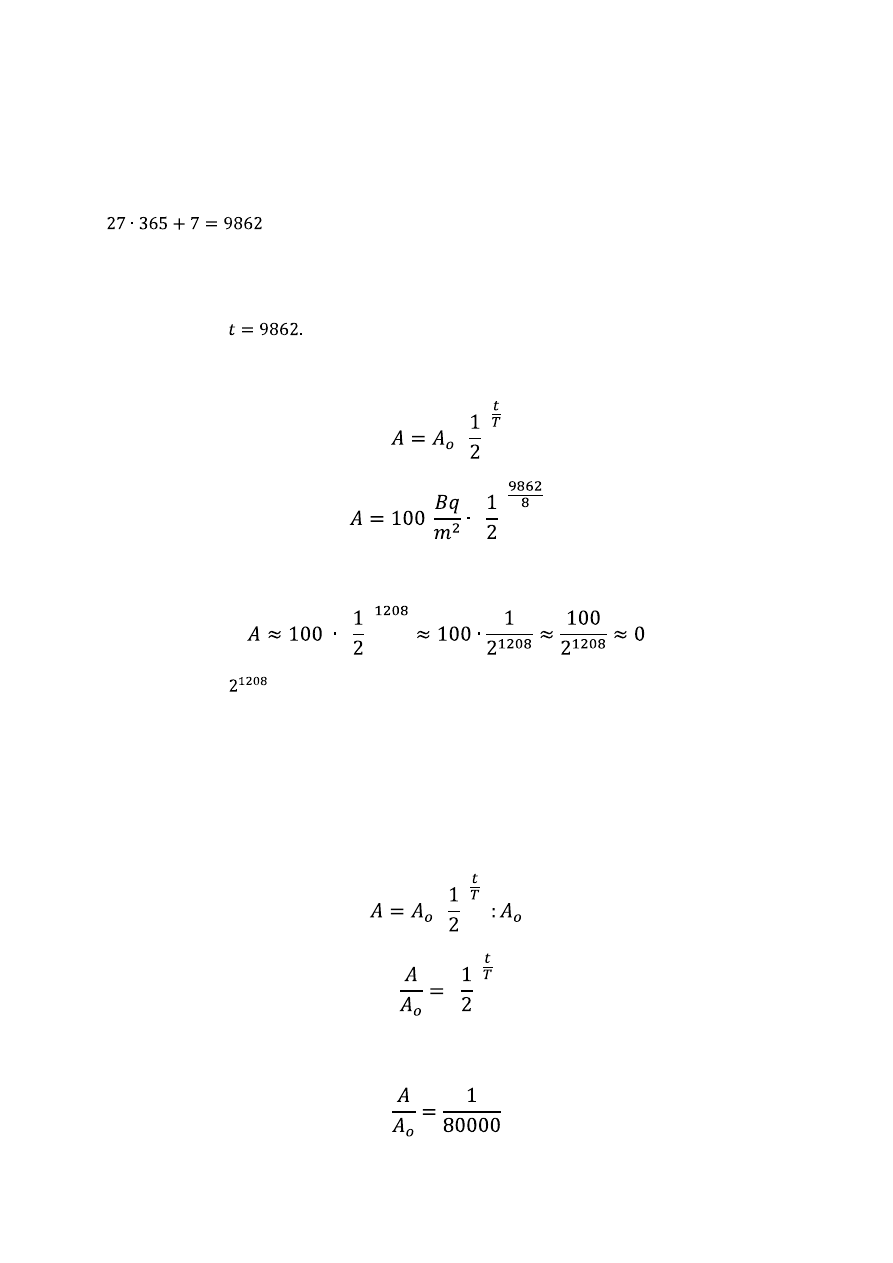
Rozwiązanie

Ad. a) Czas, który upłynął wyrażamy w dniach, ponieważ czas połowicznego rozpadu dla jodu
wyrażony jest w dniach.

.

W powyższym przeliczeniu ilość lat pomnożyliśmy przez ilość dni w roku i dodaliśmy ilość lat
przestępnych w tym okresie (rok trawa 366 dni).

Czas aktywności

Podstawiamy do wzoru

Dla wyjaśnienia,

jest liczbą bardzo dużą, posiadającą 364 liczby przed przecinkiem.

Dzieląc 100 przez tak dużą liczbę praktycznie otrzymujemy wartość zero.

Odpowiedź: Aktualnie aktywność jodu pochodzącego z awarii reaktora w Czarnobylu jest
obecnie praktycznie równa zero.

Ad. b) Z treści zadania wynika, że aktywność po wybuchu była 80 000 większa od aktywności
przed wybuchem. Podstawiając do równania otrzymujemy:

Jeżeli przyjmiemy, że aktywność początkowa A jest 80 000 razy większa od aktywności
końcowej, otrzymamy, że

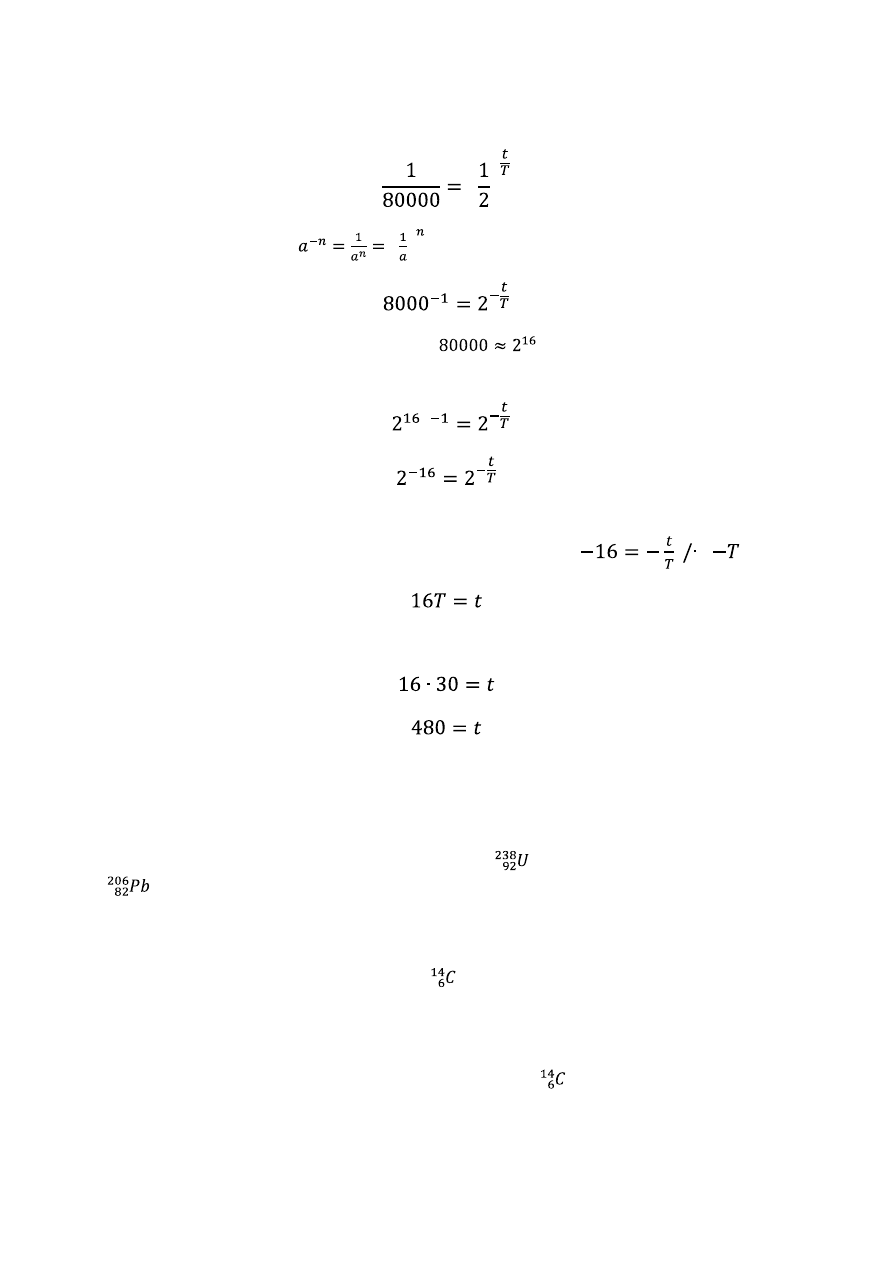
Podstawiając do wzoru, otrzymamy:

Z własności potęgowania:

, otrzymamy zależność

Z pewnym przybliżeniem możemy przyjąć, że

. Po podstawieniu do powyższego

równania, otrzymamy:

Korzystamy z własności funkcji wykładniczej – dwie potęgi o tej samej podstawie są sobie

równe, gdy wykładniki są równe. W konsekwencji otrzymujemy

:

Za T przyjmujemy czas połowicznego rozpadu dla cezu, który wynosi 30 lat.

Odpowiedź: Aktywność cezu powróci do normy po wybuchu w Czarnobylu po około 480
latach.

Dzięki rozpadowi naturalnemu możemy ustalić wiek wielu przedmiotów. Do ustalenia wieku
Układu Słonecznego możemy stosować izotop uranu

porównując go z izotopem ołowiu

. Możemy w ten sposób ustalić, ile uranu rozpadło się tworząc ołów. Materią, która

podlega badaniu, to meteoryty, które powstały w momencie powstania Układu Słonecznego.
Na tej podstawie oszacowano wiek Układu Słonecznego na około 4,75 mld lat.

Podobne zastosowanie znalazł izotop węgla

. Powstaje on w ziemskiej atmosferze i jest

pochłaniany przez rośliny w procesie fotosyntezy. Potem trafia do różnych organizmów w
łańcuchu pokarmowym. Dopóki organizm żyje, ilość tego izotopu nie ulega zmianie, bo część
izotopu ulega rozpadowi, ale w tym czasie stale go przybywa. W momencie gdy organizm
umrze, nie następuje wymiana z otoczeniem i ilość izotopu

zaczyna maleć. Określając

ilość tego izotopu w przedmiotach pochodzenia roślinnego lub zwierzęcego możemy

oszacować jego wiek. Przedmiotami tymi mogą być różne przedmioty z drewna lub szczątki
zwierzęce lub ludzkie. Metodę tą opracował amerykański chemik Willard Libby w 1949 roku.