Wprowadzenie do fizyki

Mirosław Kozłowski

rok akad. 2002/2003

Część 6a

Wstęp do

Szczególnej Teorii

Względności

Wstęp do Szczególnej Teorii

Względności cz. a

Slajd podsumowania

Koniec
pokazu

Wstęp do Szczególnej Teorii Względności, cz. a

3

6.1 Historia Szczególnej Teorii Względności

.

6.2 Pojęcie czasu w Szczególnej Teorii Względności;

Elastyczność czasu

.

Linki do stron WWW

Hyper Physics

4

Astronomy Picture of the Day

Space Photos and Images

P

hy

si

cs

W

or

ld

,

9

(2002)

5

P

hy

si

cs

W

or

ld

6.1 Historia Szczególnej Teorii

Względności

1. W. Kaufmann,

Die elektromagnetische Masse des Electrons,
Nachr. Ges. Wiss. Göttingen, 2 (1901) 143;
Phys. Z., 4 (1902) 54.

Wstęp do Szczególnej Teorii Względności, cz. a

6

Phys. Z., 4 (1902) 54.

2. A. H. Bucherer,

Phys. Zeit., 9 (1908) 755.

.

1

2

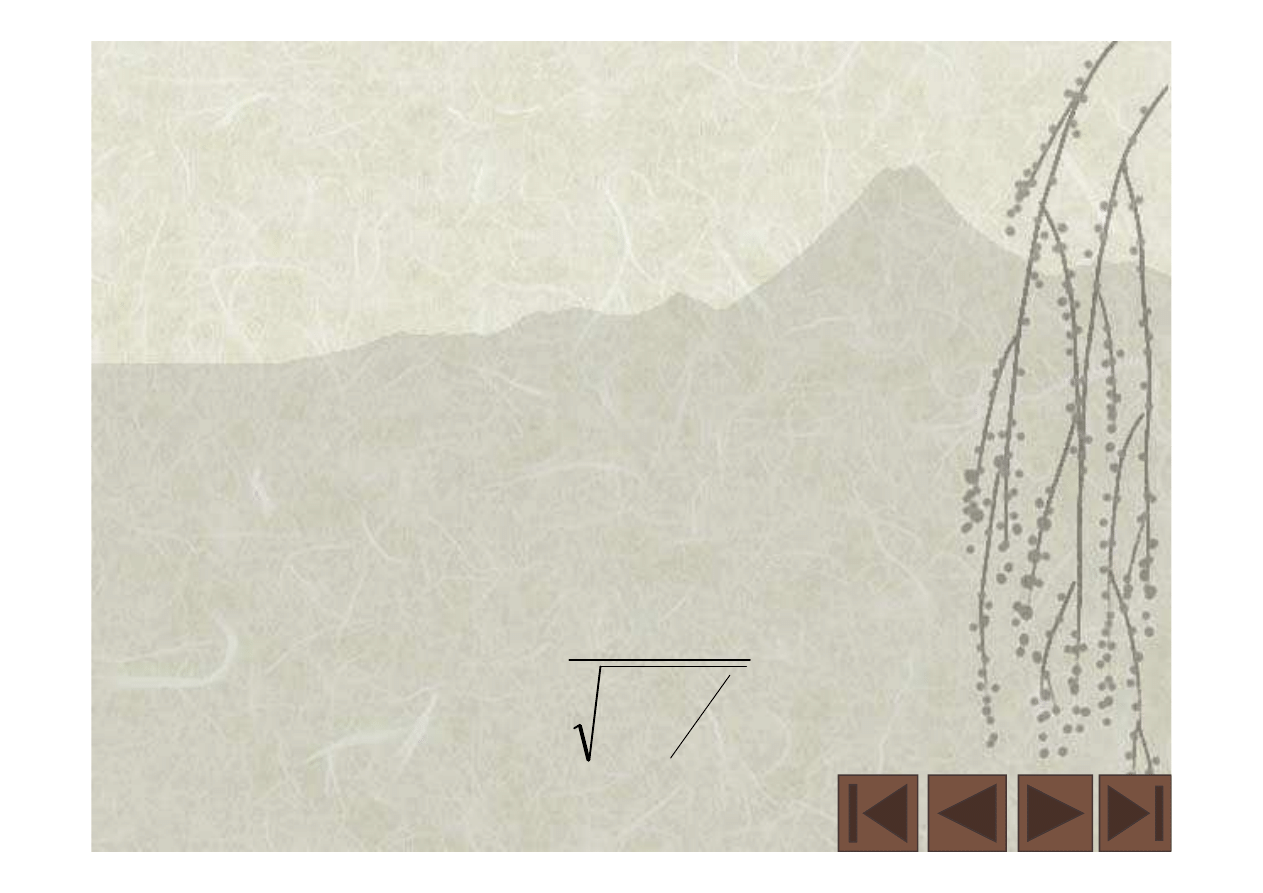
2

0

c

v

m

m

−

=

3. W. Bertozzi,

Am. J. Phys., 32 (1964)531.

4. J. Bailey et al.,

.

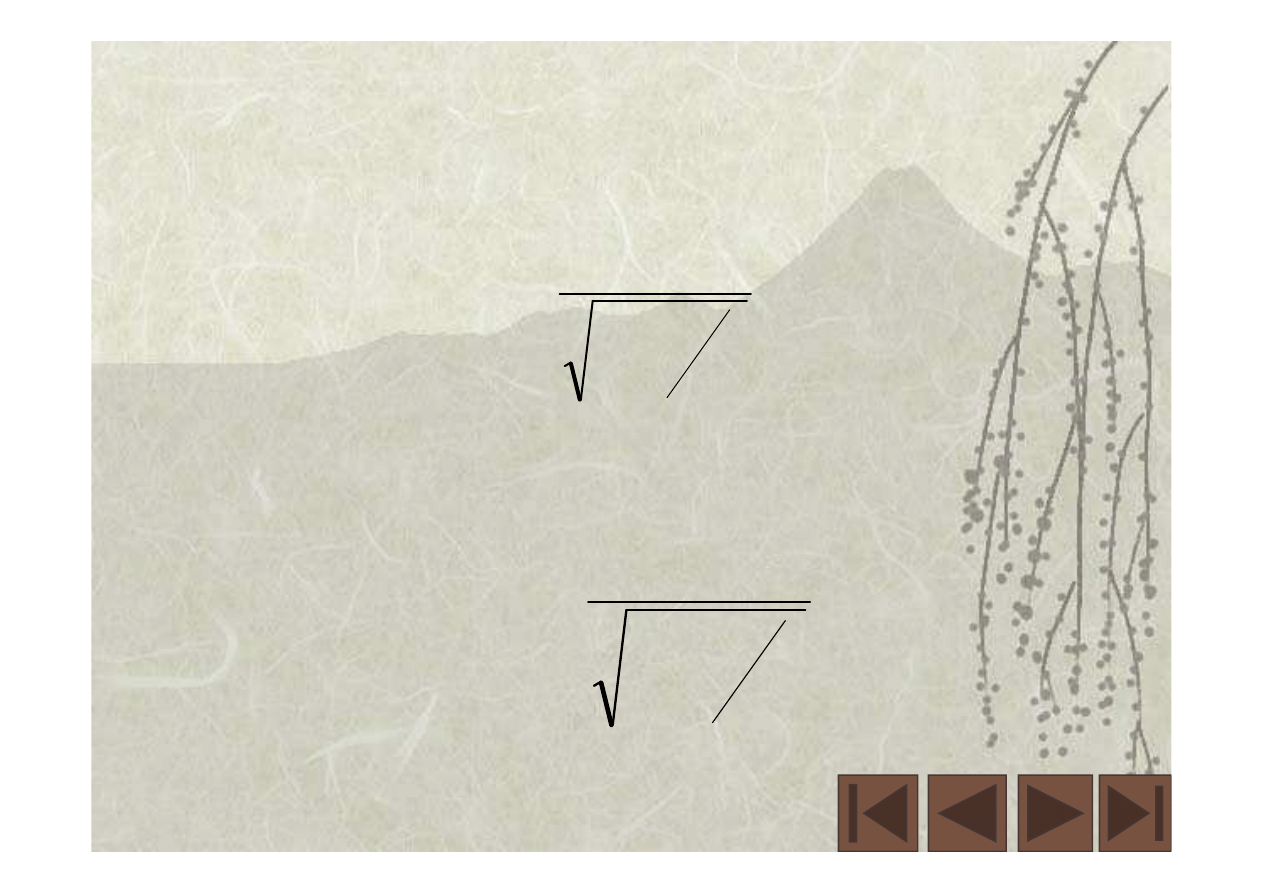
1

2

2

2

0

c

v

c

m

E

−

=

Wstęp do Szczególnej Teorii Względności, cz. a

7

4. J. Bailey et al.,

Nature, 268 (1997) 301.

.

1

2

2

0

c

v

t

t

−

∆

=

∆

5. H. Poincaré,

Sur la dynamique de l’electron,
Comptes rendus de l’Academie de Science
140 (1905) 1504.

6. A. Einstein,

Wstęp do Szczególnej Teorii Względności, cz. a

8

6. A. Einstein,

Zur Elektrodynamik bewegter Körper,
Ann. Phys. 17 (1905) 891,
(30 czerwiec 1905).

R

en

d

ic

o

n

ti

d

el

C

ir

co

lo

M

a

te

m

a

ti

co

,

w

k

tó

ry

m

u

k

az

ał

s

ię

a

rt

y

k

u

ł

H

.

P

o

in

ca

ré

„S

u

r

la

d

y

n

am

iq

u

e

d

e

l’

el

ec

tr

o

n

”.

Wstęp do Szczególnej Teorii Względności, cz. a

9

S

tr

o

n

a

ty

tu

ło

w

a

R

en

d

ic

o

n

ti

d

el

C

ir

co

lo

M

a

te

m

a

ti

co

d

i

P

a

le

rm

o

,

w

k

tó

ry

m

u

k

az

ał

s

i

„S

u

r

la

d

y

n

am

iq

u

e

d

e

l’

el

ec

tr

o

n

”.

Wstęp do Szczególnej Teorii Względności, cz. a

10

List H. Poincaré do H.A.Lorentza napisany na przełomie lat 1904 i 1905

A

n

n

a

le

n

d

er

P

h

ys

ik

,

w

k

tó

ry

m

a

rt

y

k

u

ł

A

.

E

in

st

ei

n

a

„Z

u

r

E

le

ct

ro

d

y

n

am

ik

Wstęp do Szczególnej Teorii Względności, cz. a

11

S

tr

o

n

a

ty

tu

ło

w

a

A

n

n

a

le

n

d

er

P

h

ys

ik

u

k

az

ał

s

ię

a

rt

y

k

u

ł

A

.

E

in

st

ei

n

a

„Z

u

r

E

le

ct

ro

d

y

n

am

ik

b

ew

eg

te

r

K

ö

rp

er

”.

S

tr

o

n

a

z

p

ra

cy

E

in

st

ei

n

a

o

e

le

k

tr

o

d

y

n

am

ic

e

cy

ch

w

r

u

ch

u

E

in

st

ei

n

;

A

C

en

te

n

a

ry

H

ar

v

ar

d

U

n

iv

er

si

ty

P

re

ss

1

9

8

0

Wstęp do Szczególnej Teorii Względności, cz. a

12

S

tr

o

n

a

z

p

ra

cy

E

in

st

ei

n

a

o

e

le

k

tr

o

d

y

n

am

ic

e

ci

ał

b

ę

d

ą

cy

ch

w

r

u

ch

u

z

A

.

P.

F

re

n

ch

,

E

in

st

ei

n

;

A

C

en

te

n

a

ry

V

o

lu

m

e,

H

ar

v

ar

d

U

n

iv

er

si

ty

P

re

ss

1

9

8

0

(

)

.

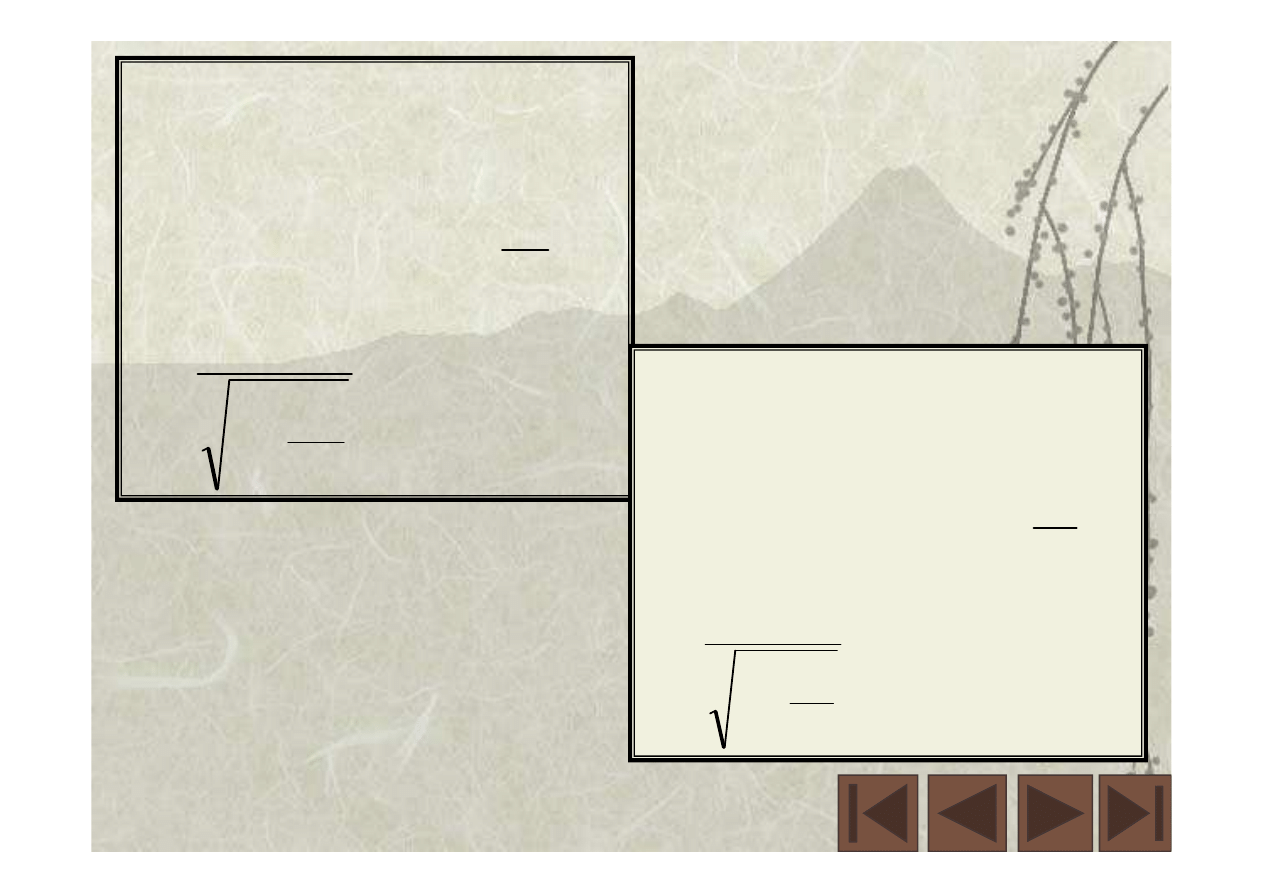
1

1

,

,

,

,

2

2

2

V

x

c

V

t

t

z

z

y

y

t

V

x

x

−

=













′

+

′

=

=

′

′

=

′

+

′

=

γ

γ

γ

(

)

,

,

y

y

Vt

x

x

=

′

−

=

′

γ

Wstęp do Szczególnej Teorii Względności, cz. a

13

1

2

c

−

.

1

1

,

,

,

2

2

c

V

x

c

V

t

t

z

z

y

y

−

=













−

=

′

=

′

=

′

γ

γ

,

,

,

,

1

,

t

t

y

y

Vt

x

x

c

=

′

=

′

−

=

′

=

∞

→

γ

Wstęp do Szczególnej Teorii Względności, cz. a

14

.

,

,

z

z

t

t

y

y

=

′

=

′

=

′

6.2 Pojęcie czasu w Szczególnej Teorii
Względności; Elastyczność czasu

w

s

p

o

cz

y

n

k

u

h

tt

p

:/

/c

as

a.

co

lo

ra

d

o

.e

d

u

/~

aj

sh

/s

r/

ti

m

e.

h

tm

l

Wstęp do Szczególnej Teorii Względności, cz. a

15

O

b

a

ze

g

ar

y

p

o

zo

st

aj

ą

w

s

p

o

cz

y

n

k

u

h

tt

p

:/

/c

as

a.

co

lo

ra

d

o

.e

d

u

/~

aj

sh

/s

r/

ti

m

e.

h

tm

l

Je

d

en

z

z

eg

ar

ó

w

p

o

ru

sz

a

si

ę

w

ia

tł

o

p

o

ru

sz

a

si

ę

h

tt

p

:/

/c

as

a.

co

lo

ra

d

o

.e

d

u

/~

aj

sh

/s

r/

ti

m

e.

h

tm

l

Wstęp do Szczególnej Teorii Względności, cz. a

16

Je

d

en

z

z

eg

ar

ó

w

p

o

ru

sz

a

si

z

p

rę

d

k

o

śc

ią

v

.

Ś

w

ia

tł

o

p

o

ru

sz

a

si

z

p

rę

d

k

o

śc

ią

c

,

c>

>

v.

h

tt

p

:/

/c

as

a.

co

lo

ra

d

o

.e

d

u

/~

aj

sh

/s

r/

ti

m

e.

h

tm

l

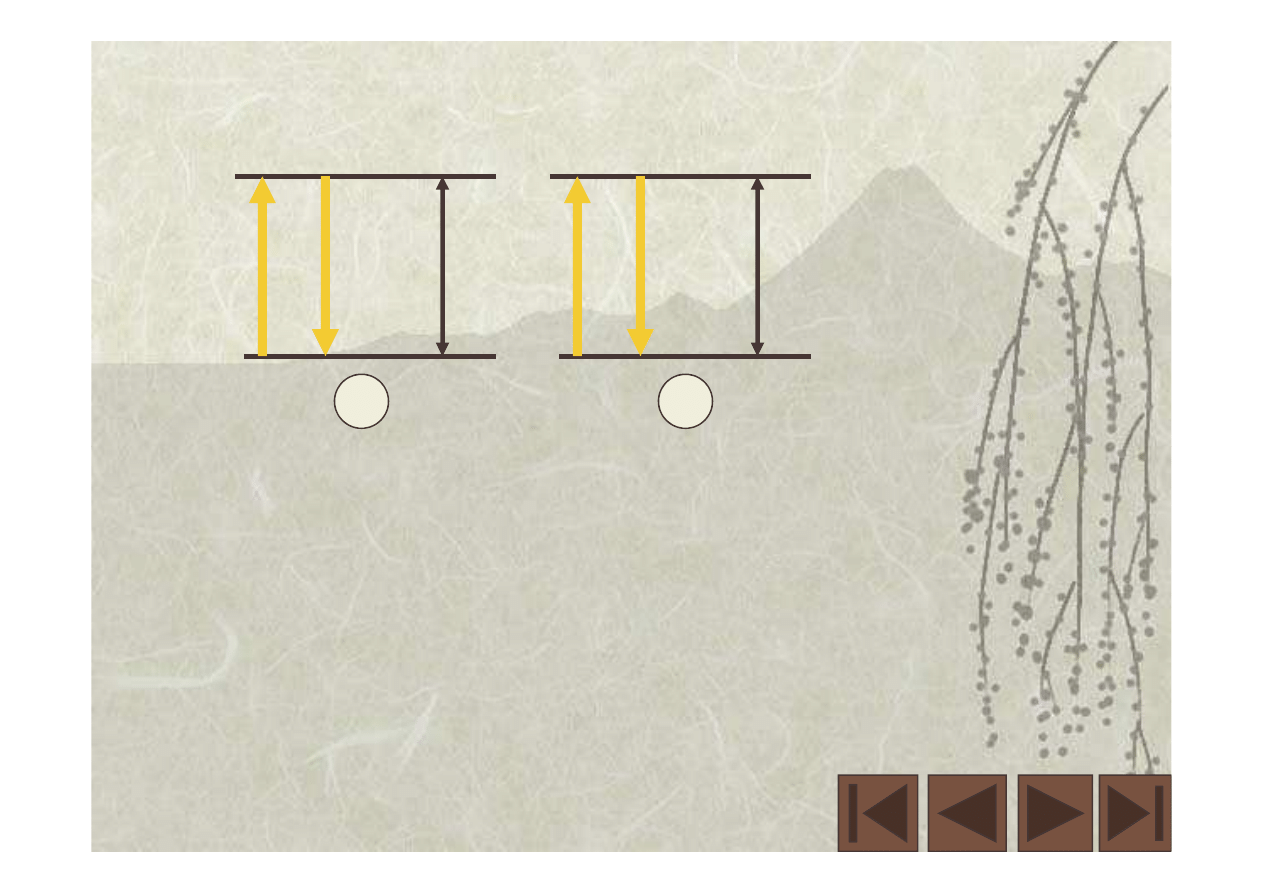
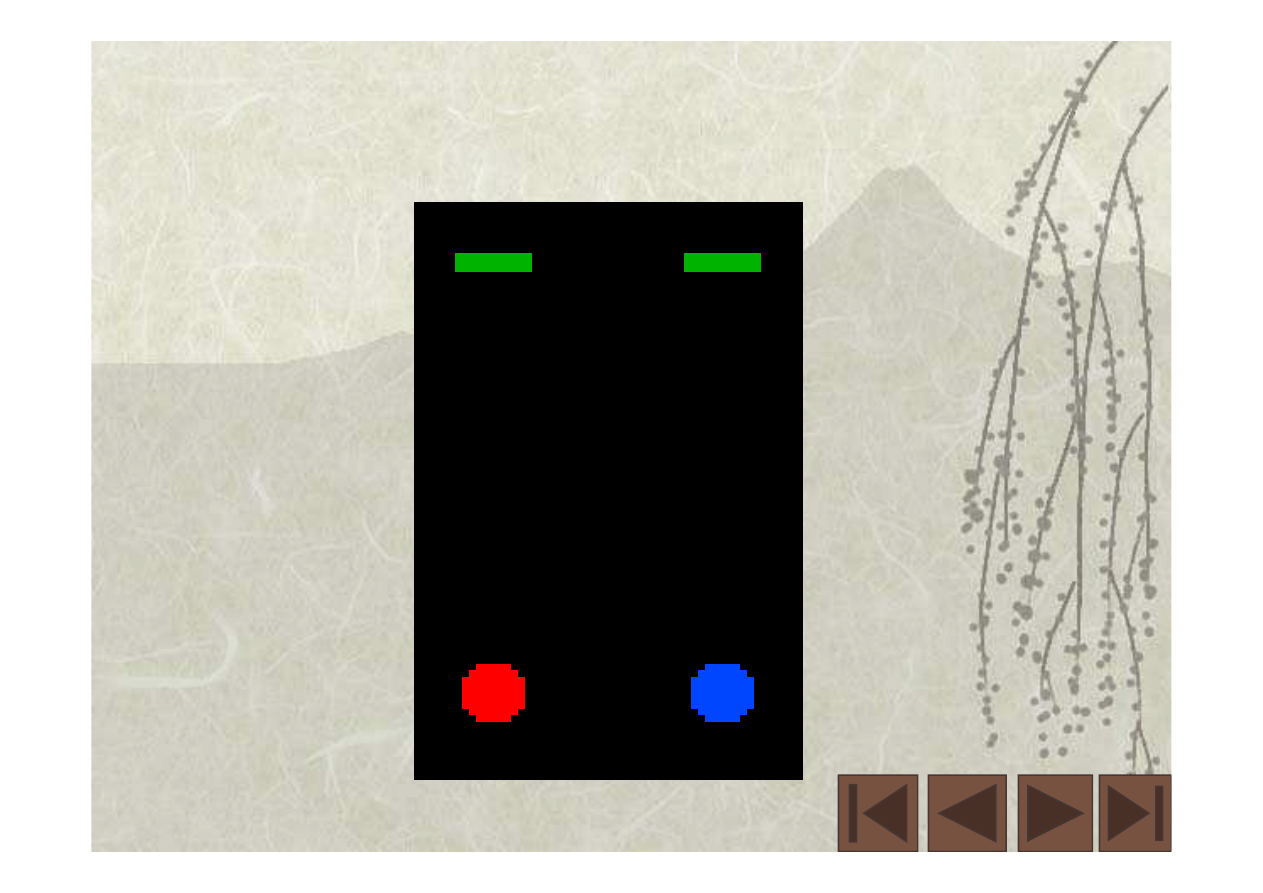
A. Dwa nieruchome zegary fotonowe

d

d

1

2

Wstęp do Szczególnej Teorii Względności, cz. a

17

jednostka czasu t

NN

= d/c,

c = prędkość absolutna,
t

NN

= jednostka czasu taka sama dla obu

zegarów (nieruchomy zegar, nieruchomy
obserwator.

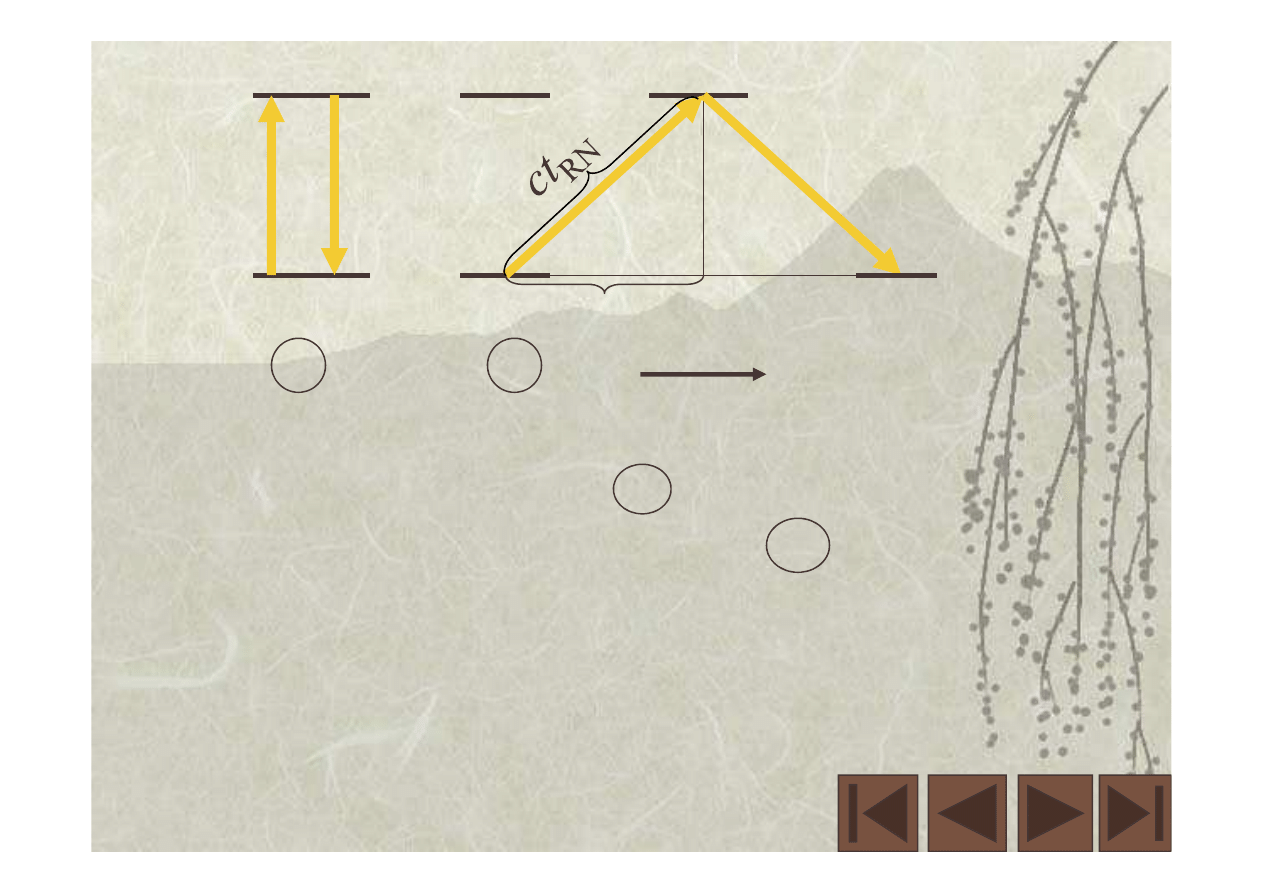
B.

1

d

t

RN

v

v

r

2

Wstęp do Szczególnej Teorii Względności, cz. a

18

= prędkość zegara 2 w układzie,

w którym spoczywa zegar 1 .

t

RN

= jednostka czasu, ruchomy zegar,

nieruchomy obserwator.

v

r

( )

( )

( ) ( )

,

,

,

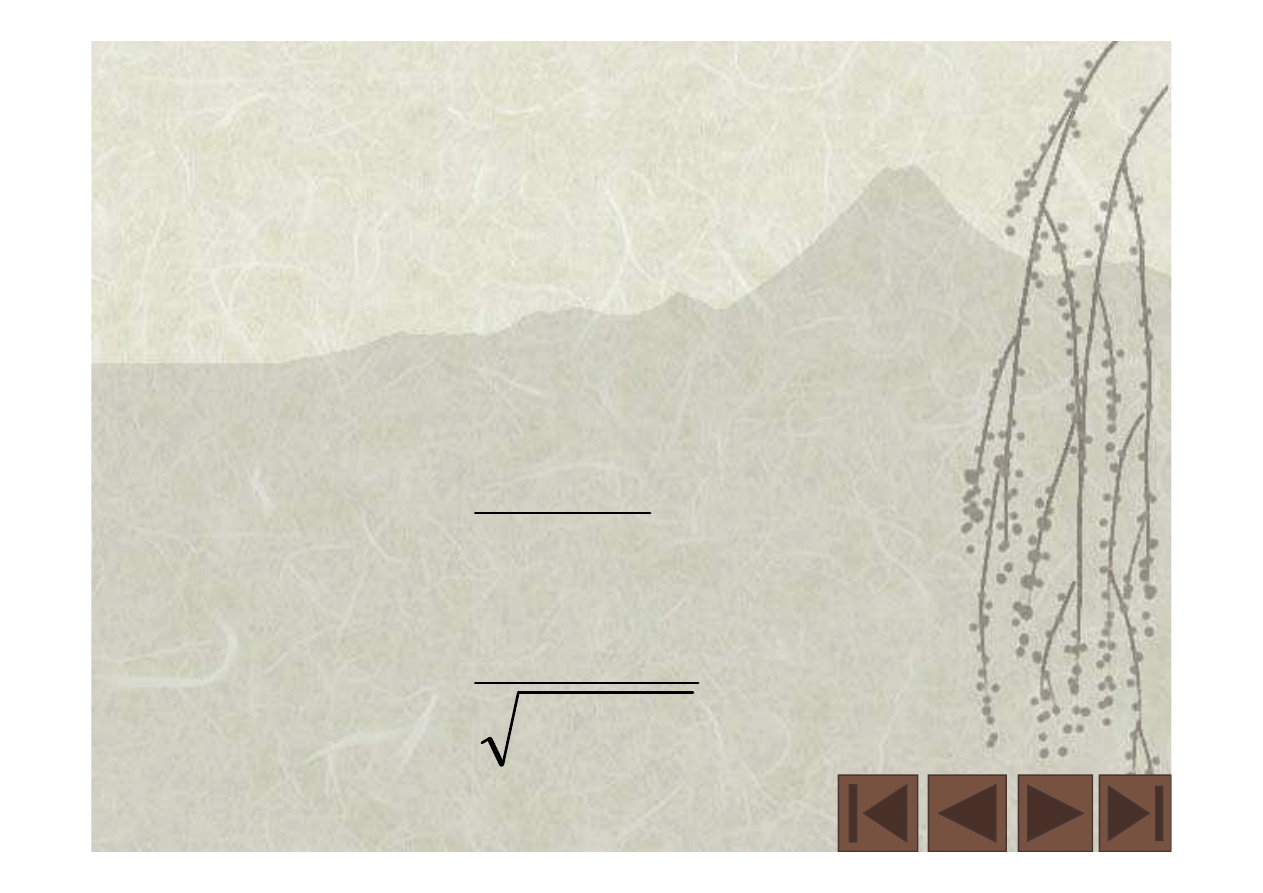
2

2

2

2

2

2

2

2

2

2

2

2

t

c

t

c

vt

ct

t

c

d

vt

d

ct

NN

RN

RN

NN

RN

RN

=

−

=

+

=

Wstęp do Szczególnej Teorii Względności, cz. a

19

.

,

2

2

2

2

2

2

2

v

c

ct

t

v

c

t

c

t

NN

RN

NN

RN

−

=

−

=

.

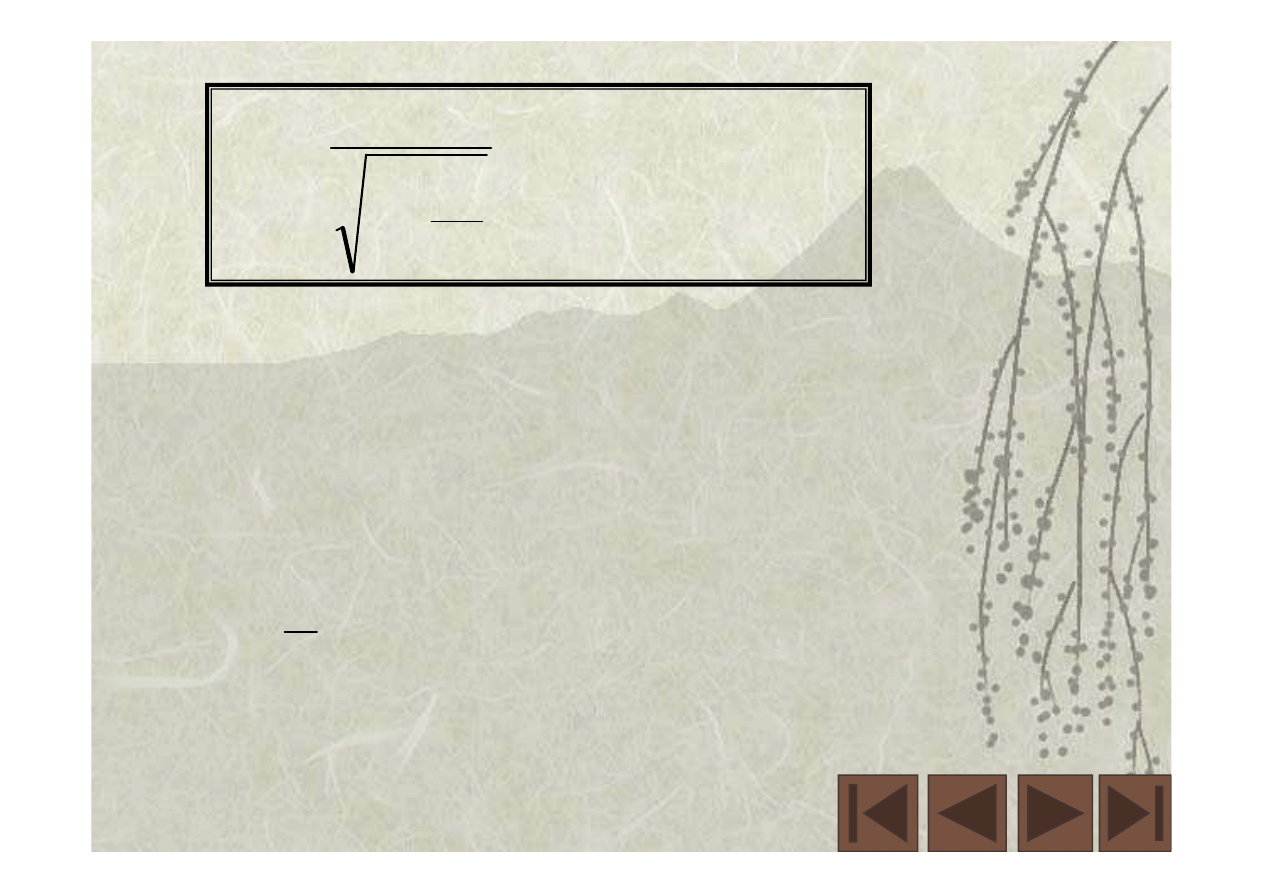
1

,

1

2

2

>

=

−

=

γ

γ

NN

NN

RN

t

c

v

t

t

.

NN

RN

t

t

>

Wnioski

Wstęp do Szczególnej Teorii Względności, cz. a

20

1. Ruchomy zegar odmierza wolniej czas niż zegar
spoczywający.
2. Dla

.

,

1

,

1

NN

RN

t

t

c

v

=

=

<<

γ

Wnioski

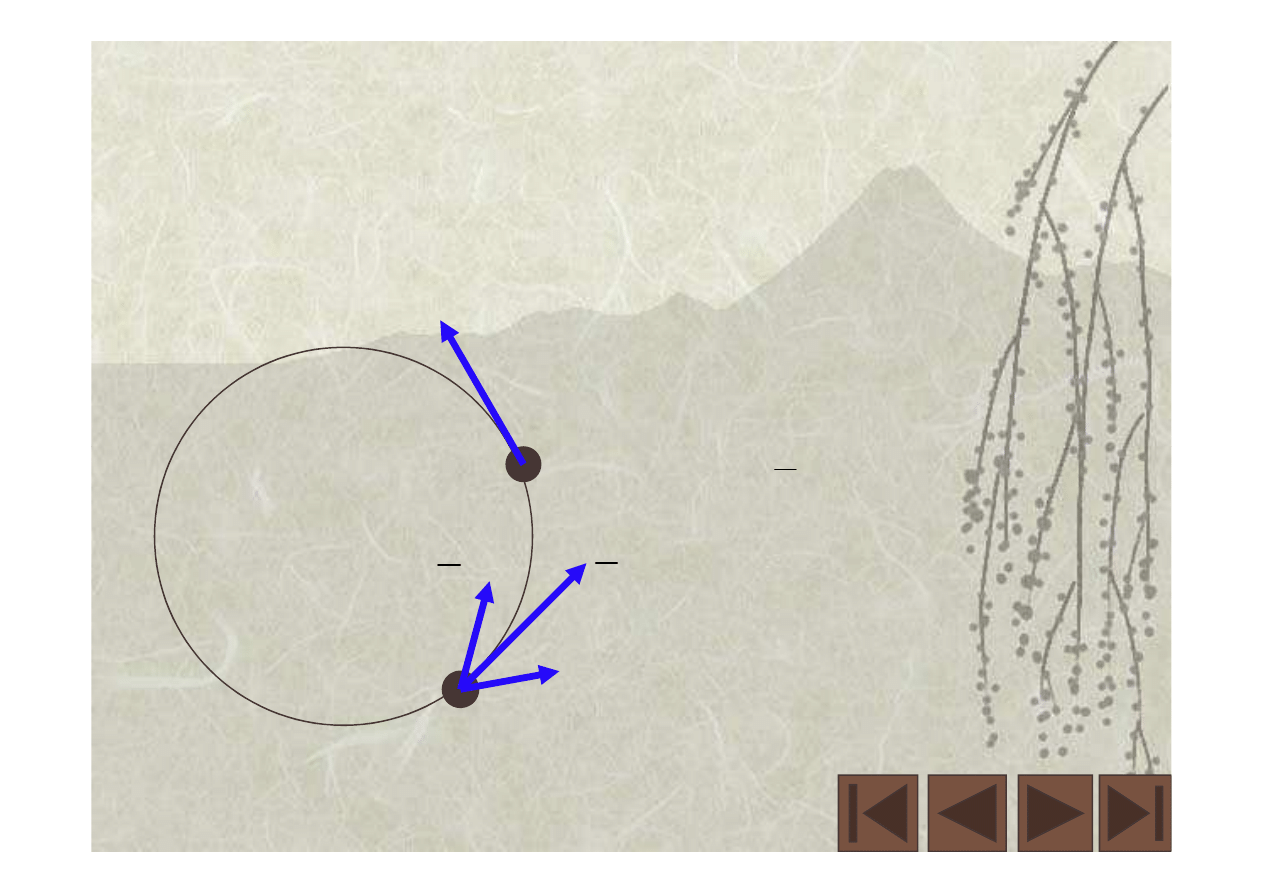
J. Bailey et al.,
Measurements of relativistic time dilatation
for positive and negative muons in a circular
orbit, Nature, vol. 268, (1977) 301.

9994

.

0

=

=

v

β

−

µ

Wstęp do Szczególnej Teorii Względności, cz. a

21

9994

.

0

=

=

c

v

β

−

µ

−

µ

e

v

µ

v

e

;

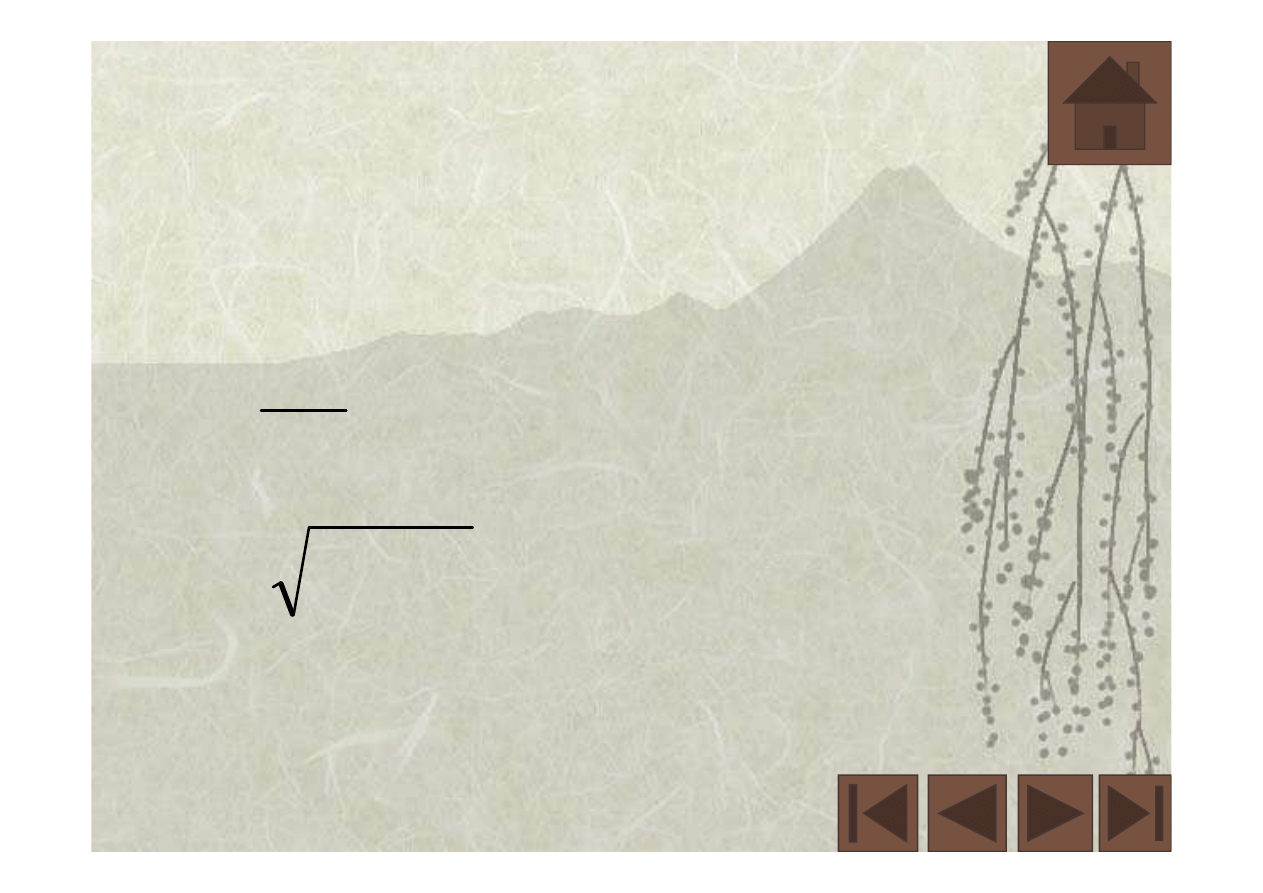
35

,

29

=

=

γ

RN

t

t

Dla mezonów µ:
t

NN

(czas życia) = 2,1948 µs,

t

RN

(czas życia) = 64,419 µs

Wstęp do Szczególnej Teorii Względności, cz. a

22

.

9994

,

0

1

2

=

−

=

−

γ

β

NN

t

To jest ostatni slajd pierwszej części rozdziału pt. „Wstęp
do Szczególnej Teorii Względności”.
Możesz:
•przejść do „Spisu treści” i wybrać kolejny rozdział,
•wrócić do materiału zawartego w tym rozdziale,
•zakończyć pokaz .

Wstęp do Szczególnej Teorii Względności, cz. a

23

Spis treści

Koniec
pokazu