Elementy szczególnej

teorii względności

Wykład 2

Opracowano np. skryptu A. Rogalski i

wykładu prof. M. Demianiuka

1

PRZYPOMINAM - Zasady zaliczania w

semestrze I

• Przedmiot w tym semestrze jest zaliczany na

ostatnich zajęciach

• Zaliczanie w formie pracy pisemnej polega na

odpo-wiedzi na 6 pytań definicyjnych i jedno
opisowe. (

Obowiązuje materiał z kursu i

wykładów)

• Podstawą do wpisania do indeksu zaliczenia

przed-miotu jest wcześniejsze zaliczenie
ćwiczeń rachun-kowych i kursu.

• Osoby które nie zaliczą przedmiotu na ostatnich

zaję-ciach przed kolejnym zaliczeniem muszą
uzyskać po-zytywny wpis z ćwiczeń i zaliczyć kurs.

Ruch mechaniczny

• Ruch mechaniczny – zmiana położenia ciała  konieczne

wskazanie innych ciał względem, których ruch się odbywa

(względne przemieszczanie się ciał)

– Ruch – zmiana w przestrzeni i w czasie

• Układ odniesienia – zbiór nieruchomych względem siebie

ciał służący do rozpatrywania ruchu innych ciał i zegar

odmierzający czas

– Ruch tego samego ciała względem różnych układów odniesienia 

różny charakter (pasażer w pociągu)

• opis ruchu – podanie położenia dla każdej chwili czasu
• Punkt materialny – ciało o znikomo małych rozmiarach w

warunkach danego zagadnienia, o danej masie i położeniu,

które można określić jak położenie punktu geometrycznego

Dynamika

• badanie przyczyn ruchu
• badanie związków między ruchem

ciała a siłami działającymi na ciało

– określenie ruchu ciała pod

działaniem znanych sił

– wyznaczenie sił działających na ciało,

gdy znany jest jego ruch

4

Masa, pęd, siła

• masa – wielkość skalarna

– charakteryzuje właściwości inercjalne ciała, czyli jego

uległość wobec oddziaływań na niego innych ciał

– mechanika klasyczna  masa ciała nie zależy od prędkości
– określenie masy poprzez porównanie z masą innego ciała

wzorca

• pęd – wielkość wektorowa

– wielkość dynamiczna charakteryzująca ruch ciała
– pęd p – iloczyn masy i prędkości ciała

• siła – wielkość wektorowa

– będąca miarą oddziaływań prowadzących do zmiany

prędkości – jeśli ciało o masie m porusza się z

przyspieszeniem a, to pozostaje ono pod działaniem siły F

definiowanej jako

v

m

p







a

m

F







5

Elementy szczególnej teorii

względności

Zasada względności Galileusza

Historia
Doświadczenie Michelsona - Morley’a

Postulaty teorii względności

Transformacje Lorentza

6

Konsekwencje transformacji Lorentza

Dodawanie prędkości

Skrócenie długości

Wydłużenie przedziałów czasowych

Mechanika relatywistyczna

Masa i pęd

Definicja siły

Relatywistyczna energia kinetyczna

Energia całkowita

Efekt Dopplera dla fal elektromagnetycznych

Grawitacja a ogólna teoria względności

7

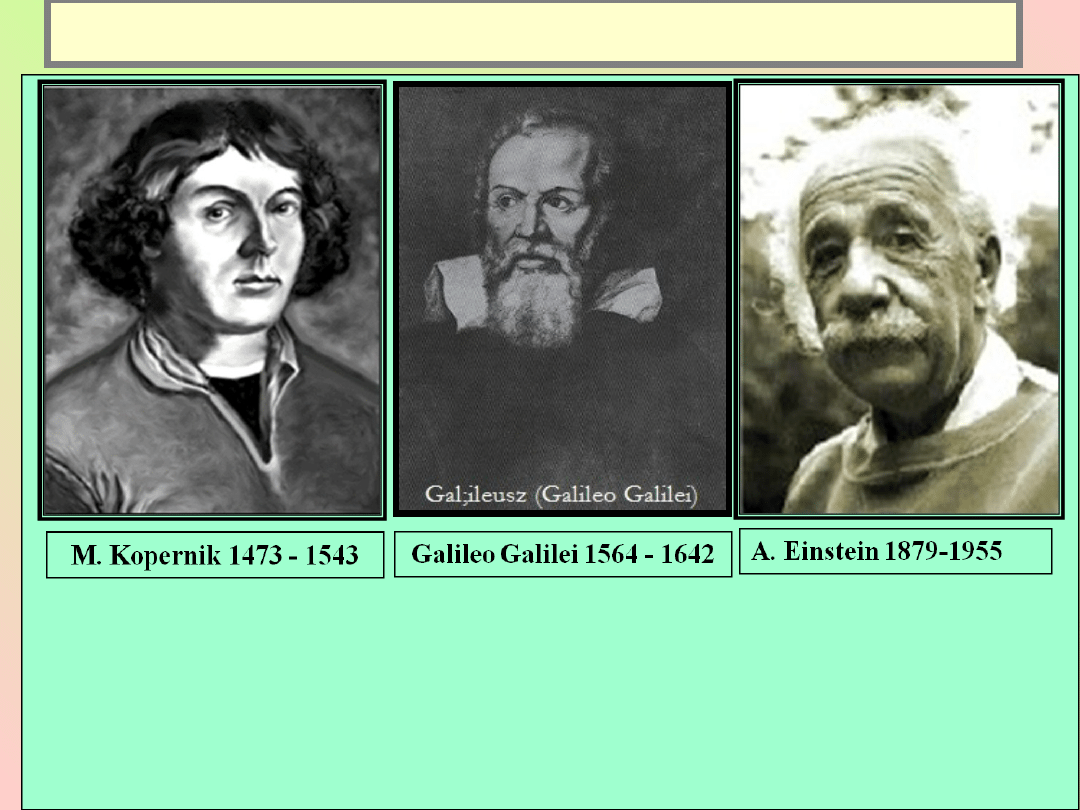
Prekursorzy rozwiązania problemu względności w

fizyce

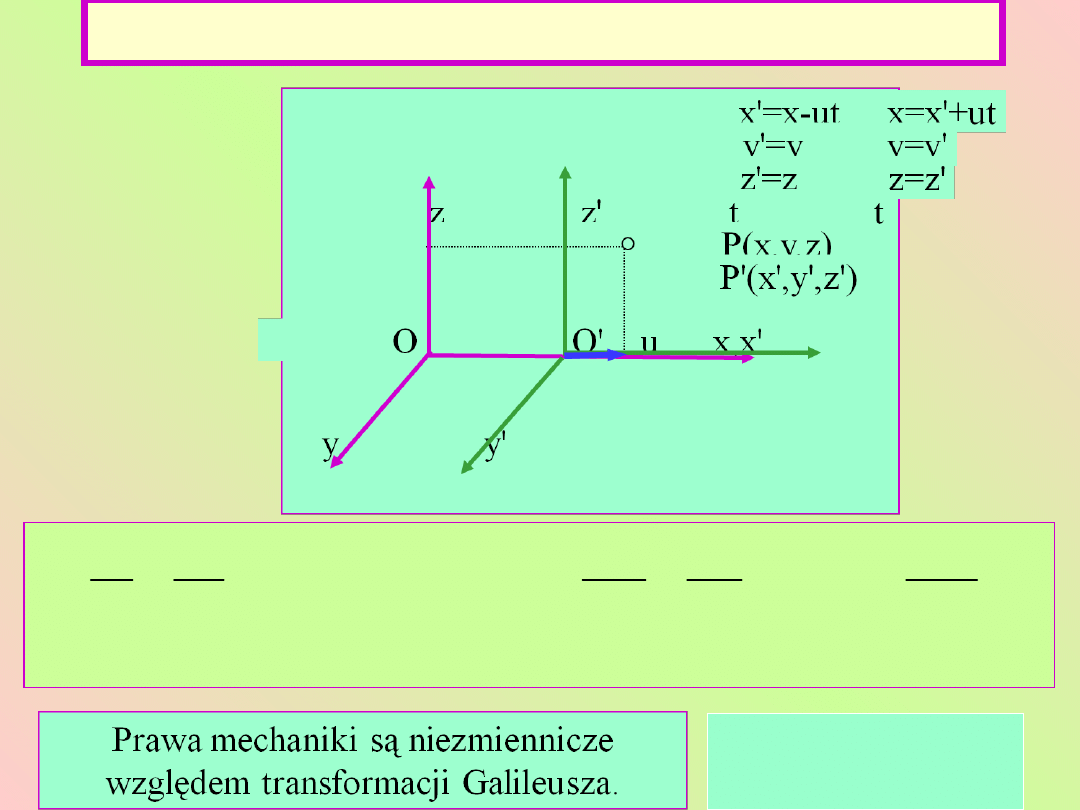
Transformacje Galileusza

Galileusza

cji

transforma

k

niezmienni

a

a

a

dt

x

d

ut

x

dt

d

dt

x

d

a

u

u

dt

dx

dt

dx

























'

'

'

)

'

(

;

'

2

2

2

2

2

v

v

ma

ma

'

Zasada względności Galileusza

Nie istnieje takie doświadczenie
mechani-czne,

przy

pomocy

którego można by stwierdzić
istnienie ruchu absolutnego lub
można by wyróżnić którykolwiek z
ukła-dów inercjalnych lub inaczej:

ze względu na prawa
mechaniki

wszystkie

układy

inercjalne

są

równoważne

.

Względność według Galileusza-Newtona

Pojęcie przestrzeni i czasu według Galileusza

•-istnieje absolutna przestrzeń niezależna od ciał;

•-ciała są "zanurzone" w tej przestrzeni;

•-istnieje

absolutny

czas

płynący

wszędzie

jednakowo i niezależnie od niczego;

•-w przestrzeni obowiązują prawa geometrii
Euklidesa;

•-informacja o zdarzeniach dociera do obserwatora
natychmiast niezależnie od ruchu układu;

•-ciała uczestniczą w dwóch ruchach: jedno
względem drugiego - i tu obowiązuje zasada
względności, oraz w ruchu względem przestrzeni
absolutnej i tu zasada względności nie może być
stosowana.

Względność w fizyce pojmowana była w sensie
mechanicznej interpretacji praw przyrody.

Postulaty teorii

względności

W końcu XIX w. Maxwell i Hertz zaproponowali

koncepcję,

że

światło

jest

promieniowaniem

elektromagnetycznym.

Od kiedy stało się wiadome, że światło ma

właściwości fa-lowe, fizykom wydało się naturalną
koniecznością zapropono-wanie ośrodka, który ten ruch
falowy miałby przenosić. Ośrodek ten był powszechnie
zwany eterem świetlnym.

W 1887 r. Michelson i Morley zaproponowali i

przepro-wadzili eksperyment w celu sprawdzenia natury
eteru świetlnego i wyznaczenia prędkości światła
względem niego.

Gdyby eter istniał, to musiałby przenikać całą

przestrzeń i musiałby być pierwotnym i bezwzględnym
układem odniesienia dla światła.

12

13

Fizycy wyciągnęli zatem wniosek, że Ziemia musi

albo pozostawać w spoczynku w tym eterze albo
poruszać się wzglę-dem niego, a w konsekwencji
inercjalny układ odniesienia dla światła musi być w
spoczynku lub poruszać się względem Ziemi.

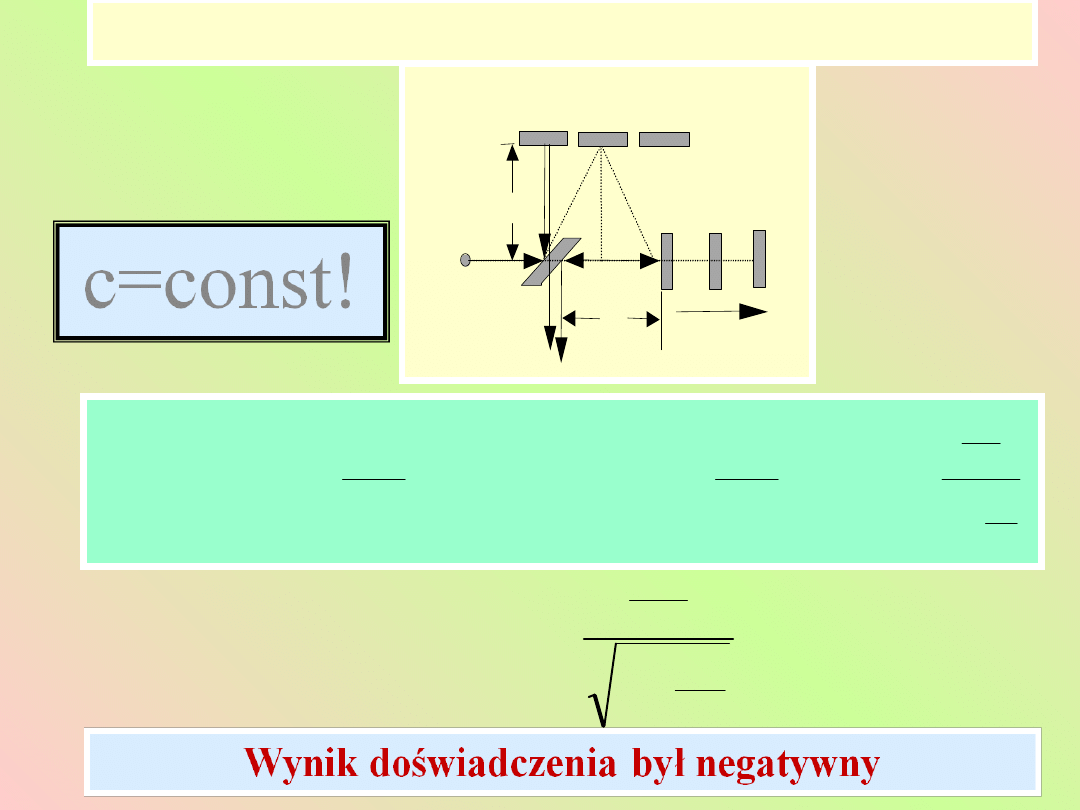
Doświadczenie Michelsona - Morley’a

A A’ A”

ct

3

ct

3

L B B’ B”
ct

1

S P ct

2

L u

ct

L ut

t

L

c u

ct

L ut

t

L

c u

t

t

L

c

u
c

1

1

1

2

2

2

1

2

2

2

2

1

 

 



 









 



;

;

;

3

2

1

2

2

3

2

3

2

2

3

2

1

2

2

)

(

)

(

t

t

t

c

u

c

L

t

ut

L

ct

















”Negatywny” wynik doświadczenia Michelsona-

Morleya spowodował przewrót w sposobie myślenia
fizyków. Powstała konieczność głębszego spojrzenia w
naturę przestrzeni i czasu.

Doświadczenie

Michelsona-Morleya

prowadzi

również do wniosku, że nie ma wyróżnionego układu
odniesienia, względem którego ośrodek w którym
rozchodziłyby się fale elektromagnetyczne byłby w
spoczynku. Z tego powodu Einstein odrzucił pojęcie eteru
i w 1905 r.

sformułował szczególną zasadę względności:

wszystkie prawa fizyki muszą być takie same we
wszystkich układach inercjalnych poruszających się
względem

siebie

ruchem

jednostajnym

prostoliniowym.

Nie

można

też

stwierdzić

bezwzględnego

spoczynku jakiegokolwiek układu.

15

Postulaty STW –Einsten 1905r

c=cons

t!

•Prędkość światła jest taka sama we
wszystkich

iner-cjalnych

układach

odniesienia

•Zasada względności obowiązuje
dla wszystkich praw fizyki.

Teoria względności opiera się na
dwóch postulatach:

o        

szczegółowej

zasadzie

względności;

o         stałości prędkości światła w
próżni.

18

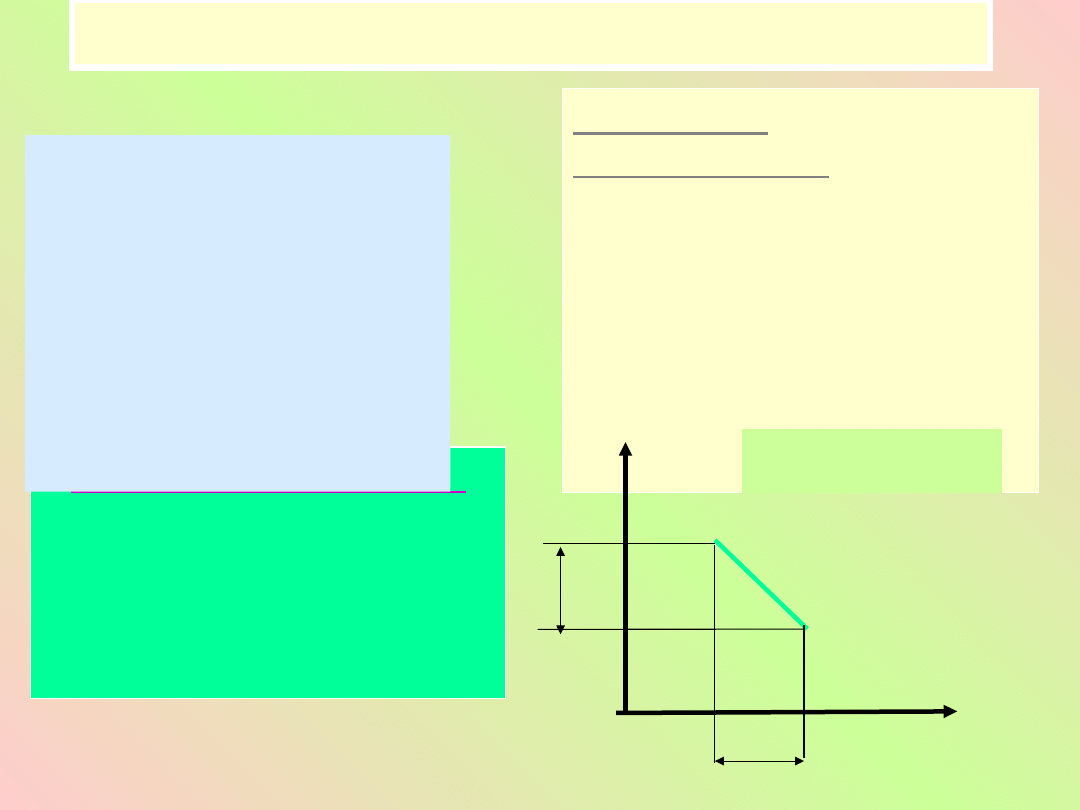
Wielkości bezwzględne i względne

Wielkości względne

•

prędkość v

•

odległość x

•

czas

t

Wielkości
bezwzględne

•

Prędkość światła c

•

masa spoczynkowa m

•

“interwał”

czasoprzestrzenny

•

2

2

2

2

dx

dt

c

ds





Pewne

wielkości

fizyczne

są

niezależnie

od

układu odniesienia
i obserwatora, a
inne

zależą

od

wzglę-dnego ruchu
obserwato-rów

ct

x

ds

dx

cd
t

Transformacje Lorentza

Transformacje Galileusza nie odpowiadają postulatom
teorii względności, ponieważ według teorii względności
prędkość światła jest równa w różnych układach
inercjalnych.

Później

przedstawimy

sposób

wyprowadzenia nowych transformacji, które będą
odpowiadały postulatom teorii względności; noszą one
nazwę transformacji Lorentza.



v



r

1



r

2

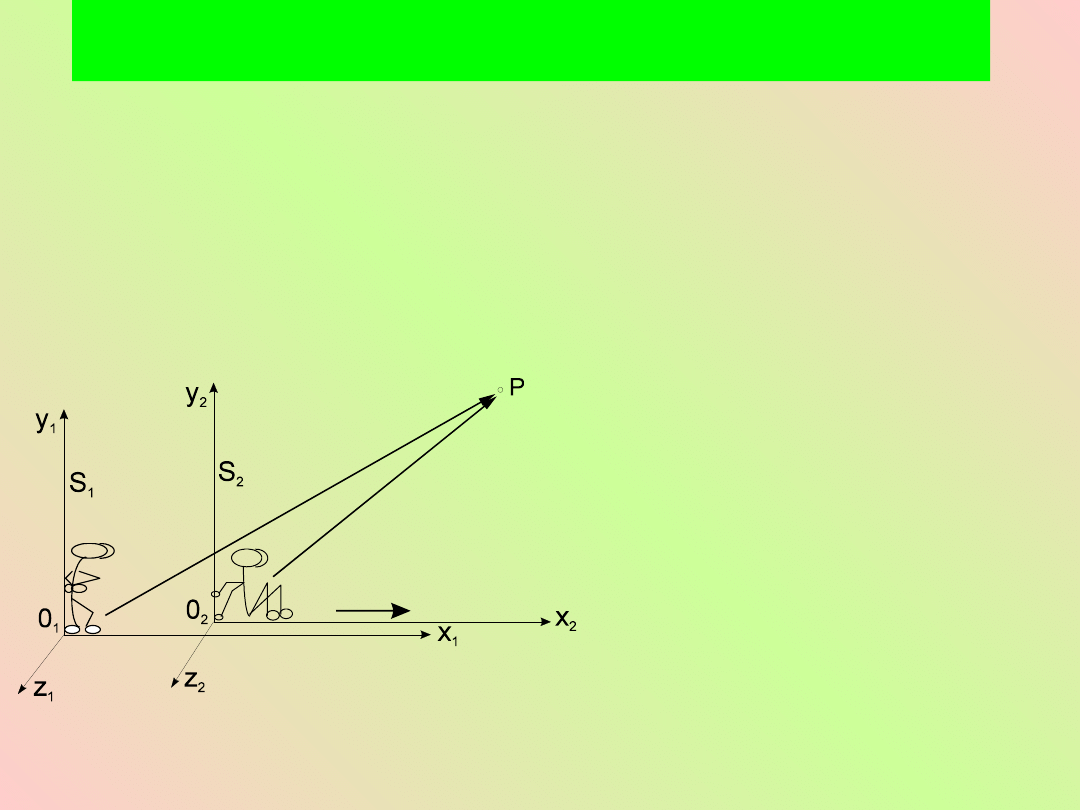
Rozważmy sytuację w
której układ inercjalny
O

1

jest w spoczynku,

a układ inercjalny O

2

porusza się ruchem
jednostajnym
prostolinio-wym

z

prędkością v=const w
kierunku osi x.

20



v



r

1



r

2

W chwili t

1

= t

2

= 0 ze

wspólnego początku układów
O

1

i O

2

wysłany jest promień

światła zdążający do punktu
P

o

współrzędnych

przestrzennych i czasowych
równych odpowie-dnio:

x

1

, y

1

, z

1

, t

1

i

x

2

, y

2

, z

2

, t

2

w układach O

1

i O

2

. Odległości r

1

i r

2

z odpowiednich

początków układów do punktu P są określone wzorami:

r

1

= ct

1

;

r

2

= ct

2

. (12)

Jesteśmy więc zmuszeni przyjąć, że czasy t

1

i t

2

mierzone

przez obserwatorów O

1

i O

2

są różne, pomimo że jest to

sprzeczne z naszym życiowym doświadczeniem. Na
podstawie wyrażeń (12) otrzymamy

21

2

2

2

2

2

2

2

2

2

2

1

2

2

1

2

1

2

1

t

c

z

y

x

t

c

z

y

x













(13)

a z warunku symetrii y

1

= y

2

oraz z

1

= z

2

. Uwzględniając

to w wyrażeniach (13) mamy:

2

1

2

2

1

2

2

2

2

2

t

c

x

t

c

x







(14)

Związki transformacyjne pomiędzy układami O

1

i O

2

powinny spełniać pewne warunki formalne:
o    

transformacja musi być liniowa; tzn. zdarzeniu w

jednym

układzie

inercjalnym

musi

odpowiadać

pojedyncze zdarzenie w drugim układzie o jednoznacznie

określonych współrzędnych;
o     ruch jednostajny musi przekształcać się w ruch

jednostajny;
o    dla małych prędkości transformacja musi sprowadzić

się do transformacji Galileusza.

22

W związku z powyższym









1

1

2

x

b

t

a

t

z

z

y

y

vt

x

x













1

2

1

2

1

1

2



gdzie γ, a oraz b są stałymi. Wstawimy teraz wyrażenia
(15) do równania (14), otrzymujemy

(15)







 



0

2

2

1

2

2

2

2

2

2

1

2

2

2

1

1

2

2

2

2

2

1



















c

c

a

v

γ

t

bc

a

v

γ

t

x

c

b

a

γ

x

Ponieważ wyrażenie to jest tożsamościowo równe zeru,
więc

0

0

2

2

0

1

2

2

2

2

2

2

2

2

2

2

2

2



















c

c

a

v

γ

bc

a

v

γ

c

b

a

γ

(16) Równania te

rozwiązujemy
względem stałych γ,
a i b

23

Otrzymujemy wówczas

2

1

1



















c

v

a



2

c

v

b 

„czynnik
Lorentza”

=
β

Wzory transformacyjne (15) przybierają teraz
postać:















 



































1

1

2

1

2

1

2

1

2

1

2

1

1

2

1

1

2

1

1

x

c

β

t

γ

β

x

c

v

t

t

z

z

y

y

vt

x

γ

β

vt

x

x

(19)

24

Transformacje odwrotne są dane wzorami:















 



































2

2

2

2

2

2

1

2

1

2

1

2

2

2

2

2

1

1

1

x

c

β

t

γ

β

x

c

v

t

t

z

z

y

y

vt

x

γ

β

vt

x

x

Transformacje te znane są jako transformacje

Lorentza, od nazwiska holenderskiego fizyka H.A.
Lorentza, który wprowadził je w 1890 r.

25

Transformacja Lorentza















 



































1

1

2

1

2

1

2

1

2

1

2

1

1

2

1

1

2

1

1

x

c

β

t

γ

β

x

c

v

t

t

z

z

y

y

vt

x

γ

β

vt

x

x

Konsekwencje transformacji

Lorentza

Dodawanie prędkości

W celu wyprowadzenia relatywistycznego prawa
dodawania prędkości musimy użyć transformacji
Lorentza (19). Prędkość wzdłuż osi x w układzie O

1

wyraża się wzorem ,

zaś w układzie O

2

wzorem

(dla

uproszczenia

rozważamy

przypadek

jednowymiarowy). Różniczkując pierwsze i ostatnie
równanie (19) otrzymujemy:

1

1

1

dt

dx

v 

2

2

2

dt

dx

v 

2

1

1

2

1









vdt

dx

dx

2

1

2

1

2

1









dx

c

v

dt

dt

27

stąd

1

1

2

1

1

1

2

1

1

1

2

2

2

1

dt

dx

c

v

v

dt

dx

dx

c

v

dt

vdt

dx

dt

dx

v















2

1

1

2

1

c

v

v

v

v

v







Otrzymaliśmy wzór na
doda-wanie prędkości,
który jest ogólniejszy od
wzoru klasy-cznego.

28

Skrócenie długości

Z teorii względności wynika, że ciała ruchome doznają
skrócenia swoich wymiarów w kierunku ich ruchu.
Załóżmy, że pewien pręt ma długość l

o

i porusza się wraz

z układem O

2

. Pręt ten w układzie O

2

spoczywa i położony

jest równolegle do osi x. Długość tego pręta jest wtedy
zdefiniowana jako różnica między współrzędnymi jego
końców A i B w układzie O

2

2

2

A

B

o

x

x

l





W układzie O

1

, pręt ten będzie się poruszał z prędkością

v. W celu wyznaczenia długości l tego pręta w układzie
O

1

należy wyznaczyć w tej samej chwili współrzędne jego

końców x

B1

i x

A1

, gdy je pręt mija. Z transformacji

Lorentza

 

2

1

1

2

1

c

v

vt

x

x

B

B







 

2

1

1

2

1

c

v

vt

x

x

A

A







29

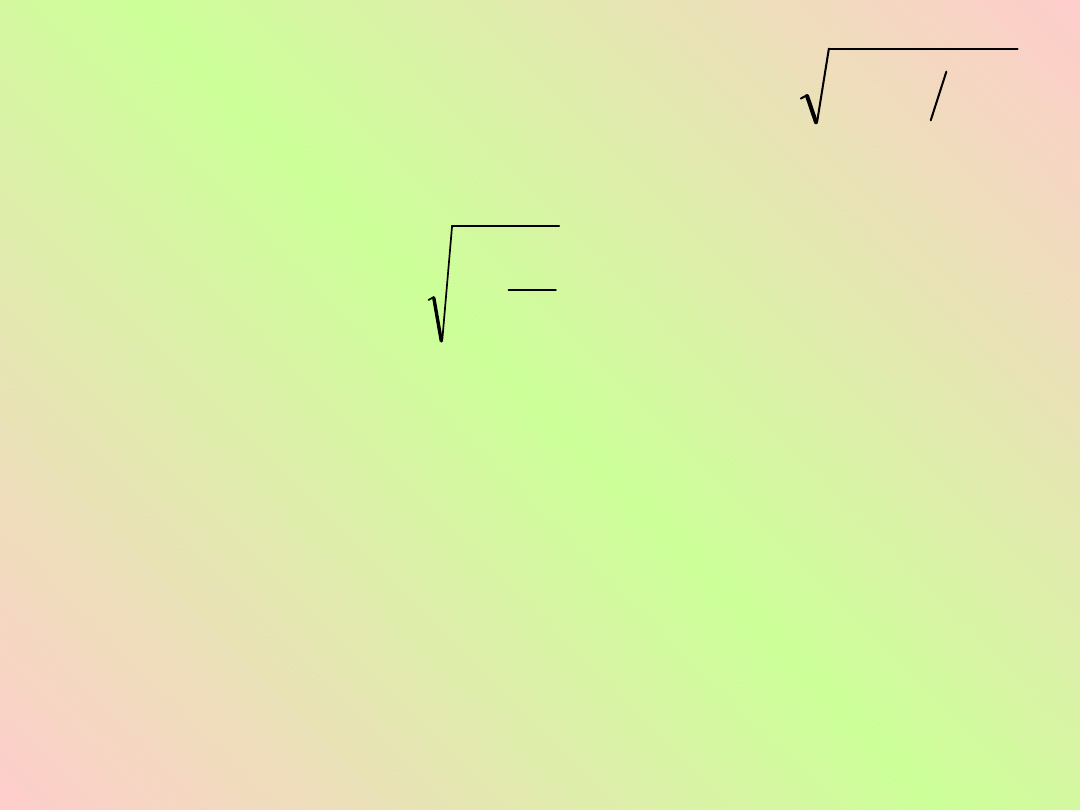
Wobec tego

 

2

2

2

1

1

1

c

v

)

x

x

(

x

x

A

B

A

B









Widzimy więc, że długość l

o

obserwator w układzie O

1

oceni jako

2

2

1

c

v

l

l

o





a więc krótszą

Ogólnie możemy powiedzieć,

że liniowe rozmiary

ciała są największe w tym układzie, względem
którego ciało spoczywa

. Skrócenie długości

zachodzi tylko w przypadku długości mierzonych
równolegle do kierunku ruchu względnego.

Należy tu wspomnieć, że Lorentz i Fitzgerald uważali, że

zjawisko

skrócenia (kontrakcji) przedmiotu znajdującego się w ruchu jest
spowodowane pewną siłą działającą na ten przedmiot w czasie
jego przechodzenia przez stacjonarny eter

. Einstein przyjął

zupełnie odmienny punkt widzenia, a mianowicie, że skrócenie to
jest właściwością samej przestrzeni jako takiej i że
bezwzględny lub wyróżniony spośród innych układ odniesienia nie
istnieje.

30

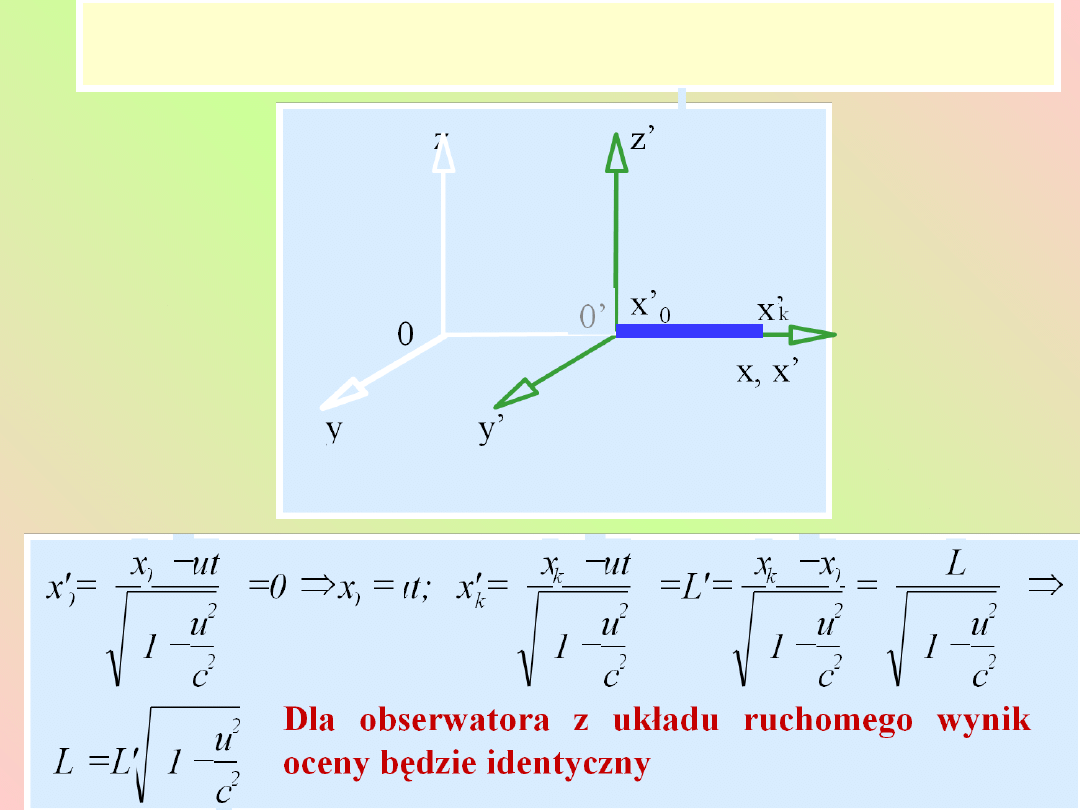
Skrócenie długości w układzie poruszającym

się widziane przez obserwatora nieruchomego

2

2

2

2

2

2

0

2

2

0

2

2

0

0

1

'

1

'

1

'

'

1

'

'

;

'

'

0

1

'

'

c

u

L

L

c

u

L

c

u

x

x

L

c

u

ut

x

x

ut

x

c

u

ut

x

x

k

k

k







































Skrócenie długości w układzie nieruchomym

widziane przez obserwatora ruchomego

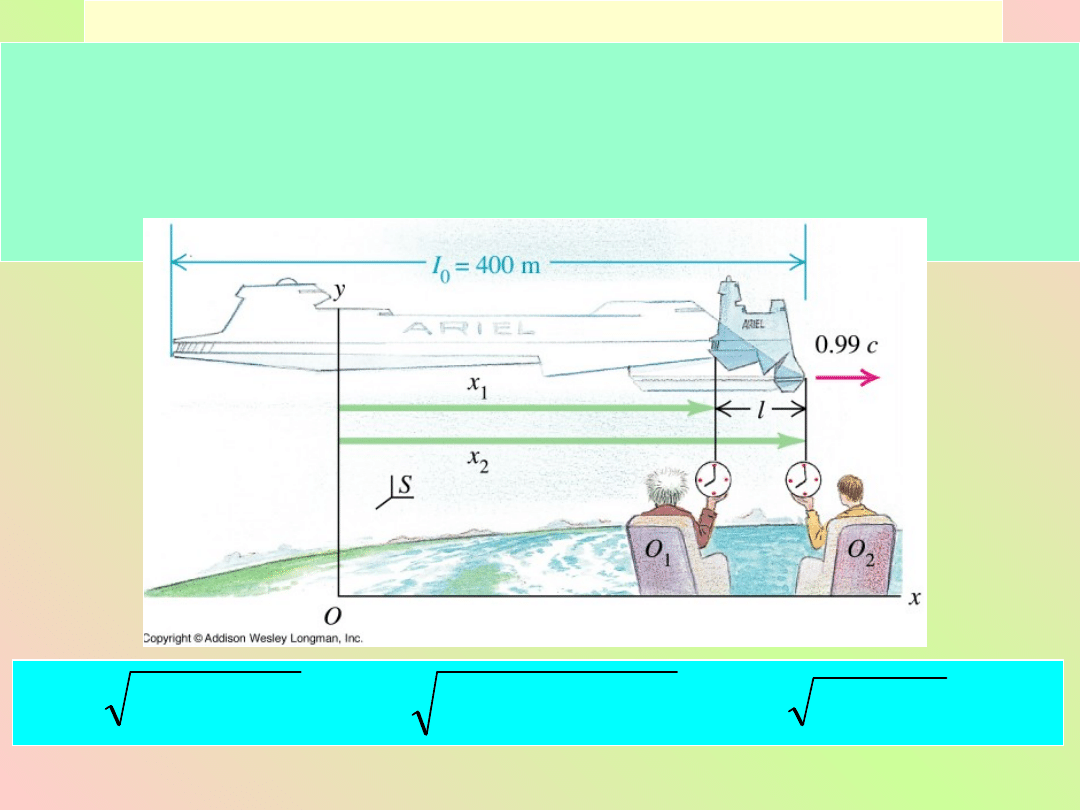
Załoga statku kosmicznego mierzy jego długość i
otrzymuje wynik l

o

= 400m. Jaką długość statku

zmierzy obserwator na Ziemi, jeśli wiadomo, że
prędkość statku u = 0.8c

240

64

.

0

1

400

)

/

8

.

0

(

1

400

/

1

2

2

2

0















c

c

c

u

l

l

Przykład

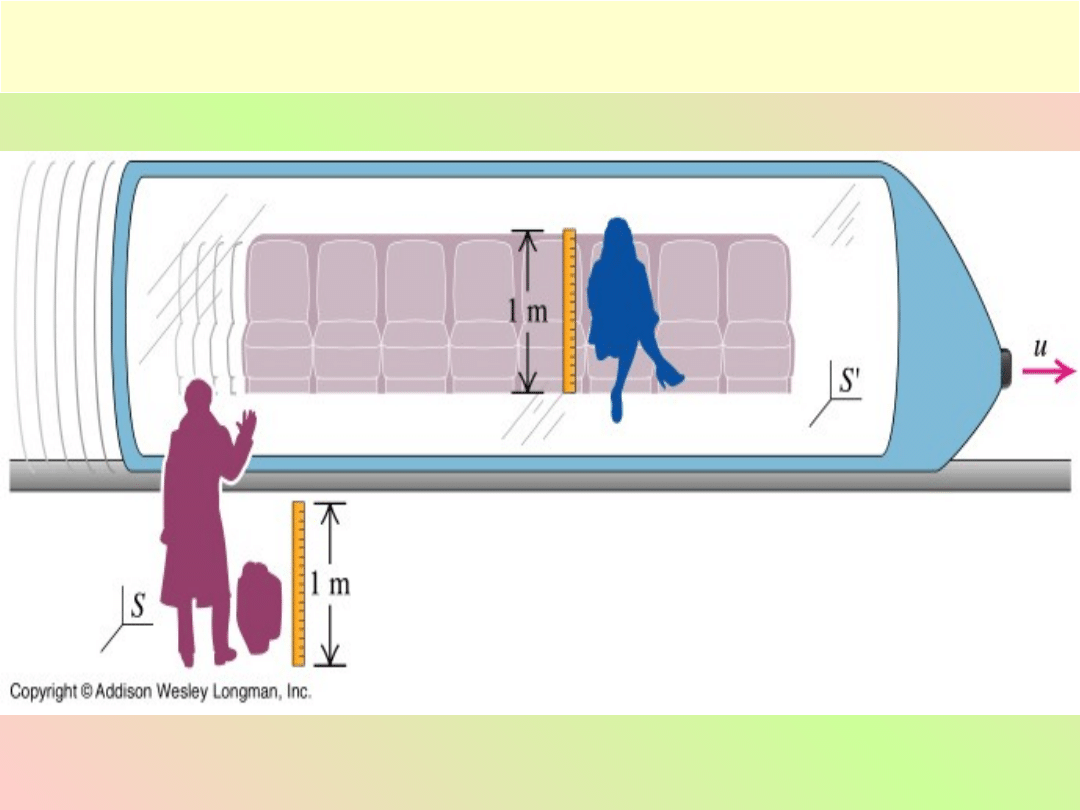
Długość w kier. prostopadłym do kier. ruchu układu

nie ulega zmianie

'

l

l







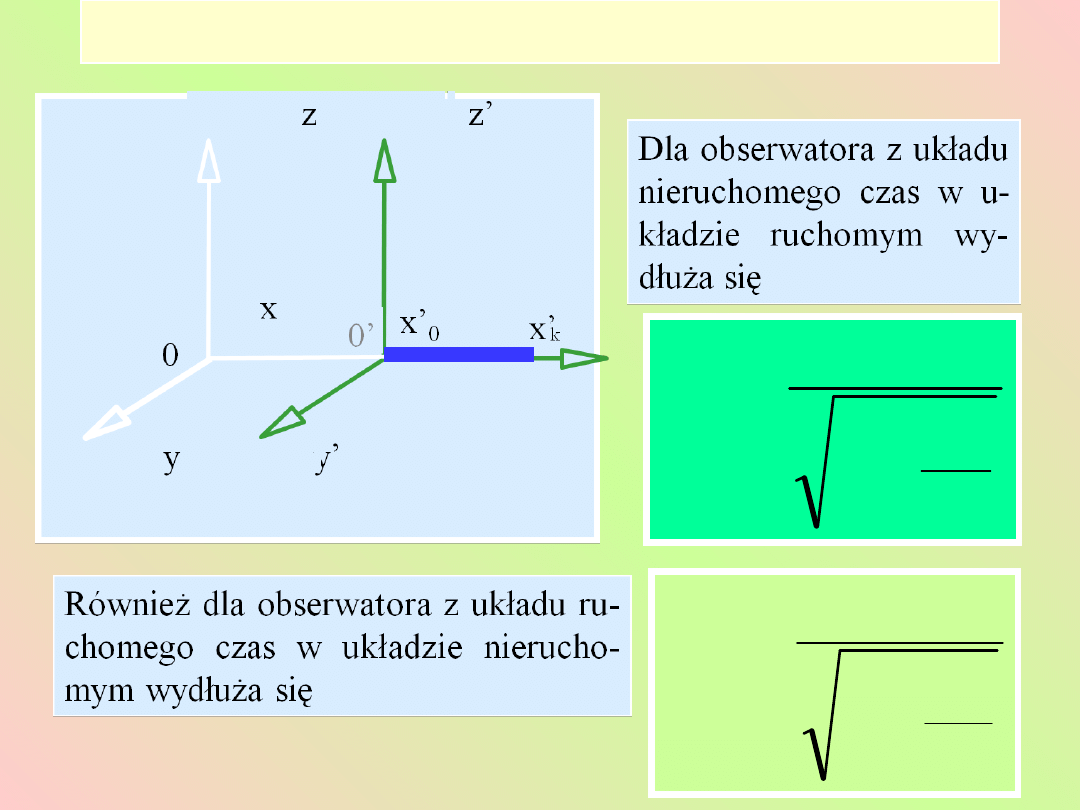
Wydłużenie przedziałów

czasowych

Następnym

ważnym

wnioskiem

z

teorii

względności jest niejednakowy przebieg czasu w
układach inercjalnych.

Wyobraźmy sobie zdarzenie zachodzące w punkcie A i
chwili t

A

(rys.). Rozważmy następnie inne zdarzenie

zachodzące w tym samym punkcie, ale w innym czasie
t

B

. Oba zdarzenia są rejestrowane w układzie O

2

, w

którym punkt A jest w spoczynku. Przedział czasu
między dwoma zdarzeniami jest równy

2

2

2

A

B

t

t

T





x

A 2

y

A 2

O

1

O

2

x

2

x

1

y

1

y

2

A

v

35

Rozważmy teraz tę samą parę zdarzeń, ale obserwowaną
z układu O

1

, poruszającego się równolegle do osi x układu

O

2

, z prędkością względną –v. Oczywiście przedział

czasowy obserwowany z układu O

1

jest określony wzorem

1

1

1

A

B

t

t

T





ale

w

układzie

O

1

wartości

współrzędnych

przestrzennych pierwszego zdarzenia nie będą takie
same jak drugiego zdarzenia, jak to było w układzie
spoczynkowym O

2

. Chwili początkowej t

A1

odpowiada

współrzędna x

A1

, chwili końcowej t

B1

– współrzędna x

B1

.

Z transformacji Lorentza (19) mamy

 

 

2

1

2

1

2

1

c

v

x

c

v

t

t

A

A

A







 

 

2

1

2

1

2

1

c

v

x

c

v

t

t

B

B

B







Po

odjęciu

stronami

tych

równości,

otrzymujemy

36

 





 

2

1

1

2

1

2

1

c

v

x

x

c

v

T

T

A

B









ale

1

1

1

vT

x

x

A

B





czyli

 

2

1

2

1

c

v

T

T





1

2

T

T 

Zatem

przedział czasu, który rozdziela dwa

następujące po sobie zdarzenia, w każdym
układzie poruszającym się względem układu
spoczywającego, jest dłuższy niż w układzie
spoczywającym.

Ponieważ

mierzony

przedział

czasowy może zostać wydłużony jedynie wskutek
zwolnienia chodu zegara używanego do pomiaru tego
przedziału, więc powyższy wniosek jest równoważny
stwierdzeniu, że poruszające się zegary chodzą wolniej
niż zegary w spoczynku.

37

Wydłużenie czasu. Czas własny

2

2

1

'

c

u

T

T









2

2

1

'

c

u

T

T









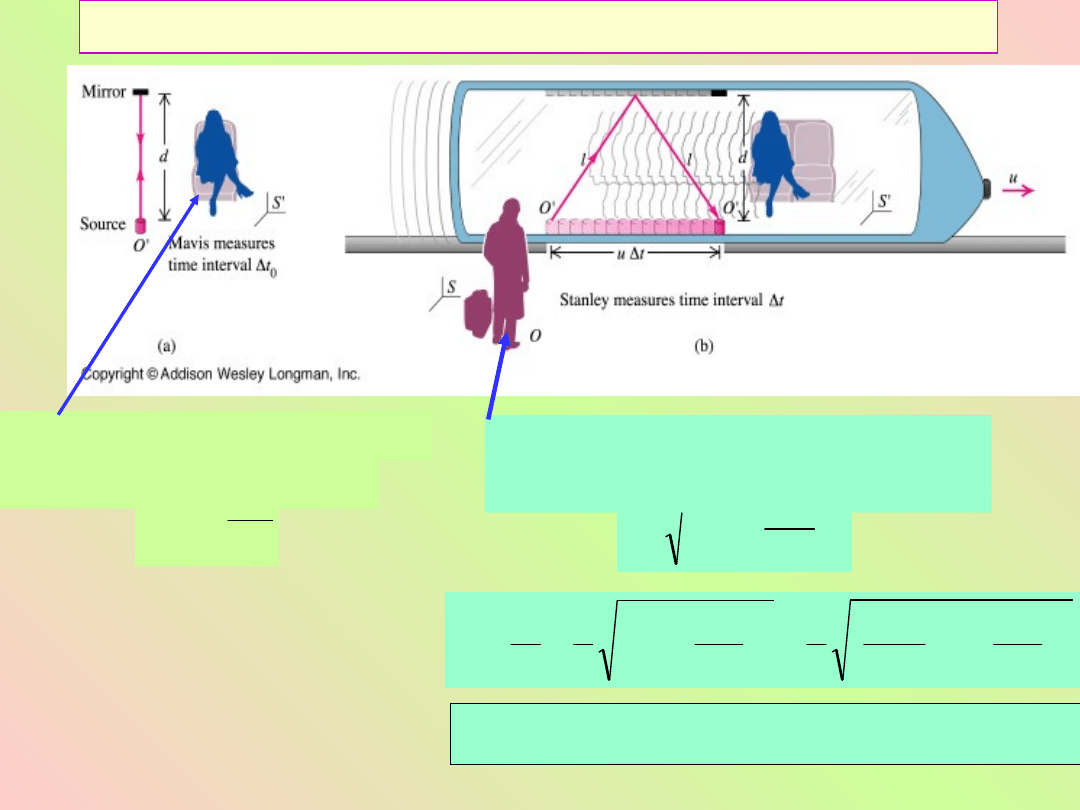
Dylatacja czasu

Czas w ruchu jest zwany czasem
własnym

Czas własny płynie wolniej !!!

2

2

1

1

c

u







0

0

2

2

0

1

t

c

u

t

t















γΔt

gdzi
e

Dylatacja czasu

2

2

)

2

(

t

u

d

l







2

2

0

2

2

)

2

(

)

2

(

2

)

2

(

2

2

t

u

t

c

c

t

u

d

c

c

l

t



















0

t



Mavis mierzy
odstęp czasu

:

Stanley mierzy odstęp
czasu:

Czas własny płynie wolniej !!!

t



c

d

t

2

0





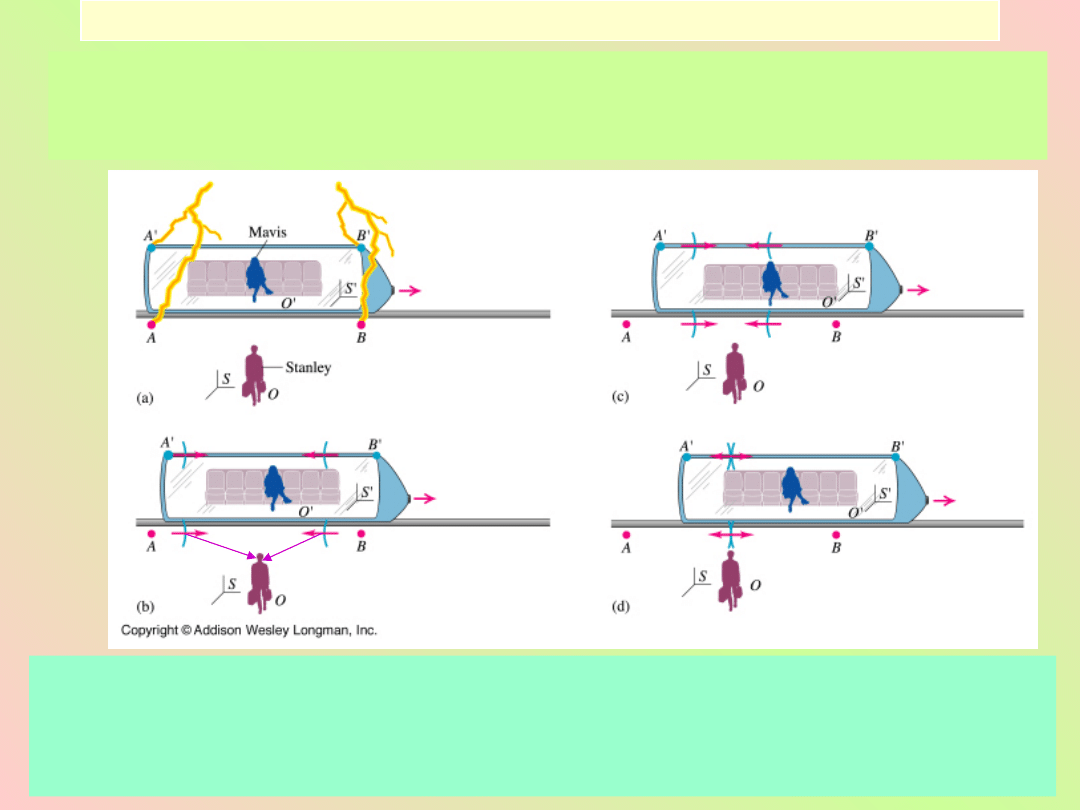
Względność jednoczesności zdarzeń

Dwa zdarzenia jednoczesne w jednym układzie odniesienia nie
są jednoczesne z punktu widzenia obserwatora znajdującego się
w układzie odniesienia poruszającym się względem pierwszego.

Mavis twierdzi, że piorun uderzył najpierw w prawe drzwi wagonu,
bo zbliża się do fali nadbiegającej od strony tych drzwi a oddala
od fali nadbiegającej od lewej strony. Wg. Stanleya, piorun
uderzył jednocześnie w prawe i lewe drzwi.

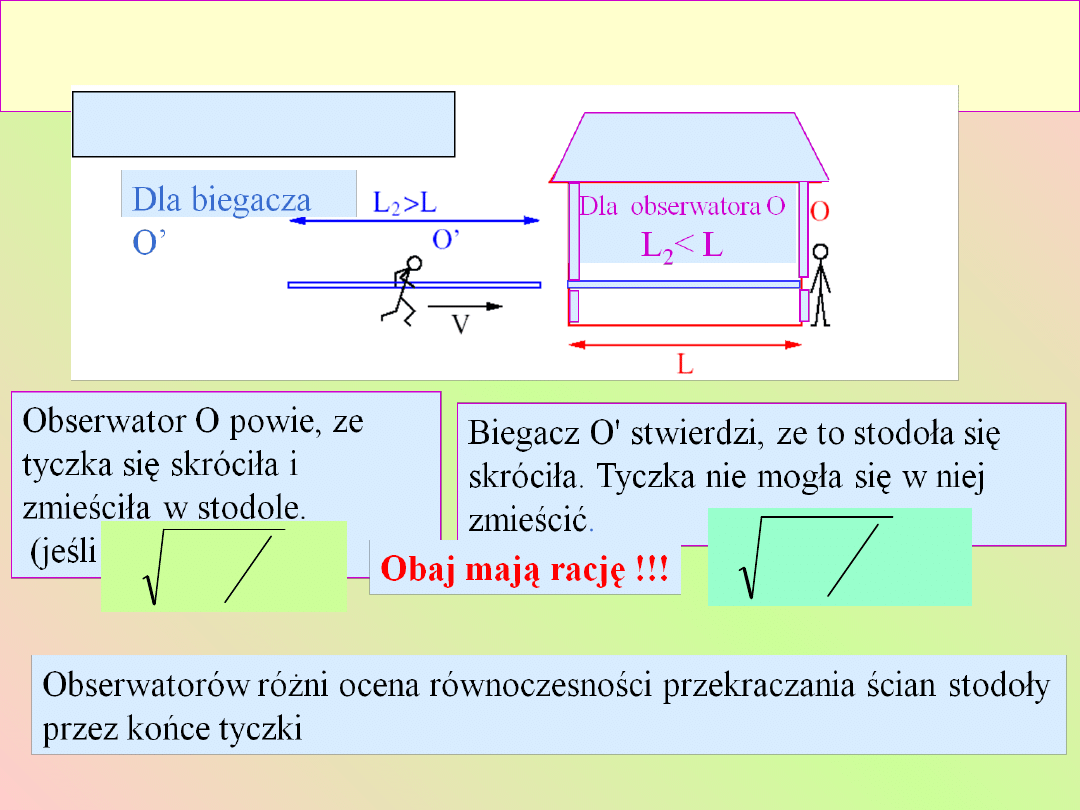
Skrócenie długości Lorentza - paradoks „tyczki w
stodole”

L

c

L





2

2

1

2

v

2

2

1

L

c

L





2

v

Dokładność GPS zależy od STW!

(GPS) Global Positioning
System

•Błąd pomiaru czasu rzędu

miliardowej części sekundy

powoduje błąd pomiaru

położenia rzędu 50 cm.

•Ze względu na ruch satelity

czas płynie wolniej o ok. 10

-8

s.

Mniejsza grawitacja nieznacznie

zmniejsza tę różnicę.

•Koniecznie zatem należy

uwzględnić STW i OTW!

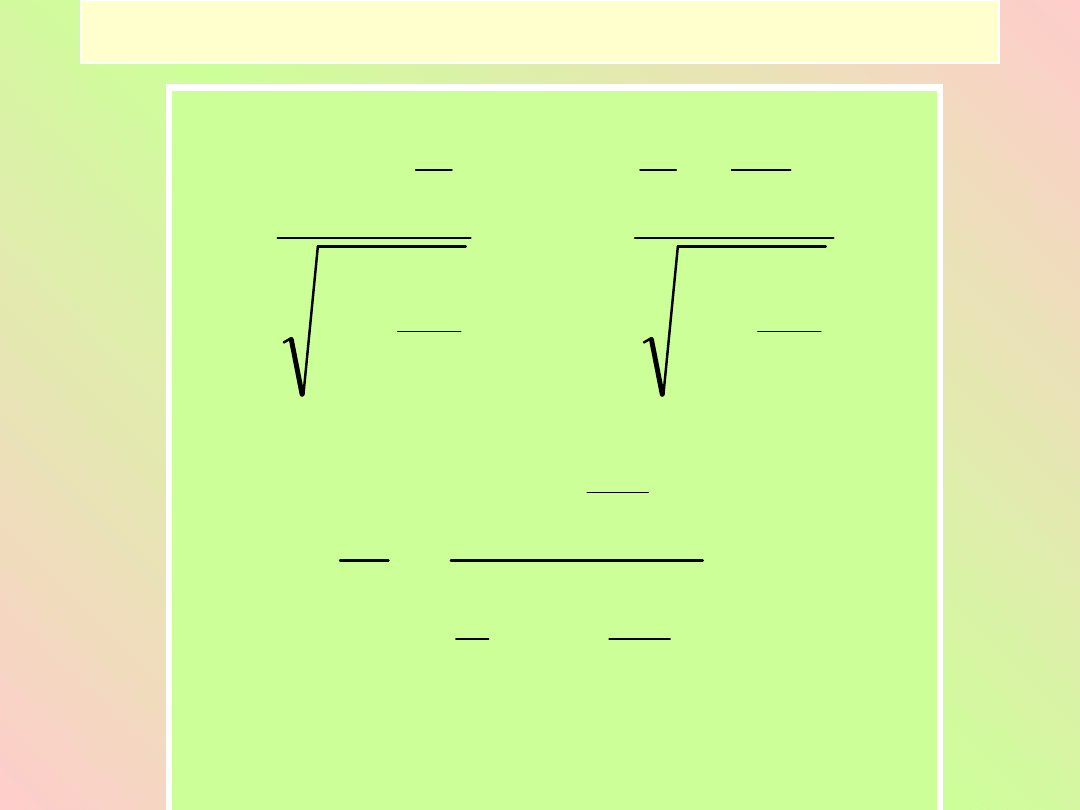
Prędkość światła

c

c

czyli

c

c

ux

x

c

c

ux

x

t

x

c

c

u

x

c

u

c

x

t

c

u

c

x

u

x

x















 



















'

;

1

'

'

'

;

1

'

;

1

'

2

2

2

2

2

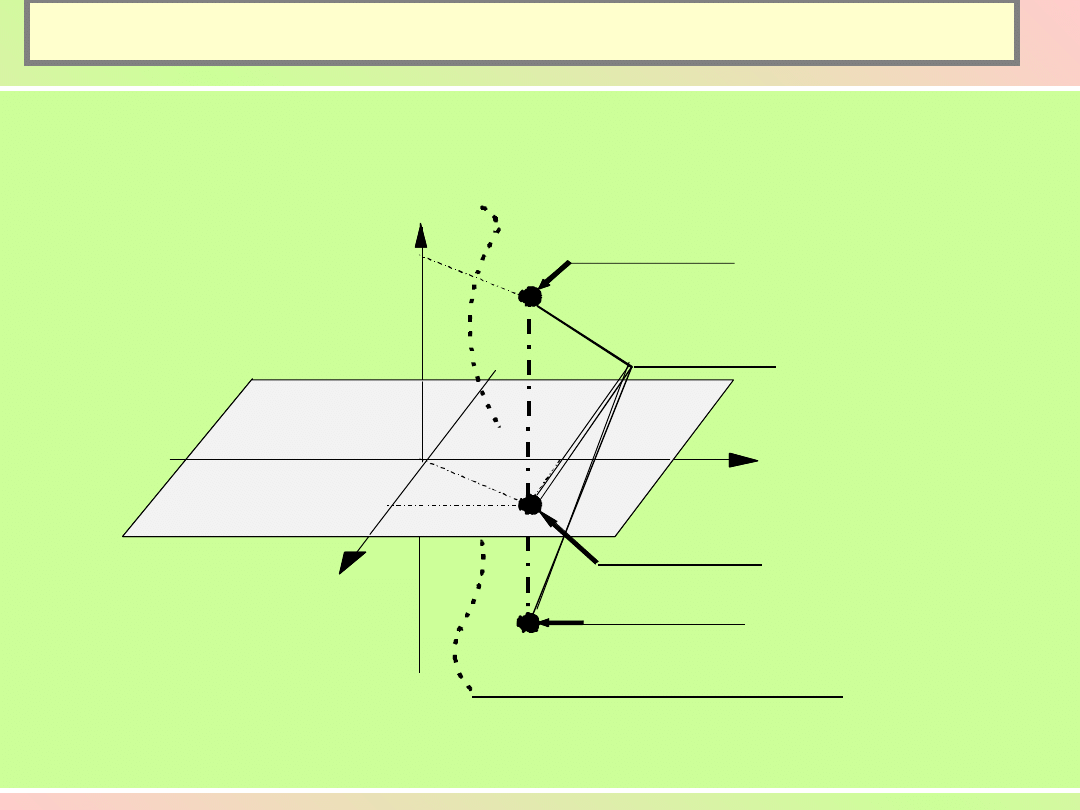
Czasoprzestrzeń.

x

y

t

zdarzenie

zdarzenie

w terazniejszosci

zdarzenie

w przeszlosci

w przyszlosci

czas

czas

T E R A Z

J U T R O

W C Z O R A J

PUNKT

SWIATA

Linia swiata(droga zycia)

punktu substancjonalnego

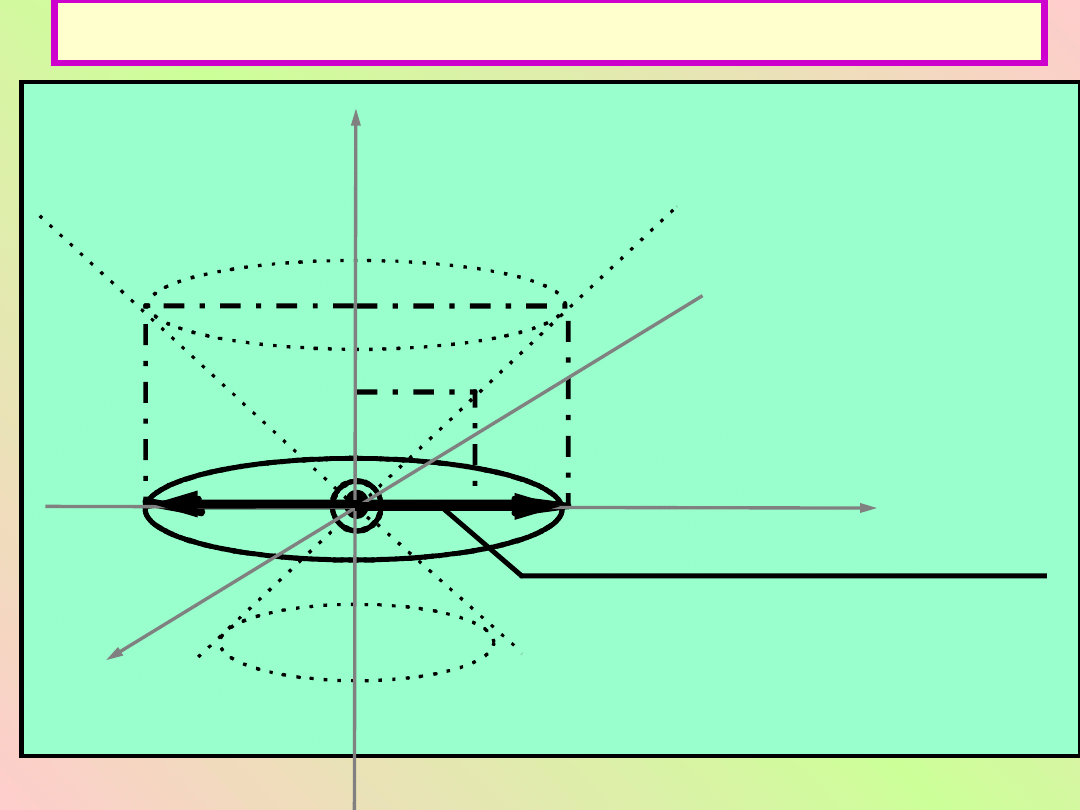
Czasoprzestrzeń.

ict

x=ct (stożek światła)

Informacja

o zdarzeniu w t=0,x=0

,y=0

x

y

absolutna przeszłość

absolutna przyszłość

Mechanika relatywistyczna

Masa i pęd

W mechanice klasycznej pęd ciała jest definiowany
jako

v

m

p







Prawo zachowania pędu izolowanego układu cząstek
jest najbardziej fundamentalnym prawem fizyki.
Izolowany układ cząstek m

1

, m

2

, ...., m

n

, nie

podlegający

działaniu

sił

zewnętrznych,

będzie

zachowywał się w czasie i przestrzeni w taki sposób, że

const

v

m

i

i

i







Kiedy zdarzenie obserwuje się z różnych, poruszających
się układów odniesienia, nie ma powodu oczekiwać, że
przestrzeń stanie się niejednorodna. Musimy zobaczyć,
jak zachowuje się powyższe równanie gdy zastosujemy
transformację Lorentza dla poruszających się układów
współrzędnych.

47

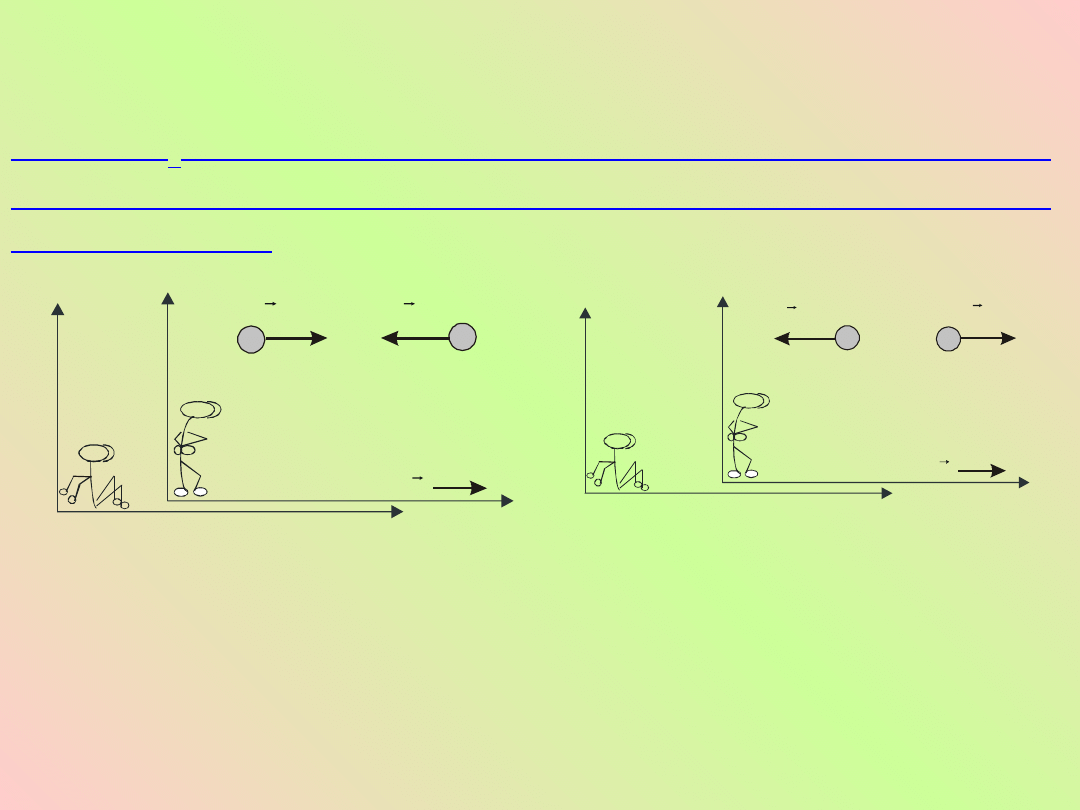
Przewidując komplikacje dotyczące masy jakie mogą
powstać, przypisujemy masie specjalny symbol m

o

.

Masa m

o

jest masą ciała w spoczynku, mierzoną w

naszym układzie odniesienia i nosi nazwę masy
spoczynkowej.

y

1

y

2

x

1

x

2

O

1

O

2

p r z e d z d e r z e n ie m

( a )

v

2

A

v

2

B

v

y

1

y

2

x

1

x

2

O

1

O

2

p o z d e r z e n iu

( b )

'

2

B

v

'

2

A

v

v

Rys. (a) Obserwator O

2

widzi dwie kule zbliżające się do siebie

z jednakowymi prędkościami. (b) Obserwator O

2

będzie widział

kule odskakujące z równymi ale przeciwnie skierowanymi
prędkościami.

48

Rozważmy dwie identyczne i idealnie sprężyste kule w
poruszającym się układzie O

2

, każda o masie

spoczynkowej m

o

(rys.). W poruszającym się układzie

O

2

, kule A i B mają prędkości odpowiednio równe

V

v

V

v

B

A















2

2

W wyrażeniach na prędkość zastosujemy transformację
Lorentza, aby powiązać obserwacje tego samego
zjawiska z obu układów. Z transformacji Lorentza
wynika, że w układzie O

1





 

c

V

v

V

c

v

v

v

v

A

A

A

















1

1

2

2

1





 

c

V

v

V

c

v

v

v

v

B

B

B



















1

1

2

2

1

Gdzie



= v/c

(31)

(32)

49

Jeżeli suma mas obserwowana z układu O

1

jest równa

M, to ta masa pozostanie stała w procesie zderzenia i
w chwili zderzenia mamy

Mv

v

m

v

m

B

B

A

A





1

1

1

1

gdzie

1

1

B

A

m

m

M





Zatem, podczas gdy obserwator O

2

widzi masy chwilowo

w spoczynku, obserwator O

1

widzi, że poruszają się one z

prędkością v. Z ostatniego równania mamy

















1

1

1

1

1

1

1

1

A

A

B

B

B

B

A

A

v

v

M

v

v

m

v

v

M

v

v

m













(34)

Po zastosowaniu równań
transformacyjnych (31) i
(32)

i

uproszczeniu,

stosunek wyrażeń (34)
wynosi

 

 

c

V

c

V

m

m

B

A











1

1

1

1

(35)

50

Korzystając z wyrażenia (31) otrzymujemy

co można przekształcić algebraicznie, otrzymując

Podobnie, korzystając z równania (32), otrzymujemy





 





2

2

2

2

2

1

1

1

1

c

V

c

v

V

c

v

A













 

 

c

V

c

V

c

v

A















1

1

1

1

2

2

2

2

1

 

 

c

V

c

V

c

v

B















1

1

1

1

2

2

2

2

1

Czynniki

oraz

mogą być teraz wyznaczone z powyższych równań i
podsta-wione do równania (35).

 





c

V





1

 





c

V





1





 

c

V

v

V

c

v

v

v

v

A

A

A

















1

1

2

2

1

 

 

c

V

c

V

m

m

B

A











1

1

1

1

51

Otrzymujemy w ten sposób następujące wyrażenie na
stosunek dwóch mas widzianych z układu O

1









2

1

2

1

1

1

1

1

c

v

c

v

m

m

A

B

B

A







Zatem masa widziana z poruszającego się układu
odniesienia nie jest równa m

o

, ale jest odwrotnie

proporcjonalna do czynnika Lorentza , który jest
zawsze większy od 1, ale zbliża się do 1 gdy prędkość
staje się bardzo mała w porównaniu z prędkością
światła c. Pozwala to sformułować ogólne twierdzenie,
że





2

1

1

c

/

v







o

B

B

A

A

m

c

v

m

c

v

m









2

2

1

1

2

2

1

1

1

1

Czyli >>>

52

o

o

m

m

m











2

1

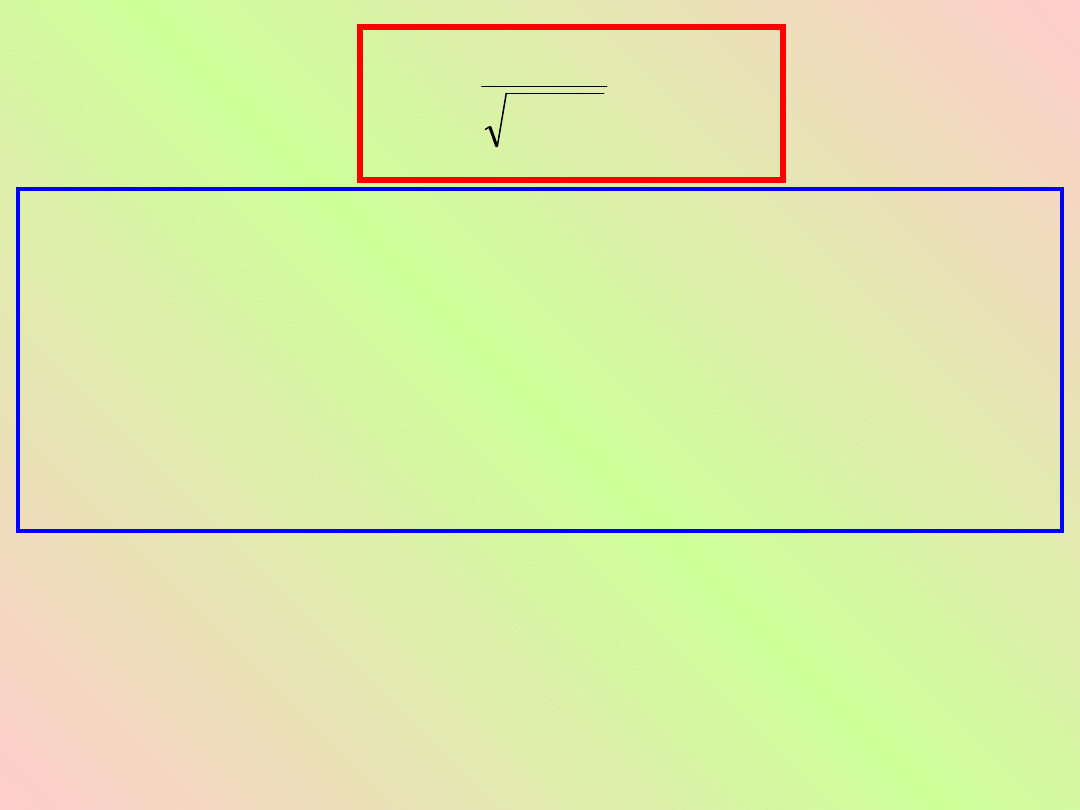
Masa ciała nie jest zatem w ogólności stała ani taka
sama dla wszystkich obserwatorów, ale jest wielkością
która:

> zależy od układu odniesienia z jakiego jest
obserwowana,

>   jest równa m

o

kiedy ciało jest w spoczynku w

układzie odniesienia z którego jest obserwowane.

Właściwości czynnika Lorentza powodują, że masa
staje się bardzo duża i w końcu zbliża się do
nieskończoności, kiedy prędkość względna zbliża się
do c.

53

Zgodnie

ze

wzorem

na

masę,

wyrażenie

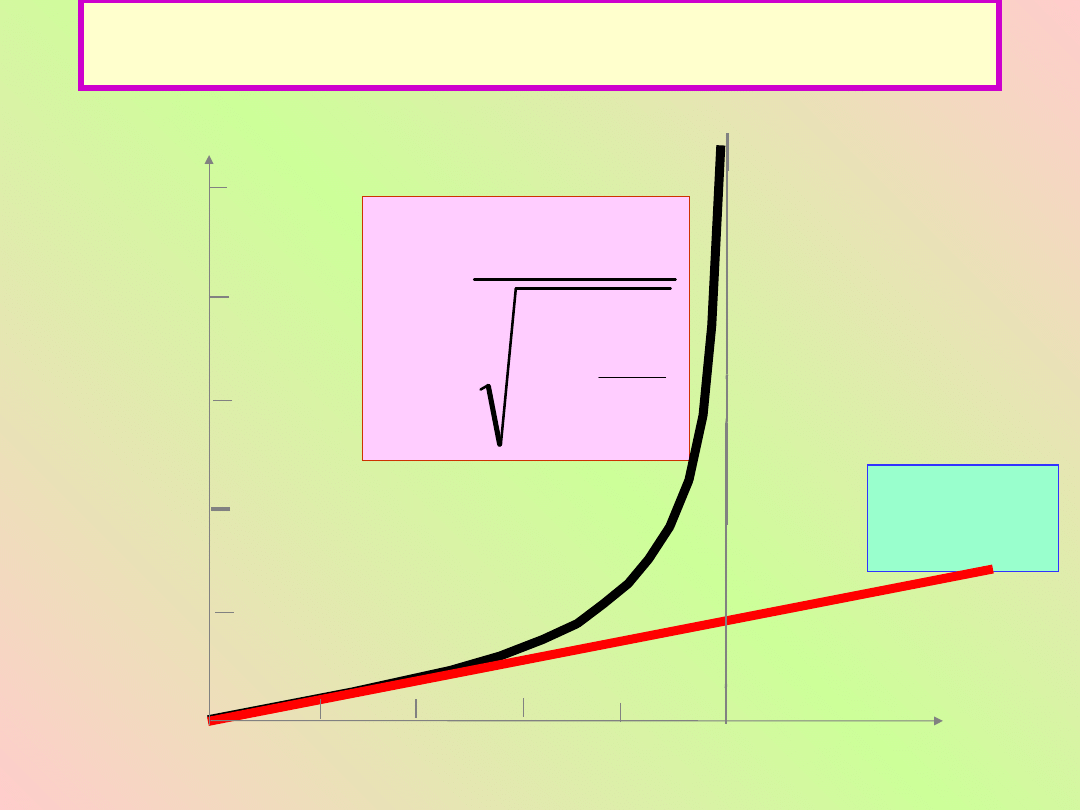
relatywistyczne na pęd ma postać

a na zachowanie pędu układu izolowanego

v

m

v

m

p

o













const

v

m

v

m

i

n

i

oi

i

n

i

i

















1

1



Teraz podam wyrażenia na kolejne wielkości bez

ich wyprowadzeń

54

Pęd klasyczny

i

pęd

relatywistyczny

p

m

0

c

2m

0

c

3m

0

c

4m

0

c

5m

0

c

2

2

1

c

m

p

o

v

v





v

0

m

p

v

0

.2c .4c .

6c

.8c

c

Definicja siły

Chociaż prawa mechaniki klasycznej nie są na tyle
uniwersalne,

aby

opisywały

także

zjawiska

relatywistyczne, to drugie prawo Newtona

jest na tyle ogólne, że stosuje się również w
mechanice relatywistycznej. Zróżniczkowanie ww.
równania prowadzi do wyrażenia

gdzie m oznacza teraz



m

o

.

 

v

m

dt

d

dt

p

d

F











dt

dm

v

dt

v

d

m

F











56

Siła i przyśpieszenie relatywistyczne

Równanie Newtona dp/dt=d/dt(mv)=F nie
jest niezmiennicze względem transformacji
Lorentza ponieważ prędkość ciała względem
układu nieruchomego wynosi v=(u+v’)/(1+
uv’/c

2

), a nie jak w przypadku transformacji

Galileusza v=u+v’ , a przyśpieszenie d

2

x’/dt’

2

nie będzie równe dx

2

/dt

2

lecz wyniesie

 

v

dt

d

dt

dp

m

F





2

2

3

2

2

2

2

dt

x

d

c

v

1

1

dt'

x'

d

'





















a

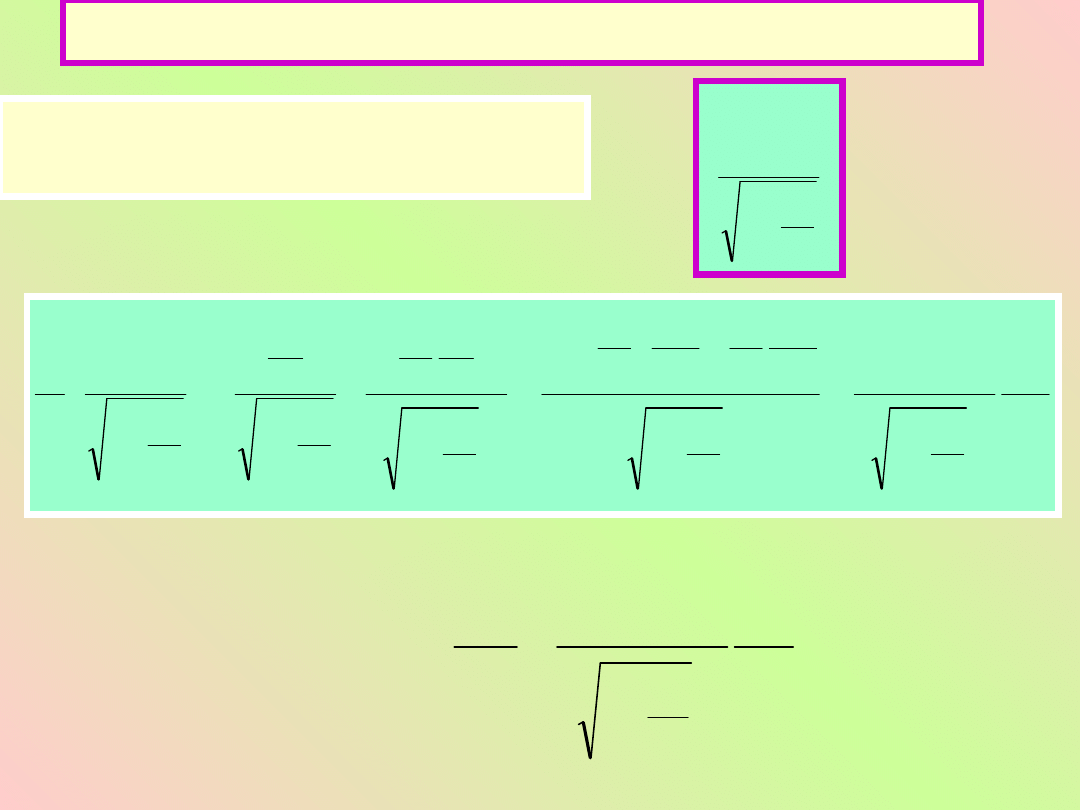
Przyśpieszenie relatywistyczne

Rozważmy pochodną po czasie
następującego wyrażenia

v

v

c

1

2

2



























d

dt

v

v

c

dv

dt

v

c

v

c

dv

dt

v

c

v

c

d x

dt

v

c

d x

dt

v

c

v

c

d x

dt

1

1

1

1

1

1

1

2

2

2

2

2

2

2

2

3

2

2

2

2

2

2

2

2

2

2

3

2

2

3

2

2





























































































Porównajmy teraz wynik różniczkowania z wzorem na
przyśpieszenie

2

2

3

2

2

2

2

dt

x

d

c

v

1

1

dt'

x'

d

'





















a

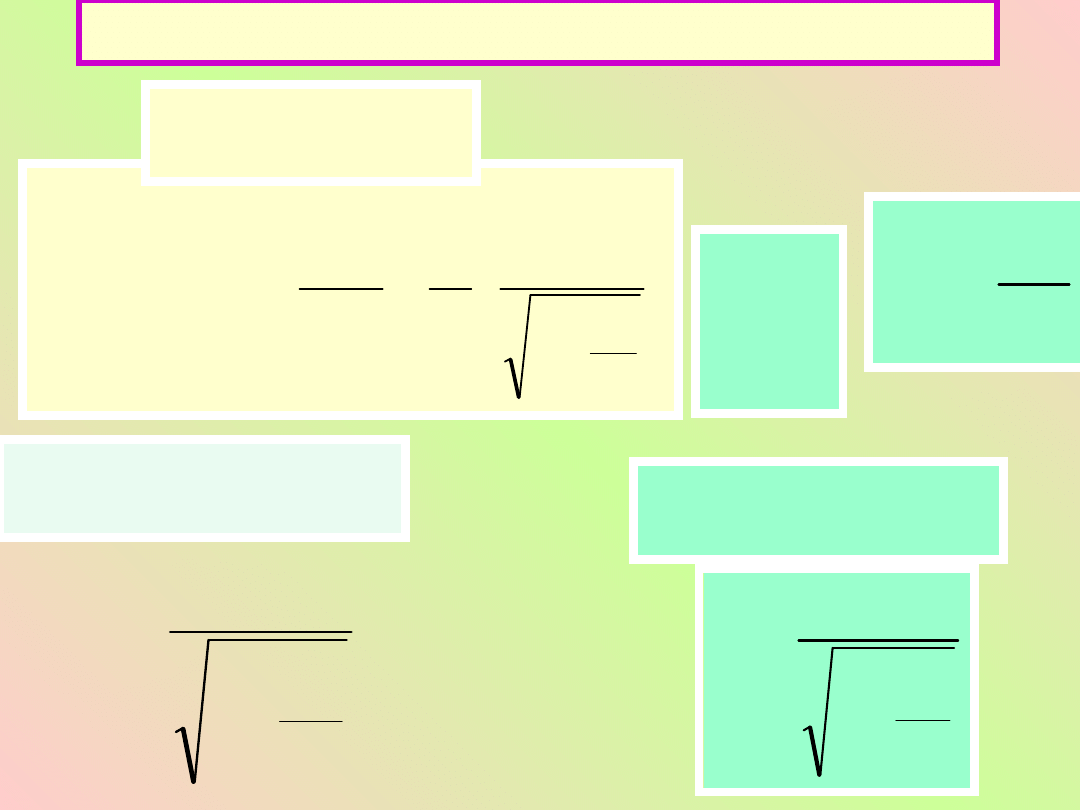
Siła, pęd i masa relatywistyczna

































2

2

o

2

2

0

c

1

m

dt

d

dt'

x'

d

m

a

m

'

F

v

v

'

0

2

2

0

v

1

c

m

m





Siła
relatywistyczna

Zatem pęd

relatywistyczny

masa

relatywistyczna

dt

dp

F 

'

Z

drugie

j

strony

2

2

0

1

c

m

p

v

v





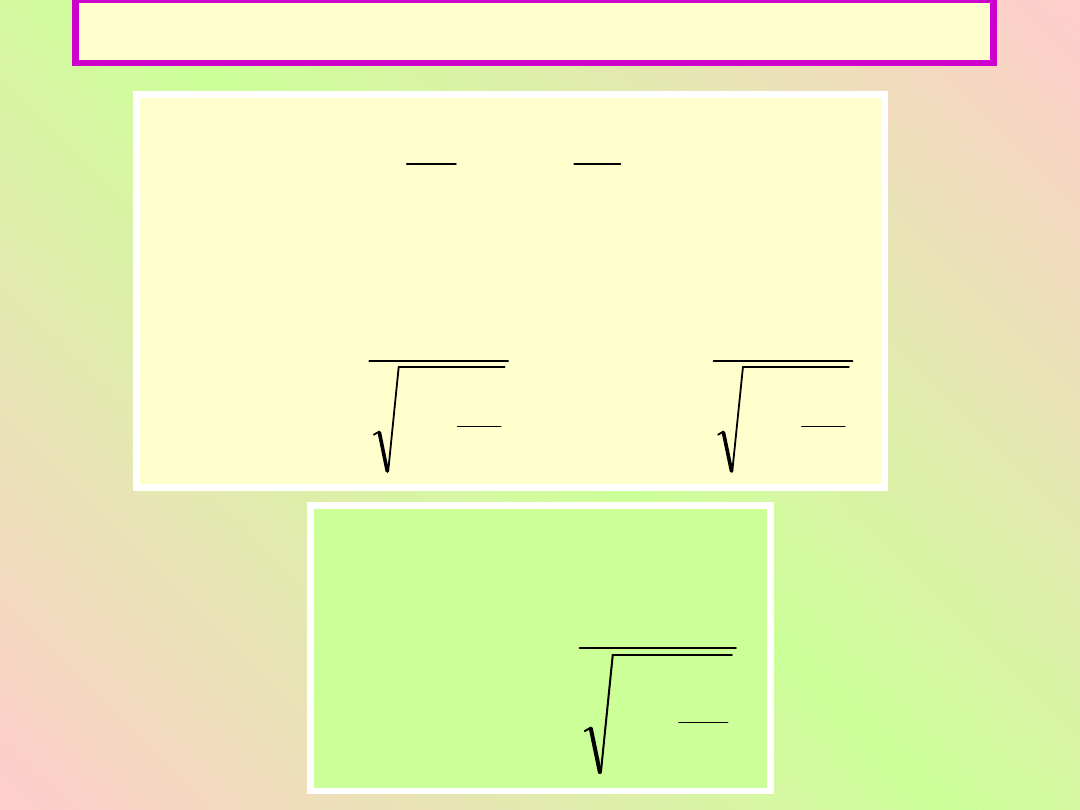
Energia relatywistyczna













































































v

v

v

x

x

p

x

x

k

c

v

v

vd

m

c

v

v

m

vd

vdp

dp

dt

dx

dx

dt

dp

Fdx

E

0

2

2

0

0

0

2

2

0

0

1

1

2

1

2

1































v

k

c

v

v

vd

m

E

0

2

2

0

1

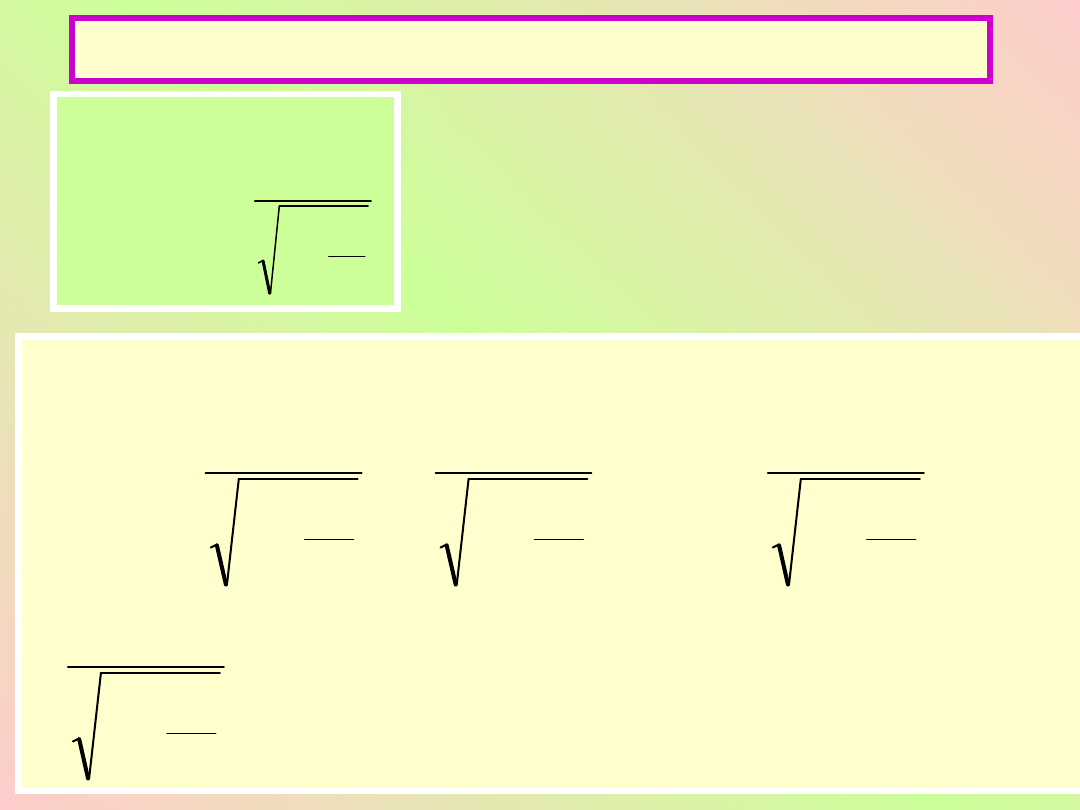
Kinetyczna energia relatywistyczna































v

k

c

v

v

vd

m

E

0

2

2

0

1

Obliczmy prawą stronę
tego równania wykonując
całkowanie przez części

2

0

2

2

0

2

2

2

0

2

2

2

2

0

0

2

2

2

2

2

0

1

1

1

1

c

m

mc

c

m

c

v

c

m

c

c

v

c

m

c

v

vdv

c

v

v

m

E

V

k













































































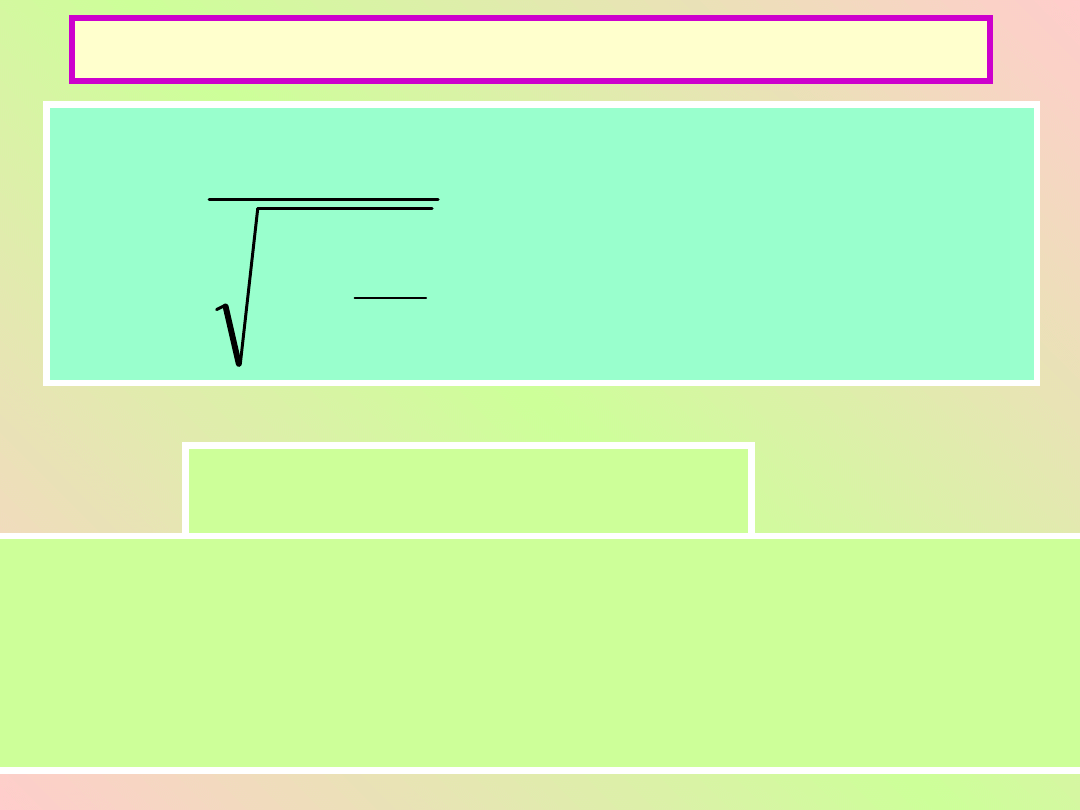
Energia relatywistyczna

Stąd energia

całkowita

2

0

2

c

m

E

mc

E

k







2

0

2

2

0

2

2

2

0

1

c

m

mc

c

m

c

v

c

m

E

k











Energia spoczynkowa

Dla m

0

= 1 gram

2

0

0

c

m

E 

1kg odważnik = 1000 gramów =1000 bomb 20-kilotonowych



Co odpowiada jednej 20-kilotonowej bombie
atomowej





J

s

m

kg

E

13

2

8

3

0

10

9

10

3

10































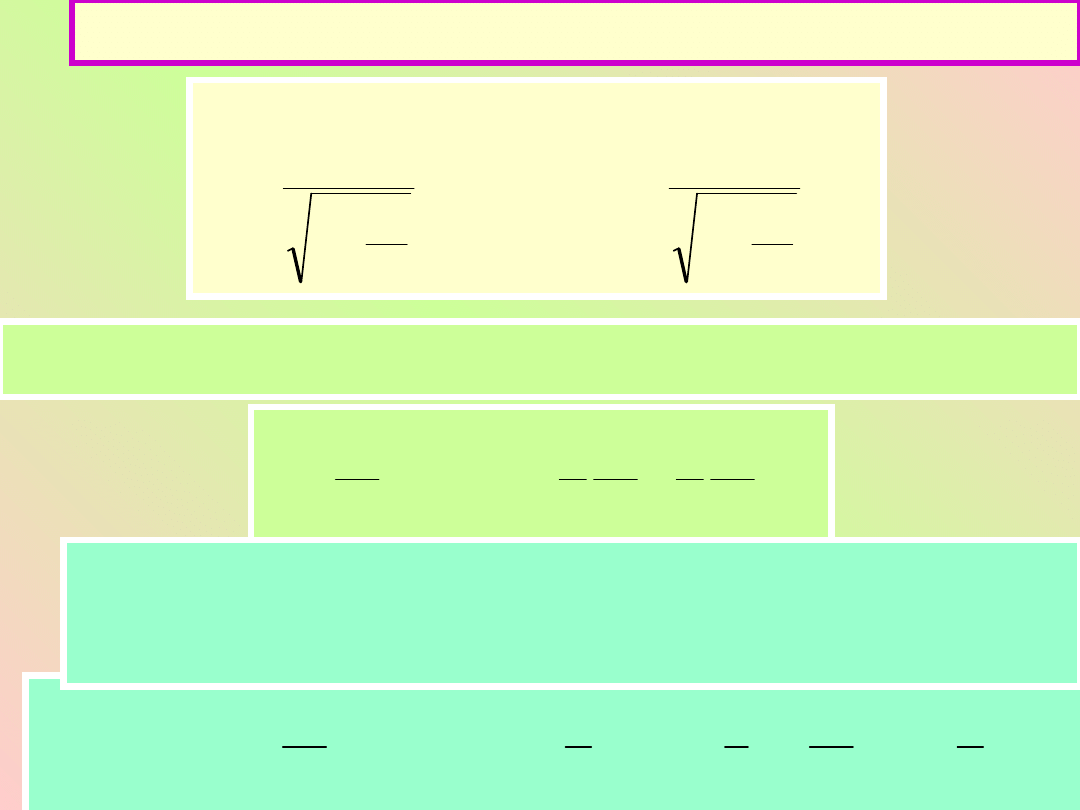
Energia kinetyczna relatywistyczna i

klasyczna

E

mc

v

c

mc

m v

m

v

c

m v

k

























0

2

2

2

1 2

0

2

0

2

0

4

2

0

2

1

1

2

3

8

1

2

/

...



Rozwijając pierwszy wyraz w nawiasie na szereg dwumianowy o

wykładniku ujemnym





































1

1

1

1

2

2

2

0

2

0

2

2

2

0

c

v

c

m

c

m

c

v

c

m

E

k

...

8

3

2

1

1

1

2

4

2

2

2

/

1

2

2

























c

v

c

v

c

v

Otrzymamy na energię kinetyczną wzór, który dla
małych prędkości w porównaniu z c przechodzi w
znany wzór z dynamiki klasycznej E

k

=1/2 mv

2

Zasada względności Einsteina

1) Układy inercjalne transformują się według wzorów

Lorentza. Względem tych przekształceń prawa
mechaniki i elektrodynamiki są niezmiennicze. Jeśli
wszystkie siły przyrody kształtują się według tych
samych praw co siły elektromagnetyczne, to

wszystkie

prawa

przyrody

muszą

być

niezmiennicze względem transformacji Lorentza

;

2)

Niemożliwym jest wykrycie ruchu absolutnego. Z

niemożliwości wykrycia ruchu absolutnego

wynika

równoważność wszystkich układów inercjalnych

.

Nie ma potrzeby zajmowania się pojęciem eteru jako
absolutnego

układu

odniesienia.

Pole

elektromagnetyczne w próżni jest realnością fizyczną i
prawa nim rządzące nie wymagają istnienia
specjalnego ośrodka (eteru);

3)

Na podstawie analizy faktów doświadczalnych i

rozważań zawartych w tzw. szczególnej teorii
względności Einstein formułuje zasadę względności w
stwierdzeniu, że

:

Wszystkie układy

inercjalne są

równoważne przy

formułowaniu praw

przyrody.

Relatywistyczna energia

kinetyczna

Aby znaleźć wyrażenie relatywistyczne na energię
kinetyczną, obliczamy pracę wykonaną w celu
zwiększenia prędkości cząstki od zera do końcowej
wartości v. Żeby uprościć to zadanie, zakładamy, że
siła i przesunięcie mają ten sam kierunek.







r

r

d

F

K

0









2

c

m

m

K

o





67

Energia całkowita

K

E

E

o





2

c

m

E

o

o



gdzie

Energia
spoczynkowa

a skoro

to

Należy zauważyć, że ta definicja energii całkowitej w
mechanice relatywistycznej nie zawiera energii
potencjalnej.

Równoważność masy i energii jest jedną z
najważniejszych konsekwencji szczególnej
teorii względności.





2

2

c

m

m

c

m

E

o

o







2

mc

E 

68

Efekt Dopplera dla fal elektromagnetycznych

zależy tylko od względnego ruchu źródła i

obserwatora, gdyż fale elektromagnetyczne

mogą rozchodzić się w próżni

.

Nie wymagają ośrodka, który mógłby stanowić układ

odniesienia.

Aby obliczyć wielkość efektu Dopplera dla fal

elektromagnetycznych,

musimy

stosować

teorię

względności.

69

Efekt Dopplera dla fal

elektromagnetycznych

v

D e te k t o r

Ź r ó d ło

y

1

y

2

x

2

x

1

0

1

0

2

Na rys. pokazano źródło światła i detektor oddalające
się ze względną prędkością v. Załóżmy, że w obu
układach mamy identyczne zegary wskazujące zero w
chwili gdy układy O

1

i O

2

znajdowały się w tym samym

miejscu. Przypuśćmy, że źródło emituje impuls światła,
gdy jego zegar wskazuje czas T

2

. Chcemy obliczyć czas

T

1

, gdy impuls dochodzi do detektora w układzie O

1

. Z

teorii względności wiemy, że obserwator w układzie
spoczywającym O

1

widzi, że zegar biegnie szybciej niż

poruszający się zegar w układzie O

2

.

70

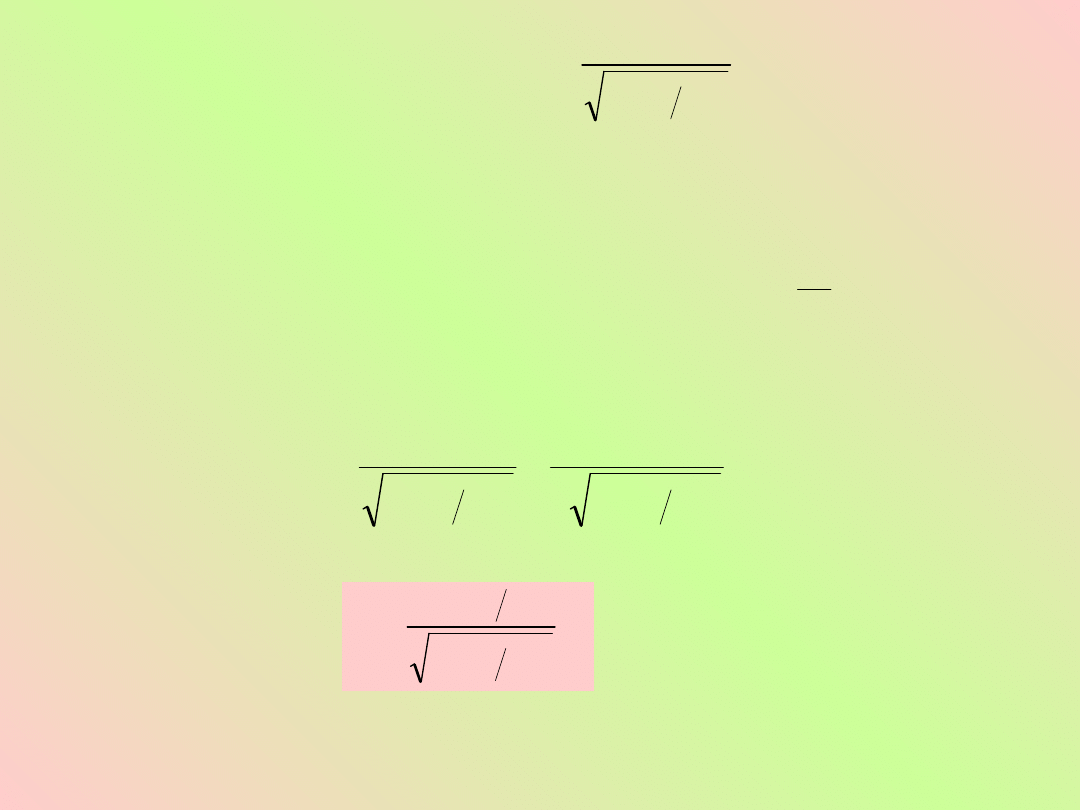
Według obserwatora O

1

(8.104)

W układzie odniesienia O

1

czas przelotu impulsu jest

równy x

1

/c. Jeżeli t

1

jest momentem przybycia impulsu

światła do O

1

, to w układzie odniesienia O

1

mamy

Wyeliminujemy x

1

biorąc pod uwagę relację (8.104) i x

1

=

vt

1

. Wówczas

czyli

 

2

2

1

1

c

v

T

t









c

x

t

przelotu

czas

t

T

1

1

1

1









 

 

2

2

2

2

1

1

1

c

v

c

vT

c

v

T

T









 

2

2

1

1

1

T

c

v

c

v

T







71

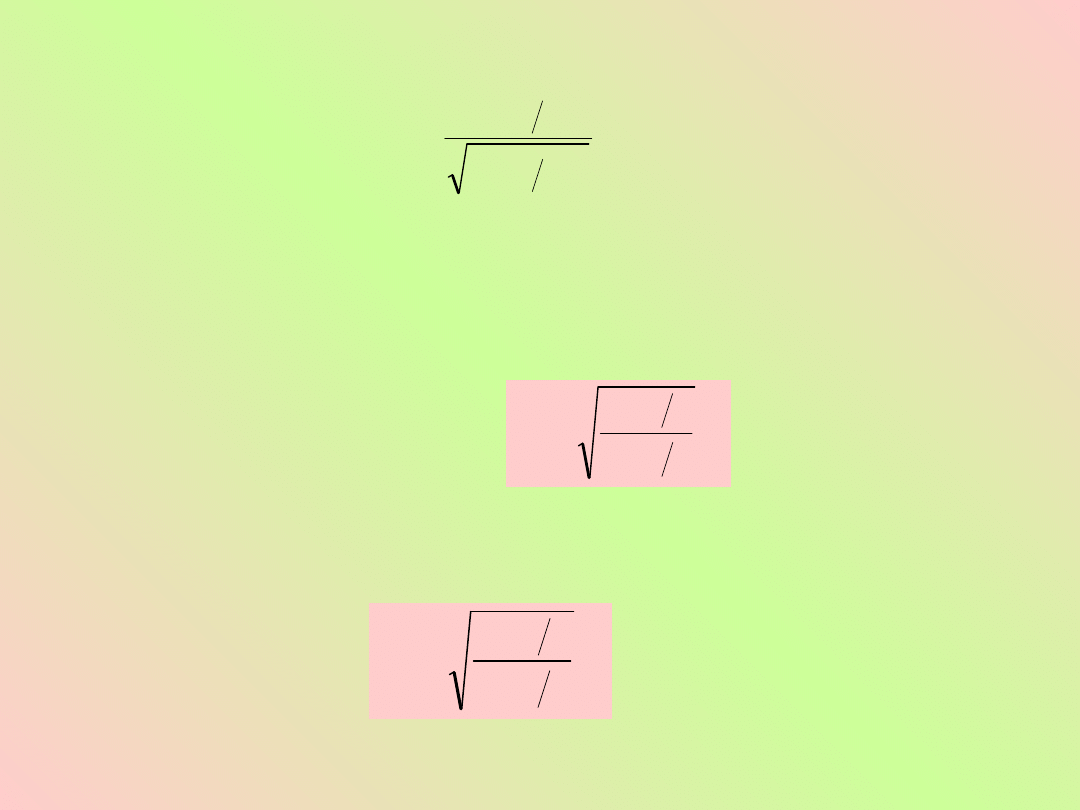
Okres czasu między dwoma kolejnymi impulsami, czyli
okres drgań, wynosi

(8.105)

gdzie



2

jest okresem zmierzonym przy źródle. Związek

między częstością a okresem jest dany wzorem f = 1/



.

W związku z tym na podstawie (8.105) otrzymujemy

Źródło i detektor oddalają się

(8.106)

W przypadku gdy źródło się przybliża, znak przy v/c
będzie odwrócony

(8.107)

 

2

2

1

1

1





c

v

c

v







2

1

1

1

f

c

v

c

v

f







2

1

1

1

f

c

v

c

v

f







72

Przy małych prędkościach względnych (v << c), po
rozwinięciu dwóch ostatnich zależności w szereg,
możemy pominąć (v/c)

2

oraz człony o wyższych

potęgach. Otrzymamy wtedy

(8.108)

przy czym znak + odnosi się do v < 0, zaś znak – do v >
0.

Zjawisko Dopplera dla fal elektromagnetycznych

ma liczne praktyczne zastosowania, np. w fizyce

atomowej, w astronomii do określenia prędkości

odległych świecących ciał niebieskich, w

radiolokacji do pomiaru prędkości i odległości

ruchomych obiektów.

2

1

1

f

c

v

f











 



73

Grawitacja a ogólna teoria

względności

To co dotychczas rozważaliśmy, nazywamy szczególną
teorią względności w odróżnieniu od ogólnej teorii
względności. Pierwsza z nich była całkowicie rozwinięta
przez Einsteina w 1905 r., podczas gdy druga – w zasadzie
w 1911 r. Ogólna teoria względności stanowi współczesną
teorię grawitacji.

Prawo powszechnego ciążenia, zwane również prawem
grawitacji, zostało sformułowane przez Newtona w 1687 r.
Prawo to mówi, że dwa ciała o masach m

1

i m

2

przyciągają

się wzajemnie siłą proporcjonalną do iloczynu ich mas i
odwrotnie proporcjonalną do kwadratu ich odległości r,

Współczynnik proporcjonalności G nosi nazwę stałej
grawitacji, która wynosi 6,6710

–11

Nm

2

/kg

2

.

2

2

1

r

m

m

G

F 

74

Siła grawitacyjna jest przykładem często spotykanej w
fizyce siły centralnej, tzn. siły której kierunek działania
przechodzi przez centrum i której wartość zależy od
odległości od tego cen-trum. Innymi przykładami siły
centralnej są siła elektrostatyczna i siła sprężystości.

Niezwykle ważną cechą siły centralnej jest to, że
moment tej siły względem centrum wynosi zero, co
oznacza, że w ruchu pod wpływem siły centralnej musi
być zachowany moment pędu cząstki. Każda z sił
centralnych jest siłą zachowawczą.

Można wykazać, że pod działaniem siły centralnej ciało
może poruszać się po krzywej stożkowej: elipsie,
paraboli lub hiperbo-li w zależności od warunków
początkowych w jakich ciało to do-staje się w pole
działania siły. Wynikają stąd sformułowane przez
Keplera w latach 1609–1619, a więc jeszcze przed
odkry-ciami Newtona, trzy prawa ruch planet.

75

W teorii grawitacji Newtona przyjmuje się, że siła
działa natychmiast, a to oznacza, że sygnał bądź
energia przekazywane są natychmiast od masy m

1

do

masy m

2

.

W ten sposób naruszone jest jedno z

podstawowych założeń teorii względności, że żaden
sygnał (żadna postać energii) nie może się rozchodzić
z prędkością większą od prędkości światła

.

Równoważność masy i energii oznacza, że światło

powinno ulegać przyciąganiu grawitacyjnemu

. I tak np.

światło przebiegające w pobliżu Słońca na drodze
porównywalnej ze średnicą Słońca równej 1,4410

9

m

w czasie t = 1,4410

9

/c = 5 s powinno ”spaść” o h =

(1/2)g

s

t

2

= 3,710

3

m, gdzie g

s

oznacza przyśpieszenie

w pobliżu Słońca. Wówczas kąt odchylenia promienia
wynosi a = h/R

s

= 510

–6

radiana czyli około 1

’’

.

Zjawisko to zaobserwowano podczas zaćmienia Słońca
jako zmianę położenia pewnych gwiazd.

76

Ogólna teoria względności odgrywa dużą rolę w dziale
astrofizyki zwanej kosmologią – nauce o powstaniu,
rozmiarach i budowie Wszechświata.

Wyjaśnia ona takie zjawiska jak:
zwiększenie długości fali przy emitowaniu światła przez
ciała o dużej masie,
zakrzywienie promienia świetlnego przechodzącego w
pobliżu powierzchni Słońca w kierunku środka Słońca,
czy też mechanizm powstawania tzw. ”czarnych dziur”
(specjalnego typu gwiazd).

77