Mody TM: 1
Fale w falowodzie
Zakładamy, że falowód jest doskonałym przewodnikiem, tak że E = 0
i B = 0 wewnątrz samego przewodnika i dlatego warunki brzegowe
przy wewnętrznej ściance rury mają postać:
t
0
=
E
(1a)
n
0
B
= (1b)
Poszukujemy rozwiązania w postaci fal monochromatycznych propa-
gujących się w kierunku osi z w postaci:
j(
)
0
0
0
j(
)
0
0
0
ˆ
ˆ
ˆ
( , , , ) (
)
ˆ
ˆ
ˆ
( , , , ) (
)
kz
t
x
y
z
kz
t
x
y
z
x y z t
E
E
E
e
x y z t
B
B
B
e
−
−
=
+
+
=
+
+
E
x
y
z
B
x
y
z
ω
ω
Okazuje się, że wielkości E
0z
i B
0z
(w ogólności zespolone) spełniają
niesprzężone równania (wynikające z równań Maxwella)
2
2
2
2
0
2
2
0
z
k
E
x
y
c
⎡
⎤
∂
∂
⎛ ⎞
+
+
−
=
⎢
⎥
⎜ ⎟
∂
∂
⎝ ⎠
⎢
⎥
⎣
⎦
ω
(2a)
2
2
2
2
0
2
2
0
z
k
B
x
y
c
⎡
⎤
∂
∂
⎛ ⎞
+
+
−
=
⎢
⎥
⎜ ⎟
∂
∂
⎝ ⎠
⎢
⎥
⎣
⎦
ω
(2b)
Pozostałe składowe wyznaczamy z równań
(
)
0
0
0
2
2
j
z
z
x
E
B
E
k
x
y
c
k
⎛
⎞
∂
∂
=
+
⎜
⎟
∂
∂
−
⎝
⎠
ω
ω
(3a)
(
)
0
0
0
2
2
j
z
z
y
E
B
E
k
y
x
c
k
⎛
⎞
∂
∂
=
−
⎜
⎟
∂
∂
−
⎝
⎠
ω
ω
(3b)
(
)
0
0
0
2
2
2
j
z
z
x
B
E
B
k
x
c
y
c
k
⎛
⎞
∂
∂
=
−
⎜
⎟
∂
∂
−
⎝
⎠
ω
ω
(3c)
(
)
0
0
0
2
2
2
j
z
z
y
B
E
B
k
y
c
x
c
k
⎛
⎞
∂
∂
=
+
⎜
⎟
∂
∂
−
⎝
⎠
ω
ω
(3d)
Mody TM: 2
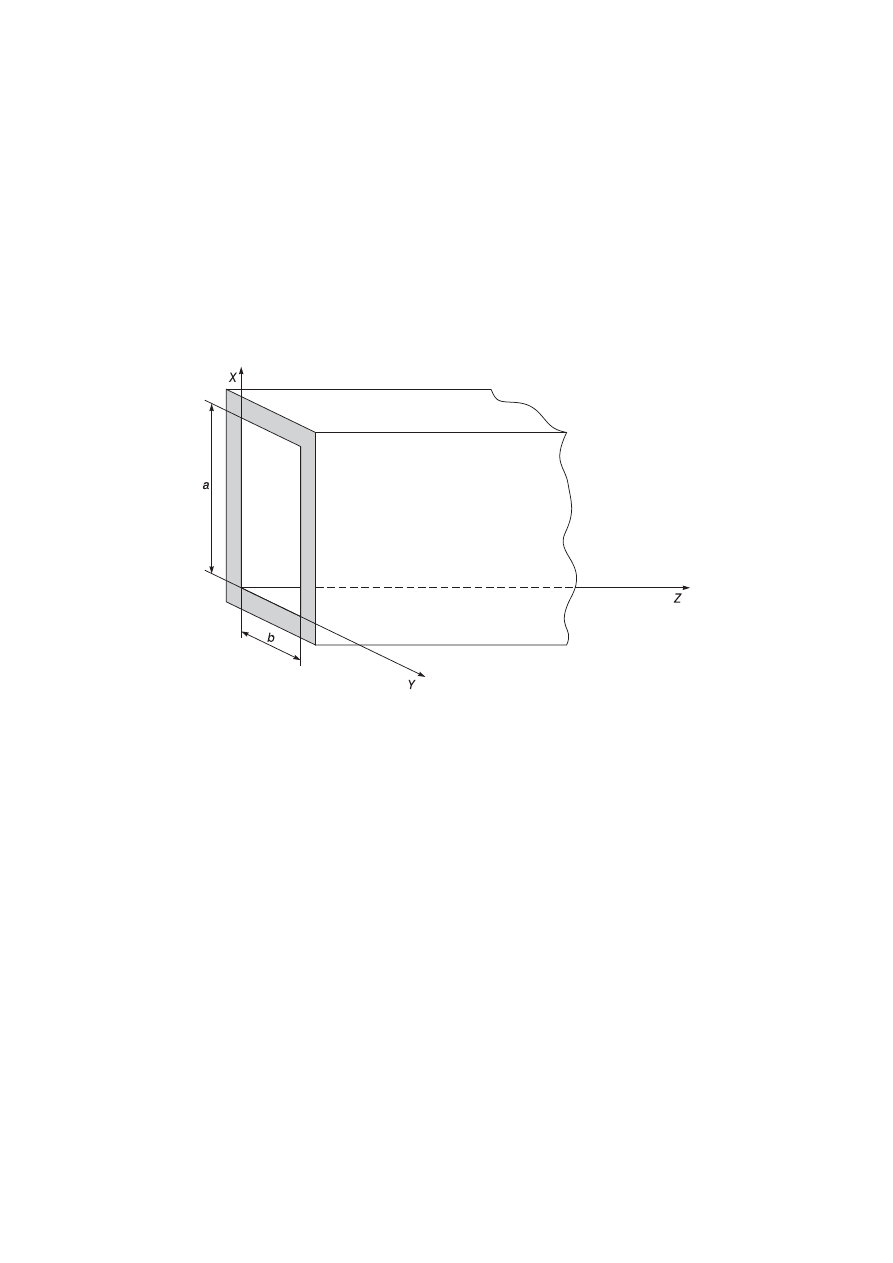
Fale TE i TM w falowodzie prostokątnym
Rozwiązując problem monochromatycznej fali biegnącej w falowo-
dzie (w szczególności w falowodzie o przekroju prostokątnym jak na
rysunku) rozpatruje się dwa typy fal wynikające z równań (2):
Fale TE (transverse electric): rozwiązujemy (2b) z warunkiem
(1b).
Fale TM (transverse magnetic): rozwiązujemy (2a) z warunkiem
(1a).
Rys. Falowód prostokątny
Pozostałe składowe wyznaczamy ze wzorów (3).
Mody TM: 3
Fale TM w falowodzie prostokątnym (ćwiczenia)
Dla modów (rozwiązań równań Maxwella) TM (poprzecznych
magnetycznych) składowa wzdłużna pola magnetycznego jest zerem
(
0
0
z
B
=
) więc rozwiązujemy równanie dla składowej wzdłużnej pola
elektrycznego
2
2
2
2
0
0
0
2
2
0
z
z
z
E
E
k
E
x
y
c
⎡
⎤
∂
∂
⎛ ⎞
+
+
−
=
⎢
⎥
⎜ ⎟
∂
∂
⎝ ⎠
⎢
⎥
⎣
⎦
ω
(2a)
z warunkiem brzegowym
t
0
=
E
(1a)
Warunek brzegowy oznacza, że składowa styczna natężenia pola elek-
trycznego na ściankach falowodu zeruje się.
Rozwiązanie metodą rozdzielenia zmiennych (Fouriera)
1. Zakładamy rozwiązanie w postaci iloczynu dwóch funkcji:
0
( , )
( )
( )
z
E
x y
X x Y y
=
⋅
(3)
Po podstawieniu do równania (2a) otrzymujemy
2
2
2
2
2
2
( )
( )
( )
( )
( )
( ) 0
X x
Y y
Y y
X x
k
X x Y y
x
y
c
⎡
⎤
∂
∂
⎛ ⎞
⋅
+
⋅
+
−
⋅
=
⎢
⎥
⎜ ⎟
∂
∂
⎝ ⎠
⎢
⎥
⎣
⎦
ω
2. Dzielimy obie strony równania przez
( )
( )
X x Y y
⋅
, co daje
2
2
2
2
2
2
( )
( )
0
( )
( )
Y y
X x
y
x
k
X x
Y y
c
∂
∂
∂
⎛ ⎞
∂
+
+
−
=
⎜ ⎟
⎝ ⎠
ω
(4)
Równanie przyjęło postać sumy trzech składników. Pierwszy zależy
wyłącznie od zmiennej x, drugi – wyłącznie od zmiennej y, a trzeci nie
zależy ani od x, ani od y (jest stały). Ich suma jest zerem. Aby to rów-
nanie było spełnione dla każdych x i y pierwszy i drugi składnik też
musi być równy jakiejś stałej. Stałe te moglibyśmy nazwać dowolnie
np. składnik pierwszy byłby równy A
x
a drugi A
y
.
Mody TM: 4
3. Dla wygody, oznaczmy je jak w poniższych wyrażeniach:
2
2
2
2
2
2
( )
( )
( )
( )
x
y
Y y
X x
y
x
k
k
X x
Y y
∂
∂
∂
∂
= −
= − (5)
Wielkości k
x
i k
y
nazywają się stałymi rozdziału. Uzyskujemy stąd
dwa równania (każde zależne wyłącznie od jednej zmiennej prze-
strzennej) które należy rozwiązać:
2
2
2
( )
( ) 0
x
d X x
k X x
dx
+
= (6a)
2
2
2
( )
( ) 0
y
d Y y
k Y y
dy
+
= (6b)
Ponadto z równania (4) uzyskujemy związek łączący k
x
i k
y
2
2
2
2
0
x
y
k
k
k
c
⎛ ⎞
− −
+
−
=
⎜ ⎟
⎝ ⎠
ω
(7)
4. Rozwiązaniem ogólnym równania (6a) jest
( )
sin(
)
cos(
)
x
x
X x
A
k x
B
k x
=
+
(8a)
Podobnie rozwiązaniem ogólnym równania (6b) jest
( )
sin(
)
cos(
)
y
y
Y y
C
k y
D
k y
=
+
(8a)
Dla wyznaczenia stałych A, B, C, D należy podstawić uzyskane roz-
wiązania do warunków brzegowych (1a).
5. Warunek (1a) oznacza, że składowa styczna natężenia pola elek-
trycznego na ściankach falowodu przyjmuje wartość zero. W naszym
przypadku jest to w szczególności składowa
0
( , )
( )
( )
z
E
x y
X x Y y
=
⋅
.
Mody TM: 5
Jeżeli przez S oznaczymy przekrój falowodu w płaszczyźnie xy to ma-
tematycznie warunki brzegowe można wyrazić w postaci
0
( , )
( )
( )
0
z
S
S
E
x y
X x Y y
=
⋅
=
gdzie
0
0,
dolny odcinek poziomy
0,
górny odcinek poziomy
0
0,
lewy odcinek pionowy
0,
prawy odcinek pionowy
x
y
b
x
a
y
b
S
y
x
a
y
b
x
a
⎧ =
∈
⎪ =
∈
⎪
= ⎨
=
∈
⎪
⎪ =
∈
⎩
Rozdzielając zmienne uzyskujemy warunki brzegowe dla funkcji X(x)
(0) 0,
( ) 0
X
X a
=
=
(9a)
oraz funkcji Y(y)
(0) 0,
( ) 0
Y
Y b
=
=
(9b)
6. Podstawiając rozwiązanie ogólne (8a) do pierwszego z warunków
brzegowych (9a) otrzymujemy
(0)
sin( 0)
cos( 0) 0
x
x
X
A
k
B
k
=
+
=
stąd stała 0
B
= .Wstawiając do drugiego otrzymujemy
( )
sin(
) 0
x
X a
A
k a
=
=
Jest to możliwe wtedy gdy
0,1,2,
x
k a
m
m
= π,
=
… (10a)
Analogicznie z analizy Y(y) otrzymujemy, że 0
D
= oraz
0,1,2,
y
k b
n
n
= π,
=
…
(10b)
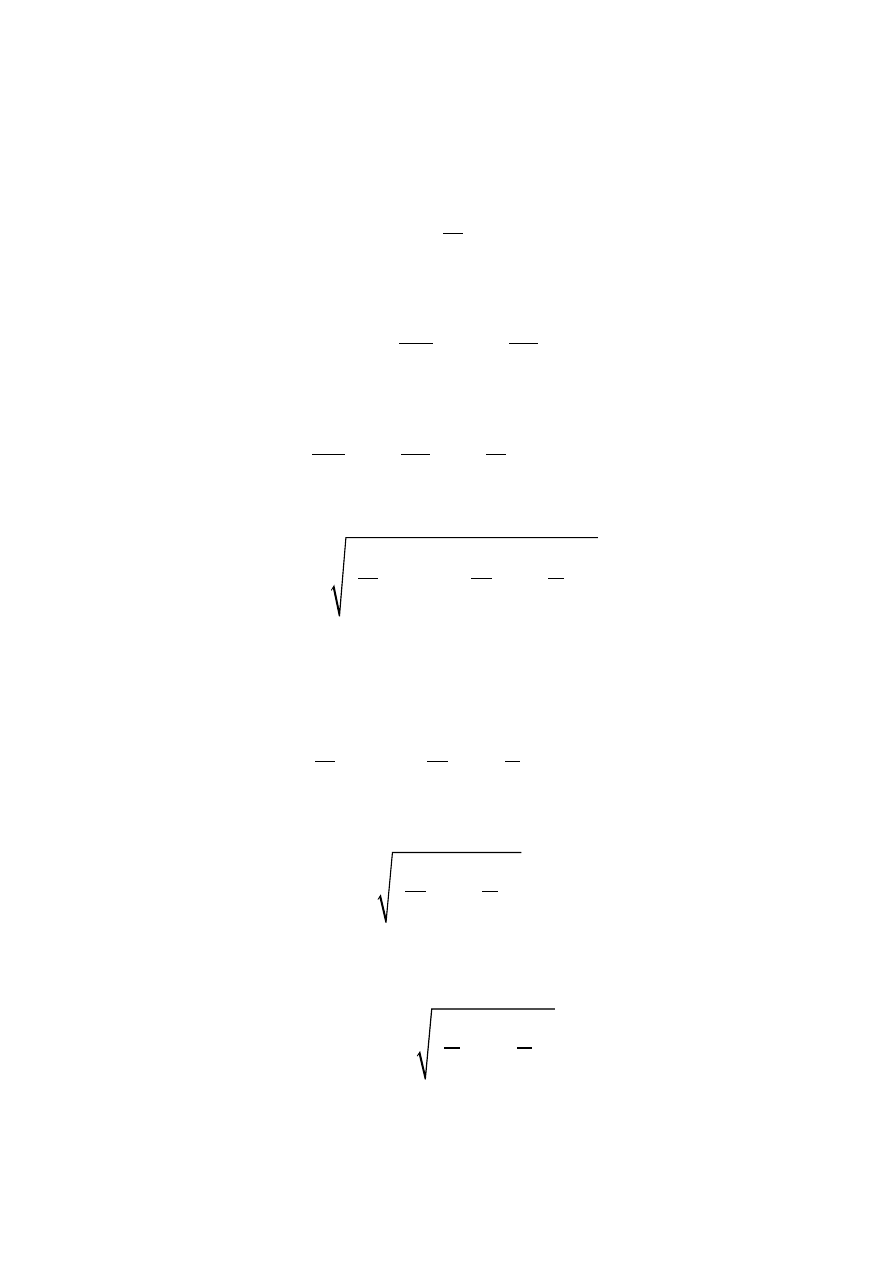
Ostatecznie
0
0
( , )
sin
sin
z
m
n
E
x y
E
x
y
a
b
π
π
⎛
⎞
⎛
⎞
=
⎜
⎟
⎜
⎟
⎝
⎠
⎝
⎠
(11)
gdzie wprowadziliśmy stałą
0
E
AC
=
.
Otrzymane rozwiązanie nazywa się modem TM
mn
.
UMOWA: Pierwszy wskaźnik dotyczy większego wymiaru przekroju
falowodu, czyli zakładamy, że
a
b
≥
, przy czym
,
0
m n
≠
.
Mody TM: 6
Wyznaczanie częstości obcięcia
Wykorzystaliśmy dwa równania powstałe po rozdzieleniu zmiennych.
Z trzeciego z nich
2
2
2
2
0
x
y
k
k
k
c
⎛ ⎞
− −
+
−
=
⎜ ⎟
⎝ ⎠
ω
po wstawieniu
x
y
m
n
k
k
a
b
π
π
=
,
=
(12)
wyznaczamy liczbę falową k:
2
2
2
2
0
m
n
k
a
b
c
π
π
⎛
⎞
⎛
⎞
⎛ ⎞
−
−
+
−
=
⎜
⎟
⎜
⎟
⎜ ⎟
⎝
⎠
⎝
⎠
⎝ ⎠
ω
Stąd
2
2
2
m
n
k
c
a
b
2
⎡
⎤
⎛ ⎞
⎛ ⎞
⎛ ⎞
=
− π
+
⎢
⎥
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎢
⎥
⎣
⎦
ω
(13)
Aby fala rozchodziła się w falowodzie bez tłumienia, liczba falowa
musi być rzeczywista. Zachodzi to wtedy, gdy wyrażenie pod pier-
wiastkiem w równaniu (13) jest dodatnie:
2
2
2
0
m
n
c
a
b
2
⎡
⎤
⎛ ⎞
⎛ ⎞
⎛ ⎞
− π
+
>
⎢
⎥
⎜ ⎟
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠
⎝ ⎠
⎢
⎥
⎣
⎦
ω
Z tej nierówności wyznaczamy warunek na częstość kołową fali ω
2
2
mn
m
n
c
a
b
⎛ ⎞
⎛ ⎞
> π
+
=
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠
ω
ω (14)
Wyrażenie
mn
ω nazywa się częstością obcięcia dla danego modu.
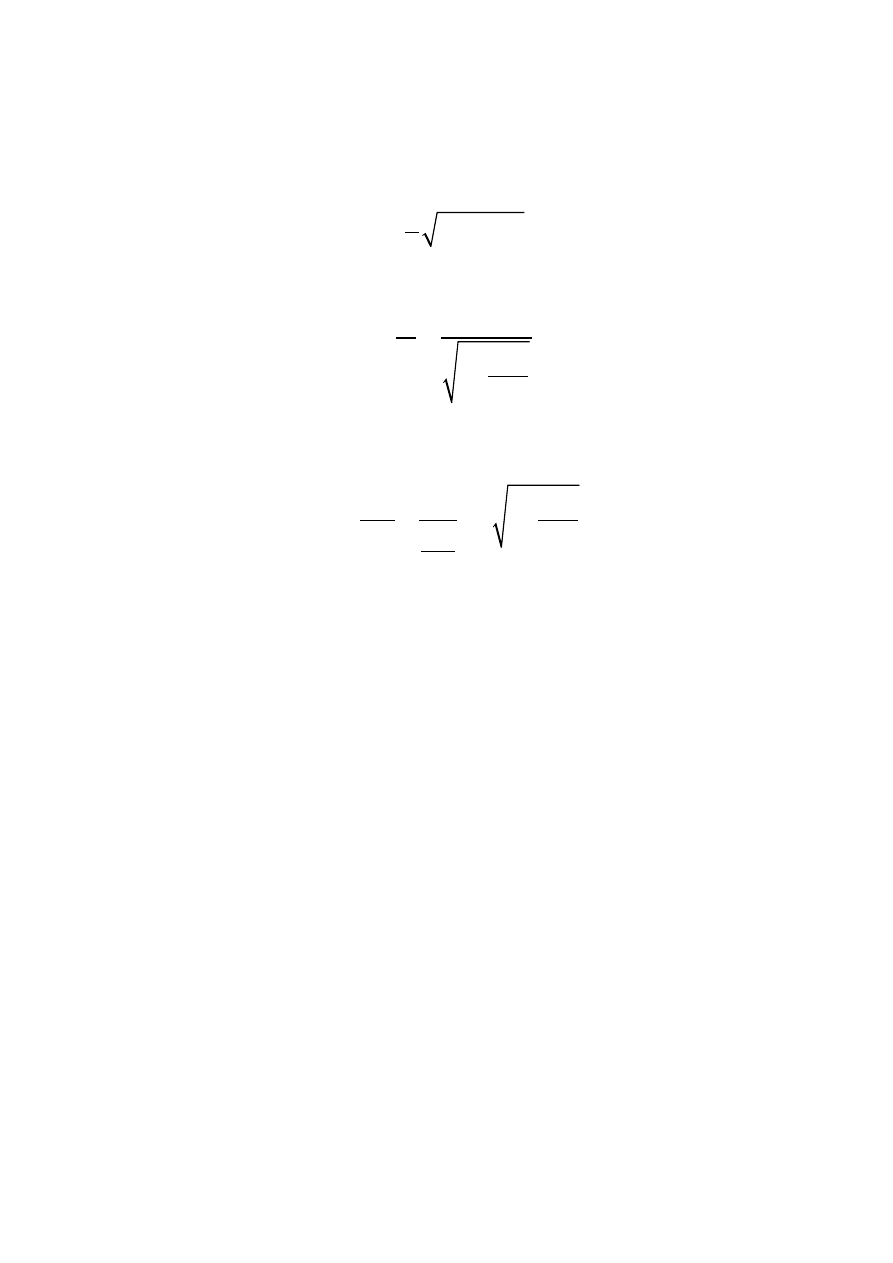
Najniższa częstość obcięcia występuje dla modu TM
11
:
2
2
11
1
1
c
a
b
⎛ ⎞
⎛ ⎞
= π
+
⎜ ⎟
⎜ ⎟
⎝ ⎠
⎝ ⎠
ω
(15)
Częstości mniejsze od niej (dla modów TM) nie propagują się.
Mody TM: 7
Wyznaczanie prędkości fazowej i grupowej
Wykorzystując wyrażenie (14) na częstość obcięcia
mn
ω , liczbę falo-
wą można wyrazić w postaci
2
2
1
mn
k
c
=
−
ω
ω (16)
Stąd prędkość fazowa wynosi
2
2
1
mn
c
k
=
=
−
ω
υ
ω
ω
(17)
i jest większa od prędkości światła w ośrodku swobodnym c. Energia
jest przenoszona z prędkością grupową
2
2
1
1
mn
g
d
c
dk
dk
d
=
=
=
− ω
ω
υ
ω
ω
(18)
i jest mniejsza od c.