Mody TE: 1

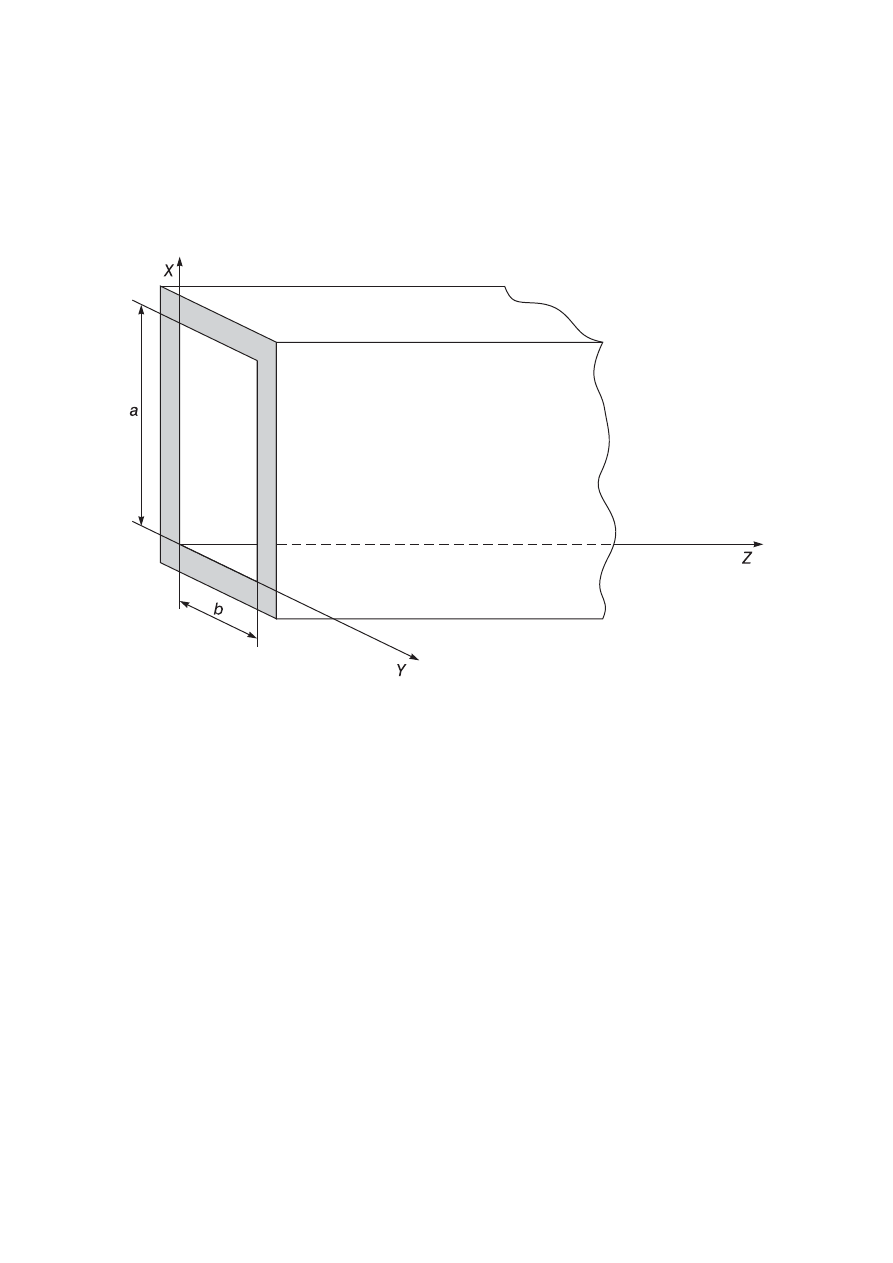
Fale w falowodzie

Rozważmy fale elektromagnetyczne propagujące się wzdłuż pustej
rury, czyli falowodu (w szczególności falowodu o przekroju prosto-
kątnym jak na rysunku).

Rys. Falowód prostokątny

Zakładamy, że falowód jest doskonałym przewodnikiem, tak że E = 0
i B = 0 wewnątrz samego przewodnika i dlatego warunki brzegowe
przy wewnętrznej ściance rury mają postać:

t

0

=

E

(1a)

n

0

B

= (1b)

Poszukujemy rozwiązania w postaci fal monochromatycznych propa-
gujących się w kierunku osi z w postaci:

j(

)

0

0

0

j(

)

0

0

0

ˆ

ˆ

ˆ

( , , , ) [

( , )

( , )

( , )]

ˆ

ˆ

ˆ

( , , , ) [

( , )

( , )

( , )]

kz

t

x

y

z

kz

t

x

y

z

x y z t

E

x y

E

x y

E

x y e

x y z t

B

x y

B

x y

B

x y e

−

−

=

+

+

=

+

+

E

x

y

z

B

x

y

z

ω

ω

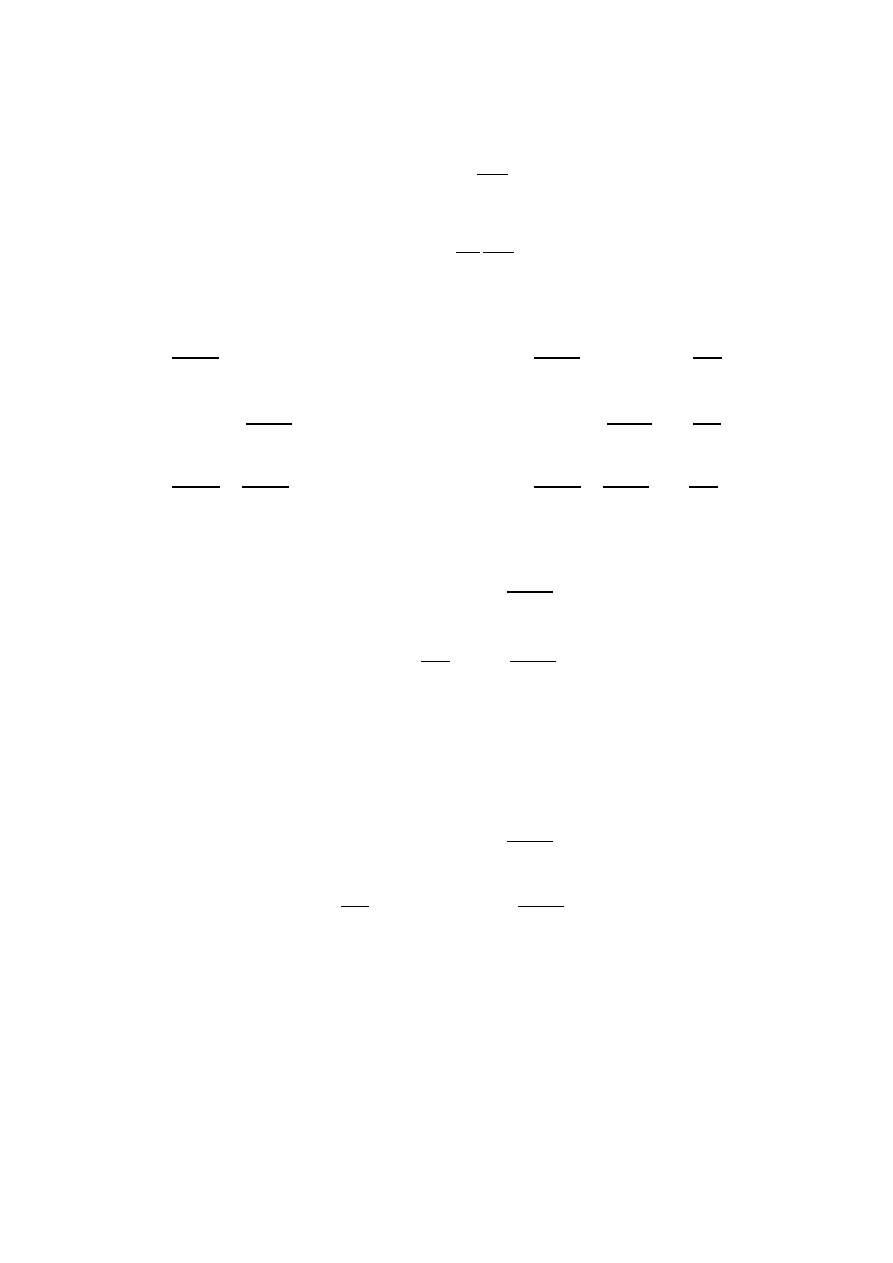
Mody TE: 2

Wstawiając te zależności do równań Maxwella

t

∂

∇ × = −

∂

B

E

2

1

c

t

∂

∇ × =

∂

E

B

uzyskujemy sześć równań

(I)

0

0

0

j

j

z

y

x

E

kE

B

y

∂

−

=

∂

ω

(IV)

0

0

0

2

j

j

z

y

x

B

kB

E

y

c

∂

−

= −

∂

ω

(II)

0

0

0

j

j

z

x

y

E

kE

B

x

∂

−

=

∂

ω

(V)

0

0

0

2

j

j

z

x

y

B

kB

E

x

c

∂

−

= −

∂

ω

(III)

0

0

0

j

y

x

z

E

E

B

x

y

∂

∂

−

=

∂

∂

ω

(VI)

0

0

0

2

j

y

x

z

B

B

E

x

y

c

∂

∂

−

= −

∂

∂

ω

Zapiszmy równania (I) i (V) w postaci układu

0

0

0

0

0

0

2

j

j

j

j

z

x

y

z

x

y

E

B

kE

y

B

kB

E

c

x

∂

⎧

+

=

⎪

∂

⎪

⎨

∂

⎪

+

=

⎪

∂

⎩

ω

ω

Można stąd wyznaczyć

0 x

B i

0 y

E względem pochodnych cząstkowych

składowych podłużnych

0 z

E i

0 z

B .

W analogiczny sposób z (II) i (IV)

0

0

0

0

0

0

2

j

j

j

j

z

x

y

z

x

y

E

kE

B

x

B

E

kB

c

y

∂

⎧

−

=

⎪

∂

⎪

⎨

∂

⎪

−

= −

∂

⎪⎩

ω

ω

można uzyskać

0 x

E i

0 y

B także względem pochodnych cząstkowych

składowych podłużnych

0 z

E i

0 z

B .

Tak wyznaczone wielkości

0 x

E i

0 y

E wstawiamy do równania (III)

a

0 x

B i

0 y

B do równania (VI).

Mody TE: 3

Okazuje się, że wielkości E

0z

i B

0z

(w ogólności zespolone) spełniają

niesprzężone równania

2

2

2

2

0

2

2

0

z

k

E

x

y

c

⎡

⎤

∂

∂

⎛ ⎞

+

+

−

=

⎢

⎥

⎜ ⎟

∂

∂

⎝ ⎠

⎢

⎥

⎣

⎦

ω

(2a)

2

2

2

2

0

2

2

0

z

k

B

x

y

c

⎡

⎤

∂

∂

⎛ ⎞

+

+

−

=

⎢

⎥

⎜ ⎟

∂

∂

⎝ ⎠

⎢

⎥

⎣

⎦

ω

(2b)

gdzie pozostałe składowe wyznaczamy z równań

(

)

0

0

0

2

2

j

z

z

x

E

B

E

k

x

y

c

k

⎛

⎞

∂

∂

=

+

⎜

⎟

∂

∂

−

⎝

⎠

ω

ω

(3a)

(

)

0

0

0

2

2

j

z

z

y

E

B

E

k

y

x

c

k

⎛

⎞

∂

∂

=

−

⎜

⎟

∂

∂

−

⎝

⎠

ω

ω

(3b)

(

)

0

0

0

2

2

2

j

z

z

x

B

E

B

k

x

c

y

c

k

⎛

⎞

∂

∂

=

−

⎜

⎟

∂

∂

−

⎝

⎠

ω

ω

(3c)

(

)

0

0

0

2

2

2

j

z

z

y

B

E

B

k

y

c

x

c

k

⎛

⎞

∂

∂

=

+

⎜

⎟

∂

∂

−

⎝

⎠

ω

ω

(3d)

Rozwiązując problem monochromatycznej fali biegnącej w falowo-
dzie rozpatruje się dwa typy fal wynikające z równań (2):

jeżeli

0

0

z

E

= mówimy o falach (modach) poprzecznych elek-

trycznych (TE) (ang. transverse electric); rozwiązujemy (2b)
z warunkiem (1b).

jeżeli

0

0

z

B

= mówimy o falach poprzecznych magnetycznych

(TM) (ang. transverse magnetic); rozwiązujemy (2a) z warunkiem
(1a).

Pozostałe składowe wyznaczamy ze wzorów (3).

Jeżeli zarówno

0

0

z

E

= jak i

0

0

z

B

= mówimy o falach poprzecz-

nych elektromagnetycznych (TEM) (ang. transverse
electromagnetic). Okazuje się, że fale TEM nie mogą występować
w pustym falowodzie.

Mody TE: 4

Fale TE w falowodzie prostokątnym (wykład)

Dla modów (rozwiązań równań Maxwella) TE (poprzecznych elek-
trycznych) składowa wzdłużna pola elektrycznego jest zerem
(

0

0

z

E

= ) więc rozwiązujemy równanie dla składowej wzdłużnej pola

magnetycznego

2

2

2

2

0

0

0

2

2

0

z

z

z

B

B

k

B

x

y

c

⎡

⎤

∂

∂

⎛ ⎞

+

+

−

=

⎢

⎥

⎜ ⎟

∂

∂

⎝ ⎠

⎢

⎥

⎣

⎦

ω

(2b)

z warunkiem brzegowym

n

0

B

= (1b)

Warunek brzegowy oznacza, że składowa normalna indukcji magne-
tycznej na ściankach falowodu zeruje się.

Rozwiązanie metodą rozdzielenia zmiennych (Fouriera)

1. Zakładamy rozwiązanie w postaci iloczynu dwóch funkcji:

0

( , )

( )

( )

z

B

x y

X x Y y

=

⋅

(3)

Po podstawieniu do równania (2b) otrzymujemy

2

2

2

2

2

2

( )

( )

( )

( )

( )

( ) 0

X x

Y y

Y y

X x

k

X x Y y

x

y

c

⎡

⎤

∂

∂

⎛ ⎞

⋅

+

⋅

+

−

⋅

=

⎢

⎥

⎜ ⎟

∂

∂

⎝ ⎠

⎢

⎥

⎣

⎦

ω

2. Dzielimy obie strony równania przez

( )

( )

X x Y y

⋅

, co daje

2

2

2

2

2

2

( )

( )

0

( )

( )

Y y

X x

y

x

k

X x

Y y

c

∂

∂

∂

⎛ ⎞

∂

+

+

−

=

⎜ ⎟

⎝ ⎠

ω

(4)

Równanie przyjęło postać sumy trzech składników. Pierwszy zależy
wyłącznie od zmiennej x, drugi – wyłącznie od zmiennej y, a trzeci nie
zależy ani od x, ani od y (jest stały). Ich suma jest zerem. Aby to rów-
nanie było spełnione dla każdych x i y pierwszy i drugi składnik też
musi być równy jakiejś stałej.

Mody TE: 5

3. Dla wygody, oznaczmy je jak w poniższych wyrażeniach:

2

2

2

2

2

2

( )

( )

( )

( )

x

y

Y y

X x

y

x

k

k

X x

Y y

∂

∂

∂

∂

= −

= − (5)

Wielkości k

x

i k

y

nazywają się stałymi rozdziału. Uzyskujemy stąd

dwa równania (każde zależne wyłącznie od jednej zmiennej prze-
strzennej) które należy rozwiązać:

2

2

2

( )

( ) 0

x

d X x

k X x

dx

+

= (6a)

2

2

2

( )

( ) 0

y

d Y y

k Y y

dy

+

= (6b)

Ponadto z równania (4) uzyskujemy związek łączący k

x

i k

y

2

2

2

2

0

x

y

k

k

k

c

⎛ ⎞

− −

+

−

=

⎜ ⎟

⎝ ⎠

ω

(7)

4. Rozwiązaniem ogólnym równania (6a) jest

( )

sin(

)

cos(

)

x

x

X x

A

k x

B

k x

=

+

(8a)

Podobnie rozwiązaniem ogólnym równania (6b) jest

( )

sin(

)

cos(

)

y

y

Y y

C

k y

D

k y

=

+

(8a)

Dla wyznaczenia stałych A, B, C, D należy podstawić uzyskane roz-
wiązania do warunków brzegowych (1b).
5. Warunek (1b) oznacza, że składowa styczna indukcji magnetycznej
na ściankach falowodu przyjmuje wartość zero. W naszym przypadku
jest to w szczególności składowa

0

( , )

x

B

x y

dana równaniem (3c)

i

0

( , )

y

B

x y

dana równaniem (3d). Składowe te wyrażają się przez po-

chodne cząstkowe składowej

0

( , )

( )

( )

z

B

x y

X x Y y

=

⋅

:

(

)

0

0

2

2

j

z

x

B

k

B

x

c

k

∂

=

∂

−

ω

(

)

0

0

2

2

j

z

y

B

k

B

y

c

k

∂

=

∂

−

ω

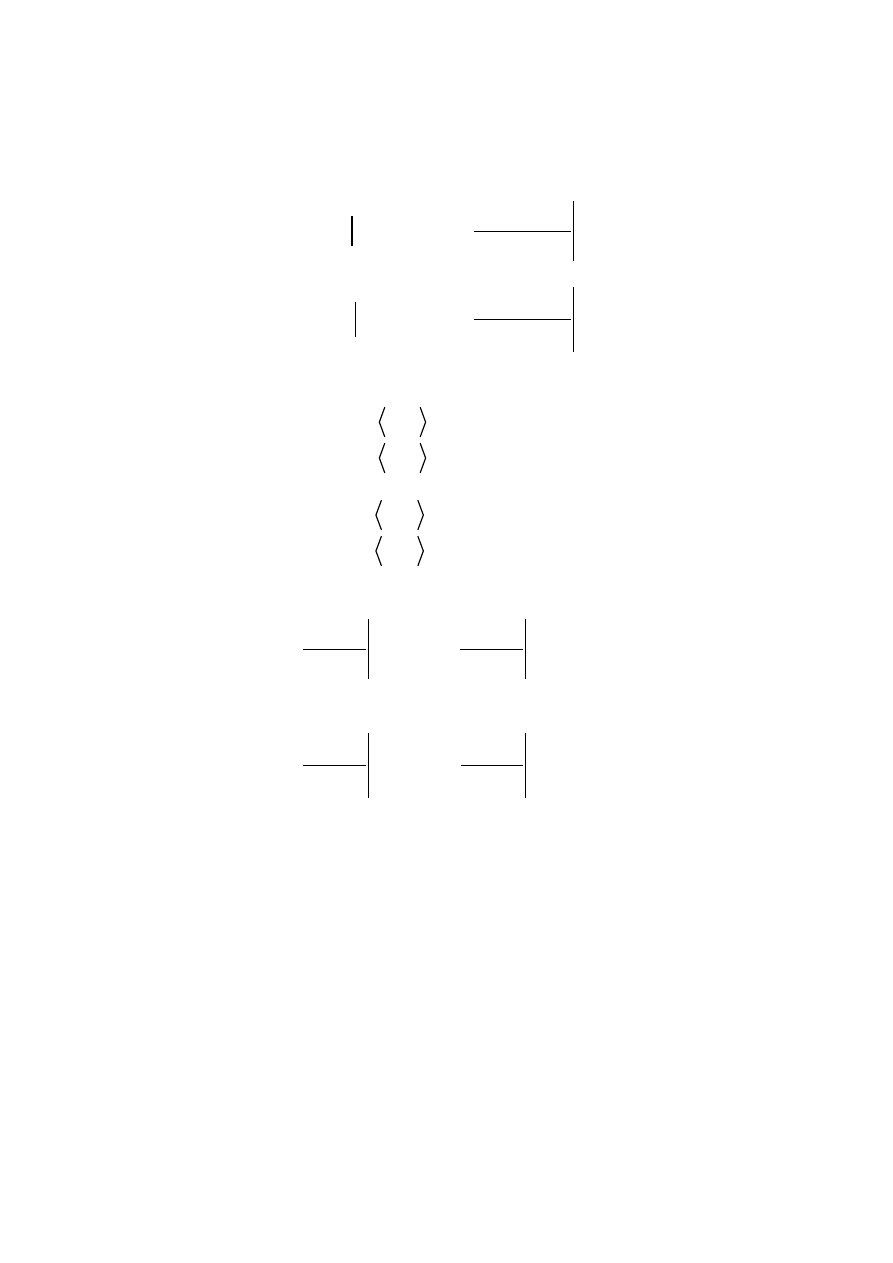
Mody TE: 6

Jeżeli (zgodnie z rysunkiem) w przekroju falowodu w płaszczyźnie xy
przez H oznaczymy odcinki poziome a przez V – odcinki pionowe, to
matematycznie warunki brzegowe można wyrazić w postaci

0

0

( , )

( , )

0

0

z

x

H

H

B

x y

B

x y

x

∂

=

⇒

=

∂

0

0

( , )

( , )

0

0

z

y

V

V

B

x y

B

x y

y

∂

=

⇒

=

∂

gdzie

0

0,

dolny odcinek poziomy

0,

górny odcinek poziomy

x

y

b

H

x

a

y

b

⎧ =

∈

= ⎨

=

∈

⎩

0

0,

lewy odcinek pionowy

0,

prawy odcinek pionowy

y

x

a

V

y

b

x

a

⎧ =

∈

= ⎨

=

∈

⎩

Rozdzielając zmienne uzyskujemy warunki brzegowe dla funkcji X(x)

0

( )

( )

0,

0

x

x a

dX x

dX x

dx

dx

=

=

=

=

(9a)

oraz funkcji Y(y)

0

( )

( )

0,

0

y

y b

dY y

dY y

dy

dy

=

=

=

=

(9b)

6. Podstawiając rozwiązanie ogólne (8a) do pierwszego z warunków
brzegowych (9a) otrzymujemy

cos( 0)

sin( 0) 0

x

x

x

x

k A

k

k B

k

−

=

stąd stała 0

A

= .Wstawiając do drugiego otrzymujemy

sin(

) 0

x

B

k a

=

Jest to możliwe wtedy gdy

0,1,2,

x

k a

m

m

= π,

=

… (10a)

Analogicznie z analizy Y(y) otrzymujemy, że 0

C

= oraz

0,1,2,

y

k b

n

n

= π,

=

…

(10b)

Mody TE: 7

Ostatecznie

0

0

( , )

cos

cos

z

m

n

B

x y

B

x

y

a

b

π

π

⎛

⎞

⎛

⎞

=

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

(11)

gdzie wprowadziliśmy stałą

0

B

BD

=

.

Otrzymane rozwiązanie nazywa się modem TE

mn

.

UMOWA: Pierwszy wskaźnik dotyczy większego wymiaru przekroju
falowodu, czyli zakładamy, że

a

b

≥

, przy czym przynajmniej jeden

wskaźnik musi być niezerowy.

Wyznaczanie częstości obcięcia

Wykorzystaliśmy dwa równania powstałe po rozdzieleniu zmiennych.
Z trzeciego z nich

2

2

2

2

0

x

y

k

k

k

c

⎛ ⎞

− −

+

−

=

⎜ ⎟

⎝ ⎠

ω

po wstawieniu

x

y

m

n

k

k

a

b

π

π

=

,

=

(12)

wyznaczamy liczbę falową k:

2

2

2

2

0

m

n

k

a

b

c

π

π

⎛

⎞

⎛

⎞

⎛ ⎞

−

−

+

−

=

⎜

⎟

⎜

⎟

⎜ ⎟

⎝

⎠

⎝

⎠

⎝ ⎠

ω

Stąd

2

2

2

m

n

k

c

a

b

2

⎡

⎤

⎛ ⎞

⎛ ⎞

⎛ ⎞

=

− π

+

⎢

⎥

⎜ ⎟

⎜ ⎟

⎜ ⎟

⎝ ⎠

⎝ ⎠

⎝ ⎠

⎢

⎥

⎣

⎦

ω

(13)

Aby fala rozchodziła się w falowodzie bez tłumienia, liczba falowa
musi być rzeczywista. Zachodzi to wtedy, gdy wyrażenie pod pier-
wiastkiem w równaniu (13) jest dodatnie:

2

2

2

0

m

n

c

a

b

2

⎡

⎤

⎛ ⎞

⎛ ⎞

⎛ ⎞

− π

+

>

⎢

⎥

⎜ ⎟

⎜ ⎟

⎜ ⎟

⎝ ⎠

⎝ ⎠

⎝ ⎠

⎢

⎥

⎣

⎦

ω

Z tej nierówności wyznaczamy warunek na częstość kołową fali ω

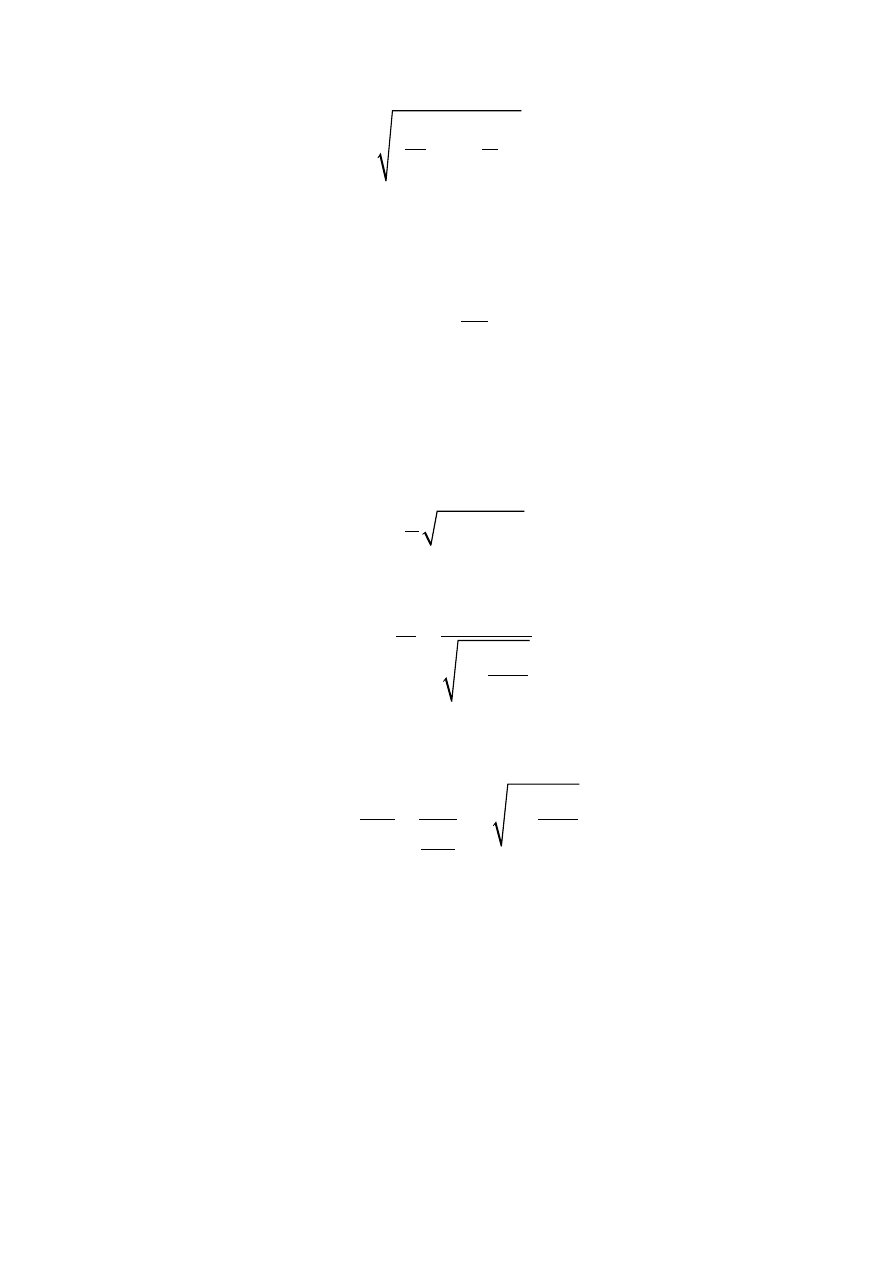
Mody TE: 8

2

2

mn

m

n

c

a

b

⎛ ⎞

⎛ ⎞

> π

+

=

⎜ ⎟

⎜ ⎟

⎝ ⎠

⎝ ⎠

ω

ω (14)

Wyrażenie

mn

ω nazywa się częstością obcięcia dla danego modu.

Najniższa częstość obcięcia dla danego falowodu występuje dla modu
TE

10

:

10

c

a

π

=

ω

(15)

Częstości mniejsze od niej nie propagują się.

Wyznaczanie prędkości fazowej i grupowej

Wykorzystując wyrażenie (14) na częstość obcięcia

mn

ω , liczbę falo-

wą można wyrazić w postaci

2

2

1

mn

k

c

=

−

ω

ω (16)

Stąd prędkość fazowa wynosi

2

2

1

mn

c

k

=

=

−

ω

υ

ω

ω

(17)

i jest większa od prędkości światła w ośrodku swobodnym c. Energia
jest przenoszona z prędkością grupową

2

2

1

1

mn

g

d

c

dk

dk

d

=

=

=

− ω

ω

υ

ω

ω

(18)

i jest mniejsza od c.