Politechnika Krakowska
Wydział Mechaniczny
Temat:
Prostowody przybliżone.
Rok akademicki:
Semestr:
Data:
Skład zespołu:
Grupa
Zespół
Numer ćwiczenia
2
Ocena
Podpis
Wprowadzenie
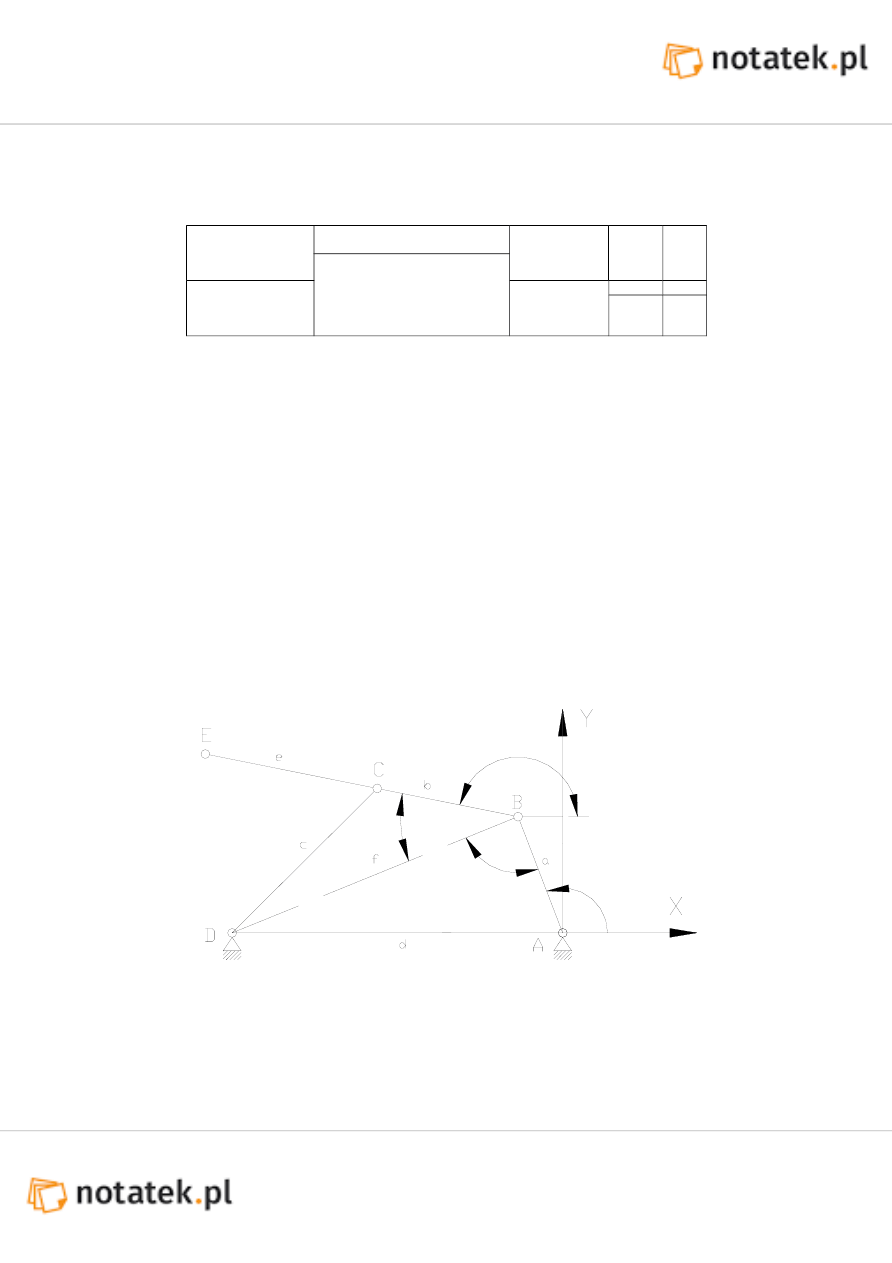
Prostowodem nazywamy mechanizm płaski, w którym określony punkt porusza się po z góry określonym torze.
Dzielą się one na:
♦
dokładne – tor wybranego punktu jest linią prostą (np. Prostowód Evansa; Prostowód Peaucelliera).
♦
przybliżone – tor wybranego punktu na pewnym odcinku nieznacznie odbiega od linii prostej.
W technice ze względu na prostą strukturę i zwartą budowę, częściej stosowane są prostowody przybliżone.
Klasycznym przykładem prostowodu przybliżonego jest mechanizm dźwigowy oparty na czworoboku
przegubowym, o odpowiednio dobranych długościach ogniw. Taką strukturę mają żurawie portowe, w których
hak porusza się po lini poziomej, co w konsekwencji eliminuje pracę podnoszenia nosiwa w czasie zmiany
wypadu.
I

DOŚWIADCZALNIE
TEORETYCZNIE
i
α
( )
i
Xe
α
( )
i
Ye
α
( )
i
d
α
( )
i
Xe
α
( )
i
Ye
α
( )
i
d
α
10
23
0,11
0,288
-264,147
119,651
-1,63987
15
27
0,92
-0,617
-267,119
120,358
-0,39738
20
32
0,43
-0,152
-270,267
121,784
0,38061
25
38
0,12
0,152
-273,626
123,846
0,78133
30
44
0,08
0,186
-277,219
126,452
0,89182
35
50
0,22
0,04
-281,061
129,505
0,79828
40
56
0,31
-0,046
-285,155
132,912
0,57643
45
63
0,27
-0,023
-289,459
136,853
0,29415
50
69
0,28
-0,039
-294,067
140,437
0,00730
55
76
0,21
0024
-298,849
144,402
-0,24027
60
83
0,11
0,117
-303,809
148,418
-0,4203
65
89
0,02
0,201
-308,914
152,435
-0,51309
70
96
0,06
0,154
-314,12
156,412
-0,51279
75
102
0,18
0,028
-319,382
160,321
-0,42445
80
108
0,21
-0,008
-324,647
164,143
-0,26516
85
114
0,29
-0,094
-329,859
167,871
-0,06335
90
119
0,22
-0,029
-334,957
171,506
0,14315
95
124
0,11
0,086
-339,876
175,061
0,30455
100
129
0,06
0,121
-344,546
178,557
0,36167
105
133
0,31
-0,133
-348,89
182,025
0,24312
110
137
0,42
-0,247
-352,827
185,504
-0,13125
Obliczenia:
(
)
(
)
(
)
β
α
β
α
ψ
ϕ
α
β
ψ
ϕ
α
sin
sin
cos
cos
180
2
cos
2
cos
180
cos
2
2
2
2
2
2
2
2
2
b
e
a
y
b
e
a
x
fb
c
b
f
arc
fa
c
a
f
arc
ad
d
a
f
E
E
o
+
+
=
+
+
=
−
−
+
=
−
+
=
−
+
=
−
−
+
=
II

[ ]
[ ]
[ ]
[ ]
[ ]
mm
d
cm
e
mm
c
mm
b
mm
a
Dane
o
o
o
200
180
125
170
70
5
110
10
:
max
min
=
=
=
=
=
=
∆
=
=
α
α
α
Wzory końcowe nie uwzględniające transformacji układu współrzędnych mają następującą postać:
(
)
(
)
(
)
(
)
17
sin
1260
449
cos
280
10
cos
7
20
sin
449
cos
280
200
cos
224
253
sin
sin
4375
17
449
cos
280
10
449
cos
280
200
α
α
α
α
α
α
α
+
−
−
+
−
−
=
−
−
=
a
a
y
x
E
E
Wyznaczamy błąd prostowodności badanego mechanizmu dla rzeczywistego i teoretycznego zakresu
zmienności kąta
α
.
Błąd prostowodności definiujemy jako iloraz szerokości prostokątnego pasa tolerancji wewnątrz którego mieści
się badany fragment toru rzeczywistego do długości tego pasa.
( )
( )
( )
( ) ( )
(
) (
)
(
) (
)
[
]
2
min
max
min
max
2
min
max
1
1
100
m
y
y
m
x
x
L
m
b
y
x
m
d
o
o
L
d
d
i
i
i
i
i
+
−
+
−
=
∆
+
+
−
⋅
=
⋅
∆
−
=
α
α
α
α
α
α
α
α
α
δ
Teoretyczny błąd prostowodności:
o
o
t
29
,
2
=
δ
Rzeczywisty błąd prostowodności:
o
o
r
79
,
0
=
δ
Prosta regresji ma postać: y=mx+b
Dla pomiarów doświadczalnych współczynniki m i b wynoszą:
m = - 0,001
b = 0,31
Dla obliczeń teoretycznych:
m = -0,764
b = -84,221
III
Wyszukiwarka
Podobne podstrony:
prostownik sprawozdanie id 4022 Nieznany
prostownik akumul 01 id 402192 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
cw med 5 id 122239 Nieznany
więcej podobnych podstron