Część III

Pomiary wybranych

wielkości fizycznych

14. Pomiary wielkości elektrycznych stałych

w czasie

Wielkości elektryczne w sposób szczególny są łatwo mierzalne przyrządami elektronicznymi,
w tym mikroprocesorowymi.

14.1. Pomiary prądu stałego

Współczesna technika pozwala na precyzyjny pomiar natężenia prądu stałego w bardzo
szerokim zakresie, od pA do setek A.

Niestety, poza samą wartością mierzonego prądu, na wynik pomiaru wpływają także inne
czynniki powodujące, że prąd wpływający do amperomierza jest różny od wydajności
prądowej J źródła prądowego. Są one zatem źródłem błędów systematycznych. Należą do
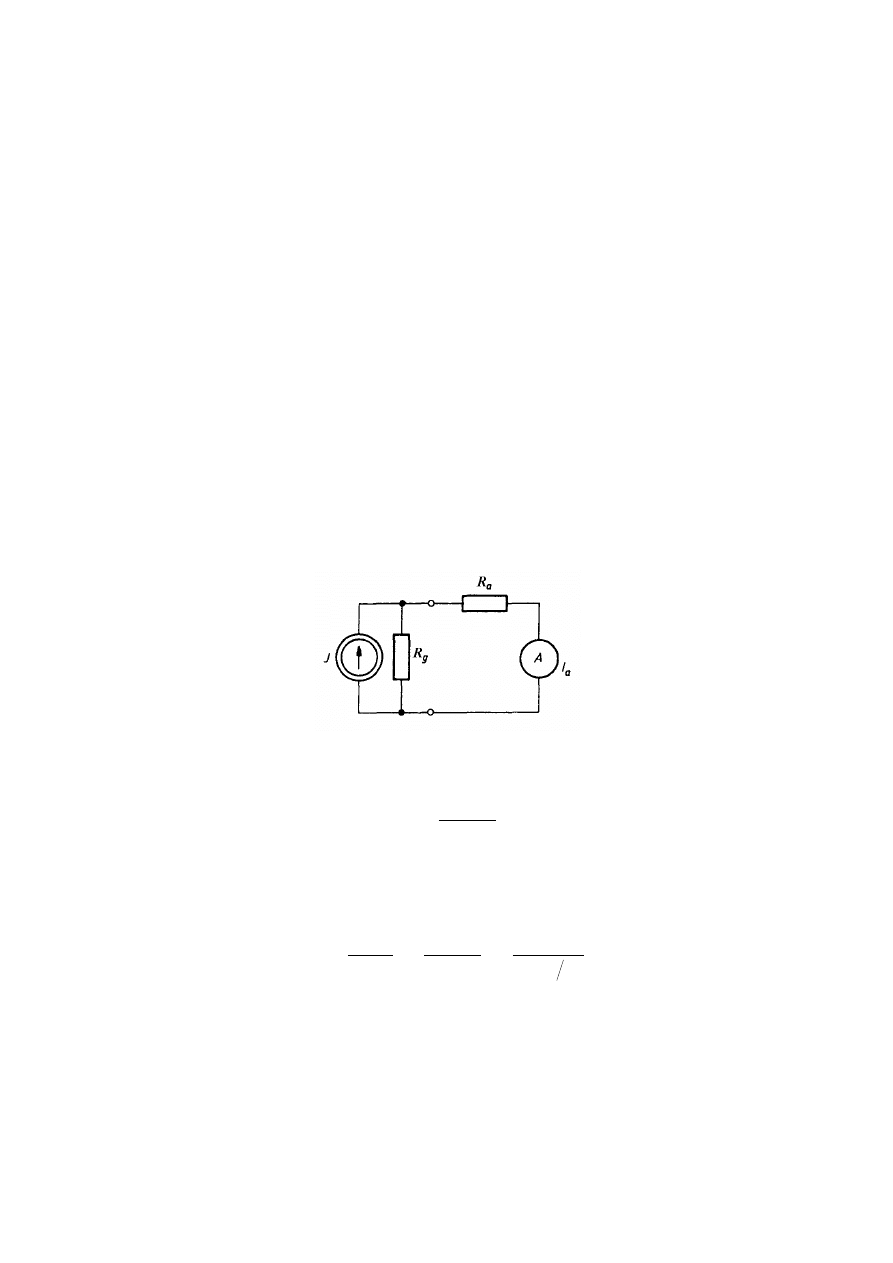
nich (rys.):



rezystancja wewnętrzna źródła prądowego R

g

,



rezystancja wewnętrzna amperomierza R

a

.

Prąd płynący przez amperomierz wynosi:

a

g

g

a

R

R

R

J

I





.

Stąd względny błąd systematyczny – błąd metody – czyli względna różnica między
wskazaniem (nawet bezbłędnie działającego) miernika a wartością wydajności ma wartość:

a

g

a

g

a

a

S

R

R

R

R

R

J

J

I

J

δ

















1

1

.

Różne metody i przyrządy stosowane są w pomiarach prądów stałych. Prześledzimy je w
ujęciu historycznym.

Amperomierze magnetoelektryczne należą do najstarszych konstruowanych mierników
wielkości elektrycznych. Cewka mechanizmu magnetoelektrycznego, pod wpływem
zachodzących zjawisk fizycznych, wychyla się o kąt proporcjonalny właśnie do natężenia
prądu.

4

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

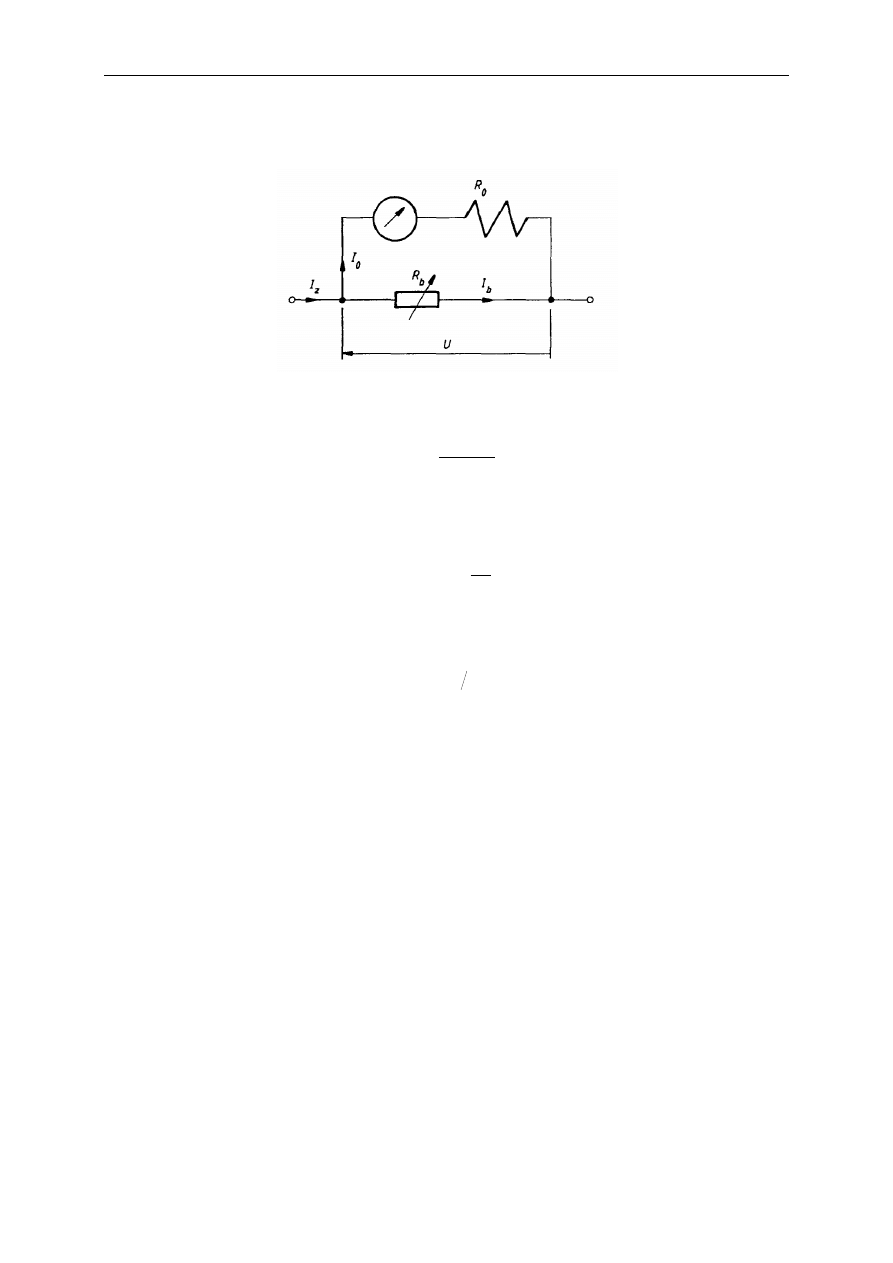
Zasadę działania takich amperomierzy wraz z ideą rozszerzanie zakresu pomiarowego przez
rezystor bocznikujący R

b

(tworzący dzielnik prądowy), pokazuje poniższy rysunek.

Wychylenie kątowe mechanizmu wynosi:

Z

b

b

I

R

R

R

I

α







0

0

,

a zakres pomiarowy I

z

jest zależny od R

b

:

















b

Z

R

R

I

I

0

0

1

.

Dla takich mierników określa się też czułość prądową, wyrażaną w [dz/mA]:

Z

Z

I

I

S





.

Amperomierze elektroniczne posiadają bloki przetwarzające napięcie, dlatego też
najczęściej konstruowane są na bazie przetwornika I/U oraz miliwoltomierza elektronicznego.
Najprostszym przetwornikiem I/U jest rezystor szeregowy.

Amperomierze cyfrowe natomiast budowane są z wykorzystaniem przetworników I/U i A/C.
Wartość mierzonego prądu określana jest w nich na podstawie cyfrowego pomiaru napięcia,
stąd podstawową strukturą wewnętrzną takiego amperomierza jest woltomierz cyfrowy.

14.2. Pomiary napięcia stałego

Technika pomiaru napięcia stałego jest również bardzo rozwinięta. Z dużą dokładnością
można mierzyć napięcia w zakresie od nV do kV. Cechą charakterystyczną współczesnych
woltomierzy jest bardzo wysoka rezystancja wejściowa, sięgająca 10

8

÷10

10

Ω.

Czynnikami wpływającymi na wynik pomiaru są:



rezystancja wewnętrzna źródła napięcia R

g

,



rezystancja wejściowa woltomierza R

we

.

14. Pomiary wielkości elektrycznych stałych w czasie

5

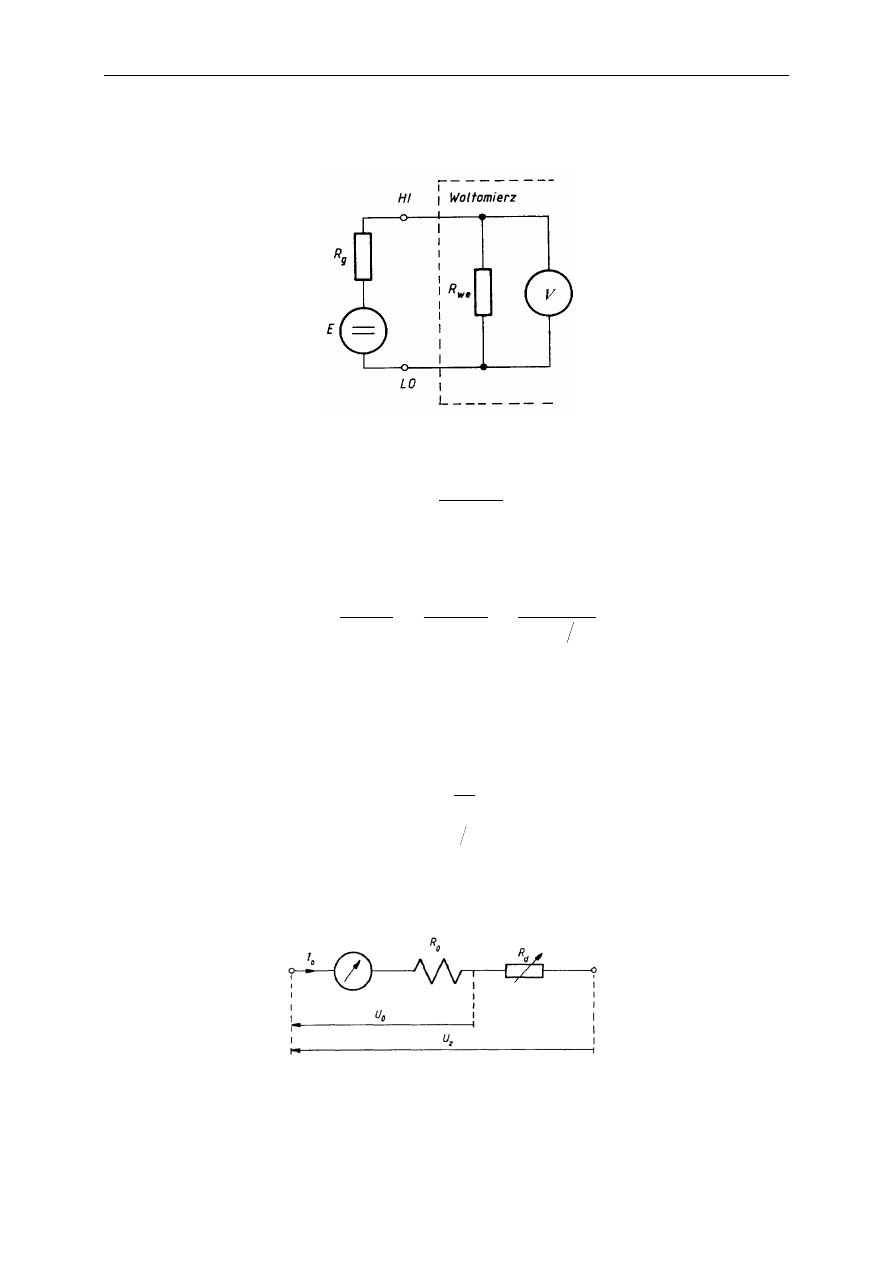
Rezystancje te powodują, że napięcie mierzone przez (nawet bezbłędnie działający)
woltomierz jest różne od siły elektromotorycznej (E) źródła – błąd systematyczny.

Powstający dzielnik napięciowy (rys.) daje:

we

g

we

V

R

R

R

E

U





.

Stąd względny błąd systematyczny:

g

we

we

g

g

V

S

R

R

R

R

R

E

E

U

E

















1

1



.

Woltomierze analogowe najczęściej wykorzystują mechanizm magnetoelektryczny i mają
identyczną strukturę jak amperomierze, a rezystancja cewki (R

0

) jest w nich naturalnym

przetwornikiem mierzonego napięcia (na poziomi mV) na natężenie prądu, na które fizycznie
reaguje cewka. Stąd ich czułość napięciowa powiązana jest z czułością prądową cewki:

U

S

R

U

S

I

S

U

I

I







0



,

Z

Z

U

U

S





.

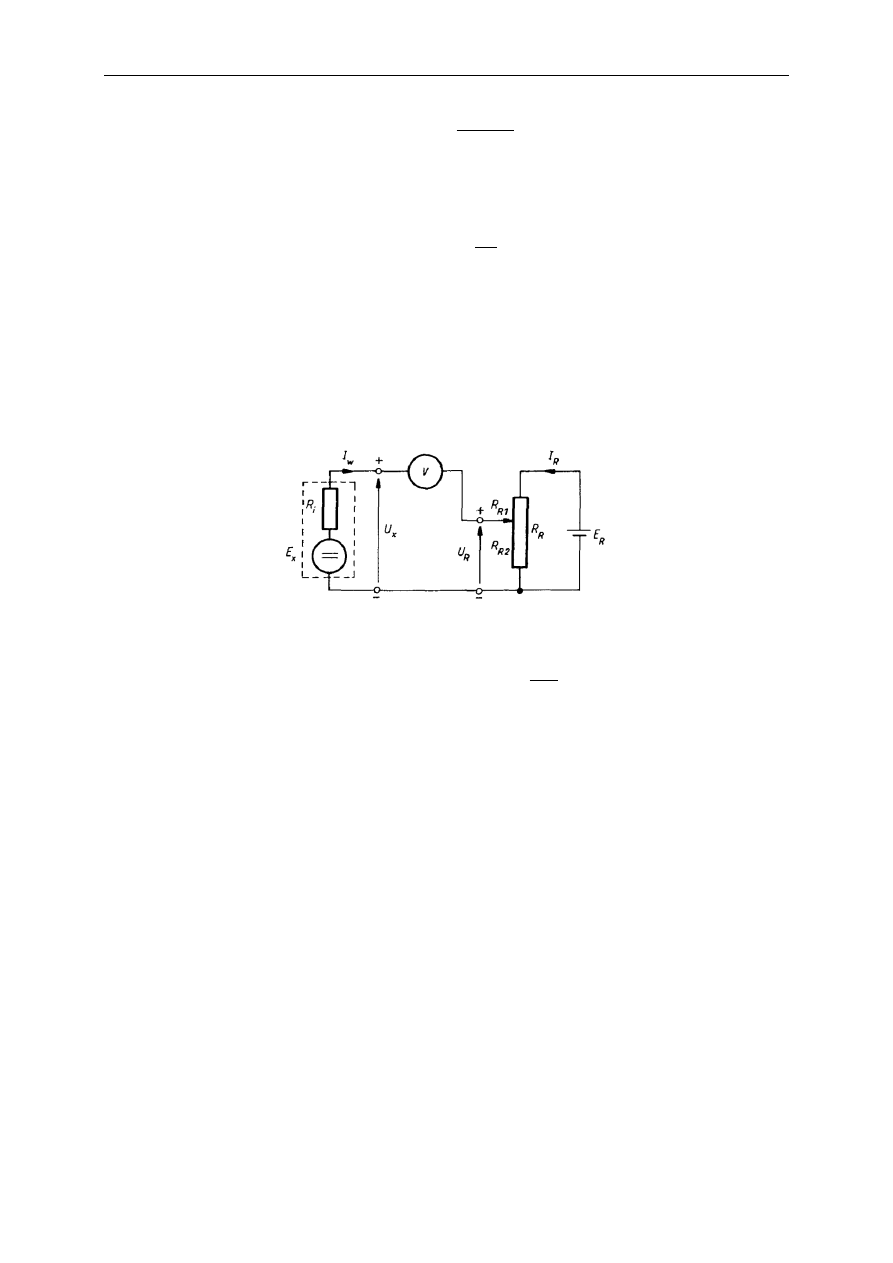
W celu umożliwienia pomiaru większych napięć, mechanizm magnetoelektryczny uzupełnia
się regulowanym rezystorem szeregowym R

d

(rys.), który tworzy dzielnik napięciowy.

Wychylenie cewki jest proporcjonalne do przyłożonego napięcia:

6

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Z

d

U

R

R

R

U

I

α









0

0

0

0

,

a aktualny zakres pomiarowy zależy od nastawy R

d

:

















0

0

1

R

R

U

U

d

Z

.

Woltomierze elektroniczne są typowymi analogowymi miernikami elektronicznymi. Do
najważniejszych bloków przetwarzających nośnik informacji, jakim jest napięcie, należą:
dzielnik napięcia, wzmacniacz napięcia, układ zwiększający R

we

i wskaźnik analogowy.

Wśród woltomierzy elektronicznych spotkać można takie, które realizują różne metody
pomiarowe, np. zerową kompensacyjną (rys.).

Wtedy:

R

R

R

R

R

R

x

x

R

R

E

R

I

U

U

E

2

2









.

Wśród woltomierzy elektronicznych spotkać można rodzinę mierników z wbudowanym
przetwornikiem A/C, którego zadaniem było przetworzenie wytworzonego już wyniku
pomiaru w postaci napięcia stałego na kod cyfrowy, który następnie sterował (lampowym)
wyświetlaczem cyfrowym. Uzyskano w ten sposób nową jakość – odczyt cyfrowy w mierniku
analogowym.

Biorąc pod uwagę rodzaj i cechy zastosowanego przetwornika A/C, podstawowe rodzaje tego
typu woltomierzy biorą soje nazwy od zastosowanego przetwornika:



woltomierze impulsowo-czasowe,



woltomierze kompensacyjne,



woltomierze całkujące.

Woltomierze cyfrowe stanowią najważniejszą grupę przyrządów pomiarowych, gdyż na ich
strukturze opiera się większość mierników mikroprocesorowych. Najważniejszą ich cechą jest
wykorzystanie przetworników A/C (rys.), przetwarzających właśnie napięcie.

14. Pomiary wielkości elektrycznych stałych w czasie

7

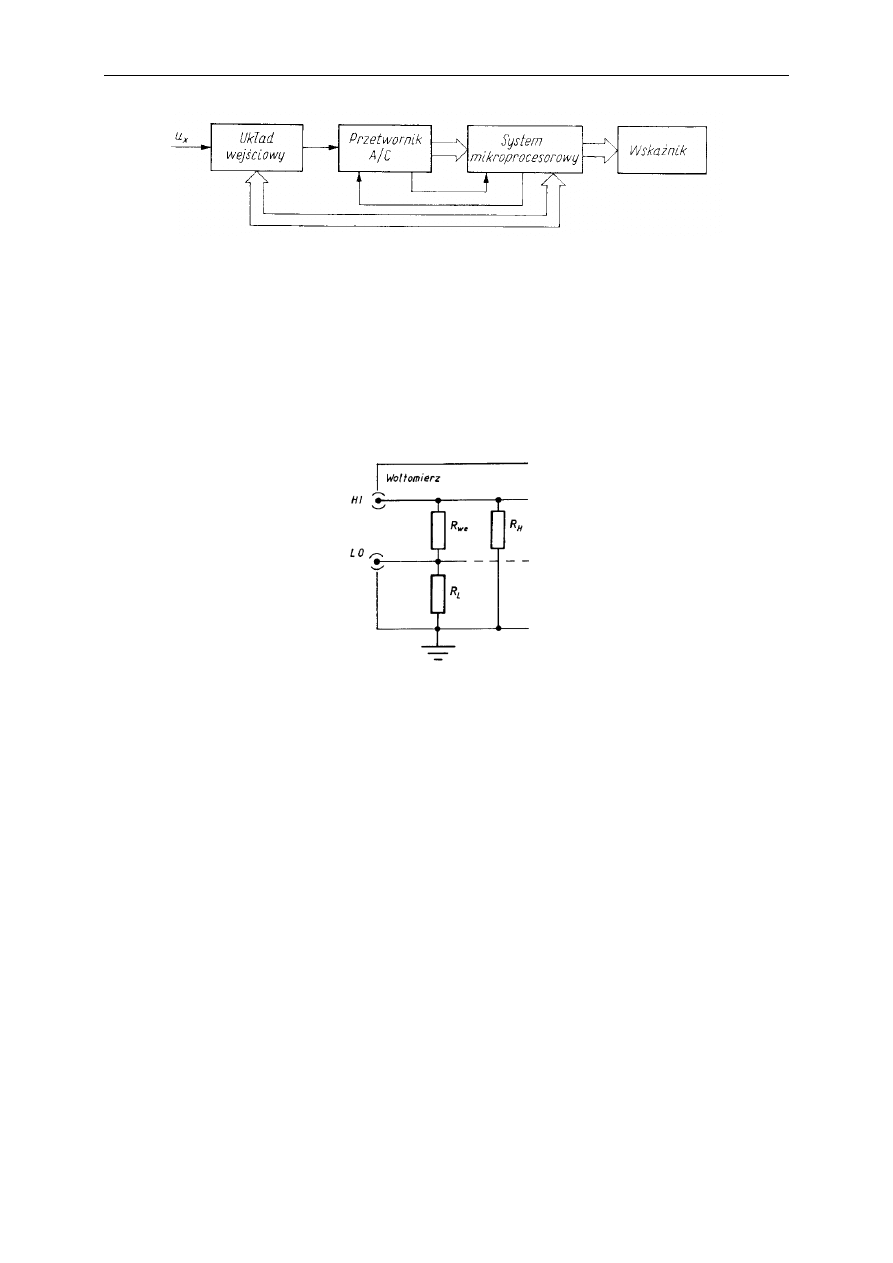
Współczesne woltomierze są zazwyczaj budowane jako złożone urządzenia
mikroprocesorowe, które poza dwoma gniazdami do przyłączenia napięci mierzonego (HI i
LO), mają jeszcze dwa dodatkowe zaciski – potencjał ekranu oraz potencjał masy przyrządu.
W zależności od konfiguracji umieszczanej na nich metalowej zworki (blaszki stalowej, którą
można zwierać wejścia), woltomierze takie mogą pracować z wejściami symetrycznymi i
niesymetrycznymi (rys.):



wejścia symetryczne: rezystancje zacisków R

H

i R

L

względem masy są jednakowe,



wejścia niesymetryczne: rezystancje R

H

i R

L

są różne.

Często zacisk LO woltomierza łączony jest z masą, a masa z ekranem.

14.3. Pomiary mocy

Moc P w obwodach prądu stałego, zależna od natężenia I przepływającego przez odbiornik
prądu i spadku napięcia U na nim, określona jest prostym równaniem:

UI

P



.

Mierniki służące do pomiaru mocy w obwodach prądu stałego nazywane są watomierzami.

Watomierze analogowe wykorzystują mechanizm elektrodynamiczny. Składa się on z dwóch
cewek prądowych, z których jedna zastępuje magnes stały występujący w mechanizmach
magnetoelektrycznych. Pole magnetyczne wytwarzane przez cewkę nieruchomą jest
proporcjonalne do płynącego przez nią natężenia prądu I

N

, a wychylenie cewki ruchomej jest

proporcjonalne do natężenia płynącego przez nią prądu I

R

oraz pola magnetycznego

wytworzonego przez pierwszą z cewek. Ostatecznie wychylenie ustroju jest proporcjonalne
do iloczynu obydwu prądów:

R

N

d

I

I

k





,

gdzie k

d

jest współczynnikiem proporcjonalności zależnym od konstrukcji miernika.

8

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

W analogowych miernikach mocy stosuje się też mechanizm ferrodynamiczny, w którym strumień magnetyczny
cewki nieruchomej jest zwiększony przez dodatkowy materiał ferromagnetyczny.

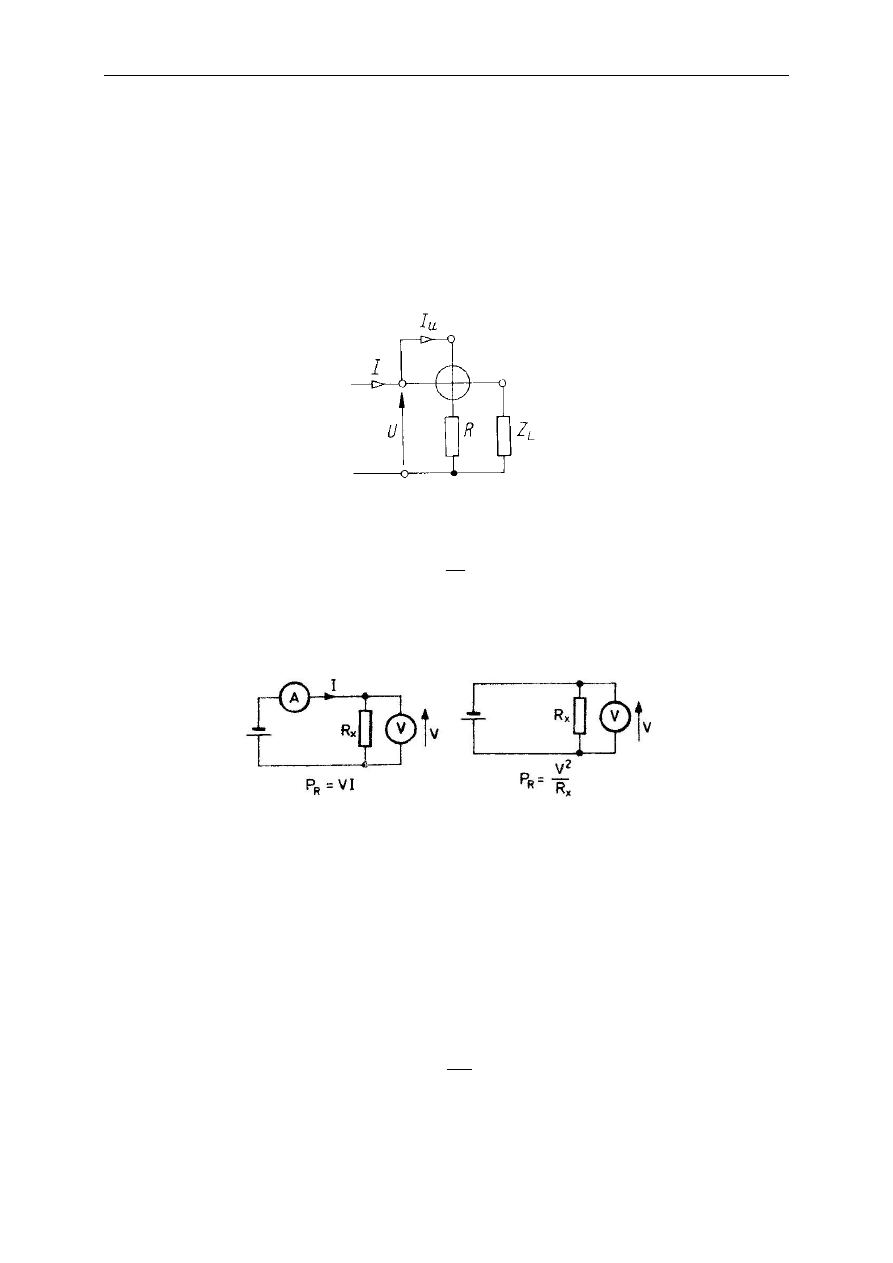
Idea bezpośredniego pomiaru mocy miernikiem analogowym pokazana jest na poniższym
rysunku. Spadek napięcia U przetwarzany jest przez rezystor R na proporcjonalny prąd I

u

,

który następnie fizycznie jest mnożony przez prąd odbiornika I w mechanizmie elektro- lub
ferrodynamicznym. Dlatego też watomierze posiadają 4 zaciski wejściowe – po parze na prąd
i napięcie, z tym, że jeden z zacisków napięciowych i jeden z prądowych są ze sobą
wewnętrznie połączone

(są one oznakowane na płycie czołowej)

.

Ostatecznie wychylenie watomierza α jest wprost proporcjonalne do mierzonej mocy:

P

k

UI

R

k

I

I

k

p

d

U

d









.

Moc można również mierzyć metodami pośrednimi (rys.). Takim pomiarom towarzyszą błędy
systematyczne: wynik pomiaru zawiera również moc energii traconej w miernikach.

Watomierze cyfrowe, obecnie mikroprocesorowe, dokonują pomiaru pośredniego: wynik
pomiaru obliczają cyfrowo na podstawie pomiaru prądu i napięcia.

14.4. Pomiary rezystancji

Rezystancję najczęściej mierzy się metodą pośrednią, zwaną też techniczną, polegającą na
pomiarze prądu I płynącego przez opornik oraz spadku napięcia U na nim, oraz
wykorzystaniu prawa Ohma:

a

V

I

U

R



.

14. Pomiary wielkości elektrycznych stałych w czasie

9

Ze względu na dwie możliwe konfiguracje połączeń mierników, rozróżnia się układy z
poprawnym pomiarem napięcia lub prądu. W przypadku poprawnego pomiaru napięcia błąd
metody dany jest równaniem:

V

x

x

x

S

R

R

R

R

R

R











.

Przy pomiarze w układzie z poprawnym pomiarem prądu błąd metody wynosi:

x

a

x

S

R

R

R





.

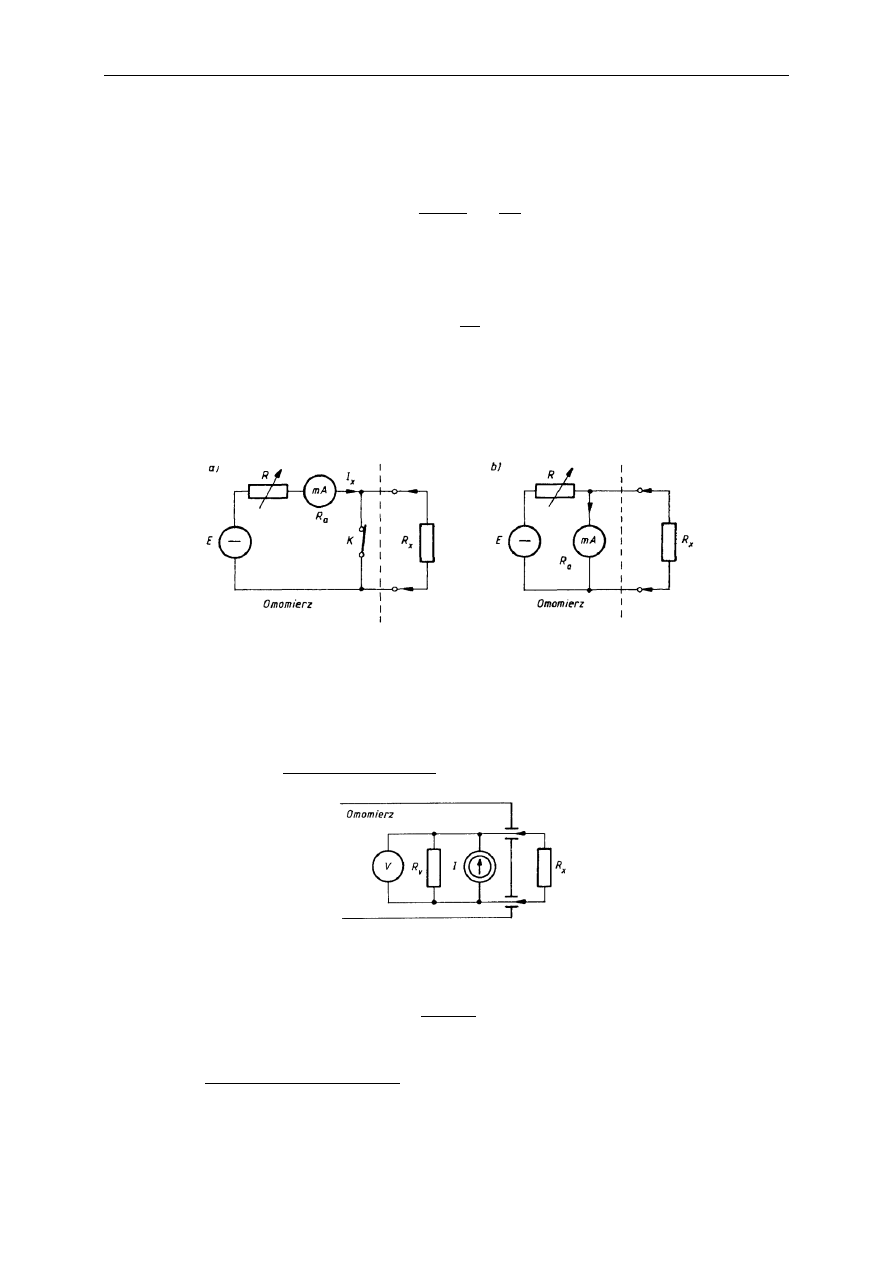
Omomierze analogowe najczęściej wykorzystują mechanizmy magnetoelektryczne. Muszą
też posiadać wewnętrzne źródło zasilania. Ich charakterystyki (a zatem też i skale) są
nieliniowe. Buduje się je w układach szeregowych (rys. a) lub równoległych (rys. b).

Omomierze elektroniczne i cyfrowe posiadają strukturę wewnętrzną zależną od poziomu
mierzonej rezystancji. Ich blokami składowymi są m.in. źródła prądowe lub napięciowe, a
pomiar (analogowy lub cyfrowy) sprowadza się do pomiaru powstałego napięcia lub natężenia
prądu.

Omomierze do pomiaru typowych rezystancji maja strukturę jak na rysunku.

Gdy spełniony jest warunek

v

x

R

R



, to:

x

v

x

v

x

V

IR

R

R

R

R

I

U







.

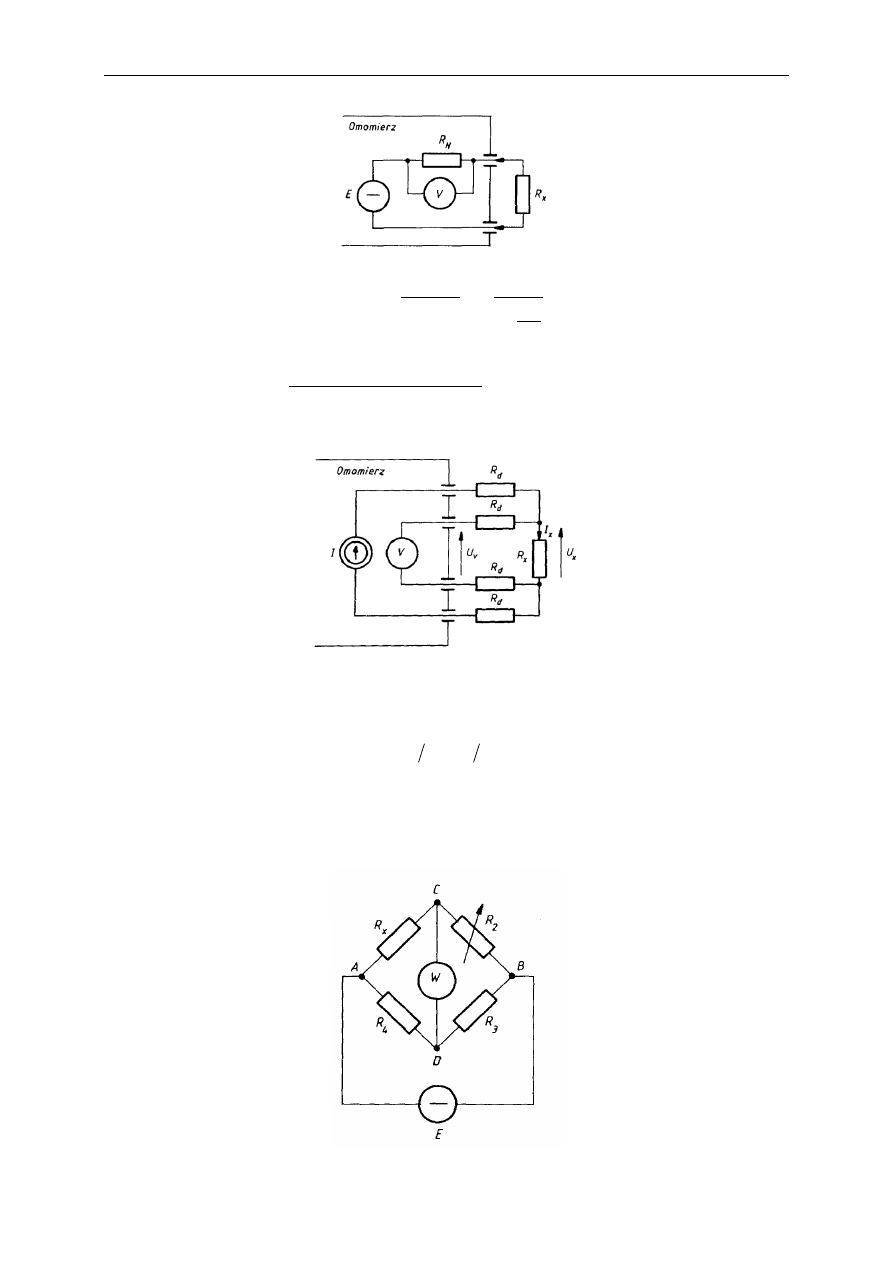
Do pomiaru bardzo dużych rezystancji stosuje się odmienne układy, w których mierzone
napięcie U

V

jest nieliniowa funkcją badanej rezystancji R

x

.

10

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

N

x

x

N

N

V

R

R

E

R

R

R

E

U









1

1

.

Omomierze do pomiaru bardzo małych rezystancji budowane są jako czterozaciskowe – po
parze na sygnały napięciowy i prądowy. Eliminuje się w ten sposób występujący w innych
układach błąd metody spowodowany rezystancją doprowadzeń.

Gdy

v

d

x

R

R

R



~

, to prąd płynący w obwodzie napięciowym powyższej struktury jest

pomijalnie mały, co daje

x

v

U

U



oraz

I

I

x



, zatem:

x

x

x

v

zm

R

I

U

I

U

R







.

Rezystancję można też mierzyć metodami bezpośrednimi zerowymi.

Poniższy rysunek przedstawia Mostek Wheatstone'a realizujący pomiar metodą
kompensacyjną (regulowany wzorzec).

14. Pomiary wielkości elektrycznych stałych w czasie

11

Napięcie między węzłami wynosi:







3

2

4

4

2

3

3

2

2

4

R

R

R

R

R

R

R

R

E

R

R

R

E

R

R

R

E

U

x

x

x

x

CD

















.

Po zrównoważeniu mostka wskazywanym przez wskaźnik W (brak przepływu prądu między
węzłami C i D) mamy

0



CD

U

, zatem

4

2

3

R

R

R

R

x



i ostatecznie

3

4

2

R

R

R

R

x



.

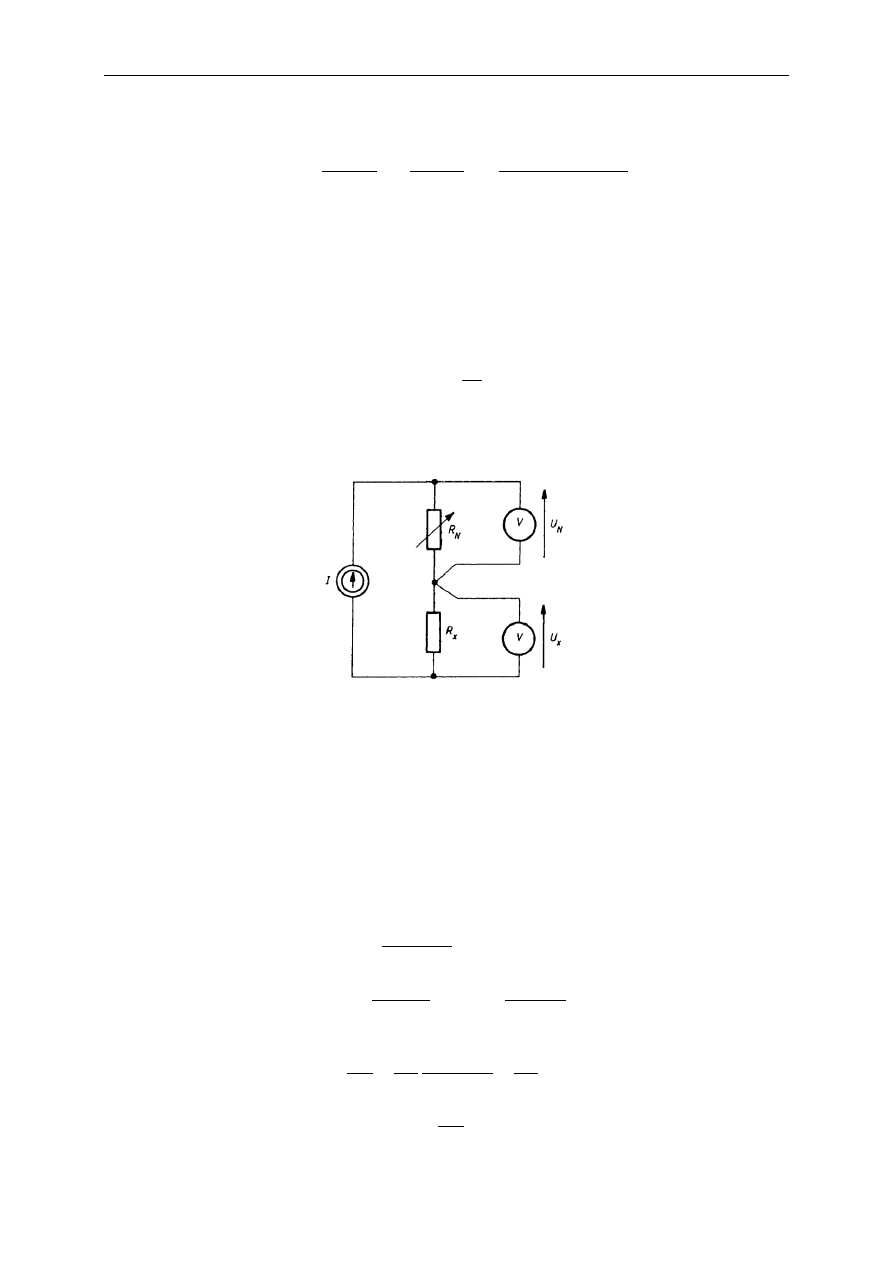
Kolejną metodą zerową jest metoda porównawcza, zwana podstawieniową (rys.).

Może ona być realizowana w dwóch etapach za pomocą jednego woltomierza i opornicy
dekadowej (regulowany wzorzec rezystancji), którą w drugiej fazie reguluje się tak długo, aż
wskazywane napięcie U

N

jest takie samo jak U

x

uzyskane przy pierwszym pomiarze:

N

x

x

N

R

R

U

U







.

Jeżeli nie da się odpowiednio dokładnie doregulować opornicy (

x

N

U

U



), można wyznaczyć

R

x

z poniższych wzorów, zauważając, że

v

N

x

R

R

R



~

:

,

,

,

,

,

,

v

N

v

N

N

v

x

v

x

x

v

v

v

v

N

x

N

x

v

R

R

R

R

I

U

R

R

R

R

I

U

I

R

U

R

R

R

I

I























.

,

N

N

x

x

N

x

v

x

v

N

N

x

N

x

R

U

U

R

R

R

R

R

R

R

R

R

U

U











12

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

14.5. Zagadnienia kontrolne

Czynniki wpływające na dokładność pomiaru prądu stałego
Czynniki wpływające na dokładność pomiaru napięcia stałego
Podstawowe metody pomiaru napięcia stałego
Zasady pomiarów bezpośrednich i pośrednich mocy przy prądach stałych
Podstawowe metody pomiaru rezystancji elektrycznej

15. Sygnały pomiarowe i ich parametry

15.1. Pojęcia podstawowe

Większość wielkości fizycznych zmienia swoją wartość w czasie.

Czas – pojęcie dobrze znane z życia codziennego – w fizyce i filozofii bywa różnie
interpretowany.

Spór o to, czy czas rzeczywiście istnieje, czy też jest tworem abstrakcyjnym porządkującym wrażenia odbierane
przez człowieka, toczyli m.in. Newton i Leibniz. Fakt, że chronologię pewnych zdarzeń pamiętamy (przeszłość)
a innych jeszcze nie znamy (przyszłość) powoduje, że przypisujemy czasowi kierunek, zwany strzałką czasu.
Jako istotna wielkość fizyczna czas występuje w teorii względności Einsteina.

Sygnał pomiarowy to podlegająca pomiarowi zmienna w czasie wielkość fizyczna będąca
nośnikiem informacji o stanie badanego obiektu.

W metrologii i innych dziedzinach nauki i techniki sygnały rzeczywiste opisywane są za
pomocą modeli matematycznych.

Model matematyczny sygnału to najczęściej funkcja (lub szereg funkcyjny), której
argumentem jest czas. Takie podejście umożliwia wykonywanie operacji matematycznych na
badanych sygnałach.

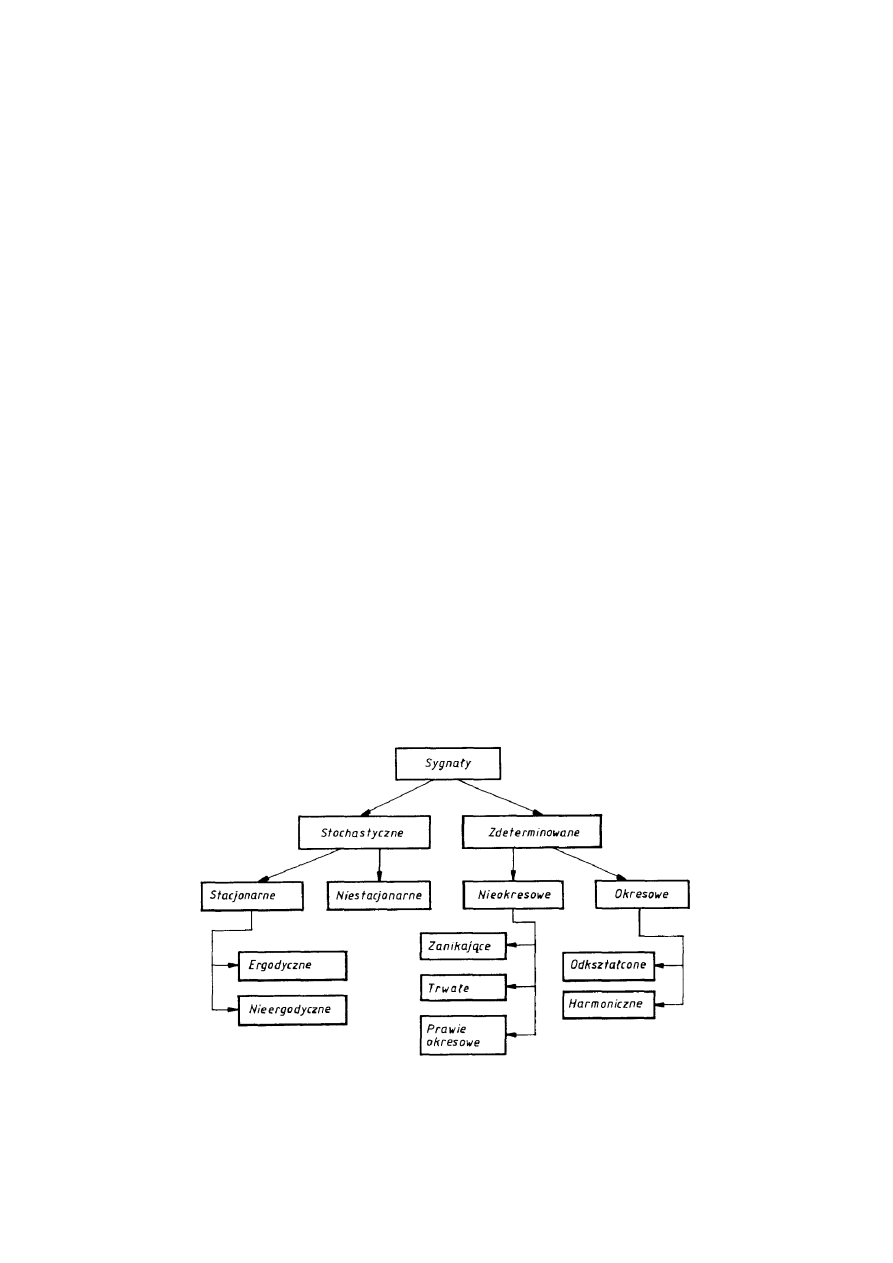
Klasyfikacja sygnałów (rys.) najczęściej bierze pod uwagę ich charakter: zdeterminowany
(tzn. że na podstawie skończonego czasu obserwacji można z zadaną dokładnością
przewidzieć wartość sygnału w przyszłości) i stochastyczne (których przyszłej wartości nie da
się dokładnie określić, lecz jedynie z pewnym prawdopodobieństwem).

Rys. Przykład klasyfikacji sygnałów.

Sygnały stochastyczne stacjonarne cechują się niezmiennością swych parametrów (jak np. wartość średnia czy
wariancja) w czasie, natomiast parametry sygnałów niestacjonarnych zmieniają się.

14

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Przykładem sygnałów stochastycznych analizowanych w metrologii są szumy, które stają się
źródłem błędów przypadkowych.

Najprostsze do analizy są sygnały okresowe, tzn. takie, których wartości powtarzają się ze
stałym okresem czasu:

  



kT

t

x

t

x





,

gdzie T to okres, a k jest liczbą całkowitą.

Sygnały okresowe opisane są matematycznie przez funkcje okresowe (lub szeregi funkcji
okresowych). Należą do nich sygnały harmoniczne (zwane też sinusoidalnymi):

 































t

T

X

t

X

t

x

π

2

cos

cos

,

gdzie X jest amplitudą sygnału, ω to pulsacja, a φ jest kątem przesunięcia fazowego (zwanym krótko „fazą”),

i sygnały odkształcone, na które można spojrzeć jak na odkształcone sinusoidy i zgodnie z
twierdzeniem Fouriera będące złożeniem sygnałów harmonicznych:

 











k

k

k

t

k

X

t

x





cos

.

Szczególnym rodzajem sygnałów odkształconych są sygnały impulsowe, odgrywające ważną rolę w elektronice
cyfrowej.

Sygnały deterministyczne nieokresowe mogą mieć zanikającą energię, lub być trwałe (w czasie obserwacji).
Interesującą klasą są sygnały prawie okresowe, a wśród nich takie, których „okres” zawsze mieści się w
pewnych granicach, lecz nigdy nie powtarza.

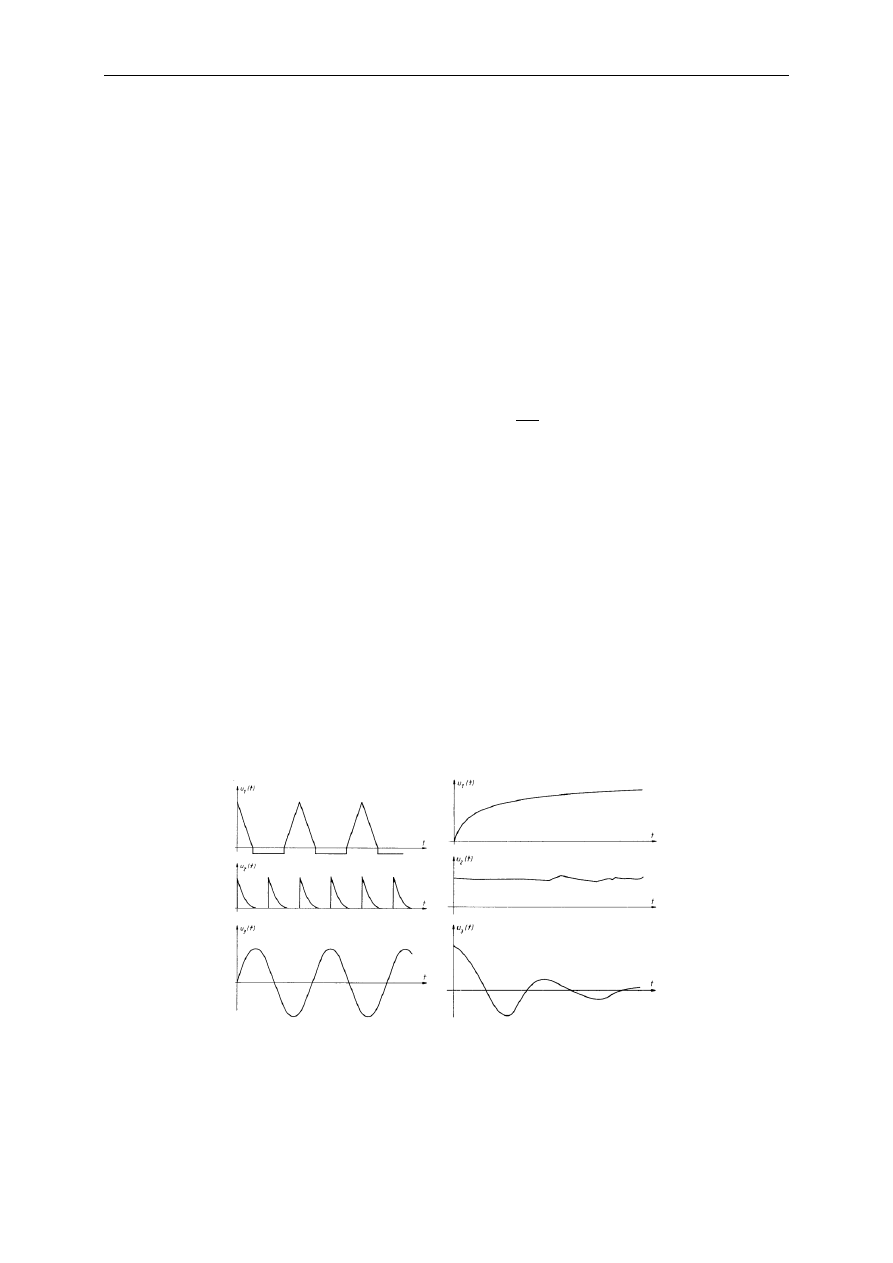
Poniżej pokazane są przykłady sygnałów: odkształconych, harmonicznego, trwałych i zanikającego.

15. Sygnały pomiarowe i ich parametry

15

15.2. Parametry sygnałów

Sygnały pomiarowe charakteryzowane są m.in. za pomocą ich parametrów. Parametry te
można pogrupować pod względem opisywanych cech fizycznych.

Parametry energetyczne związane są z energią przenoszoną przez sygnał. Definiowane są za
pomocą wartości chwilowych x(t). Definicje najważniejszych, wprowadzonych już wcześniej
parametrów energetycznych sygnałów okresowych, są następujące:

− wartość średnia:

 







T

t

t

śr

t

t

x

T

X

0

0

d

1

,

− wartość średnia wyprostowana:

 







T

t

t

śrw

t

t

x

T

X

0

0

d

1

,

− wartość międzyszczytowa:

 

 

 

 

t

x

t

x

X

T

t

T

t

pp

,

0

,

0

min

max









,

− i najważniejszy parametr – wartość skuteczna:

 







T

t

t

sk

t

t

x

T

X

0

0

d

1

2

.

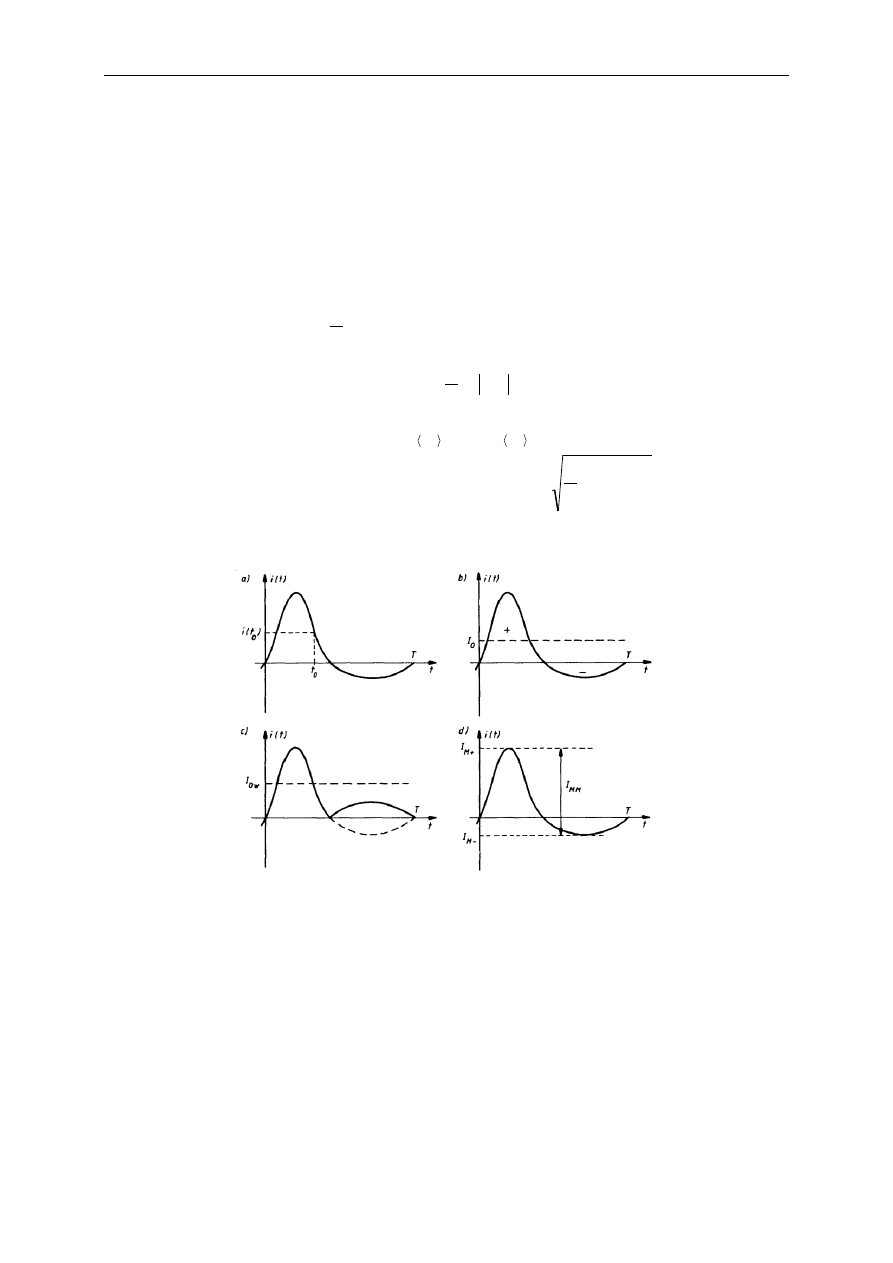
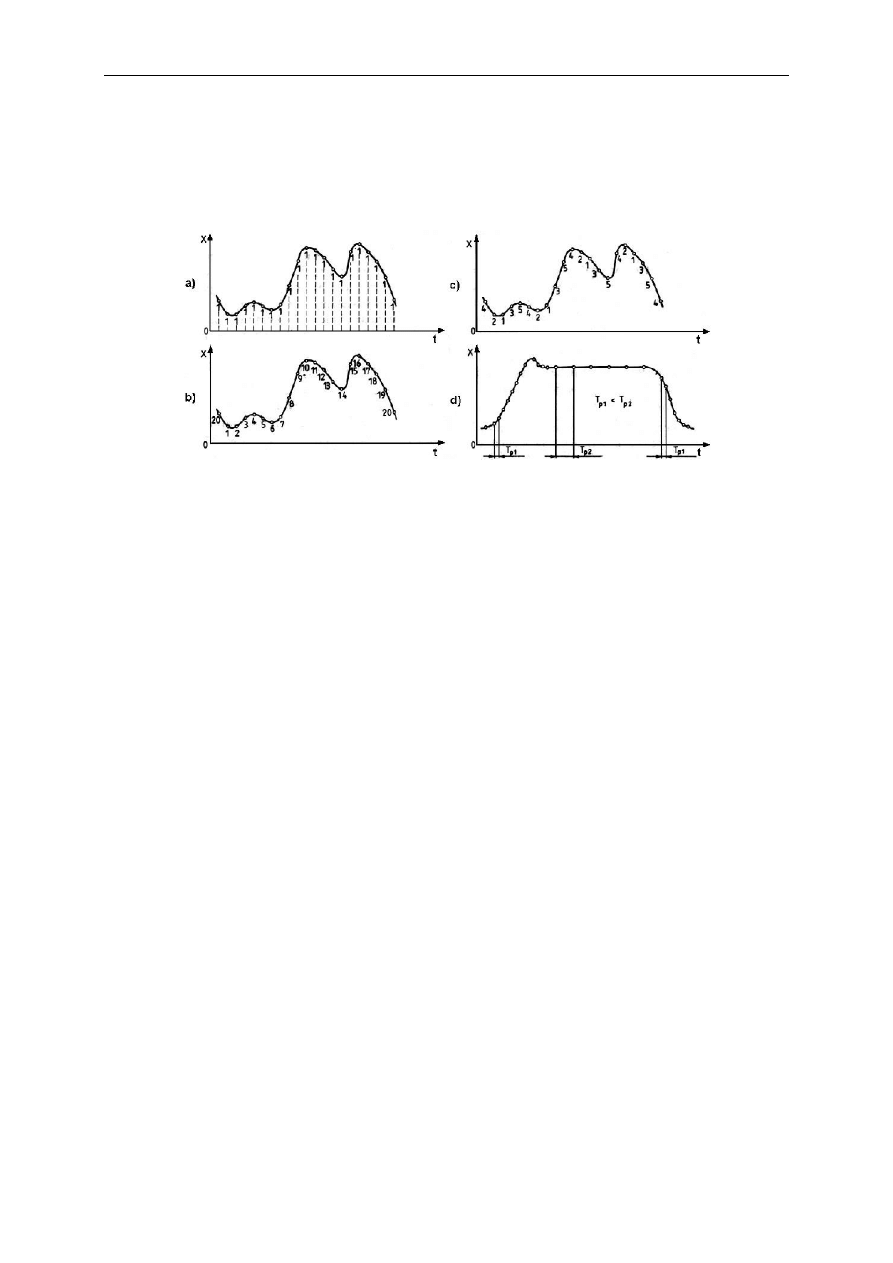
Interpretacja geometryczna niektórych z nich pokazana jest na poniższym rysunku.

Rys. Interpretacja geometryczna: a) wartości chwilowej, b) wartości średniej

c) wartości średniej wyprostowanej, d) wartości międzyszczytowej

Ponieważ energia elektryczna przesyłana jest w sieci energetycznej za pomocą sygnału
sinusoidalnego (harmonicznego), jego zniekształcenie może wpływać np. na działanie
urządzeń odbiorczych czy też mierników zużycia energii. Dlatego też zdefiniowano
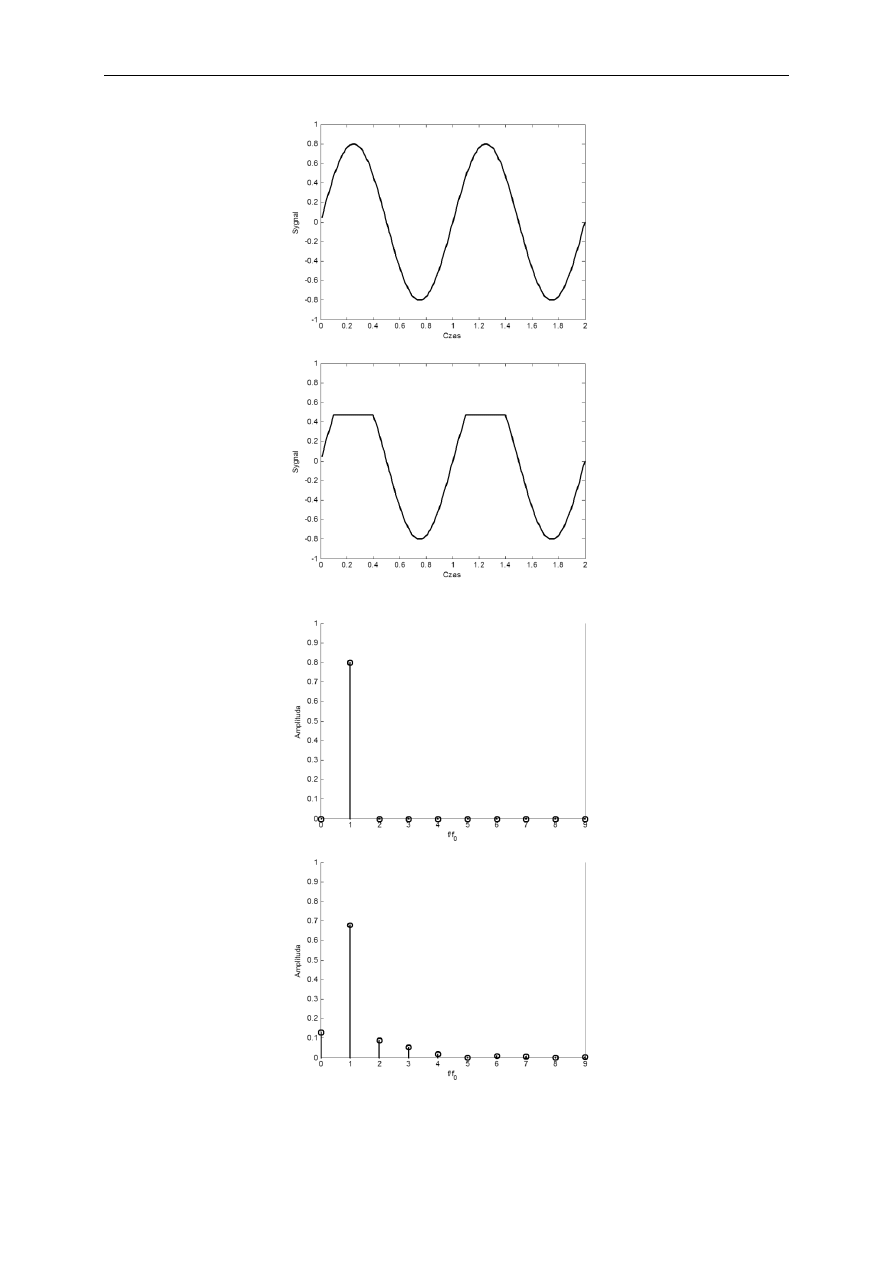
dodatkowe parametry energetyczne określające stopień zniekształcenia. Wykorzystują one
fakt, iż idealna sinusoida ma tylko jedną składową częstotliwościową, a sygnały odkształcone,
zgodnie z twierdzeniem Fouriera, więcej harmonicznych (rys.). Energia wyższych
harmonicznych (ich wartość skuteczna) jest zatem miarą odkształcenia.

16

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Rys. Sygnał sinusoidalny oraz sinusoidalny zniekształcony (górny panel) z odpowiadającymi im widmami

częstotliwościowymi (panel dolny)

15. Sygnały pomiarowe i ich parametry

17

Najistotniejszy z tych parametrów – współczynnik zawartości harmonicznych h

1

(współczynnik zniekształceń nieliniowych) – odnosi energię wyższych harmonicznych
(licznik) do energii harmonicznej podstawowej (mianownik):

1

2

4

2

3

2

2

1

2

4

2

3

2

2

1

X

X

X

X

X

X

X

X

h

sk

sk

sk

sk





















,

gdzie X

sk

to wartość skuteczna, a X to amplituda odpowiedniej harmonicznej. Współczynnik

zawartości harmonicznych h można też definiować następująco (stosunek energii wyższych
harmonicznych do całkowitej energii sygnału):





























2

3

2

2

2

1

2

4

2

3

2

2

2

4

2

3

2

2

X

X

X

X

X

X

X

X

X

X

h

sk

sk

sk

sk

.

Pomiędzy tak zdefiniowanymi współczynnikami zachodzi zależność:

2

1

1 h

h

h





.

Parametry czasowe określają przebieg sygnału w czasie. W przypadku sygnałów
okresowych podstawowym ich parametrem jest pulsacja ω [rad] (zwana też częstością),
powiązana z częstotliwością f [Hz] i okresem T [s]:

T

f

ω

π

2

π

2





.

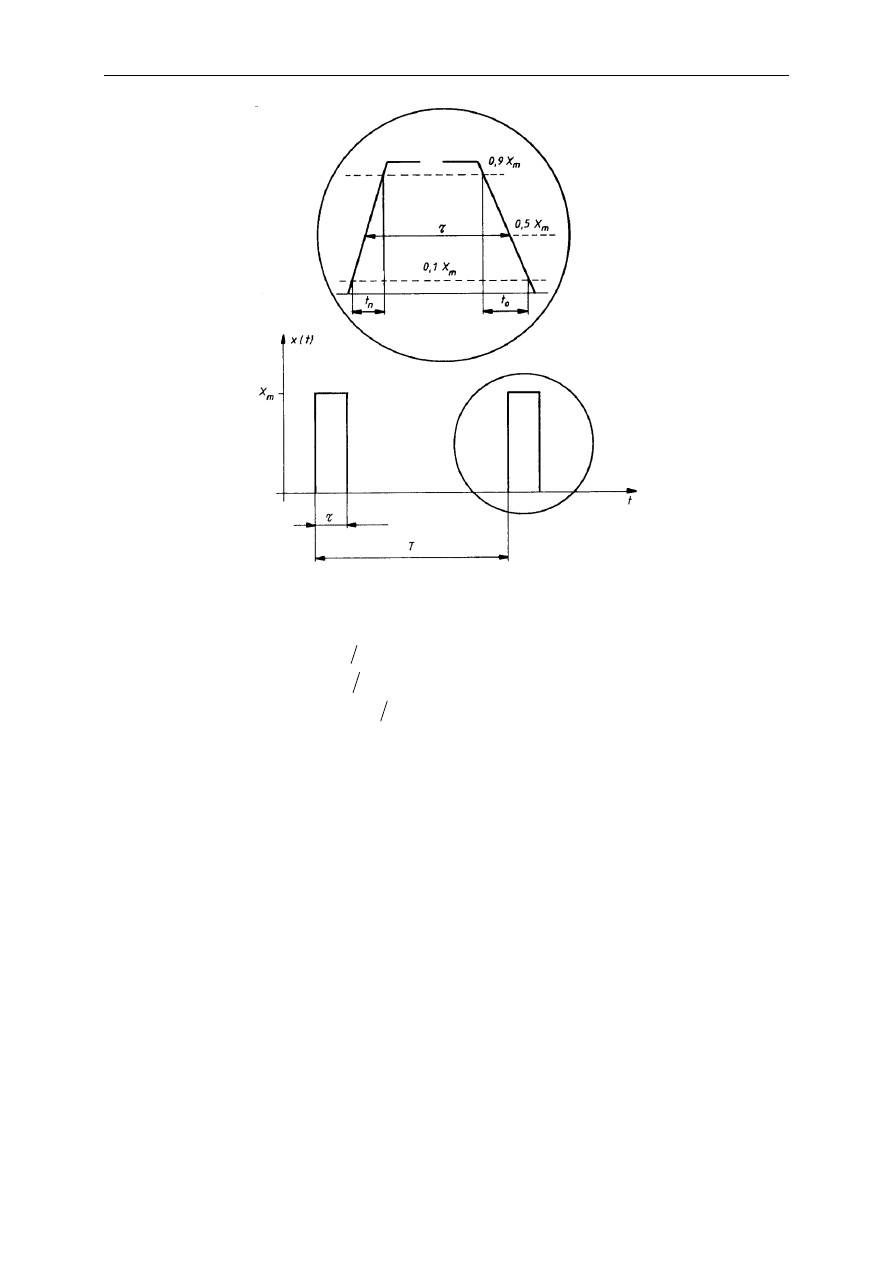
Istotna grupa parametrów czasowych opisuje właściwości impulsów, które powinny być
zbliżone kształtem do prostokątów, co fizycznie jest nieosiągalne. Należą do nich (rys.):
− czas trwania impulsu τ,
− czas narostu impulsu t

n

,

− czas opadania impulsu t

o

,

− wypełnienie sygnału impulsowego

T

τ

ε



.

18

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Parametry charakteryzujące kształt to kolejna grupa parametrów opisujących sygnały
okresowe. Należą do nich:

− współczynnik kształtu

śr

sk

X

X

k



,

− współczynnik szczytu

sk

p

p

X

X

k



,

− współczynnik uśredniania

śr

p

u

X

X

k



.

Pomiędzy tymi współczynnikami zachodzą następujące zależności:

.

,

1

k

k

k

k

k

k

p

u

p

u









Wartości parametrów charakteryzujących kształt (które dla typowych sygnałów można obliczyć teoretycznie)
wykorzystywane były m.in. do przeskalowywania analogowych mierników np. wartości średniej wyprostowanej
czy szczytowej określonego typu sygnału (najczęściej sinusoidalnego) na mierniki wartości skutecznej.

15.3. Zagadnienia kontrolne

Cechy podstawowych rodzajów sygnałów pomiarowych
Podstawowe parametry sygnałów okresowych

16. Pomiary częstotliwości, czasu i fazy

16.1. Pomiary częstotliwości

Częstotliwość f definiujemy jako liczbę powtórzeń zjawiska o okresie T zachodzących w
jednostce czasu:

T

f

1



.

Istnieje kilka podejść do pomiaru częstotliwości. Podstawowe polega na pomiarze czasu
trwania



całkowitej liczby N pełnych okresów – wtedy:



N

f



.

W przypadku badania zjawisk falowych, dla których znana jest szybkość



rozchodzenia się

fali w medium, częstotliwości określa się pośrednio przez pomiar długości fali



:







f

.

Do innych stosowanych metod należą:

− metoda porównawcza (porównanie ze wzorcem częstotliwości – np. metoda interferometryczna),
− metody rezonansowe (poszukiwane jest maksimum rezonansu obiektu z regulowanym wzorcem

częstotliwości).

Najpopularniejszymi obecnie miernikami częstotliwości są proste częstościomierze cyfrowe
(należą one do wyjątków wśród urządzeń cyfrowych, gdyż nie wykorzystują
mikroprocesorów). Typowe częstościomierze cyfrowe umożliwiają pomiar częstotliwości w
zakresie od 0.001 Hz do kilkudziesięciu GHz.

Zastosowana w nich pośrednia metoda pomiaru polega na zliczaniu liczby okresów o
mierzonej częstotliwości f

x

we wzorcowym przedziale czasu



( zwanym czasem

bramkowania).

Mierniki służące do cyfrowego pomiaru częstotliwości i parametrów pokrewnych zbudowane
są następujących podstawowych bloków:
− układ wejściowy (przekształca każdy okres sygnału wejściowego na jeden impuls),
− generator kwarcowy (generator częstotliwości wzorcowej f

k

, zwykle 5 lub 10 MHz, o

dokładności rzędu 10

-8

),

− dzielnik częstotliwości (częstotliwość na wyjściu tego bloku jest m-tą dziesiętna

podwielokrotnością częstotliwości wejściowej),

− układ sterowania bramką (odmierza wzorcowy odcinek czasu T

w

=



),

− bramka (przekazuje impulsy z wejścia na wyjście tylko przez czas



),

− licznik (zlicza N dochodzących do niego impulsów),
− urządzenie odczytowe (najczęściej cyfrowy wyświetlacz LED lub LCD).

20

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

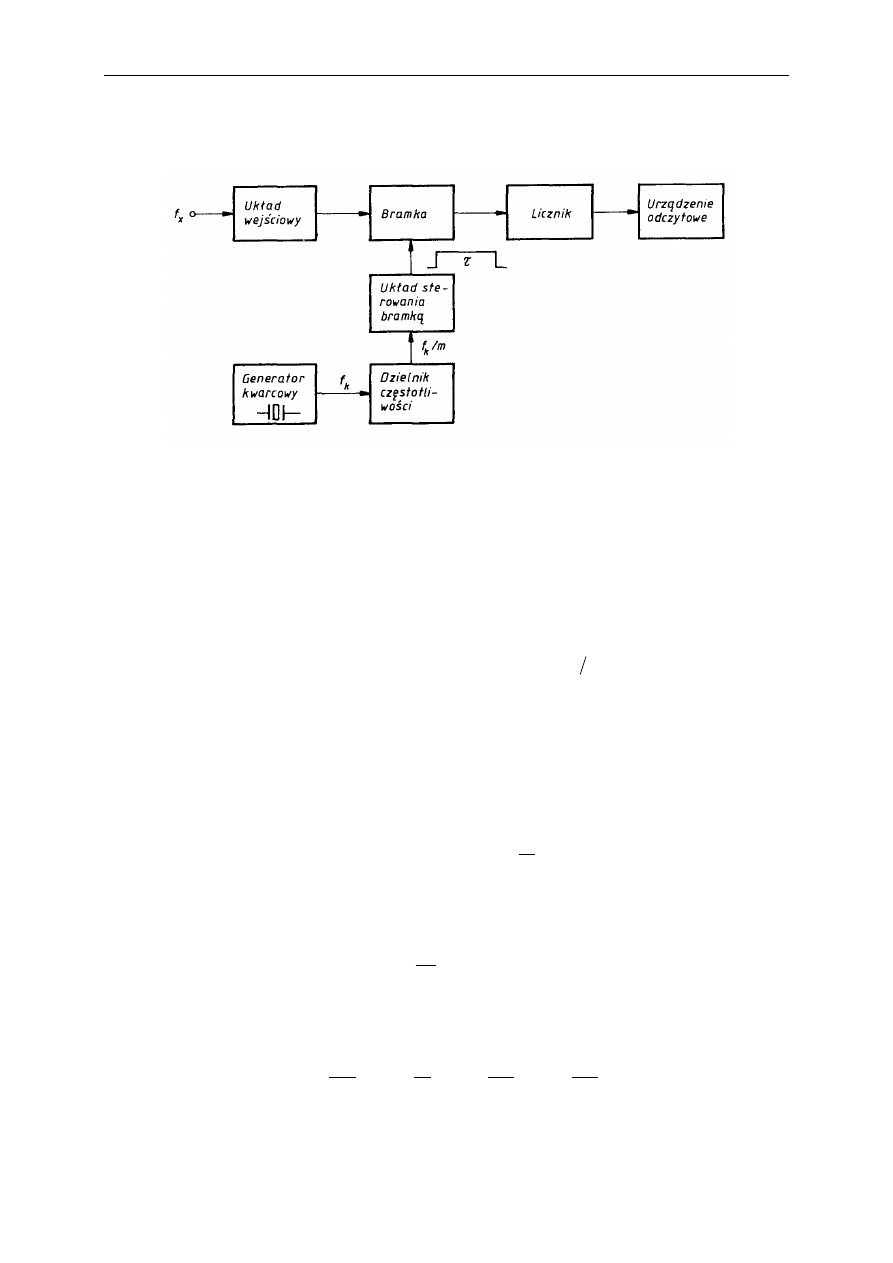
Schemat blokowy przyrządu mierzącego częstotliwość przez zliczanie okresów przedstawia
poniższy rysunek.

Rys. Schemat blokowy częstościomierza cyfrowego stosującego zliczanie okresów.

Układ wejściowy formuje impulsy, które po przejściu przez bramkę w czasie



zliczane są

przez układ licznika cyfrowego. Prezentowana przez urządzenie odczytowe liczba całkowita
jest zawsze liczbą N zliczonych impulsów. Ostateczny wynik pomiaru formowany jest przez
wyświetlenie przecinak na odpowiedniej pozycji, co jest możliwe dzięki temu, ze



jest

dziesiętna wielokrotnością lub podwielokrotnością 1 sekundy (np. 50 zliczonych impulsów w
ciągu sekundy daje wskazanie 50 Hz, a tka sama ilość zliczona w czasie 10 s daje wynik 5,0
Hz).

Dla wyniku uzyskiwanego z dzielenia innych wartości (

τ

N

f

x



) błąd względny pomiaru

pośredniego jest sumą błędów względnych pomiarów bezpośrednich:

δτ

N

δ

f

δ

x





.

Dokładność pomiaru częstotliwości tą metodą zależy zatem od dokładności zliczania
impulsów przez licznik, która typowo wynosi:

N

N

δ

N

1

1

Δ









oraz od dokładności wyznaczania czasu bramkowania



, która jest bardzo wysoka, gdyż

k

k

k

f

f

m

mT















i zazwyczaj pomijalna. Ostatecznie wzór na błąd względny można przekształcić do postaci:

τ

f

f

δ

τ

f

f

δ

N

f

δ

N

N

f

δ

x

k

x

k

k

x

1

1

1

Δ















.

16. Pomiary częstotliwości, czasu i fazy

21

Wynika stąd, że błąd pomiaru tą metodą jest odwrotnie proporcjonalny do mierzonej
częstotliwości. Dlatego też do pomiaru bardzo małych częstotliwości używa się tych samych
mierników cyfrowych, lecz w innej konfiguracji bloków składowych.
Metoda pośrednia polegająca na pomiarze okresu pozwala na badanie sygnałów o małych
częstotliwościach.

Tym razem bramka otwierana jest na jeden okres badanego sygnału, a licznik zlicza impulsy
o dużej częstotliwości wytwarzane przez generator kwarcowy (po przejściu przez dzielnik
częstotliwości). Wtedy (

w

f

τ 1



):

x

k

x

w

x

mf

f

f

f

τ

T

N







,

a stąd:

k

x

k

x

x

f

δ

N

δ

T

δ

f

m

N

f

T











1

.

Ponieważ

x

x

T

f

1



, to

k

x

x

f

δ

N

δ

T

δ

f

δ







.

Ostatecznie:

k

x

k

k

x

k

x

f

mf

f

δ

f

mf

f

δ

N

f

δ











1

.

Z powyższej zależności wynika, że przy pomiarze tą metodą błąd względny jest wprost
proporcjonalny do mierzonej częstotliwości, zatem jest ona przydatna do pomiaru małych
częstotliwości.

Używając częstościomierza umożliwiającego pomiar obiema metodami, stajemy przed
problemem doboru odpowiedniej metody pomiaru częstotliwości. Kryterium w tym

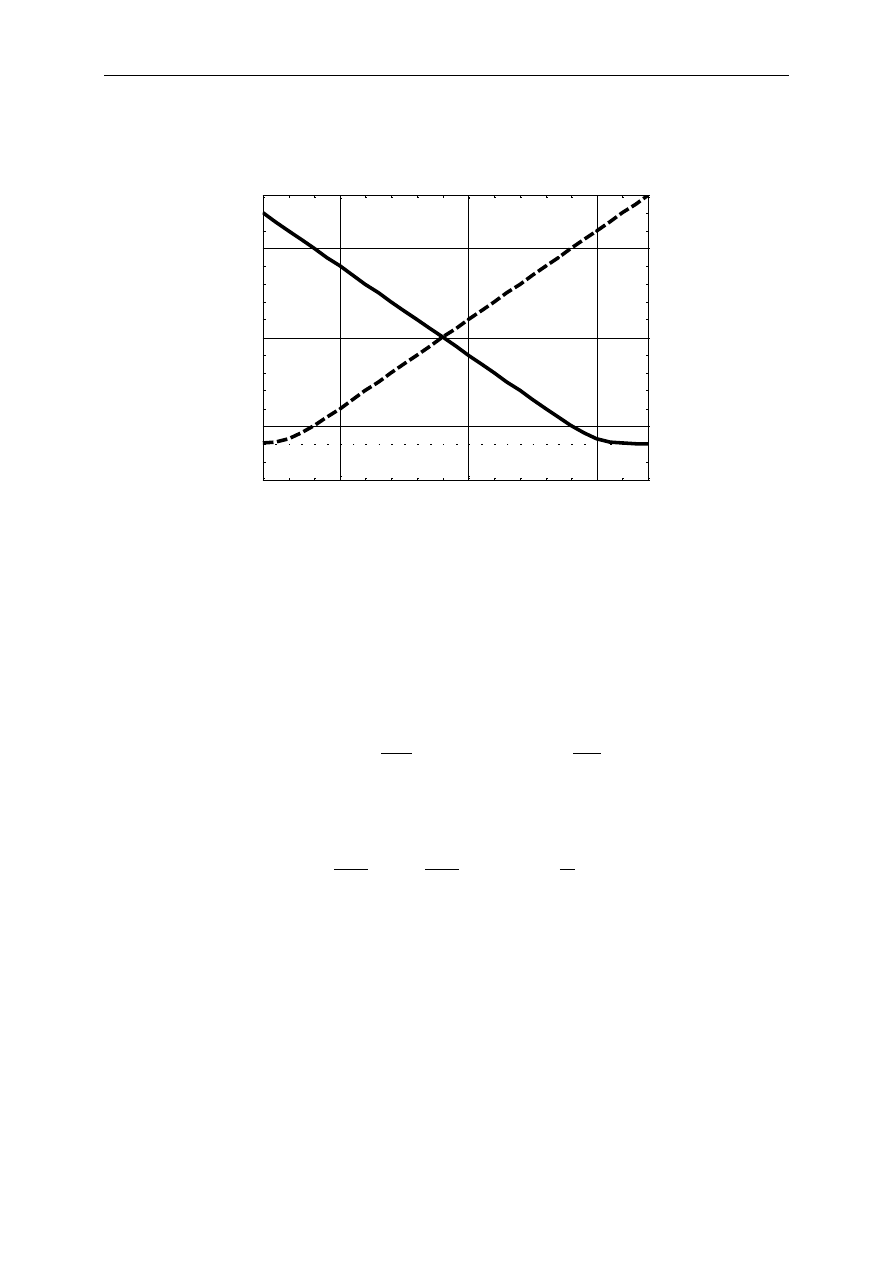
22

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

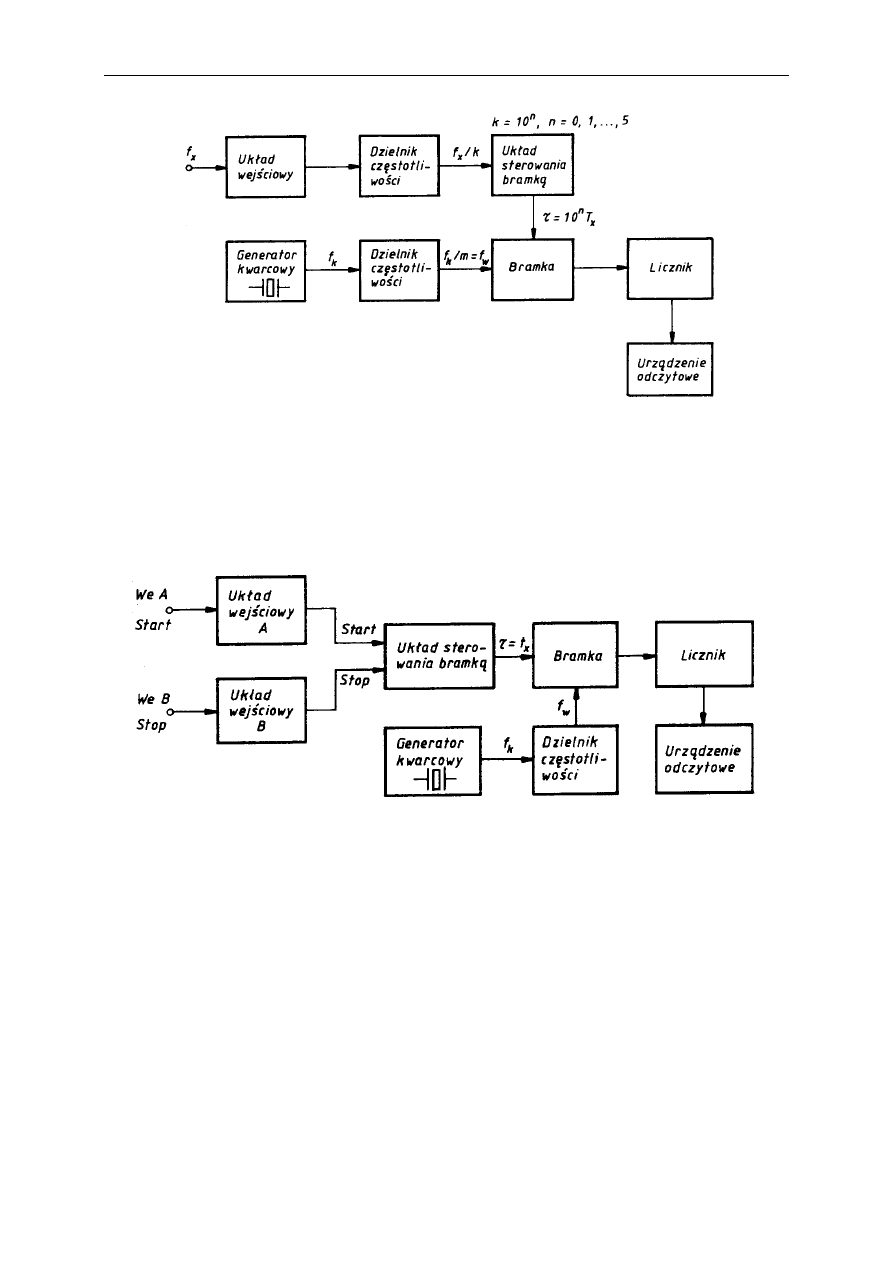
przypadku powinien być błąd pomiaru, który należy minimalizować. Warto zatem przyjrzeć
się ilustracji zależności błędów pomiaru częstotliwości obiema metodami (rys.).

Jak widać, błąd

)

(

z

x

f

δ

metody polegającej na zliczaniu impulsów maleje z mierzona

częstotliwością, a błąd

)

(

p

x

f

δ

metody polegającej na pomiarze okresu rośnie. Istnieje zatem

częstotliwość graniczna, dla której są one równe:

)

(

)

(

:

p

gr

z

gr

gr

f

f

f







.

Wykorzystując wyprowadzone poprzednio wzory na błędy względne obu metod:

m

f

f

f

δ

f

δ

x

k

k

z

x





)

(

oraz

k

x

k

p

x

f

mf

f

δ

f

δ





)

(

,

można tę częstotliwość wyznaczyć:

k

gr

k

gr

k

gr

k

k

f

m

f

f

mf

f

δ

mf

f

f

δ

1











.

Jeżeli mierzona częstotliwość jest większa od granicznej (co określa się np. w pomiarze
próbnym), to należy stosować metodę przez zliczanie okresów, a jeżeli niższa, to metodę
pomiaru okresu.

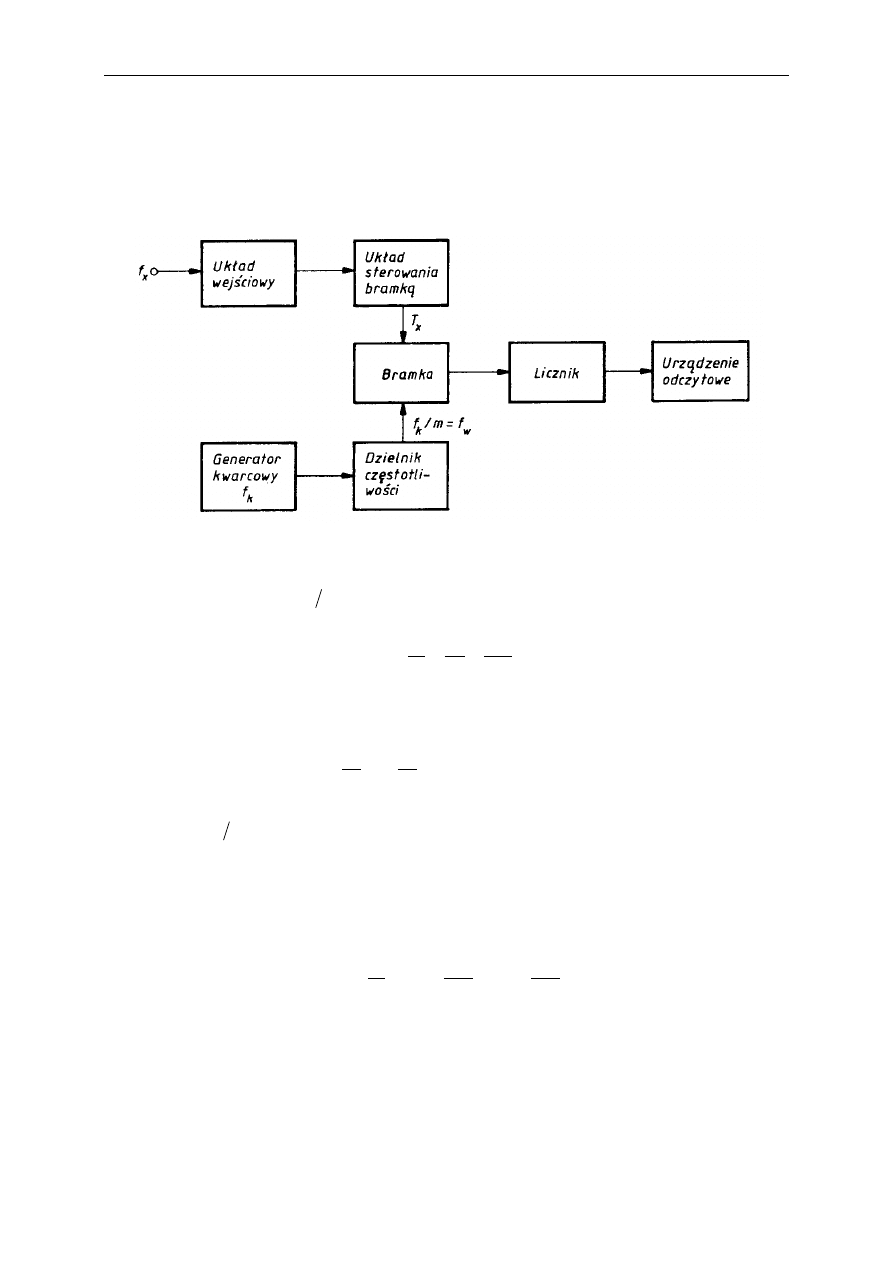
Częstościomierze cyfrowe umożliwiają też pomiar okresu średniego, co uzyskuje się przez
włączenie dodatkowego bloku dzielnika częstotliwości w tor sygnału mierzonego (rys.).

10

0

10

5

10

10

10

-5

10

0

10

5

f [Hz]

B

la

d

w

z

g

le

d

n

y

16. Pomiary częstotliwości, czasu i fazy

23

16.2. Pomiar odcinka czasu

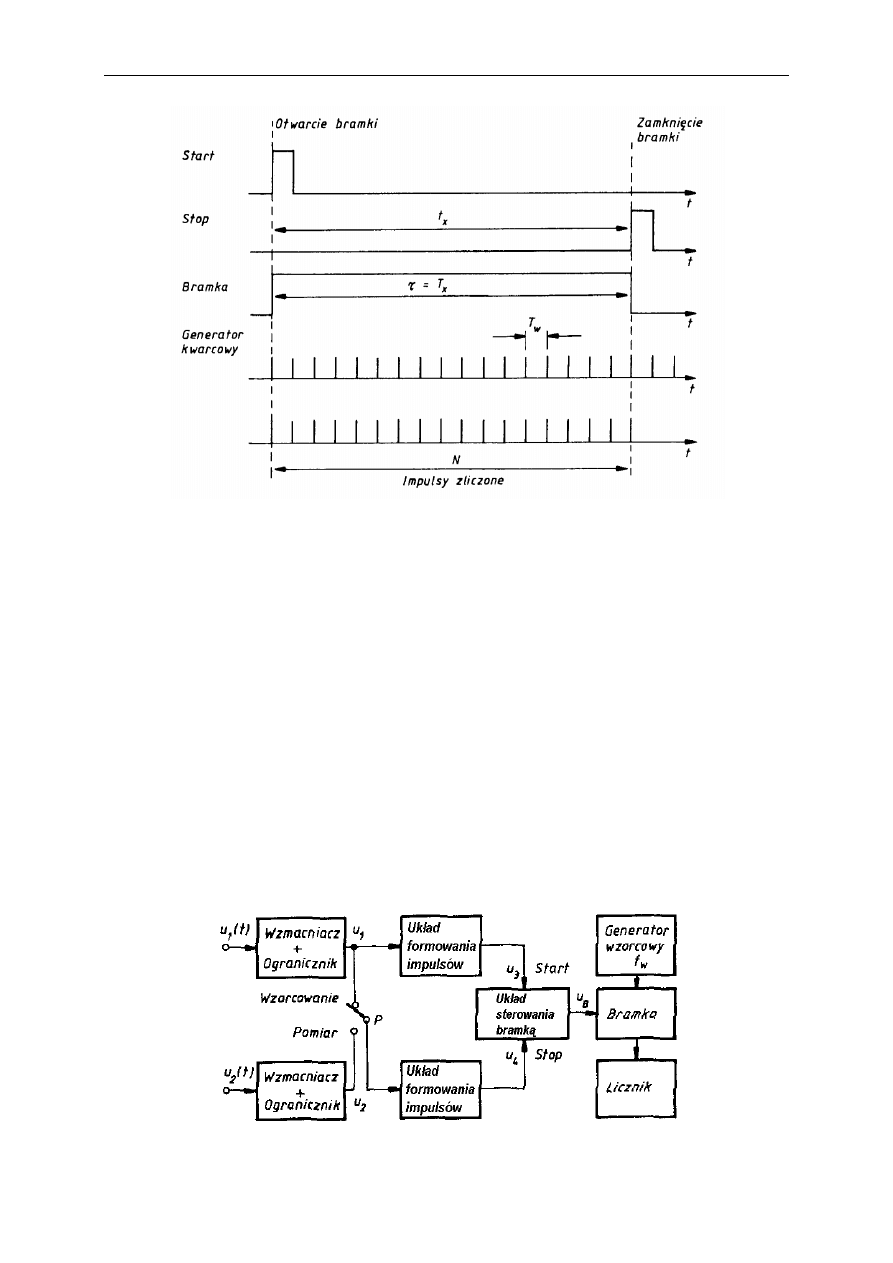
Pomiar odcinka czasu wymaga podana informacji o początku i końcu pomiaru, stąd potrzebne
są dwa układy wejściowe (Start i Stop).

Impulsy formowane w tych układach (ich zbocze narastające lub opadające) otwierają i
zamykają bramkę, a tym samym wyznaczają czas zliczania impulsów zegarowych (rys.).
Liczba zliczonych impulsów jest wprost proporcjonalna do mierzonego odcinka czasu, a
częstotliwość f

w

będąca naturalną potęgą 10 powoduje, że wyświetlana liczba (z przecinkiem

zapalonym na odpowiedniej pozycji) wyrażona jest w jednostkach czasu.

24

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

16.3. Pomiar kąta przesunięcia fazowego

Przesunięcie

fazy

dwóch

sygnałów

sinusoidalnych:

 





1

1

1

1

sin









t

U

t

u

i

 





2

2

2

2

sin









t

U

t

u

definiowane jest jako różnica kątów, będących ich argumentami:



 



2

1

2

1





















t

.

Różnicę tę – kąt przesunięcia fazowego – mierzy się zazwyczaj dla sygnałów o tej samej
częstotliwości (ω

1

= ω

2

), wtedy:

2

1













.

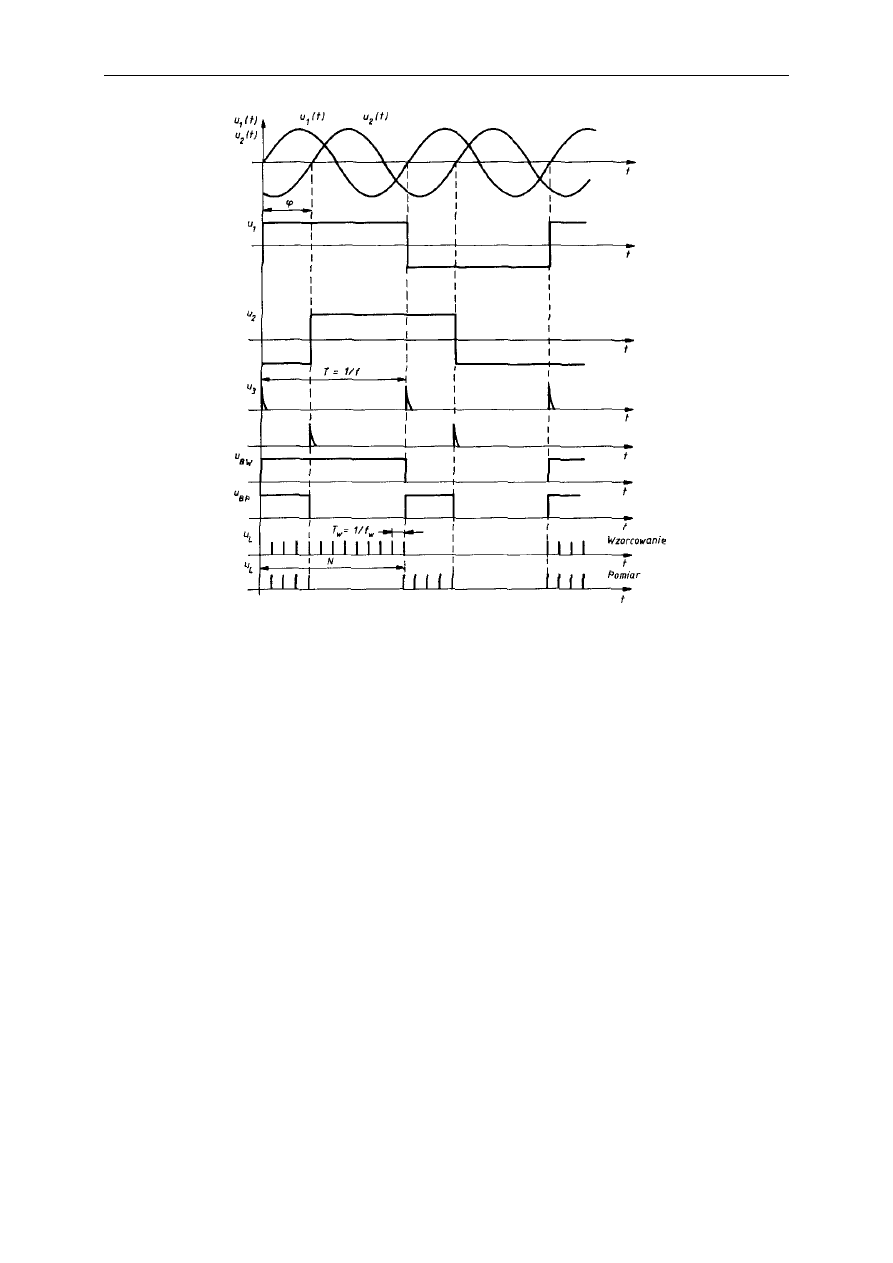
Zasada pomiaru jest podobna do pomiaru odcinka czasu z tym, że przebiega w dwóch fazach:
wzorcowania i pomiaru, a klucz przełączający modyfikuje tory układów wejściowych, na
które składają się bloki wzmacniacza i ogranicznika oraz układu formowania impulsów.

16. Pomiary częstotliwości, czasu i fazy

25

16.4. Zagadnienia kontrolne

Zasady działania i układy cyfrowych częstościomierzy małych i dużych częstotliwości
Zasada działania i układ pomiaru odcinka czasu

17. Przyrządy do rejestracji i obserwacji

sygnałów zmiennych

17.1. Rejestratory

Rejestratory elektromechaniczne X-t to analogowe przyrządy do wizualizacji sygnałów
zmiennych w czasie. Przetwarzają one mierzoną wielkość w przemieszczenie liniowe lub
kątowe i dokonują zapisu tego przemieszczenia w funkcji czasu. Ich parametry, a zwłaszcza
częstotliwość graniczna nie przekraczająca 100 Hz, nie są zbyt wygórowane. Nośnikiem
zapisu jest taśma, krążek lub arkusz papieru.

Rejestratory analogowe dzieli się na rejestratory o przetwarzaniu bezpośrednim i pośrednim
(elektroniczne).

Rejestratory o przetwarzaniu bezpośrednim pobierają stosunkowo dużą moc z obiektu.
Typowo, stosowane do rejestracji sygnałów i > 0,5 A i u > 0,5 V. Ich główne bloki składowe
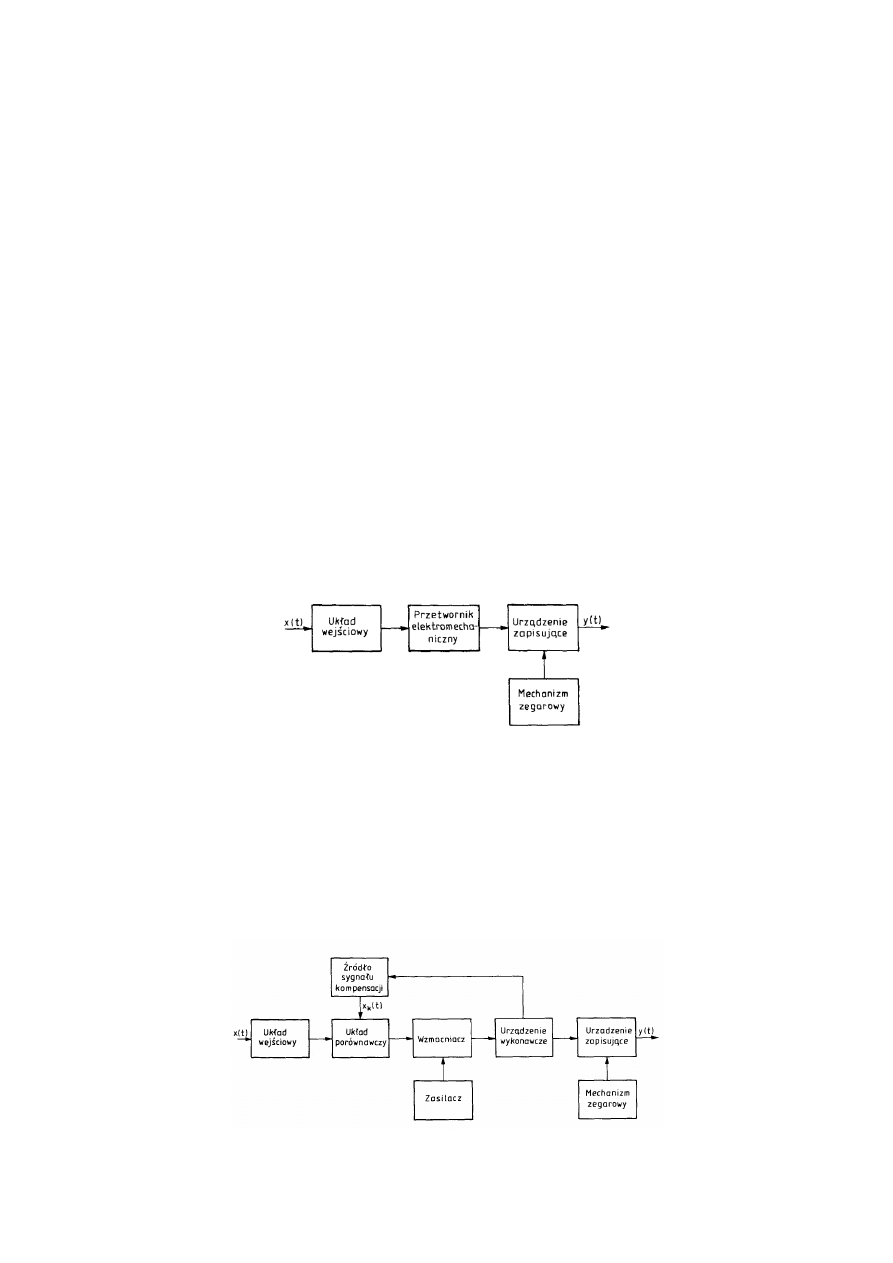
to: układ wejściowy kondycjonujący sygnał, przetwornik elektromechaniczny zamieniający
sygnał elektryczny na proporcjonalne do niego przemieszczenie oraz urządzenie zapisujące
sterowane mechanizmem zegarowym skalującym oś czasu (rys.).

Rys. Schemat blokowy rejestratora o przetwarzaniu bezpośrednim.

Rejestratory o przetwarzaniu pośrednim są urządzeniami elektronicznymi, wyposażonymi w
dodatkowe bloki. Ich cechą jest to, że pobierają energię ze źródła pomocniczego, dzięki
czemu nie obciążają obiektu badanego. Budowane są w różnych strukturach, m.in. w układzie
przetworników kompensacyjnych napięcia. Sygnał wyjściowy z układu porównawczego
(różnicowego) jest wzmacniany i wykorzystywany do sterowania regulowanym źródłem
sygnału kompensacji x

k

. Sygnał ten podąża za sygnałem rejestrowanym x. Jednocześnie

sygnał powstający w urządzeniu wykonawczym steruje urządzeniem zapisującym (rys.)

Rys. Schemat blokowy rejestratora o przetwarzaniu pośrednim (układ kompensacyjnego przetwornika napięcia)

17. Przyrządy do rejestracji i obserwacji sygnałów zmiennych

27

Rejestratory elektromechaniczne X-Y posiadają dwa wejścia. Wejście Y zastępuje
mechanizm zegarowy, dzięki czemu jeden sygnał fizyczny może być rejestrowany względem
drugiego. Urządzenia takie sterowane cyfrowo (z komputera) noszą nazwę ploterów.

Rejestratory z taśmą magnetyczną przyniosły nowe, lepsze właściwości, co związane jest z
zastosowanym nośnikiem informacji i możliwością regulacji szybkości jego przesuwu. Przede
wszystkim częstotliwość graniczna zwiększyła się do 10 MHz. Szybsze odtwarzanie
zarejestrowanych informacji niż ich rejestracja pozwalało na wizualizację sygnałów
wolnozmiennych (np. miesięczne wahania temperatury), a odtwarzanie wolniejsze niż
rejestracja dawało opcję „lupy” rozciągającej interesujące fragmenty. Wadą tych
rejestratorów jest częsty brak wizualizacji sygnału w czasie jego rejestracji.

Rejestratory cyfrowe stosowane współcześnie posiadają wewnętrzną strukturę woltomierza
jedno- lub wielokanałowego (z wieloma przetwornikami A/C lub z jednym przełączanym – tj.
multipleksowanym) i znajdują zastosowanie w bardzo wielu obszarach działalności
człowieka.

17.2. Oscyloskopy

Oscyloskopy są urządzeniami elektronicznymi umożliwiającymi zarówno obserwację
przebiegów sygnałów okresowych jak i (niezbyt precyzyjne) pomiary ich parametrów
czasowych i niektórych energetycznych, takich jak:
− amplituda,
− okres (i tym samym częstotliwość),
− parametry czasowe impulsów,
− kąt przesunięcia fazowego,
− charakterystyki elementów nieliniowych.

Podstawowe właściwości typowych oscyloskopów to:

− duża impedancja wejściowa (R

we

~10 M



, C

we

10÷50 pF),

− duża czułość napięciowa (1÷10

4

mV/dz),

− duży zakres częstotliwościowy.


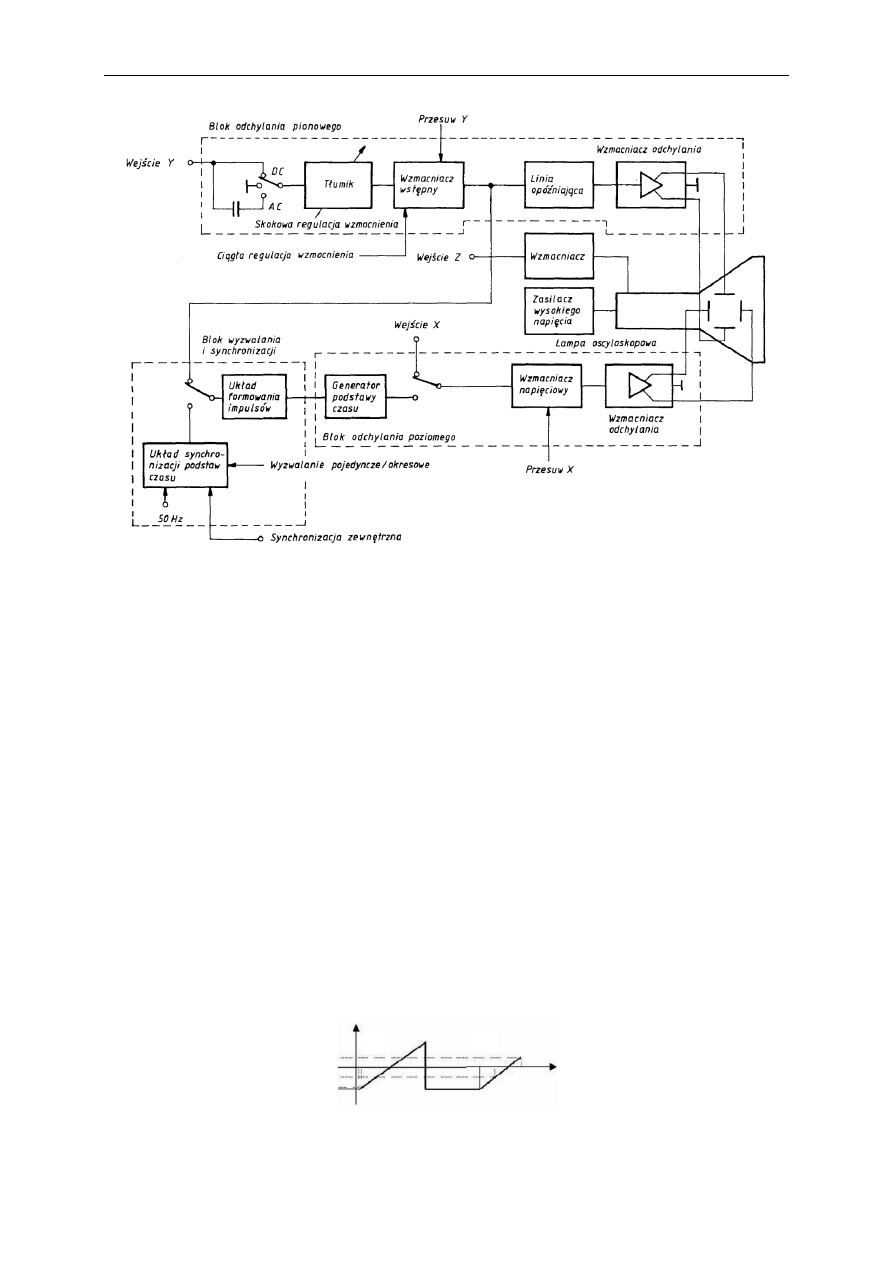
Oscyloskop analogowy zbudowany jest z (rys.):

− lampy oscyloskopowej z układami zasilania,
− bloku odchylania pionowego,
− bloku odchylania poziomego,
− bloku wyzwalania i synchronizacji.

28

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Rys. Schemat blokowy oscyloskopu analogowego.

Obraz powstaje na pokrytym luminoforem ekranie lampy oscyloskopowej w miejscu
uderzenia strumienia elektronów emitowanych przez działko elektronowe. Kierunek
strumienia ustalany jest przez pole elektrostatyczne wytwarzane przez płytki odchylania
pionowego i poziomego.

Obrazowany sygnał wejściowy podawany jest do bloku odchylania pionowego (Wejście Y),
powodując proporcjonalne wychylanie się plamki świetlnej w górę i w dół. W jego skład
wchodzą:



układ wyboru trybu pracy (AC, DC lub GND),



tłumik i wzmacniacz wstępny (regulacja wzmocnienia obserwowanego sygnału),



końcowy wzmacniacz odchylania.

Zadaniem bloku odchylania poziomego jest przesuwanie plamki w poziomie. W
podstawowym trybie pracy odchylaniem poziomym steruje sygnał wytwarzany w generatorze
podstawy czasu. Jest to sygnał piłokształtny (rys.). Jego liniowy narost powoduje
równomierne przesuwanie się plamki z lewej na prawa stronę ekranu, a raptowny spadek
wartości daje w efekcie szybki powrót strumienia z prawej strony na lewą (na tyle szybki, że
nie pozostawia on widocznego śladu na luminoforze). Zamiast sygnału z generatora, plamka
może być odchylana w poziomie sygnałem zewnętrznym podanym na Wejście X.

Rys. Sygnał piłokształtny wytwarzany przez generator podstawy czasu.

17. Przyrządy do rejestracji i obserwacji sygnałów zmiennych

29

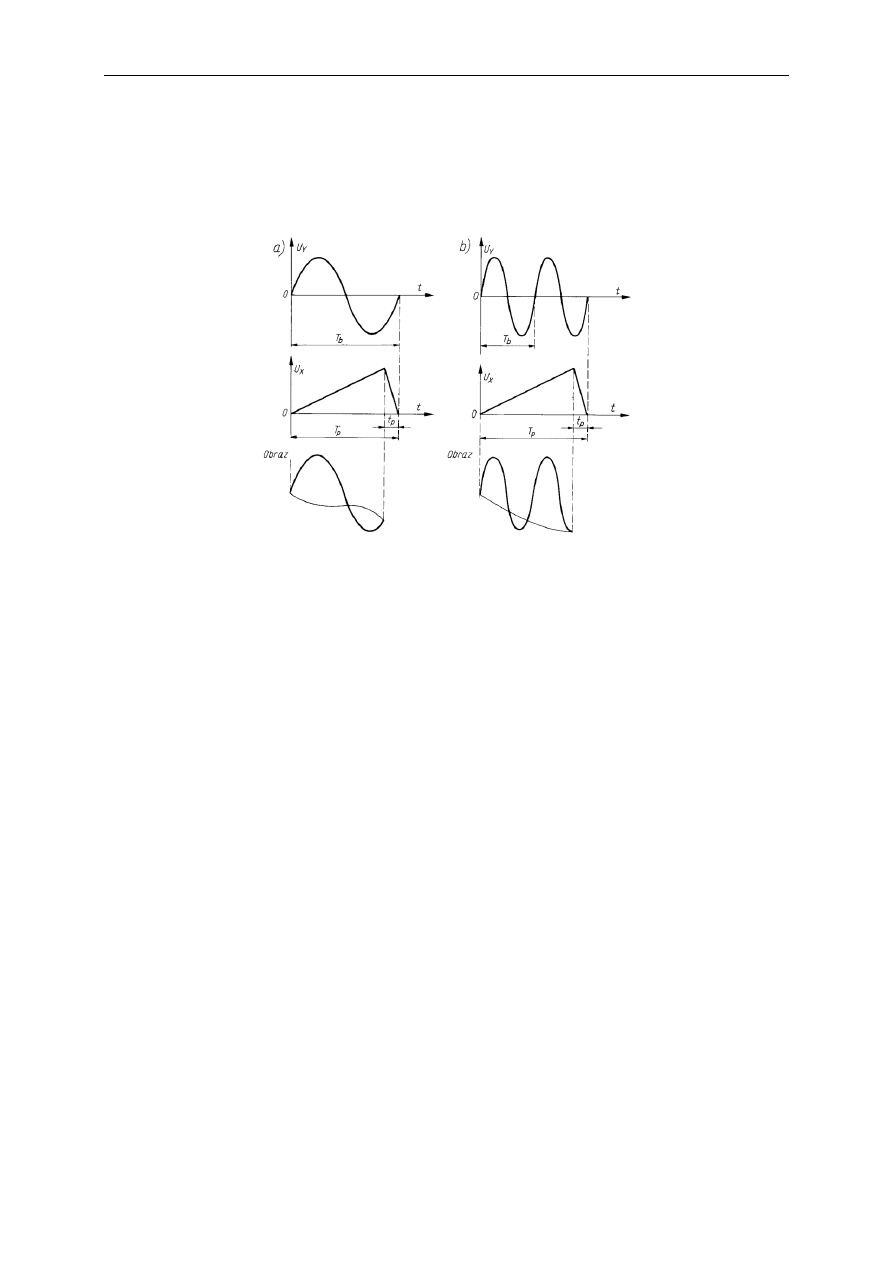
Przykład powstawania obrazu na ekranie lampy oscyloskopowej pokazuje poniższy rysunek.
Panel górny to dwa obserwowane sygnały okresowe o różnych częstotliwościach. Na panelu
środkowym pokazano sygnały podstawy czasu, a na dolnym trajektorie plamek świetlnych i
powstające obrazy obserwowanych sygnałów.

Rys. Przykład ilustrujący powstawanie obrazu na ekranie lampy oscyloskopowej.

Aby obraz był stabilny, narost sygnału podstawy czasu musi rozpoczynać się zawsze w tej
samej fazie sygnału obserwowanego. Odpowiada za to blok wyzwalania i synchronizacji.
Wstępnie przetworzony sygnał obrazowany, po przekroczeniu ustalonego poziomu wartości,
wyzwala układ formowania impulsów, a wytworzony impuls wyjściowy wyzwala narost
sygnału odchylania poziomego. W efekcie czas oczekiwania na początek narostu tego sygnału
zależy od sygnału obrazowanego. W ten sposób odchylanie poziome jest zsynchronizowane z
sygnałem obserwowanym.

Oscyloskop może pracować w kilku trybach, w zależności od ustawienia przełączników na
płycie czołowej. Po pierwsze należy wybrać zawartość sygnału obserwowanego:



AC: tylko składowa zmienna (np. wtedy, gdy jest nałożona na dużo większą składową
stałą),



DC: sygnał pełny (tj. składowa stała wraz ze zmienną),



GND: na odchylanie poziome podawany jest potencjał zerowy (tzw. masa oscyloskopu).

Większość oscyloskopów analogowych to przyrządy jednostrumieniowe (jeden strumień
elektronów) i dwukanałowe (możliwość jednoczesnego podłączenia i obserwacji dwóch
sygnałów zewnętrznych). Możliwe są następujące tryby pracy:



suma: na ekranie widoczny jest sygnał będący sumą sygnałów podanych na oba kanały
(podstawa czasu piłokształtna),



przemienny: na przemian rysowane są pojedyncze przebiegi sygnałów z kanału A i B
(podstawa czasu piłokształtna) – dzięki bezwładności żarzenia się luminoforu obserwator
widzi oba sygnały,



kluczowany (czopowany): w jednym przebiegu (piłokształtnego) sygnału podstawy czasu
fragmentami rysowane są oba sygnały, a w przebiegu następnym uzupełniane są brakujące
fragmenty przebiegów poprzednich,

30

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)



X-Y: na płytki odchylania poziomego lampy oscyloskopowej podawany jest sygnał z

Wejścia X, a na odchylanie pionowe – jak zwykle z Wejścia Y (jeżeli są to sygnały
sinusoidalne o różnych częstotliwościach pozostających w stosunku liczb naturalnych, to
na ekranie powstają krzywe Lissajous – rys.).

Rys. Przykłady krzywych Lissajous.

Pomiar amplitudy, okresu (częstotliwości) czy fazy sygnałów okresowych polega na
ustawieniu pokręteł wzmocnienia sygnału wejściowego i rozciągu podstawy czasu w pozycji
wyskalowanej oraz na odczycie (w milimetrach) wartości wybranych parametrów z
powstającego obrazu i kresek podziałki umieszczonej na ekranie lampy oscyloskopowej.
Wartości te przeliczane są następnie z uwzględnieniem nastawionej czułości i rozciągu czasu.

Zakres częstotliwościowy typowego oscyloskopu analogowego obejmuje pasmo 0÷400 MHz.
W celu obserwacji sygnałów szybciej zmiennych zbudowano oscyloskopy o przetwarzaniu
bezpośrednim (pozbawione bloków przetwarzania sygnału obrazowanych, które ograniczały
pasmo częstotliwościowe) pozwalające na obserwację sygnałów o widmie sięgającym 3 GHz.

Oscyloskop próbkujący jest modyfikacją oscyloskopu analogowego, wyposażoną w układ
próbkująco-pamiętający i rozbudowany blok synchronizacji. Sygnał obrazowany próbkowany
jest raz w okresie i wartość ta steruje położeniem plamki w pionie do czasu, gdy nowa
wartość z innego okresu (zwykle oddalonego w czasie od poprzedniego) zostanie pobrana i
„zapali” plamkę obok. Ponieważ dzieje się to setki lub tysiące razy w ciągu sekundy,
uzyskiwany jest stabilny obraz oberwanego sygnału. Sygnał taki może mieć częstotliwość do
20 GHz.

Oscyloskop cyfrowy to najpopularniejszy obecnie przyrząd do obserwacji i pomiaru
parametrów sygnałów okresowych. Pierwsze oscyloskopy cyfrowe posiadały lampy
oscyloskopowe (wraz z przetwornikiem C/A i odpowiednimi blokami analogowymi).
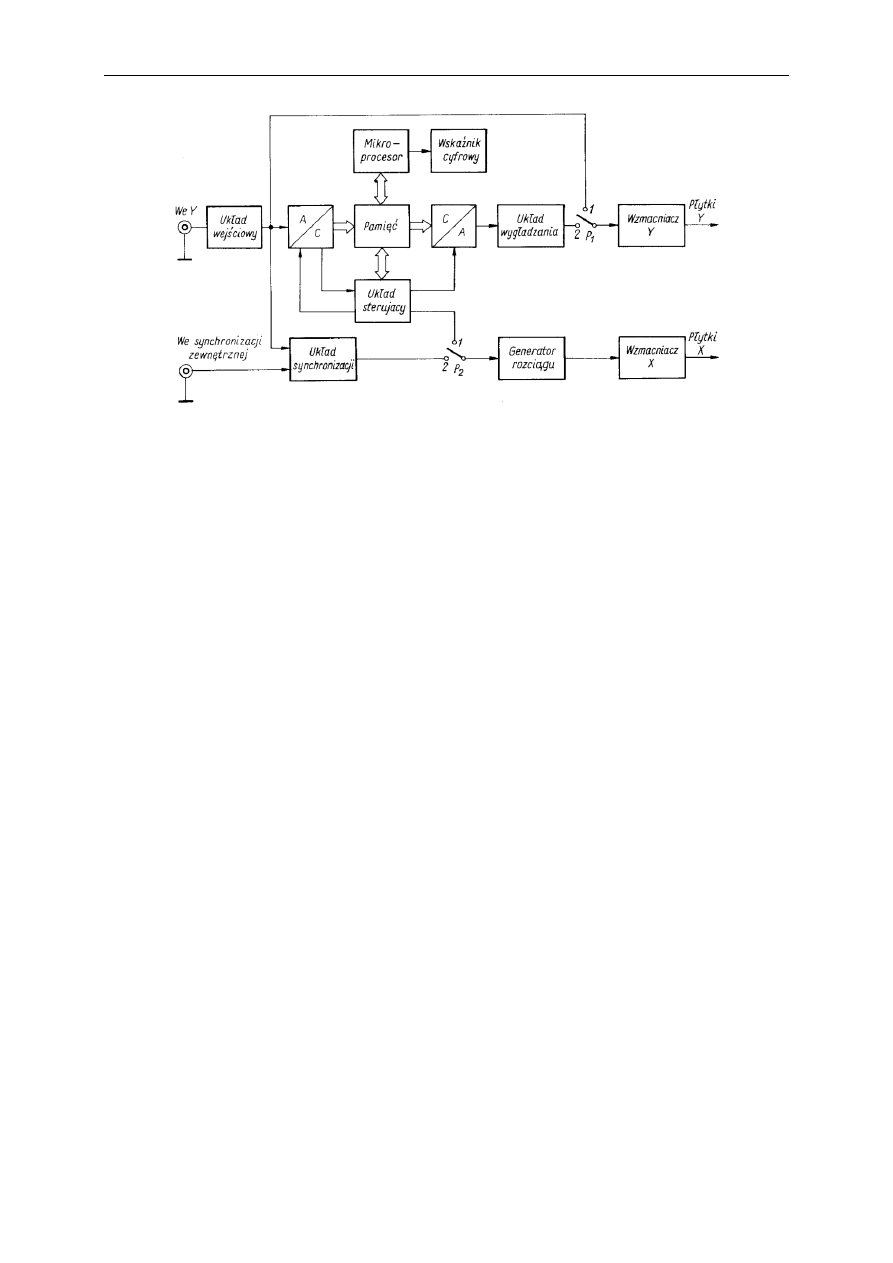
Oscyloskopy nowszej generacji posiadają mikroprocesor oraz graficzny wyświetlacz LCD
(rys.)

17. Przyrządy do rejestracji i obserwacji sygnałów zmiennych

31

Główne bloki współczesnego oscyloskopu cyfrowego to:



analogowy układ wejściowy (wstępne dopasowanie poziomu obserwowanego sygnału),



przetwornik A/C,



pamięć próbek,



układ sterowania (mikroprocesor),



wyświetlacz LCD.

Parametry przetwornika A/C muszą odpowiadać wymaganiom stawianym przed
oscyloskopami cyfrowymi, określonymi przede wszystkim przez maksymalną częstotliwość
rejestrowanych sygnałów i rozdzielczość stosowanych wyświetlaczy LCD. Użyteczny zakres
częstotliwościowy sięga 100 GHz, zatem rozdzielczość przetworników nie może być duża
(wynika to z zależności między czasem przetwarzania, liczbą bitów wyjściowych i
złożonością konstrukcyjną). Dlatego też typowo stosuje się przetworniki 8-bitowe (256 linii
na wyświetlaczu LCD), rzadziej 10- (1024 poziomy) lub 12-bitowe (4096 poziomów).

Zastosowanie mikroprocesora i pamięci próbek pozwala na poszerzenie trybów pracy
oscyloskopów cyfrowych o funkcje niedostępne wcześniej. Oto przykładowe tryby pracy:



rejestracja sygnału;



praca z odświeżaniem przebiegu z pamięci:
• z obrazem przesuwanym (kolejne próbki wyświetlane są po prawej stronie ekranu, a

pozostałe przesuwane o jedna pozycje w lewo),

• z obwiednią (obrysowywane są maksymalne i minimalne wartości w okresie),
• różnicowa (obraz jest odświeżany tylko wtedy, gdy nowo zarejestrowany fragment

różni się od aktualnie wyświetlanego bardziej niż ustalona wartość);



praca z uśrednianiem (uśrednianych jest wiele wcześniej zapamiętanych okresów, co
redukuje zakłócenia losowe: następuje zwiększenie stosunku sygnału do szumu);



praca z różnymi sposobami próbkowania (rys.):
• próbkowanie równomierne (ze stałą częstotliwością),
• próbkowanie sekwencyjne (w czasie każdego okresu pobierana jest tylko jedna próbka,

a kolejne próbki są przesunięte w czasie w odniesieniu do początku okresu o stałą
wartość odwzorowując ostatecznie cały okres: stosowane w przypadku przebiegów o
częstotliwości większej niż szybkość działania przetwornika A/C),

32

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

• próbkowanie pseudoprzypadkowe (próbki są pobierane w przypadkowych punktach

obserwowanego sygnału: umożliwia to pozorne zwiększenie zakresu częstotliwości
oscyloskopu),

• próbkowanie ze zmienną częstotliwością (zależną od dynamiki badanego sygnału).

Rys. Różne sposoby próbkowania: a) równomierne, b) sekwencyjne, c) pseudoprzypadkowe, d) ze zmienna

częstotliwością.

17.3. Zagadnienia kontrolne

Zasada działania rejestratorów o przetwarzaniu bezpośrednim i pośrednim
Powstawanie obrazu w oscyloskopie
Podstawowe bloki i zasada działania oscyloskopu analogowego i cyfrowego

18. Pomiary napięć i prądów zmiennych

18.1. Impedancja elektryczna

Impedancja elektryczna – ważna wielkość fizyczna będąca uogólnieniem rezystancji
elektrycznej – ma swoją interpretacje matematyczną i fizyczną.

Od strony matematycznej impedancja Z jest liczba zespoloną. Posiada zatem część
rzeczywistą Re(Z) i urojoną Im(Z):

 

 

1

gdzie

,

Im

Re









j

Z

j

Z

Z

.

Część rzeczywista impedancji elektrycznej zwana jest rezystancją R, a część urojona
reaktancją X. W obwodach elektrycznych wartość obu części może zależeć od pulsacji ω i
tym samym od aktualnej częstotliwości f (lub widma złożonego z wielu częstotliwości)
sygnału w obwodzie:

   

 

f

jX

R

Z

π

2

gdzie

,















.

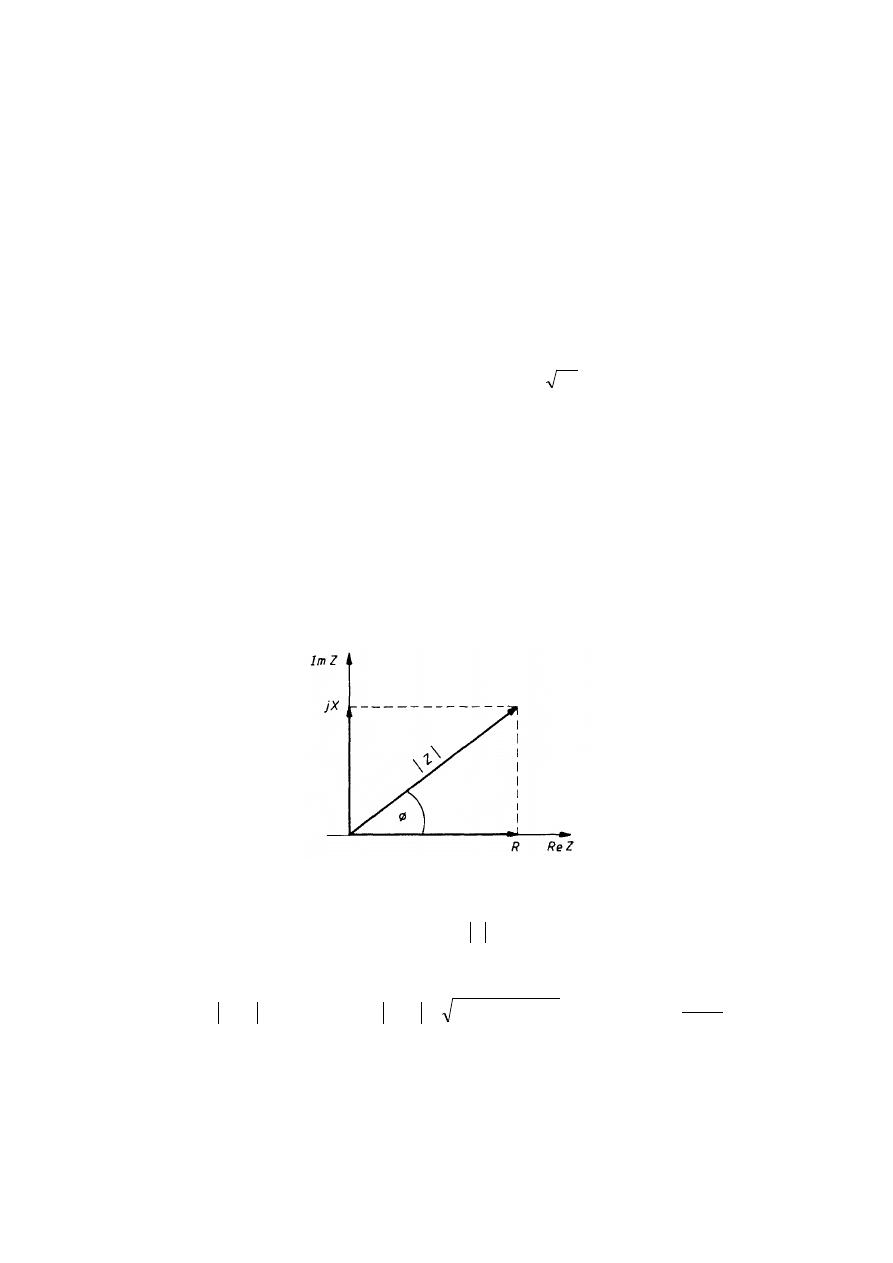
Jako liczba zespolona, impedancja elektryczna jest wektorem, który można przedstawić na
płaszczyźnie zespolonej (część rzeczywistą na osi odciętych, a część urojoną na osi rzędnych
– rys.).

Rys. Przedstawienie impedancji elektrycznej na płaszczyźnie zespolonej.

Zatem, alternatywnie w stosunku do R i X, impedancję można też charakteryzować za pomocą
pary innych liczb: jej modułu (długości wektora) Z oraz kąta φ utworzonego przez wektor i
oś odciętych, które również mogą zależeć od pulsacji:

 

 

 

 

 

 

 

 

 























R

X

X

R

Z

Z

Z

j

arctg

i

gdzie

,

e

2

2











.

Ta cecha impedancji elektrycznej pozwala przedstawić jej interpretację fizyczną.
Zauważając, że transformując harmoniczne napięcie u(t) i prąd i(t) w dziedzinę częstotliwości
otrzymujemy liczby zespolone U(ω) i I(ω), uogólnione prawo Ohma można zapisać jako:

34

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

 

 

 







I

U

Z



.

Zatem impedancja mówi o związku pomiędzy napięciem i prądem zmiennym, opisanym w
dziedzinie częstotliwości. W szczególności moduł impedancji odpowiada stosunkowi wartości
skutecznych napięcia i prądu (w przypadku sygnałów harmonicznych również stosunkowi ich
amplitud):

 

sk

sk

I

U

Z





i wyraża straty energetyczne w obiekcie (podobnie jak rezystancja w obwodach prądu
stałego). Natomiast kąt utworzony przez wektor impedancji i oś odciętych jest kątem
przesunięcia fazowego między harmonicznym napięciem i prądem.

Trzy elementy bierne występujące w układach elektronicznych: oporniki o rezystancji R,
kondensatory o pojemności C i cewki o indukcyjności L maja swoje impedancje Z

R

, Z

C

i Z

L

w idealnym przypadku wyrażone następująco:

 

 

 

 

.

,

1

1

,

L

ω

j

ω

jX

ω

Z

C

ω

j

C

ω

j

ω

jX

ω

Z

R

Z

L

L

C

C

R















Z powyższych wzorów wynika, że wartość rezystancji opornika nie zależy od częstotliwości, kondensator
przepuszcza prąd zmienny (jego impedancja maleje z częstotliwością) i nie przepuszcza prądu stałego (gdy
ω = 0), a cewka bez przeszkód przepuszcza prąd stały (jest zwarciem) i tłumi prądy o rosnącej częstotliwości.

Jednocześnie idealny opornik jedynie rozprasza energie elektryczną (jego impedancja posiada tylko część
rzeczywistą), a w idealnym kondensatorze i cewce nie ma strat energii, może ona być jednak magazynowana i
bezstratnie oddawana (impedancje posiadają tylko część urojoną).

Reguły wyznaczania impedancji wypadkowej dla połączeń szeregowych i równoległych są takie same, jak w
przypadku rezystancji.

18.2. Pomiary napięć przemiennych

Pomiar napięcia zmiennego wymaga połączenia źródła napięcia z woltomierzem, co
najczęściej wykonuje się za pomocą przewodów zbudowanych z wielu skręconych żyłek
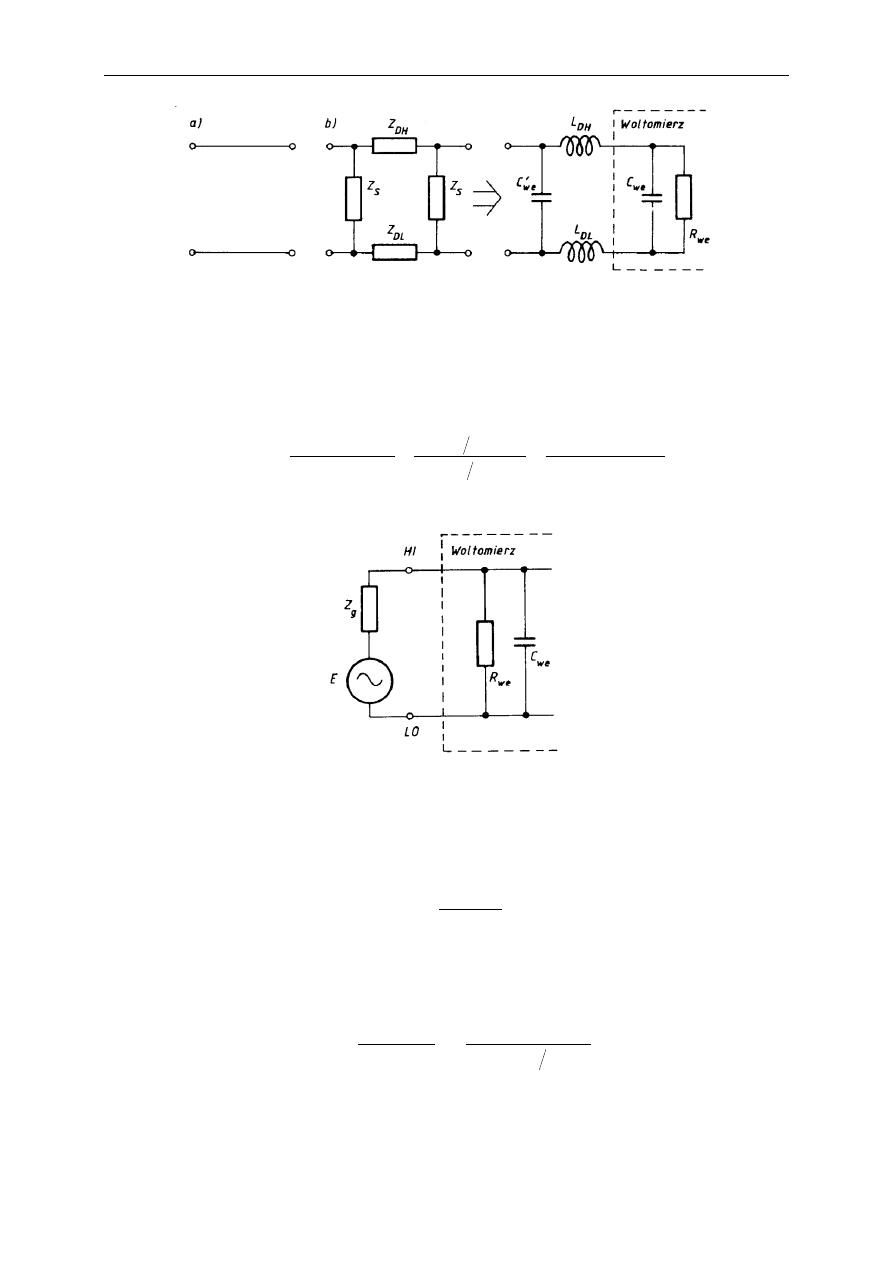
miedzianych (duża odporność na zgięcia) osłoniętych z zewnątrz warstwą izolatora (rys. a).
Takie podejście wprowadza do układu pomiarowego impedancję połączeń (rys. b). Składają
się na nią impedancje cewek utworzonych przez skręcone druty miedziane (indukcyjności
L

DH

i L

DL

) oraz impedancja kondensatora powstałego z dwóch przewodników (przewody

łączące) rozdzielonych dielektrykiem (pojemność C'

we

). Pojemność ta połączona jest z zawsze

istniejącą pojemnością wejściową woltomierza C

we

(która nie manifestuje swej obecności

przy pomiarach napięcia stałego).

18. Pomiary napięć i prądów zmiennych

35

Rys. Impedancyjne właściwości przewodów łączących i wejścia woltomierza.

W efekcie, wraz z rosnącą częstotliwością zwiększa się porcja energii przepływającej przez C'

we

, niedostarczonej

do woltomierza, co zmniejsza jego wskazania (błąd systematyczny pomiaru – błąd metody).

Pojemność wejścia C

we

wraz z rezystancją R

we

tworzą impedancje wejściową woltomierza

Z

we

. Impedancja ta odzwierciedla właściwości dynamiczne miernika, istotne przy pomiarach

napięć zmiennych, i zależy od częstotliwości:

 

 

 









1

π

2

1

1























we

we

we

we

we

we

we

Cwe

Rwe

Cwe

Rwe

we

C

R

f

R

j

C

j

R

C

j

R

Z

Z

Z

Z

f

Z









.

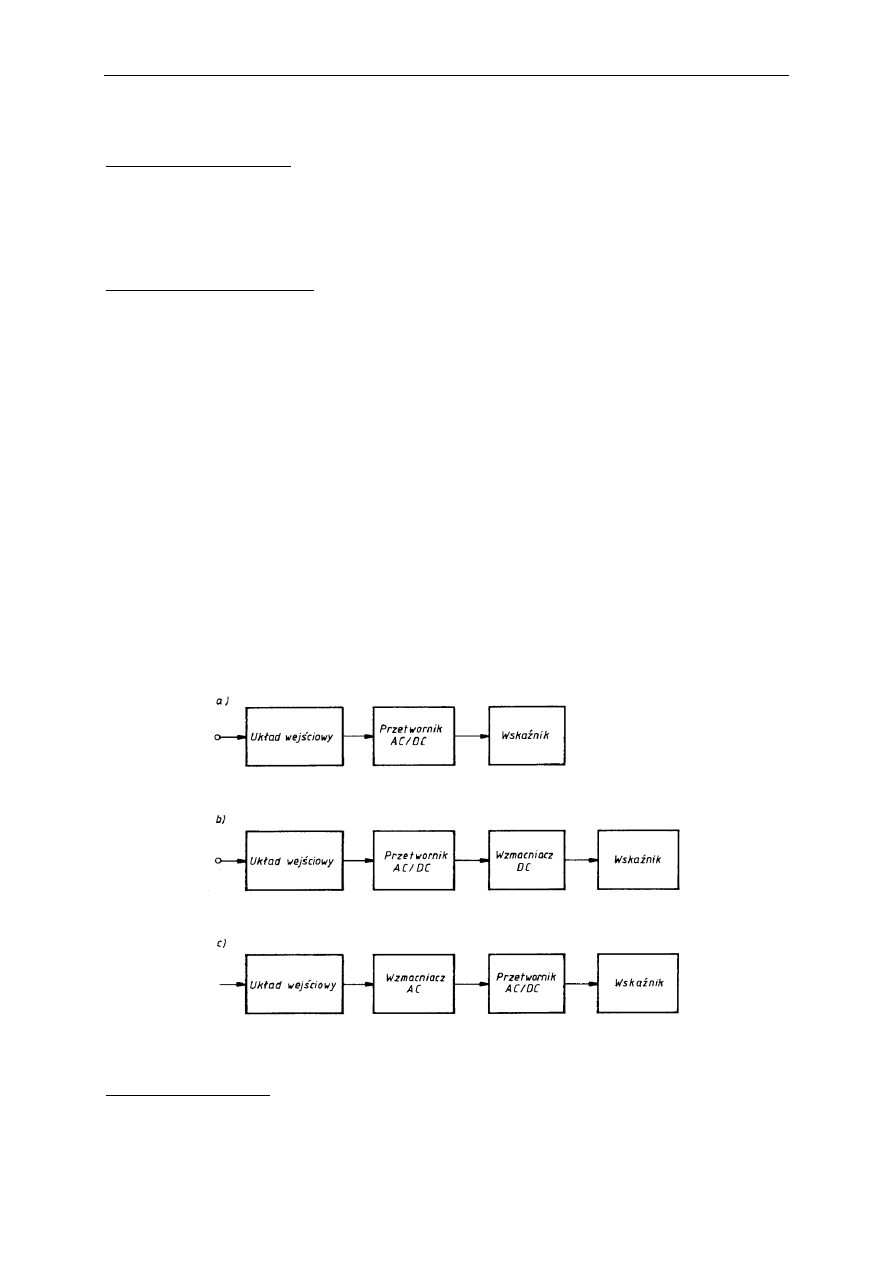
Rys. Schemat układu do pomiaru napięcia zmiennego.

Oznaczając impedancję wewnętrzną źródła (wraz z impedancją doprowadzeń) jako Z

g

(rys.)

można (z dzielnika napięciowego) wyznaczyć wzór na napięcie wskazywane przez
woltomierz:

we

g

we

V

Z

Z

Z

E

U





,

a następnie wzór na względny błąd systematyczny pomiaru siły elektromotorycznej E (błąd
metody):

 

 

   

f

Z

f

Z

E

E

f

U

f

E

g

we

V











1

1



.

Wynika z niego, że błąd ten zależy od stosunku impedancji wejściowej woltomierza do impedancji wewnętrznej
źródła (który powinien być jak największy) i od częstotliwości mierzonego sygnału.

36

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Woltomierze wartości skutecznej

Woltomierze analogowe wymagają zastosowania odpowiedniej zasady pomiaru, czyli
zjawiska fizycznego zamieniającego wartość skuteczna napięcia na proporcjonalne zjawisko
mechaniczne, co nie jest w tym przypadku łatwe. Przykładowym rozwiązaniem jest
woltomierz elektrostatyczny stosowany do pomiaru wartości skutecznej dużych napięć (do
MV) o dużej częstotliwości (do 300 MHz).

Woltomierze elektroniczne wartości skutecznej budowane były z wykorzystaniem
mechanizmów magnetoelektrycznych (reagujących na prąd lub małe napięcie stałe) i
przetworników AC/DC wytwarzających sygnał stały proporcjonalny do U

sk

, takich jak

przetworniki:



wartości średniej wyprostowanej,



wartości szczytowej,



wartości skutecznej (zawierające kwadratory).

Wadą pierwszych dwóch rozwiązań był błąd systematyczny pomiaru powodowany kształtem sygnału
mierzonego innym niż sinusoidalny (mierniki skalowane były zgodnie ze współczynnikiem kształtu).

Woltomierze elektroniczne budowane były w następujących strukturach, w zależności od
przeznaczenia:



struktura podstawowa do pomiaru typowych napięć przemiennych z przetwornikiem

wartości średniej wyprostowanej lub skutecznej między układem wejściowym a
wskaźnikiem (rys. a),



struktura do pomiaru wielkich częstotliwości (do 1 GHz) z wejściowym przetwornikiem

wartości szczytowej (najczęściej w sondzie, rys. b),



struktura do pomiaru małych napięć (nV÷mV, do 30 MHz) ze wstępnym wzmacniaczem

napięcia zmiennego (rys. c).

Rys. Schematy blokowe ukazujące struktury woltomierzy elektronicznych.

Woltomierze cyfrowe wartości skutecznej posiadają wewnętrzną strukturę identyczną z
omówioną wcześniej strukturą woltomierzy DC. Do wyznaczania wartości skutecznej
wykorzystywane są w nich odpowiednie procedury programowe obliczające U

sk

na podstawie

18. Pomiary napięć i prądów zmiennych

37

rejestrowanych próbek mierzonego sygnału (lub rzadziej przetworniki AC/DC umieszczone
między układem wejściowym i przetwornikiem A/C).

18.3. Pomiary wartości skutecznej prądu

Amperomierze analogowe wartości skutecznej były równie rzadko spotykane, co
woltomierze (z podobnych powodów). Przykładem takiego miernika może być amperomierz
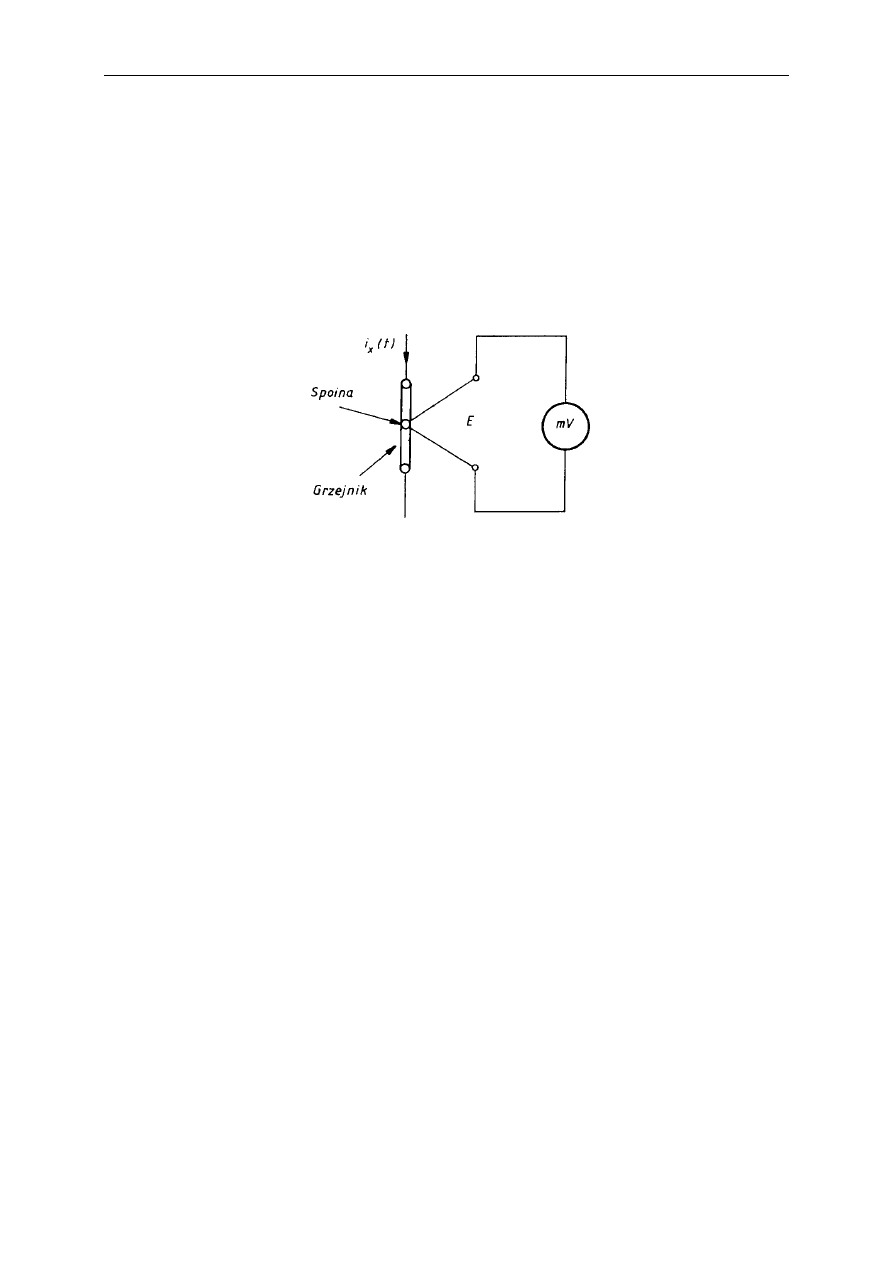
termoelektryczny stosowany do pomiaru natężenia prądu wielkiej częstotliwości (rys.).

Rys. Zasada działania amperomierza termoelektrycznego.

W amperomierzach termoelektrycznych prąd zmienny przepływający przez mały grzejnik powodował
wydzielenie się ciepła (jak wiadomo – proporcjonalnie do wartości skutecznej prądu), a dalej temperatura
grzejnika przetwarzana była na (w przybliżeniu) stałe napięcie ogniwa termoelektrycznego. Napięcie to
mierzone było w strukturze miliwoltomierza DC wyskalowanego w mA wartości skutecznej.

Amperomierze elektroniczne i cyfrowe mają omówiona wcześniej strukturę wewnętrzną
odpowiednio woltomierza elektronicznego lub cyfrowego, uzupełnioną o przetwornik i/u
(układ budowany z wykorzystaniem precyzyjnego rezystora).

18.4. Multimetry

Obecnie mierniki napięć i prądów stałych i zmiennych jaki i rezystancji najczęściej budowane
są jako jedno urządzenie zwane multimetrem.

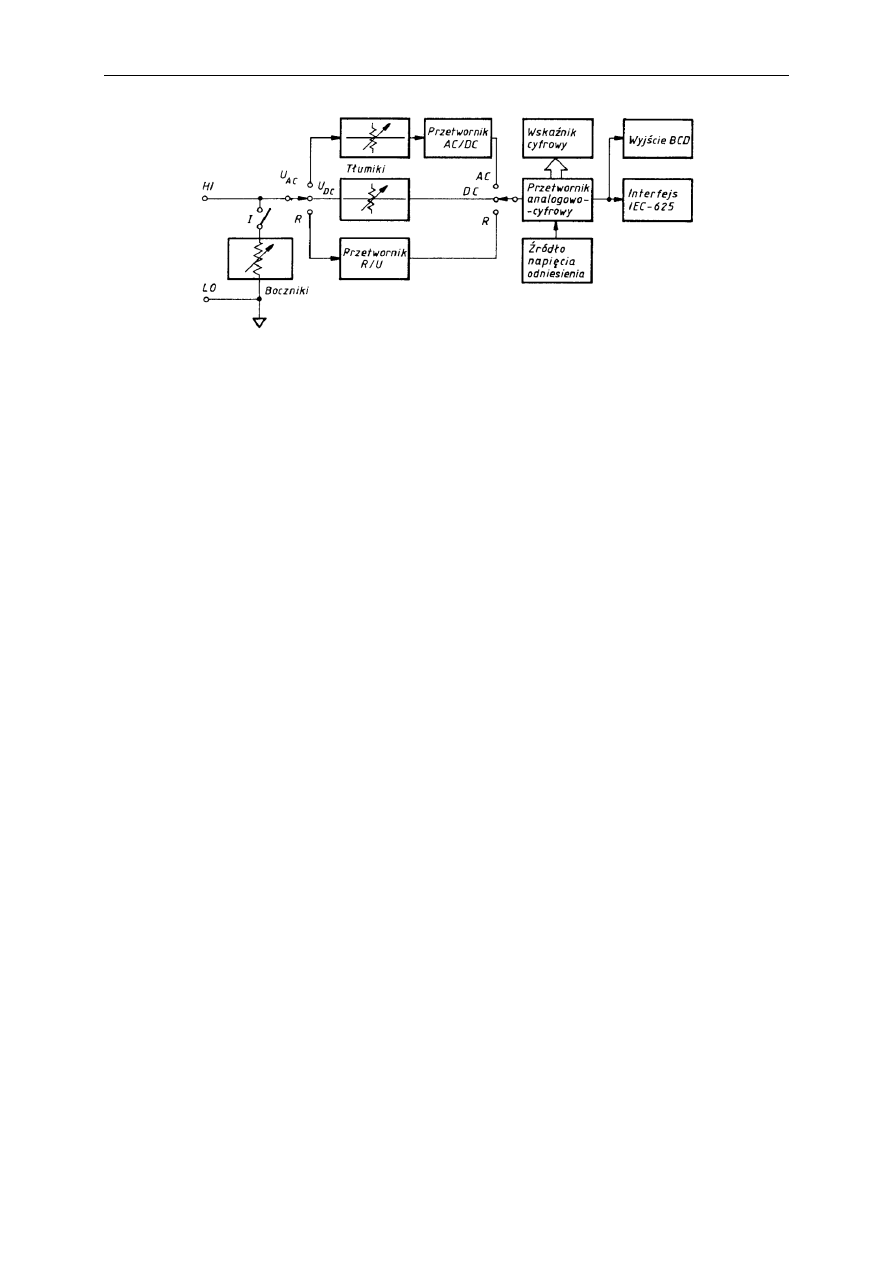
Multimetry pierwotnie budowane były jako nieprogramowalne, posiadające strukturę
wewnętrzną prostego woltomierza cyfrowego z przetwornikiem A/C, uzupełnionego o
dodatkowe bloki przetworników (I/U, R/U, AC/DC) i przełączników (rys.).

38

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Rys. Schemat blokowy przedstawiający ideę budowy multimetru.

Współczesne multimetry mikroprocesorowe są programowalne (tzn. posiadają program
zarządzający ich działaniem). Nie muszą korzystać z przetworników AC/DC, gdyż wyniki
pomiaru obliczane są na podstawie spróbkowanego sygnału mierzonego i definicji danego
parametru.

18.5. Zagadnienia kontrolne

Fizyczna interpretacja impedancji elektrycznej
Związek częstotliwościowych właściwości napięć przemiennych z dokładnością ich pomiaru
Budowa i działanie woltomierze i amperomierze napięć przemiennych
Zasada działania multimetrów cyfrowych

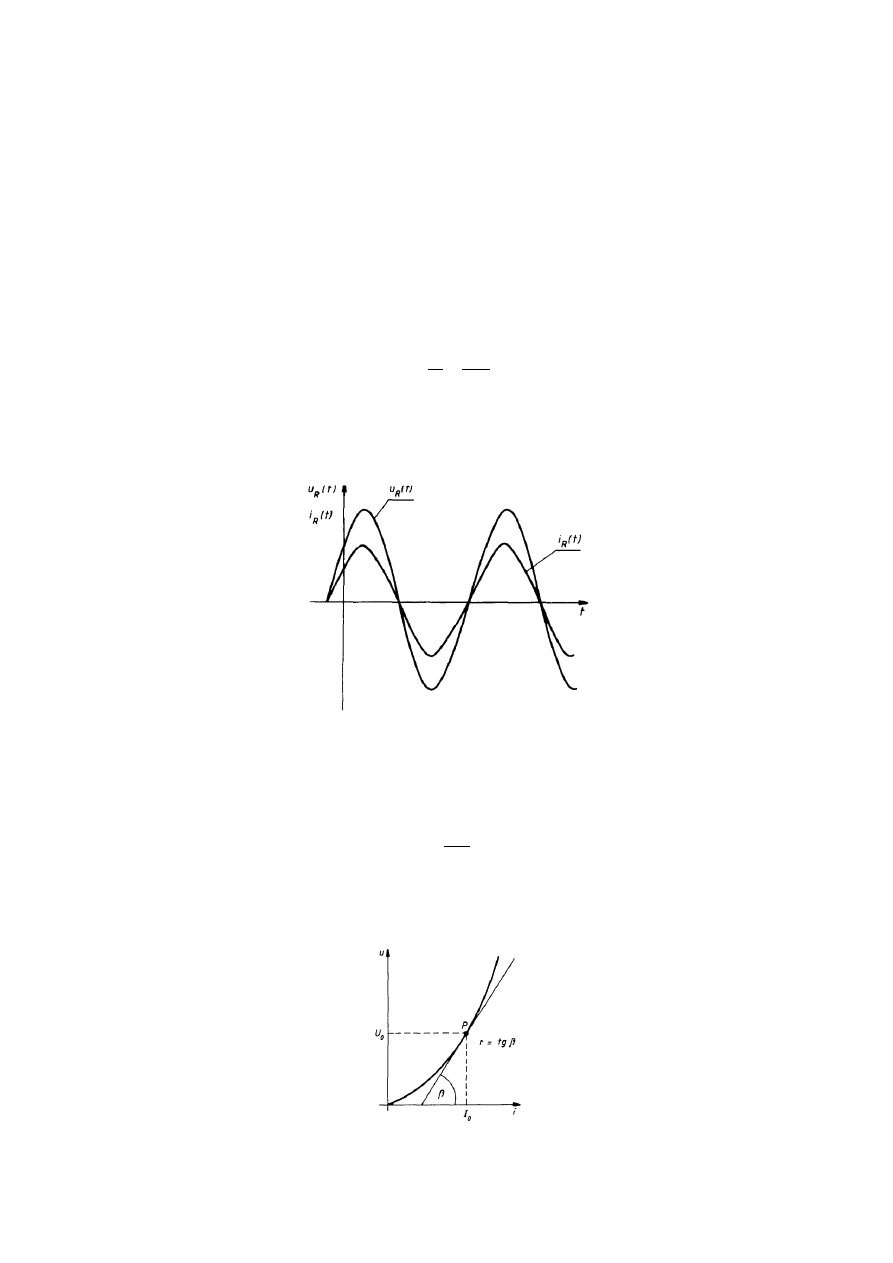
19. Właściwości elementów biernych

19.1. Idealne charakterystyki elementów biernych

Rezystor idealny (opornik), będący elementem rozpraszającym energie elektryczną
(zamieniającym ją najczęściej na ciepło), opisany jest przez rezystancję statyczną wynikającą
z prawa Ohma. Mówi ono o związku zarówno między napięciem i prądem stałym na
elemencie jak i ich wartościami chwilowymi:

 

 

t

i

t

u

I

U

R





.

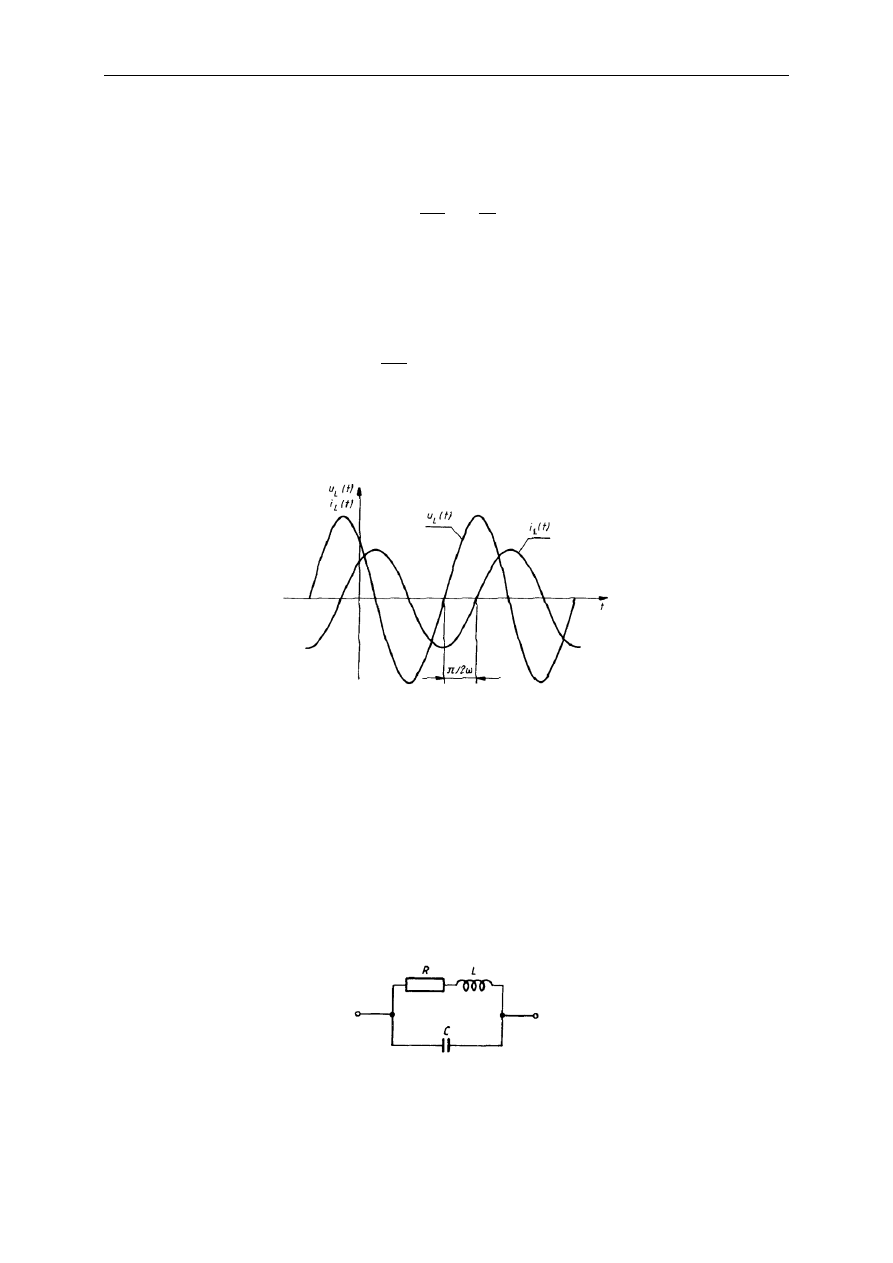
Cechą charakterystyczna idealnego rezystora jest brak przesunięcia fazowego między
napięciem i prądem przemiennym (rys.).

Rys. Napięcie i prąd przemienny w idealnym rezystorze.

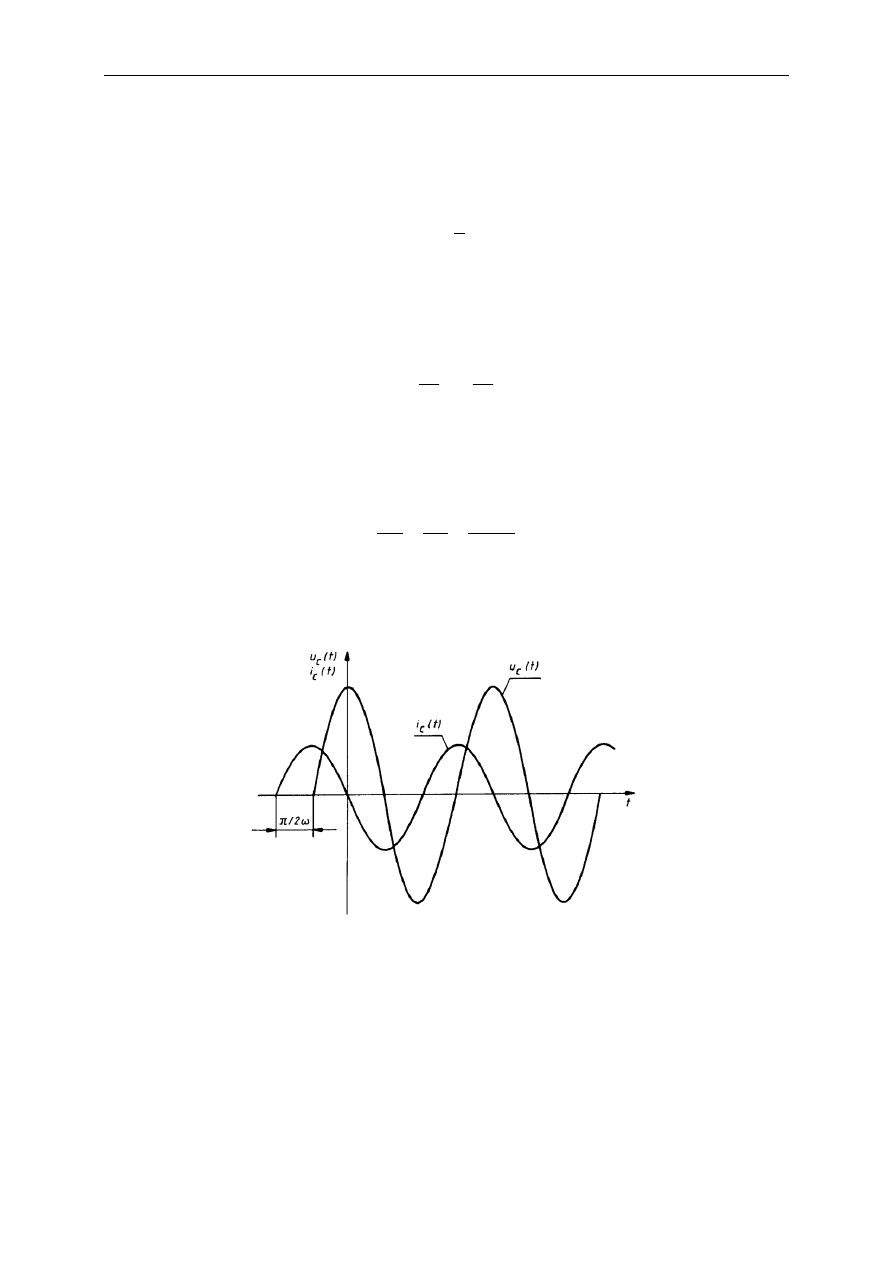
Statyczne charakterystyki prądowo-napięciowe niektóre elementów i układy elektronicznych
są nieliniowe (rys.). W takim przypadku definiuje się rezystancję dynamiczną:

dI

dU

r



.

W szczególnym przypadku zależności U(I) i pewnym zakresie tej charakterystyki rezystancja dynamiczna może
być zerowa lub ujemna.

Rys. Przykład nieliniowej statycznej charakterystyki prądowo-napięciowej.

40

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Kondensator idealny gromadzi energię elektryczną w polu elektrostatycznym wytwarzanym
przez ładunek elektryczny q zgromadzony pod wpływem przyłożonego napięcia u i może ją
oddawać bezstratnie. Możliwość tę wyraża wartość parametru C zwanego pojemnością:

u

q

C



.

Korzystając z powyższej zależności oraz definicji natężenia prądu (zmiana ładunku w czasie)
można przedstawić związek miedzy prądem i napięciem zmiennym w idealnym kondensatorze
w dziedzinie czasu:

dt

du

C

dt

dq

i





.

Związek między napięciem i prądem w kondensatorze idealnym w dziedzinie częstotliwości
wyrażony jest przez impedancję Z

C

omówioną wcześniej. Wynika z niej m.in., ze stosunek

napięcia do prądu skutecznego zależy od częstotliwości:

fC

C

I

U

sk

sk

π

2

1

1







Cechą charakterystyczną idealnego kondensatora jest przesuniecie fazowe miedzy napięciem i
prądem harmonicznym wynoszące –



/2 rad (–90°).

Rys. Napięcie i prąd przemienny w idealnym kondensatorze.

Cewka indukcyjna idealna gromadzi energię elektryczną w strumieniu magnetycznym Φ
wywołanym przez przepływający prąd i i może ją bezstratnie oddawać. Możliwość tę
charakteryzuje parametr L zwany indukcyjnością:

iL

Φ



.

19. Właściwości elementów biernych

41

Ponieważ wartość napięcia w cewce odpowiada zmianie stłumienia magnetycznego w czasie,
powyższe równanie pozwala wyznaczyć związek pomiędzy napięciem i prądem zmiennym w
cewce idealnej w dziedzinie czasu:

dt

di

L

dt

dΦ

u





.

Związek między napięciem i prądem w cewce idealnej w dziedzinie częstotliwości dany jest
przez wcześniej omówioną impedancję Z

L

. Wynika z niej m.in., ze stosunek napięcia do prądu

skutecznego w następujący sposób zależy od częstotliwości:

fL

L

I

U

sk

sk

π

2







.

Cechą charakterystyczną idealnej cewki jest przesuniecie fazowe miedzy napięciem i prądem
harmonicznym wynoszące



/2 rad (90°).

Rys. Napięcie i prąd przemienny w idealnej cewce.

19.2. Rzeczywiste właściwości elementów biernych

Rezystor rzeczywisty (opornik elektryczny) jest elementem wykonywanym różnymi
technologiami, co powoduje, że poza rozpraszaniem energii elektrycznej zachodzą w nim
jeszcze inne (poboczne) zjawiska fizyczne. Należy do nich przede wszystkim gromadzenie
ładunku elektrycznego miedzy metalicznymi końcówkami opornika (powstaje z nich i
powietrza kondensator bocznikujący o małej pojemności C) oraz generacja strumienia
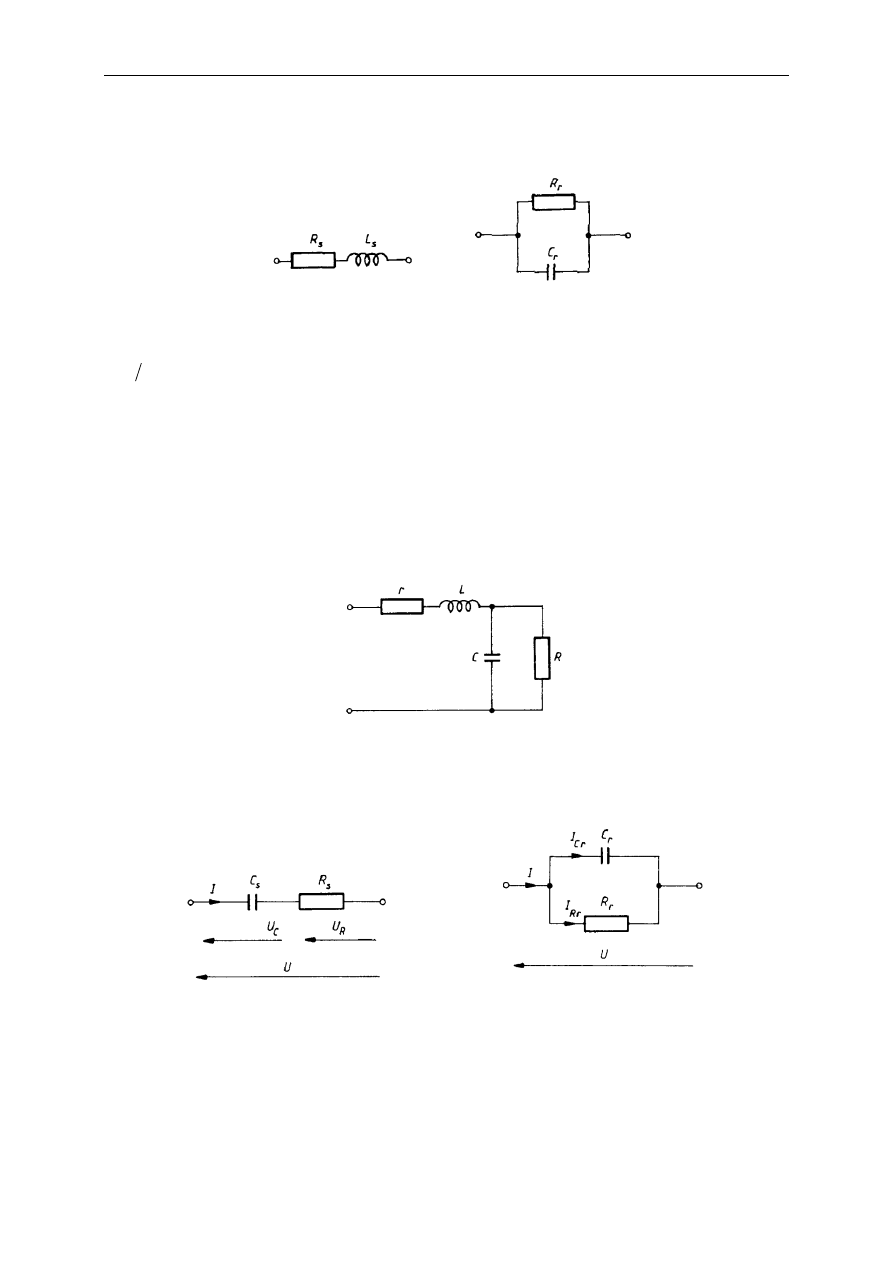
magnetycznego wskazująca na obecność indukcyjności L (rys.).

Rys. Schemat zastępczy rezystora rzeczywistego.

42

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

W praktyce rezystor rzeczywisty przy małych częstotliwościach (tj.

1

2



LC



) opisuje się

dwuelementowym schematem zastępczym, szeregowym lub równoległym, w zależności od
wartości rezystancji (rys.)

Rys. Schematy zastępcze rezystora o małej i dużej rezystancji przy niskich częstotliwościach.

O „małej rezystancji” mówimy, gdy spełniony jest warunek





1

2



RC



, a o „dużej” gdy





1

2



R

L



.

O rozbieżności między właściwościami rzeczywistego rezystora i idealnego można przekonać się
eksperymentalnie, mierząc jego impedancję w szerokim przedziale częstotliwości (rezystor idealny posiadałby
stałą część rzeczywista i zerową reaktancje, a rzeczywisty ma impedancję zależną od częstotliwości).

Kondensator rzeczywisty również cechuje się dodatkowymi właściwościami fizycznymi,
poza gromadzeniem ładunku, wynikającymi z jego budowy. Opisują je parametry
pasożytnicze, takie jak: rezystancja doprowadzeń r, indukcyjność doprowadzeń L oraz
(bardzo duża, lecz skończona) rezystancja dielektryka R (rys.)

Rys. Schemat zastępczy kondensatora rzeczywistego.

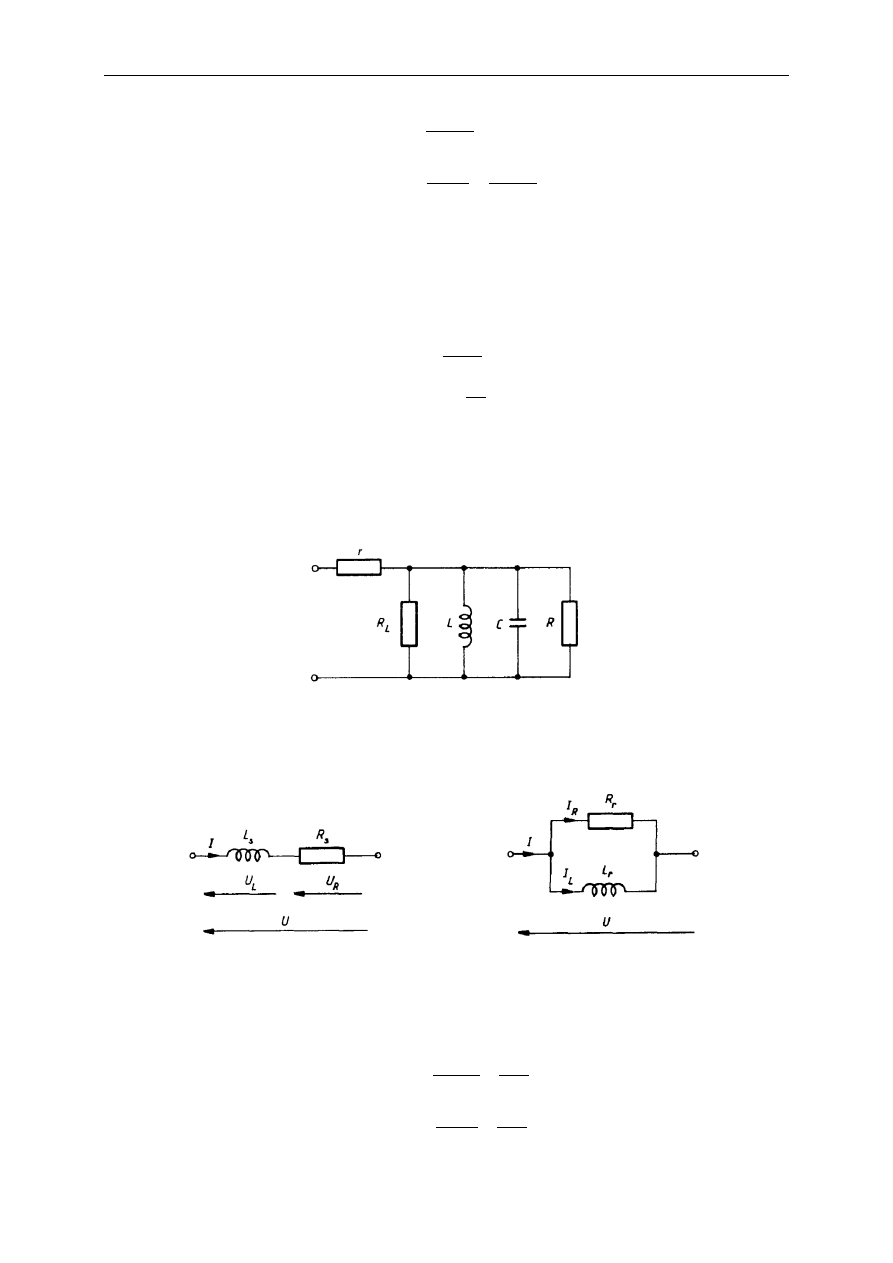
Ostatecznie, w praktyce stosuje się prostsze schematy dwuelementowe, szeregowy lub
równoległy, zaniedbując resztkową indukcyjność (rys.).

Rys. Szeregowy i równoległy schemat zastępczy kondensatora rzeczywistego

Charakteryzując kondensator rzeczywisty, zamiast jego rezystancji pasożytniczej (szeregowej
R

s

lub równoległej R

r

) podaje się wartość jednego parametru: współczynnika strat D

(zwanego też tangensem kąta stratności tg



), który dla schematu szeregowego i równoległego

definiowany jest następująco:

19. Właściwości elementów biernych

43

 

 

.

1

,

r

r

C

R

s

s

C

R

C

R

I

I

tg

D

C

R

U

U

tg

D

























Interesującym faktem poznawczym jest to, że schemat szeregowy i równoległy jednakowo dobrze opisują
kondensator rzeczywisty i nie da się eksperymentalnie (tzn. poprzez pomiar) rozróżnić, którym z nich lepiej jest
opisać badany kondensator. W efekcie każdemu kondensatorowi rzeczywistemu należy przypisać dwie wartości
pojemności: szeregową C

s

i równoległą C

r

. Związek między nimi, a także rezystancją szeregową i równoległą,

podają poniższe równania:

.

1

1

,

1

1

2

2











 







D

R

R

D

C

C

s

r

s

r

Cewka indukcyjna rzeczywista podczas przepływu prądu zmiennego również ujawnia
różnorodność zachodzących zjawisk fizycznych (rys.). Poza dominującą indukcyjnością L,
uwidacznia się rezystancja przewodnika R

L

, z którego cewka jest wykonana, rezystancja

doprowadzeń r oraz kondensator pasożytniczy wytworzony przez przewodniki doprowadzeń i
powietrze (C i R).

Rys. Schemat zastępczy cewki rzeczywistej.

Upraszczając analizę, właściwości cewki rzeczywistej opisuje się stosując jej szeregowy lub
równoległy schemat zastępczy (rys.).

Rys. Szeregowy i równoległy schemat zastępczy cewki rzeczywistej.

Parametrem, który opisuje jakość cewki, jest jej dobroć Q, zdefiniowana w układzie
szeregowym i równoległym następująco:

 

 

.

,

r

r

R

L

s

s

R

L

L

R

I

I

tg

Q

R

L

U

U

tg

Q

























44

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Analogicznie do kondensatora, również cewka rzeczywista ma dwie indukcyjności: szeregową L

s

i równoległą

L

r

, jednoznacznie powiązane ze sobą (tak jak i rezystancje R

s

i R

r

):





.

1

,

1

1

2

2

Q

R

R

Q

L

L

s

r

s

r





















19.3. Zagadnienia kontrolne

Parametry elektryczne rzeczywistych elementów biernych

20. Pomiary impedancji

Właściwości rzeczywistych elementów biernych powodują, że ich pomiary w istocie są
pomiarami impedancji elektrycznej. Szczególnie istotne, nie tylko w elektronice, są pomiary
pojemności i indukcyjności wraz ze współczynnikiem strat i dobrocią badanych elementów.

Pomiary impedancji zdominowane są przez pomiary bezpośrednie metodami mostkowymi
(metoda zerowa kompensacyjna).

20.1. Mostki czterogałęźne

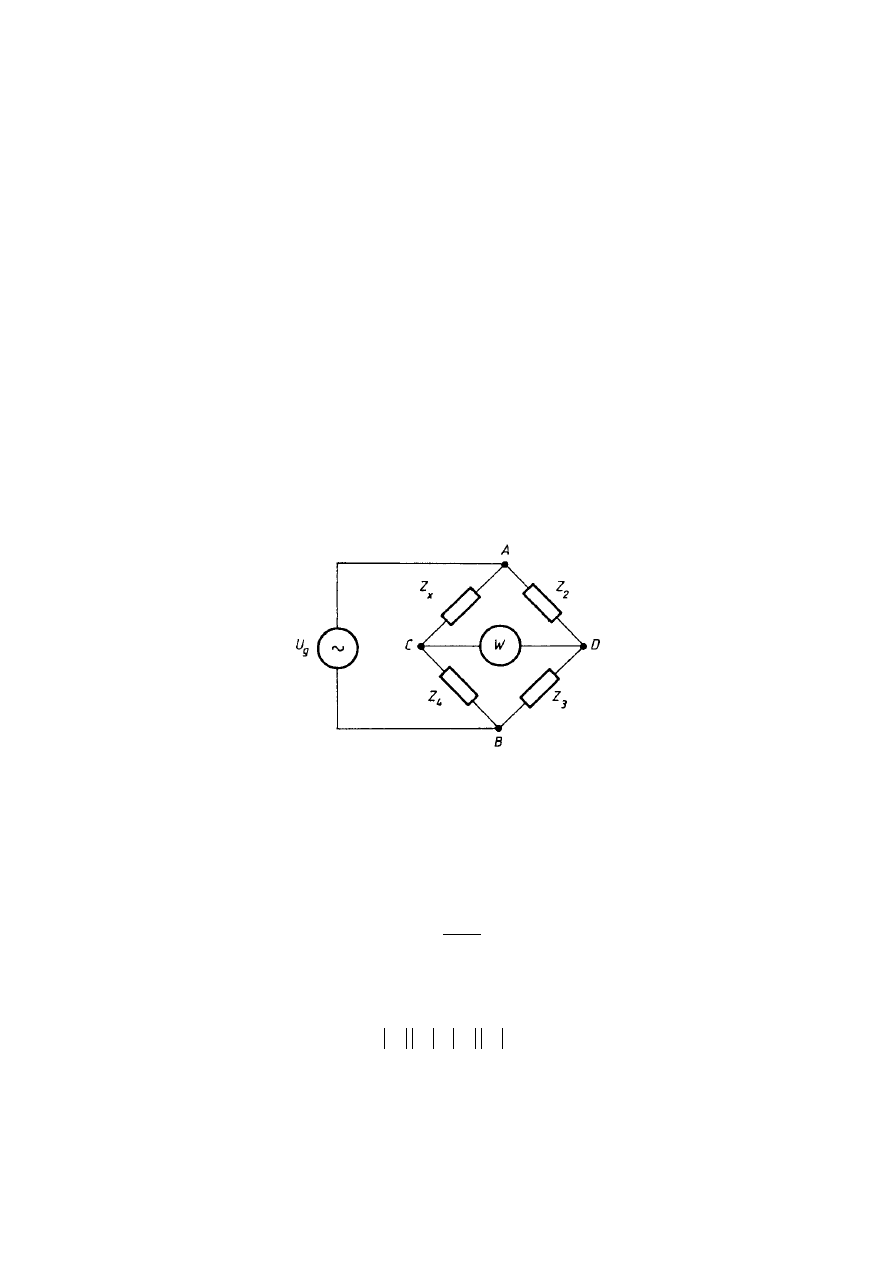
Zasadę pomiaru impedancji za pomocą mostka czterogałęźniego przedstawia rys. Układ
pobudzany jest (pomiar parametrów biernych) przez napięcie przemienne przyłożone do
węzłów A i B. Badana impedancja Z

x

znajduje się w jednym z ramion, a impedancje

wzorcowe (z których Z

3

lub Z

4

jest regulowana) w pozostałych. Równoważenie mostka

prowadzi do wyrównania się potencjałów w węzłach C i D (U

CD

= 0) i zaniku prądu miedzy

nimi, co wykrywane jest przez wskaźnik zrównoważenia (najczęściej czuły galwanometr).

Rys. Schemat mostka czterogałęźnego do pomiaru impedancji.

Z warunku równowagi mostka wynika równość impedancji:

4

2

3

Z

Z

Z

Z

x



,

a stąd:

3

4

2

Z

Z

Z

Z

x



.

Ponieważ impedancja jest wielkością zespoloną, pierwsza z powyższych równości implikuje:

,

,

4

2

3

4

2

3

















x

x

Z

Z

Z

Z

lub

















.

Im

Im

,

Re

Re

4

2

3

4

2

3

Z

Z

Z

Z

Z

Z

Z

Z

x

x





46

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Te podwójne równości prowadzą do wniosku, że aby zrównoważyć mostek impedancyjny,
należy regulować dwie wielkości. Dlatego też do równoważenia części rzeczywistej
(rezystancji) używa się regulowanego rezystora, a części urojonej (reaktancji) – regulowanego
kondensatora. Ostatecznie w mostkach czterogałęźnych stosuje się cztery wzorce: dwa stałe
(rezystory) i dwa regulowane.

Dokładność pomiaru mostkami czterogałęźnymi zależy od:



dokładności elementów wzorcowych (R i C),



rozdzielczości wzorców,



czułości wskaźnika równowagi (błąd nieczułości),



wpływu na pomiar dodatkowych zjawisk o naturze elektrycznej.

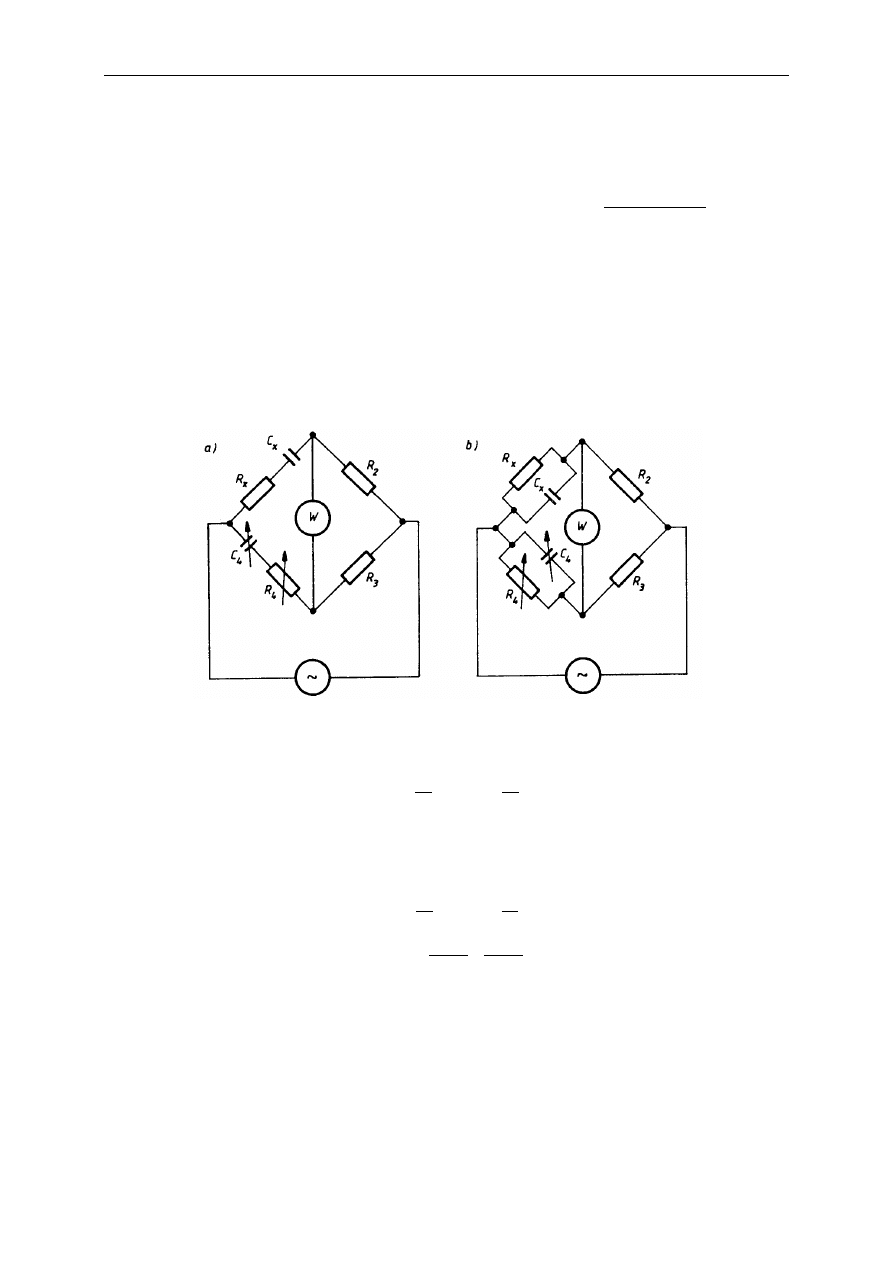
Mostki do pomiaru pojemności budowane są w dwóch konfiguracjach (rys.): do pomiaru
pojemności szeregowej (mostek Sauty'ego-Wiena) i równoległej (mostek Nernsta).

Rys. Mostek uniwersalny do pomiaru pojemności: a) szeregowy, b) równoległy.

Zrównoważenie mostka dla modelu szeregowego daje:

,

,

,

4

4

3

2

4

2

3

4

C

R

C

R

tg

D

R

R

R

R

R

R

C

C

s

s

s

s

















a mostka dla modelu równoległego:

.

1

1

,

,

4

4

3

2

4

4

3

4

C

R

C

R

tg

D

R

R

R

R

R

R

C

C

r

r

r

r

















Układ równoległy jest wygodniejszy do pomiaru pojemności kondensatorów o dużym współczynniku strat D,
natomiast układ szeregowy – odwrotnie.

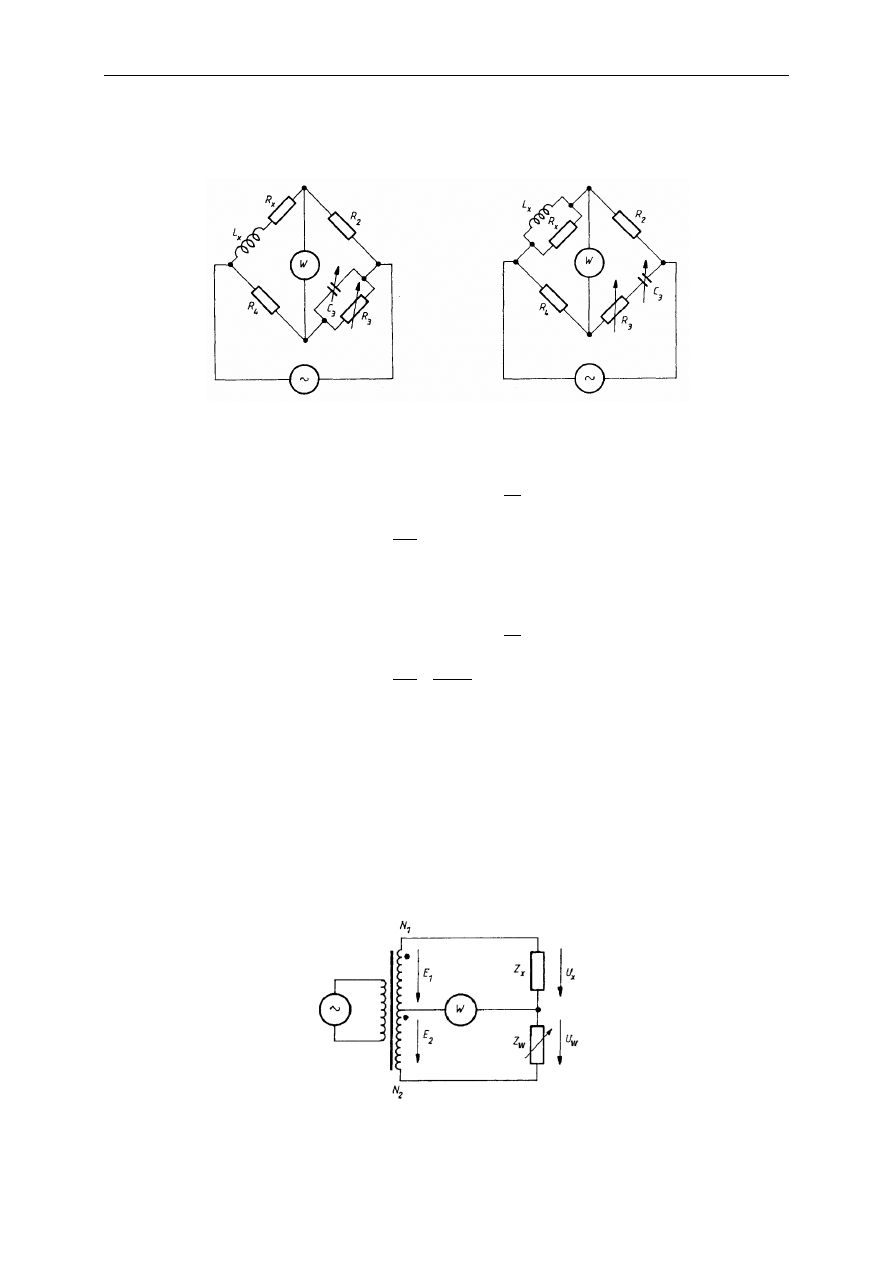
Mostki do pomiaru indukcyjności budowane są w dwóch analogicznych konfiguracjach
(rys.): do pomiaru indukcyjności szeregowej (mostek Maxwella-Wiena) i równoległej
(mostek Haya).

20. Pomiary impedancji

47

Warte zauważenia jest zastosowanie do regulacji reaktancji kondensatora wzorcowego zamiast cewki. Wynika to
z większej precyzji wzorców pojemnościowych. Jednocześnie w mostku przekonfigurowane zostaje połączenie i
umieszczenie wzorców regulowanych.

Rys. Mostek uniwersalny do pomiaru indukcyjności: a) szeregowy, b) równoległy.

Zrównoważenie mostka dla modelu szeregowego daje:

,

,

,

3

3

3

2

4

3

4

2

C

R

R

L

Q

R

R

R

R

C

R

R

L

s

s

s

s













a mostka dla modelu równoległego:

.

1

,

,

3

3

3

2

4

3

4

2

C

R

L

R

Q

R

R

R

R

C

R

R

L

r

r

r

r













Układ równoległy jest wygodniejszy do pomiaru indukcyjności cewek o dużej dobroci Q, a szeregowy –
odwrotnie.

20.2. Mostki transformatorowe

W mostkach tych dwa spadki napięć w ramionach zastąpione są siłami elektromotorycznymi
E

1

i E

2

wtórnych uzwojeń transformatora (rys.).

Rys. Mostek transformatorowy do pomiaru impedancji.

48

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Z warunku równowagi mostka wynika:

.

,

2

1

2

1

2

1

N

N

Z

Z

Z

Z

U

U

N

N

E

E

w

x

w

x

w

x









Powyższe podejście prowadzi do zastąpienia stosunku impedancji we wzorze wykorzystywanym do
wyznaczenia wyniku pomiaru stosunkiem liczby uzwojeń wtórnych. Dzięki temu uzyskuje się większa
dokładność i powtarzalność wskazań (liczba zwojów jest precyzyjnie określona i niezależna od czynników
zewnętrznych).

Inne sposoby pomiaru impedancji to:



metody rezonansowe,



mierniki z przetwarzaniem impedancji w przedział czasu.

20.3. Półautomatyczne i automatyczne pomiary impedancji

W mostki półautomatycznych jeden z elementów wzorcowych dostrajany jest ręcznie, a drugi
automatycznie. Mostki automatyczne budowane są jako przyrządy cyfrowe, w których za
równoważenie mostka odpowiedzialny jest mikroprocesor.

20.4. Zagadnienia kontrolne

Metody mostkowe pomiaru impedancji: zasada i realizacje
Zasada pomiaru impedancji mostkami transformatorowymi

21. Pomiary mocy sygnałów harmonicznych

21.1. Definicje mocy

Moc chwilowa p w obwodzie prądu zmiennego jest iloczynem chwilowych wartości napięcia
i natężenia prądu:

     

t

i

t

u

t

p





.

Ponieważ u i i zmieniają się okresowo (rozważamy sygnały harmoniczne), to moc chwilowa również jest
sygnałem okresowym.

Moc czynna P mierzona w watach [W] jest wartością średnią mocy chwilowej:

 







T

t

t

dt

t

p

T

P

0

0

1

.

Wyraża ona rozpraszanie (zamianę na ciepło) energii elektrycznej przez odbiornik lub jej zamienianie na inną
postać lub pracę.

Można pokazać, że w obwodach z sygnałami sinusoidalnymi moc czynną można wyrazić za
pomocą wartości skutecznych napięcia i prądu oraz kąta przesunięcia fazowego φ między
tymi sygnałami:



cos

sk

sk

I

U

P



.

Wynika stąd, że dla idealnego rezystora

R

U

I

U

P

sk

sk

sk

2





, a dla idealnego kondensatora i cewki

0



P

.

Moc pozorna S mierzona w woltamperach [VA] opisuje amplitudę oscylacji mocy
chwilowej:

sk

sk

I

U

S





.

Moc bierna Q mierzona w warach [var] jest mocą pulsującą między nadajnikiem i
odbiornikiem:



sin





sk

sk

I

U

Q

.

Ze wzoru tego wynika, że dla idealnego rezystora

0



P

(nie oddaje on mocy elektrycznej, która do niego

dociera), a dla idealnego kondensatora i cewki

sk

sk

I

U

P



(tzn. nie rozpraszają one energii elektrycznej).

Związek miedzy mocą pozorną, czynną i bierną łatwo znaleźć posługując się zależnościami
trygonometrycznymi:

2

2

2

Q

P

S





.

50

Miernictwo elektroniczne – komentarz do wykładu

(© A.G. Polak 2013)

Ponieważ różni odbiorcy w różnym stopniu pobierają energię dostarczaną przez sygnał elektryczny,
charakteryzuje się ich za pomocą współczynnika mocy K

p

:



cos





S

P

K

p

.

21.2. Pomiary mocy

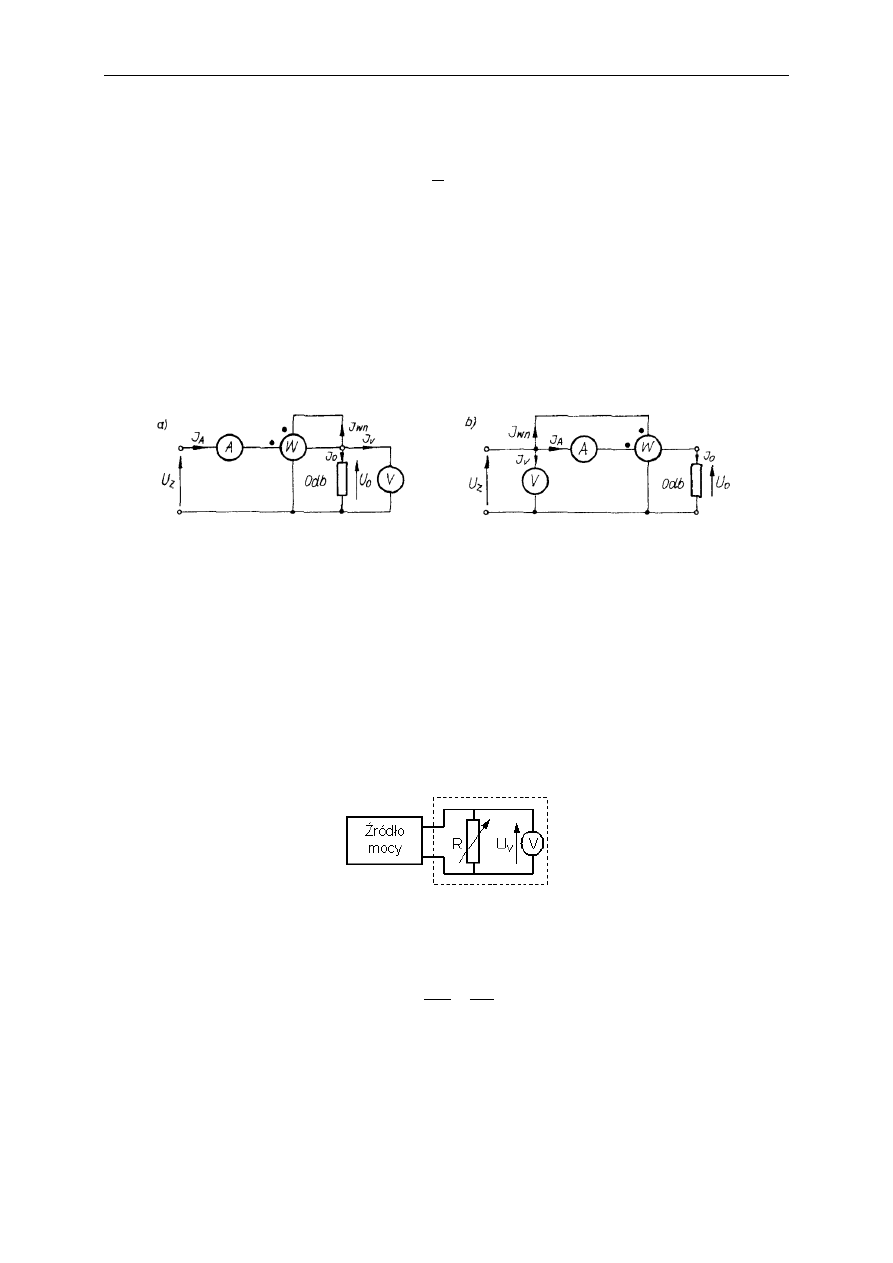
Pomiar mocy odbieranej bezpośrednio mierzy się watomierzem, gdyż jest to moc czynna.
Watomierz jednak zwykle podłącza się jednocześnie z amperomierzem i woltomierzem
wartości skutecznej (rys.), co można zrobić w dwóch układach: z poprawnym pomiarem
napięcia (a) i prądu (b).

Rys. Układy pomiaru mocy za pomocą watomierza.

Wartości odczytane z mierników pozwalają wyznaczyć nie tylko moc czynna, ale również
bierną i pozorną.

Dodatkowo kontrola przez amperomierz aktualnej wartości skutecznej prądu zabezpiecza watomierz przed
uszkodzeniem w przypadku φ zbliżonego do π/2, kiedy P ≈ 0.

Pomiar mocy metodą absorpcyjną służy do charakteryzowania źródła energii poprzez
maksymalną moc, jaka może z niego pobrać odbiornik. Jest to zatem pomiar mocy czynnej i
może być realizowany w układzie jak na rys., gdzie miernik składa się z regulowanego
rezystora (odbiornik mocy) i woltomierza wartości skutecznej wyskalowanego w watach.

Rys. Zasada pomiaru mocy metodą absorpcyjną.

W takim przyrządzie:

R

U

R

U

P

V

sk

2

2





.

Pomiar polega na takim doregulowaniu R, aby miernik wskazywał maksimum mocy. Pozwala
to określić maksymalną mocy oddawaną przez źródło oraz rezystancję dopasowania.

21. Pomiary mocy sygnałów harmonicznych

51

21.3. Pomiar energii elektrycznej

Energia elektryczna sygnału harmonicznego (mierzona często w kilowatogodzinach)
odpowiada mocy czynnej scałkowanej w czasie pomiaru t

pom

:

 





p o m

t

dt

t

P

W

0

.

W miernikach analogowych zazwyczaj wykorzystuje się w tym celu przetworniki
indukcyjne (aluminiowa tarcza porusza się pod wpływem wirowego pola magnetycznego
wytworzonego przez dwie cewki, przez które płyną prądy proporcjonalne do chwilowych
wartości natężenia prądu i napięcia).

Mierniki cyfrowe realizują pomiar stosując zasady wykorzystywane w miernikach
analogowych lub w oparciu o związek energii i mocy, przeliczając rejestrowane próbki
napięcia i prądu.

21.4. Zagadnienia kontrolne

Co opisuje moc czynna, a co bierna; sposoby ich pomiaru
Na czym polegają pomiary wielkości nieelektrycznych

22. Pomiary wielkości nieelektrycznych

Większość z otaczających człowieka wielkości to wielkości nieelektryczne. Z drugiej strony
najpopularniejsze obecnie przyrządy pomiarowe to cyfrowe (mikroprocesorowe) urządzenia
elektroniczne lub optoelektroniczne.

Idea pomiarów wielkości nieelektrycznych miernikami elektronicznymi polega na
zastosowaniu czujników wielkości nieelektrycznych, przetwarzających je na elektryczne.
Pomiar sprowadza się zatem do omówionego wcześniej pomiaru wielkości elektrycznych
aktywnych i biernych, przede wszystkim:



napięcia,



natężenia prądu,



rezystancji,



pojemności,



indukcyjności.

Przypomnijmy, że przetwornik to urządzenie (lub element) odwzorowujący wielkość
wejściową na wielkość wyjściową w zdefiniowany sposób z wykorzystaniem wybranego
zjawiska fizycznego. W przyrządach pomiarowych zwykle kilka przetworników łączonych
jest szeregowo tworząc łańcuch przetwarzania.

Czujnik jest pierwszym elementem łańcucha przetworników. Ma on bezpośredni kontakt z
polem pomiarowym i reaguje na wartość wielkości mierzonej wytwarzając proporcjonalną do
niej wartość wielkości wyjściowej. W miernikach elektronicznych jest nią wielkość
elektryczna.

Do głównych zalet elektronicznego pomiaru wielkości nieelektrycznych należą:



analogowe przetwarzanie sygnału pomiarowego (wzmacnianie, filtracja, itd.),



przetwarzanie cyfrowe sygnału (obróbka matematyczna),



przesyłanie sygnału i/lub wyniku pomiaru na odległość,



sterowanie elektryczne badanymi obiektami.

Czujniki pomiarowe dzieli się na dwa typy: parametryczne i generacyjne, biorąc pod uwagę
to, czy muszą być pobudzane, czy tez same wytwarzają wyjściowy sygnał elektryczny.

Główne grupy mierzonych wielkości nieelektryczne to:
– wymiary geometryczne,
– siły i momenty sił,
– prędkość i przyspieszenie,
– ciśnienia i przepływy,
– moc, praca i energia mechaniczna oraz cieplna,
– temperatura, ilość ciepła,
– promieniowanie,
– właściwości fizykochemiczne.

W każdym przypadku wykorzystywane są specjalistyczne czujniki przetwarzające te
wielkości na wielkości elektryczne.