
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 1 -
WEKTORY
¾
UKŁAD ORTOKARTEZJAŃSKI
¾
WEKTOR
¾
DZIAŁANIA NA WEKTORACH
¾
KOMBINACJA LINIOWA WEKTORÓW
¾
WARUNEK KOLINEARNOŚCI DWÓCH WEKTORÓW
¾
ILOCZYN SKALARNY
¾
ILOCZYN WEKTOROWY
¾
ILOCZYN MIESZANY TRÓJKI WEKTORÓW
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 2 -
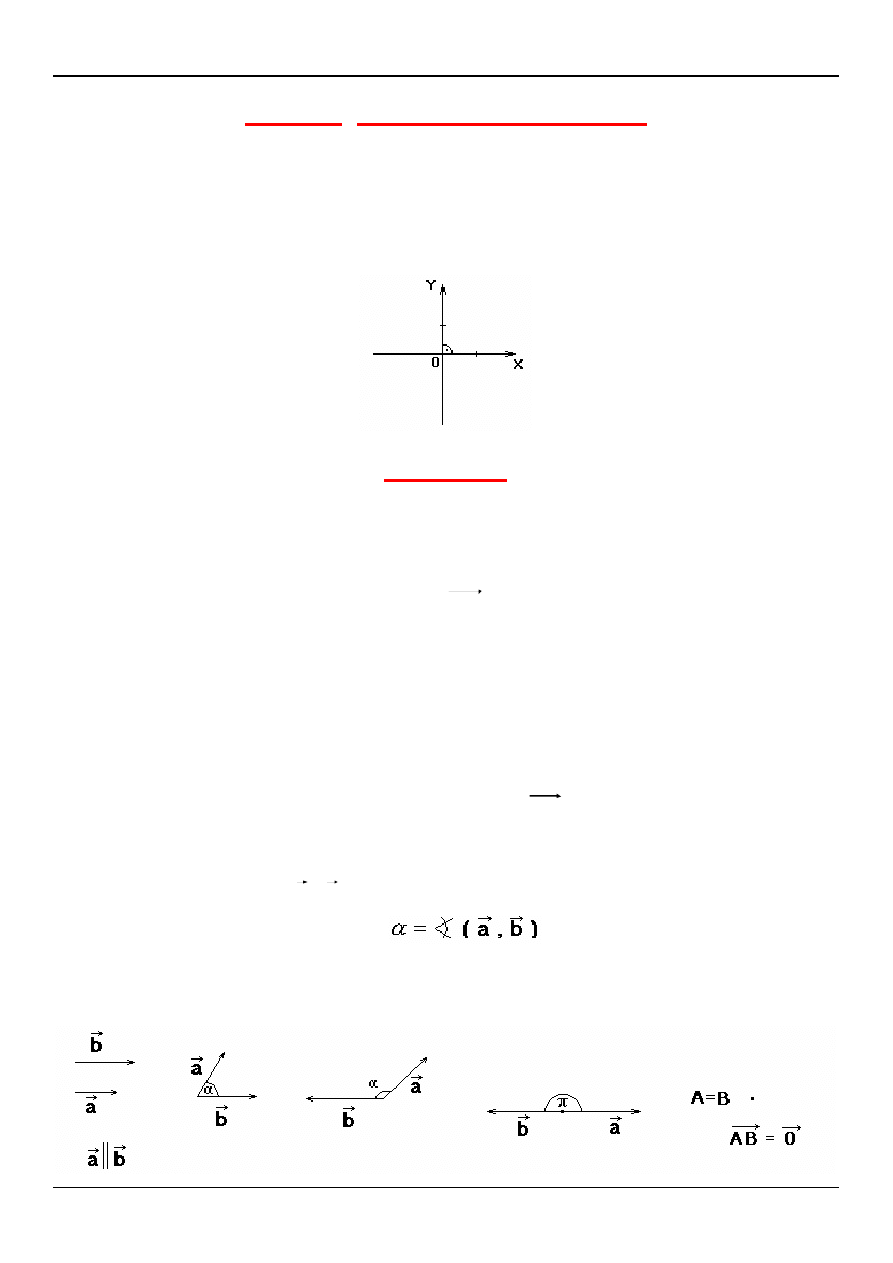
UKŁAD ORTOKARTEZJAŃSKI
Układem ortokartezjańskim na płaszczyźnie nazywamy uporządkowaną parę regularnych
osi liczbowych Ox i Oy wzajemnie prostopadłych mających wspólny początek O i
wspólną jednostkę długości.
Układ taki oznaczamy Oxy
WEKTOR
Parą uporządkowaną punktów (A,B) czyli odcinek skierowany o początku A i końcu B
nazywamy wektorem i oznaczamy symbolem
AB
Wektor charakteryzują trzy parametry:
- kierunek
- zwrot
- długość
Punkt zaczepienia wektora jest dowolny – rozpatrujemy, więc wektory swobodne.
W przypadku gdy A=B wtedy mówimy, że wektor
AB
m
a długość 0 ale kierunek i
zwrot nieokreślony.
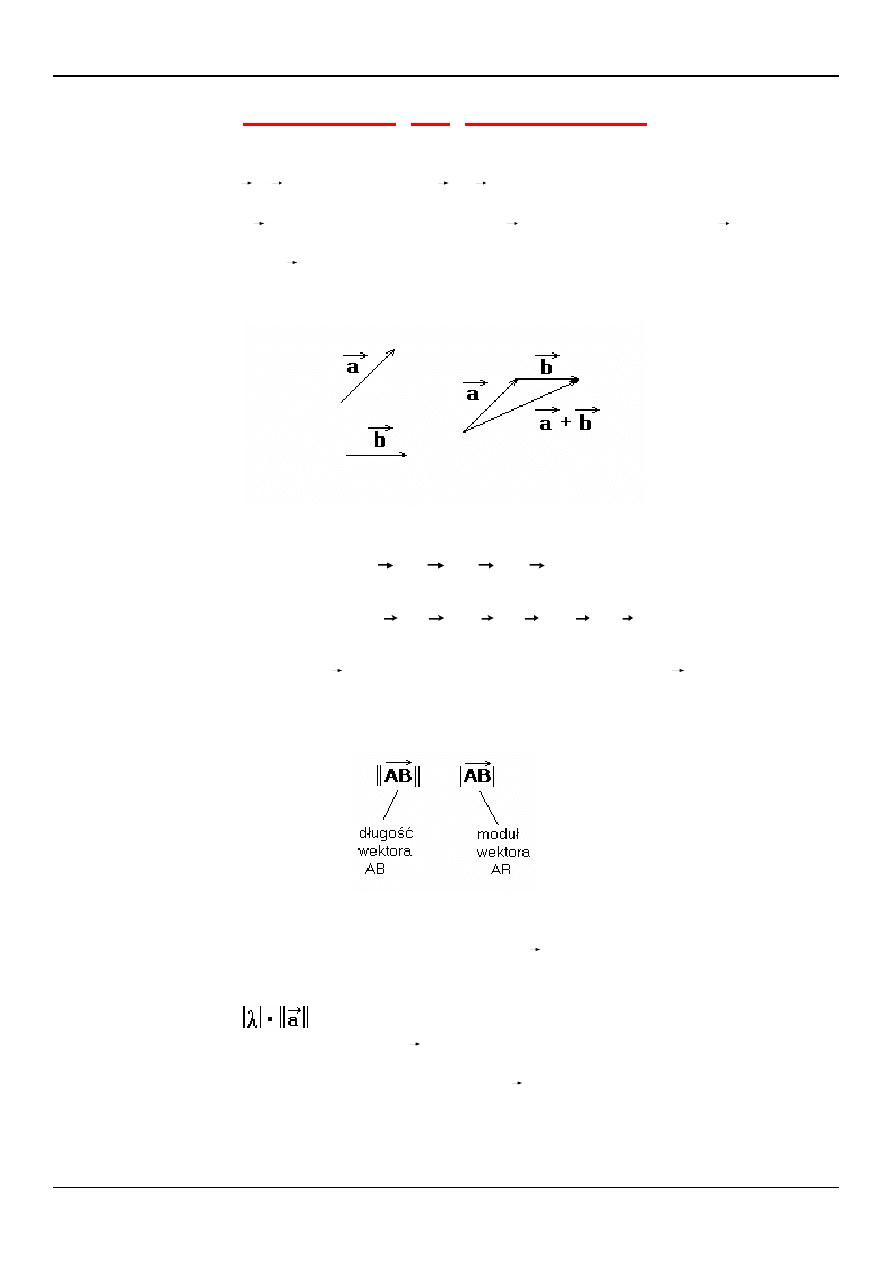
Kąt między wektorami
a
i
b
oznaczamy
Jego miara spełnia nierówność
0 ≤ α ≤ π
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 3 -
DZIAŁANIA NA WEKTORACH
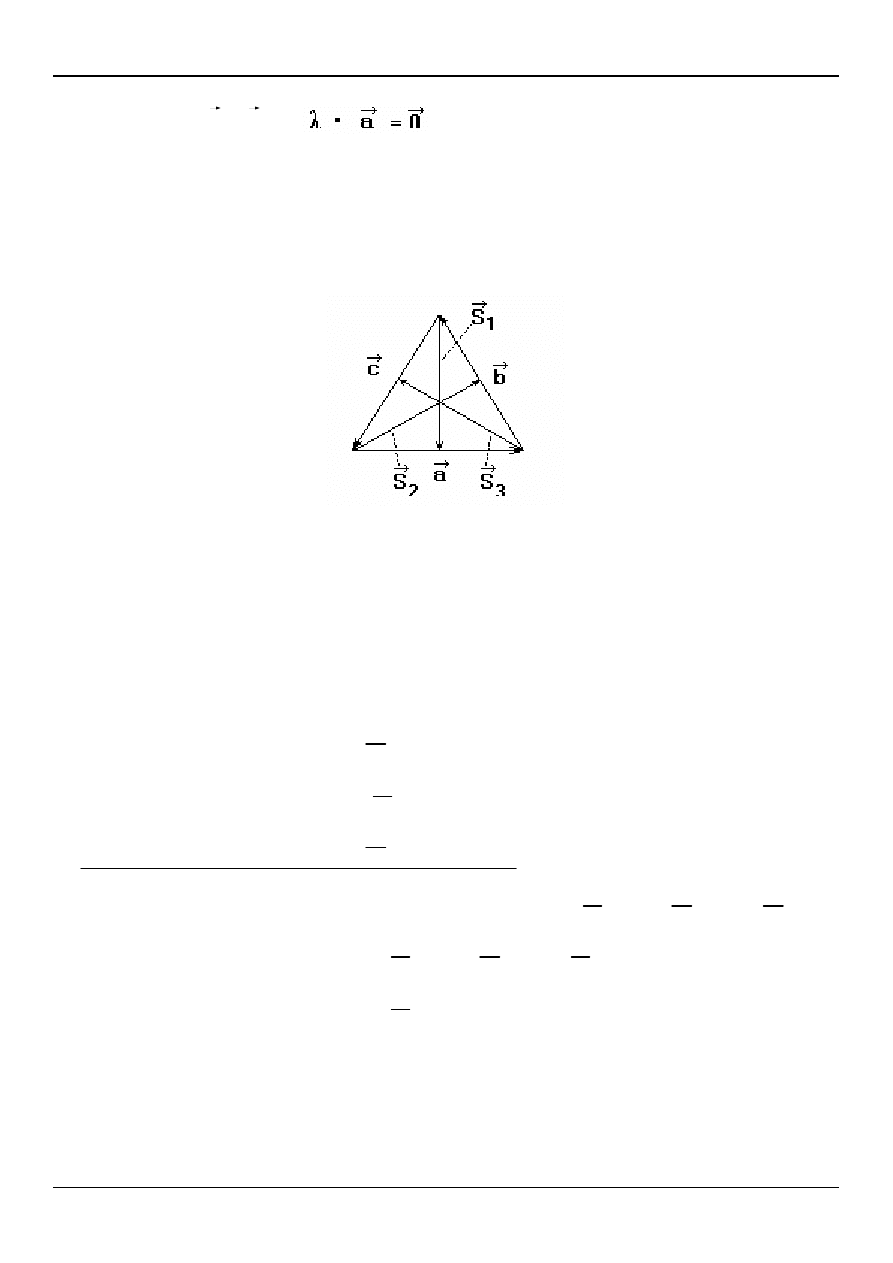
SUMA WEKTORÓW
Sumą wektorów
a
i
b
oznaczoną przez
a
+
b
nazywamy wektor o początku w
początku wektora
a
i o końcu w końcu wektora
b
, gdy początek wktora
b
pokrywa
się z końcem wektora
a
.
Dodawanie wektorów jest:
przemienne
a
b
b
a
+
=
+
łączne
( )
( )
c
b
a
c
b
a
+
+
=
+
+
dla każdego wektora
a
istnieje wektor do niego przeciwny
a
−
.
ILOCZYN WEKTORA I LICZBY
Iloczynem różnej od zera λ i niezerowego wektora
a
nazywamy wektor:
- o długości
- o kierunku takim jak kierunek
a
- kierunek zwrocie takim jak zwrot wektora
a
gdy λ >0 i przeciwnym gdy λ<0
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 4 -
Gdy λ=0 lub
a
≡
0
to
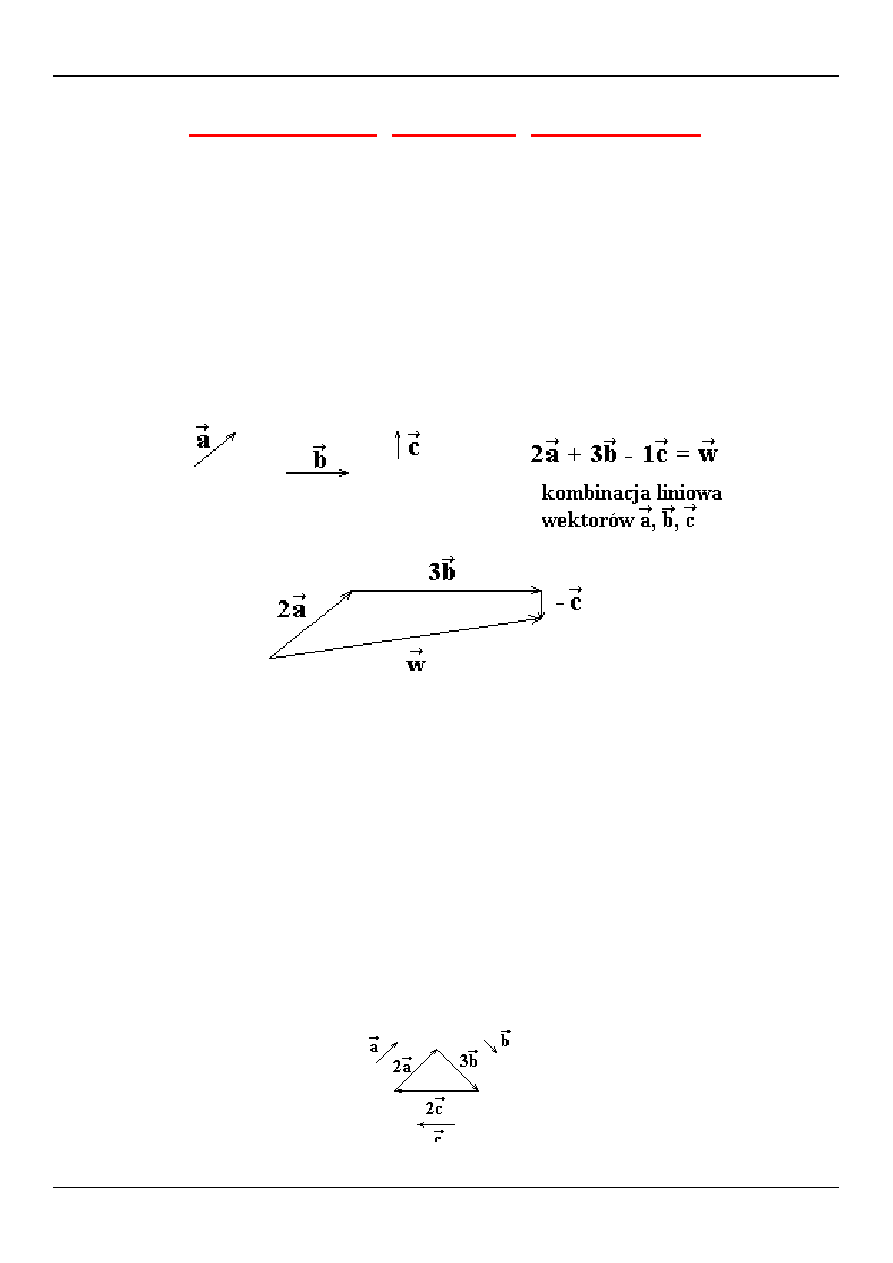
ZADANIE:
Wykazać, że ze środkowych trójkąta można zbudować trójkąt
0
s
s
s
)
c
b
a
(
s
s
s
c
b
a
s
s
s
c
b
a
c
b
a
s
s
s
b
a
s
c
b
s
a
c
s
0
s
s
s
:
T
0
c
c
-
0
c
b
a
:
Z
3
2
1
2
3
3
2
1
2
3
2
3
2
3
3
2
1
2
1
2
1
2
1
3
2
1
2
1
1
2
1
2
2
1
1
3
2
1
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
r
=
+
+
+
+
=
+
+
+
+
=
+
+
+
+
+
+
+
=
+
+
+
+
=
+
=
+
=
=
+
+
=
+
=
+
+
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 5 -
KOMBINACJA LINIOWA WEKTORÓW
Kombinacją liniową wektorów
1,2...n
i
a
i
=
r
nazywamy wektor
n
n
2
2
1
1
a
λ
...
a
λ
a
λ
r
r
r
+
+
+
gdzie
1,2...n
i
λ
i
=
są liczbami rzeczywistymi
Wektory
1,2...n
i
a
i
=
r
nazywamy liniowo zależnymi, jeżeli istnieje ich nie trywialna
kombinacja liniowa równa zeru:
0
a
λ
...
a
λ
a
λ
n
n
2
2
1
1
r
r
r
r
=
+
+
+
tzn. taka w której nie wszystkie współczynniki
λ
1
są zerami:
np.

PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 6 -
b
3
-
a
2
c
2
0
c
2
b
3
a
2
zalezne
liniowo
są
r
r
r
r
43
42
1
r
r
r
−
=
=
+
+
Wektory są liniowo zależne, jeżeli jeden z tych wektorów można przedstawić za
pomocą pozostałych.
Dwa wektory nazywamy kolinearnymi, jeżeli są liniowo zależne.
Zatem dwa wektory są kolinearne, gdy jeden z nich jest wektorem zerowym lub gdy
jeden z nich powstaje z drugiego w wyniku pomnożenia przez liczbę (równoległe).
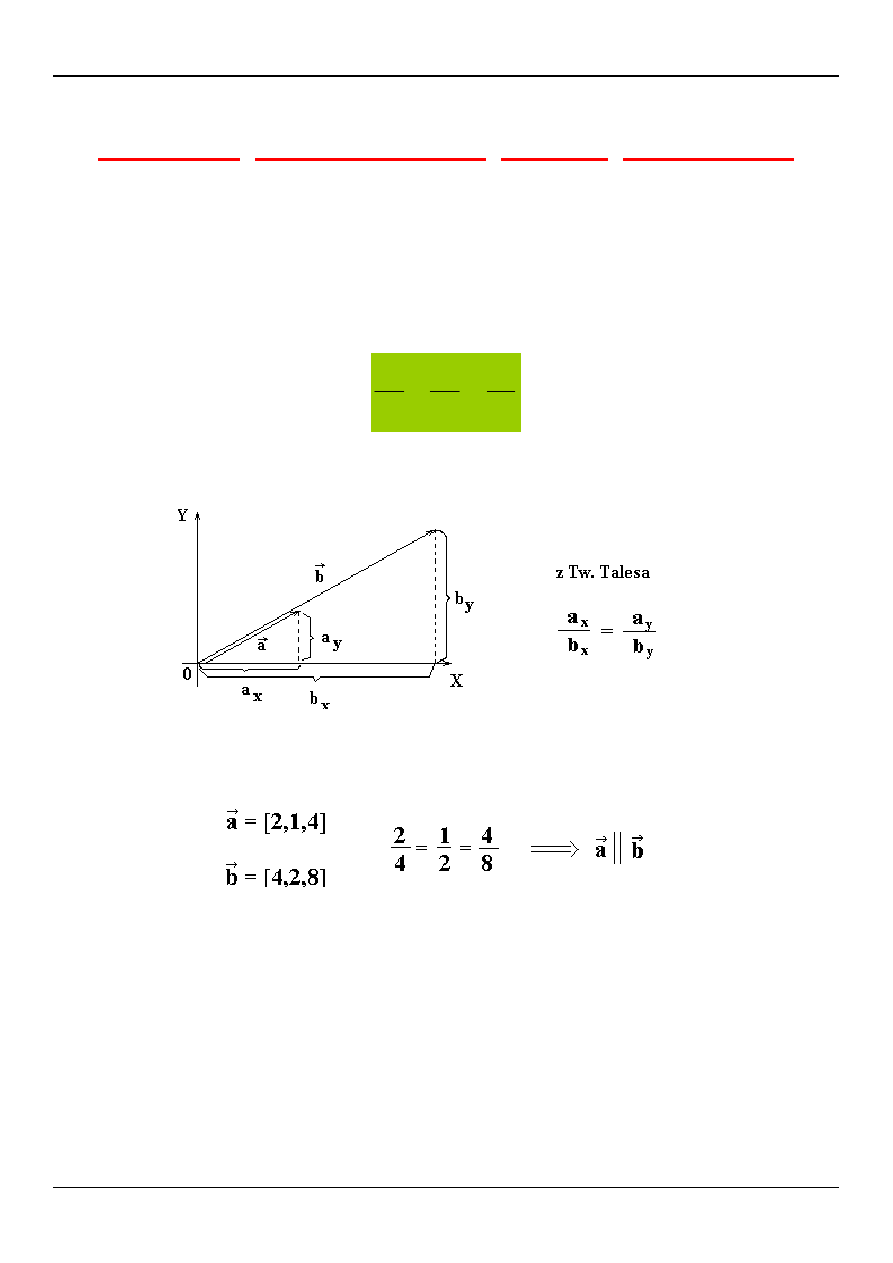
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 7 -
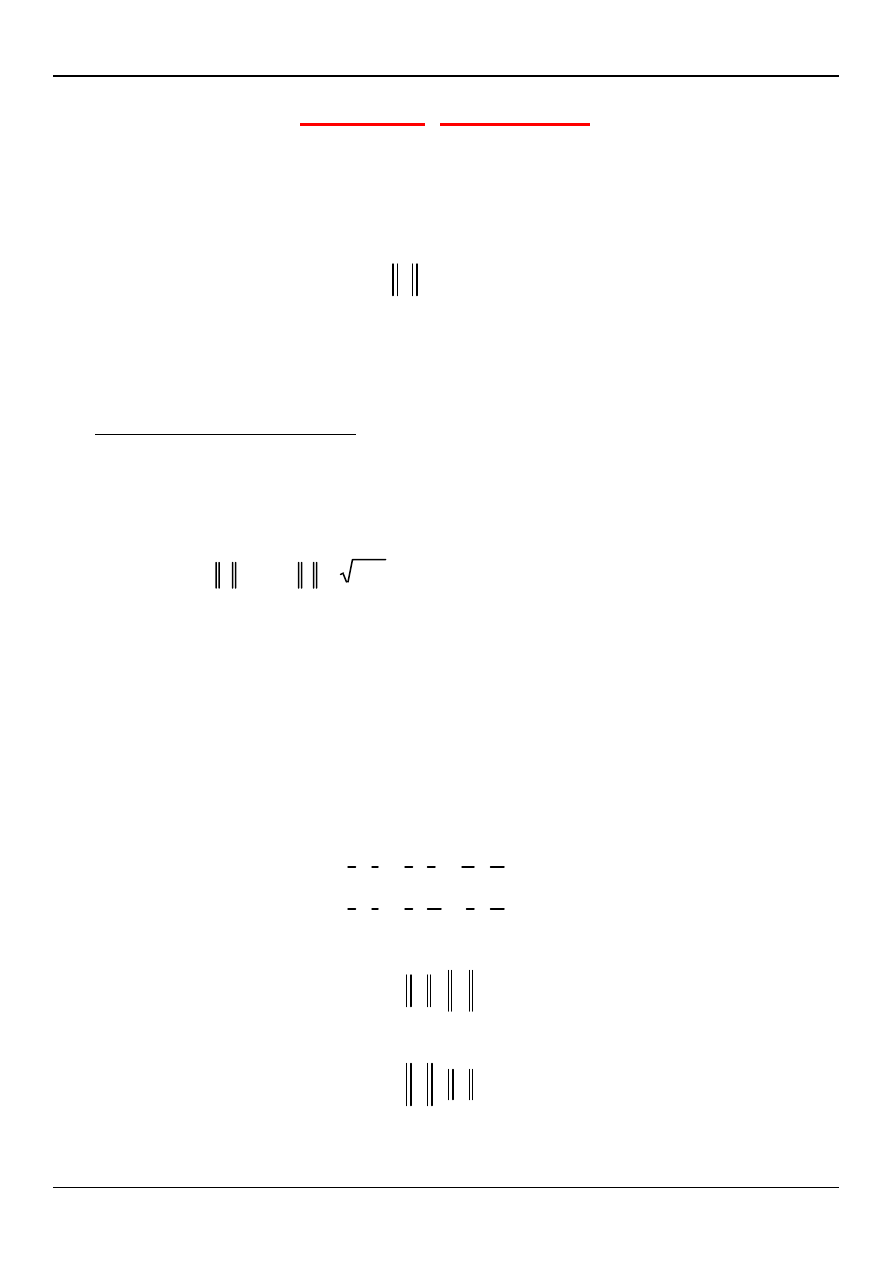
WARUNEK KOLINEARNOŚCI DWÓCH WEKTORÓW
Kolinearność wektorów
]
b
,
b
,
[b
b
]
a
,
a
,
[a
a
z
y
x
z
y
x
=
=
r
r
ma miejsce gdy:
z
z
y
y
x
x
b
a
b
a
b
a
=
=
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 8 -
ILOCZYN SKALARNY
Iloczynem skalarnym dwóch wektorów
b
,
a
r
r
oznaczonym przez
b
a
r
o
r
nazywamy liczbę
równą iloczynowi długości tych wektorów i cosinusa kąta między nimi zawartego.
)
b
,
a
(
cos
b
a
b
a
r
r
r
r
r
o
r
<
⋅
⋅
=
W przypadku gdy
0
b
a
0
b
lub
0
a
=
=
=
r
o
r
r
r
Własności iloczynu skalarnego
1.
a
b
b
a
r
o
r
r
o
r
=
2.
c
a
b
a
)
c
b
(
a
r
o
r
r
o
r
r
r
o
r
+
=
+
3.
λ)
b
(
a
b
)
a
(λ
)
b
a
(
λ
⋅
=
⋅
=
⋅
r
o
r
r
o
r
r
o
r
4.
a
a
a
a
a
a
2
r
r
r
r
r
o
r
⋅
=
=
Wersorem (lub wektorem jednostkowym) nazywamy każdy wektor o długości 1.
W przestrzeni R
3
wersory osi Ox, Oy, Oz oznaczać będziemy odpowiednio i, j, k.
Z def. Iloczynu skalarnego mamy:
0
k
j
k
i
j
i
1
k
k
j
j
i
i
=
⋅
=
⋅
=
⋅
=
⋅
=
⋅
=
⋅
cos(-α
a
b
a
b
||
cosα
b
a
b
a
⋅
⋅
=
⋅
⋅
=
r
r
r
o
r
r
r
r
o
r

PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 9 -
Iloczyn skalarny dwóch wektorów
]
b
,
b
,
[b
b
i
]
a
,
a
,
[a
a
z
y
x
z
y
x
=
=
r
r
jest równy
sumie iloczynów jednoimiennych współrzędnych wektorów.
z
z
y
y
x
x
b
a
b
a
b
a
b
a
+
+
=
r
o
r
Dowód
Wektory można przedstawić w postaci
z
z
y
y
x
x
z
y
x
z
y
x
z
y
x
z
y
x
b
a
b
a
b
a
b
a
)
k
b
j
b
i
(b
)
k
a
j
a
i
(a
b
a
k
b
j
b
i
b
b
oraz
k
a
j
a
i
a
a
+
+
=
+
+
⋅
+
+
=
+
+
=
+
+
=
r
o
r
r
o
r
r
r
Warunek prostopadłości wektorów
Jeżeli
0
b
i
0
a
≠
≠
r
r
oraz
]
b
,
b
,
[b
b
,
]
a
,
a
,
[a
a
z
y
x
z
y
x
=
=
r
r
to
0
b
a
b
a
b
a
tzn.
0
b
a
b
a
z
z
y
y
x
x
=
+
+
=
⋅
⇔
⊥
r
r
r
r
Mówimy, że przestrzeń i wprowadzony w niej układ ortokartezjański Oxyz mają
orientację dodatnią (lub są zorientowane w prawo) jeżeli układ Oxyz ma dla patrzącego
z półprzestrzeni zawierającej dodatnią półoś Oz orientację dodatnią.
W przeciwnym razie mówimy, że przestrzeń i układ mają orientację ujemną
(lub są zorientowane w lewo).
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 10 -
ILOCZYN WEKTOROWY
Iloczynem wektorowym
b
a
r
r ×
uporządkowanej pary dwóch wektorów niekolinearnych
b
i
a
r
r
w przestrzeni zorientowanej nazywamy wektor:
- którego długość
)
b
,
a
(
sin
b
a
b
a
r
r
r
r
r
r
<
⋅
⋅
=
×
-
który jest prostopadły do wektorów
b
i
a
r
r
tzn.
b
)
b
a
(
,
a
)
b
a
(
r
r
r
r
r
r
⊥
×
⊥
×
- zwrot wektora
b
a
r
r ×
jest taki, że uporządkowana trójka
}
b
a
,
b
,
a
{
r
r
r
r
×
ma orientacją
zgodną z przyjętą orientacją przestrzeni.
- jeżeli wektory
b
i
a
r
r
są kolinearne to
0
b
a
=
×
r
r
Własności iloczynu wektorowego
1.
a
b
b
a
r
r
r
r
×
−
=
×
2.
c
a
b
a
)
c
b
(
a
r
r
r
r
r
r
r
×
+
×
=
+
×
3.
a
)
b
(λ
b
)
a
(λ
)
b
a
(
λ
r
r
r
r
r
r
×
⋅
=
×
⋅
=
×
⋅
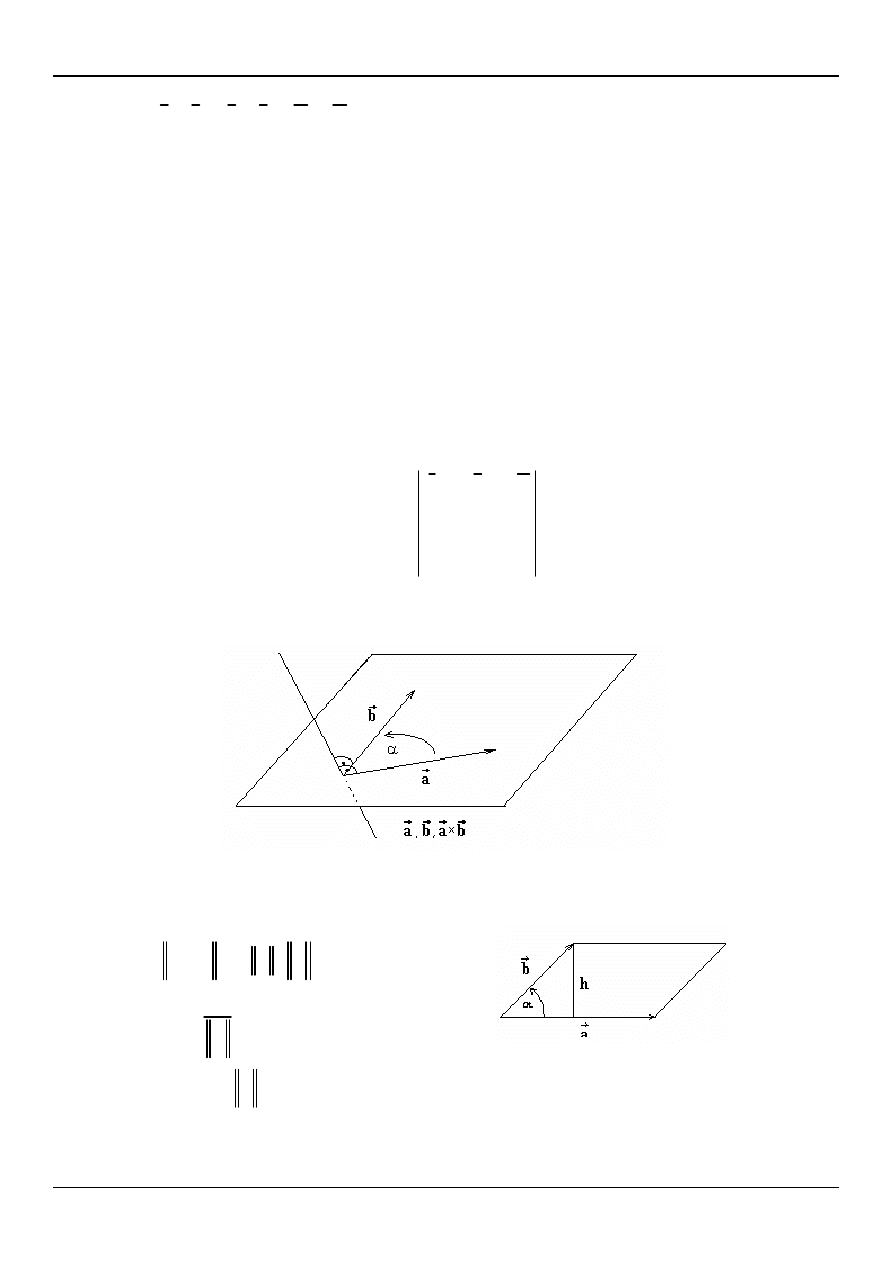
4. długość wektora
b
a
tj.
b
a
r
r
r
r
×
×
jest równa liczbowo polu równoległoboku
rozpiętego na wektorach
b
i
a
r
r
.
5.
j
i
k
i
k
j
k
j
i
=
×
=
×
=
×
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 11 -
6.
0
k
k
j
j
i
i
=
×
=
×
=
×
Jeżeli
]
b
,
b
,
[b
b
i
]
a
,
a
,
[a
a
z
y
x
z
y
x
=
=
r
r
wtedy
]
b
a
b
a
,
b
a
b
a
,
b
a
b
[a
b
a
x
y
y
x
z
x
x
z
y
z
z
y
−
−
−
=
×
r
r
Posługując się symbolem wyznacznika możemy zapisać
z
y
x
z
y
x
b
b
b
a
a
a
k
j
i
b
a
=
×
r
r
sinα
b
h
sinα
b
h
S
sinα
b
a
b
a
⋅
=
=
=
⋅
⋅
=
×
r
r
r
r
r
r
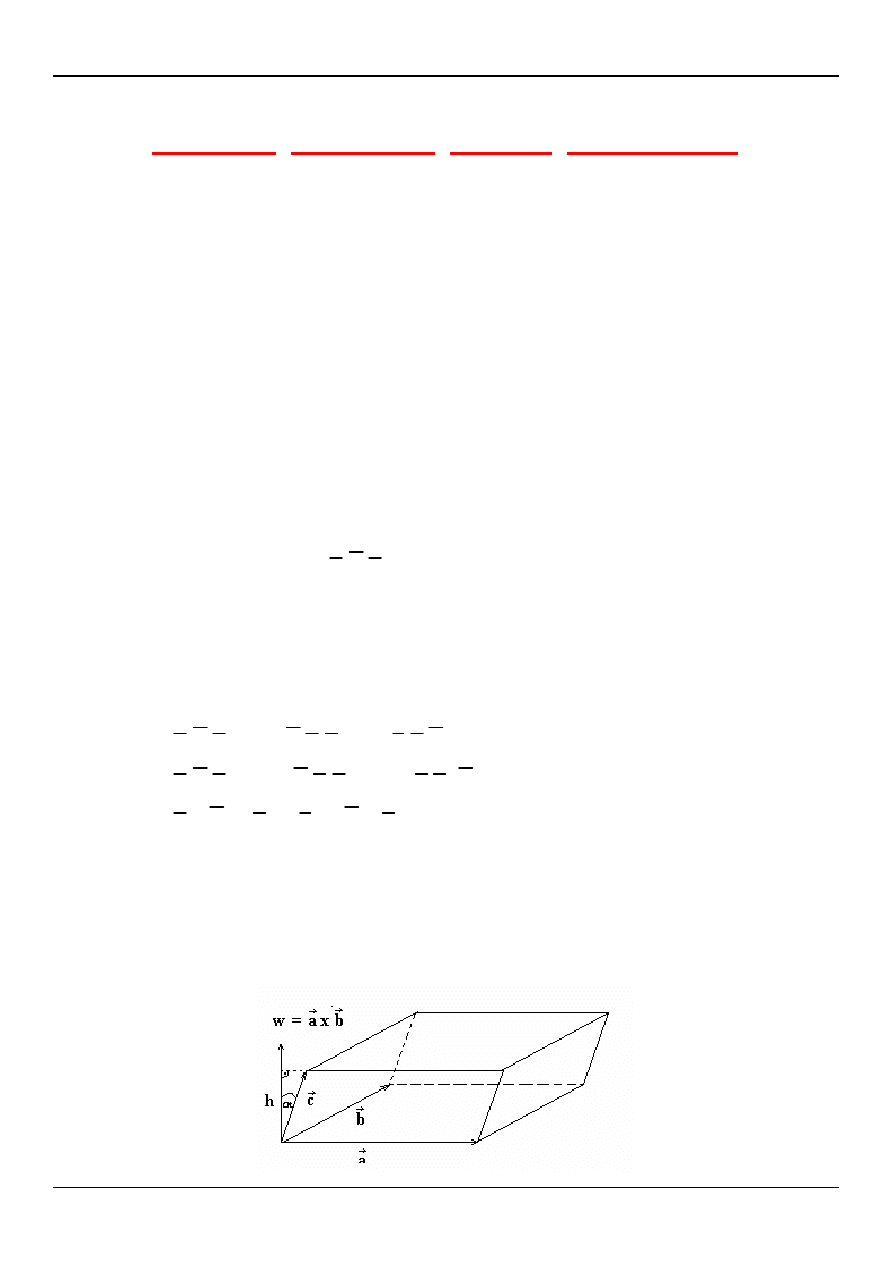
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 12 -
ILOCZYN MIESZANY TRÓJKI WEKTORÓW
Iloczynem mieszanym uporządkowanej trójki wektorów
]
c
,
b
,
a
[
r
r
r
w przestrzeni
zorientowanej nazywamy liczbę
)
c
,
b
,
a
(
r
r
r
określoną
c
)
b
a
(
)
c
b
a
(
r
o
r
r
r
r
r
×
=
Tw.
Jeżeli
]
c
,
c
,
[c
c
,
]
b
,
b
,
[b
b
,
]
a
,
a
,
[a
a
z
y
x
z
y
x
z
y
x
=
=
=
r
r
r
=
z
y
x
z
y
x
z
y
x
c
c
c
b
b
b
a
a
a
)
c
b
a
(
Stąd wynikają własności iloczynu wektorowego mieszanego.
1.
)
b
a
c
(
)
a
c
b
(
)
c
b
a
(
=
=
2.
)
b
c
a
(
)
c
a
b
(
-
)
c
b
a
(
−
=
=
3.
)
c
b
(
a
c
)
b
a
(
×
=
×
o
o
Wartość bezwzględna iloczynu mieszanego trzech wektorów jest równa liczbowo
objętości równoległościanu rozpiętego na tych wektorach.
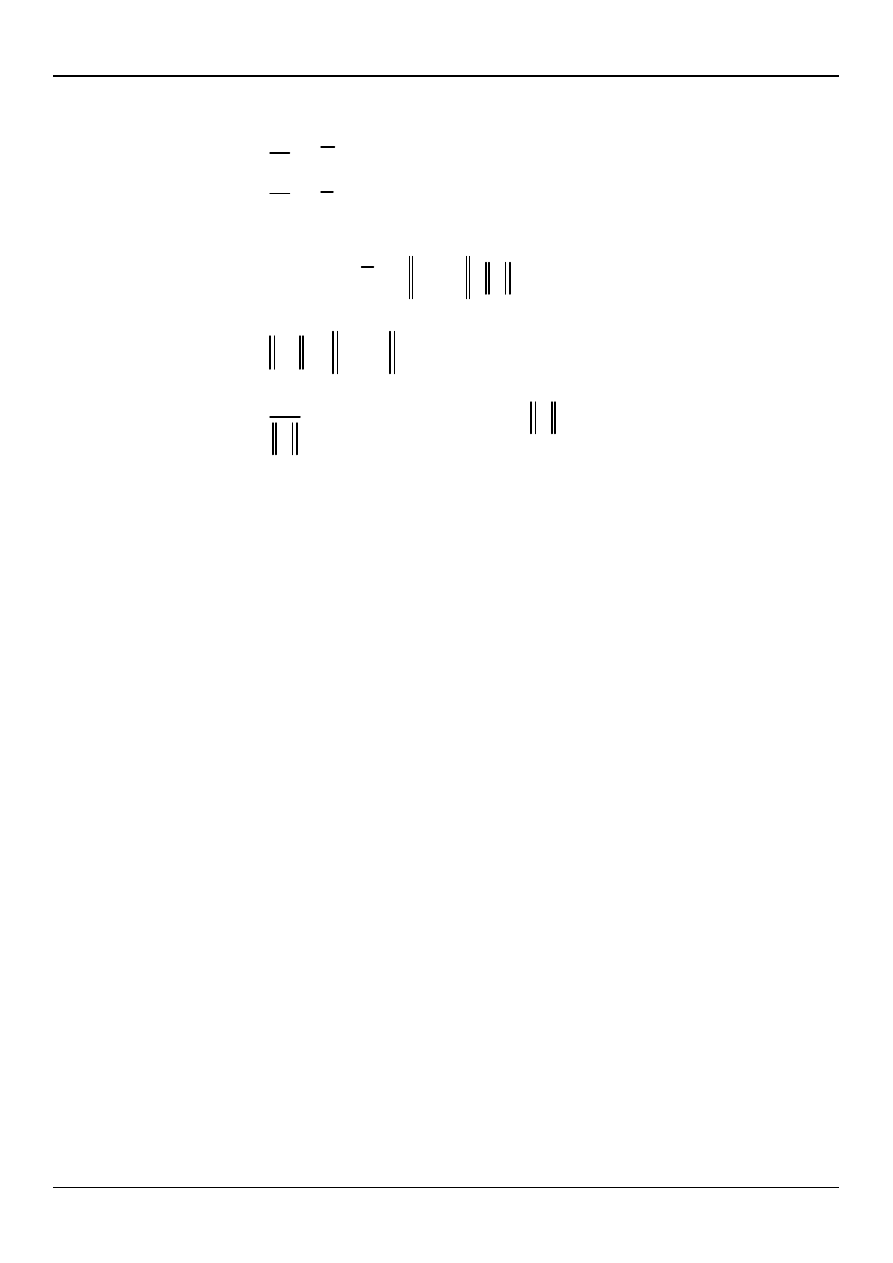
PADER collection
MATEMATYKA – Semestr II – Wektory
dr Stanisław Kiełtyka
- 13 -
cosα
c
h
cosα
c
h
S
b
a
w
cosα
c
b
a
c
)
b
a
(
a
w
b
w
h
S
w
⋅
=
⇒
=
=
×
=
⋅
⋅
×
=
×
⊥
⊥
r
r
r
r
r
4
8
47
6
r
8
7
6 r
r
43
42
1
o
r
r
r
Wyszukiwarka
Podobne podstrony:
matematyka 01 Wektory
zestaw 01 wektory 26 02 2012 id Nieznany
01 Wektory
01 Wektoryid 2971 Nieznany (2)
R A Salvatore Nowa era Jedi 01 Wektor Pierwszy
01 Wektory
A01 Wektory (01 12)
A01 Wektory (01 12)
A01 Wektory (01 12)
TD 01
Ubytki,niepr,poch poł(16 01 2008)
więcej podobnych podstron