1. Przekształcenia izometryczne
2. Operacje symetrii możliwe w sieci
3. Iloczyn przekształceń
4. Symbole elementów symetrii

Wykład 3

Przekształcenia izometryczne w sieci

krystalicznej

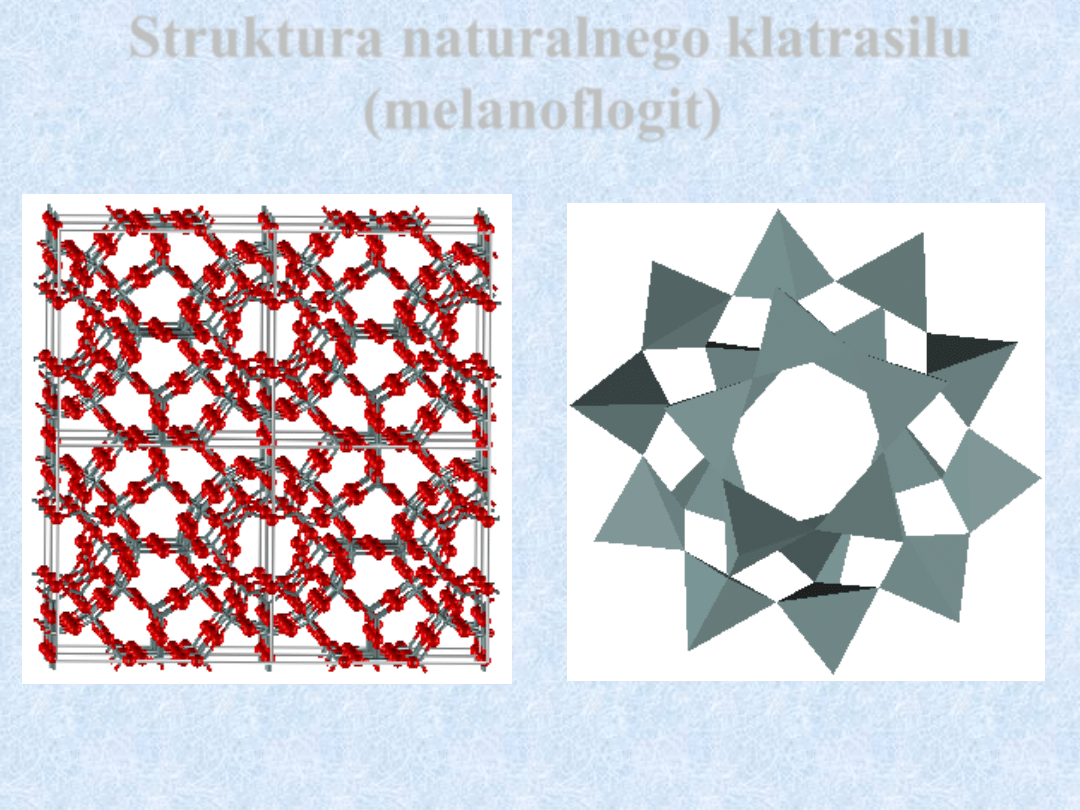
Struktura naturalnego klatrasilu

(melanoflogit)

Pseudokryształy - Daniel Shechtman Nagroda

Nobla 2011

srebro/aluminium quasicrystal

Icosahedron

Przekształcenia izometryczne

Przekszta łcenie izometryczne (z grec. izo- ten sam, metri –
odległość;) to przekształcenie, które w wyniku jego
zastosowania nie powoduje zmian odległości między dwoma
dowolnymi, przekształcanymi punktami:







r



=



T(r)



gdzie:





r



- odległość między dowolnymi dwoma punktami,





T(r)



- odległość między tymi samymi punktami po przekształceniu T

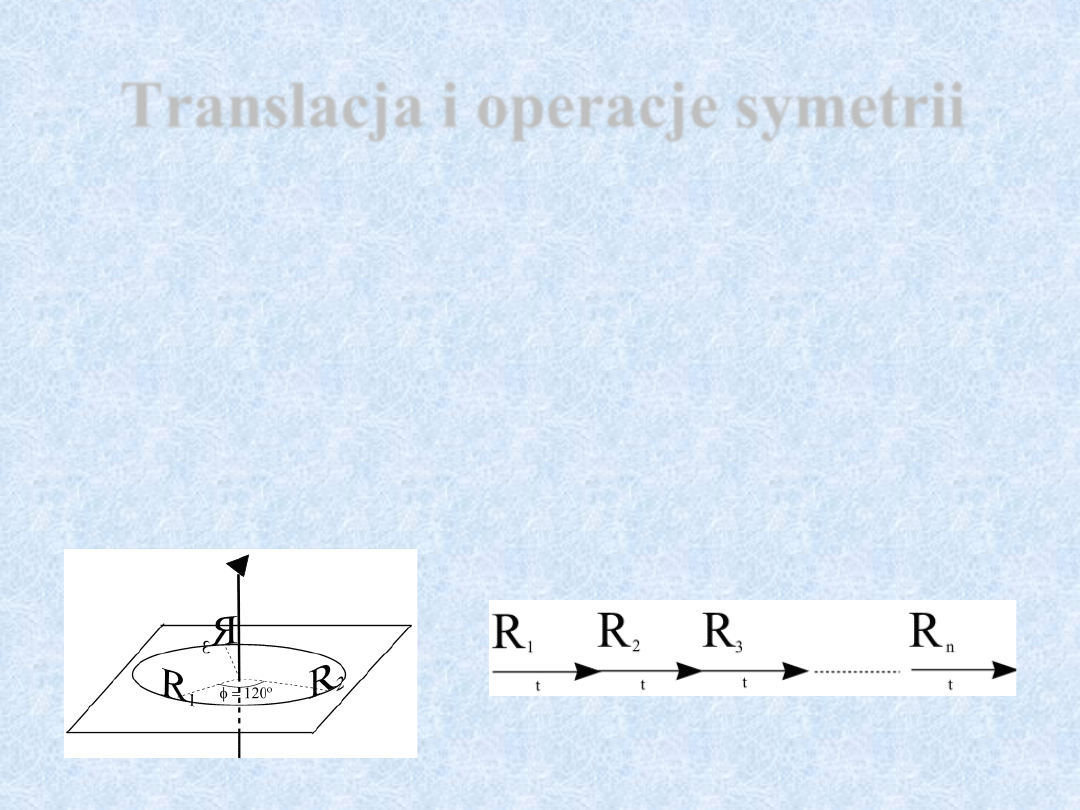
Translacja i operacje symetrii

Zamknięte

1. oś obrotu
2. centrum inwersji (symetrii)
3. płaszczyzna symetrii
4. oś inwersyjna (obrót i

odbicie w centrum)

Otwarte

1. oś śrubowa (obrót +

translacja)

2. płaszczyzna poślizgowa

(odbicie + translacja)

Obrót wokół osi

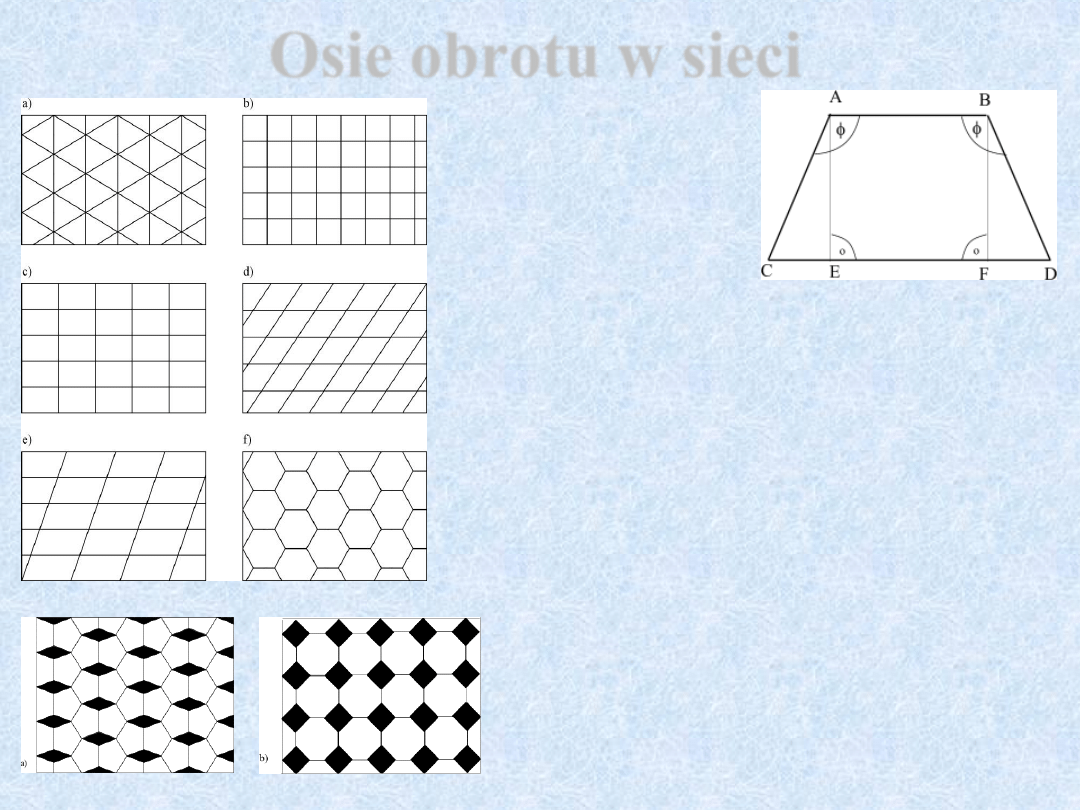
Osie obrotu w sieci

CD = k·AB

gdzie:

k -

liczba całkowita

,

CD = CE + EF + FD

natomiast:

EF = AB

z definicji funkcji cosinus oraz ujemnej
wartości tej funkcji w przedziale kątowym
180-270o:

CE = FD = -

AB·cos



z powyższych równań można
wyprowadzić zależność:

k·AB = AB + 2·(-AB·cos



)

co łatwo można przekształcić w:

k·AB = AB(1-2cos



)

skąd:

cos



= (1-k)/2

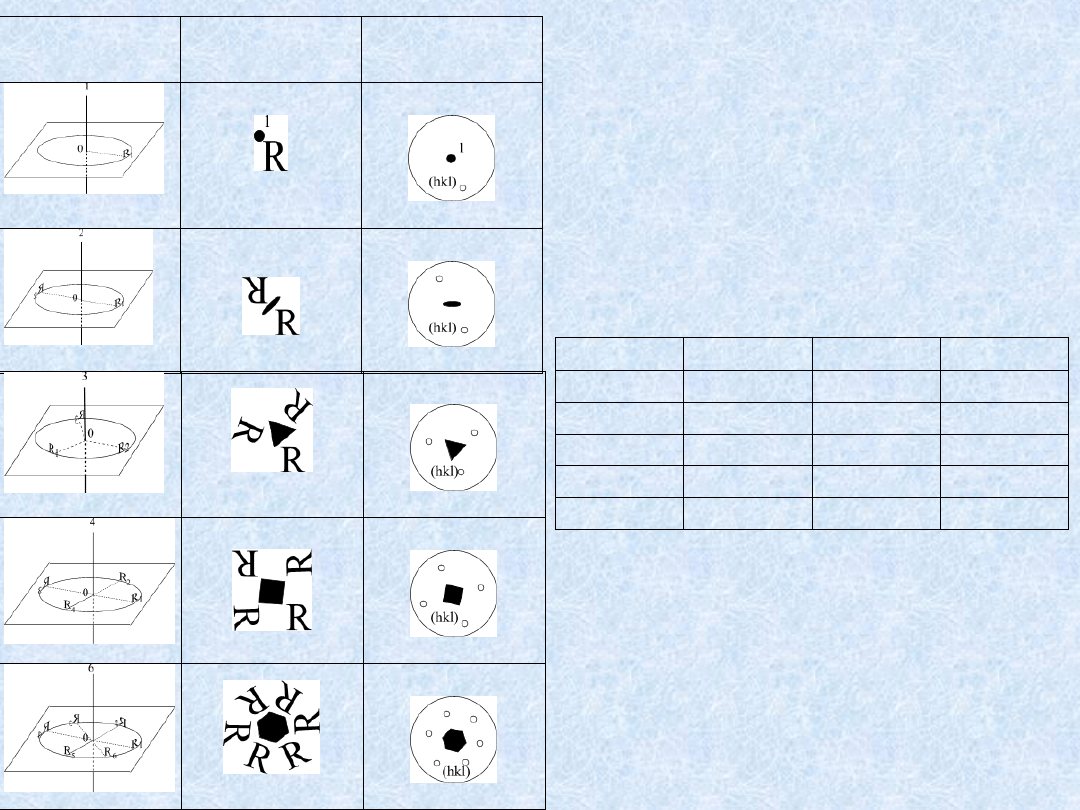
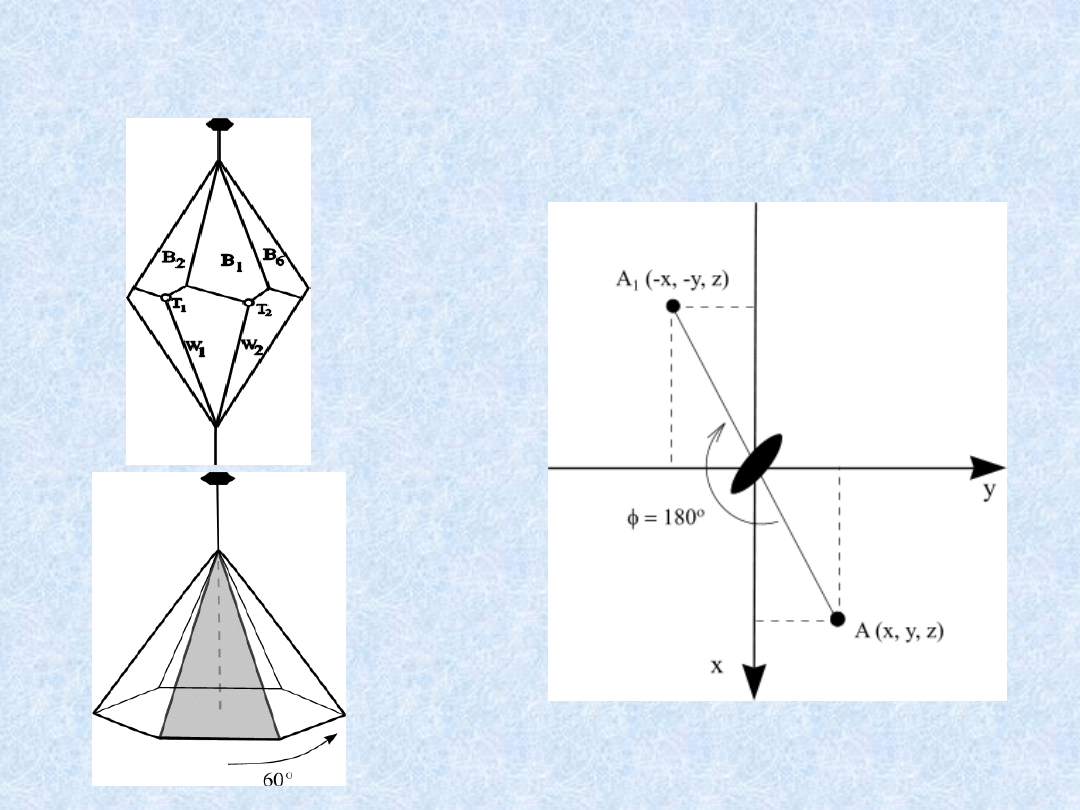
Właściwa oś symetrii X

Działanie

właściwej

osi

symetrii X na element „R”

Projekcja

stereograficzna

bieguna

ściany

(hkl)

przekształcanego względem
właściwej osi symetrii X



= 360

o



= 180

o



= 120

o



= 90

o



= 60

o

k

cos





krotność osi

3

-1

180

o

2

2

-½

120

o

3

1

0

90

o

4

0

½

60

o

6

-1

1

360

0

1

Krotność osi

dozwolona w sieci

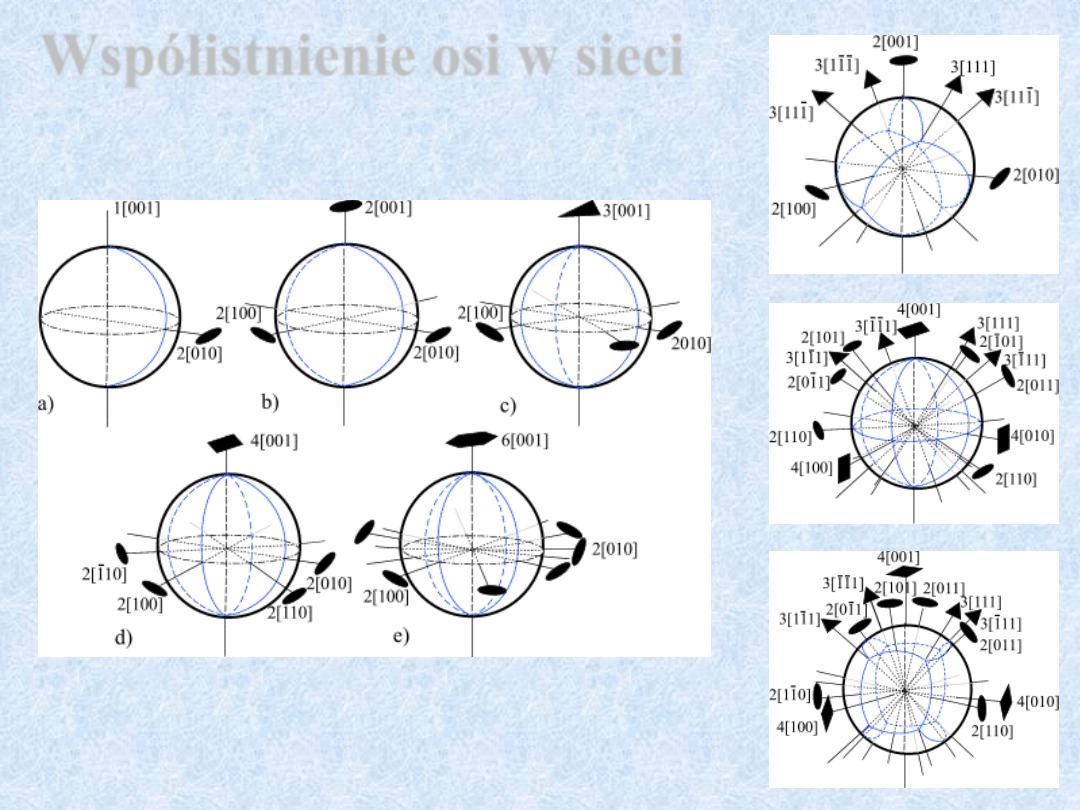
Współistnienie osi w sieci

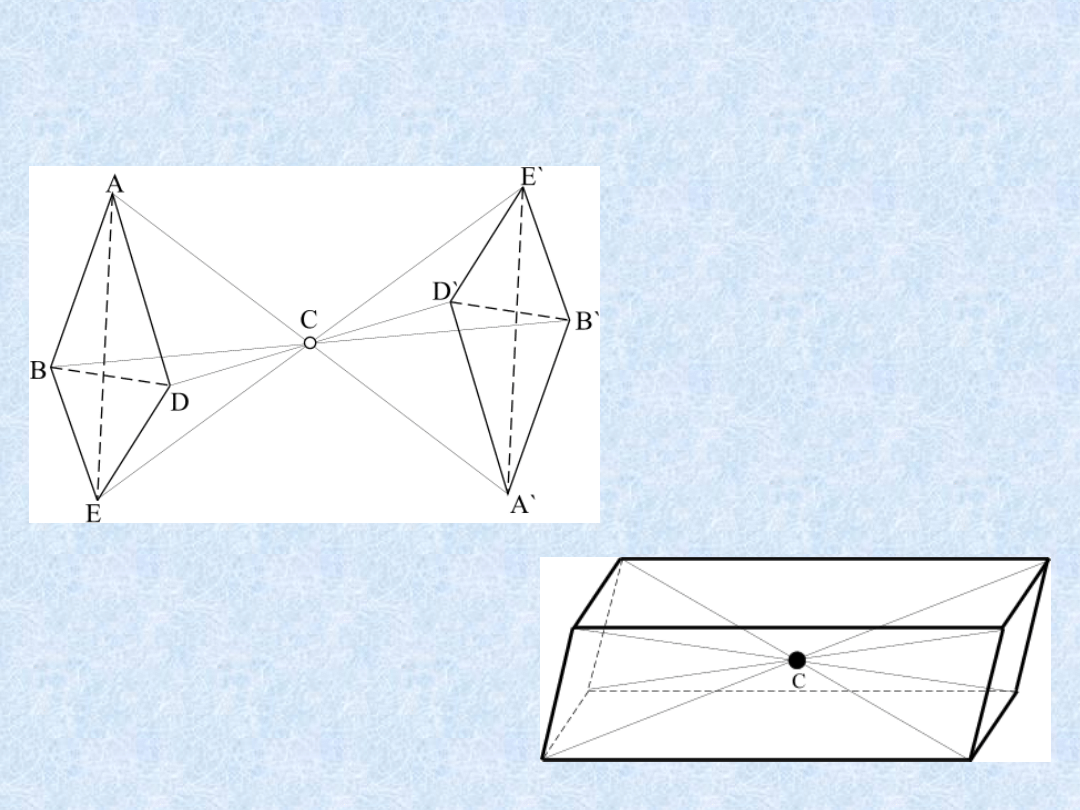
Centrum inwersji (symetrii)

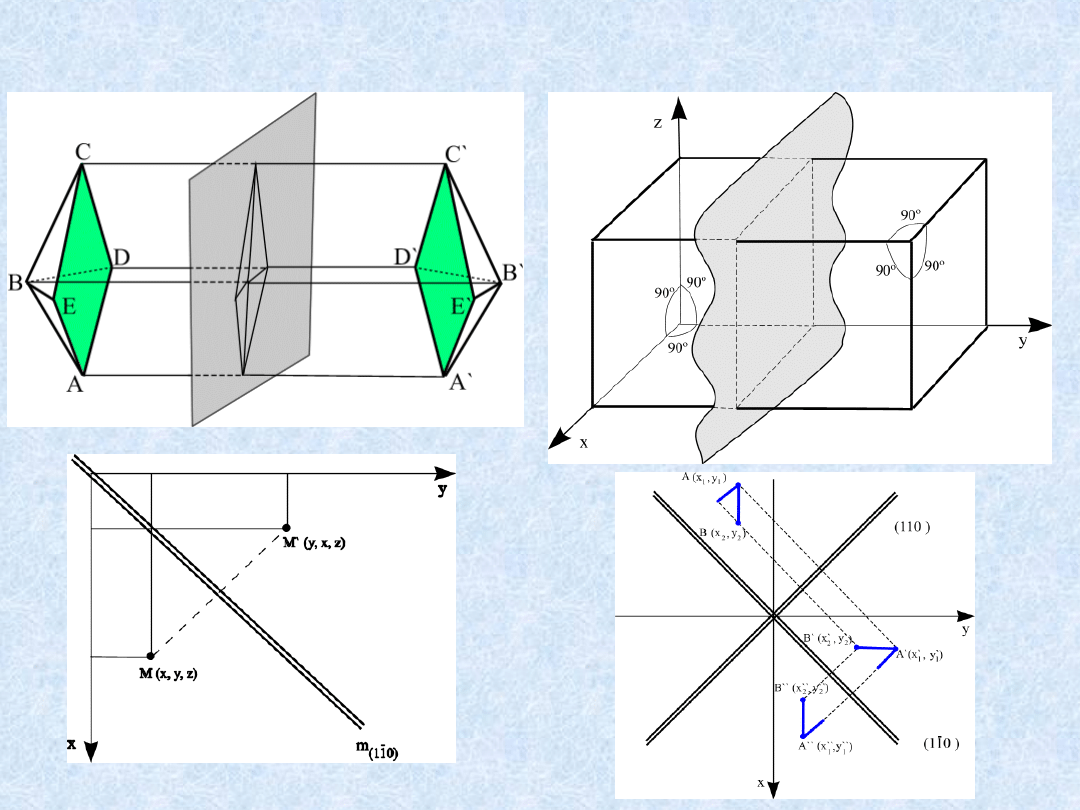
Płaszczyzna symetrii

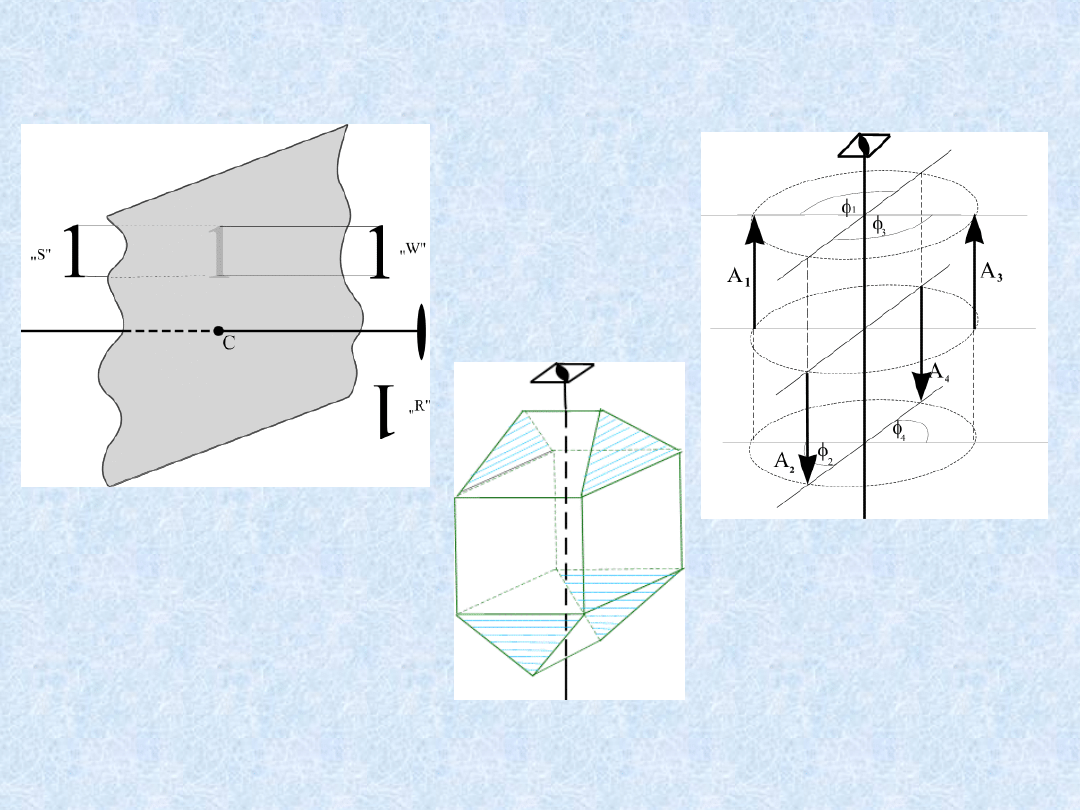
Iloczyn operacji symetrii

iloczyn dwóch operacji symetrii jest również operacją symetrii

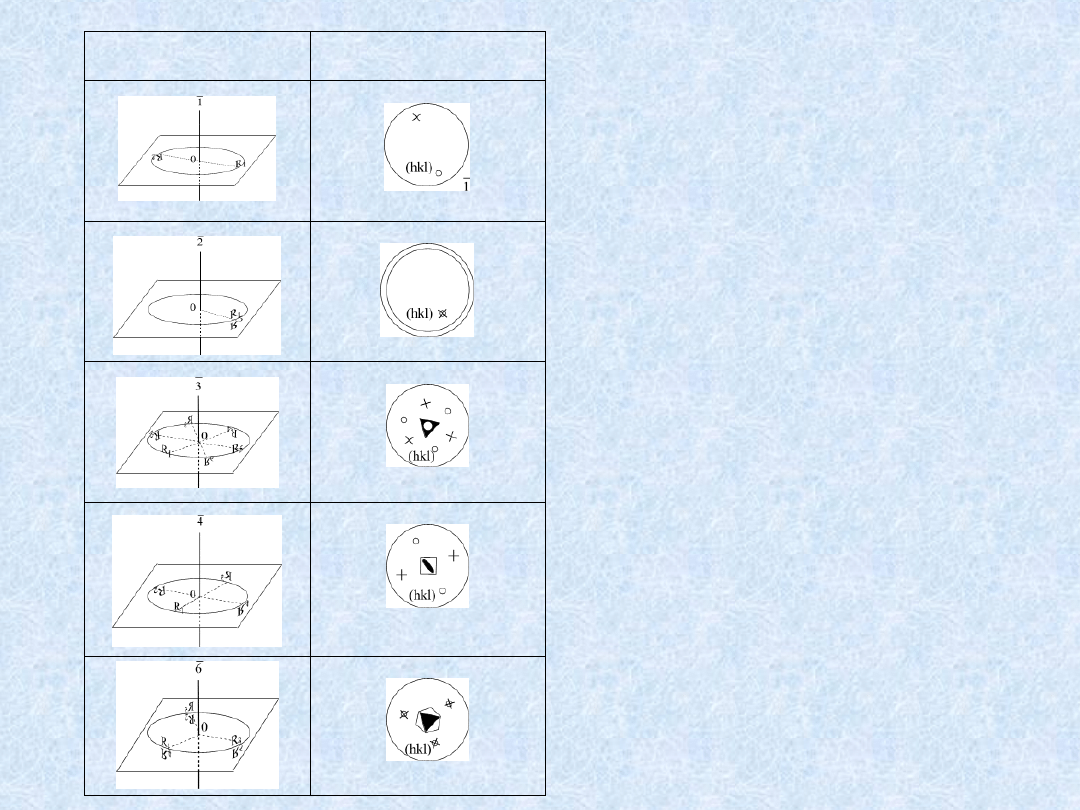
Działanie inwersyjnej osi symetrii



X

na element „R”

Projekcja

stereograficzna

bieguna

ściany

(hkl)

przekształcanego

względem inwersyjnej osi symetrii



X

Inwersyjne

osie symetrii

Zamknięte operacje symetrii

Operacje symetrii

Elementy symetrii

PROSTE

obrót

obrót o 360

o

obrót o 180

o

obrót o 120

o

obrót o 90

o

obrót o 60

o

oś jednokrotna

oś dwukrotna

oś trójkrotna

oś czterokrotna

oś sześciokrotna

odbicie względem płaszczyzny

płaszczyzna symetrii

odbicie

względem

centrum

inwersji (inwersja)

centrum inwersji

ZŁOŻONE

obrót z
inwersją

obrót o 360

o

i inwersja

obrót o 180

o

i inwersja

obrót o 120

o

i inwersja

obrót o 90

o

i inwersja

obrót o 60

o

i inwersja

oś jednokrotna inwersyjna



centrum

inwersji

oś dwukrotna inwersyjna



płaszczyzna

symetrii

oś trójkrotna inwersyjna

oś czterokrotna inwersyjna

oś sześciokrotna inwersyjna

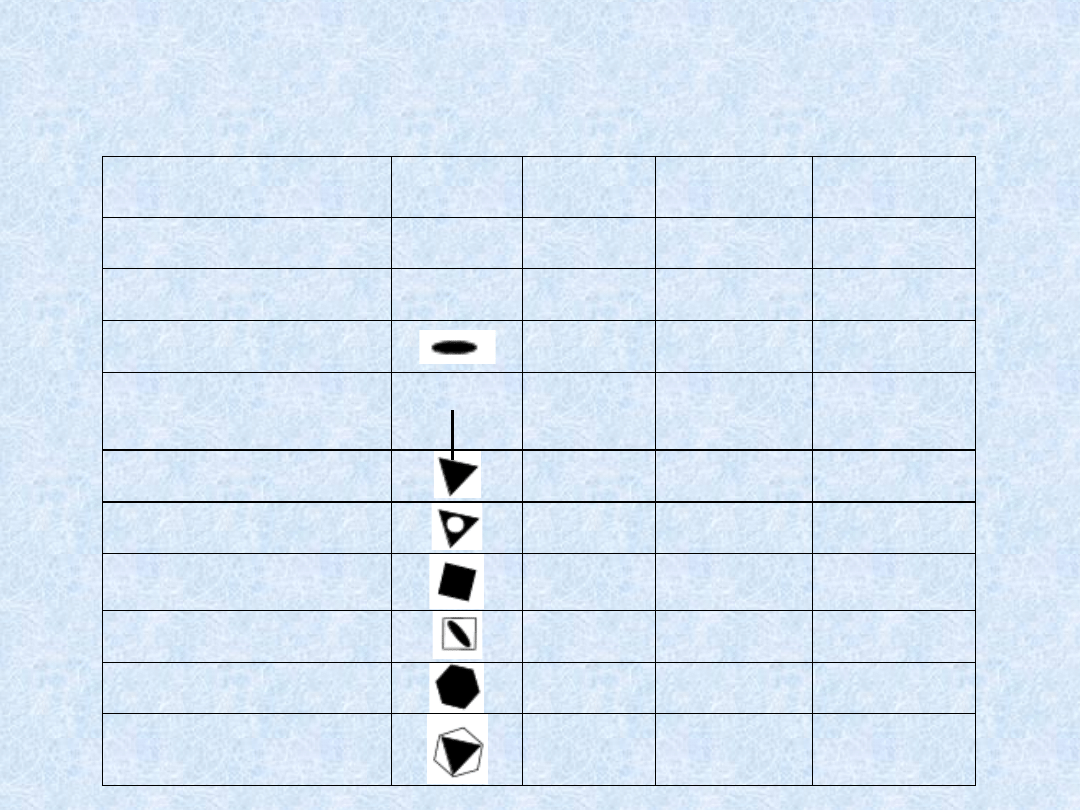
Symbole elementów symetrii

występujących w sieci przestrzennej

Element symetrii

Symbol
graficzny:

Kreutza –
Zaremby

Schoenfliesa

Hermanna -
Mauguina

Oś jednokrotna- identyczność
(obrót o 360

o

)

L

1

= E

C

1

1

Oś jednokrotna inwersyjna
(obrót o 360

o

i inwersja)

◦

C

i



1

Oś dwukrotna
(obrót o 180

o

)

L

2

z

C

2

2

Oś dwukrotna inwersyjna –
płaszczyzna zwierciadlana
(obrót o 180

o

i inwersja)

P

y

C

s

m

Oś trójkrotna
(obrót o 120

o

)

L

3

z

,L

3

111

C

3

3

Oś trójkrotna inwersyjna
(obrót o 120

o

i inwersja)

A

3

S

3



3

Oś czterokrotna
(obrót o 90

o

)

L

4

z

C

4

4

Oś czterokrotna inwersyjna
(obrót o 90

o

i inwersja)

A

4

z

S

4



4

Oś sześciokrotna
(obrót o 60

o

)

L

6

z

C

6

6

Oś sześciokrotna inwersyjna
(obrót o 60

o

i inwersja)

A

6

z

S

6



6