
T. Pankowski, Model relacyjny
1
Tadeusz Pankowski
www.put.poznan.pl/~tadeusz.pankowski
Relacyjne bazy
Relacyjne bazy
danych
danych
T. Pankowski, Model relacyjny
2
T. Pankowski, Model relacyjny
3
Model danych
Model danych
¾ Model danych:
•
Aspekt strukturalny
: Zbiór struktur danych, zbiór operacji na
tych strukturach, zbiór zależności między danymi.
•
Aspekt semantyczny
: Ustalenie znaczeń – znaczenie
(semantyka) struktur danych względem wiedzy o świecie
rzeczywistym, określenie semantyki (wartości) operacji.
•
Aspekt pragmatyczny
: Określenie zasad korzystania z
modelu danych w systemie bazy danych dla rozwiązywania
konkretnych problemów (reprezentacja stanu systemu
rzeczywistego, formułowanie zapytań, wykonywanie
transakcji, ...).
T. Pankowski, Model relacyjny
4
Baza danych
Baza danych
Baza danych:
• jest logicznie spójnym zbiorem danych posiadających określoną strukturę,
na których można wykonywać określone operacje (
aspekt składniowy i
operacyjny
);
• reprezentuje pewien fragment świata rzeczywistego zwanego dziedziną
przedmiotową (
application domain
); zmiany w dz.p. odzwierciedlane są w
bazie danych (
aspekt semantyczny
);
• jest projektowana, tworzona i utrzymywana z punktu widzenia
przydatności dla określonych zastosowań, którymi zainteresowana jest
określona grupa użytkowników (
aspekt pragmatyczny
).
Z bazą danych związane są:
• źródło, z którego wyprowadzane są dane (dz.p.);
• określony poziom interakcji ze zdarzeniami zachodzącymi w dz.p.;
• grupa użytkowników czynnie zainteresowana zawartością bazy danych.
T. Pankowski, Model relacyjny
5
Relacyjny model danych
Relacyjny model danych
¾ E.F. Codd, "A relational model of data for large shared
data banks", Communications of ACM 13 (3), 1970, ss.
377-387.
¾ Model danych (podstawa teoretyczna):
• struktury: dane proste (atomowe), krotki, tabele
(relacje);
• operacje: operacje algebry relacji, rachunki relacji,
operacje aktualizacji;
• zależności: zależności funkcyjne (klucze główne),
zależności referencyjne (klucze obce), ograniczenia na
wartości, ...
T. Pankowski, Model relacyjny
6
Relacyjne (SQL
Relacyjne (SQL
-
-
owe) bazy danych
owe) bazy danych
¾ Relacyjne bazy danych = SQL-owe bazy danych
• wykraczają istotnie poza teoretyczny model relacyjny (włączają
koncepcje obiektowości, XML, programowanie),
¾ SQL-owe bazy danych
• standard SQL-92
• standard SQL:1999, SQL:2003
¾ Najważniejsze relacyjne SZBD:
• Oracle 9i, 10g
• MS SQL Server 2000, 2005, 2008
• DB2, Sybase, Interbase, ...
¾ Inne systemy relacyjne
• dBASE, Clipper, Xbase (stare systemy powszechne w Polsce)
• Access (Microsoft)
• MySQL, PostgreSQL (oprogramowanie wolne).
7
Relacyjny model danych
Relacyjny model danych
8
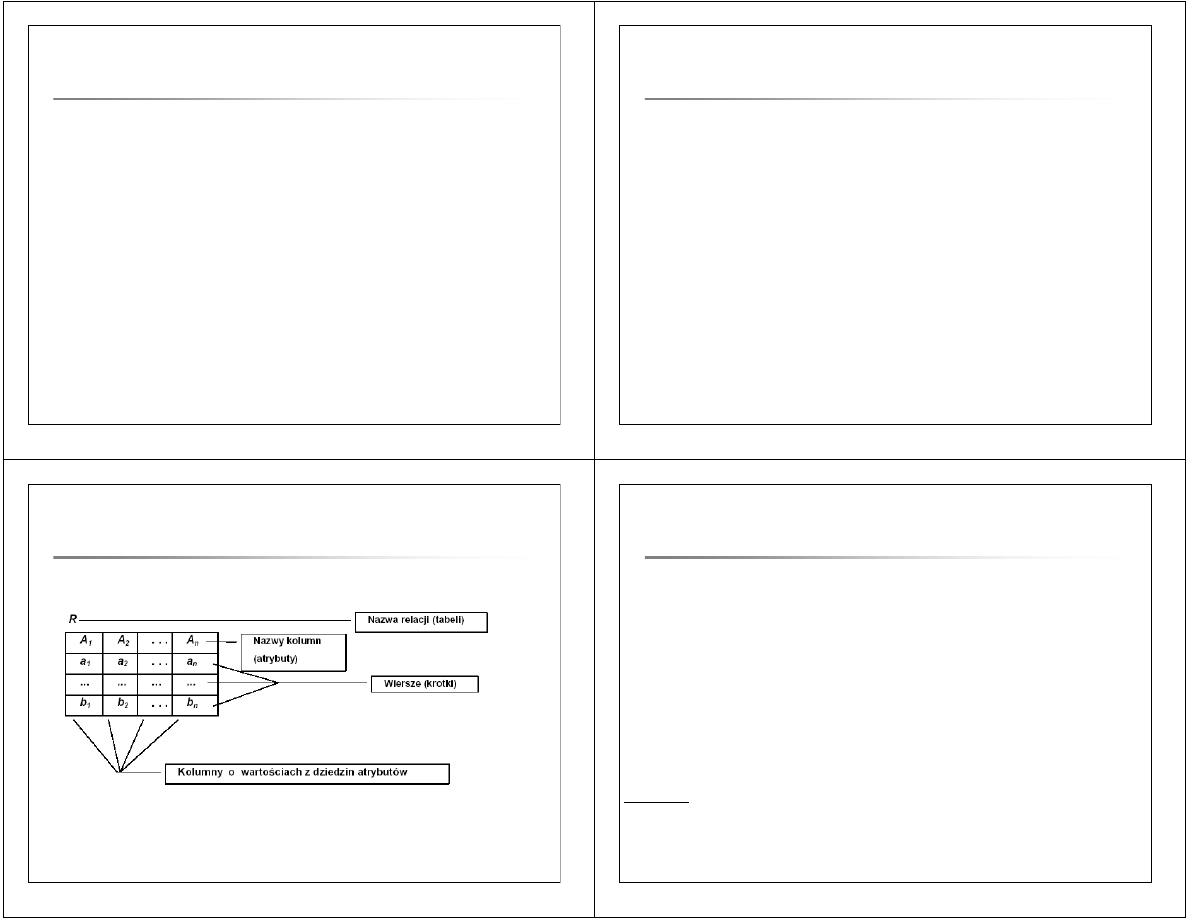
Relacyjny model danych
Relacyjny model danych
Atrybut
– symbol, nazwa
(np.
Nazwisko
,
NrEwid
, DataUr, Cena, ...),
U = {A
1
,...,A
n
} – zbiór
atrybutów
.
Dziedzina atrybutu
– Dom(
A
), zbiór dopuszczalnych wartości atrybutu A.
Wszystkie wartości są proste (atomowe).
Wyróżniona
wartość pusta
NULL
∈ Dom(A).
Krotka
(wiersz, rekord) typu U
r
= [A
1
:a
1
,...,A
n
:a
n
], a
i
∈ Dom(A
i
), [ ] – krotka pusta,
r
= (a
1
,..., a
n
) – zapis uproszczony, gdy ustalona jest kolejność atrybutów,
Tabela
(
relacja
) R typu U –
skończony zbiór
(
wielozbiór –
mogą występować
duplikaty!) krotek typu U.
Formalnie:
Krotka jest funkcją z U do V=Dom(A
1
)
∪ ... ∪ Dom(A
n
),
r
: U
→ V,
r
(
A
i
) =
r.A
i
∈ Dom(A
i
)

T. Pankowski, Model relacyjny
9
Algebra relacji
Algebra relacji
Att – nieskończony i przeliczalny zbiór atrybutów,
Val – zbiór wartości
Algebrą relacji nazywamy następującą strukturę:
AlgRel
Att,Val
= (Tab, {
∪
X
, –
X
,
π
X
,
δ
XÆY
, ´,
σ
E
}),
gdzie:
Tab – zbiór wszystkich tabel utworzonych nad zbiorami Att i Val;
∪
X
– suma mnogościowa tabel typu X, X
⊂ Att (X jest skończony),
–
X
– różnica mnogościowa tabel typu X,
π
X
– projekcja tabeli na zbiór X,
δ
XÆY
– przemianowanie tabeli poprzez zmianę nazw z X na
odpowiadające im nazwy z Y,
´
– złączenie tabel o dowolnych typach,
σ
E
– selekcja z tabeli według warunku E.
T. Pankowski, Model relacyjny
10
Operacje na tabelach (relacjach)
Operacje na tabelach (relacjach)
Dwie grupy operacji (wyrażalne za pomocą sześciu
podstawowych):
1. Operacje mnogościowe - wynikają z faktu, że
tabela jest zbiorem:
•
suma, różnica, przekrój.
2. Operacje relacyjne - wynikają z faktu, że tabela
jest (wielo)zbiorem funkcji:
•
projekcja, przemianowanie, złączenie (naturalne i
iloczyn kartezjański), selekcja, złączenia zewnętrzne,
podzielenie.
T. Pankowski, Model relacyjny
11
Operacje mnogo
Operacje mnogo
ś
ś
ciowe
ciowe
–
–
suma
suma
• R, S – tabele jednakowego typu U,
• Wynik – tabela typu U.
• Suma mnogościowa (union):
R
∪ S = { t | t ∈ R ∨ t ∈ S}.
• SQL
(UNION – usuwa duplikaty, UNION ALL – pozostawia duplikaty)
select * from Student
union
select * from Pracownik
Student
Pracownik
Student
∪
ALL
Pracownik
T. Pankowski, Model relacyjny
12
Suma mnogo
Suma mnogo
ś
ś
ciowa
ciowa
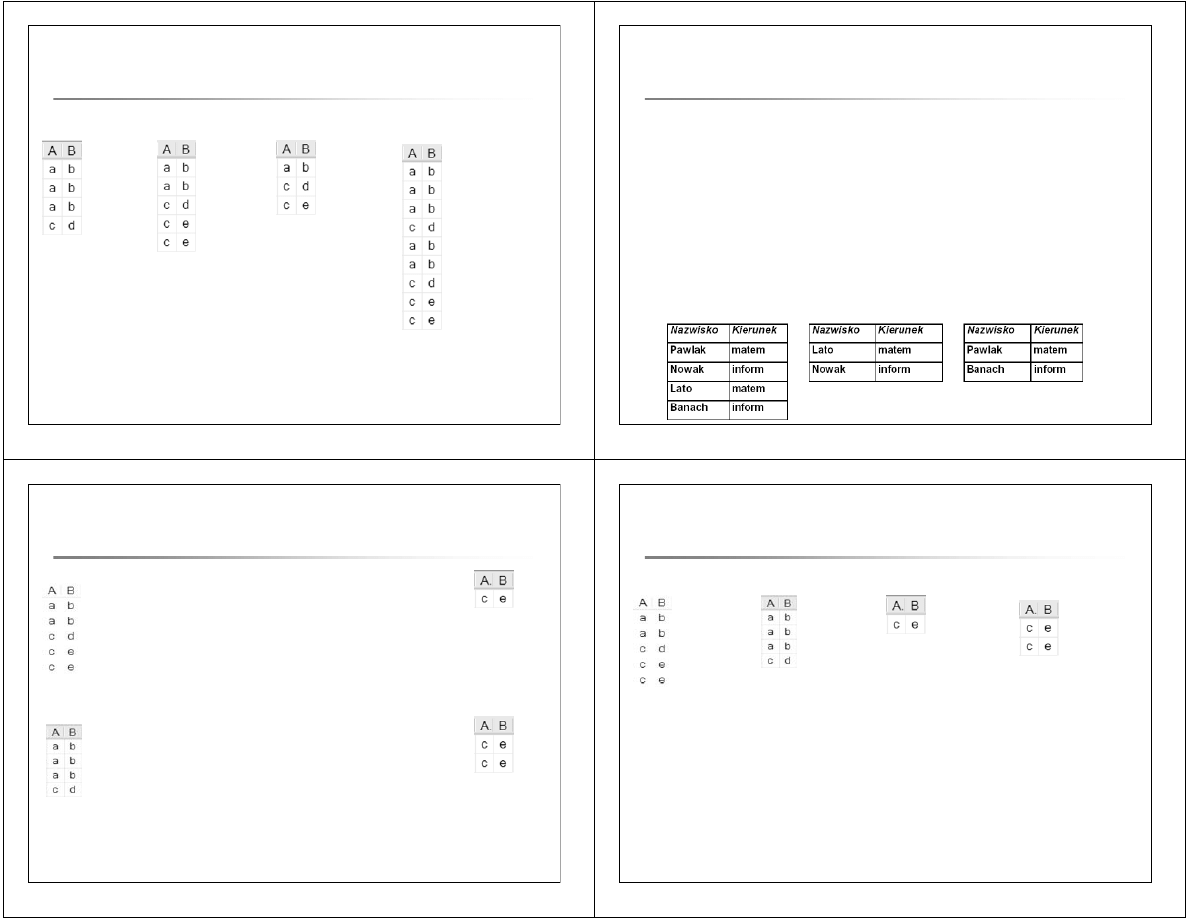
R
S
R
∪ S = { t | t ∈ R ∨ t ∈ S} –
wynik jest zbiorem, nie zawiera duplikatów
select * from R union select * from S
R
∪
ALL
S = { (k+j)*t | k*t
∈ R ∨ j*t ∈ S} –
wynik jest wielozbiorem, zawiera duplikaty.
(k*t
∈ R oznacza, że krotka t występuje k razy w tabeli R)
select * from R union all select * from S
T. Pankowski, Model relacyjny
13
Suma mnogo
Suma mnogo
ś
ś
ciowa
ciowa
R
S
R
∪ S
R
∪
ALL
S
T. Pankowski, Model relacyjny
14
Operacje mnogo
Operacje mnogo
ś
ś
ciowe
ciowe
–
–
r
r
ó
ó
ż
ż
nica
nica
• R, S – tabele jednakowego typu U,
• Wynik – tabela typu U.
• Różnica mnogościowa (difference):
R – S = { t | t
∈ R ∧ t ∉ S}.
• SQL
(EXCEPT – usuwa duplikaty):
select * from Student EXCEPT select * from Pracownik P
select * from Student as S
where not exists (select * from Pracownik P
where S.Nazwisko=P.Nazwisko
and S.Kierunek = P.Kierunek)
Student
Pracownik
Student – Pracownik
T. Pankowski, Model relacyjny
15
R
R
ó
ó
ż
ż
nica mnogo
nica mnogo
ś
ś
ciowa
ciowa
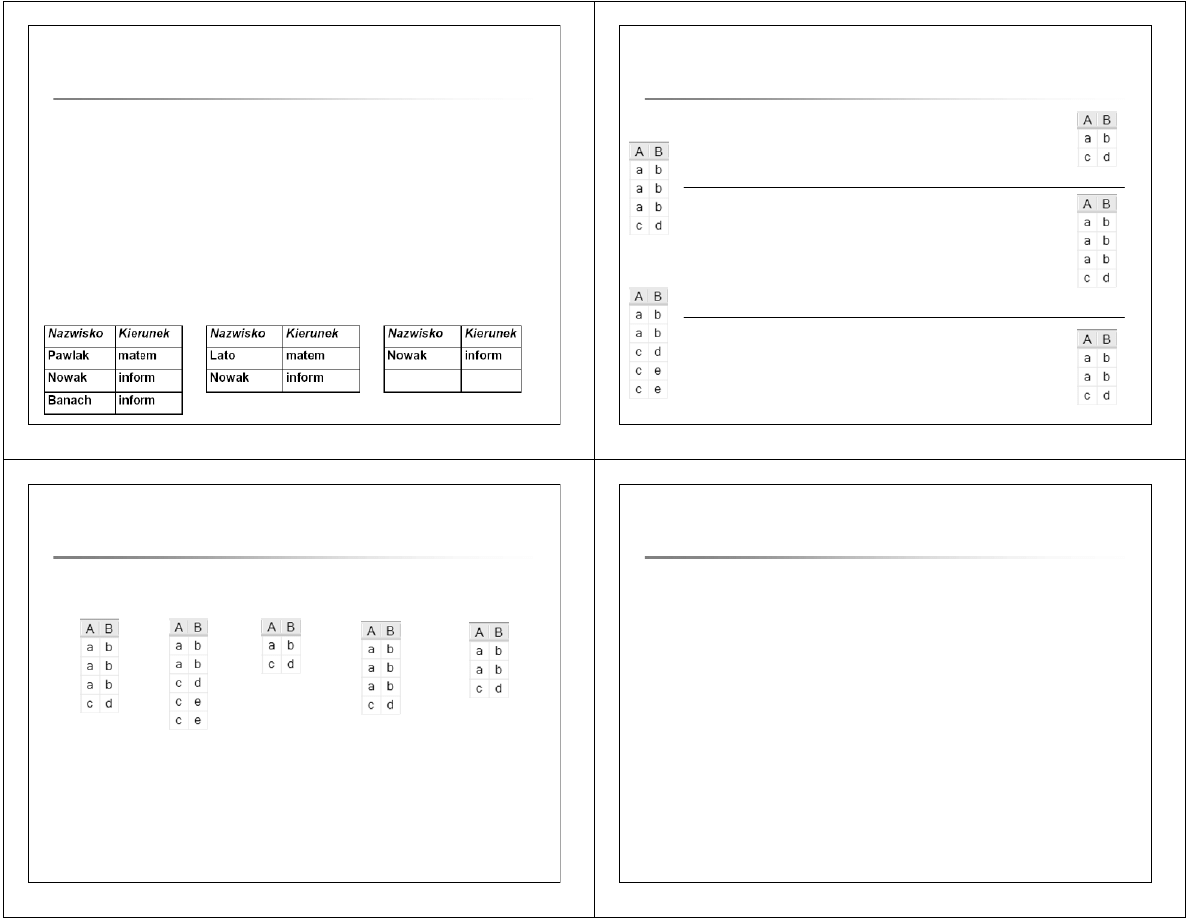
R
S
S – R = { t | t
∈ S ∧ t ∉ R} –
wynik jest zbiorem, nie zawiera duplikatów
select * from S except select * from R
S –
LDup
R = { k*t | k*t
∈ S ∧ t ∉ R} –
wynik jest wielozbiorem, zawiera duplikaty
select * from S
where not exists(
select * from R
where R.A=S.A and S.B=R.B)
T. Pankowski, Model relacyjny
16
R
R
ó
ó
ż
ż
nica mnogo
nica mnogo
ś
ś
ciowa
ciowa
R
S
S – R
S–
LDup
R
T. Pankowski, Model relacyjny
17
Operacje mnogo
Operacje mnogo
ś
ś
ciowe
ciowe
–
–
przekr
przekr
ó
ó
j
j
• R, S – tabele jednakowego typu U,
• Wynik – tabela typu U.
• Przekrój mnogościowy (intersection):
R
∩ S = { t | t ∈ R ∧ t ∈ S}.
• SQL
(INTERSECT – usuwa duplikaty):
:
select * from Student INTERSECT select * from Pracownik P
select * from Student as S
where exists (select * from Pracownik P
where S.Nazwisko=P.Nazwisko
and S.Kierunek = P.Kierunek)
Student
Pracownik
Student
∩
Pracownik
18
Przekr
Przekr
ó
ó
j mnogo
j mnogo
ś
ś
ciowy
ciowy
R
S
R
∩ S = { t | t ∈ R ∧ t ∈ S} –
wynik jest zbiorem, nie zawiera duplikatów
select * from R intersect select * from S
R
∩ S = S ∩ R
R
∩
LDup
S = { k*t | k*t
∈ R ∧ t ∈ S} –
wynik jest wielozbiorem, zawiera duplikaty
select * from R
where exists(
select * from S
where R.A=S.A and S.B=R.B)
select * from S
where exists(
select * from R
where R.A=S.A and S.B=R.B)
19
Przekr
Przekr
ó
ó
j mnogo
j mnogo
ś
ś
ciowy
ciowy
R
S
R
∩ S
R
∩
LDup
S
S
∩
LDup
R
T. Pankowski, Model relacyjny
20
Operacje na krotkach
Operacje na krotkach
–
–
projekcja
projekcja
Przykład:
π
{A,C}
([A:a, B:b, C:c]) = [A:a, C:c]
Def. (
projekcja krotki na zbiór atrybutów
)
Niech r będzie krotką typu U, i niech X będzie podzbiorem U, X
⊆ U.
Projekcją
(rzutem, ograniczeniem) (ang.
projection
) krotki r na zbiór X,
co oznaczamy
π
X
(r), nazywamy krotkę t typu X taką, która jest identyczna
z krotką
r na zbiorze atrybutów X, tj.:
t =
π
X
(r), jeśli dla każdego A
∈X,
t.A = r. A.
Gdy X = {} ({} oznacza zbór pusty), to projekcja jest krotką pustą []
Przykład:
π
{}
([A:a, B:b, C:c]) = [].
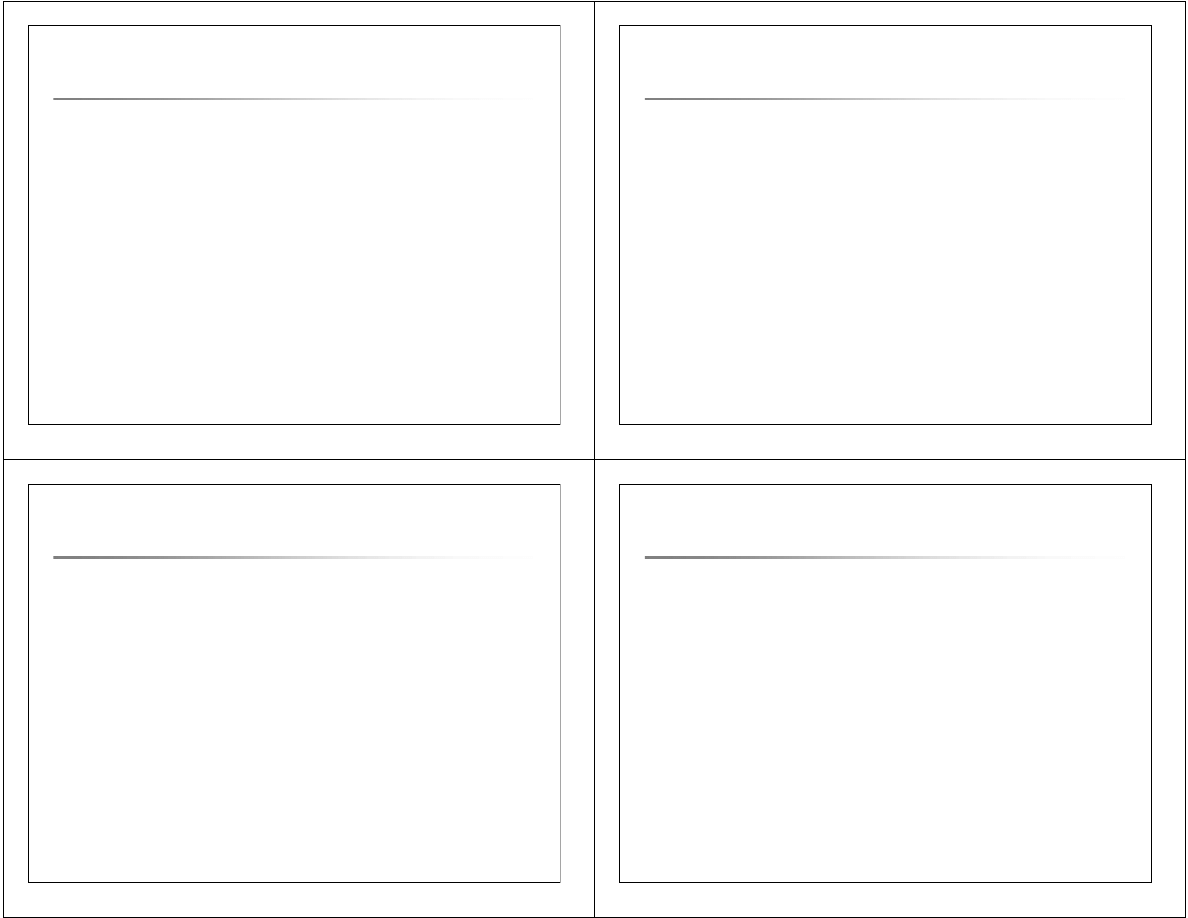
21
Operacje na krotkach
Operacje na krotkach
–
–
przemianowanie
przemianowanie
Przykład:
δ
A Æ D
([A:a, B:b, C:c]) = [D:a, B:b, C:c].
Def: (
przemianowanie atrybutów w krotce)
Niech r będzie krotką typu U, B atrybutem w U i C atrybutem nie należącym do U.
Przemianowaniem atrybutu B na C w krotce r, co oznaczamy
δ
B Æ C
(r), nazywamy
krotkę t powstałą z r przez zamianę atrybutu B na C, tj. taką krotkę t typu
U – {B}
∪ {C}, że:
t.A = r. A, dla każdego A
∈ U – {B},
t.C = t.B.
Uogólnienie na ciągi atrybutów:
Niech X=(B
1
, …, B
k
) i Y=(C
1
, …, C
k
) będą ciągami atrybutów, X
⊆ U, Y ∩ U = {}.
Przemianowanie atrybutów z X na odpowiadające im atrybuty z Y w krotce r
definiujemy następująco:
δ
X Æ Y
(r) =
δ
Bk Æ Ck
(... (
δ
B1 Æ C1
(r))...)
T. Pankowski, Model relacyjny
22
Operacje na krotkach
Operacje na krotkach
–
–
z
z
łą
łą
czenie
czenie
Def: (
złączenie krotek
)
Niech dane będą:
r – krotka typu X, s – krotka typu Y.
Jeśli zbiór r
∪ s jest krotką, to nazywamy go
złączeniem naturalnym
r i s i
oznaczamy r ´ s.
Jeśli r
∪ s nie spełnia warunków krotki, to mówimy, że r i s są
niezłączalne
.
Przykład:
[A:a,B:b,C:c] ´ [D:d,E:e] = [A:a,B:b,C:c,D:d,E:e] – krotki rozłącznych typów;
[A:a,B:b,C:c] ´ [B:b,E:e] = [A:a,B:b,C:c,E:e] – krotki nierozłącznych typów;
[A:a,B:b,C:c] ´ [] = [A:a,B:b,C:c] – złączenie z krotką pustą nie zmienia krotki;
[A:a, B:b, C:c] i [B:d, E:e] – krotki niezłączalne !
suma [A:a, B:b, C:c, B:d, E:e] nie jest krotką bo atrybut B występuje dwa razy –
raz z wartością 'b' i powtórnie z wartością 'd'.
T. Pankowski, Model relacyjny
23
W
W
ł
ł
a
a
ś
ś
ciwo
ciwo
ś
ś
ci projekcji i z
ci projekcji i z
łą
łą
czenia krotek
czenia krotek
π
{}
(
t
) = [] – wynikiem projekcji krotki na zbiór pusty jest krotka pusta [];
r
´
s = s
´
t
– złączenie krotek jest przemienne;
r
´
(
s
´
t
) = (
r
´
s
)
´
t
– złączenie krotek jest łączne;
r
´
[] =
r
– krotka pusta jest elementem neutralnym dla złączenia;
r
´
r
=
r
– złączenie krotki z samą sobą nie zmienia krotki;
T. Pankowski, Model relacyjny
24
Spe
Spe
ł
ł
nianie warunku przez krotk
nianie warunku przez krotk
ę
ę
Def: (
warunek nad zbiorem atrybutów U)
Niech
U
będzie zbiorem atrybutów, a Const – zbiore stałych (liczb, tekstów).
Niech:
A, A'
∈ U,
c
∈ Const,
θ ∈ {=, !=, <, <=, >, >=, like, ... } – operator porównania
Warunkiem
nad U nazywamy wyrażenie logiczne
E
o następującej składni:
E
::=
A
θ
c
|
A
θ
A'
| (
E
) | not
E
|
E
or
E
|
E
and
E
Krotka
r
typu U
spe
ł
nia
warunek
E
,
E
(
r
) = TRUE,
jeśli wyrażenie powstałe z
E
przez podstawienie za każde wystąpienie atrybutu
A
wartości
r.A
jest prawdziwe.
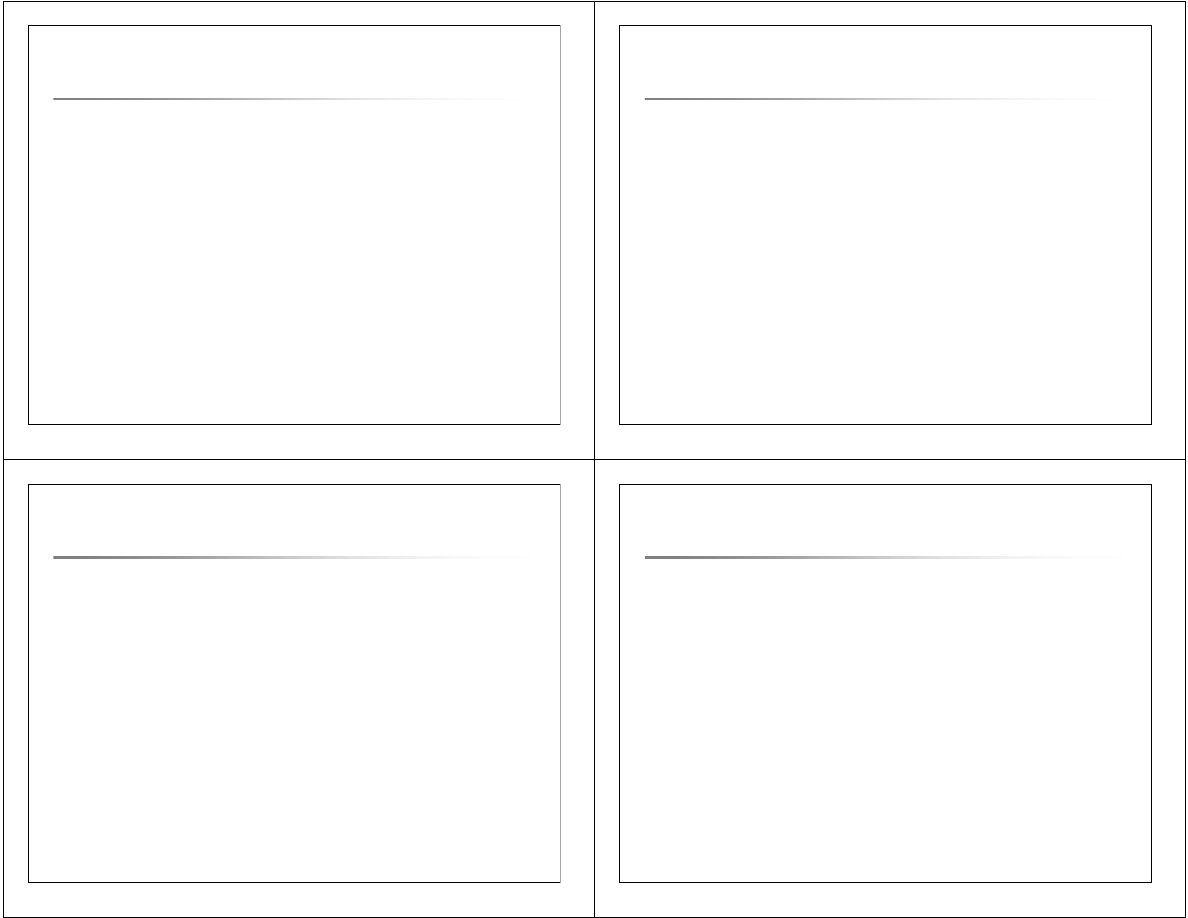
T. Pankowski, Model relacyjny
25
Spe
Spe
ł
ł
nianie warunku przez krotk
nianie warunku przez krotk
ę
ę
Przykład:
E
:= (Kierunek=’mat’ or Kierunek=‘fiz’)
(Kierunek=’mat’ or Kierunek=‘fiz’)([NrStud:2345, Kierunek:’mat’]) = TRUE
(Kierunek=’mat’ or Kierunek=‘fiz’)([NrStud:2345, Kierunek:’inf’]) = FALSE
(Kierunek=’mat’ or Kierunek=‘fiz’)([NrStud:2345, Kierunek:NULL]) = UNKNOWN
T. Pankowski, Model relacyjny
26
Spe
Spe
ł
ł
nianie warunku przez krotk
nianie warunku przez krotk
ę
ę
Krotki:
r
= [NrStud:2345, Kierunek:’mat’]
s
= [NrStud:2346, Kierunek:NULL]
Warunek:
E
≡ Kierunek=’mat’
Spełnianie:
E(r) = TRUE
E(s) != TRUE, E(s) = UNKNOWN
Uwaga:
Występowanie wartości NULL powoduje, że działamy w logice
trójwartościowej z wartościami logicznymi:
{TRUE, FALSE, UNKNOWN} (lub {T, F, U}).
Dowolne porównanie z NULL daje wartość logiczną UNKNOWN.
t
.
A
θ NULL = UNKNOWN,
NULL
θ
v
= UNKNOWN dla każdego
v
, również równego NULL.
T. Pankowski, Model relacyjny
27
Operacje na tabelach
Operacje na tabelach
1. Projekcja:
π
X
(R) = {
π
X
(r) | r
∈ R }
2. Przemianowanie:
δ
X Æ Y
(R) := {
δ
X Æ Y
(r) | r
∈ R }
3. Złączenie naturalne:
R ´ S = {r ´ s | r
∈ R, s ∈ S }
5. Selekcja:
σ
E
(R ) = {r | r
∈ R ∧ E (r ) = TRUE}
T. Pankowski, Model relacyjny
28
Operacje na tabelach
Operacje na tabelach
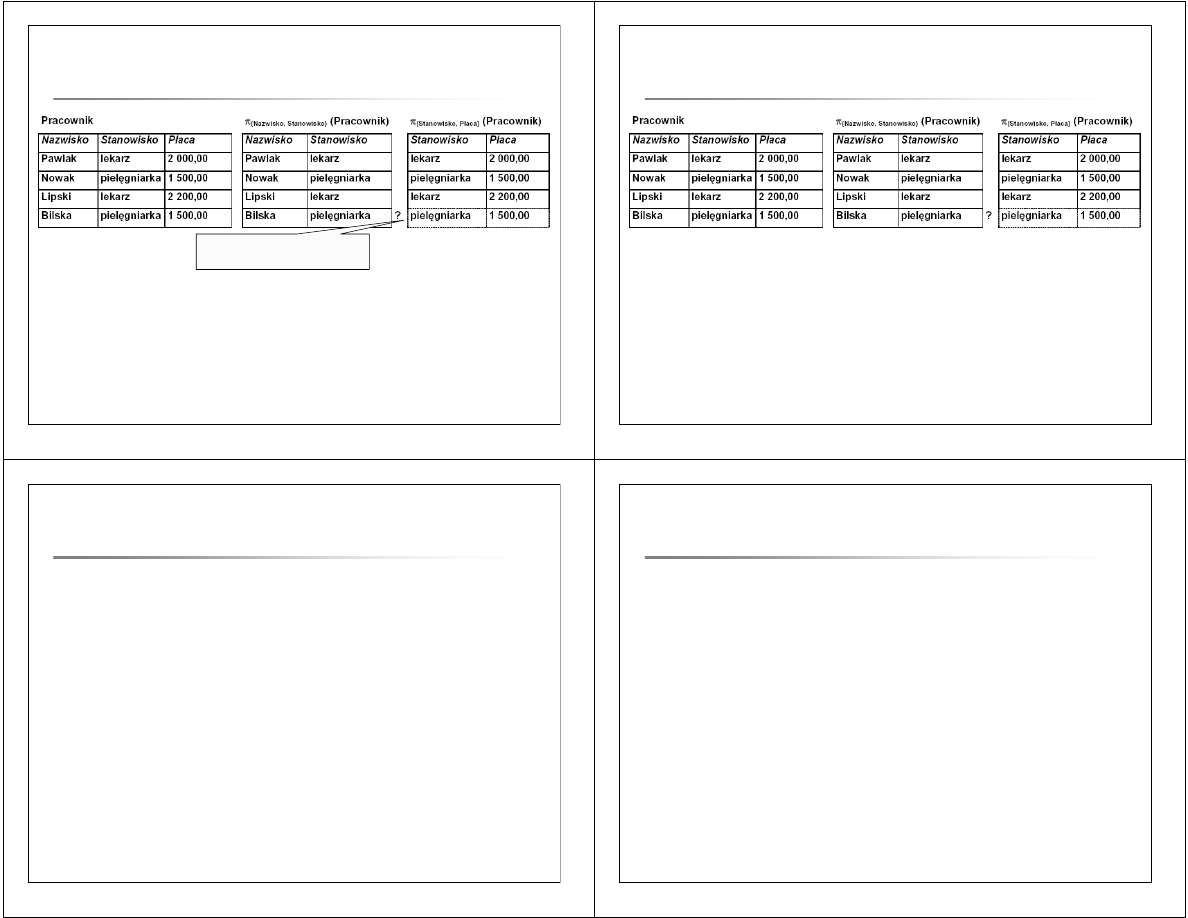
Projekcja:
π
X
(R) = {
π
X
(r) | r
∈ R }
T. Pankowski, Model relacyjny
29
Projekcja
Projekcja
Szczególny przypadek:
π
{}
(R) = if R = {} then {} else {[]}
Problem duplikatów
Czy (pielęgniarka, 1 500,00) powinna dwa razy występować w
π
{Stanowisko, Płaca}
(Pracownik)?
-
tak, jeśli chcemy wyliczyć średnią płacę,
-
nie, jeśli sporządzamy wykaz stanowisk i płace na tych stanowiskach.
T. Pankowski, Model relacyjny
30
Projekcja
Projekcja
SQL:
select Stanowisko, Płaca
from
Pracownik
usuwanie duplikatów:
select distinct Stanowisko, Płaca
from
Pracownik
T. Pankowski, Model relacyjny
31
Operacje na tabelach
Operacje na tabelach
Przemianowanie:
δ
A Æ B
(R) := {
δ
A Æ B
(r) | r
∈ R }
T. Pankowski, Model relacyjny
32
Przemianowanie
Przemianowanie
(przyk
(przyk
ł
ł
ad)
ad)
Dla relacji:
Studenci(IdStud, Nazwisko, Data_ur, Miejscowość)
δ
Miejscowość Æ Miasto
(Studenci)
SQL:
select IdStud, Nazwisko, Data_ur, Miejscowość as Miasto
from Studenci
T. Pankowski, Model relacyjny
33
Operacje na tabelach
Operacje na tabelach
Złączenie naturalne:
R ´ S = {r ´ s | r
∈ R, s ∈ S }
T. Pankowski, Model relacyjny
34
Z
Z
łą
łą
czenie naturalne
czenie naturalne
(c.d.)
(c.d.)
><
T. Pankowski, Model relacyjny
35
Z
Z
łą
łą
czenie naturalne
czenie naturalne
(c.d.)
(c.d.)
><
T. Pankowski, Model relacyjny
36
Z
Z
łą
łą
czenie naturalne
czenie naturalne
(c.d.)
(c.d.)
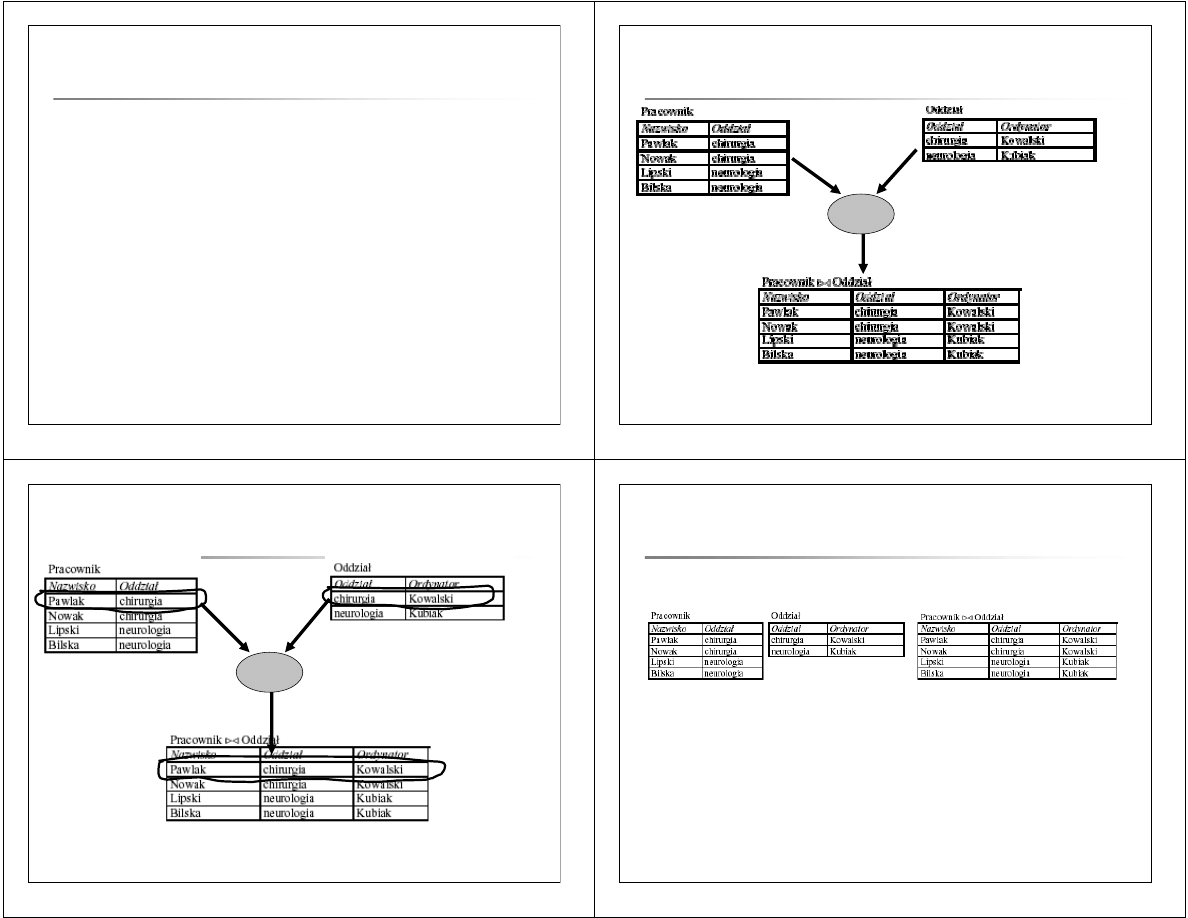
W złączenie naturalnym dwóch tabel R i S typów odpowiednio X i Y:
• atrybuty występujące w X mogą występować także w Y,
• relacja wynikowa zawiera sumę atrybutów z X i Y (bez powtórzeń),
• łączone są te krotki, które na wspólnych atrybutach mają jednakowe
wartości.
T. Pankowski, Model relacyjny
37
Z
Z
łą
łą
czenie naturalne
czenie naturalne
(c.d.)
(c.d.)
SQL:
select Nazwisko,
P.Oddział, Ordynator
from Pracownik P, Oddział O
where P.Oddział = O.Oddział
lub:
select Nazwisko,
P.Oddział, Ordynator
from Pracownik P join Oddział O
on P.Oddział = O.Oddział
T. Pankowski, Model relacyjny
38
Z
Z
łą
łą
czenie
czenie
–
–
w
w
ł
ł
a
a
ś
ś
ciwo
ciwo
ś
ś
ci
ci
Szczególne przypadki złączenia:
R – relacja typu X,
S – relacja typu Y.
1. Jeśli X = Y, to R ´ S = R
∩ S
złączenie naturalne jest przekrojem mnogościowym.
2. Jeśli X
∩ Y = {}, to złączenie jest iloczynem
kartezjańskim.
3.
R ´ {[]} = R.
4.
R ´ {} = {}.
T. Pankowski, Model relacyjny
39
Z
Z
łą
łą
czenie
czenie
–
–
w
w
ł
ł
a
a
ś
ś
ciwo
ciwo
ś
ś
ci
ci
Twierdzenie (właściwości złączenia naturalnego i kartezjańskiego)
R – tabela typu U, wówczas:
1.
R
´
S = S
´
R
złączenie jest przemienne.
2.
(R
´
S)
´
T = R
´
(S
´
T)
złączenie jest łączne.
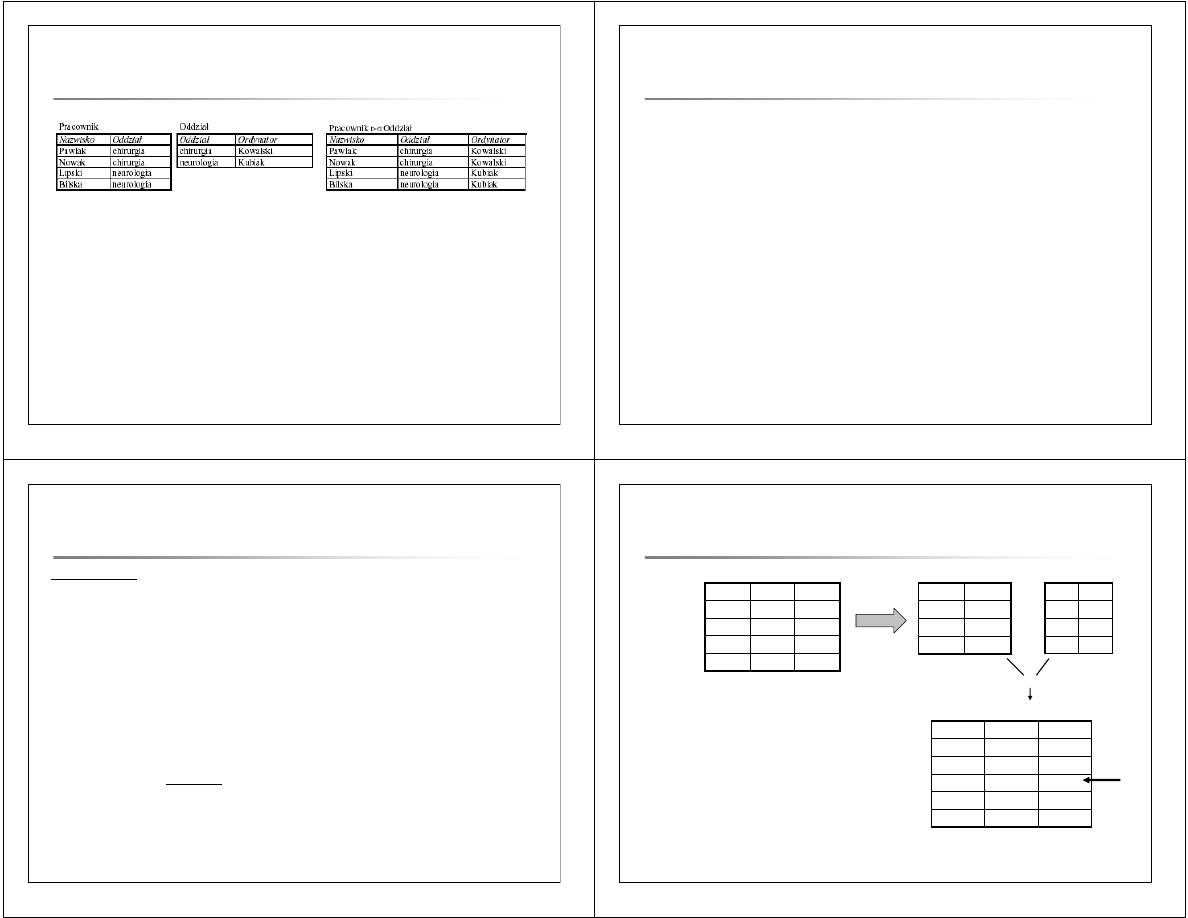
3.
Jeśli X
⊆ U, to R
´
π
X
(R) = R
złączenie tabeli z dowolną swoją projekcją daje w wyniku R.
4.
Jeśli X
∪ Y = U, to R ⊆ π
X
(R)
´
π
Y
(R)
tabela jest zawarta w złączeniu dowolnych dwóch swoich
projekcji, których suma typów jest równa typowi relacji.
Zachodzi zawieranie a nie równość (!).
T. Pankowski, Model relacyjny
40
Ilustracja w
Ilustracja w
ł
ł
a
a
ś
ś
ciwo
ciwo
ś
ś
ci (4)
ci (4)
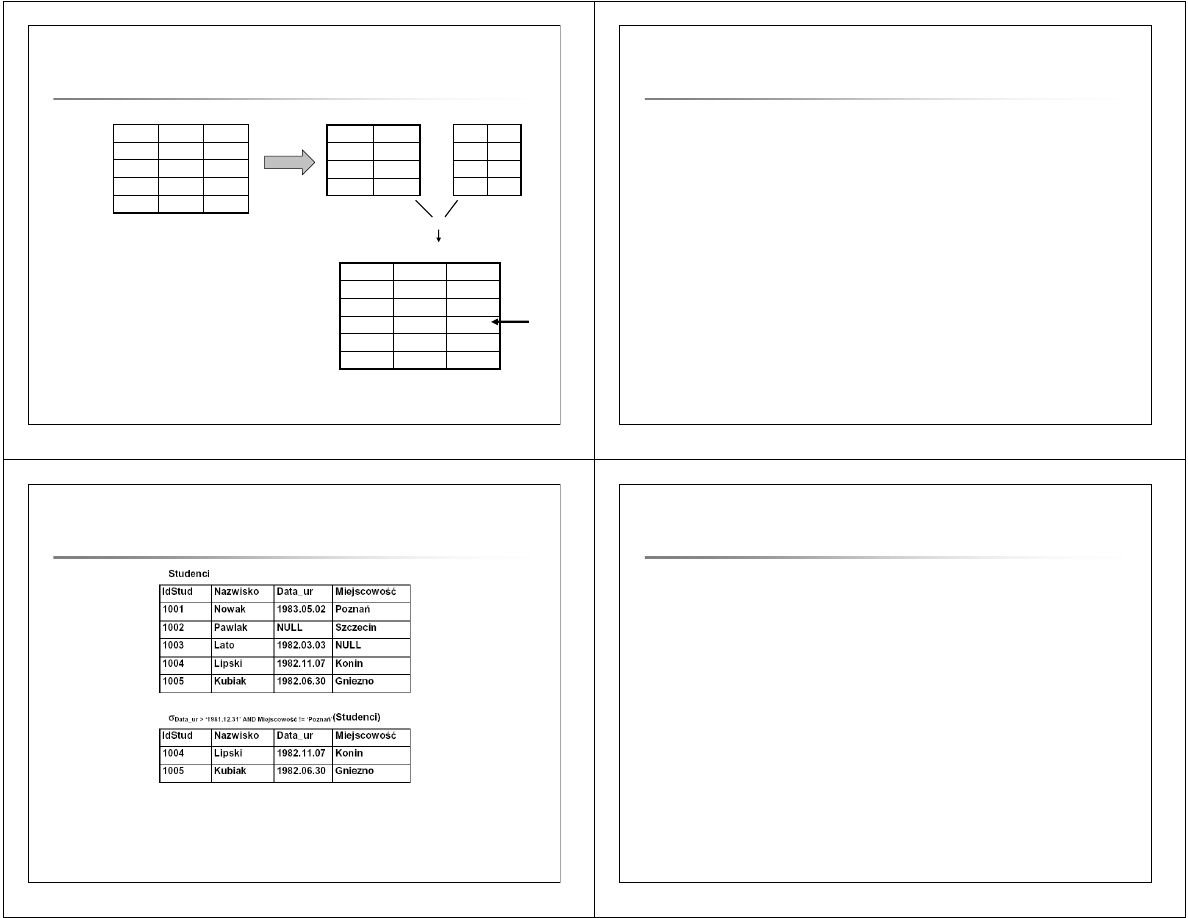
Sprz
⊂ π
{IdKli,IdTow}
(Sprz)
´
π
{IdKli,Data}
(Sprz),
krotka [a, y, 1] nie należy do Sprz !
3
y
b
2
y
a
2
x
a
1
x
a
Data
IdTow
IdKli
3
y
b
2
y
a
1
y
a
2
x
a
1
x
a
Data
IdTow
IdKli
y
b
y
a
x
a
IdTow
IdKli
Sprz
3
b
2
a
1
a
Data
IdKli
π
IdKli,IdTow
(Sprz)
π
IdKli,Data
(Sprz)
π
IdKli,IdTow
(Sprz) ´
π
IdKli,Data
(Sprz)
?
´
T. Pankowski, Model relacyjny
41
Ilustracja w
Ilustracja w
ł
ł
a
a
ś
ś
ciwo
ciwo
ś
ś
ci (4)
ci (4)
3
y
b
2
y
a
2
x
a
1
x
a
Data
IdTow
IdKli
3
y
b
2
y
a
1
y
a
2
x
a
1
x
a
Data
IdTow
IdKli
y
b
y
a
x
a
IdTow
IdKli
Sprz
3
b
2
a
1
a
Data
IdKli
π
IdKli,IdTow
(Sprz)
π
IdKli,Data
(Sprz)
π
IdKli,IdTow
(Sprz) ´
π
IdKli,Data
(Sprz)
?
´
T. Pankowski, Model relacyjny
42
Operacje na tabelach
Operacje na tabelach
Selekcja:
σ
E
(R ) = {r | r
∈ R ∧ E (r ) = TRUE}
Wynikiem selekcji jest zbiór tych krotek tabeli
R
,
które spełniają warunek
E
.
T. Pankowski, Model relacyjny
43
Selekcja
Selekcja
-
-
przyk
przyk
ł
ł
ad
ad
select *
from Studenci
where Data_ur > ’1981.12.31’ and Miejscowosc < > ‘Poznań’
T. Pankowski, Model relacyjny
44
Pochodne operacje na tabelach
Pochodne operacje na tabelach
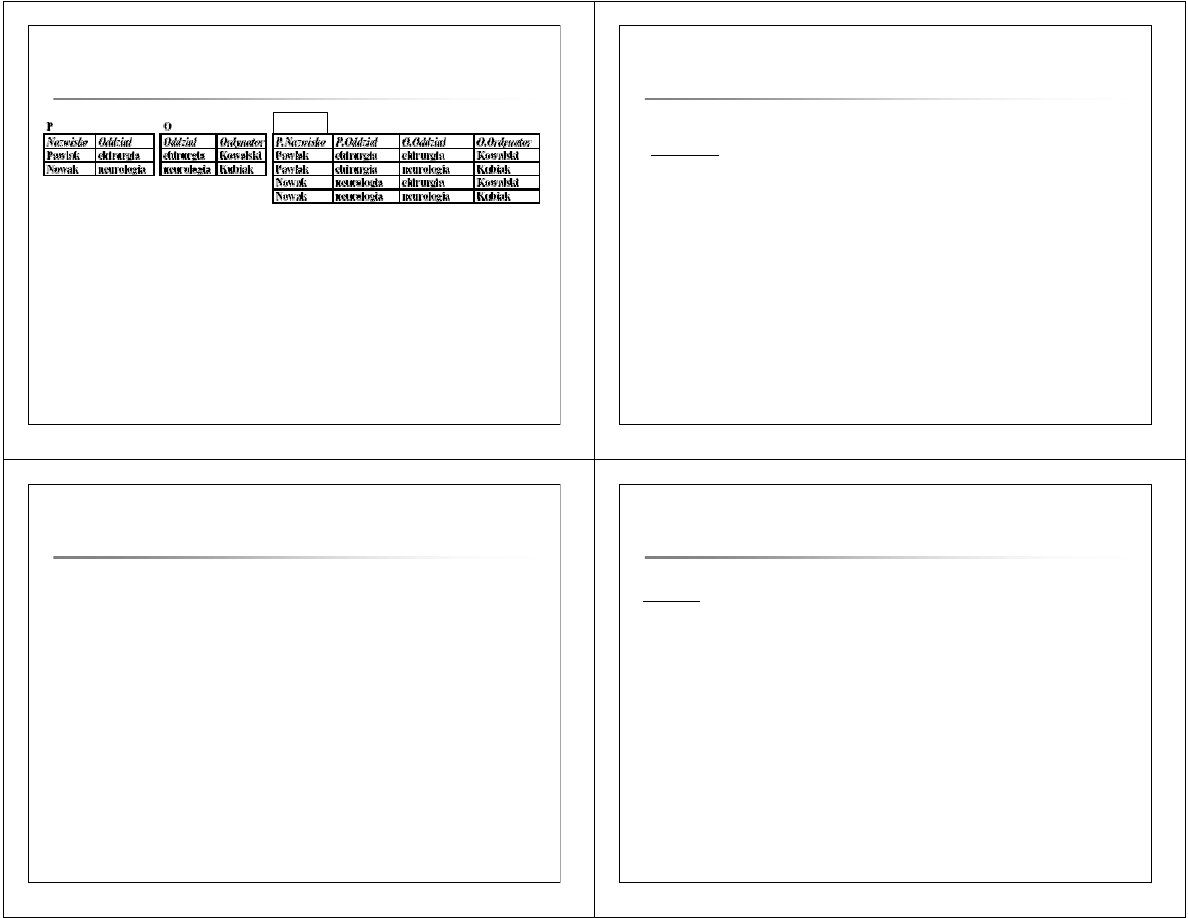
Iloczyn kartezjański:
R
M
×
N
S =
δ
X Æ M.X
(R) ´
δ
Y Æ N.Y
(S)
Każda krotka z
R
jest łączona z każdą krotką z
S
.
Jeśli R ma n
R
kolumn i m
R
wierszy, a
S ma n
S
kolumn i m
S
wierszy, to
R
N
×
M
S ma n
R
+ n
S
kolumn i m
R
*m
S
wierszy.
T. Pankowski, Model relacyjny
45
Iloczyn kartezja
Iloczyn kartezja
ń
ń
ski
ski
(c.d.)
(c.d.)
SQL:
select P.Nazwisko,
P.Oddział, O.Oddział, O.Ordynator
from Pracownik P, Oddział O
lub
select P.*,
O.*
from Pracownik P, Oddział O
P
P
×
O
O
T. Pankowski, Model relacyjny
46
Z
Z
łą
łą
czenie warunkowe,
czenie warunkowe,
θ
θ
-
-
z
z
łą
łą
czenie (
czenie (
θ
θ
-
-
join
join
)
)
Definicja (
θ-złączenie)
Niech R i S będą tabelami typów odpowiednio X i Y, a E
niech będzie warunkiem selekcji nad zbiorem atrybutów X
∪ Y.
Z
łą
czeniem (warunkowym)
tabel R i S, względem warunku
E, nazywamy selekcję złączenia naturalnego R i S
względem warunku E
R
´
E
S =
σ
E
(R ´ S),
T. Pankowski, Model relacyjny
47
Z
Z
łą
łą
czenia zewn
czenia zewn
ę
ę
trzne
trzne
(OUTER JOIN)
(OUTER JOIN)
Celem wprowadzenia złączenia zewnętrznego jest to, aby w relacji
wynikowej zawarte były wszystkie krotki należące do jednego z
argumentów (relacji leżącej po lewej bądź po prawej stronie
operatora), albo do obydwu tych argumentów i to niezależnie od
tego, czy dla danej krotki istnieje dopasowana do niej krotka
należąca do drugiej relacji, czy nie.
Wyróżniamy:
1. Złączenie zewnętrzne lewostronne - LEFT OUTER JOIN
2. Złączenie zewnętrzne prawostronne - RIGHT OUTER JOIN
3. Złączenie zewnętrzne pełne - FULL OUTER JOIN
T. Pankowski, Model relacyjny
48
Z
Z
łą
łą
czenie zewn
czenie zewn
ę
ę
trzne lewostronne
trzne lewostronne
LEFT OUTER JOIN (LOJ)
LEFT OUTER JOIN (LOJ)
Definicja
Niech R i S będą tabelami typów odpowiednio X i Y, a E niech będzie
warunkiem selekcji nad zbiorem atrybutów X
∪ Y.
Lewostronnym złączeniem zewnętrznym tabel R i S względem E, co
oznaczamy, R +
´
E
S, nazywamy następującą tabelę typu X
∪ Y:
R +
´
E
S = R
´
E
S
∪ {t
´
Null(Y – X) | t
∈ R – π
X
(R
´
E
S)}
Do wyniku należą więc wszystkie krotki lewego operanda (R) złączone
bądź z dopasowanymi krotkami tabeli S, bądź z wartościami NULL, gdy
brak dla nich w S dopasowanych krotek.
T. Pankowski, Model relacyjny
49
Z
Z
łą
łą
czenie zewn
czenie zewn
ę
ę
trzne lewostronne
trzne lewostronne
-
-
przyk
przyk
ł
ł
ad
ad
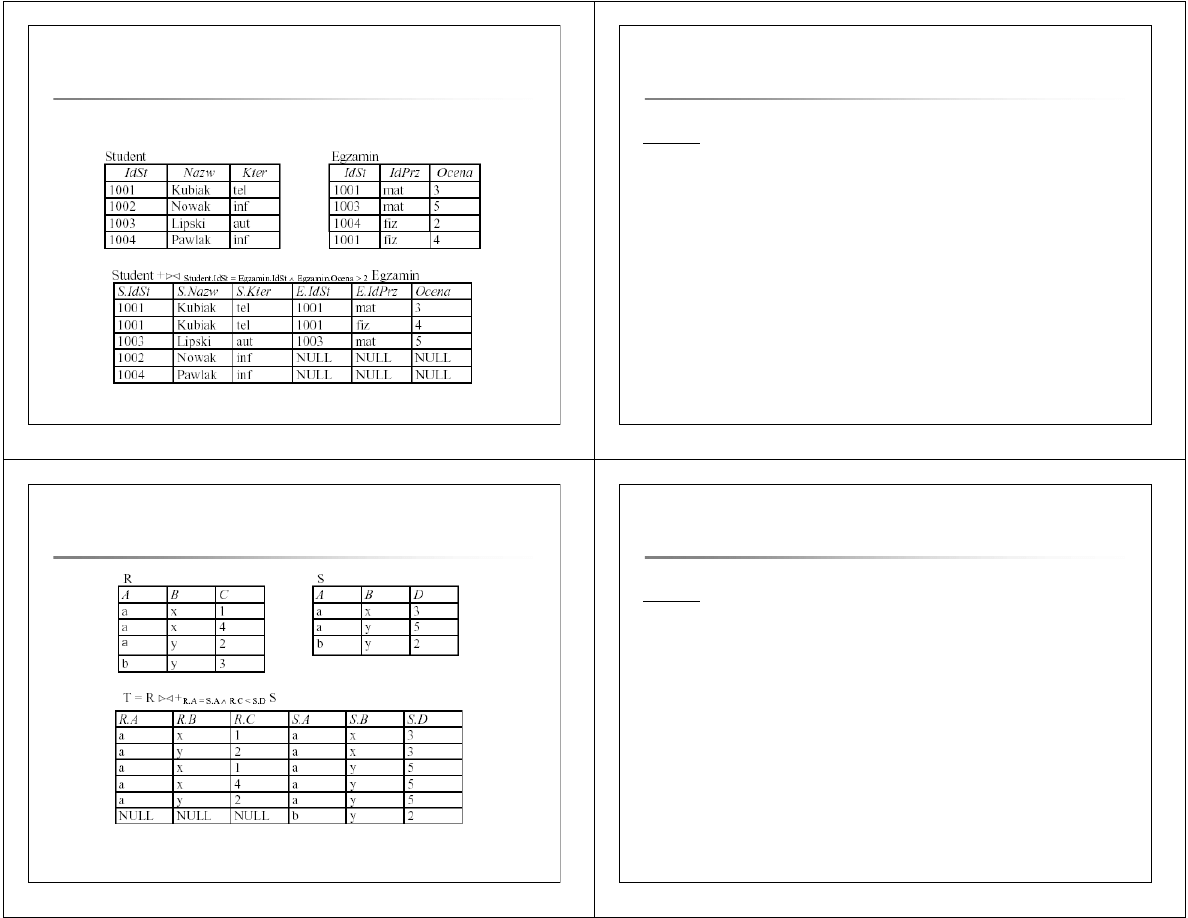
Podaj dane o wszystkich studentów wraz z informacjami
o zdanych przez nich egzaminach:
T. Pankowski, Model relacyjny
50
pra
pra
wostronne
wostronne
RIGHT
RIGHT
OUTER
OUTER
JOIN
JOIN
(ROJ)
(ROJ)
Definicja
Niech R i S będą tabelami typów odpowiednio X i Y, a E niech będzie
warunkiem selekcji nad zbiorem atrybutów X
∪ Y.
Prawostronnym złączeniem zewnętrznym tabel R i S względem E, co
oznaczamy, R
´
+
E
S, nazywamy następującą tabelę typu X
∪ Y:
R
´
+
E
S = R
´
E
S
∪ {Null(X – Y)
´
t| t
∈ S – π
Y
(R
´
E
S)}
Do wyniku należą więc wszystkie krotki prawego operanda (S) złączone
bądź z dopasowanymi krotkami tabeli R, bądź z wartościami NULL, gdy
brak dla nich w R dopasowanych krotek.
T. Pankowski, Model relacyjny
51
Z
Z
łą
łą
czenie zewn
czenie zewn
ę
ę
trzne
trzne
pra
pra
wostronne
wostronne
-
-
przyk
przyk
ł
ł
ad
ad
T. Pankowski, Model relacyjny
52
Z
Z
łą
łą
czenie zewn
czenie zewn
ę
ę
trzne
trzne
pe
pe
ł
ł
ne
ne
FULL
FULL
OUTER JOIN
OUTER JOIN
(FOJ)
(FOJ)
Definicja
Niech R i S będą tabelami typów odpowiednio X i Y, a E niech będzie
warunkiem selekcji nad zbiorem atrybutów X
∪ Y.
Pełnym złączeniem zewnętrznym tabel R i S względem E, co
oznaczamy, R +
´
+
E
S, nazywamy sumę mnogościową złączeń lewo- i
prawostronnego tabel R i S względem warunku E:
R +
´
+
E
S = R +
´
E
S
∪
R
´
+
E
S
T. Pankowski, Model relacyjny
53
Z
Z
łą
łą
czenie zewn
czenie zewn
ę
ę
trzne
trzne
pe
pe
ł
ł
ne
ne
-
-
przyk
przyk
ł
ł
ad
ad
Podaj wszystkich studentów, wszystkich pracowników wraz z
informacjami o promotorstwie prac magisterskich.
T. Pankowski, Model relacyjny
54
Podzielenie (
Podzielenie (
division
division
)
)
Definicja
Niech dane będą relacje R(U) i S(X) i niech X
⊆ U.
Podzieleniem relacji R(U) przez S(X) nazywamy relację R
÷ S, taką że:
R
÷ S := {t ∈ π
U – X
(R) |
∀ s ∈ S. t ´ s ∈ R}.
T. Pankowski, Model relacyjny
55
Podzielenie
Podzielenie
-
-
przyk
przyk
ł
ł
ad
ad
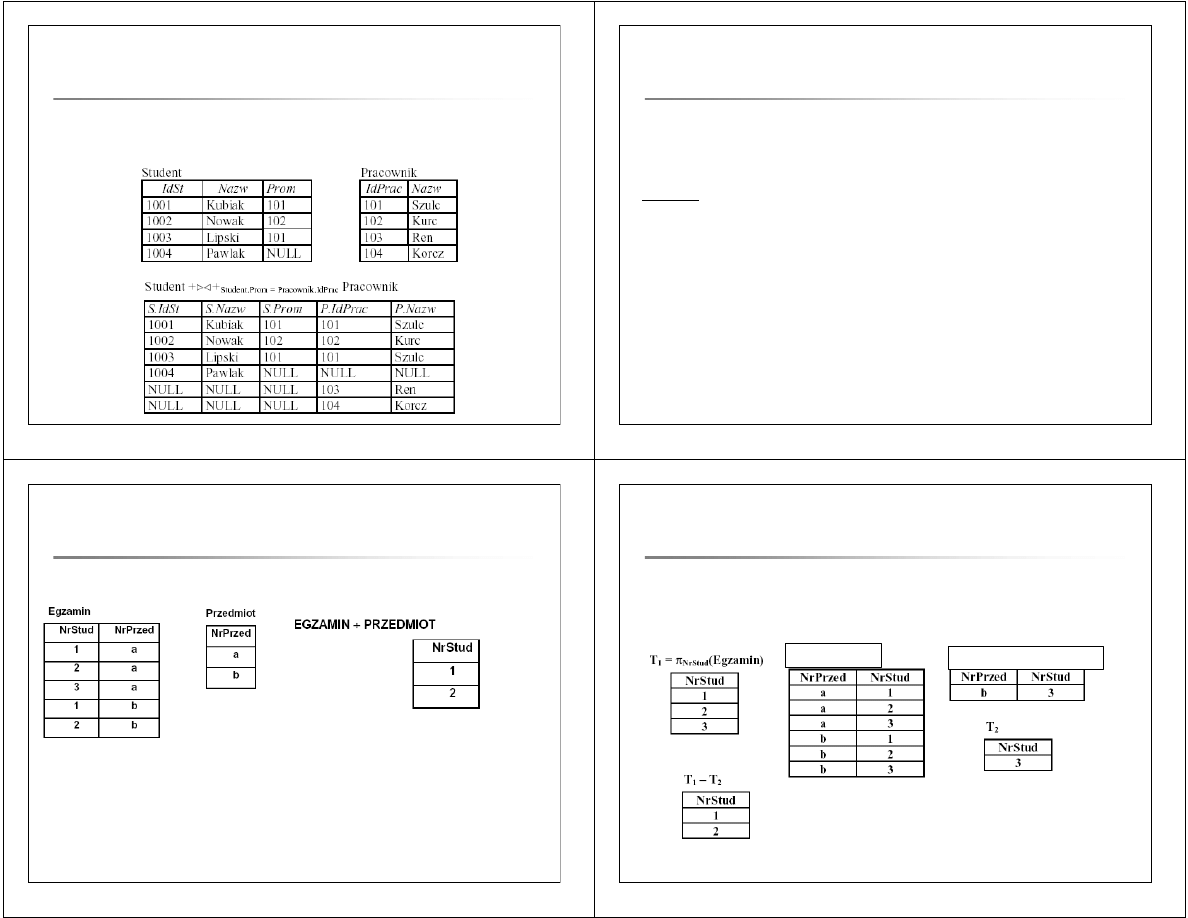
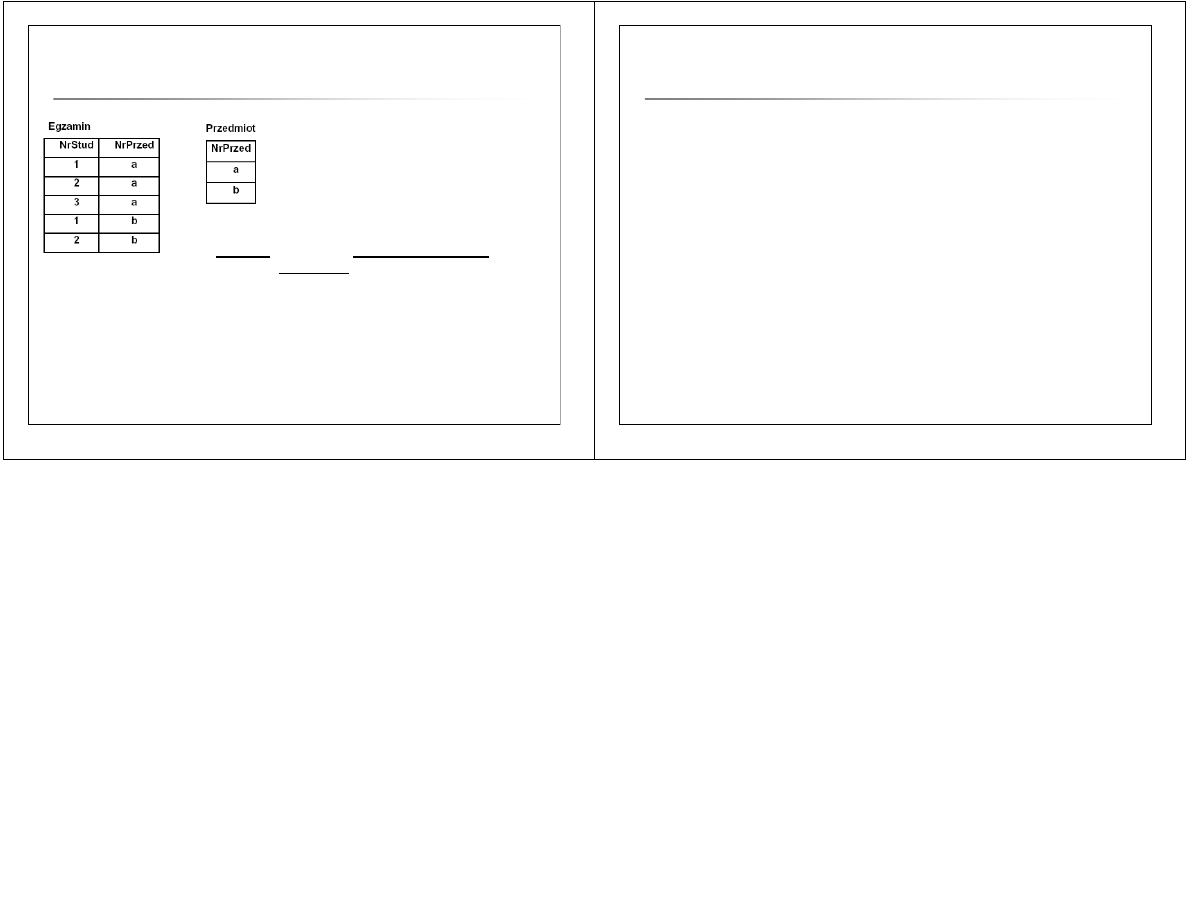
Podaj numery studentów, którzy zdawali egzamin z ka
ż
dego przedmiotu.
T. Pankowski, Model relacyjny
56
Podzielenie
Podzielenie
–
–
wyra
wyra
ż
ż
enie za pomoc
enie za pomoc
ą
ą
innych operacji
innych operacji
T1
← π
U – X
(R)
T2
← π
U – X
((S
´
T1) – R)
T = T1 – T2
T1
← π
NrStud
(Egzamin)
T2
← π
NrStud
((Przedmiot
´
T1) – Egzamin)
T = T1 – T2
Przedmiot
´
T1 – Egzamin
Przedmiot
´
T1
57
Podzielenie
Podzielenie
(c.d)
(c.d)
Podaj numery studentów, którzy zdawali egzamin z ka
ż
dego przedmiotu.
Wyraża zapytanie typu „dla-każdego”
Schemat rozumowania (z podwójną negacją):
studenci, dla których nie istnieje przedmiot,
z którego nie zdawali egzaminu
select distinct E.NrStud
from Egzamin E
where not exists (select *
from Przedmiot P
where not exists (select *
from Egzamin E1
where E1.NrPrzed = P.NrPrzed and E1.NrStud = E.NrStud)))
58
Podzielenie
Podzielenie
(c.d)
(c.d)
{e.NrStud | Egzamin(E)
∧ ∀
p(Przedmiot(p)
⇒
∃
e1 (Egzamin(e1)
∧
e1.NrPrzed=p.NrPrzed
∧
e1.NrStud= e.NrStud))}
Zast
ą
pienie
∀
:
∀
x(
ϕ ⇒ ϕ
’)
⇔ ¬
(
∃
x(
ϕ ∧ ¬ϕ
’))
{e.NrStud | Egzamin(E)
∧ ¬ ∃
p(Przedmiot(p)
∧
¬ ∃
e1 (Egzamin(e1)
∧
e1.NrPrzed=p.NrPrzed
∧
e1.NrStud= e.NrStud))}
select E.NrStud
from Egzamin E
where not exists (select *
from Przedmiot P
where not exists (select *
from Egzamin E1
where E1.NrPrzed = P.NrPrzed and E1.NrStud = E.NrStud)))
Wyszukiwarka
Podobne podstrony:
model relacyjny
Bazy danych model relacyjny
11 SV650K1 '01 Model
12 SV650SK1 '01 Model
Microsoft PowerPoint 03 model relacyjny id 299067
model relacyjny
Żebro 01 Model 000
Podciąg 01 Model 000
11 SV650K1 01 Model
Projekt BD Relacyjne Bazy Danych obligat ET II II 01
2005 01 podst model
(paper model)(mały modelarz 01 1959)polski parowóz pt 47 TXHIJ2ZLF4EVBIUZNK4BG4RLCURZMRTJCMLX3MI
01 Mathematical model of power network
[03] Bazy Danych Relacyjny Model Danych
2005 01 rozsz model
Budownictwo ogólne projekt Model (01)
więcej podobnych podstron