Autor: Grzegorz Lenc,

Strona

1

/

11

INSTRUKCJA

LABORATORIUM

ELEKTROTECHNIKI

BADANIE TRANSFORMATORA

Autor: Grzegorz Lenc,

Strona

2

/

11

Badanie transformatora

Celem ćwiczenia jest poznanie zasady działania transformatora oraz wyznaczenie

parametrów schematu zastępczego.

Podstawy teoretyczne

Działanie transformatora polega na wzajemnym oddziaływaniu elektromagnetycznym

uzwojeń (najczęściej dwóch) niepołączonych galwanicznie, nawiniętych na wspólnym rdzeniu (

rys.1)

Jeżeli do zacisków uzwojenia pierwotnego (uzwojenia, do którego doprowadza się energię)

przyłożymy napięcie sinusoidalne zmienne U

1

, to w uzwojeniu będzie płynął prąd o wartości I

1

,

który wywoła powstanie strumienia

1

1

I

s

l

z

u

s

H

u

⋅

⋅

⋅

=

⋅

⋅

⋅

=

Φ

µ

µ

(1)

gdzie:
µ – przenikalność magnetyczna,

l

z

I

H

1

1

=

– natężenie pola magnetycznego,

s – przekrój poprzeczny rdzenia transformatora,
l – długość obwodu magnetycznego,
z

1

– liczba zwojów uzwojenia pierwotnego.

Jeżeli założyć, że w pewnym zakresie natężenia pola magnetycznego µ = const., to przy

sinusoidalnym prądzie wartość chwilowa strumienia magnetycznego będzie równa:

t

m

ϖ

sin

Φ

=

Φ

(2)

gdzie:

Ф

m

– wartość maksymalna strumienia,

ω = 2 Π f – pulsacja.

Zmienny strumień magnetyczny wzbudza w obydwóch uzwojeniach siłę elektromotoryczną,

o wartościach chwilowych równych:

dt

d

z

e

Φ

−

=

1

;

dt

d

z

e

Φ

−

=

2

2

(3)

i wartościach skutecznych:

Autor: Grzegorz Lenc,

Strona

3

/

11

1

1

1

44

,

4

2

2

fz

f

z

E

m

m

Φ

=

Φ

Π

=

2

2

2

44

,

4

2

2

fz

f

z

E

m

m

Φ

=

Φ

Π

=

(4)

zatem przekładnia transformatora:

2

1

2

1

z

z

E

E

=

(5)

Z powodu bardzo małych strat energii przetwarzanej w transformatorze (ok. 2 – 3 %),

można przyjąć, że moc doprowadzona do uzwojenia pierwotnego jest prawie równa mocy

oddawanej przez uzwojenie wtórne, tzn.:

U

1

I

1

≈ U

2

I

2

(6)

czyli:

2

1

1

2

2

1

2

1

z

z

I

I

U

U

E

E

=

=

≈

(7)

i

1

R

1

z

1

z

2

Φ

s1

Φ

r

i

2

R

2

Φ

s2

u

1

u

2

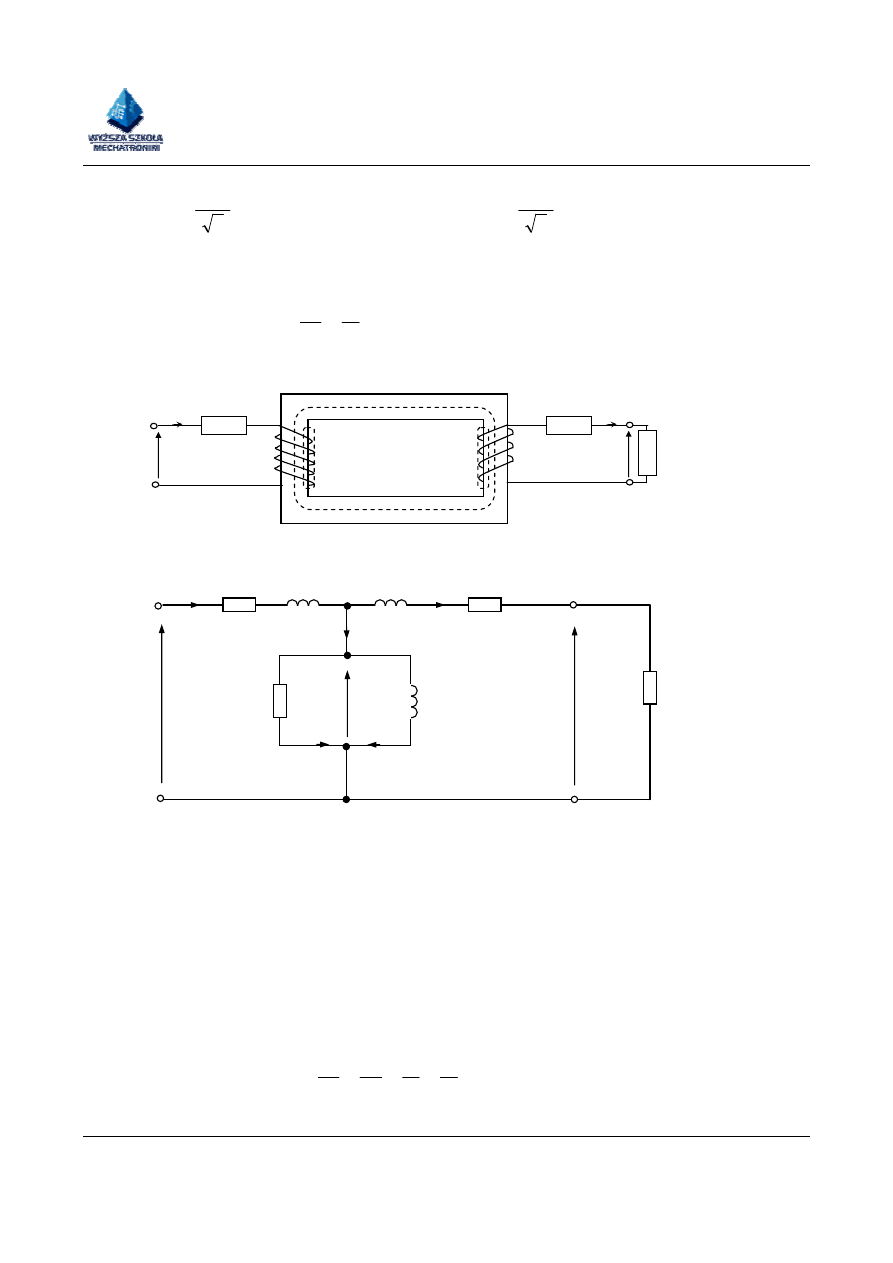
Rys. 1. Transformator dwuuzwojeniowy z rdzeniem ferromagnetycznym

I

1

L's

2

Z'

0

R

1

Ls

1

R'

2

R

Fe

X

µ

U'

2

E

1

I

µ

I

Fe

U

1

Rys. 2. Schemat zastępczy transformatora dwuuzwojeniowego

Autor: Grzegorz Lenc,

Strona

4

/

11

Siły elektromotoryczne e

1

oraz e

2

indukowane w uzwojeniach spełniają różne zadania. sem

e

1

przeciwdziała przyłożonemu napięciu U

1

, a e

2

odgrywa rolę źródła energii i od jej wartości

zależy wartość prądu i

2

.

Prąd i

2

przepływając przez zwoje z

2

wytwarza strumień magnetyczny, który zgodnie z

regułą Lenza będzie osłabiał strumień magnetyczny Ф, a co za tym idzie, sem e

1

.

Zmniejszenie wartości e

1

powoduje wzrost natężenia prądu pierwotnego i

1

, co kompensuje

rozmagnesowujące oddziaływanie prądu wtórnego i

2

. Jak z tego widać, każdej zmianie prądu i

2

odpowiada zmiana prądu i

1,

czyli można uważać, że praktycznie wartość maksymalna strumienia

głównego Ф

m

nie ulega zmianie, o ile napięcie zasilające pozostaje wartością stałą.

Przy przepływie prądu zmiennego przez uzwojenie nawinięte na rdzeń wykonany z

materiału ferromagnetycznego powstają straty histerezowe i wiroprądowe. Jeżeli prąd płynący w

uzwojeniu ma częstotliwość f, to punkt pracy przemieszcza się po pętli histerezy f razy na sekundę.

Moc tracona na przemagnesowanie (straty histerezowe) jest proporcjonalna do częstotliwości i do

pola powierzchni pętli histerezy. Do określenia wartości strat w rdzeniu stosowane są wzory

empiryczne. Wzór Richtera pozwala obliczyć straty jednostkowe histerezowe w W/kg :

2

100

m

B

f

Ph

ε

=

(8)

gdzie:

ε –

współczynnik materiałowy zawarty w granicach 2,8 ÷ 4,4.

Zgodnie z prawem indukcji elektromagnetycznej zmienny strumień magnetyczny indukuje

w środowisku przewodzącym siły elektromotoryczne, które powodują w nim przepływ prądów

wirowych. Prądy te powodują dodatkowe straty czynne i grzanie rdzenia.

Starty jednostkowe wiroprądowe w W/kg, wg wzoru Richtera obliczamy:

2

2

100

m

W

B

f

P













=

δ

(9)

gdzie:

δ – współczynnik materiałowy zawarty w granicach (1,1 ÷ 22,4 )

W celu ograniczenia prądów wirowych, rdzenie transformatorów wykonuje się z cienkich

blach stalowych( z dodatkiem krzemu ), między sobą izolowanych.

Całkowite straty magnetyczne w rdzeniu są sumą strat histerezowych i wiroprądowych i

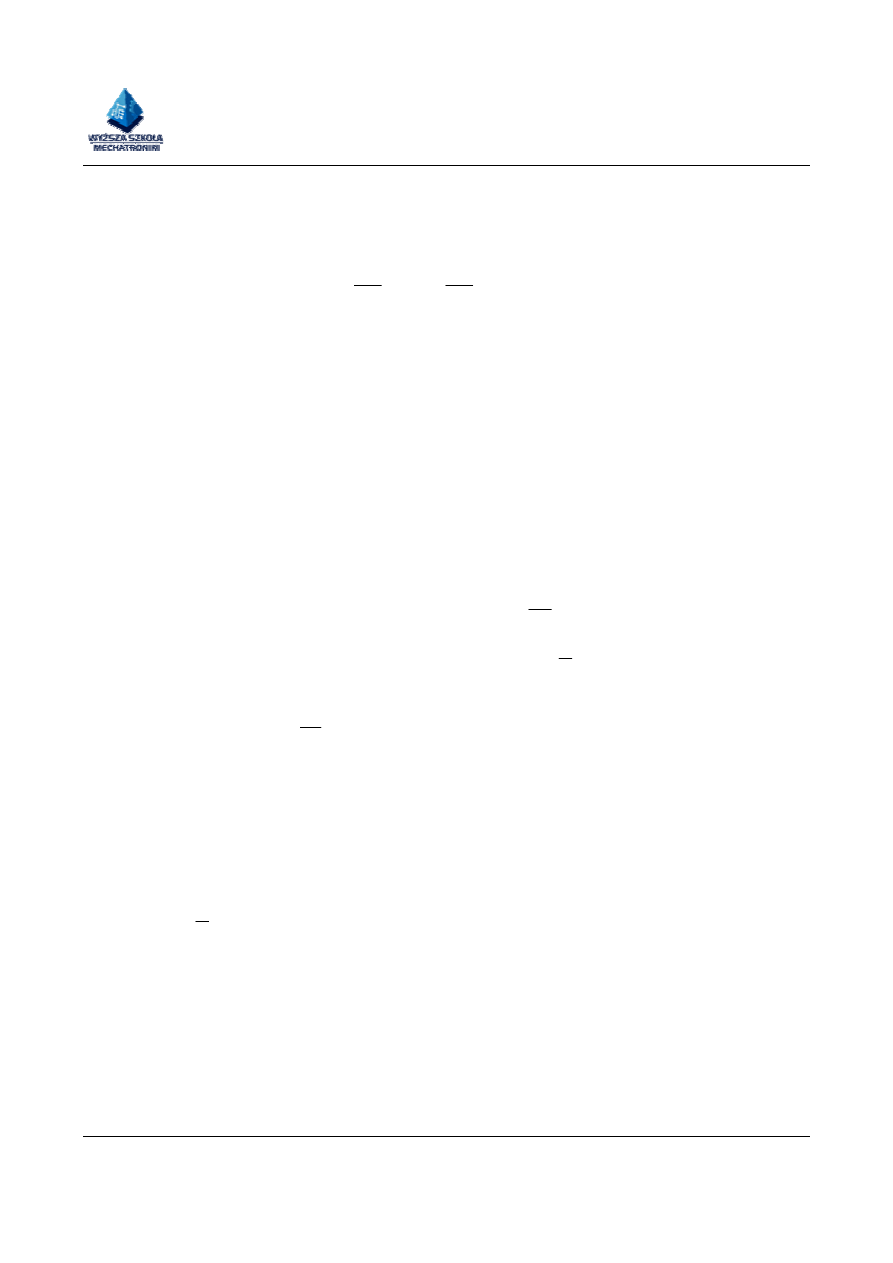
Autor: Grzegorz Lenc,

Strona

5

/

11

podawane są zazwyczaj w W/kg:

W

n

Fe

P

P

P

+

=

(10)

2

2

2

100

100

m

m

Fe

B

f

B

f

P













+

=

δ

ε

(11)

Równania napięciowe transformatora uwzględniające rezystancję i reaktancję rozproszenia

uzwojeń można zapisać w następujący sposób:

(

)

1

1

1

1

1

E

I

L

j

R

U

S

+

+

=

ω

(12a)

(

)

2

2

2

2

2

U

I

L

j

R

E

S

+

+

=

ω

(12b)

gdzie:

R

1

, R

2

– rezystancje uzwojeń transformatora,

L

S1

, L

2

–indukcyjność rozproszenia uzwojeń transformatora,

E

1

, E

2

– siły elektromotoryczne( napięcia magnesujące ).

Jeśli przez R

Fe

oznaczymy rezystancję odwzorowującą zjawisko strat w stali ( P

Fe

= R

Fe

I

Fe

2

),

a przez X

µ

reaktancję magnesowania, to uwzględniając zależności:

2

0

2

I

Z

U

=

2

1

E

E

=

ϑ

'

2

1

I

I

I

I

Fe

+

+

=

µ

'

1

2

2

I

I

ϑ

=

otrzymamy równanie napięć uzwojenia wtórnego transformatora w następującej postaci:

2

2

2

2

2

1

'

'

z

I

L

j

I

R

E

s

=

+

=

ϑ

ϖ

ϑ

ϑ

(14a)

czyli

2

2

2

2

2

2

2

1

'

'

U

I

jX

I

R

E

ϑ

ϑ

ϑ

+

+

=

(14b)

gdzie:

2

2

2

'

ϑ

R

R

=

– rezystancja uzwojenia wtórnego sprowadzona do obwodu pierwotnego,

2

2

2

'

ϑ

X

X

=

– reaktancja rozproszenia wtórnego sprowadzona do obwodu pierwotnego,

ϑ

2

2

' U

U

=

– napięcie na zaciskach wtórnych sprowadzone do obwodu pierwotnego,

ϑ

1

'

2

2

I

I

=

– prąd w uzwojeniu wtórnym sprowadzony do obwodu pierwotnego.

Po uwzględnieniu wprowadzonych wielkości równanie (4) przyjmuje postać:

'

'

'

'

'

2

2

2

2

2

1

U

I

jX

I

R

E

+

+

=

(15)

(13)

Autor: Grzegorz Lenc,

Strona

6

/

11

Równanie powyższe pozwala na galwaniczne połączenie obwodu pierwotnego i wtórnego w
schemacie zastępczym transformatora ( rys 2)

Wykres wskazowy transformatora odpowiadający schematowi zastępczemu oraz równaniom

(12a) i (15) przedstawia (rys 3).

Wartości elementów schematu zastępczego można wyznaczyć z pomiarów w stanie zwarcia

i w stanie jałowym.

Stanem jałowym transformatora nazywamy stan, w którym transformator jest nie obciążony

(I

2

= 0 i Z

2

= ∞ ). Odpowiadają mu schemat zastępczy i wykres wskazowy przedstawione na ( rys 4)

W czasie próby stanu jałowego napięcie i strumień osiągają wartości znamionowe,

U

1

jX

1

I

1

R

1

I

1

-E

1

I

0

I

2

'

I

µ

I

1

I

Fe

I

2

'

R

2

'I

2

'

U

2

'

jX

2

'

I

2

'

E

2

Φ

12

Rys. 3. Wykres wskazowy transformatora

X

2

R

1

X

1

R

2

R

Fe

X

µ

E

I

µ

I

Fe

U

1

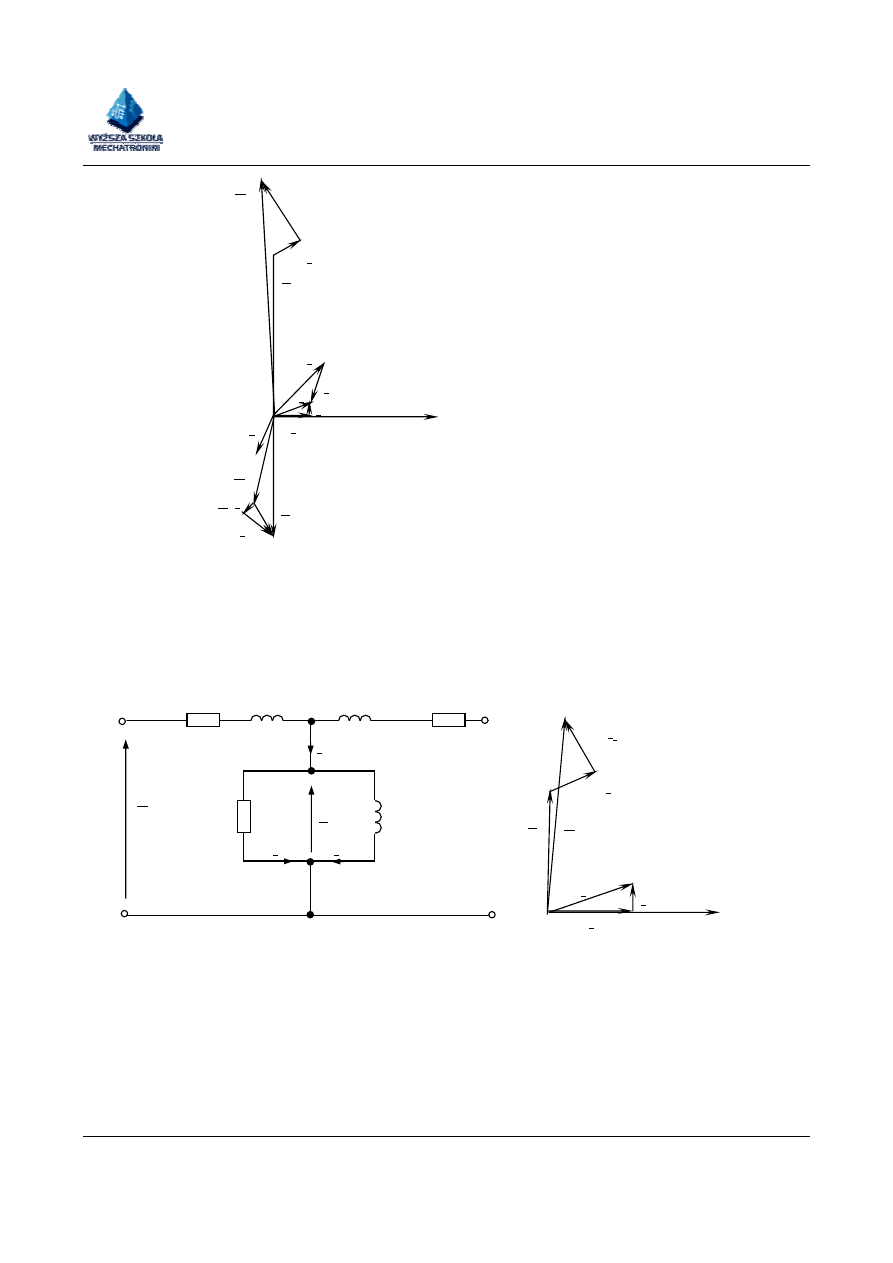
Rys. 4. Stan jałowy transformatora , schemat zastępczy i wykres wskazowy

I

0

I

0

X

1

I

0

E

1

U

1

I

µ

I

Fe

Φ

R

1

I

0

Autor: Grzegorz Lenc,

Strona

7

/

11

natomiast prąd jest bardzo mały w porównaniu z prądem znamionowym, dlatego straty w
uzwojeniach są pomijalnie małe, a moc czynna pobierana przez transformator jest równa w
przybliżeniu stratom mocy w stali:

Fe

R

U

P

2

1

0

=

(16)

Na podstawie próby biegu jałowego można również określić moc bierną niezbędną do

przemagnesowania rdzenia

µ

X

U

Q

2

1

0

=

(17)

Gdy uzwojenie wtórne transformatora zostanie zwarte ( U

2

= 0, Z

abc

= 0 ), wówczas transformator

znajduje się w stanie zwarcia.

Próbę zwarcia wykonuje się w ten sposób, że napięcie zasilające U

1

podnosi się do takiej

wartości, przy której prąd wtórny jest równy prądowi znamionowemu I

2z

= I

2n

= I

2.

Wartość

napięcia U

1

podczas tej próby wynosi około 0,1 U

n,

wobec tego strumień główny jest dużo mniejszy

od strumienia znamionowego, a co za tym idzie straty w żelazie oraz straty histerezowe są
pomijalnie małe.
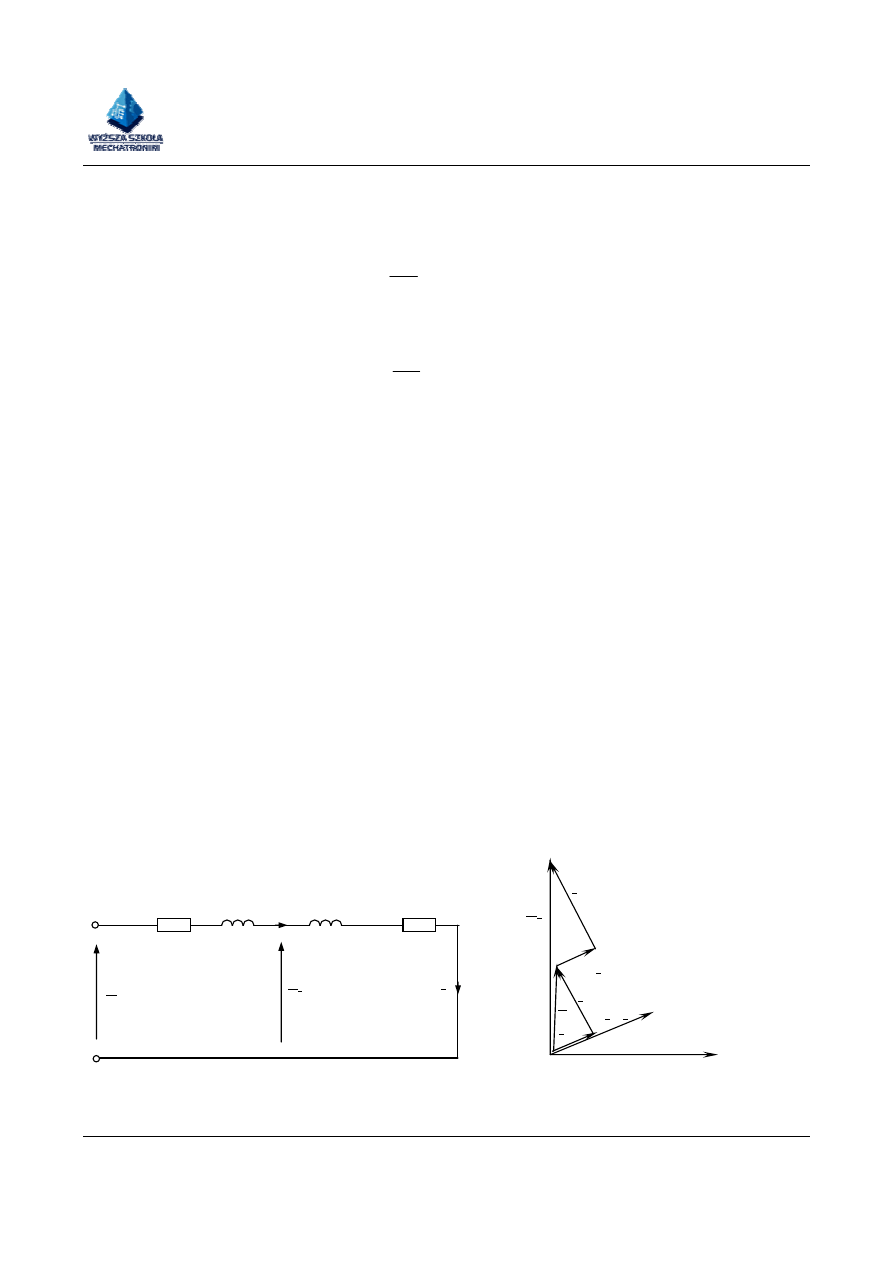
Schemat zastępczy transformatora i wykres wskazowy w stanie zwarcia przedstawia (rys 5 )

Moc pobierana przez transformator w stanie zwarcia wynika ze strat mocy czynnej i biernej

w uzwojeniach transformatora.

Moc czynna:

2

2

R

I

P

=

(18)

gdzie:

'

2

1

2

R

R

R

+

=

'

2

1

R

R

≈

Moc bierna:

z

X

I

Q

2

=

(19)

gdzie:

'

2

1

X

X

X

z

+

=

'

2

1

X

X

≈

X

2

'

R

1

X

1

R

2

'

E

1

U

1

I

2

U

1

I

2

X

2

'

I

1

=I

2

I

2

R

2

'

E

1

R

1

I

1

I

1

X

1

Ф

Rys.5. Stan zwarcia transformatora schemat zastępczy i wykres wskazowy

Autor: Grzegorz Lenc,

Strona

8

/

11

Część praktyczna

Wykonanie pomiarów

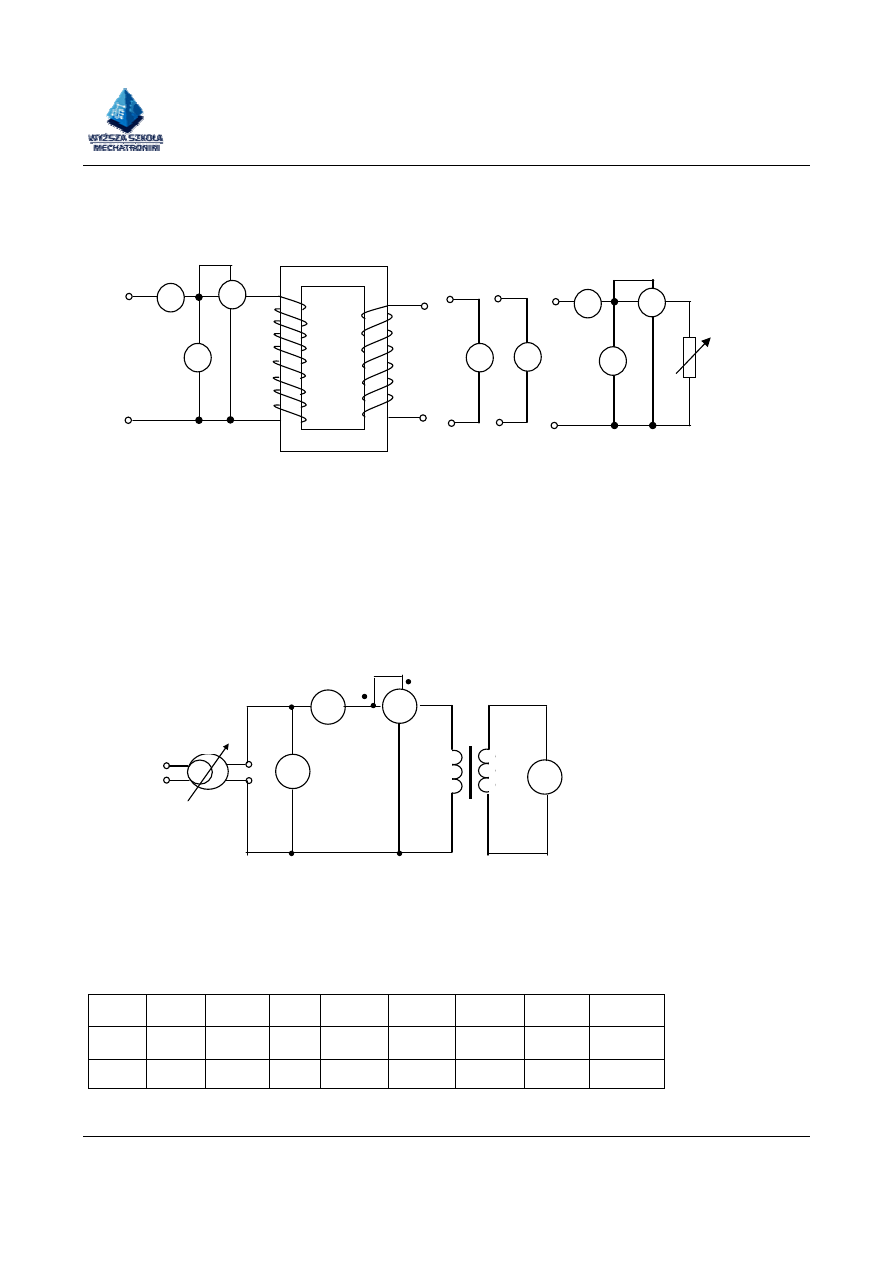
2 .1 Stan jałowy transformatora

W układzie przedstawionym na rys. 6.a zmieniając napięcie U

1

w granicach od 0 do 1,2 U

n

(U

n

–

napięcie znamionowe), odczytać wskazania mierników. Wyniki pomiarów przedstawić w tabeli jak
niżej

Lp.

U

1

I

1

P

1

U

2

cos φ

ϑ

X

µ

R

Fe

[V]

[A]

[W]

[V]

–

–

[Ω]

[Ω]

1

A

V

W

A

V

A

V

W

Rys.6. Schemat pomiarowy do badania transformatora: a) w stanie jałowym b) w stanie zwarcia
c) w stanie obciążenia

V

2

A

A

1

V

1

W

1

Tr

Autor: Grzegorz Lenc,

Strona

9

/

11

Pomijając spadki napięcia na rezystancji reaktancji uzwojenia pierwotnego obliczyć wartości R

Fe

oraz X

µ

schematu zastępczego transformatora:

ϕ

cos

1

1

I

U

R

Fe

=

;

ϕ

µ

sin

1

1

I

U

X

=

Na podstawie wyników pomiarów dla biegu jałowego transformatora wykreślić na

wspólnym wykresie charakterystyki:

( )

1

0

U

f

I

=

;

( )

1

0

U

f

P

=

;

( )

1

cos

U

f

=

ϕ

;

oraz wyznaczyć przekładnie transformatora

2

1

U

U

=

ϑ

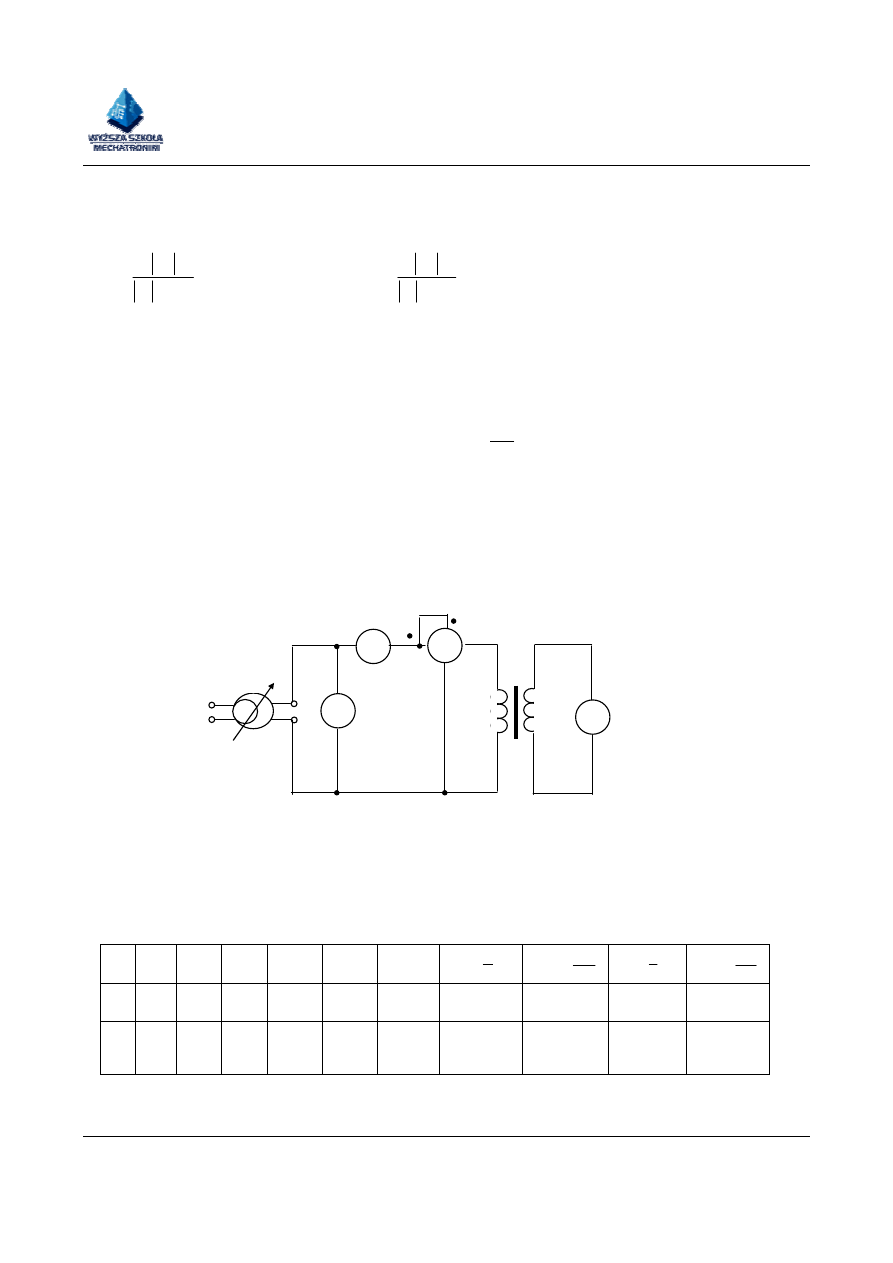
2.Stan zwarcia transformatora

Przy badaniu stanu zwarcia transformatora należy tak ustawić napięcie wejściowe U

1

(ułamek napięcia znamionowego), by prąd wyjściowy I

2

nie przekraczał prądu znamionowego

uzwojenia wtórnego I

2N

.

Schemat ideowy obwodu do badania transformatora w stanie zwarcia

W układzie przedstawionym na rysunku zmieniając napięcie zasilające od zera do wartości

U

1z

, dla którego wartość prądu I

2

= I

2n

, odczytać wskazania mierników Wyniki pomiarów zapisać

w tabeli jak niżej

Lp.

I

2

I

1z

U

1z

P

1z

R

z

X

z

z

R

R

2

1

1

=

2

1

2

ϑ

R

R

=

z

X

X

2

1

1

=

2

1

2

ϑ

X

X

=

[A]

[A]

[V]

[W]

[Ω]

[Ω]

[Ω]

[Ω]

[Ω]

[Ω]

1

A

2

A

A

1

V

1

W

1

Tr

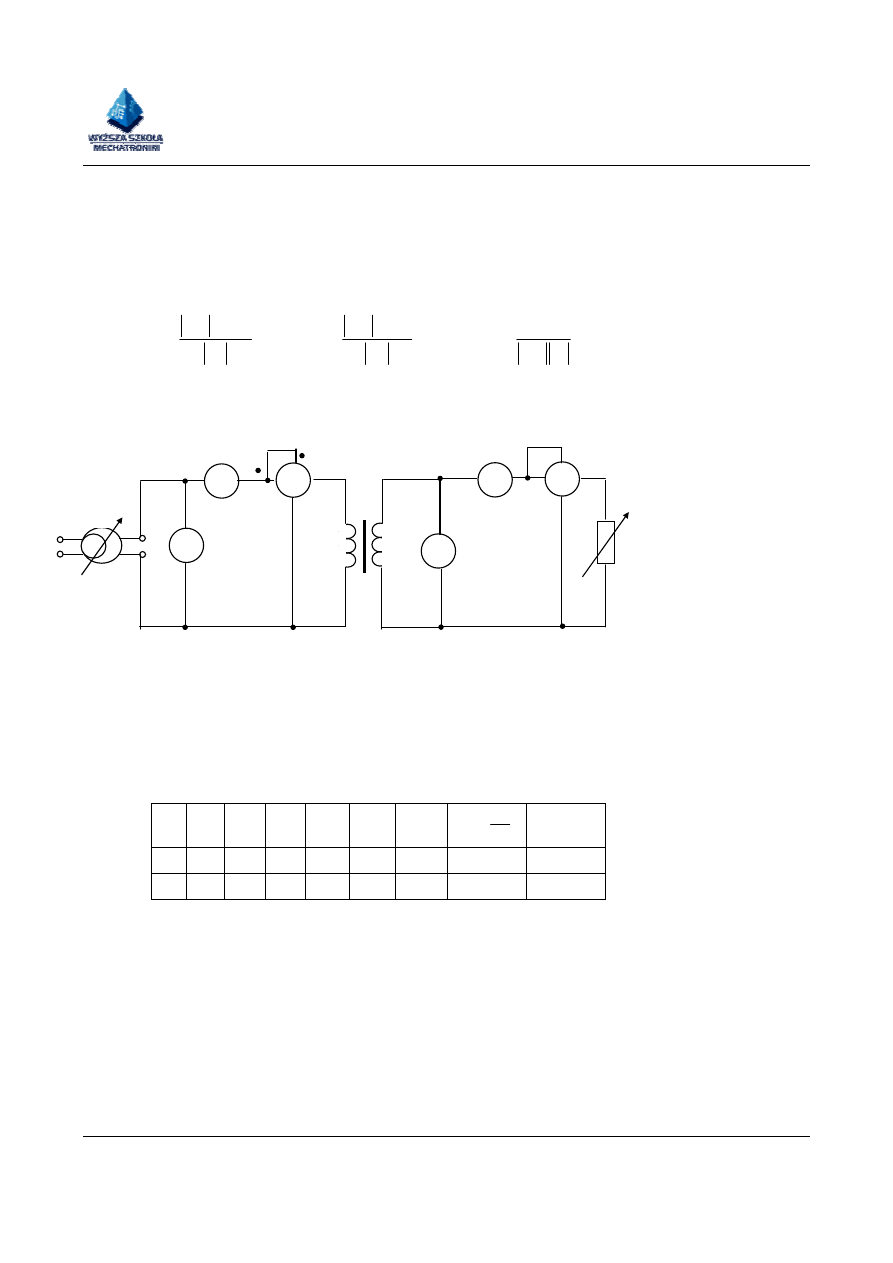
Autor: Grzegorz Lenc,

Strona

10

/

11

Korzystając z wyników pomiarów dla stanu zwarcia transformatora, określić napięcie

zwarcia oraz parametry R

1

, X

1

, R

2

, X

2,

schematu zastępczego transformatora:

z

z

z

I

U

R

1

1

cos

ϕ

=

;

z

z

z

I

U

X

1

1

sin

ϕ

=

;

z

z

I

U

P

1

1

cos

=

ϕ

2.3. Stan obciążenia transformatora













Schemat ideowy do badania transformatora w stanie obciążenia.

W układzie przedstawionym na rysunku utrzymując napięcie pierwotne U

1

=U

1n

=const,

zmieniać rezystancję obciążenia R

2

w taki sposób, aby prąd I

2

zmieniał się w granicach od

0 <

I

2

< I

2n

Wyniki pomiarów zapisać w tabeli

Lp. U

1

I

1

P

1

I

2

U

2

P

2

1

2

P

P

=

η

cos φ

[V] [A] [W] [A] [V]

[W]

–

–

1

Na podstawie wyników pomiarów, otrzymanych przy badaniu transformatora w stanie

obciążenia, obliczyć sprawność η oraz cos φ. Wykonać we wspólnym układzie współrzędnych
charakterystyki obciążenia transformatora.

( )

2

2

I

f

U

=

;

( )

2

1

I

f

I

=

;

( )

2

I

f

=

η

;

( )

2

cos

I

f

=

ϕ

V

2

A

A

1

V

1

W

1

A

2

W

2

Tr

R

obc

Autor: Grzegorz Lenc,

Strona

11

/

11

LABORATORIUM ELEKTROTECHNIKI

ET003 – BADANIE TRANSFORMATORA

Specyfikacja S003

W skład stanowiska laboratoryjnego wchodzą:

•

Autotransformator

•

Transformator

•

2 x Amperomierz

•

2 x Woltomierz

•

2 x Watomierz

•

Rezystory

•

Stanowisko do badania transformatora