KMBiM

 

GEOMETRIA WYKREŚLNA

Rok I, semestr I (zimowy)

WILiŚ  PG

ĆWICZENIE NR 4 T

Rok akademicki 2007/2008

Imię i Nazwisko

Nr indeksu

Grupa

Data

Ocena

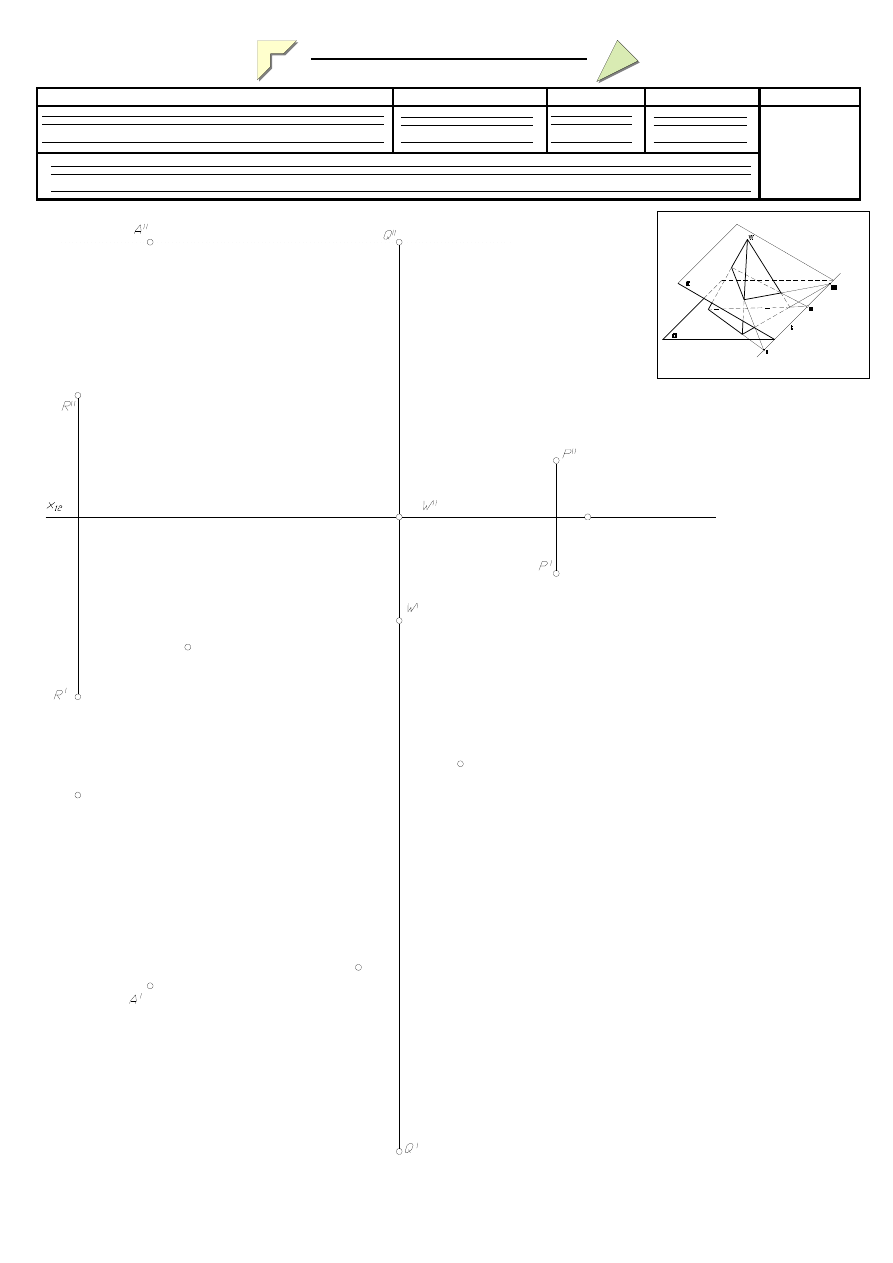
POLECENIE  Przekrój wielościanu płaszczyzną

1. Opisz wierzchołki ostrosłupa o wierzchołku W, którego podstawą jest pięciokąt znajdujący się 

na płaszczyźnie równoległej do rzutni π

1.

 Narysuj odnoszące i tworzące ostrosłupa.

2. Sprowadź płaszczyznę tnącą PQR do położenia rzutującego w trzecim rzucie. Wyznacz oś x

13

.

3. Narysuj trzeci rzut ostrosłupa.
4. Wyznacz przekrój ostrosłupa płaszczyzną PQR.
5. Sprawdź uzyskany przekrój za pomocą kolineacji we wszystkich rzutach.
6. Ustal widoczność bryły ograniczonej przekrojem.  
7. Wyeksponuj wynik według wytycznych graficznych.

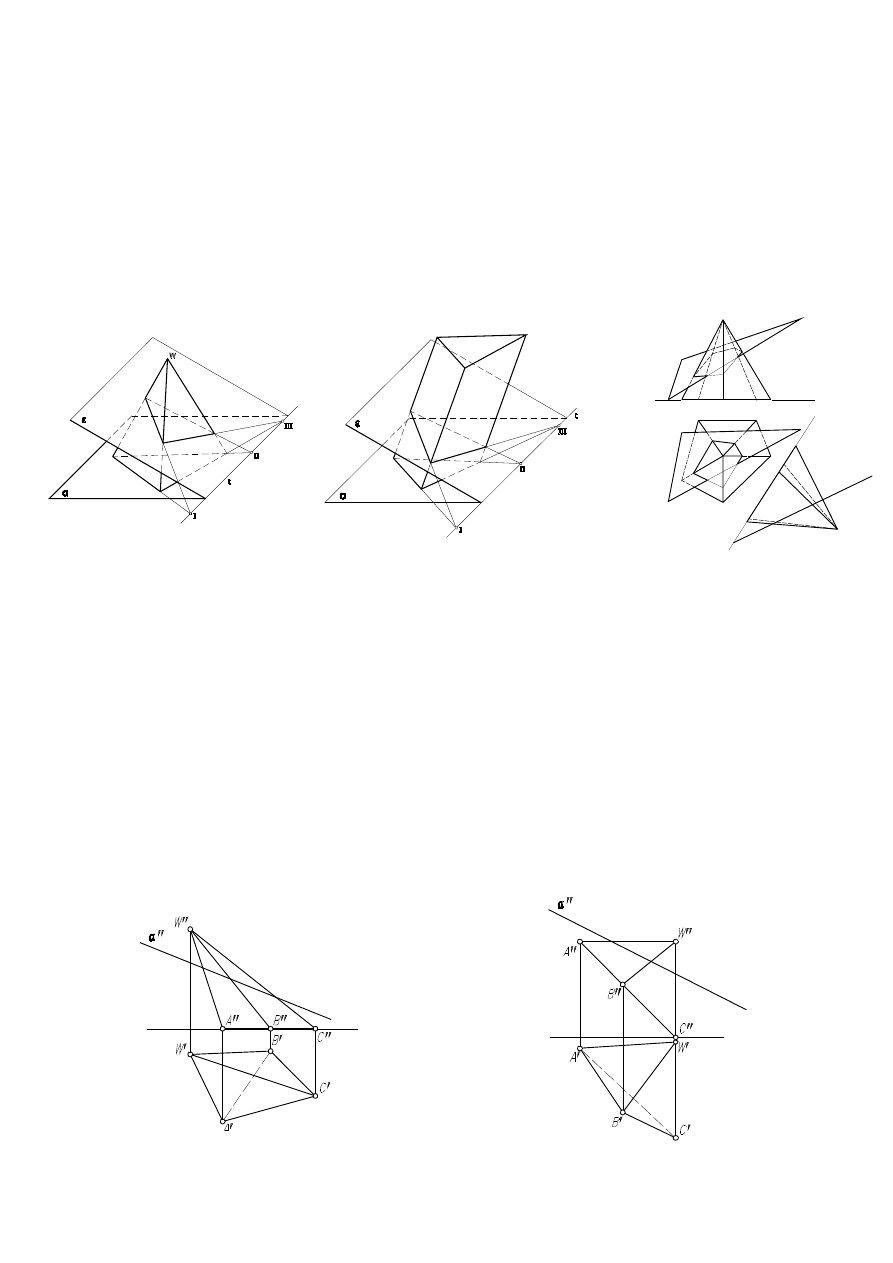
ZAGADNIENIE    Kolineacja, powinowactwo, przekroje wielościanów.

      

Rys.1. Kolineacja

Rys.2. Powinowactwo

t        –   oś kolineacji/powinowactwa
ε        –   płaszczyzna tnąca
α        –   płaszczyzna podstawy
I,II,III –  punkty wspólne prostych odpowiadających 

sobie na płaszczyźnie α i ε

Rys.3. Przekrój ostrosłupa 

płaszczyzną trójkąta

.

ZADANIA

1. Narysuj dowolny ostrosłup, którego podstawa znajduje się na jednej z rzutni. Jako płaszczyznę tnącą 

przyjmij dowolną płaszczyznę rzutującą:

a) poziomo-rzutującą,
b) pionowo-rzutującą.
Wyznacz przekrój.

2. Podaj cechy przekroju wielościanu. Jaki wielobok jest przekrojem czworościanu?

3. Narysuj przekrój ostrosłupa ABCW płaszczyzną 

α (

 rys. 1 i 2)

.

Rys.1.

Rys.2.

...............................................................

Poprzez niniejszy podpis oświadczam, że znam Regulamin Studiów i Regulamin Przedmiotu oraz, że niniejsza praca wykonana została przeze mnie samodzielnie.