Prof. Piotr Chrzan

WYKŁAD

DYSKONTOWE METODY

OCENY PRZEDSIĘWZIĘĆ INWESTYCYJNYCH

1. Rodzaje i cechy wydatków inwestycyjnych

2. Wartość bieżąca netto

3. Wewnętrzna stopa zwrotu

4. Zmodyfikowana wewnętrzna stopa zwrotu

5. Zdyskontowany okres zwrotu nakładów inwe-

stycyjnych

6. Wskaźnik rentowności inwestycji

7. Porównywanie projektów o różnych okresach

użytkowania

1

Prof. Piotr Chrzan

1. Rodzaje i cechy wydatków inwestycyjnych

Inwestowanie określa się jako finansowe angażowanie się

w jakieś przedsięwzięcie w nadziei uzyskania przyszłych

korzyści

Przedsięwzięcie jest to zespół czynności wzajemnie ze sobą

powiązanych, które mogą być akceptowane lub odrzucone

w całości.

Podział przedsięwzięć według celu, który mają zrealizować:

1. Przedsięwzięcia zastępujące istniejące dotychczas obiek-

ty przedsiębiorstwa

2. Przedsięwzięcia zwiększające skalę dotychczasowej

działalności

3. Przedsięwzięcia o charakterze strategicznym

4. Przedsięwzięcia wynikające z poprawy bezpieczeństwa

pracy, ekologii, dostosowania działalności do obowiązu-

jących przepisów

2

Prof. Piotr Chrzan

Cechy inwestowania

– wartość zaangażowania finansowego znana i pewna

– przyszłe korzyści jedynie możliwe, a więc niepewne

Inwestowanie (Inwestycje) dzielą się na:

– finansowe (akcje, obligacje, depozyty bankowe)

– rzeczowe (zakup maszyny, budowa zakładu)

Obie formy inwestowania są komplementarne.

Inwestowanie, spekulacja, hazard

Inwestorzy –podmioty inwestujące (indywidualni, instytu-

cjonalni (przedsiębiorstwa)

Przedmiotem badań analizy przedsięwzięć inwestycyjnych

przedsiębiorstwa (firmy) są wydatki inwestycyjne, które

przedsiębiorstwo ponosi na swoja działalność i związane z

nimi decyzje inwestycyjne.

Wydatki inwestycyjne rozpatrywane są jako nakłady, które

przedsiębiorstwo ponosi na konkretne aktywa materialne, a w

ich ramach na majątek trwały.

Decyzje inwestycyjne – ile?, w co? i jak inwestować?

Decyzje finansowe – jak pozyskiwać kapitał w celu realizacji

inwestycji?

3

Prof. Piotr Chrzan

Cechy nakładów i decyzji inwestycyjnych

– istotne obciążenie finansowe przedsiębiorstwa

– nakłady inwestycyjne angażowane są na długi okres

czasu

– decyzje inwestycyjne z reguły nieodwracalne lub bardzo

kosztowne

– korzyści uzyskuje się w przyszłości, nieraz odległej

– zawsze istnieje element ryzyka i niepewności czy prze-

widywane korzyści zastana osiągnięte

– znaczny wpływ na osiągnięcie celów finansowych

przedsiębiorstwa

– determinują przyszły kierunek rozwoju przedsiębiorstwa

– wpływają na poziom przyszłego niezbędnego majątku

obrotowego

Związki inwestowania z pozostałymi sferami działalności

przedsiębiorstwa

4

Prof. Piotr Chrzan

Analiza zdyskontowanych przepływów pieniężnych netto

Discounted Cash Flow Analysis

Przepływy środków pieniężnych – rzeczywisty przepływ śro-

dków pieniężnych netto, w przeciwieństwie do przepływów

bilansowych (metoda memoriałowa).

Przyrostowe przepływy środków pieniężnych – przepływy

środków pieniężnych netto przypisywane przedsięwzięciu

inwestycyjnemu.

Alternatywny koszt kapitału jest to stopa k dochodu (zwrotu)

jaką przedsiębiorstwo traci inwestując ten kapitał w przed-

sięwzięcie analizowane i rezygnując z lokaty kapitału w naj-

bardziej efektywne z możliwych przedsięwzięć alternatyw-

nych.

Koszt alternatywny (koszt utraconych korzyści) można roz-

ważać jako:

– koszt pozyskania kapitału przez przedsiębiorstwo

– stopę dochodu, której można oczekiwać od przedsię-

wzięcia podobnego.

5

Prof. Piotr Chrzan

2. . Wartość bieżąca netto

NPV Net Present Value

Wartość obecna netto

Wartość teraźniejsza netto

Wartość zaktualizowana netto

CIF – Cash In Flow (wpływy środków pieniężnych)

CIF

t

– wpływy środków pieniężnych w okresie t

COF – Cash Out Flow (odpływy środków pieniężnych)

COF

t

– odpływy środków pieniężnych w okresie t

CF

– Cash Flow (przepływ środków pieniężnych netto)

CF

t

–

przepływ środków pieniężnych w okresie t

dla

t=

0,1,2,

...

n

t

t

t

COF

CIF

CF

−

=

+

t

CF – dodatnie przepływy środków pieniężnych

⎩

⎨

⎧

<

≥

=

+

0

CF

dla

0

0

CF

dla

CF

CF

t

t

t

t

−

t

CF – ujemne przepływy środków pieniężnych

⎩

⎨

⎧

>

≤

−

=

−

0

CF

dla

0

0

CF

dla

CF

CF

t

t

t

t

dla

t=

0,1,2,

...

n

−

+

−

=

t

t

t

CF

CF

CF

6

Prof. Piotr Chrzan

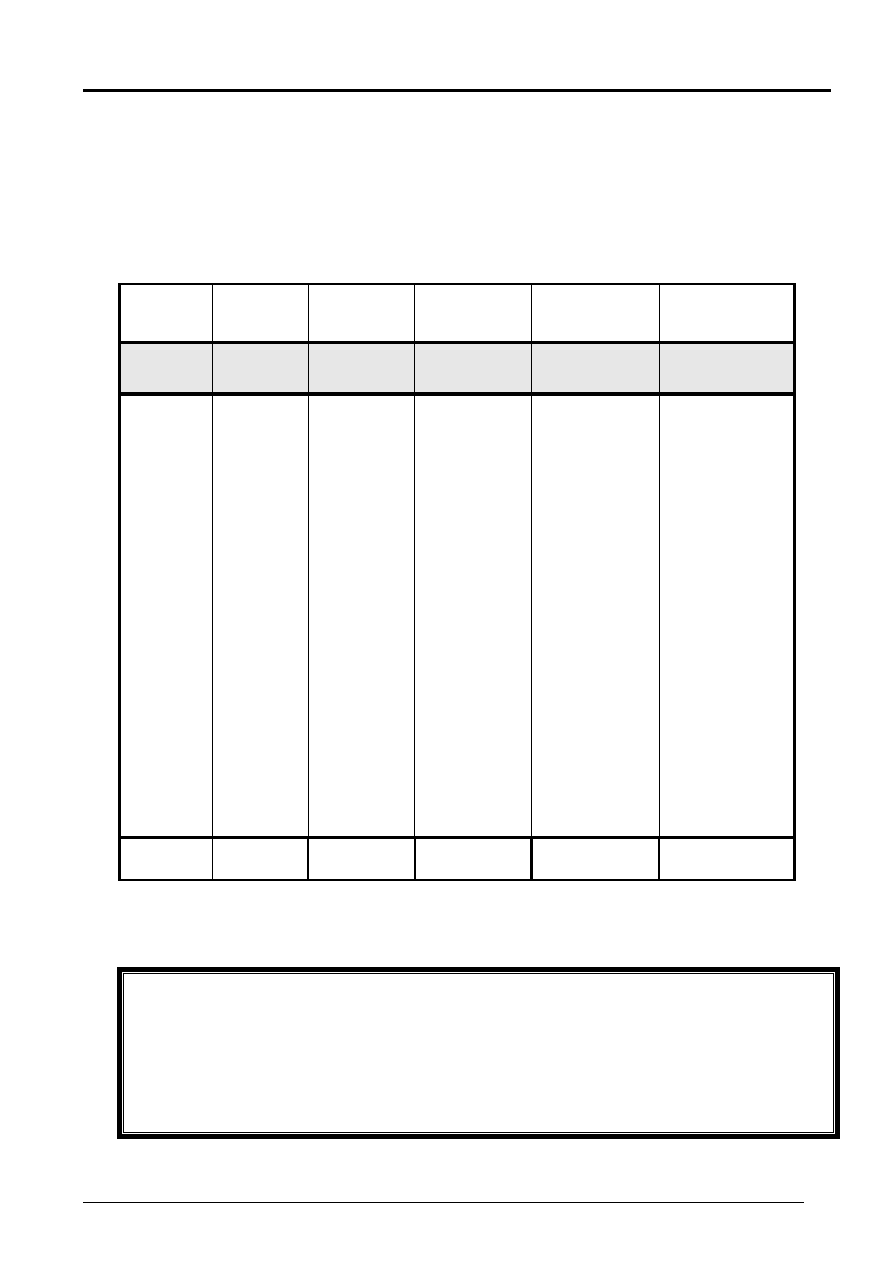
Przykład 1.

Przepływy środków pieniężnych w tys. zł.

związanych z realizacją przedsięwzięcia inwestycyjnego A.

Tabela 1.

Rok Wpływ

Odpływ Przepływ

Dodatni

przepływ

Ujemny

przepływ

t

CIF

t

COF

t

CF

t

+

t

CF

−

t

CF

0 0 10 -10 0

10

1 0 5 -5 0

5

2 0 1 -1 0

1

3 0 1 -1 0

1

4 0 1 -1 0

1

5 0 1 -1 0

1

6 8 1 7 7

0

7 9 1 8 8

0

8 10 1 9

9

0

9 11 1 10 10

0

10 12 0 12 12

0

Razem

50 23 27 46

19

Wartość bieżąca netto inwestycji (Net Present Value)

jest

to zaktualizowana na moment t = 0 wartość strumienia

przepływów pieniężnych netto CF

t

tej inwestycji.

7

Prof. Piotr Chrzan

∑

=

−

+

=

n

0

t

t

t

)

k

1

(

CF

NPV

gdzie: CF

t

– przepływy środków pieniężnych w okresie t

k – Koszt kapitału (wymagana stopa zwrotu inwestycji)

n – okres życia inwestycji

CF

t

= CIF

t

– COF

t

CIF

t

– wpływy środków pieniężnych

COF

t

– odpływy środków pieniężnych

∑

∑

=

−

=

−

+

−

+

=

n

0

t

t

t

n

0

t

t

t

)

k

1

(

COF

)

k

1

(

CIF

NPV

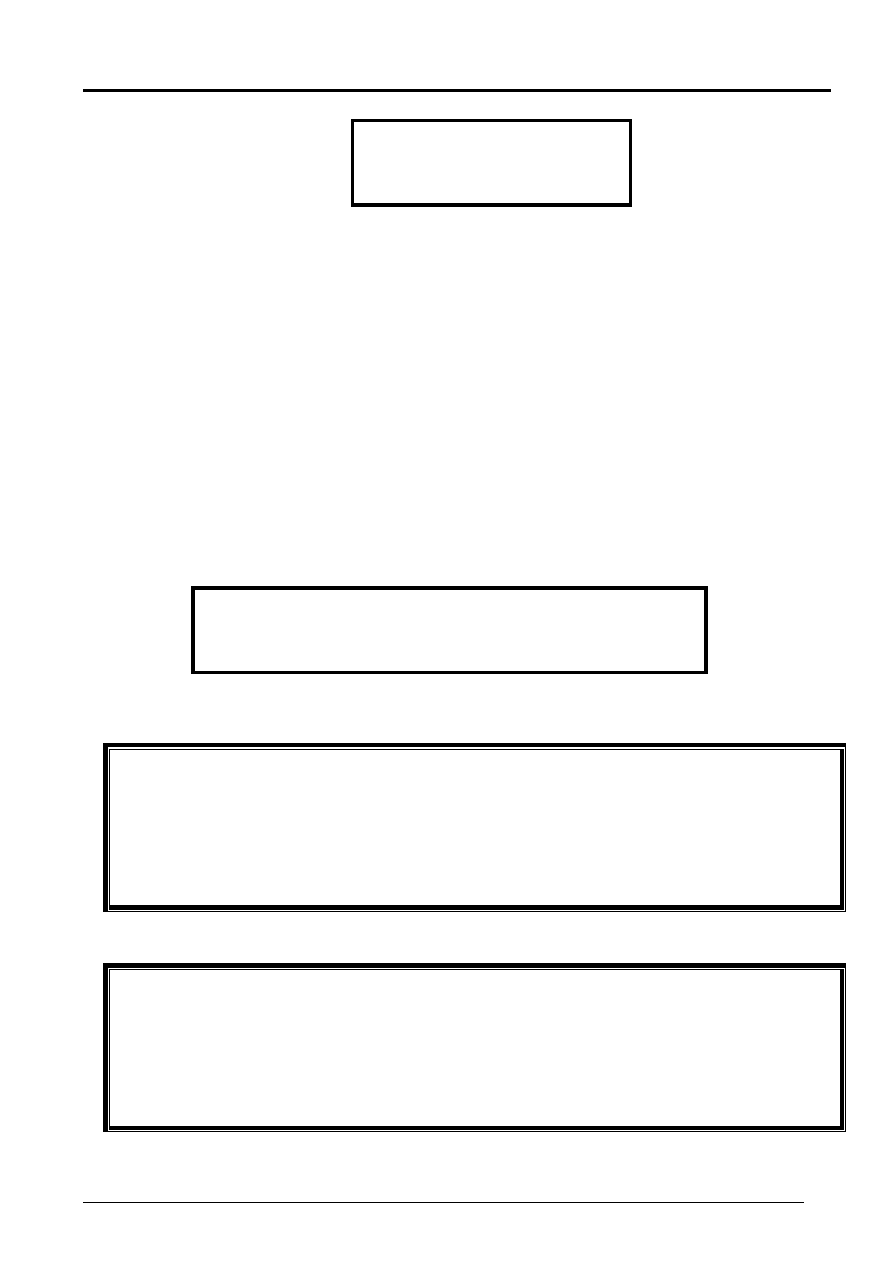
NPV mierzy nadwyżkę zaktualizowanych na moment t=0

wpływów nad zaktualizowanymi na ten moment odpływa-

mi.

NPV mierzy nadwyżkę sumy zdyskontowanych na moment

t=0 wpływów nad sumą zdyskontowanych na ten moment

odpływów.

8

Prof. Piotr Chrzan

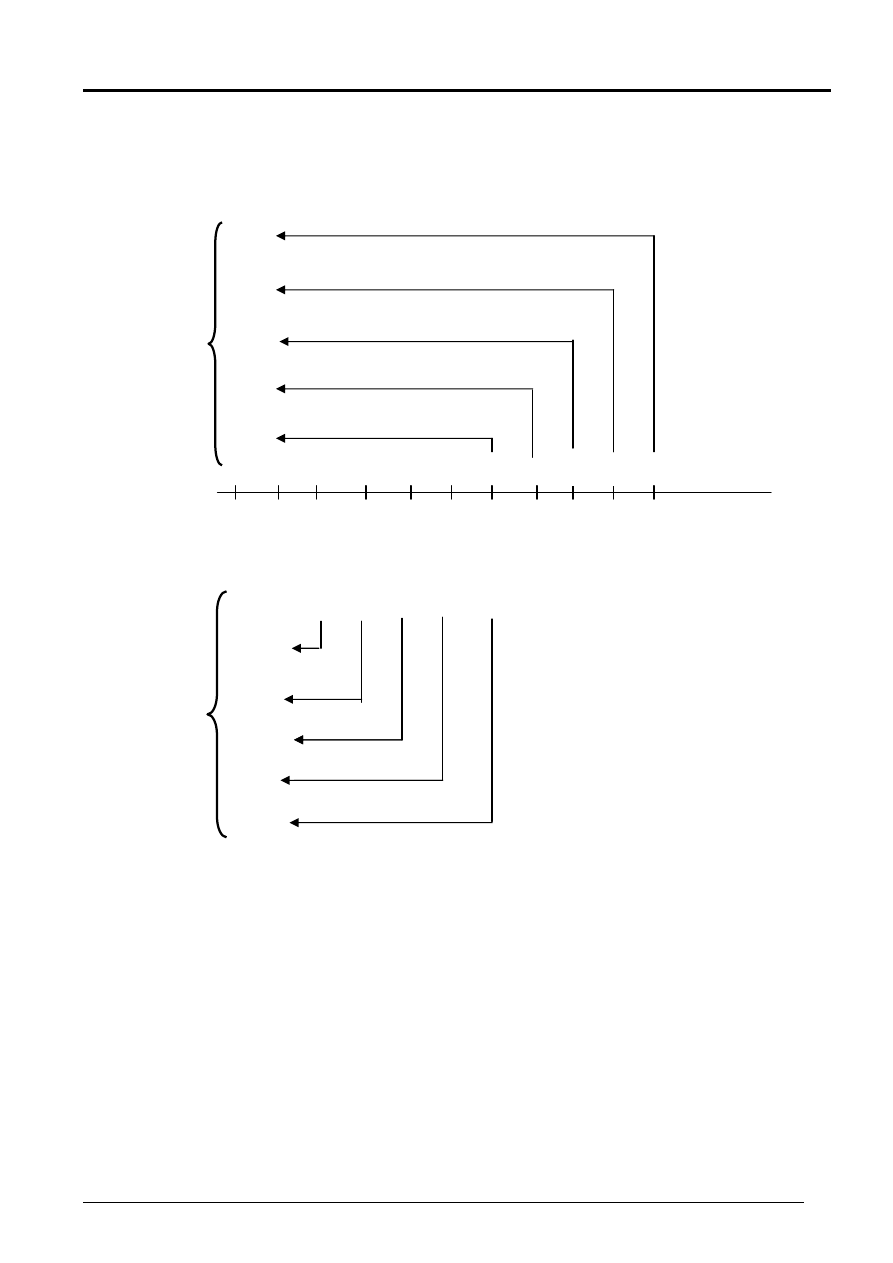
Przykład 2.

Wyznaczyć NPV projektu A dla kosztu kapitału k=10%.

t=0 1 2 3

5

4

6

8 9 10

7

3,95

4,11

4,20

4,24

4,63

21,13

7

12

9 10

8

17,43

-0,62

-0,75

-0,83

-4,55

-10 -5 -1 -1 -1

-0,68

-0,75

-0,83

-4,55

-10 -5 -1 -1 -1

-0,62

-1

-17,43

`

NPV = 21,13 – 17,43 = 3,7

Uzasadnienie metody NPV

Jeżeli projekt ma dodatnie NPV, tzn. ze dostarcza więcej

środków pieniężnych niż potrzeba do obsłużenia długu i

przyniesienia wymaganej stopy dochodu akcjonariuszom. O

te dodatkowe środki wzrasta wartość firmy.

9

Prof. Piotr Chrzan

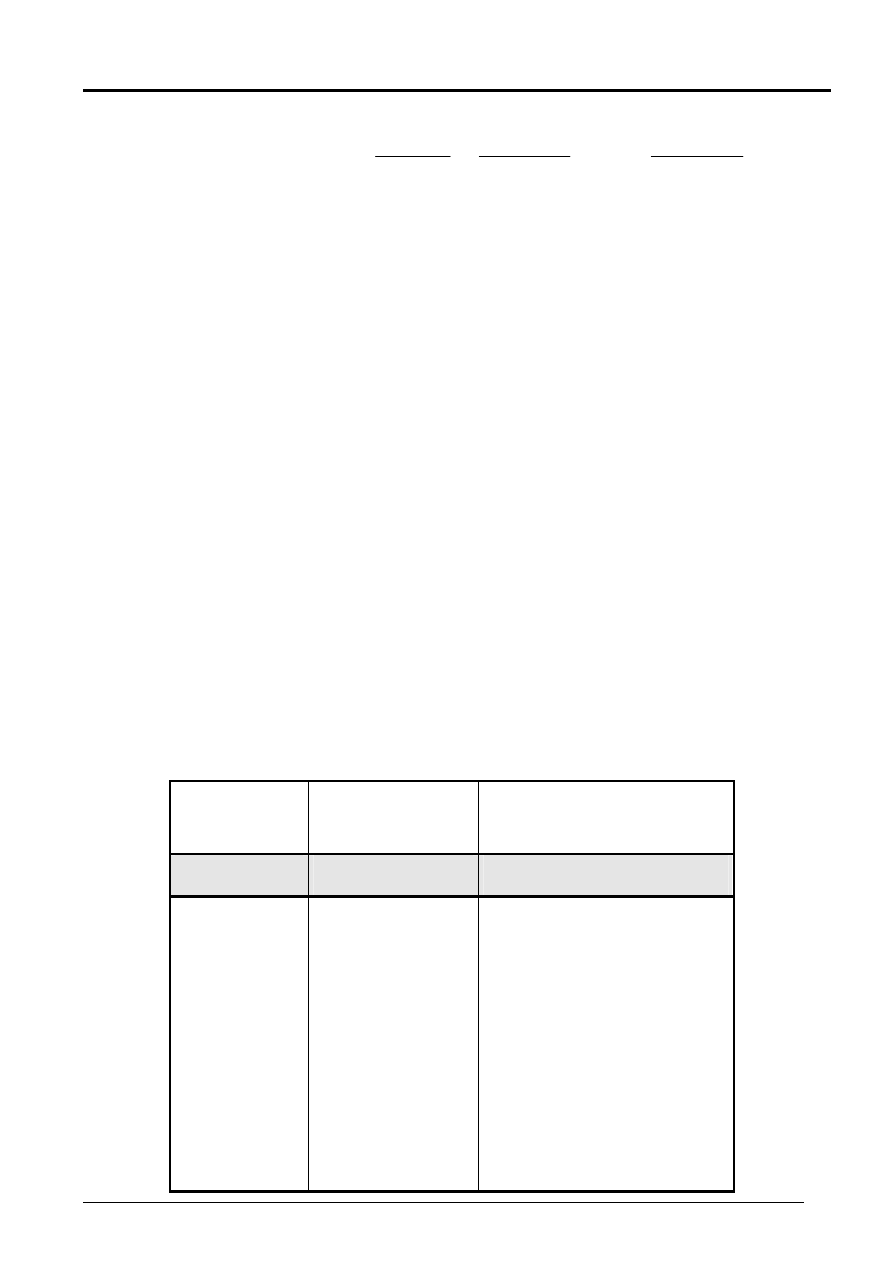
n

n

2

2

1

0

)

k

1

(

CF

)

k

1

(

CF

)

k

1

(

CF

CF

)

k

(

NPV

+

+

+

+

+

+

+

=

L

NPV(k) – funkcja wymierna zmiennej stopy procentowej k

(kosztu kapitału)

v = (1+k)

-1

– czynnik dyskontujący

n

n

2

2

1

0

v

CF

v

CF

v

CF

CF

)

v

(

NPV

+

+

+

+

=

L

NPV(v)– wielomian n-tego stopnia czynnika dyskontującego v

Przykład 3

Wyznaczyć NPV inwestycji A dla różnych stóp procento-

wych k.

NPV(v) = –10–5v–v

2

–v

3

–v

4

–v

5

+7v

6

+ 8v

7

+9v

8

+10v

9

+ 12v

10

Tabela 2.

Stopa

procentowa

Czynnik

dyskontujący

Wartość bieżąca netto

inwestycji

k

v

NPV(k)=NVP

0.05 0.9524

12.6746

0.06 0.9434

10.5357

0.07 0.9346

8.5858

0.08 0.9260

6.8060

0.09 0.9174

5.1808

0.10 0.9090

3.6955

0.11 0.9009

2.3370

0.12 0.8928

1.0937

10

Prof. Piotr Chrzan

0.13 0.8850

-0.0450

0.15 0.8696

-2.0457

0.16 0.8621

-2.9239

0.17 0.8547

-3.7302

0.18 0.8474

-4.4709

0.19 0.8403

-5.1517

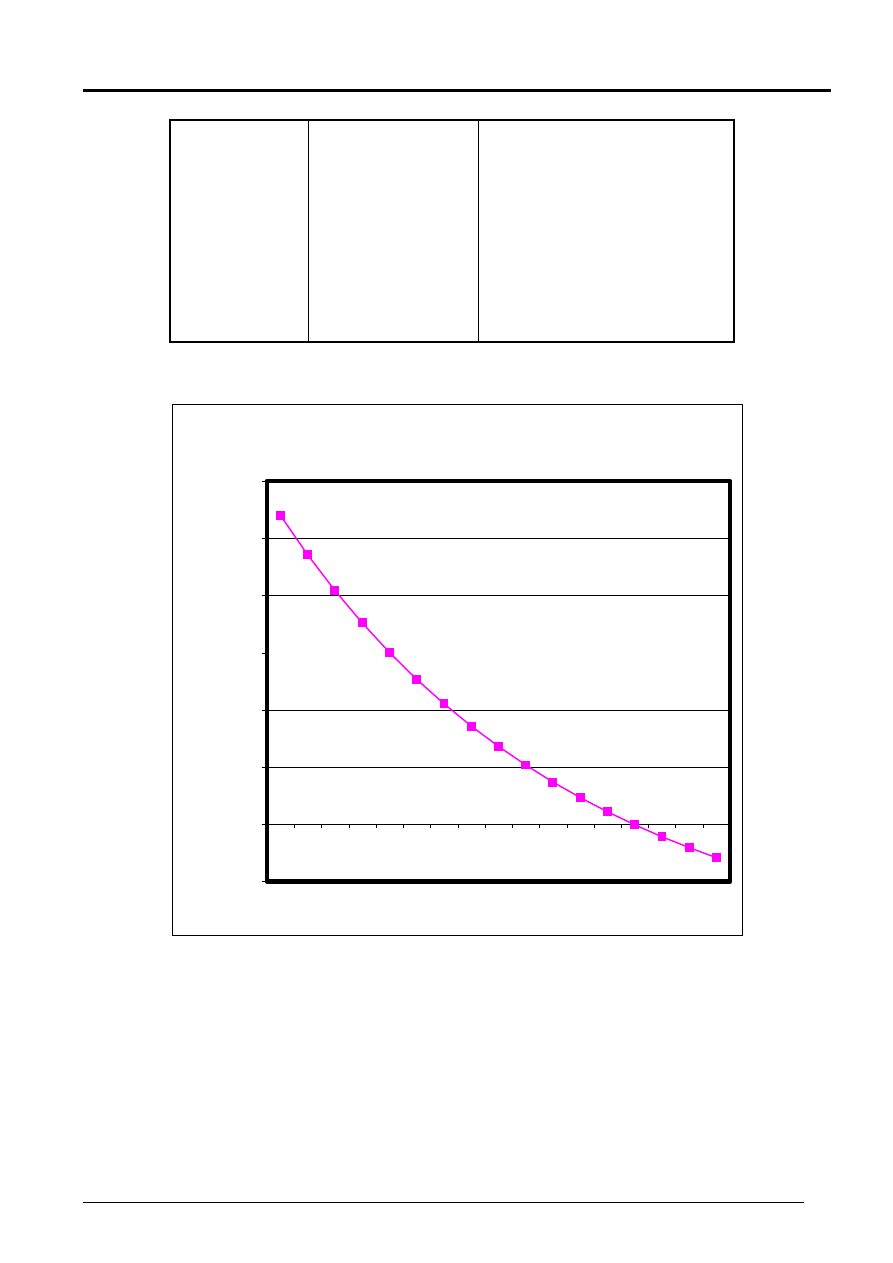
Rys.1

WYKRES FUNKCJA NPV(k)

27,00

23,56

20,44

17,60

15,02

12,67

8,59

6,81

5,18

3,70

2,34

1,09

-0,04

-1,09

-2,05

-2,92

10,54

-5,00

0,00

5,00

10,00

15,00

20,00

25,00

30,00

k

0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15

Stopa Kosztu Kapitału

Warto

ść

Bie

żą

ca Projektu-A

k

g

– graniczny koszt kapitału (minimalna stopa zwrotu z in-

westycji)

NPV(k

g

) > 0 - inwestycja akceptowana

NPV(k

g

)

≤ 0 - inwestycja odrzucona

Dla k

g

= 0,10 (10%) NPV = 3,6955

≈ 3,7 j.p.

11

Prof. Piotr Chrzan

– zainwestowanie odpowiednich kwot COF

t

(wydatki) wy-

generuje 3,7 j.p. więcej niż złożenie tych kwot na lokacie

bankowej oprocentowanej10%

– inwestycja generuje stopę zwrotu wyższą od kosztu kapi-

tału k = 10%

– jeżeli inwestor dla realizacji przedsięwzięcia skorzysta z

kredytu oprocentowanego na 10%, to uzyskane wpływy

wystarczą na spłatę kredytu i procentu, a ponadto wyge-

neruje nadwyżkę 3,7 j.p.

– jeżeli inwestycja zostanie zrealizowana, to wartość firmy

wzrosnie o 3,7 j.p.

Kryterium 1 – Maksimum NPV

Przy ustalonej granicznej stopie kosztu kapitału (minimalnej

wymaganej stopie zwrotu) k

g

z kilku rozpatrywanych projek-

tów inwestycyjnych najlepszy jest ten dla którego NPV(k

g

)

przyjmuje wartość największą.

Wady kryterium NPV

12

Prof. Piotr Chrzan

ƒ aby skorzystać z kryterium należy ustalić graniczną sto-

pę k

g

ƒ można porównywać jedynie projekty o tym samym cza-

sie trwania

ƒ projekt o małej wartości NPV może mieć dużą stopę

zwrotu

ƒ projekt o dużej wartości NPV nie musi mieć największej

stopy zwrotu

W przypadku zmiennych kosztów kapitału k

t

∑

=

−

+

=

n

0

t

t

t

t

)

k

1

(

CF

NPV

gdzie:

CF

t

– przepływy środków pieniężnych w okresie t=0,1,2, ... n

k

t

– koszt kapitału w okresie t =1,2, ... n (k

0

=0)

13

Prof. Piotr Chrzan

3. Wewnętrzna stopa zwrotu

(

Internal Rate of Return - IRR)

Wewnętrzną stopę zwrotu

określa się jako stopę procentową

dla której wartość bieżąca netto inwestycji jest równa zero.

NPV(IRR) = 0

0

)

IRR

1

(

CF

NPV

n

0

t

t

t

=

+

=

∑

=

−

t

t

t

COF

CIF

CF

−

=

dla t=0,1,2, ...n

∑

∑

=

−

=

−

+

=

+

n

0

t

t

t

n

0

t

t

t

)

IRR

1

(

COF

)

IRR

1

(

CIF

)

IRR

(

COF

PV

)

IRR

(

CIF

PV

=

PV(wpływów) = PV(odpływów)

IRR – stopa procentowa, dla której PV wpływów z projektu

równa się PV jego odpływów (kosztów)

IRR – oczekiwana średnia stopa dochodu z projektu

14

Prof. Piotr Chrzan

Uzasadnienie metody IRR

Jeżeli IRR przekracza koszt funduszy użytych do sfinanso-

wania projektu, to pozostaje nadwyżka, która jest kumulowa-

na przez właścicieli

n

n

0

t

t

t

)

IRR

1

(

0

)

IRR

1

(

CF

NPV

−

=

−

+

⋅

=

+

=

∑

0

CF

)

IRR

1

(

CF

)

IRR

1

(

CF

)

IRR

1

(

CF

n

1

n

1

n

1

n

0

=

+

+

+

+

+

+

+

−

−

L

Wielomian n-tego stopnia zmiennej stopy procentowej IRR

Przykład 4.

Projekt inwestycyjny o przepływach pieniężnych netto

t 0 1 2

CF

t

-100 230 -132

NPV(IRR) = –100 + 230(1+IRR)

-1

– 132(1+IRR)

-2

= 0

–100(1+IRR)

2

+ 230(1+IRR) – 132 = 0 /:(–100)

(1+IRR)

2

– 2,3(1+IRR) + 1,32 = 0

IRR

1

= 0,1 IRR

2

= 0,2

(IRR – 0,1)(IRR – 0,2) = 0

15

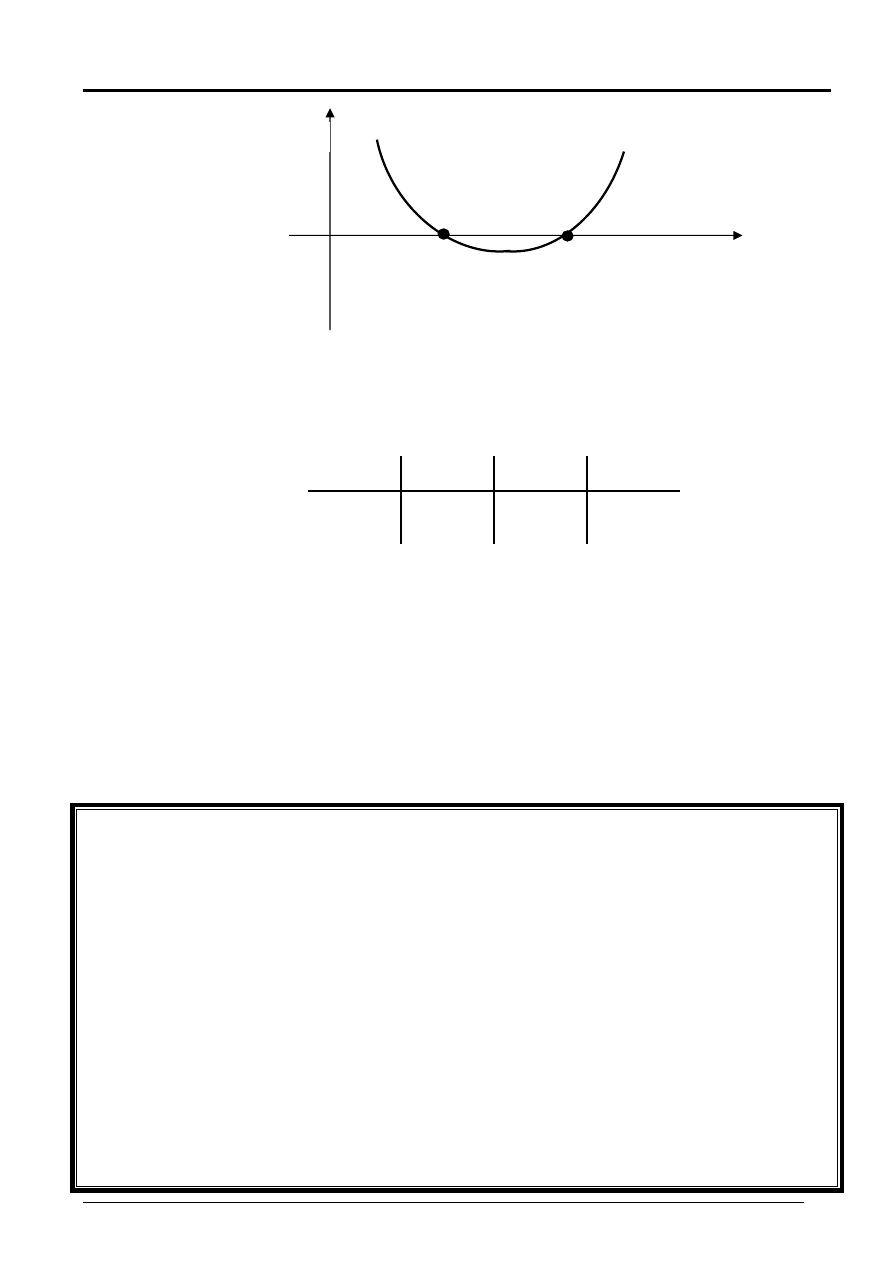
Prof. Piotr Chrzan

NPV

k

0,1

0,2

Przykład 5

Projekt inwestycyjny o przepływach pieniężnych netto:

t 0 1 2

CF

t

-100 200 -101

NPV(IRR) = –100 + 200(1+IRR)

-1

– 101(1+IRR)

-2

= 0

–100(1+IRR)

2

+ 200(1+IRR) – 101 = 0 /:(-100)

(1+IRR)

2

– 2(1+IRR) + 1,01 = 0

IRR

2

= -0,01 (IRR jest liczbą zespoloną)

Twierdzenie 1. (Kartezjusza)

Jeżeli W(x) jest wielomianem n-tego stopnia zmiennej x o postaci:

0

1

1

n

1

n

n

n

a

x

a

...

x

a

x

a

)

x

(

W

+

+

+

+

=

−

−

,

to liczba dodatnich pierwiastków równania W(x)=0

(z uwzględnieniem ich krotności) jest równa liczbie zmian

znaków w ciągu współczynników)

0

1

2

n

1

n

n

a

,

a

,..

.,

a

,

a

,

a

−

−

(zera

pomijamy) lub jest od tej liczby mniejsza o liczbę parzystą.

16

Prof. Piotr Chrzan

Wniosek.1.

Jeżeli strumień przepływów pieniężnych netto CF

t

zmienia

znak tylko jeden raz, to istnieje dokładnie jeden pierwiastek

dodatni równania PV(IRR) = 0. (IRR jest jednoznacznie

określona).

CF

t

– typowy rozkład w czasie (jednoznaczne IRR)

CF

t

– nietypowy rozkład w czasie (niejednoznaczne IRR)

Do wyznaczenia IRR–

dodatniego pierwiastka równania

NPV(IRR)=0 możemy stosować metody iteracyjne:

– metodę równego podziału,

– metodę interpolacji liniowej.

Przykład 6.

Wyznaczyć IRR projektu inwestycyjnego A z przykładu 1.

Z tabeli 2 wynika, że IRR

∈<0,12; 0,13>.

17

Prof. Piotr Chrzan

Tabela 3

Stopa

procentowa

Wartość bieżąca przepływów

pieniężnych netto

k

NPV(k)

0,12 1,094
0,13 -0,050
0,125 0,512
0,1275 0,230
0,12875 0,092
0,12937 0,024
0,12968 -0,010
0,129525 0,007
0,1296025

-0,002

IRR

≈12,96% dla projektu A

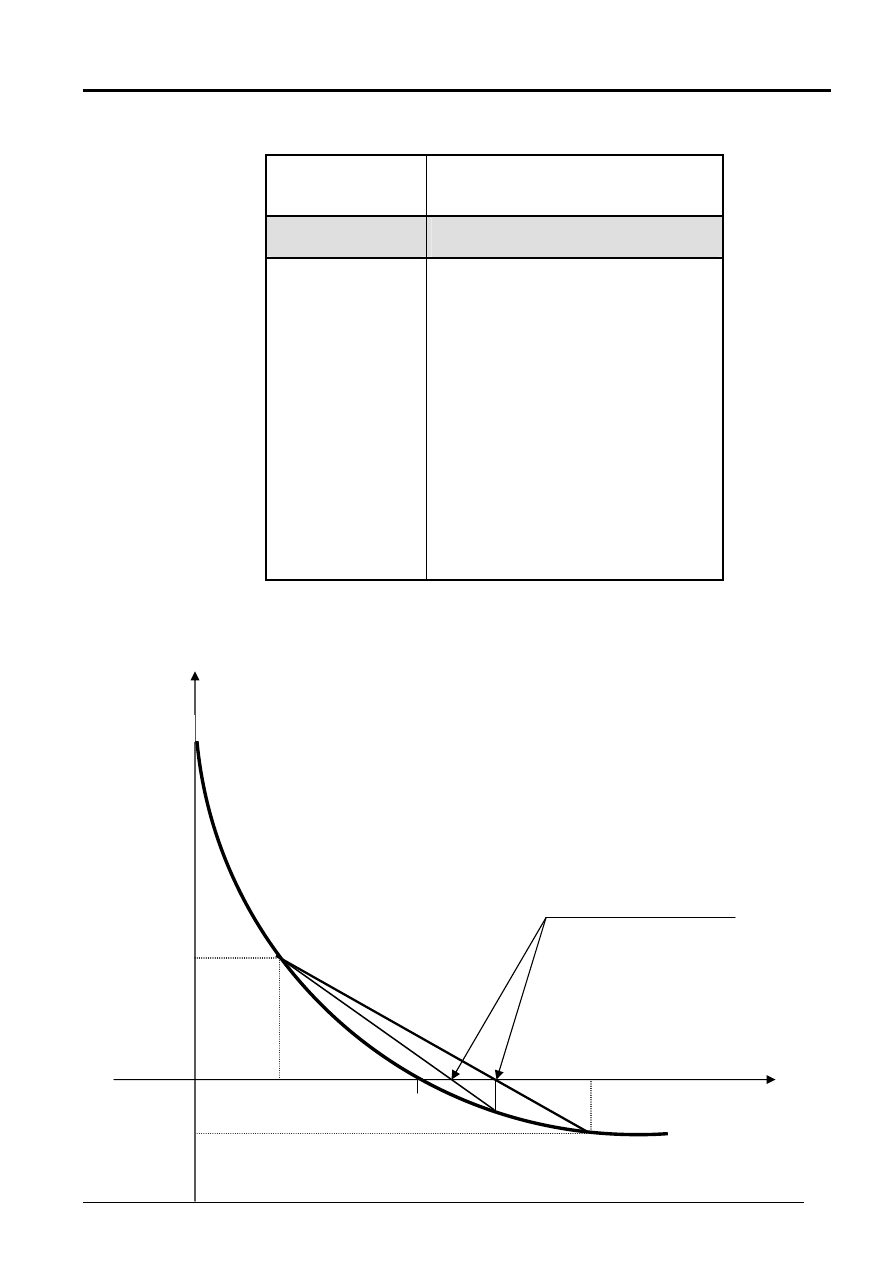
Metoda interpolacji liniowej

Przybliżona
wartość IRR

IRR

2

−

1

k

+

1

k

k

IRR

−

NPV

1

)

NPV

,

k

(

P

1

1

2

−

−

18

)

NPV

,

k

(

P

1

1

1

+

+

NPV

+

1

NPV

IRR

1

Prof. Piotr Chrzan

IRR

)

NPV

NPV

(

)

k

k

(

NPV

k

IRR

1

1

1

1

1

1

1

≈

−

−

−

=

+

−

+

−

+

+

Przykład. Obliczenie IRR metoda interpolacji liniowej

12

,

0

k

1

=

+

0937

,

1

NPV

1

=

+

13

,

0

k

1

=

−

0450

,

0

NPV

1

−

=

−

)

0937

,

1

0450

,

0

(

)

12

,

0

13

,

0

(

0937

,

1

12

,

0

IRR

1

−

−

−

−

=

1296

,

0

0096

,

0

12

,

0

)

00878

,

0

(

0937

,

1

12

,

0

IRR

1

=

+

=

−

−

=

IRR

≈ 12,96

k

g

– graniczna stopa kosztu kapitału

IRR

≥ k

g

- inwestycję akceptujemy

IRR < k

g

- inwestycję odrzucamy

Kryterium 2. Maksimum IRR

Z kilku rozważanych projektów inwestycyjnych najlepszym

jest ten, dla którego IRR przyjmuje wartość największą.

19

Prof. Piotr Chrzan

Wady kryterium 2

ƒ nie można go stosować do porównywania projektów in-

westycyjnych o różnym czasie trwania

ƒ nie można go stosować w przypadku porównywania pro-

jektów inwestycyjnych różniących się skalą wielkości

ƒ nie można go stosować w przypadku częstych zmian

znaku przepływów pieniężnych netto.

Miara ryzyka projektu – Margines bezpieczeństwa

M

b

= IRR – k

g

Margines bezpieczeństwa odpowiada na pytanie, w jakim

stopniu może zmienić się koszt kapitału, nie prowadząc do

ujemnej wartości NPV projektu

gdzie: M

b

– margines bezpieczeństwa

IRR

–

wewnętrzna stopa zwrotu

k

g

– graniczna stopa (koszt kapitału)

20

Prof. Piotr Chrzan

Porównanie metod NPV i IRR

Przykład 7.

Rozważmy projekty S i L o następujących przepływach pie-

niężnych netto:

t

0 1 2 2 4

Projekt S– CF

t

–1000 500 400 300 100

Projekt L– CF

t

–1000 100 300 400 600

IRR

S

= 14,5%

IRR

L

= 11,8%

NPV

S

(7,2%)=NPV

L

(7,2%)

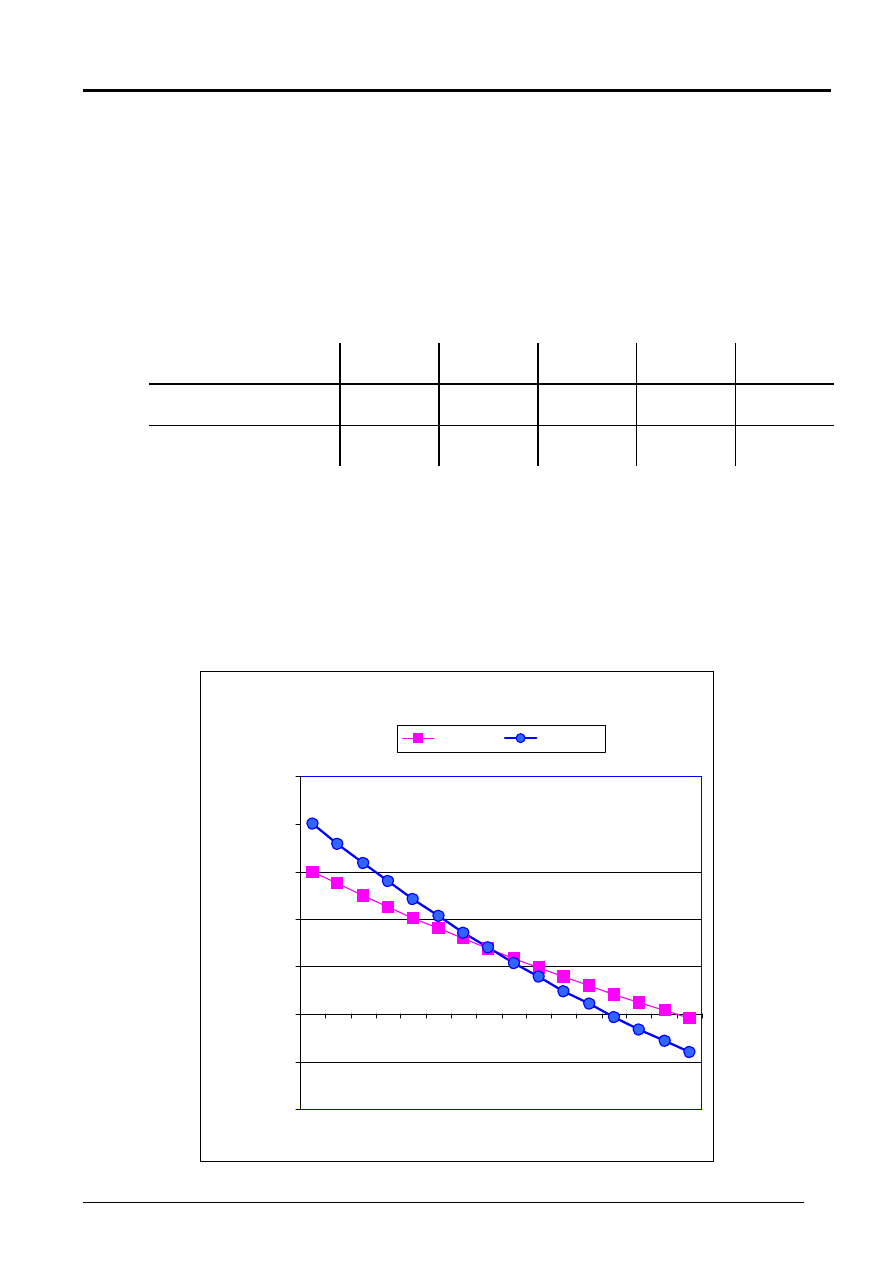
Rys. 2. Wykresy funkcji NPV(k) projektów S i L

WYKRESY FUNKCJI NPV(k)

-200,00

-100,00

0,00

100,00

200,00

300,00

400,00

500,00

k

0,

01

0,

03

0,05

0,

07

0,0

9

0,11

0,13

Stopa Kosztu Kapitału

NPV-Projektu

Projekt-S

Projekt-L

21

Prof. Piotr Chrzan

Projekty S i L wzajemnie się wykluczają.

Jeżeli koszt kapitału k >7,2%, to NPV

S

> NPV

L

i IRR

S

>IRR

L

.

Obie metody prowadzą do identycznych wyborów.

Jeżeli koszt kapitału k< 7,2%, to NPV

L

> NPV

S

i IRR

S

>IRR

L

.

Istnieje konflikt kryteriów.

Przyczyny konfliktów kryteriów NPV i IRR

ƒ istnieje różnica w skali (rozmiarze) projektów

ƒ istnieje różnica w rozkładzie w czasie przepływów pie-

niężnych netto CF

t

projektów

Metoda NPV

zakłada, że przepływy środków pieniężnych

+

t

CF zostaną powtórnie reinwestowane po koszcie kapitału.

Metoda IRR

zakłada, że przepływy środków pieniężnych

+

t

CF zostaną powtórnie zainwestowane ze stopą IRR

Można wykazać, ze najlepsze założenie to założenie o re-

inwestowaniu środków po koszcie kapitału.

Projekty niezależne

– NPV i IRR przynoszą takie same decy-

zje o przyjęciu lub odrzuceniu projektu

22

Prof. Piotr Chrzan

Projekty wzajemnie się wykluczające

– NPV i IRR mogą

przynieść różne decyzje o przyjęciu lub

odrzuceniu projektu.

Dla projektów wzajemnie się wykluczających powinno sto-

sować się

NPV

4. Zmodyfikowana wewnętrzna stopa zwrotu

MIRR – Modyfied Internal Rate of Return

+

t

CF – dodatnie przepływy środków pieniężnych netto

−

t

CF – ujemne przepływy środków pieniężnych netto

k

– stopa kosztu kapitału

r

– stopa reinwestycji kapitału

k

≠ r lub k = r

t

n

0

t

t

t

)

k

1

(

CF

)

CF

(

PV

−

=

−

−

+

=

∑

t

n

n

0

t

t

t

)

r

1

(

CF

)

CF

(

FV

−

=

+

+

+

=

∑

n

t

t

)

MIRR

1

)(

CF

(

FV

)

CF

(

PV

−

+

−

+

=

23

Prof. Piotr Chrzan

Zmodyfikowana wewnętrzna stopa zwrotu -MIRR

Zmodyfikowana wewnętrzna stopa zwrotu to taka stopa pro-

centowa, która zrównuje wartość przyszłą dodatnich prze-

pływów pieniężnych netto z wartością bieżącą ujemnych

przepływów pieniężnych netto.

Zmodyfikowana wewnętrzna stopa zwrotu

oznacza wartość

stopy procentowej, dla której wartość przyszła reinwestowa-

nych według sposobności rynkowych wpływów netto jest rów-

na wartości bieżącej wydatków netto.

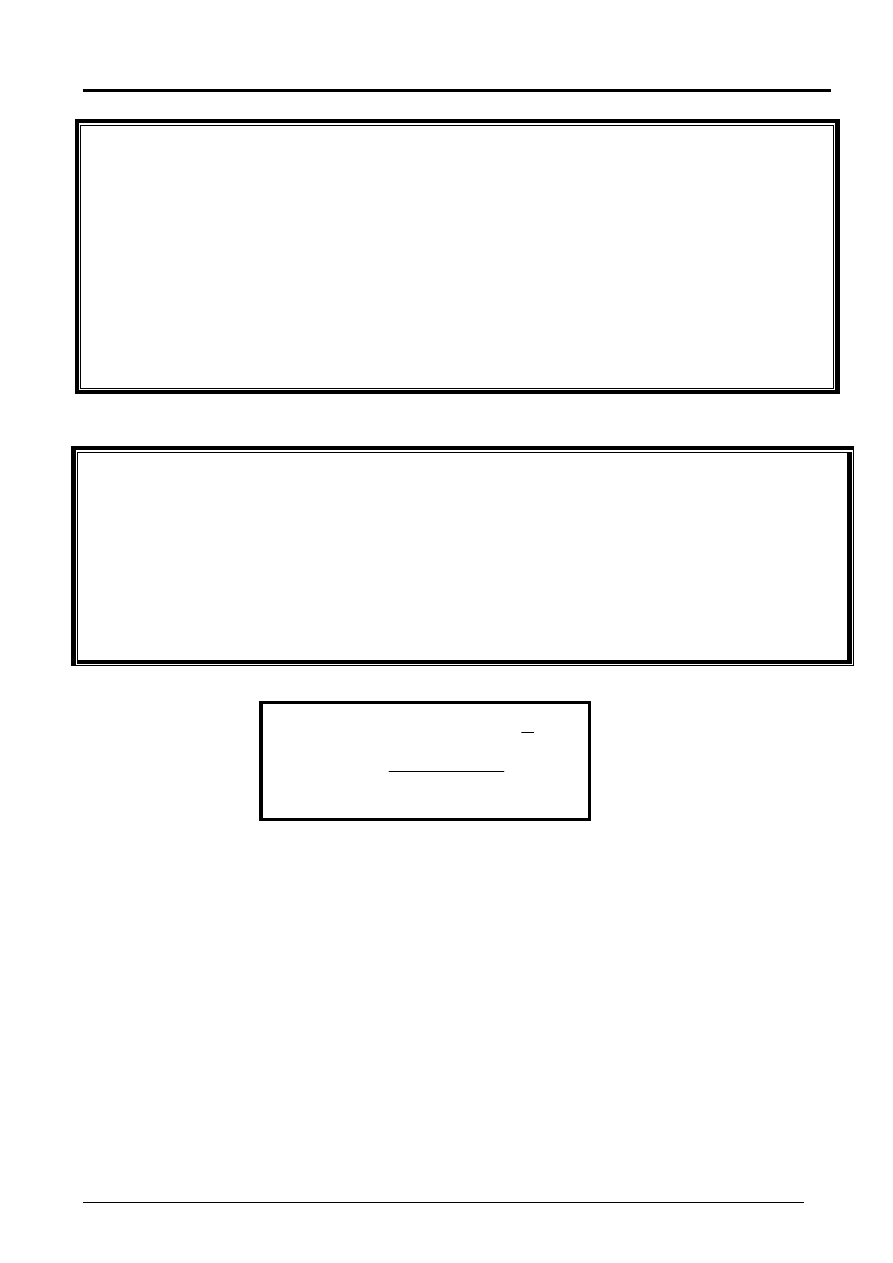
1

)

CF

(

PV

)

CF

(

FV

MIRR

n

1

t

t

−

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

−

+

gdzie: MIRR - zmodyfikowana wewnętrzna stopa zwrotu

FV(

+

t

CF ) – wartość przyszła dodatnich przepływów pienięż-

nych netto

PV(

−

t

CF ) – wartość bieżąca ujemnych przepływów pienięż-

nych netto

n – czas realizacji projektu

k

g

– graniczna stopa kosztu kapitału

24

Prof. Piotr Chrzan

Jeżeli MIRR

≥ k

g

– inwestycję akceptujemy

Jeżeli MIRR < k

g

– inwestycję odrzucamy

Przykład 8.

Obliczyć MIRR projektu A. Koszt kapitału k

g

= 10%,

stopa reinwestycji r = 10%

v = (1+k

g

)

–1

czynnik dyskontujący

u = (1+r) – czynnik procentowy

Tabela 3

Rok

Wydatki

netto

Przychody

netto

Zaktualizowane

wydatki netto

Zaktualizowane

przychody netto

t

−

t

CF

+

t

CF

t

t

v

CF

⋅

−

t

n

t

u

CF

−

+

⋅

0 10

0

10,000

0,000

1

5

0

4,545

0,000

2 1

0

0,826

0,000

3 1

0

0,751

0,000

4 1

0

0,683

0,000

5 1

0

0,321

0,000

6 0

7

0,000

10,249

7 0

8

0,000

10,648

8 0

9

0,000

10,890

9 0

10

0,000

11,000

10 0

12

0,000

12,000

Suma

17,427

54,787

25