
Prof. Piotr Chrzan
PV(
−
t
CF ) = 17,427
FV(
+
t
CF ) = 54,787
1
427
,
17
787
,
54
MIRR
10
1
−
⎟
⎠
⎞
⎜
⎝
⎛
=
1214
,
0
1
143
,
3
MIRR
10
=
−
=
MIRR = 12,14% > k
g
= 10%
Kryterium 3. Maksimum MIRR
Z kilku rozważanych projektów inwestycyjnych najlepszy
jest ten, dla którego MIRR przyjmuje wartość największą.
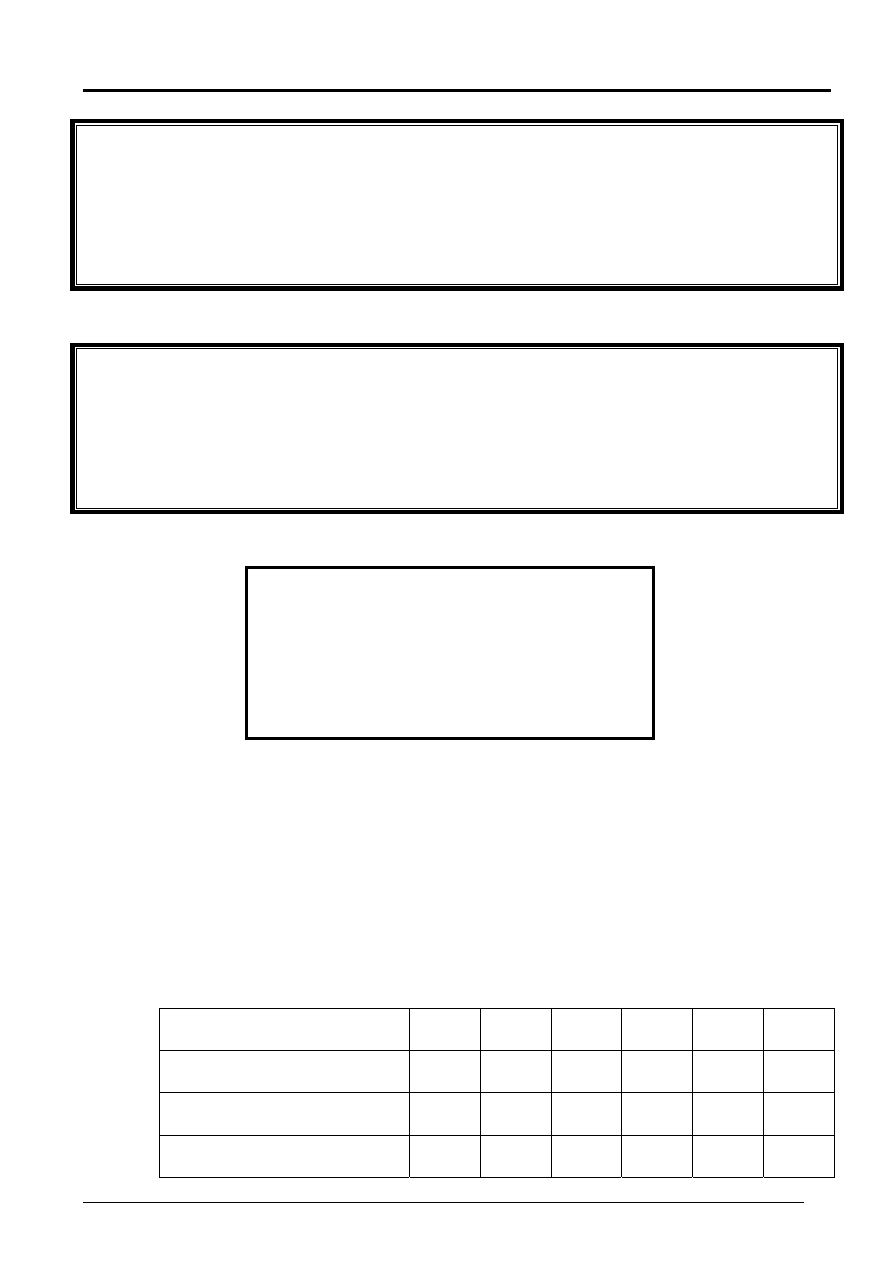
5. Zdyskontowany okres zwrotu nakładów inwe-
stycyjnych
Zdyskontowany okres zwrotu –
Discounted Payback Period –DPP
n
*
– DPP przy ustalonej stopie kosztu kapitału k
g
n
*
– liczba okresów (lat)
26
Prof. Piotr Chrzan
Zdyskontowany okres zwrotu
jest to okres, po którym war-
tość bieżąca przepływów pieniężnych netto (CF
t
) przekroczy
po raz pierwszy zero.
Zdyskontowany okres zwrotu
jest to okres, po którym war-
tość bieżąca wpływów przekroczy po raz pierwszy wartość
bieżącą wydatków.
0
)
k
1
(
CF
)
k
(
NPV
0
)
k
1
(
CF
)
k
(
NPV
*
n
0
k
t
g
t
g
1
*
n
0
k
t
g
t
g
≥
+
=
<
+
=
∑
∑
=
−
−
=
−
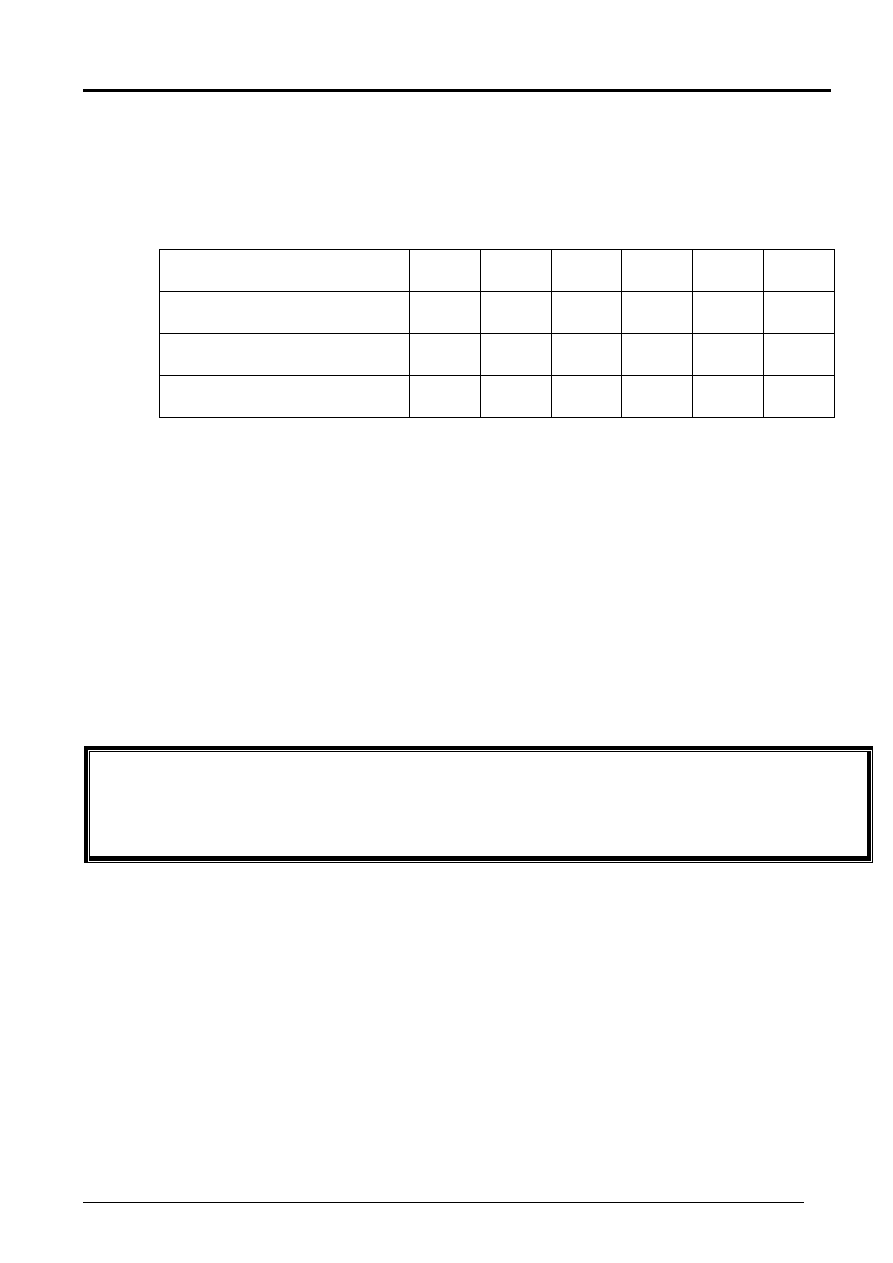
Przykład 9.
Wyznaczyć zdyskontowany okres zwrotu projektów inwesty-
cyjnych S i L z przykładu 7. Koszt kapitału k
g
= 10%.
Projekt S
Czas t
0
1
2
3
*
4
Przepływy CF
t
–1000 500 400 300 100
Zdyskontowane CF
t
–1000 455 331 225 68
Szereg skumulowany
DCF
t
–1000 –545 –214 11 79
27
Prof. Piotr Chrzan
Projekt S – DPP = n
*
= 3 lata
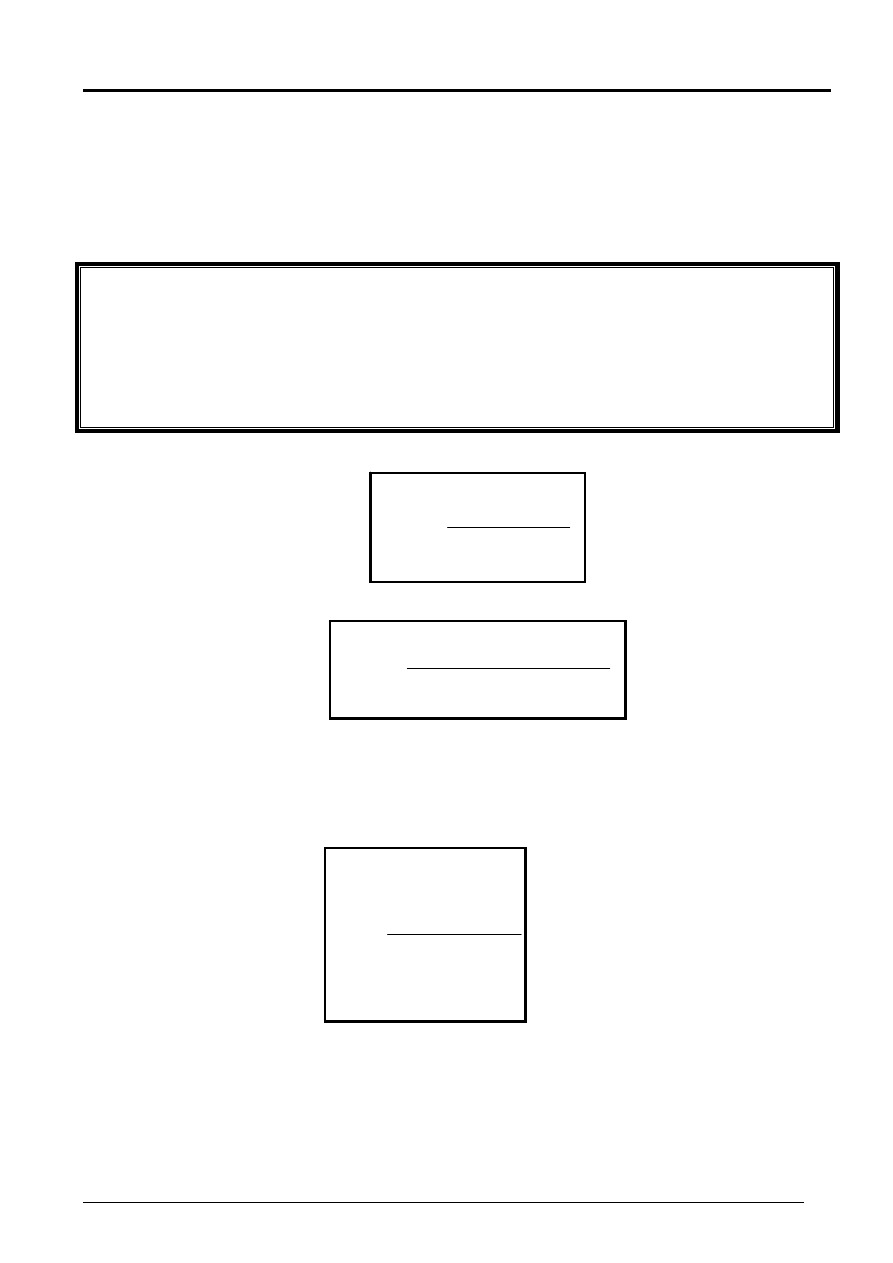
Projekt L
Czas
t 0 1 2 3
4
*
Przepływy CF
t
–1000 100 300 400 600
Zdyskontowane CF
t
–1000
91 248 301 410
Szereg skumulowany
DCF
t
–1000 –909 –661 -360 50
Projekt L – DPP = n
*
= 4 lata
DPP – dostarcza informacji jak długo fundusze będą zamro-
żone w projekcie (płynność projektu).
Kryterium 4. Minimum DPP
Z kilku rozważanych projektów inwestycyjnych najlepszy jest
ten, dla którego DPP przyjmuje wartość najmniejszą.
n
*
– DPP – miara ryzyka płynności projektu
Wady DPP
należy ustalić graniczną stopę kosztu kapitału k
g
preferuje projekty, które w krótkim okresie czasu osią-
gają dodatnie znaczne przepływy netto
+
t
CF
28
Prof. Piotr Chrzan
6. Wskaźnik rentowności inwestycji
Profitability Index –PI
Wskaźnik rentowności inwestycji
jest ilorazem wartości bie-
żącej dodatnich przepływów netto CF
+
do wartości bieżącej
ujemnych przepływów netto CF
–
.
)
CF
(
PV
)
CF
(
PV
PI
t
t
−
+
=
)
wydatków
(
PV
)
wplywów
(
PV
PI
=
PI – informuje o jednostkowej efektywności nakładów – ile
wpływów na jednostkę wydatków
∑
∑
=
−
=
+
⋅
⋅
=
n
0
t
t
t
t
n
0
t
t
v
CF
v
CF
PI
gdzie: v = (1 + k
g
)
-1
k
g
– koszt kapitału
PI – wskaźnik rentowności inwestycji
29

Prof. Piotr Chrzan
Jeżeli NPV
≥ 0
to
PI
≥ 1
PI
≥ 1 – projekt akceptujemy
PI < 1 – projekt odrzucamy
Przykład 10.
Wyznaczyć wskaźnik rentowności inwestycji projektu A z
przykładu 1. Koszt kapitału k
g
=10%
5
4
3
2
10
9
8
7
6
v
v
v
v
v
5
10
v
12
v
10
v
9
v
8
v
7
PI
+
+
+
+
+
+
+
+
+
=
v = (1+0,1)
-1
= 0,9090
2120
,
1
4272
,
17
12264
,
21
PI
≈
=
Kryterium 5. Maksimum PI
Z kilku rozważanych projektów inwestycyjnych najlepszy jest
ten, dla którego PI przyjmuje wartość największą.
30
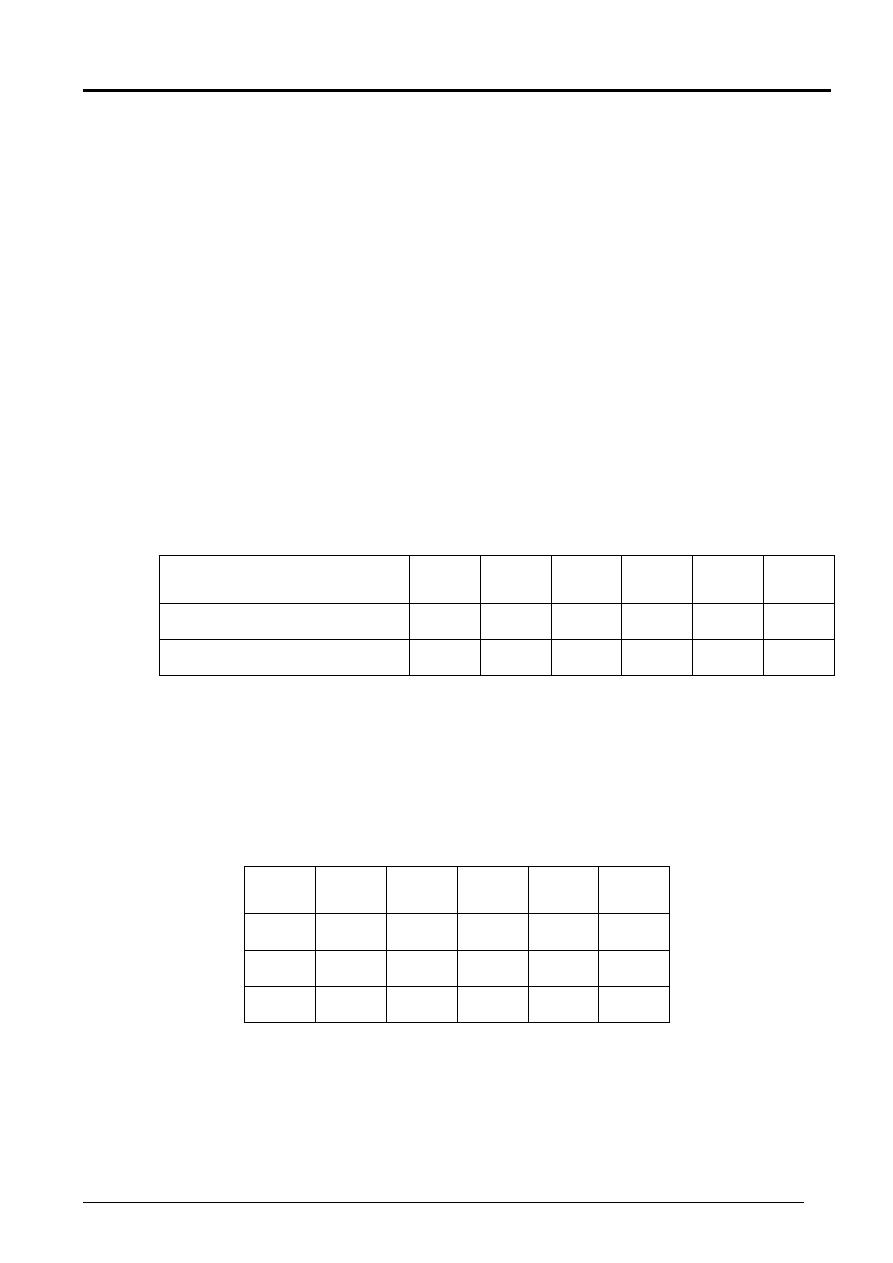
Prof. Piotr Chrzan
7. Porównywanie projektów o różnych okresach
użytkowania
Koncepcja łańcucha zastępowań – wspólnego okresu użyt-
kowania
Założenie:
Projekt o krótszym okresie użytkowania może być
powtórzony tyle razy, ile trzeba, aby okresy użytkowania by-
ły takie same.
Przykład 11. Koncepcja łańcucha zastępowań
t 0 1 2 3
4
*
Projekt X CF
t
–25 16 16 – –
Projekt Y CF
t
–60 20 20 20 20
Koszt kapitału k
g
= 10%
NPV
X
= 27,69 < NPV
Y
= 33,97
Projekt :2X
t 0 1 2 3
4
*
CF
t
–25 16 16 0 0
CF
t
0 0 –25 16 16
–25 16 –9 16 16
NPV
2X
= 50,57 > NPV
Y
= 33,97
Ze względu na kryterium NPV „projektu 2X” jest bardziej
korzystny.
31

Prof. Piotr Chrzan
Wady koncepcji łańcucha zastępowań
zakłada się, że koszty odtworzeniowe sa stałe w czasie
nie uwzględnia się zmian technologicznych
Metoda równoważnej raty rocznej – nieskończony okres
użytkowania
1. Obliczyć NPV każdego projektu
2. Dla każdego projektu obliczyć stałą ratę PMT renty
płatnej w okresie użytkowania projektu, której wartość
bieżąca jest równa NPV projektu.
3. Dla każdego projektu obliczyć wartość bieżącą renty
nieskończonej
g
k
PMT
V
=
gdzie:
V – wartość bieżąca renty nieskończonej
PMT – stała rata renty płatnej w okresie użytkowania projektu
k
g
– koszt kapitału
Kryterium 5. Maksimum V (PMT)
Z kilku rozważanych projektów inwestycyjnych najlepszy jest
ten, dla którego V(PMT) przyjmuje wartość największą.
32

Prof. Piotr Chrzan
Przykład 12. Koncepcja równoważnej raty rocznej. Dane z
przykładu 11.
Projekt
X NPV
X
= PMT
X
1
,
0
|
2
a
91
,
15
74
,
1
69
,
27
PMT
X
=
=
Projekt
Y NPV
Y
= PMT
Y
1
,
0
|
4
a
72
,
10
17
,
3
97
,
33
PMT
Y
=
=
V
X
= 15,91/0,1=159,1
V
Y
= 10,72/0,1=107,2
Projekt X lepszy od projektu Y.
33
Wyszukiwarka
Podobne podstrony:
18 Metody dys cz1
18. Metody przybliżone rozwiązywania zadań optymalizacji dyskretnej I, pytania egzamin inżynierski A
18. Metody przybliżone rozwiązywania zadań optymalizacji dyskretnej II, pytania egzamin inżynierski
T.18 Metody wyznaczania cen za uslugi transportowe, Podstawy logistyki, Transport i spedycja
2009.12.18. Metody kształcenia
Wykład 18 Metody analityczne w terapii monitorowanej OK
18 strukr wyrazowych(1), metodyka pracy korekcyjno-kompensacyjnej
18 Skura P Metody
2008 Metody komputerowe dla inzynierow 20 D 2008 1 8 22 18 59id 26588 ppt
Gimnazjum kl I metodyk s 015 18 kat1 (1)
18 EW ZEW Osordek Metodyczny do metody Johna
metodyka 18.11.2010, STUDIA, na studia, metodyka
18(45) Metody tworzenia systemów informatycznychid 17860 ppt
2008 Metody komputerowe dla inzynierow 18 D 2008 1 8 22 16 21id 26586 ppt
Metoda 18 struktur wyrazowych, terapia pedagogiczna, Metodyka zajęć korekcyjno- kompensacyjnych dzie
więcej podobnych podstron