Prędkość

Wielkość wektorowa, która określa zarówno szybkość ruchu, jak i jego kierunek w danej chwili.

Prędkość chwilowa:

( ) ( )

dt

r

d

t

t

t

r

t

r

v

t

t









≡

−

−

≡

→

0

0

0

lim

Jednostką jest metr na sekundę.

Przyspieszenie

Wielkość wektorowa, która określa zmiany wektora prędkości w czasie (zarówno wartości, jak i kierunku).

Przyspieszenie chwilowe:

( ) ( )

2

2

0

0

0

lim

dt

r

d

dt

v

d

t

t

t

v

t

v

a

t

t











=

≡

−

−

≡

→

Jednostka: metr na sekundę na sekundę.

Tor ruchu to w kinematyce krzywa zakreślona w przestrzeni przez poruszający się punkt materialny. Na
podstawie kształtu toru ruchu, ruchy można sklasyfikować jako:

•

prostoliniowe,

•

krzywoliniowe,

o

krzywoliniowe płaskie,

o

krzywoliniowe przestrzenne.

Ruch punktu we współrzędnych prostokątnych

Położenie punktu w przestrzeni możemy określić za pomocą trzech współrzędnych w prostokątnym układzie
współrzędnych Oxyz:

x=f

1

(t) y=f

2

(t) z=f

3

(t)

Są to równania ruchu punktu.
Promień-wektor danego punktu A jest to wektor łączący początek nieruchomego układu współrzędnych i dany
punkt; jest to wektor określający położenie w przestrzeni danego punktu. Gdy punkt się porusza, jego promień-
wektor r zmienia z upływem czasu swą wartość i kierunek. r=r(t)
Promień wektor można przedstawić w postaci sumy geometrycznej:
r=ix(t)+jy(t)+kz(t)
gdzie i,j,k oznaczają wersory odpowiednich osi obranego układu współrzędnych.
Prędkością punktu nazywamy zmianę wektora wodzącego względem czasu, tj. jego pochodną względem czasu

v

dt

r

d

t

r

t







=

=

∆

∆

>

−

∆

0

lim

. Wzór ten można zapisać również w postaci sumy geometrycznej v=v

x

i+v

y

j+v

z

k , a stąd

uzyskujemy wzory na współrzędne prędkości

dt

dx

v

x

=

dt

dy

v

y

=

dt

dz

v

z

=

Wartość prędkości określa wzór:

2

2

2

z

y

x

v

v

v

v

+

+

=

Przyspieszeniem punktu jest pochodną prędkości względem czasu albo drugą pochodną wektora wodzącego

względem czasu.

2

2

dt

r

d

dt

v

d

a





=

=

. Tak jak w przypadku prędkości, możemy uzyskać wzory na współrzędne

przyspieszenia

2

2

dt

x

d

dt

v

d

a

x

x

=

=



;

2

2

dt

y

d

dt

v

d

a

y

y

=

=



;

2

2

dt

z

d

dt

v

d

a

z

z

=

=



Gdzie

2

2

2

z

y

x

a

a

a

a

+

+

=

Ruch punktu we współrzędnych biegunowych

Prędkość:

Przyspieszenie:

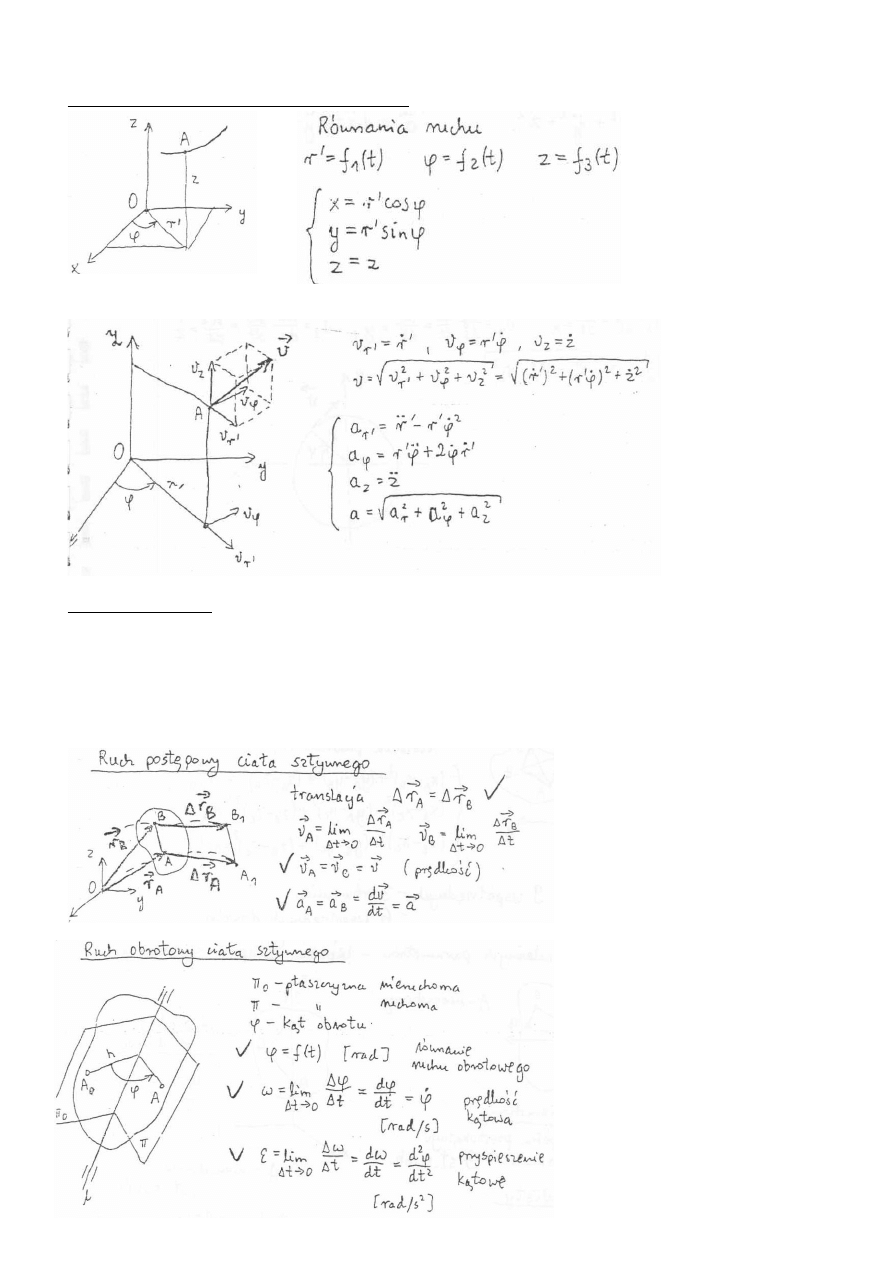
Ruch punktu we współrzędnych walcowych:

Przyspieszenie i prędkość:

-------------------------------------------------------------------------------------------------------------------------

Stopniem swobody

nazywa się możliwość wykonania ruchu ciała niezależnego od innych ruchów.

Punkt materialny ma na płaszczyźnie dwa, a w przestrzeni trzy stopnie swobody.
Ciało doskonale sztywne ma na płaszczyźnie trzy, a w przestrzeni sześć stopni swobody.
Trzy stopnie swobody ciała sztywnego na płaszczyźnie oznaczają możliwość dwóch przesunięć niezależnych w
kierunku osi x i y oraz możliwość obrotu ciała w płaszczyźnie Oxy. Sześć stopni swobody ciała w przestrzeni
oznaczają możliwość trzech niezależnych przesunięć w kierunku osi x, y i z oraz możliwość niezależnego obrotu
ciała wokół tych osi.
-------------------------------------------------------------------------------------------------------------------------

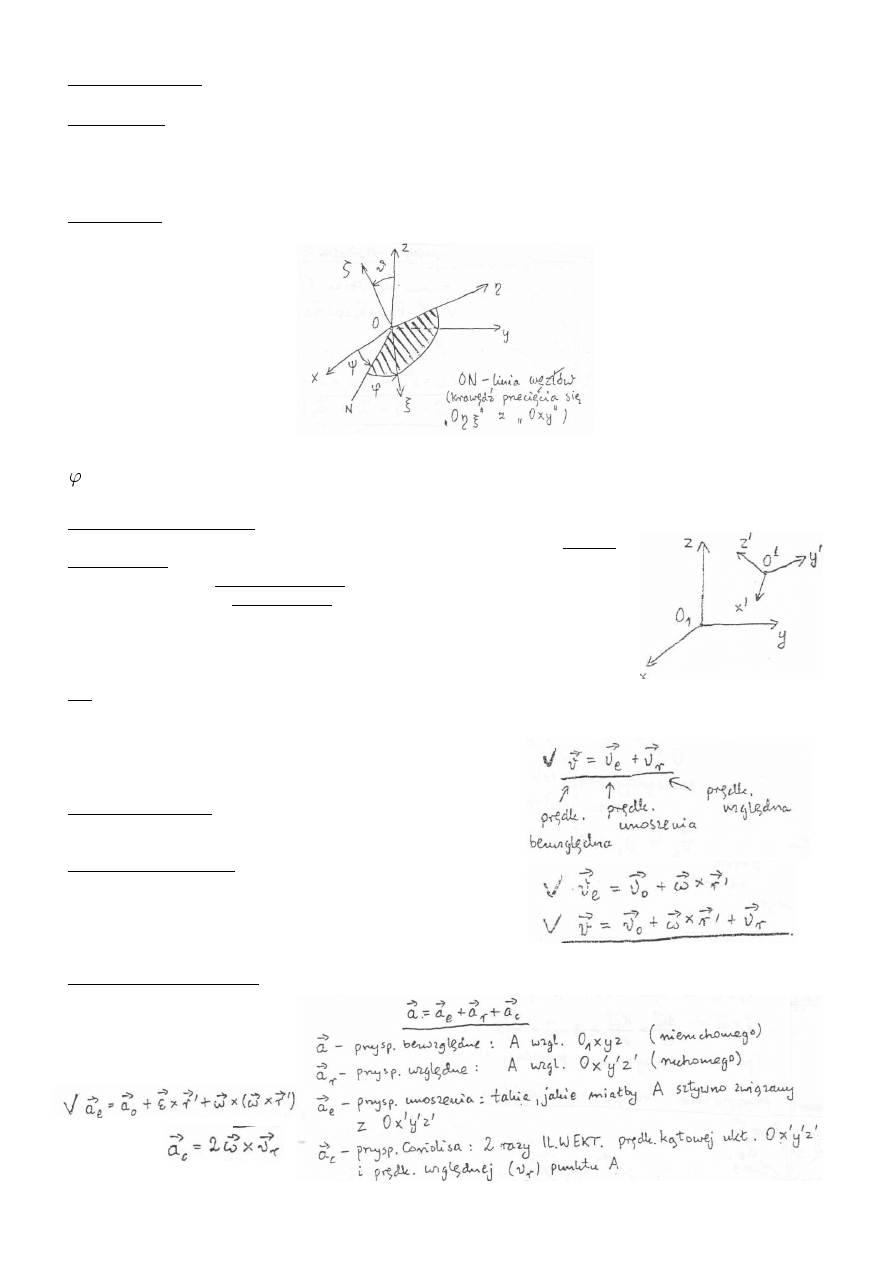
jest to taki ruch ciała sztywnego w
którym wszystkie jego punkty doznają
tych samych przesunięć

Jest to ruch ciała sztywnego wokół
chwilowej osi obrotu

.

Ruchem płaskim

ciała sztywnego nazywamy ruch, podczas którego wszystkie punkty ciała poruszają się w

płaszczyznach równoległych do pewnej nieruchomej płaszczyzny zwanej płaszczyzną kierującą

Ruch kulisty

to ruch ciała sztywnego, podczas którego jeden jego punkt zwany środkiem ruchu kulistego jest

nieruchomy. Ciało sztywne może obracać się tylko dookoła osi przechodzących przez punkt nieruchomy 0, który
nazywamy środkiem ruchu kulistego (ma trzy stopnie swobody). Torem dowolne punktu jest powierzchnia kuli o
środku w punkcie zwanym środkiem ruchu kulistego. W ruchu tym mamy dwa układy odniesienia związane ze
sobą za pomocą trzech kątów zwanych kątami Eulera.

Kąty Eulera to

układ trzech kątów, za pomocą których można jednoznacznie określić wzajemną orientację dwu

kartezjańskich układów współrzędnych o jednakowej skrętności w trójwymiarowej przestrzeni euklidesowej.

θ — kąt mierzony od osi z do osi Oζ; jest to kąt nutacji.
ψ — kąt mierzony od osi x do osi węzłów ON ; jest to kąt precesji.

— kąt mierzony od osi węzłów ON do osi Oξ; jest to kąt obrotu własnego.

Ruch względny(złożony)

Ruch punktu lub bryły względem układu nieruchomego(Oxyz) nazywamy ruchem
bezwzględnym, a ruch tego samego punktu lub bryły względem układu
ruchomego(O’x’y’z’) ruchem względnym. Ruch układu ruchomego względem
układu nieruchomego to ruch unoszenia.

Tor, jaki zakreśli punkt w układzie nieruchomym, nazywamy torem bezwzględnym , a w układzie ruchomym
torem względnym. Każdy z punktów toru względnego, zatem i punkt znajdujący się w tym samym miejscu co
punkt , zakreśli pewien tor . Ruch tego punktu względem układu
nieruchomego nazywamy ruchem unoszenia punktu w rozważanej
chwili.

Prędkość względna – prędkość tego samego punktu w ruchomym
układzie odniesienia skierowana wzdłuż stycznej do toru
względnego.
Prędkość bezwzględna – prędkość punktu względem
nieruchomego układu odniesienia skierowana wzdłuż stycznej do
toru bezwzględnego. Prędkość ta jest równa sumie geometrycznej
prędkości unoszenia v

e

oraz prędkości względnej v

r

.

Przyśpieszenie bezwzględne punktu w ruchu złożonym jest równe sumie trzech przyśpieszeń: unoszenia a

u

,

względnego a

w

i Coriolisa : a

c