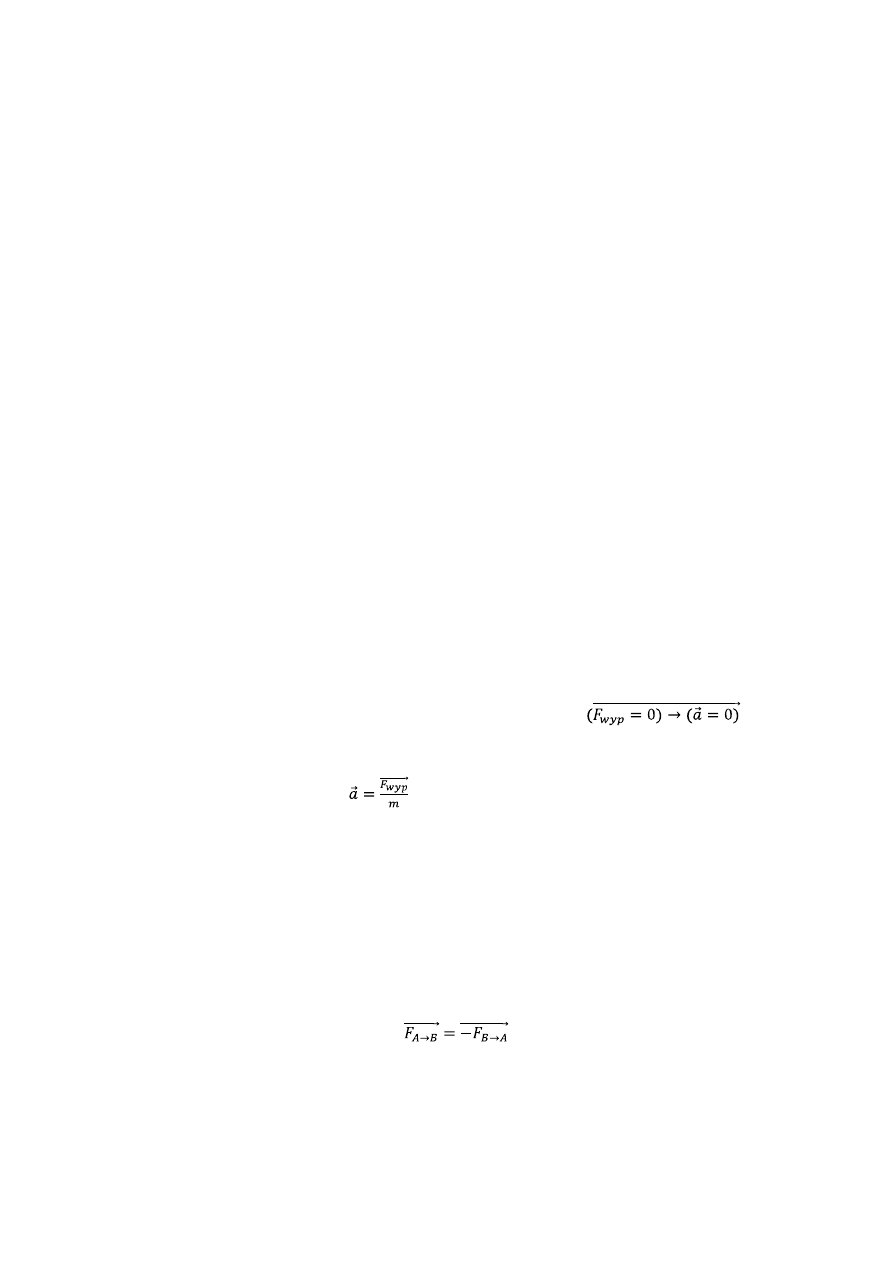
Fizyka egzamin:
1. Przemieszczenie, prędkośd i przyspieszenie w ruchu postępowym oraz obrotowym bryły
sztywnej. Związek wielkości kątowych z liniowymi.
Ruch postępowy to ruch, w którym wszystkie punkty bryły doznają równych i równoległych
przemieszczeo, gdyż wszystkie zakreślają tory o takim samym kształcie i wszystkie mają takie same
prędkości. Wynika z tego, że w ruchu postępowym wszystkie punkty bryły mogą byd reprezentowane
przez jeden punkt – środek ciężkości, a cały ruch może byd opisany tak, jak ruch punktu materialnego.
Ruch obrotowy to ruch, w którym wszystkie punkty bryły zataczają współśrodkowe okręgi
wokół osi obrotu. Oś obrotu to linia, na której leżą punkty bryły pozostające w spoczynku podczas
obrotu. W ruchu obrotowym wszystkie punkty bryły mają taką samą szybkośd kątową u i różne
szybkości liniowe v (styczne do toru), ponieważ v = r·ω Jeśli szybkośd kątowa rośnie lub maleje,
to ruch obrotowy jest odpowiednio przyspieszony lub opóźniony i dla takich ruchów istnieje
przyspieszenie lub opóźnienie kątowe, które jest zdefiniowane tak jak w ruchu po okręgu.
Aby wprawid bryłę w ruch obrotowy wokół osi albo zwiększyd lub zmniejszyd prędkośd kątową, to
musimy zadziaład na nią siłą. Wpływ tej siły na ruch obrotowy wynika z II zasady dynamiki dla bryły
sztywnej i jest związany z momentem siły oraz momentem bezwładności bryły.
2. Zasady dynamiki Newtona dla ruchu punktu materialnego oraz obrotowego bryły sztywnej
wokół stałej osi.
Punkt materialny:
I. Zasada – zasada bezwładności:
Każde ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym
prostoliniowym, dopóki działanie innych ciał nie zmusi go do zmiany tego stanu;
Ciało pozostaje w stanie spoczynku lub stałej prędkości, gdy jest pozostawione
samo sobie (działająca na nie siła wypadkowa jest równa zeru);
II. Zasada:
Zmiana ruchu jest proporcjonalna do przyłożonej siły i zachodzi w
kierunku działającej siły;
Jeżeli na ciało działa stała, niezrównoważona siłą wypadkowa , to ciało to
porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem
proporcjonalnym do tej siły a odwrotnie proporcjonalnym do masy – miary
bezwładności tego ciała.
III. Zasada:
Działania na siebie dwóch ciał są zawsze równe, lecz przeciwnie
skierowane;
Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało
drugie na pierwsze jest równa i przeciwnie skierowana do siły, jaką
ciało pierwsze działa na drugie ciało;
Ruch obrotowy bryły sztywnej:
I Zasada:
W inercjalnym układzie odniesienia bryła nie obraca się lub obraca się ruchem jednostajnym,
gdy nie działają na nią żadne momenty sił lub, gdy momenty działające równoważą się
wzajemnie:
II Zasada:
Moment siły jest równy stosunkowi momentu przyrostu pędu do czasu, w jakim ten przyrost
nastąpił, czyli jest równy szybkości zmian momentu pędu:
3. Praca i energia. Zasada zachowania energii mechanicznej:
Praca-
miara ilości
energii
przekazywanej między
układami fizycznymi
w
procesach
mechanicznych
,
elektrycznych
,
termodynamicznych
i innych.
gdzie:
– siła
–
przemieszczenie
gdy wektor siły nie jest stały lub
przemieszczenie
nie jest prostoliniowe, praca jest
sumą prac wykonanych na niewielkich odcinkach, na tyle małych, że spełnione są
powyższe warunki. Wyraża ją wówczas wzór
całkowy
gdzie:
W
– praca,
L
– całkowita droga, jaką pokonuje ciało
– siła,
–
wektor przesunięcia
,
α – kąt między wektorem siły i przesunięcia.
Energia kinetyczna (
)
–
energia
ciała
związana z
ruchem
jego masy. Jednostką
jest
dżul.
W opisywalnych przez
mechanikę
układach, może dochodzić do przemian
w
energię potencjalną
(
) i odwrotnie (przykładem takiego układu jest
wahadło
).
Sumę
nazywamy
energią mechaniczną
. Jak wynika z
zasady zachowania
energii
jest w układzie stała.
Energia potencjalna
– jest to energia związana z konfiguracją układu ciał działających
na siebie silami zachowawczymi.
Zmiana energii potencjalnej układu jest liczba przeciwną do wielkości pracy wykonanej nad
układem przez siły oddziaływania pomiędzy elementami układu podczas zmiany jego
konfiguracji.
Zasada zachowania energii mechanicznej:
W układzie izolowanym, w którym wszystkie występujące siły wewnętrzne są siłami
zachowawczymi energia mechaniczna ma wartośd stałą.
4. Definicja środka masy układu punktów materialnych. Druga zasada dynamiki dla układu
punktów materialnych – wyprowadzenie wzoru. Pęd układu punktów materialnych. Zasada
zachowania pędu dla układu punktów materialnych.
Dla układu punktów materialnych istnieje taki punkt, zwany środkiem masy, który porusza się
tak jak gdyby cała masa układu była skupiona w tym punkcie, a wszystkie siły zewnętrzne
działające na układ były przyłożone do tego punktu. Ruch dowolnego ciała lub układu
punktów materialnych można opisad rozpatrując ruch środka masy (który można sobie
wyobrazid jako ruch całości układu) plus ruch poszczególnych punktów materialnych
względem środka masy.
Pęd cząstki definiujemy jako masę cząstki pomnożoną przez jej prędkośd. Pęd układu jest
równy sumie pędów poszczególnych cząstek.
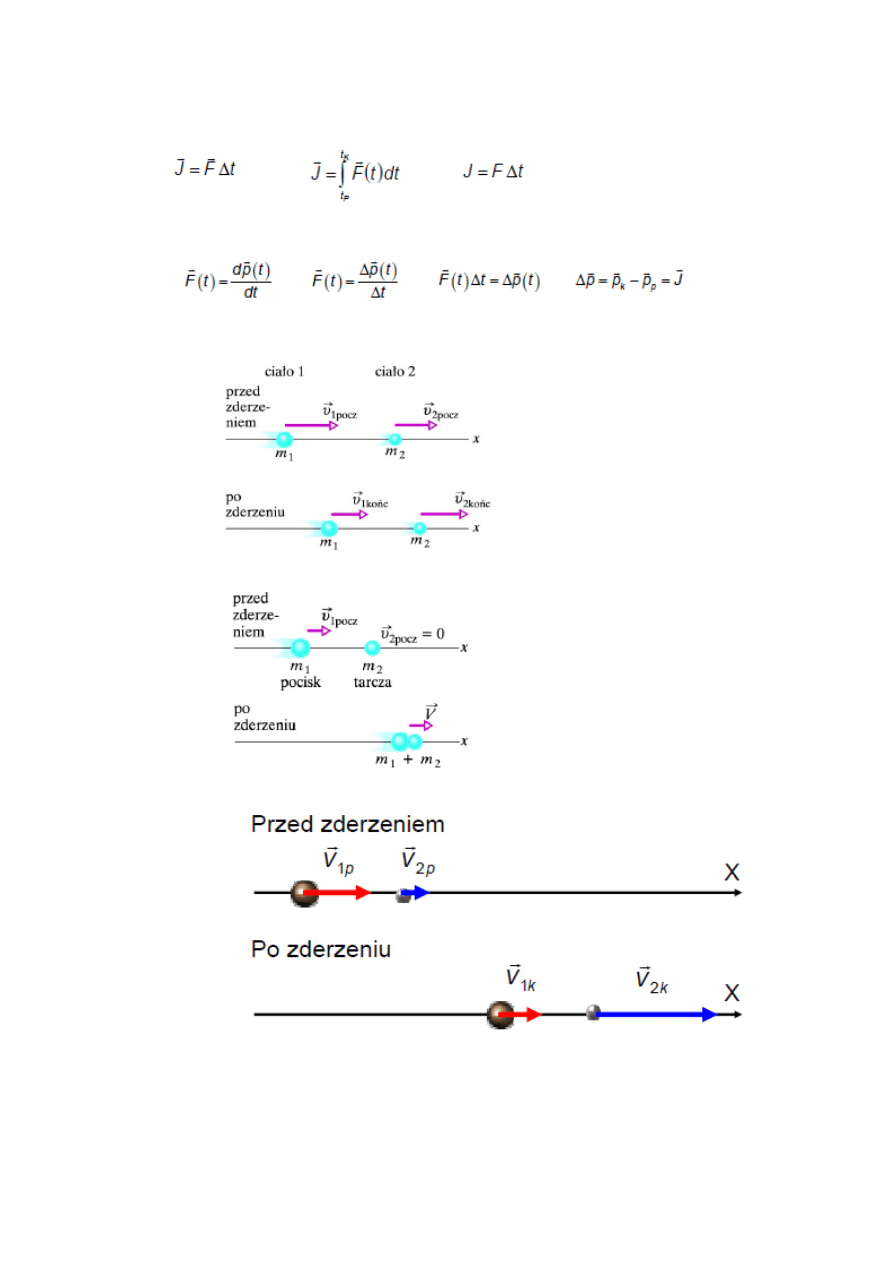
5. Zderzenia. Impuls siły. Klasyfikacja zdarzeo.
Impuls siły – równa się iloczynowi siły i czasu jej działania:
Zderzenie -
oznacza
oddziaływanie
pomiędzy poruszającymi się względem siebie ciałami,
trwające przez pewien skończony czas.
Klasyfikacja zderzeo:
a)Zderzenie niesprężyste w jednym wymiarze
b)Zderzenie całkowicie niesprężyste
c)Zderzenie sprężyste w jednym wymiarze
6. Moment pędu układu cząstek. Druga zasada dynamiki dla ruchu obrotowego układu
cząstek - wyprowadzenie wzoru. Zasada zachowania momentu pędu dla układu cząstek.
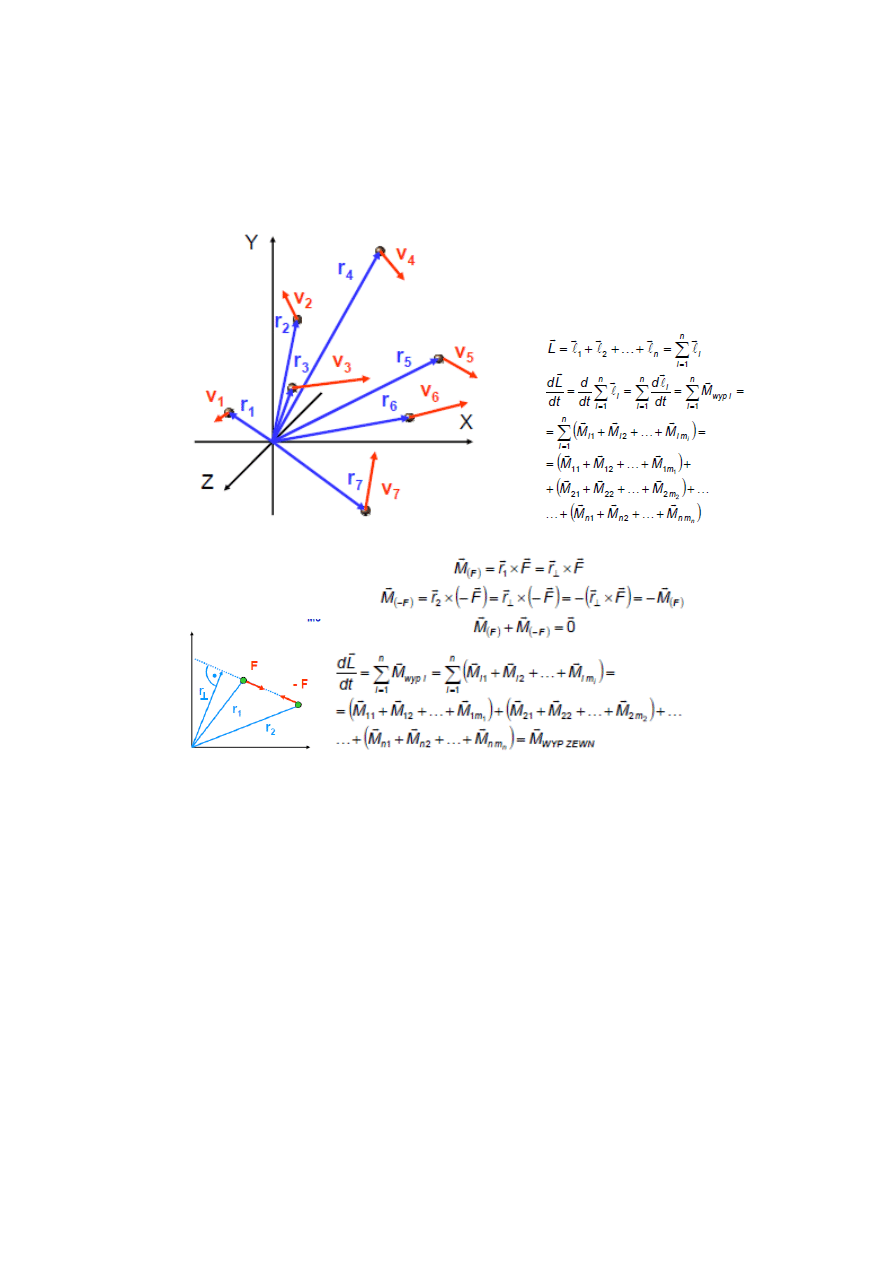
Moment pędu układu punktów materialnych jest sumą wektorową momentu pędu
wszystkich punktów materialnych. Zmiana momentu pędu w czasie jest równa momentowi
sił M działających na układ
Wyprowadzenie wzoru:
Zasada zachowania momentu pędu -
Dla dowolnego
izolowanego układu
punktów
materialnych całkowita suma ich
momentów pędu
jest stała.
7. Drgania harmoniczne. Prędkośd, przyspieszenie siła i energia w ruchu harmonicznym.
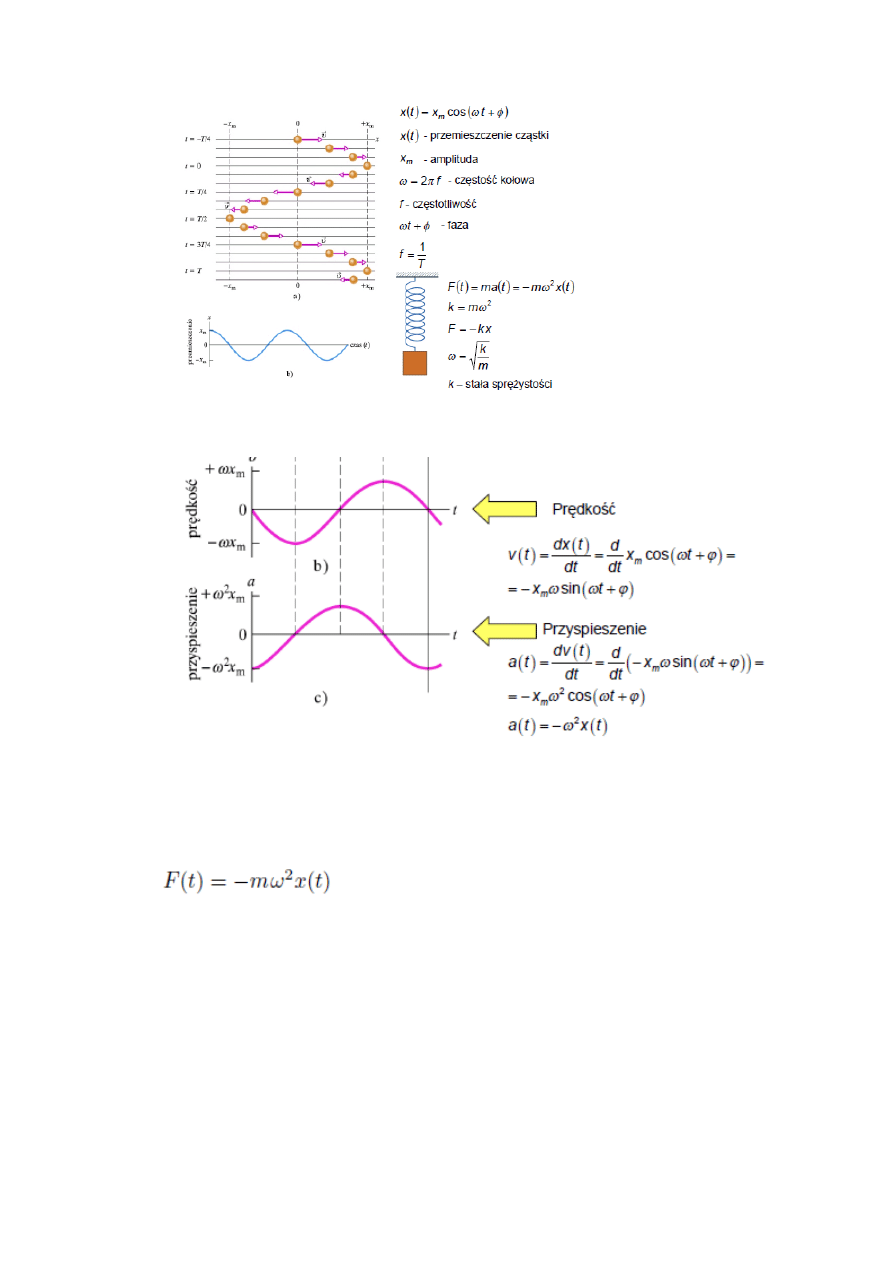
Prędkośd i przyspieszenie:
Siła:
W przypadku ruchu harmonicznego wartośd przyspieszenia a nie jest stała zatem siła F
wywołująca ruch harmoniczny musi byd zmienna.
Energia:
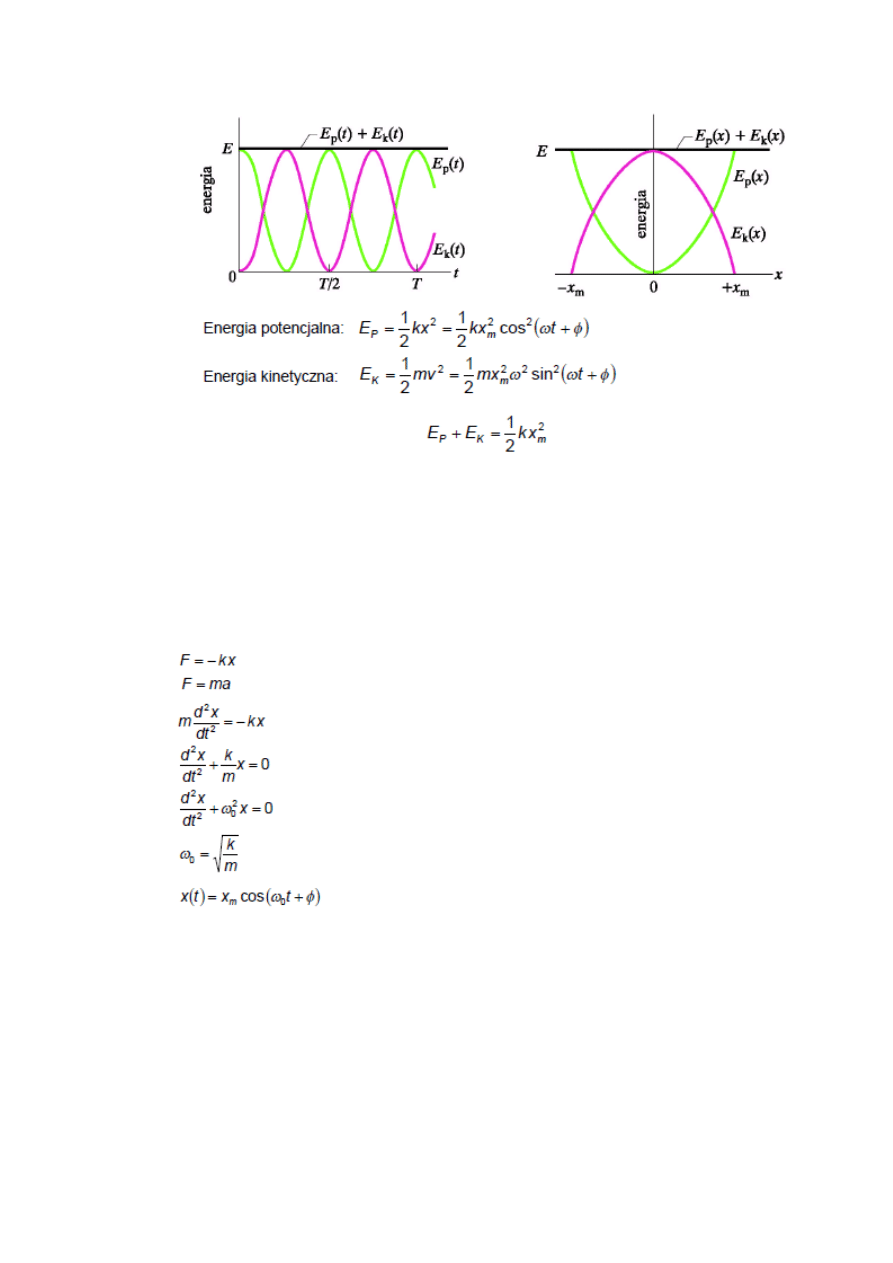
8. Drgania harmoniczne proste, tłumione oraz wymuszone. Równania ruchu i ich rozwiązania.
Rezonans.
Ruch harmoniczny prosty jest ruchem drgającym. Ruch ten odbywa się pod wpływem siły
zwróconej zawsze w stronę położenia równowagi i posiadającej wartośd wprost
proporcjonalną do wychylenia z położenia równowagi.
Ruch harmoniczny tłumiony występuje wtedy, gdy na ciało działa dodatkowo siła
oporu ośrodka proporcjonalna do prędkości:
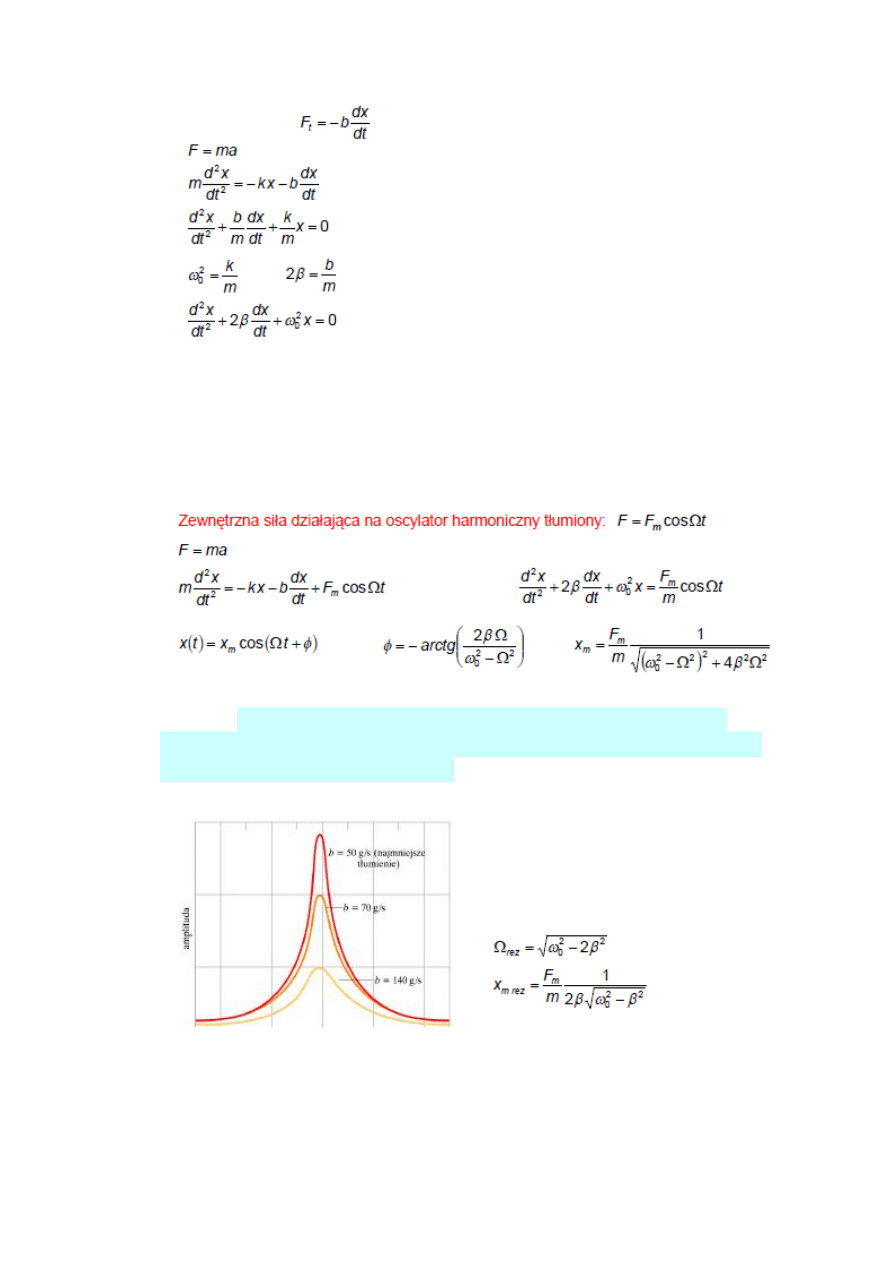
Drgania wymuszone - Ruch możemy podtrzymad poprzez przyłożenie zewnętrznej siły
okresowej. Zasadniczą role w podtrzymaniu tego ruchu odgrywa związek pomiędzy
częstością oscylacji własnych układu, a częstością siły wymuszającej. Częstośd tych drgao
jest narzucona przez okresową siłę wymuszającą, ale zarówno ich amplituda jak i faza
zależą od relacji pomiędzy częstością siły wymuszającej a częstością drgao własnych
układu.
Rezonans -
Stan, w którym amplituda drgao osiąga największą wartośd,
nazywamy stanem rezonansu. Odpowiadająca częstośd siły wymuszającej
nosi nazwę częstości rezonansowej.
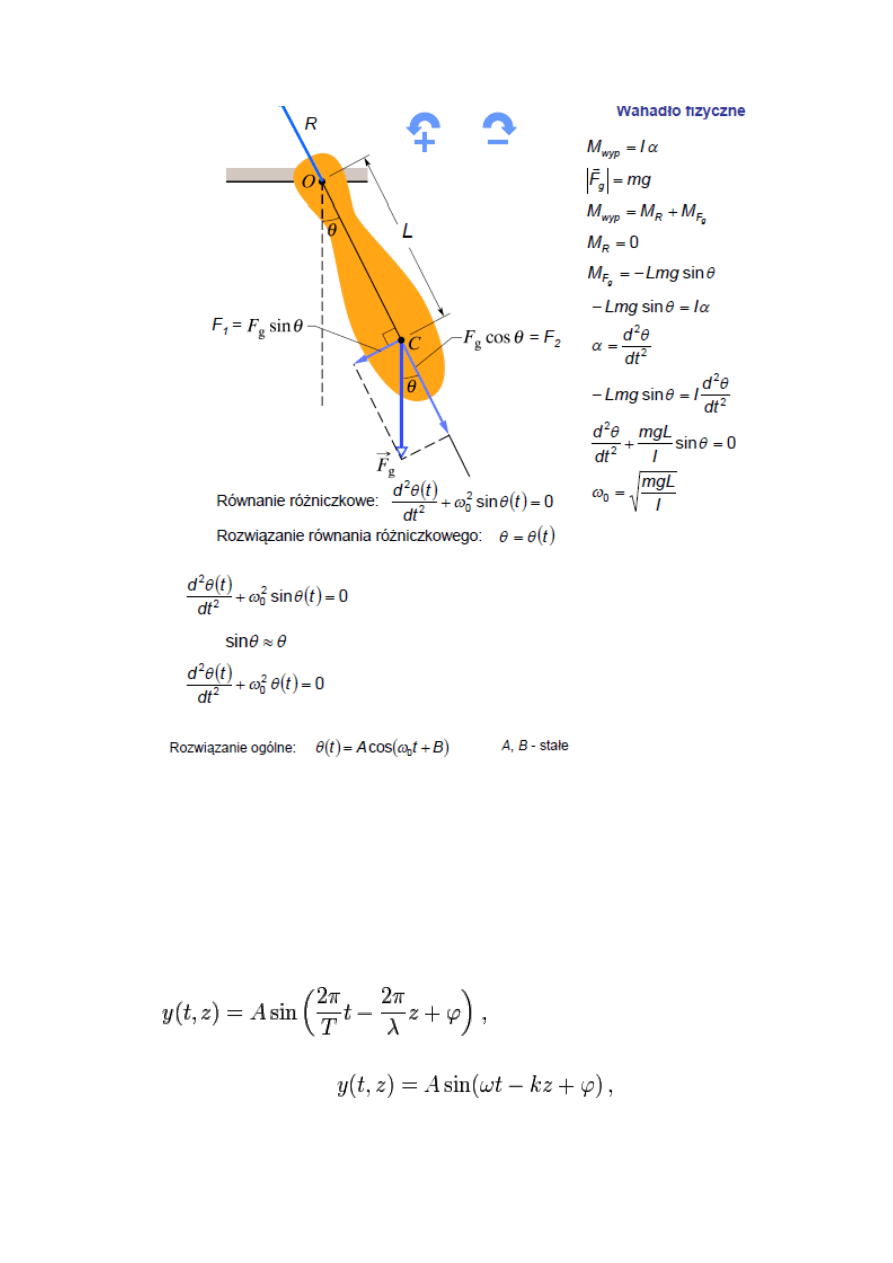
9. Wahadło fizyczne. Sformułowanie równania ruchu. Rozwiązanie równania ruchu.
Wahadło fizyczne - Bryła sztywna
, która może wykonywad obroty dookoła poziomej osi
przechodzącej ponad środkiem ciężkości tej bryły.
10. Jednowymiarowa harmoniczna fala poprzeczna – opis matematyczny.
Matematycznie fala to rozwiązanie równania falowego . Jest to dowolna funkcja
różniczkowalna spełniająca to równanie. Rozwiązania równania falowego tworzą przestrzeo
liniową , która jest przestrzenią Hilberta . Jako bazę tej przestrzeni można wybrad drgania
podstawowe w postaci przebiegów harmonicznych. Dowolne rozwiązanie równania
falowego, a więc dowolną falę można przedstawid jako sumę szeregu funkcji bazowych, a
więc przebiegów harmonicznych, co jest zasadą analizy harmonicznej odkrytej
przez Fouriera
.
co może być zapisane prościej, przyjmując:
gdzie:
A – amplituda fali,
T – okres drgań ,
λ – długość fali,
ω – częstość kołowa zwana krótko częstością lub pulsacją fali,
,
k – liczba falowa ,
φ – faza początkowa