Zadanie nr 3:

Pręt o długości L = x m, średnicy d=10 cm poddano działaniu wiejącego powietrza (nie chce mi się klepać oznaczeń z tablicy znaków więc przyjmijmy, że gęstość oznaczymy przez p=1,2 kg/m³, a współczynnik lepkości „mi” oznaczymy przez u=1,8 * 10^-5 Pa * s). Z jaką prędkością wiał wiatr, jeśli zmierzona siła oporu wynosiła F = 2N.

W moich danych x = 6

Więc obliczenie prędkości dokonuje się ze wzoru na siłę oporu:

We wzorze występuje współczynnik C_D który zależy od liczby Reynoldsa Re i od prędkości właśnie. S jest to pole przekroju pręta, więc S = L*d.

Wyznaczając ze wzoru v otrzymujemy, że:

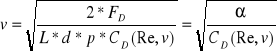
Obliczamy prędkość metodą iteracyjną.

Wyliczając współczynnik alfa otrzymujemy, że:

Teraz aby wyliczyć prędkość podstawiamy to metodą iteracyjną. Ja jako v₁ wziąłem sobie 2 m/s.

Mając daną prędkość, gęstość, objętość i współczynnik lepkości możemy obliczyć liczbę Reynoldsa, potrzebną do znalezienia współczynnika C_D.

Teraz możemy wyznaczyć C_D1. Współczynnik ten obliczamy ze wzoru dla powierzchni walcowej.

Mając współczynnik podstawiamy go z powrotem do wzoru na prędkość i sprawdzamy czy uzyskaliśmy taką samą prędkość, jaką założyliśmy na początku.

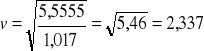
Uzyskana prędkość nie jest taka jak założone 2 m/s, więc iteracyjnie postępujemy ponownie. Tym razem wyliczamy liczbę Reynoldsa podstawiając otrzymane v₂=2,337 m/s.

A więc korzystając z tych samych wzorów co powyżej:

Re₂=15580

C_D2=1,0155

Podstawiamy nową wartość do wzoru: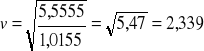

Wartość prędkości otrzymanej jest prawie identyczna jak podstawianej.

Teraz widzimy, że wartość prędkości różni się o 0,08%, co może być wynikiem zaokrąglania przy rachunku etc., dlatego też prędkość wiatru powinna ustalać się w okolicy 2,338 m/s. Zapewne podstawiając ponownie i licząc jeszcze raz uzyska się taką wartość lub zbliżoną.

Patrzymy na odpowiedzi i widzimy, że I w zadaniu 3 to 2,33895, więc będzie to poprawna odpowiedź.

Dziękuję za doczytanie do końca!

---