Rea

kcje

red

oks

Jedną z najważniejszych reakcji chemicznych w świecie
jest reakcja fotosyntezy:

ditlenek węgla

→ węglowodany

6 CO

2(g)

+ 6 H

2

O

(c)

→ C

6

H

12

O

6(s)

+ 6 O

2(g)

Inną równie istotną z praktycznego punktu widzenia
jest reakcja spalania metanu:

metan

CH

4(g)

+ 2 O

2(g)

→ CO

2(g)

+ 2H

2

O

(c)

re

a

k

cj

e

re

d

o

k

s

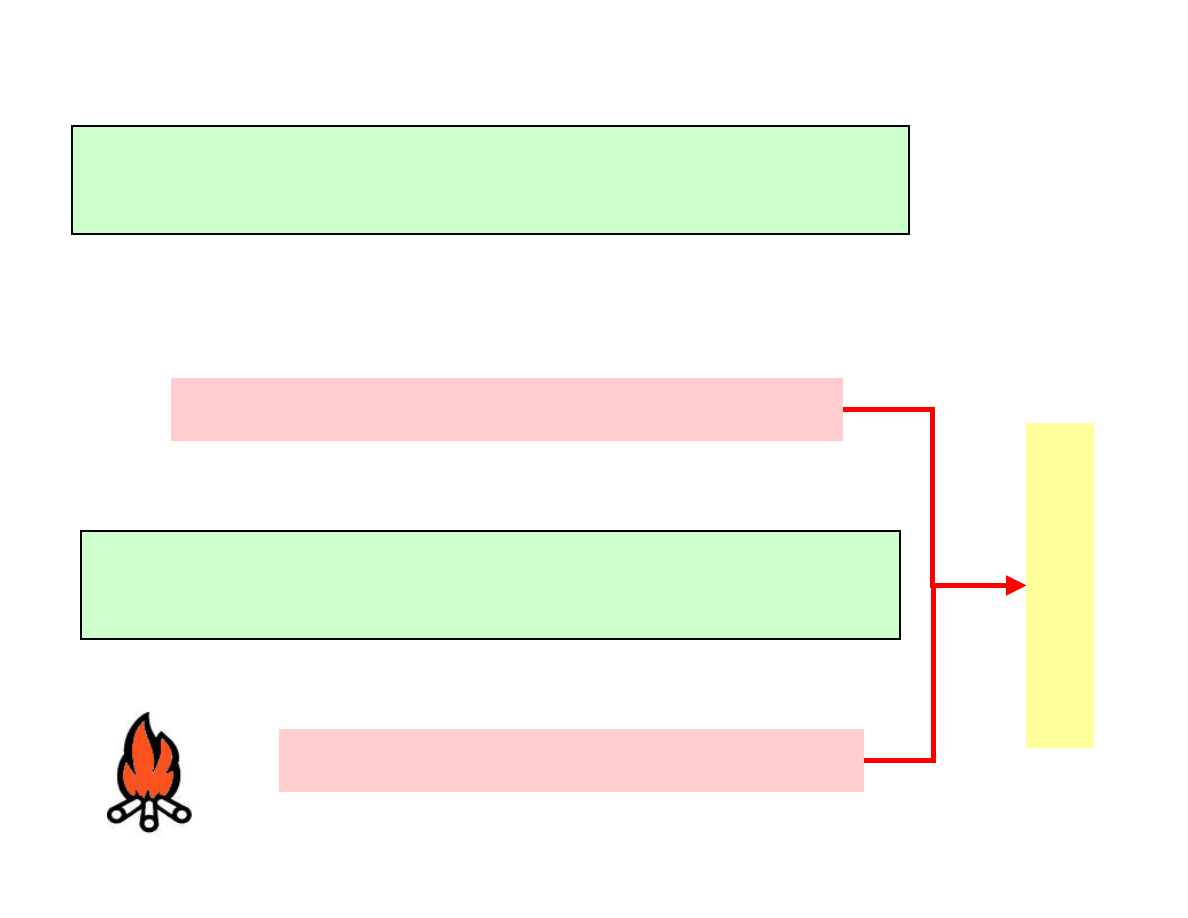
W przypadku reakcji kwas - zasada

w przypadku reakcji redoks

kwas zasada + proton

reduktor utleniacz + elektron

2 Mg

(s)

+ O

2 (g)

→ 2 MgO (Mg

2+

; O

2-

)

Reakcje redoks

Przez długi czas termin „utlenianie” dotyczył reakcji z tlenem:

Istotnym etapem reakcji jest przeniesienie elektronów z
jednej substancji na drugą

2 Mg

(s)

+ Cl

2 (g)

→ 2 MgCl

2

(Mg

2+

; 2 Cl

-

)

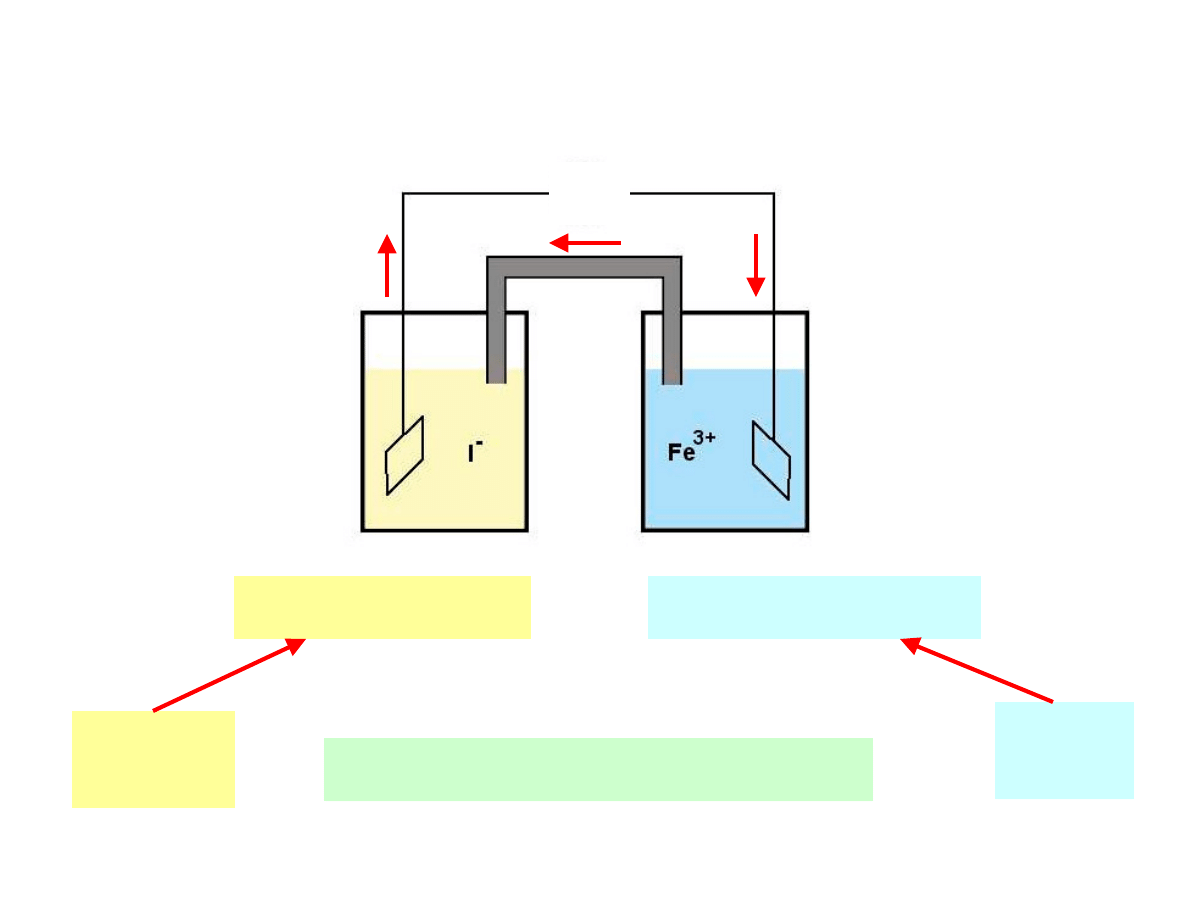
Schemat utleniania I

-

za pomocą Fe

3+

I

-

→

1/2

I

2

+ e

Fe

3+

+ e

→ Fe

2+

w całym układzie zaszła więc reakcja:

Fe

3+

+ I

-

→ Fe

2+

+

1/2

I

2

reakcja

utleniania

reakcja

redukcji

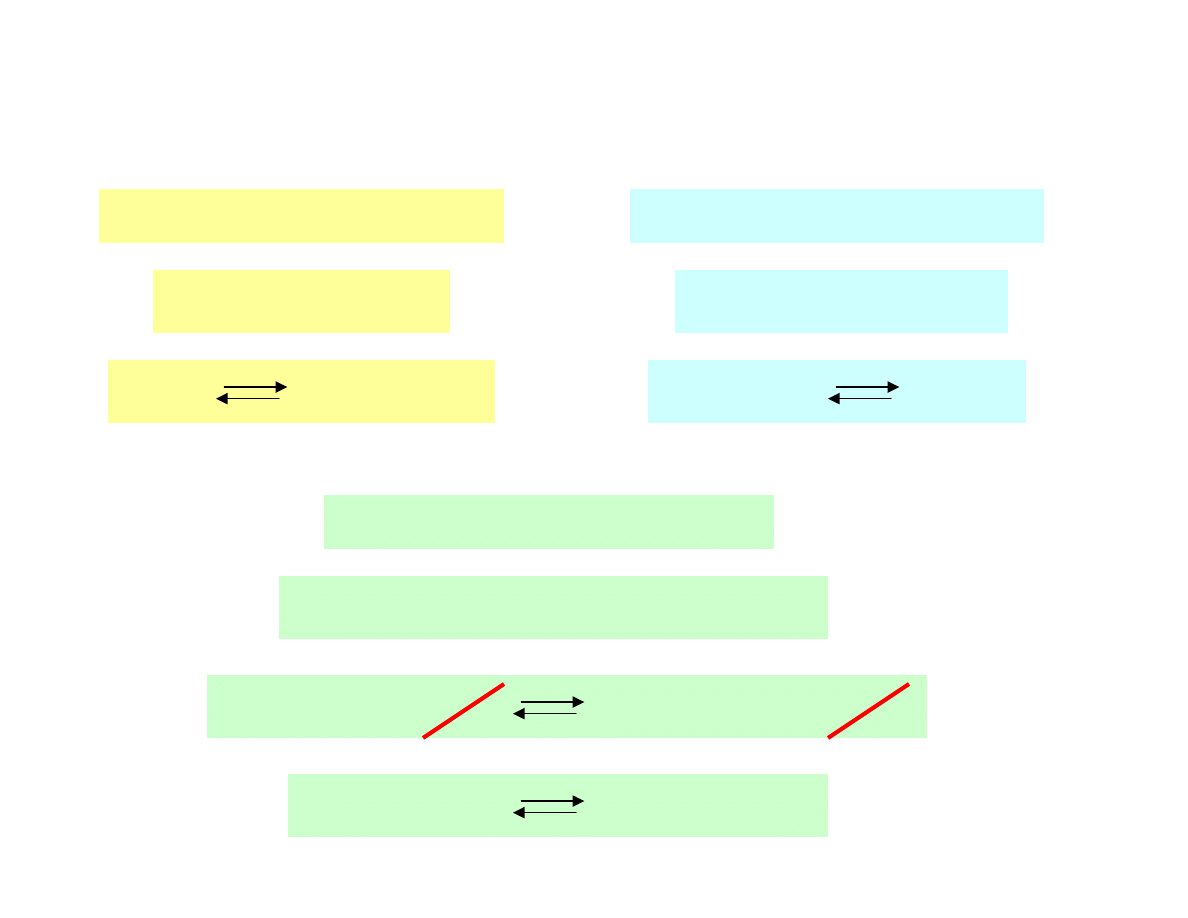
Reakcje redoks

I

-

→

1/2

I

2

+ e

Fe

3+

+ e

→ Fe

2+

Fe

3+

+ I

-

→ Fe

2+

+

1/2

I

2

reakcja utleniania

reakcja redukcji

red

1

utl

1

+ ne

reakcja utleniania-redukcji

utl

2

+ red

1

+ ne red

2

+ utl

1

+ ne

utl

2

+ ne red

2

utl

2

+ red

1

red

2

+ utl

1

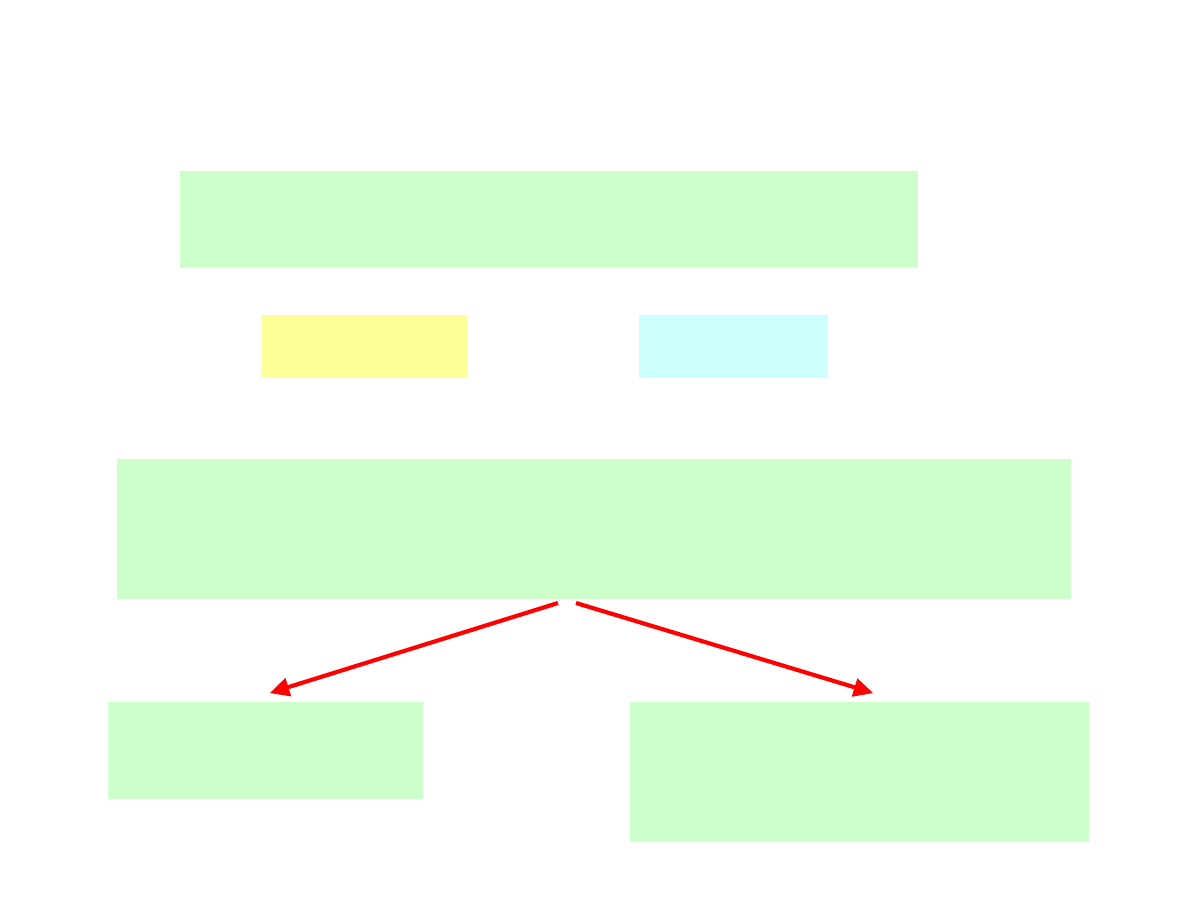
Reakcje redoks

w reakcji utleniania-redukcji uczestniczą zawsze

dwie sprzężone pary redoks

red

1

/ utl

1

utl

2

/ red

2

żadna z tych reakcji oddzielnie nie przebiegnie,

zarówno roztwory jonów Fe

3+

jak i I

-

nie ulegają zmianom,

dopóki są izolowane

zmieszać roztwory

ze sobą

włączenie ich w obwód

zapewniający swobodny

przepływ elektronów

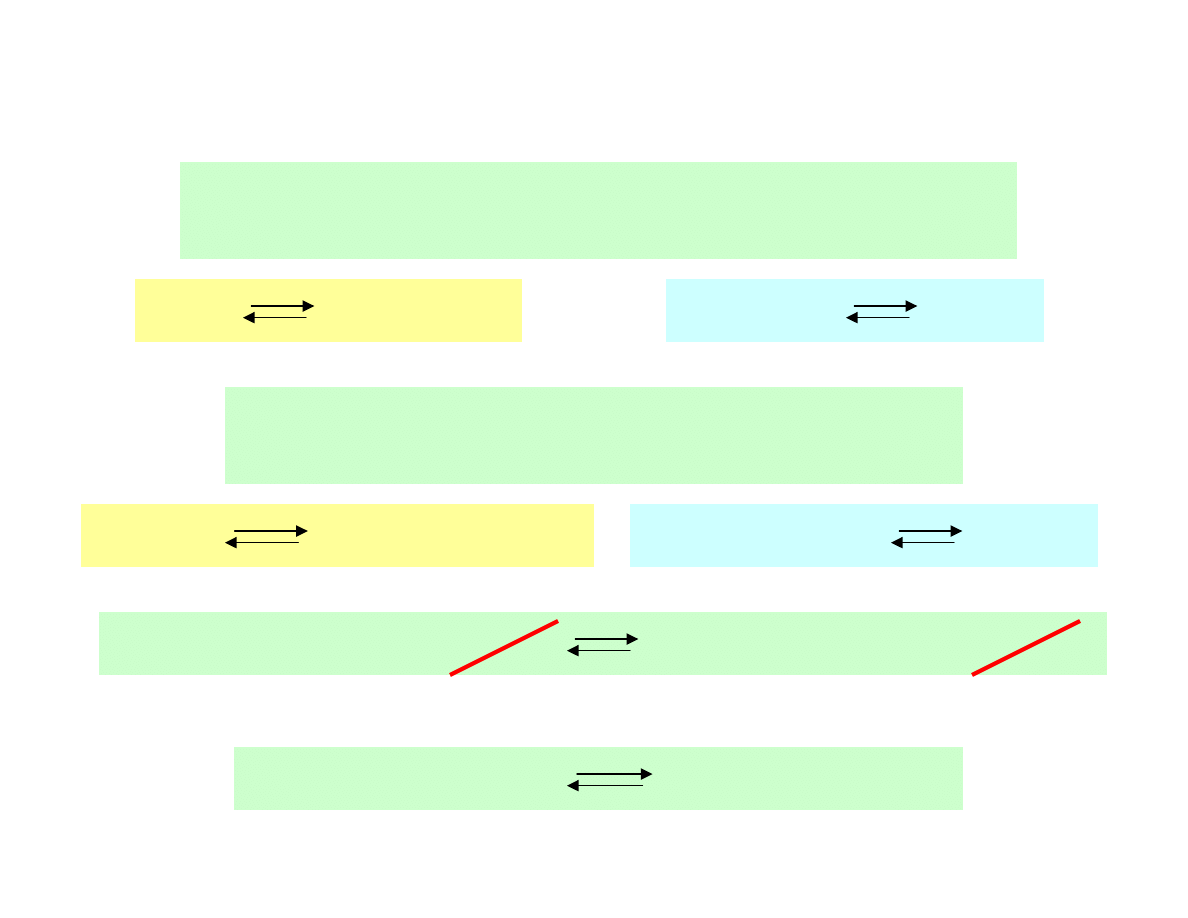
Reakcje redoks

jeżeli każda z reakcji połówkowych przebiega z

wydzieleniem lub pobraniem innej liczby elektronów:

n

2

red

1

+ n

1

utl

2

+ n

1

n

2

e n

2

utl

1

+ n

1

red

2

+ n

2

n

1

e

n

2

red

1

+ n

1

utl

2

n

2

utl

1

+ n

1

red

2

dodając równania stronami trzeba uwzględnić

odpowiednie mnożniki (nww n

1

i n

2

)

red

1

utl

1

+ n

1

e

utl

2

+ n

2

e red

2

n

2

red

1

n

2

utl

1

+ n

2

n

1

e

n

1

utl

2

+ n

1

n

2

e n

1

red

2

Wielkość charakteryzująca dany układ pod względem jego
właściwości redoks to potencjał redoks

Potencjały redoks

można go wyliczyć z wzoru Nernsta

•E

o

- potencjał standardowy danego układu redoks

•R - stała gazowa (8.314 J/(mol· K))
•T - temperatura bezwzględna (K)
•n - liczba elektronów biorąca udział w reakcji
•F - stała Faradaya (96 490 C/mol)
•a

red

- aktywność reduktora w odpowiednim środowisku reakcji

•a

utl

- aktywność utleniacza (sprzężonego z reduktorem)

utl

red

o

a

a

ln

nF

RT

E

E

−

=

!!!

!!!

Potencjały redoks

utl

red

o

a

a

ln

nF

RT

E

E

−

=

utl

red

o

a

a

log

n

0.059

E

E

−

=

podstawiając wartości stałe i zamieniając logarytm naturalny (ln) na
logarytm dziesiętny (log) - w temperaturze 25

o

C otrzymujemy:

w przypadku gdy a

utl

= a

red

utl

red

o

a

a

log

n

0.059

E

E

−

=

0

E = E

o

Potencjały redoks

utl

utl

red

red

o

f

c

f

c

log

n

0.059

E

E

⋅

⋅

−

=

biorąc pod uwagę fakt że:

przy założeniu, że w stosowanych zwykle w analizie układach
można przyjąć że f

utl

= f

red

a = f· c

utl

red

o

c

c

log

n

0.059

E

E

−

=

[utl]

[red]

log

n

0.059

E

E

o

−

=

utl

red

utl

red

o

f

f

log

n

0.059

c

c

log

n

0.059

E

E

−

−

=

Potencjały redoks

]

]

+

+

−

=

4

2

o

II)

Sn(IV)/Sn(

[Sn

[Sn

log

2

0.059

E

E

dla układu Sn(IV)/Sn(II) mamy:

w przypadku układu MnO

4

-

/Mn

2+

dla którego równanie

połówkowe ma następującą postać:

8

]

][

]

+

+

−

=

+

H

[MnO

[Mn

log

5

0.059

E

E

-

4

2

o

/Mn

MnO

2

-

4

MnO

4

-

+ 8H

+

+ 5 e Mn

2+

+ 4H

2

O

Potencjały redoks

podobnie rzecz się ma dla układu CrO

4

2-

/Cr

3+

dla którego

równanie połówkowe ma postać:

]

]

][

2

8

−

−

+

−

=

+

−

4

3

o

/Cr

CrO

[CrO

OH

[Cr

log

3

0.059

E

E

3

2

4

CrO

4

2-

+ 4H

2

O + 3 e Cr

3+

+ 8OH

-

Potencjały redoks

ponieważ nie można obliczyć ani wyznaczyć bezwzględnych
wartości potencjałów ustala się je w odniesieniu do pewnego
potencjału przyjętego jako potencjał zerowy

standardowa elektroda wodorowa

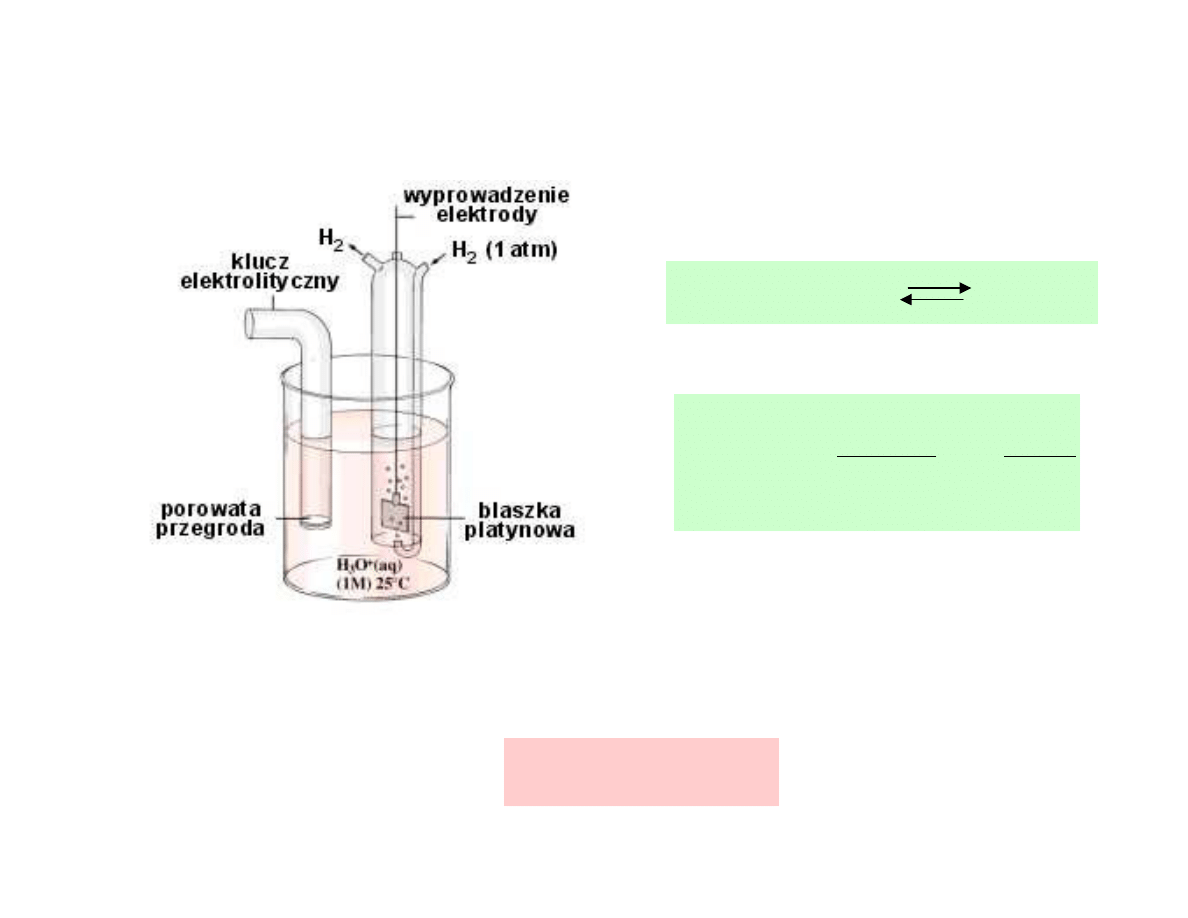
Elektroda wodorowa

2H

+

(aq)

+ 2e H

2(g)

2
H

H

o

a

p

log

2

0.059

E

E

2

+

−

=

w warunkach standardowych a

H+

= 1 oraz p

H2

=1

E = E

o

= 0 V

Szereg napięciowy metali

Metal

E

o

, V

Metal

E

o

, V

Li

+

/ Li

-3,04

Cd

2+

/ Cd

-0,40

K

+

/ K

-2,93

Co

2+

/ Co

-0,28

Ba

2+

/ Ba

-2,91

Ni

2+

/ Ni

-0,26

Ca

2+

/ Ca

-2,86

Sn

2+

/ Sn

-0,14

Ce

3+

/ Ce

-2,48

Pb

2+

/ Pb

-0,13

Mg

2+

/ Mg

-2,36

2H

+

/ H

2

0

U

3+

/ U

-1,80

Bi

3+

/ Bi

0,32

Al

3+

/ Al

-1,70

Cu

2+

/ Cu

0,34

Ti

3+

/ Ti

-1,21

Cu

+

/ Cu

0.52

Mn

2+

/ Mn

-1,18

Ag

+

/ Ag

0,80

Zn

2+

/ Zn

-0,76

Hg

2+

/ Hg

0,86

Cr

3+

/ Cr

-0,74

Pt

2+

/ Pt

1,20

Fe

2+

/ Fe

-0,44

Au

3+

/ Au

1,52

Szereg napięciowy metali

• zdolność do wymiany elektronów w układzie metal + jony

innego metalu jest tym większa im dalej od siebie
położone są oba metale w szeregu napięciowym

Znajomość położenia układu redoks w szeregu napięciowym
pozwala nam przewidywać kierunek reakcji

Fe + Cu

2+

→ Cu + Fe

2+

ale

Fe + Zn

2+

→ nie zachodzi

za to można:

Cu + 2Ag

+

→ Cu

2+

+ 2Ag

Szereg napięciowy metali

• litowce i berylowce (początek szeregu napięciowego)

reagują z wodą według schematu:

Znajomość położenia układu redoks w szeregu napięciowym
pozwala nam przewidywać kierunek reakcji

metal + woda

→ wodorotlenek metalu + wodór

• Metale stojące przed wodorem wypierają go z kwasów:

metal + kwas

→ sól + wodór

2Na + 2H

2

O

→ 2NaOH + H

2

(

↑

)

Równowagi reakcji redoks

siła napędowa reakcji redoks

Na podstawie standardowych potencjałów układów
można wyliczyć stałe równowagi reakcji redoks

różnica potencjałów układów

n

2

red

1

+ n

1

utl

2

n

2

utl

1

+ n

1

red

2

1

2

1

2

]

]

]

]

n

n

n

n

2

1

2

1

[utl

[red

[red

[utl

K

=

n

2

red

1

n

2

utl

1

+ n

2

n

1

e

n

1

red

2

n

1

utl

2

+ n

1

n

2

e

2

2

n

1

n

1

2

1

o

1

1

]

[utl

]

[red

log

n

n

0.059

E

E

−

=

1

1

n

2

n

2

2

1

o

2

2

]

[utl

]

[red

log

n

n

0.059

E

E

−

=

Równowagi reakcji redoks

gdy układ osiągnie stan równowagi wówczas:

E

2

=E

1

2

2

1

1

n

1

n

1

2

1

o

1

n

2

n

2

2

1

o

2

]

[utl

]

[red

log

n

n

0.059

E

]

[utl

]

[red

log

n

n

0.059

E

−

=

−

2

2

1

1

n

1

n

1

n

2

n

2

2

1

o

1

o

2

]

[red

]

[utl

]

[utl

]

[red

log

n

n

0.059

E

E

=

−

Równowagi reakcji redoks

stała

równowagi K

można obliczyć stopień
przereagowania utleniacza
czy reduktora jeśli znane są
potencjały standardowe obu
układów redoks

0.059

n

)n

E

(E

logK

2

1

o

1

o

2

−

=

logK

n

n

0.059

E

E

2

1

o

1

o

2

=

−

Potencjały standardowe niektórych układów redoks

w roztworach wodnych

reduktory

silne

utleniacze

układ redoks

E

o

, V

AsO

4

3-

+ H

2

O + 2e = AsO

3

3-

+ 2OH

-

-0.71

Fe(OH)

3

+ e = Fe(OH)

2

+ OH

-

-0.56

CrO

4

2-

+ 4H

2

O + 3e = Cr(OH)

3

+ 5 OH

-

-0.12

2H

+

+ 2e = H

2(g)

0.00

Fe(CN)

6

3-

+ e = Fe(CN)

6

4-

0.36

I

2(s)

= 2e = 2I

-

0.54

MnO

4

-

+ H

2

O

+ 3e = MnO

2

+ 4 OH

-

0.57

NO

3-

+ 4H

+

+ 3e = NO + 2H

2

O

0.96

O

2(g)

+ 4H

+

+ 4e = 2H

2

O

1.23

Cr

2

O

7

2-

+ 14H

+

+ 6e = 2Cr

3+

+ 7H

2

O

1.33

ClO

3

-

+ 6H

+

+ 6e = Cl

-

+ 3H

2

O

1.45

MnO

4

-

+ 8H

+

+ 5e = Mn

2+

+ 4H

2

O

1.52

F

2(g)

+ 2e = 2F

-

2.92

2H

2

O + 2e H

2(g)

+ 2OH

-

2Na + 2H

2

O

→ H

2(g)

+ 2Na

+

+ 2OH

-

woda jako utleniacz

2H

2

O O

2(g)

+ 4H

+

+ 4e

2F

2

+ 2H

2

O

→ O

2(g)

+ 4HF

woda jako reduktor

Potencjały redoks

teoretycznie należałoby oczekiwać, że wszystkie reakcje redoks
dla których wartości:

E

o

< 0 V

(potencjał standardowy wody jako utleniacza)

E

o

> 1.23 V

(potencjał standardowy wody jako reduktora)

oraz

nie będą mogły przebiegać w wodzie

zarówno reakcja redukcji jak i utleniania wody
należą do reakcji zahamowanych

Potencjały redoks

Reakcje zahamowane

Z wartości potencjałów redoks poszczególnych układów można
przypuszczać że H

2(g)

przy pH=0 powinien redukować wszystkie

utleniacze o wyższym potencjale

tak dzieje się jednak rzadko - dlaczego?

wysoki potencjał pierwszego stadium przemiany

zahamowanie procesu rozkładu wody wynika zaś
z wysokiego potencjału wydzielania gazowego wodoru

H

2

H

(g)

+ H

+

+ e

2.1 V

H

+

+ e H

(g)

-2.1 V

Amfoteryczne substancje redoks

związki które w reakcji z silnymi utleniaczami zachowują się
jak reduktory, a w reakcji z silnymi reduktorami reagują jak
utleniacze to

amfoteryczne substancje redoks

.

Typowe przykłady:

Mn(II)

Mn(IV)

Mn(VI)

Mn(VII)

Mn

2+

MnO

2

MnO

4

2

−−−−

MnO

4

−

Br(-I)

Br(0)

Br(V)

Br

−

Br

2

BrO

3

−

O(-II)

O(-I)

O(0)

Η

2

Ο

H

2

O

2

O

2

N(II)

N(III)

N(V)

NO

NO

2

−−−−

NO

3

−

Amfoteryczne substancje redoks

O(-II)

O(-I)

O(0)

Η

2

Ο

H

2

O

2

O

2

H

2

O

2

+ 2H

+

+ 2e 2 H

2

O

2I

−

+ H

2

O

2

+ 2H

+

→ I

2

+ 2 H

2

O

H

2

O

2

jako

utleniacz

H

2

O

2

O

2

+ 2H

+

+ 2e

2MnO

4

−

+ 5H

2

O

2

+ 6H

+

→ 2Mn

2+

+ 5O

2

+ 8 H

2

O

H

2

O

2

jako

reduktor

utl

red

1

1

1

o

1

1

a

a

log

n

0.059

pH

n

m

0.059

E

E

−

⋅

⋅

−

=

Wpływ środowiska na reakcje redoks

Cr(OH)

3

+ 5 OH

−

CrO

4

2

−

+ 4H

2

O + 3e

MnO

4

−

+ 8H

+

+ 5e

Mn

2+

+ 4H

2

O

1

m
H

utl

red

1

o

1

1

a

a

a

log

n

0.059

E

E

+

⋅

−

=

log a

H+

=

−pH

im mniejsze pH tym E

1

większe

Wpływ kwasowości na reakcje redoks

MnO

4

−

+ 8H

+

+ 5e

Mn

2+

+ 4H

2

O

−

+

−

⋅

⋅

−

=

4

2

MnO

Mn

o

1

1

a

a

log

5

0.059

pH

5

8

0.059

E

E

po podstawieniu wartości E

1

o

= 1.52 V, n

1

=5 i m

1

= 8

jeśli założymy, że a

MnO4−

= a

Mn2+

Dla rozpatrywanego układu:

dla pH =

0 E

1

= 1.52

− 0.0 + 0.012 ·log1 = 1.52V

1.24V

1

log

.

5

8

0.059

.

E

3

pH

dla

1

=

⋅

−

⋅

⋅

−

=

=

012

0

3

52

1

.95V

1

log

.

5

8

0.059

.

E

6

pH

dla

1

0

012

0

6

52

1

=

⋅

−

⋅

⋅

−

=

=

Wpływ kwasowości na reakcje redoks

−

−

⋅

−

=

2
4

3

CrO

5
OH

Cr(OH)

o

1

1

a

a

a

log

3

0.059

E

E

Dla drugiego z rozpatrywanych układów:

Cr(OH)

3

+ 5 OH

−

CrO

4

2

−

+ 4H

2

O + 3e

−

−

−

⋅

−

=

2
4

3

CrO

Cr(OH)

OH

o

1

1

a

a

log

3

0.059

a

log

3

5

.

E

E

059

0

−

−

⋅

⋅

+

=

2
4

3

CrO

Cr(OH)

o

1

1

a

a

log

3

0.059

pOH

3

5

.

E

E

059

0

pOH=14-pH

−

−

⋅

⋅

−

⋅

⋅

+

=

2
4

3

CrO

Cr(OH)

o

1

1

a

a

log

3

0.059

pH

3

5

.

3

5

.

E

E

059

0

14

059

0

im > pH
tym <E

1

Wpływ kwasowości na reakcje redoks

po podstawieniu wartości E

1

o

= -0.12 V

jeśli założymy, że a

Cr(OH)3

= a

CrO42−

Dla drugiego z rozpatrywanych układów:

dla pH =

1

E

1

= -0.12 + 1.38 - 0.098 ·

1

= 1.16V

Cr(OH)

3

+ 5 OH

−

CrO

4

2

−

+ 4H

2

O + 3e

1

log

3

0.059

pH

3

5

.

.

E

E

o

1

1

−

⋅

⋅

−

+

=

059

0

38

1

dla pH =

7

E

1

= -0.12 + 1.38 - 0.098 ·

7

= 0.57V

dla pH =

12

E

1

= -0.12 + 1.38 - 0.098 ·

12

= 0.08V

log 1 = 0

]

ML

[

L]

][

[M

log

n

0.059

log

n

0.059

E

]

ML

[

L]

][

[M

log

n

0.059

E

E

n

m

o

n

m

o

+

+

+

+

−

−

=

−

=

β

β

Wpływ kompleksowania na reakcje redoks

Jeżeli w układzie redoks znajdzie się czynnik kompleksujący
postać utlenioną lub zredukowaną albo też obie postacie,
to podstawowa równowaga redoks ulegnie zasadniczej zmianie

M

n+

+ ne M

m+

Mn

n+

+ L ML

n+

o

E

1

]

ML

[

L]

][

[M

log

n

0.059

E

E

n

m

o

+

+

−

=

1

]

M

[

]

[M

log

n

0.059

E

E

n

m

o

+

+

−

=

]

L

][

M

[

]

[ML

n

n

+

+

=

β

β

⋅

=

+

+

]

L

[

]

[ML

]

M

[

n

n

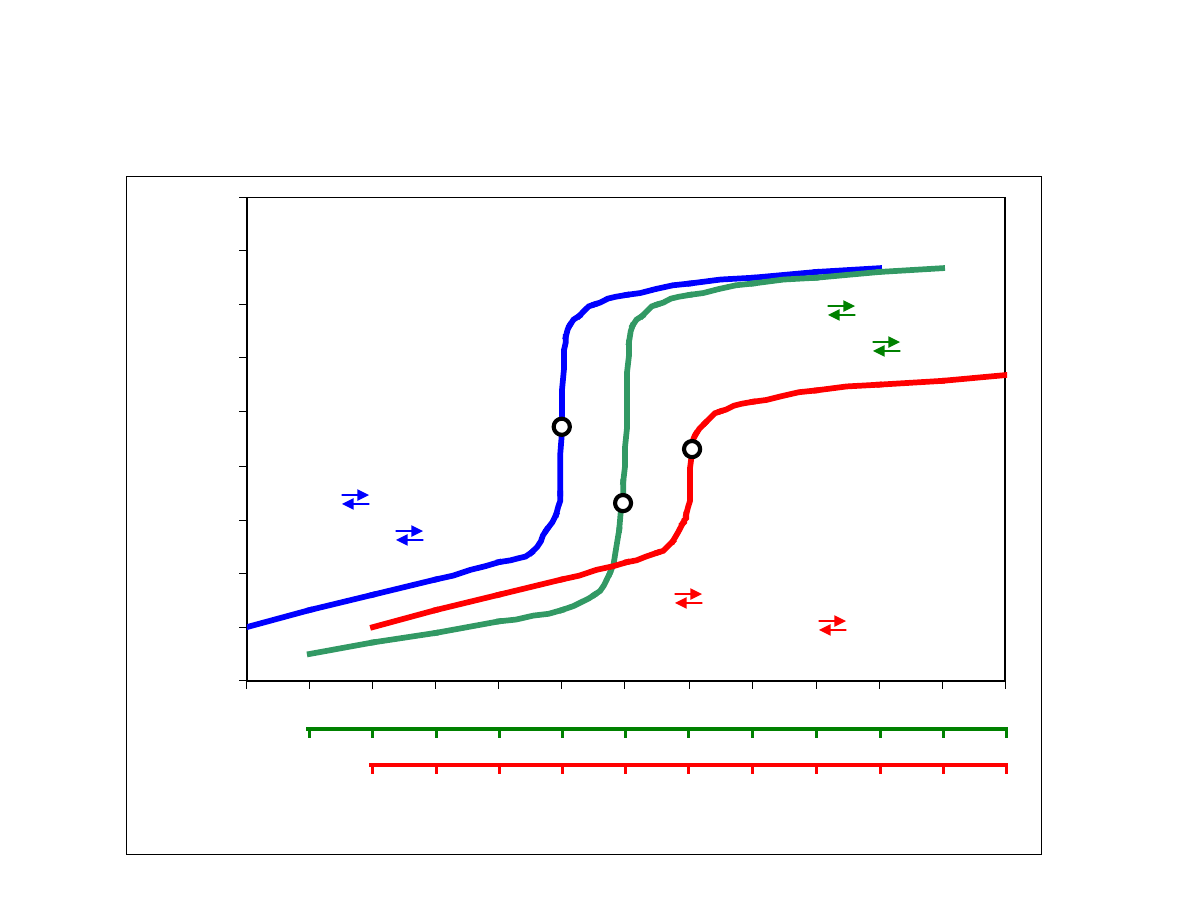
0.5

0.6

0.7

0.8

0.9

1

1.1

1.2

1.3

1.4

0

2

4

6

8

10

12

14

16

18

20

22

24

objętość titranta [ml]

E

[

V

]

0 2 4 6 8 10 12 14 16 18 20 22

0 2 4 6 8 10 12 14 16 18 20

Krzywe miareczkowania redoks

PR

Fe(II) Fe(III) + e
Ce(IV) + e Ce(III)

PR

Fe(II) Fe(III) + e
Cr

2

O

7

2-

+ 6e +14H

+

2Cr

3+

+ 7H

2

O

PR

As(III) As(V) + 2e
Ce(IV) + e Ce(III)

Wskaźniki redoks

PK miareczkowania redoks można wyznaczyć:

potencjometrycznie

(śledząc zmiany potencjału)

wizualnie

(stosując barwne wskaźniki redoks)

odwracalne lub nieodwracalne
sprzężone układy redoks, w których
formy są różnie zabarwione

kryterium doboru wskaźnika -
właściwy potencjał standardowy
lub w konkretnym środowisku

potencjał formalny

układu redoks

Wskaźniki redoks

utl

1

+ red

2

→ red

1

+ utl

2

jeżeli weźmiemy
prostą reakcję redoks:

]

utl

[red

log

n

0.059

E

E

1

1

o
utl

utl

[

]

−

=

to potencjał roztworu

przed PK

jest określony zmianami utleniacza:

zakładając dokładność wskazania PK =

±0.1%:

1

.

0

9

.

99

[

] =

]

utl

[red

1

1

n

0.18

E

0.1

log

n

0.059

E

E

o
utl

o
utl

utl

−

=

−

=

9

.

99

Wskaźniki redoks

utl

1

+ red

2

→ red

1

+ utl

2

jeżeli weźmiemy
prostą reakcję redoks:

potencjał roztworu

po PK

jest określony przez niewielki nadmiar

reduktora (podobne założenie 0.1%):

n

0.18

E

99.9

log

n

0.059

E

E

o
red

o

red

red

+

=

−

=

1

.

0

zatem potencjał wskaźnika E

Ind

musi znajdować się w przedziale:

n

0.18

E

E

n

0.18

E

o
red

Ind

o
utl

+

<

<

−

ciekawe przykłady wskaźników:

• nadmanganian MnO

4

-

(manganometria)

• jod + skrobia

(jodometria)