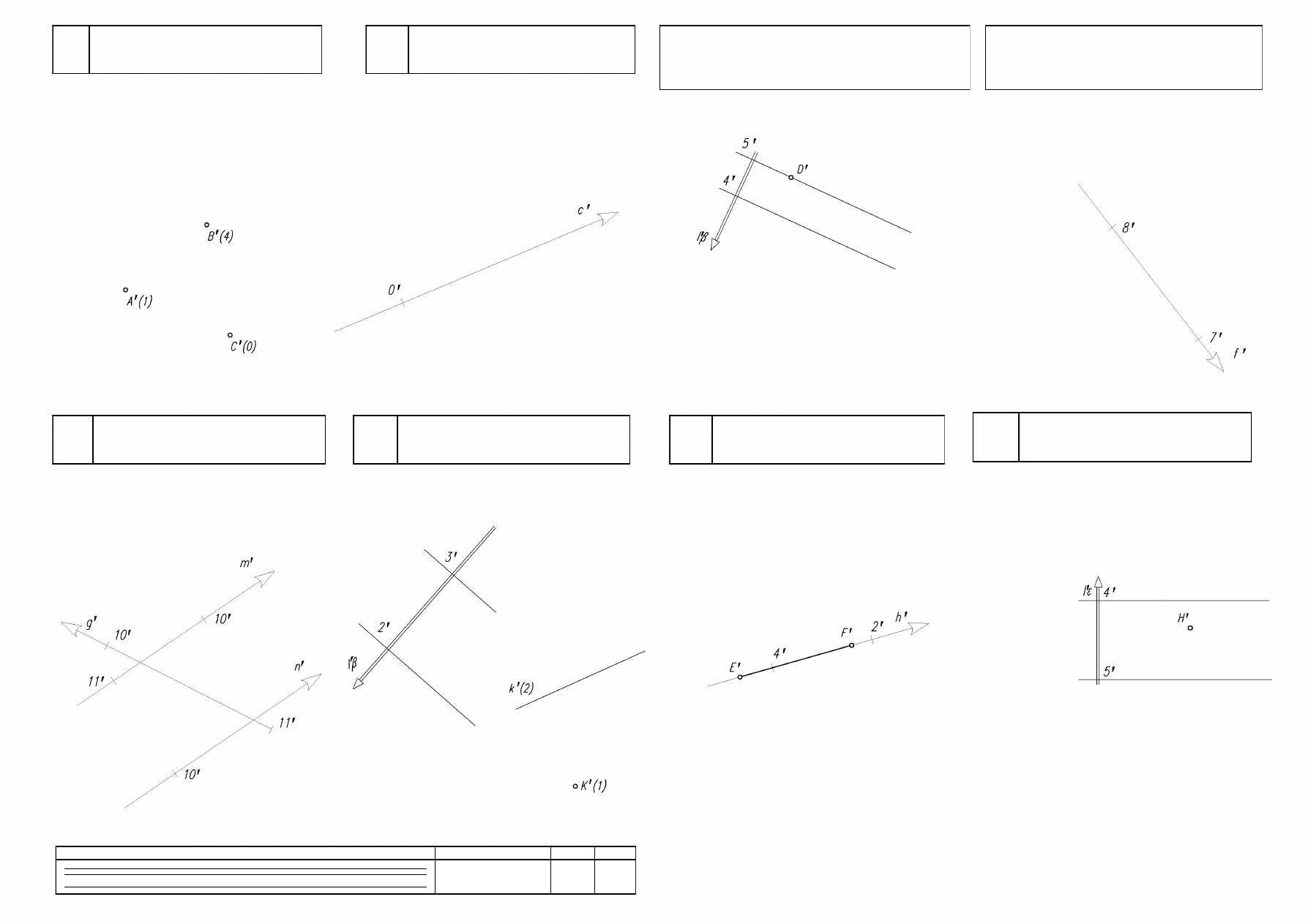
1.
Przedstaw płaszczyznę α=ABC jej
planem warstwicowym. Opisz warstwice
i linię spadu płaszczyzny.
2.
Przyjmij, że prosta c jest nachylona do
rzutni pod kątem 60˚. Uzupełnij stopnie
prostej, j=3 cm
3.
Przez dany punkt D na płaszczyźnie
bprzyjmij
prostą d leżącą na płaszczyźnie i nachyloną do
rzutni pod kątem 22,5˚. Wykreśl moduł prostej i
oznacz w konstrukcji. j=1,5 cm
4.
Po obu stronach prostej f poprowadź
dwie różne płaszczyzny
eoraz g
nachylone do rzutni pod tym samym
kątem 30˚. j=1,5cm
5.
Wskaż punkt przebicia prostej g z
płaszczyzną
d=mn, m równoległe do n.
6.
Wyznacz krawędź pomiędzy
płaszczyznami
b oraz g=Kk.
7.
Wyznacz rzeczywistą długość odcinka EF
znajdującego się na prostej h, j=2 cm
8.
Wyznacz punkty K i L odległe o 2 cm od
punktu H płaszczyzny
ei znajdujące się
na warstwicy 4. j = 2,5 cm
Imię i Nazwisko
Nr indeksu
Grupa
Ocena
Wyszukiwarka
Podobne podstrony:
GW CW08 B TRANSP
GW CW08 Przyklad
GW CW08 A
GW CW08 Przyklad
GW CW08 B
GW CW12Bv02
GW CW15 Dla chetnych
Cw08 Matlab2
GW PROJEKT D
GW Praca semestralna zasady i wytyczne
egzamin inżynierski, GW
cw08
więcej podobnych podstron