Mechanika budowli

Metoda sił – przykład ramy z ukośnymi prętami

Przykład zaczerpnięto z książki „Podstawy mechaniki budowli” M. Palucha

Temat:
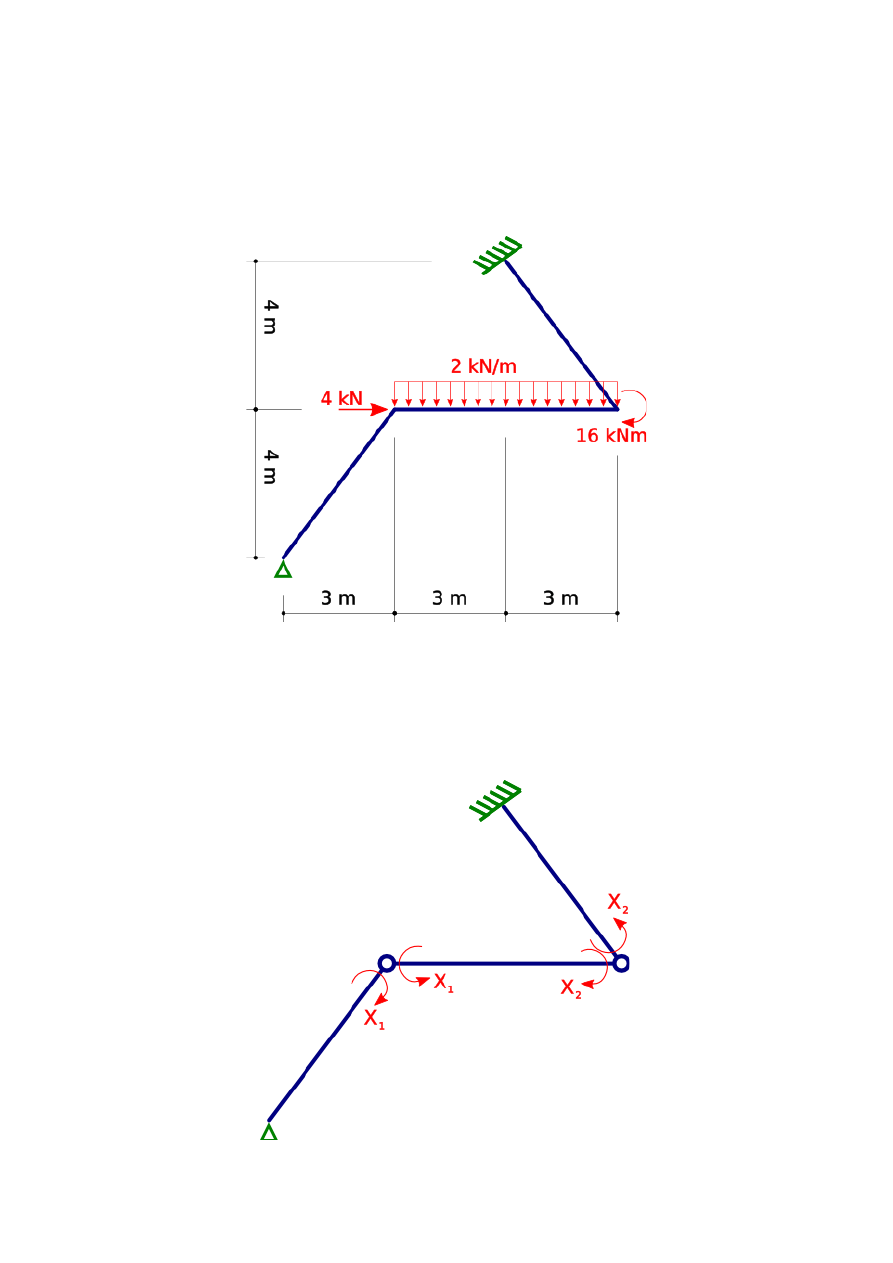
Skonstruuj wykres momentów zginających dla statycznie niewyznaczalnej ramy jak na Rys. 1.

Rys. 1. Rama statycznie niewyznaczalna

Stopień statycznej niewyznaczalności dla rozważanej ramy wynosi SNS=2. W celu skonstruowania
układu podstawowego należy więc z układu odrzucić dwa więzy zewnętrzne lub wewnętrzne. W
tym przykładzie ze względu na proste rachunki na etapie wyprowadzania macierzy podatności i
wektora wyrazów wolnych zdecydowano się na przyjęcie układu podstawowego jak na Rys. 2.

Rys. 2. Układ podstawowy

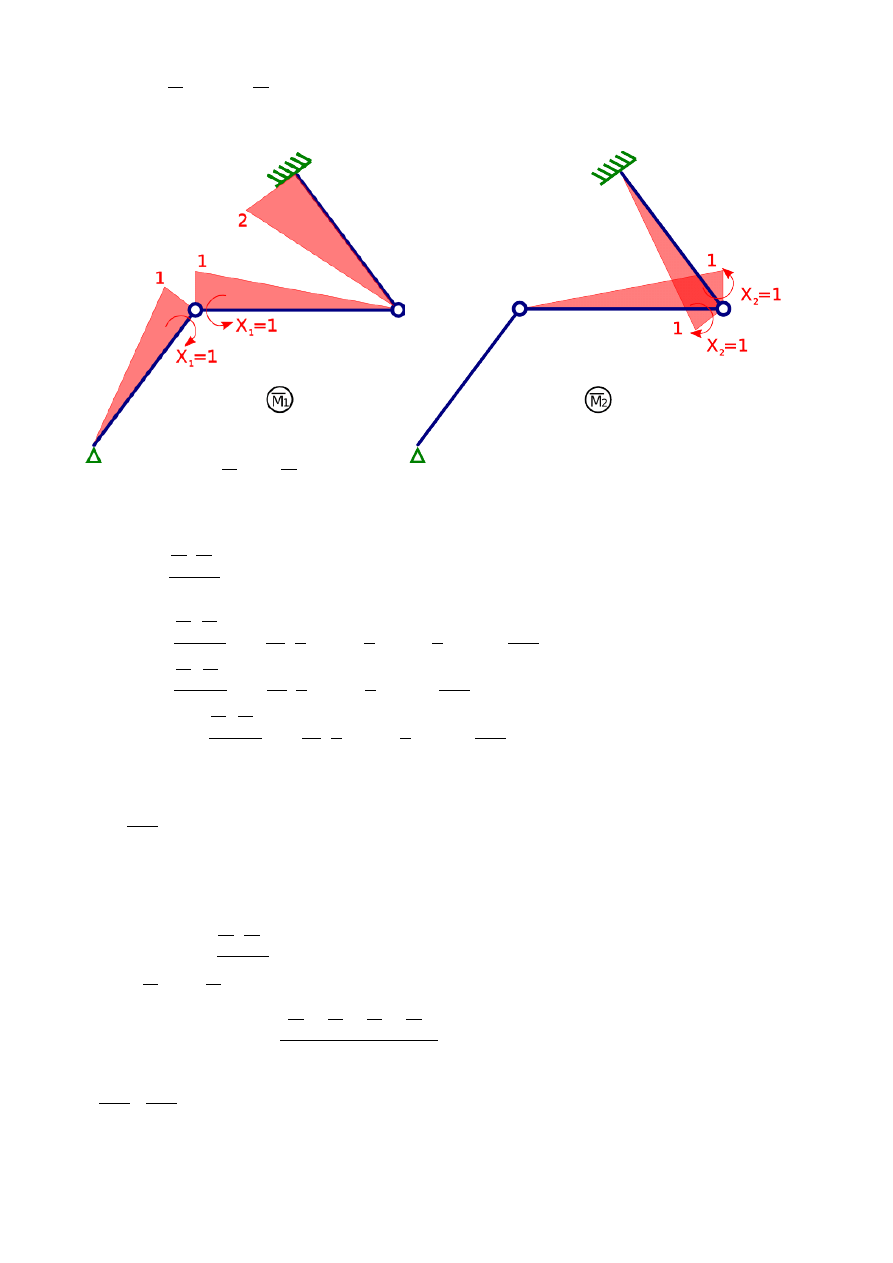
Wykresy

M

1

oraz M

2

od obciążeń jednostkowych na kierunkach niewiadomych X

1

i

X

2

są przedstawione na Rys. 2.

Rys. 3. Wykresy M

1

i M

2

Przemieszczenia na kierunkach niewiadomych

X

1

i

X

2

wywołane jednostkowymi

obciążeniami na tych samych kierunkach można obliczyć ze wzoru:

δ

ij

=

∑∫

M

i

M

j

EI

d s

δ

11

=

∑∫

M

1

M

1

EI

d s=

1

EI

(

1
3

1⋅1⋅5+

1
3

1⋅1⋅6+

1
3

2⋅2⋅5

)

=

31

2 EI

δ

22

=

∑∫

M

2

M

2

EI

d s=

1

EI

(

1
3

1⋅1⋅6+

1
3

1⋅1⋅5

)

=

11

3 EI

δ

12

=δ

21

=

∑∫

M

1

M

2

EI

d s=

1

EI

(

1
6

1⋅1⋅6+

1
6

1⋅2⋅5

)

=

8

3 EI

Ostatecznie macierz podatności:

Δ=

1

3 EI

[

31

8

8

11

]

Sprawdzenie 1:
Należy sprawdzić czy zachodzi:

∑

i

∑

j

δ

ij

=

∑∫

M

s

M

s

EI

d s

gdzie M

s

=

∑

i

M

i

czyli w rozwiązywanym zadaniu:

δ

11

+δ

21

+δ

21

+δ

22

=

∑∫

(

M

1

+

M

2

)(

M

1

+

M

2

)

EI

d s

Po podstawieniu wartości liczbowych otrzymujemy

58

3 EI

=

58

3 EI

Wykonywanie tego sprawdzenia jest zalecane zaraz po obliczeniu wszystkich wartości

δ

ij

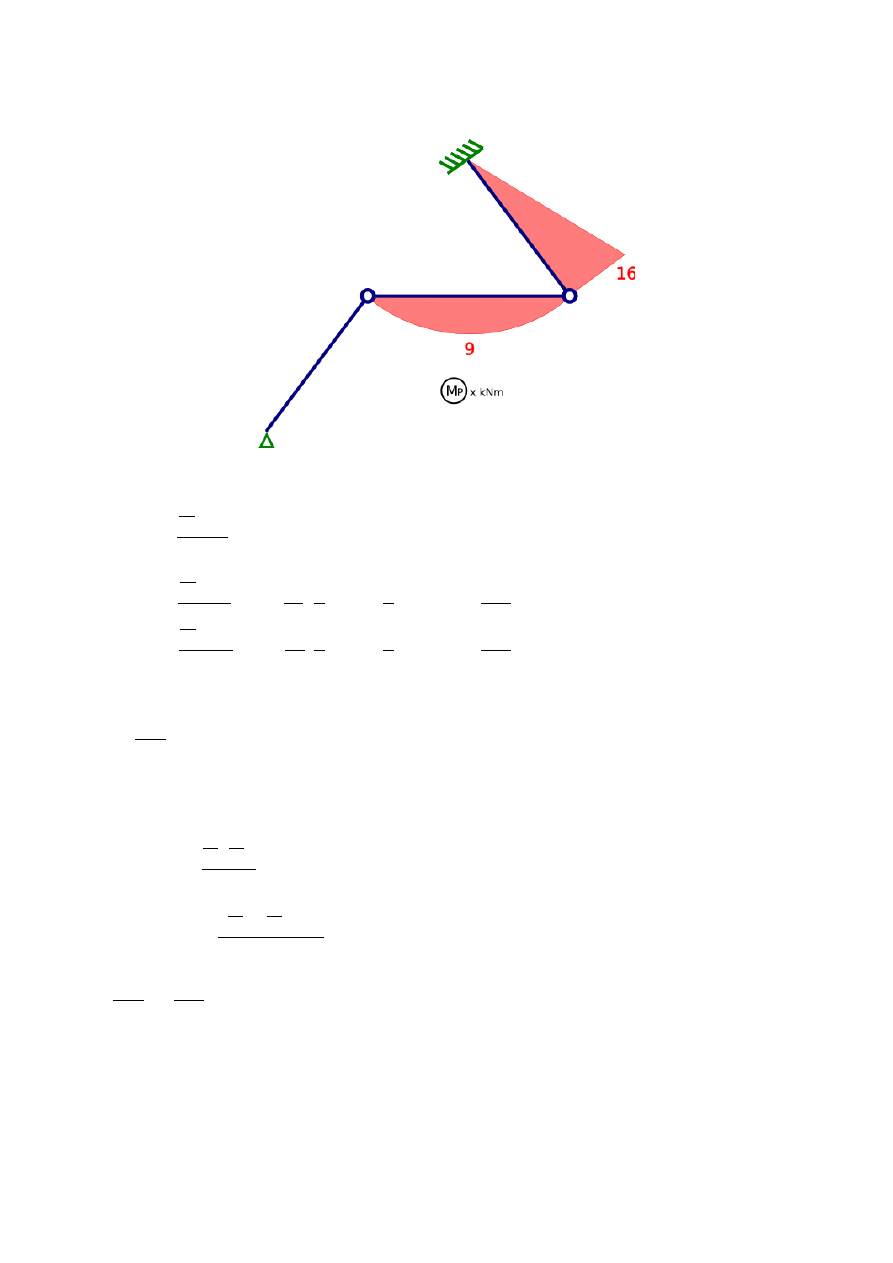
W celu obliczenia przemieszczeń na kierunkach niewiadomych X

1

i X

2

wywołanych

działaniem obciążenia zewnętrznego należy skonstruować wykres

M

P

:

Rys. 4. Wykres M

P

Szukane przemieszczenia

Δ

1P

oraz

Δ

2P

mogą być teraz obliczone ze wzoru:

Δ

iP

=

∑∫

M

i

M

P

EI

d s

Δ

1P

=

∑∫

M

1

M

P

EI

d s=−

1

EI

(

1
3

1⋅9⋅6+

1
6

2⋅16⋅5

)

=−

134
3 EI

Δ

2P

=

∑∫

M

2

M

P

EI

d s=−

1

EI

(

1
3

1⋅9⋅6+

1
3

1⋅16⋅5

)

=−

134
3 EI

Wektor wyrazów wolnych:

Δ

P

=

1

3 EI

[

−

134

−

134

]

Sprawdzenie 2:
Należy sprawdzić czy zachodzi:

∑

i

Δ

iP

=

∑ ∫

M

s

M

P

EI

d s

czyli w rozwiązywanym zadaniu:

Δ

1P

+Δ

2P

=

∑∫

(

M

1

+

M

2

)

M

P

EI

d s

Po podstawieniu wartości liczbowych otrzymujemy

−

268

3 EI

=−

268

3 EI

Wykonywanie tego sprawdzenia jest zalecane zaraz po obliczeniu wszystkich wartości

Δ

iP

Układ równań kanonicznych metody sił przyjmie więc (po przemnożeniu przez 3 EI ) postać:

[

31

8

8

11

]

[

X

1

X

2

]

+

[

−

134

−

134

]

=

[

0
0

]

Co prowadzi do:

[

X

1

X

2

]

=

1

227

[

11 −8

−

8 31

][

134
134

]

[

X

1

X

2

]

=

[

1,451

11,126

]

Końcowy wykres momentów zginających można otrzymać z:

M=

∑

i

M

i

⋅

X

i

+

M

P

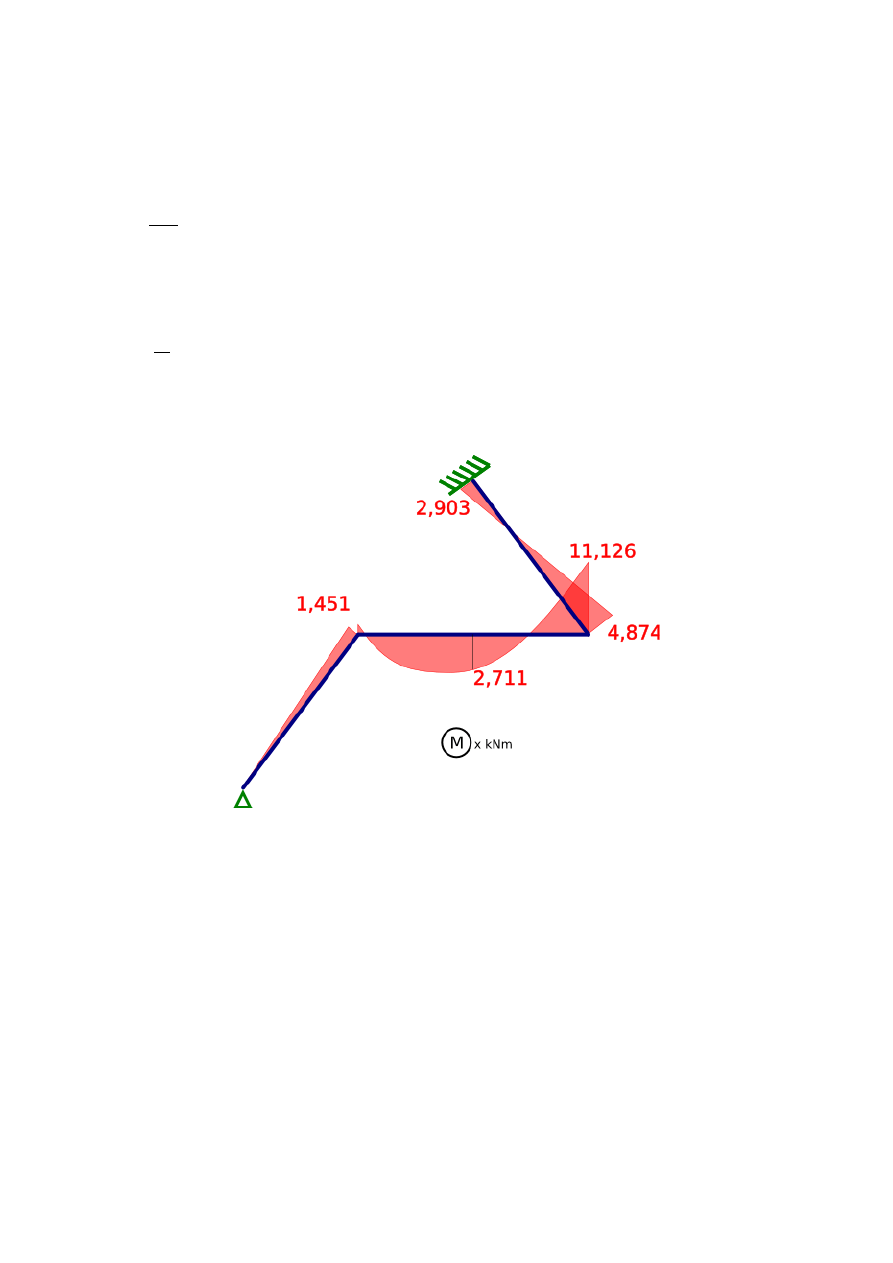
Końcowy wykres momentów zginających jest przedstawiony na Rys. 5.

Rys. 5. Końcowy wykres momentów zginających

Przed przystąpieniem do konstruowania wykresów sił poprzecznych i sił osiowych należy wykonać
sprawdzenie końcowego wykresu momentów zginających.

Sprawdzenie 3:
Sprawdzenie to polega na obliczeniu przemieszczenia rozważanej ramy w kierunku zablokowanym
przez jeden z rzeczywistych więzów. W tym celu należy przyjąć układ podstawowy metody sił
(najlepiej inny niż ten wykorzystany podczas rozwiązywania ramy) i obciążyć go siłą jednostkową
na kierunku jednego z odrzuconych więzów (patrz Rys. 6).

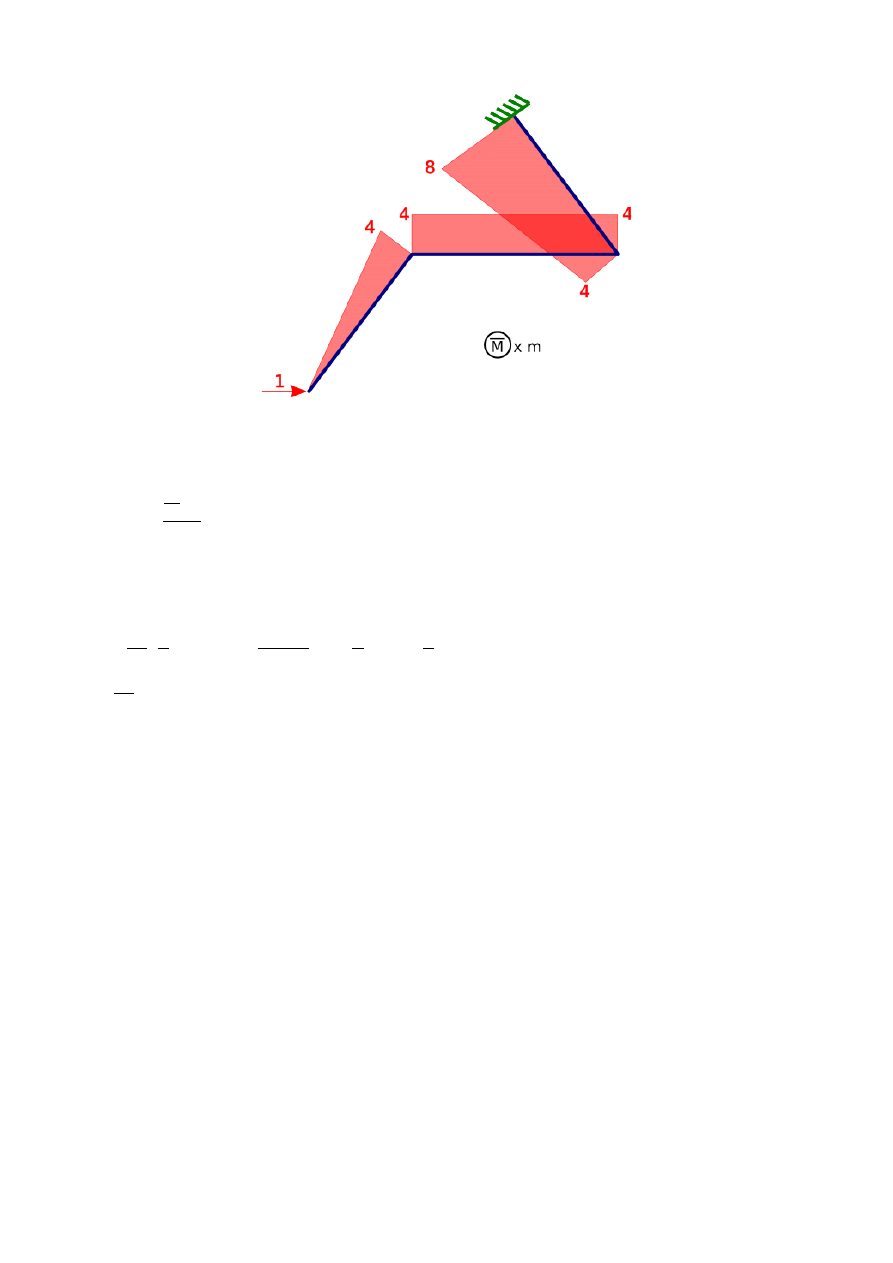
Rys. 6. Wykres momentów zginających od siły
jednostkowej na kierunku odrzuconego więzu

W rozpatrywanym przykładzie poziome przemieszczenie lewego dolnego węzła ramy, zgodnie ze
wzorem redukcyjnym, wynosi:

u=

∑∫

M M

EI

d s

Jeżeli wykres momentów jest skonstruowany prawidłowo to obliczane przemieszczenie musi
uzyskać wartość równą zero.

Δ=

1

EI

(

1
3

4⋅1,451⋅5+

12,578

2

6⋅4−

2
3

9⋅6⋅4+

5
6

(

46,442−38,989+11,610−38,989)

)

=

=

1

EI

(

160,608−160,605)≈0

Oznacza to, że przemieszczenie poziome podpory nieprzesuwnej, obliczone przy zastosowaniu
otrzymanego wcześniej końcowego wykresu momentów zginających, odpowiada wartości
rzeczywistej (podpora nieprzesuwna ma zablokowaną możliwość przesuwu we wszystkich
kierunkach). To z kolei jest przesłanką do uznania otrzymanego wykresu momentów zginających za
prawidłowy.

Wykresy sił poprzecznych i osiowych należy skonstruować samodzielnie.