Ć

w. 8 Programowanie Pascal (2) - obliczenia numeryczne

Pętla warunkowa

while.. do...

(dopóki .. wykonuj..)

Postać ogólna instrukcji:

while

W

B

do

instrukcja;

Instrukcja wewnętzna (także sekwencji – instrukcje otoczone słowami kluczo-

wymi begin i end) jest wykonywana wielokrotnie, dopóki wyrażenie logiczne W

B

jest

prawdą. Tak jak w "pętli" repeat instrukcje muszą mieć wpływ na wartość W

B

, tak

aby pętla kiedyś się skończyła.

W pętli while instrukcje są ponawiane gdy warunek jest prawdziwy, w odróżnie-

niu od pętli repeat, w której prawdziwość warunku wymusza zakończenie iteracji.
W "pętli" while warunek jest sprawdzany przed wykonaniem instrukcji – w pętli re-
peat jest sprawdzany po jej wykonaniu.

Przykład:

y:= 5;

while y>1 do

begin

y:= y–0.5;

y:= y*0.1;

end;

Ć

wiczenie

Sprawdzi

ć

powy

ż

szy przykład, wykonuj

ą

c program krokowo (F7). Wyprowa-

dza

ć

warto

ś

ci zmiennych y i k w ka

ż

dym kroku p

ę

tli oraz po jej zako

ń

czeniu

wykorzystuj

ą

c procedur

ę

write.

Wyrażenia arytmetyczne

Służą one do zapisu wykonywania operacji obliczeniowych w trakcie przebiegu

programu. Wyrażeniem arytmetycznym może być stała, zmienna lub zapis złożonej
operacji na stałych, zmiennych i funkcjach (standardowych, bibliotecznych lub wła-
snych użytkownika) z użyciem operatorów arytmetycznych. Ponadto używamy na-
wiasów (tylko okrągłych!) w celu zmiany kolejności działań.

Definicja wyrażenia

ma postać:

wyrażenie = stała
wyrażenie = zmienna
wyrażenie = identyfikator_funkcji (wyrażenie)
wyrażenie = wyrażenie operator wyrażenie

Z definicji wynika, że wyrażenia po prawej stronie mogą mieć każdą z postaci de-

finiowanych, a zatem np. argument funkcji może być np. inną funkcją (tzw. zagnież-
dżanie funkcji), a operatorami można łączyć wiele wyrażeń.

Wyrażenia używane są najczęściej w instrukcjach przypisania po prawej stronie

operatora przypisania :=

„dopóki” ...„wykonuj”

Operatory arytmetyczne

Rozróżniamy następujące operatory:

•

jednoargumentowe

–

zmiana znaku,

+

powielenie znaku,

•

dwuargumentowe

o

multiplikatywne

*

mnożenie,

/

dzielenie (rzeczywiste),

■

div■ dzielenie całkowite (obydwa argumenty operacji muszą być

całkowite, wynik jest całkowity),

■

mod■ reszta z dzielenia całkowitego (jak wyżej),

(znak ■ przedstawia spację),

o

addytywne

+ dodawanie,
– odejmowanie.

Kolejność wykonywania operacji określają następujące reguły:

•

Wyrażenia w nawiasach wykonywane najwcześniej (od najbardziej wewnętrz-
nych),

•

Kolejność operacji (od najwcześniej wykonywanych):

1. jednoargumentowe,
2. multiplikatywne,
3. addytywne.

UWAGA:

•

Dla operatorów tej samej wagi - kolejność działań od lewej do prawej.

•

Jeżeli w wyrażeniu są tylko argumenty całkowite i nie ma dzielenia rzeczywiste-
go (/) to wynik jest typu integer.

•

Jeżeli występuje chociaż jeden element typu real lub dzielenie rzeczywiste to wy-
nik jest typu real.

Funkcje standardowe

Istnieje możliwość użycia w wyrażeniu funkcji standardowych (w kontekście

identycznym jak zmienne proste) w postaci:

identyfikator_funkcji (argument)

Argumentem może być wyrażenie odpowiedniego typu. Zestaw funkcji standar-

dowych przedstawia tabela:

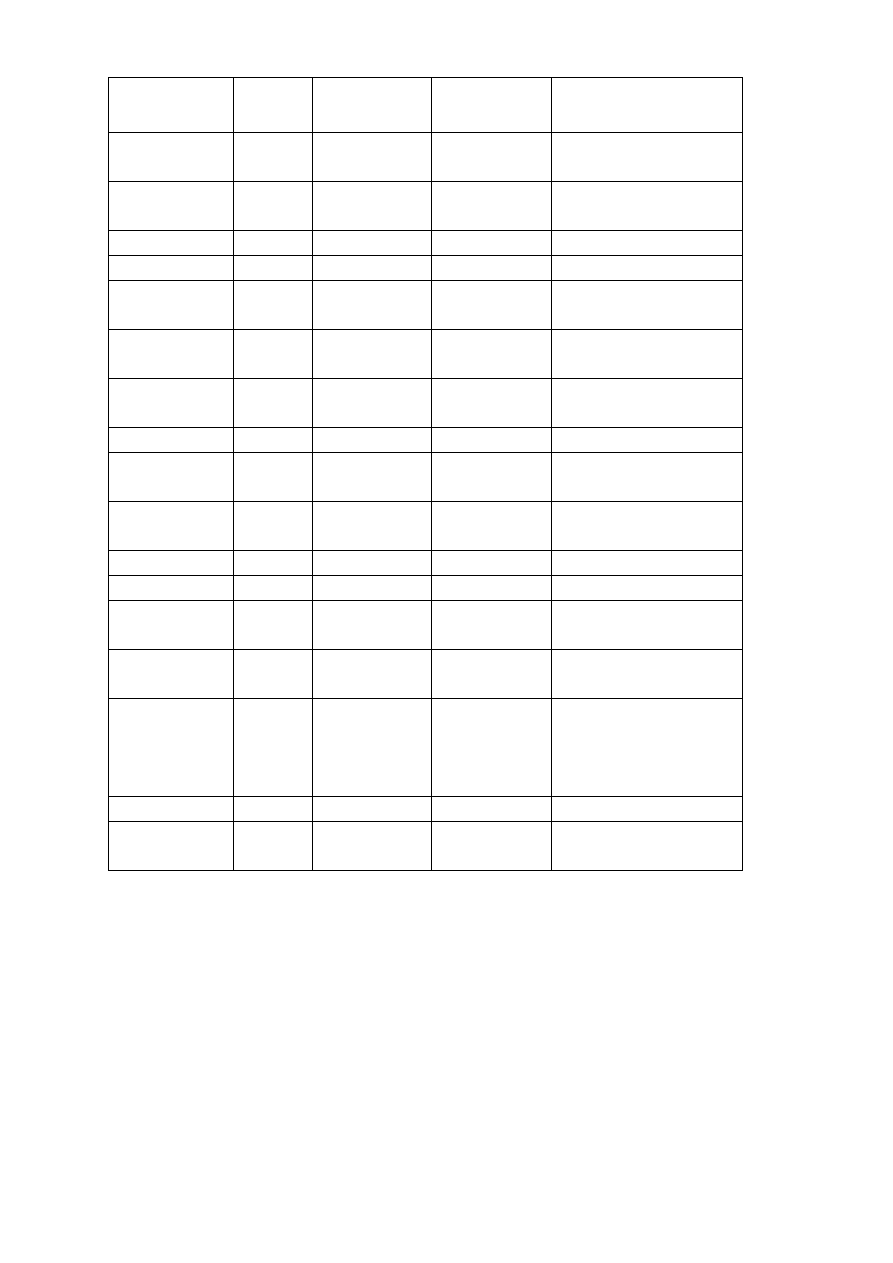
Funkcje standardowe

Znaczenie

Nazwa

funkcji

Typ wyniku

Typ

argumentu

Przykład

wartość
bezwzględna

abs

całkowity
rzeczywisty

całkowity
rzeczywisty

abs(-2)

pierwiastek
kwadratowy

sqrt

rzeczywisty rzeczywisty sqrt(5.45)

kwadrat

sqr

rzeczywisty rzeczywisty sqr(x-5)

e

x

exp

rzeczywisty rzeczywisty exp(-x/2)

logarytm
naturalny

ln

rzeczywisty rzeczywisty ln(2*x-4)

sinus

sin

rzeczywisty

rzecz. (ra-
diany)

sin(3*alfa)

cosinus

cos

rzeczywisty

rzecz. (ra-
diany)

cos(beta/2)

arcus tangens arctan rzeczywisty rzeczywisty arctan(fi)
część całko-
wita

int

rzeczywisty

całkowity
rzeczywisty

int(2.5)

część
ułamkowa

frac

rzeczywisty

całkowity
rzeczywisty

frac(3.6)

zaokrąglenie round całkowity

rzeczywisty round(3.6)

obcięcie

trunc

całkowity

rzeczywisty trunc(3.6)

znak następ-
ny

succ

porządkowy porządkowy succ (

'

g

'

)

znak po-
przedni

pred

porządkowy porządkowy pred(

'

j

'

)

znak
o podanym
kodzie
ASCII

chr

znakowy

całkowity

chr(49)

kod znaku

ord

całkowity

znakowy

ord(

'

1

'

)

długość tek-
stu

length łańcuchowy całkowity

length(

'

alfa

'

)

W wyrażeniach istotne są wszelkie ograniczenia obszaru określoności funkcji, np.

użycie ln(-3), sqrt(-5.0) spowoduje błędy wykonania.

Brak w języku operatora lub funkcji standardowej potęgowania, stąd stosuje się:

x

4

=

x*x*x*x

lub

sqr (x)*sqr (x)

lub

sqr (sqr (x)),

Można wykorzystac funkcję:

power(podstawa,wykładnik)

jej użycie wymaga dopisania deklaracji modułu Math w sekcji uses.

uses sysutils,math;
begin

writeln( power(5.1, 3.7);
readln;

end.

Brak w języku również innych, często potrzebnych funkcji, jak na przykład tan-

gens czy logarytm dziesiętny. Trzeba wówczas korzystać z elementarnych wzorów
matematycznych:

log ݔ =

୪୬ ௫

௟௡ଵ଴

tg ݔ =

ୱ୧୬ ௫

ୡ୭ୱ ௫

Należy zwrócić uwagę na możliwość wystąpienia przekroczenia dopuszczalnych

zakresów wartości zmiennych przy obliczeniach.

Poniższe wyrażenie w postaci matematycznej:

można zapisać w przykładowej postaci

1/(2*pi)*sin(3*x-3)

lub

1/2/pi*sin(3*x-3)

W przypadku zastosowania w instrukcji przypisania wyrażenia zawierającego

zmienną, której aktualnie przypisujemy wartość, np.:

x := x + 5 ;

obliczana jest wartość wyrażenia (wartość x powinna być wcześniej określona),
a następnie uaktualniana wartość zmiennej, np. w ciągu instrukcji:

...

x := 5 ;
x := sqr(x) ;

{x b

ę

dzie równe 25}

x := x +2 ;

{powi

ę

kszenie poprzedniej warto

ś

ci x o 2, x b

ę

dzie równe 27}

...

Funkcje standardowe nie wymagają deklaracji ich użycia.

Pisząc wyrażenie należy szczególnie uważać na:

-

operatory arytmetyczne – szczególnie mnożenia:

2*x

, a nie 2x,

-

format wykładniczy – np.

1.34E-8

(10

7

to 1e7 a nie e7),

-

argumenty funkcji trygonometrycznych – podajemy je w radianach, w przypadku
konieczności używania kąta w stopniach należy przeliczyć kąt na radiany wyra-
ż

eniem stopnie*pi/180, (pi jest predefiniowaną nazwą stałej).

-

hierarchię działań – odpowiednie stosowanie nawiasów,

-

brak w języku operacji potęgowania, brak funkcji tangens, cotangens, logarytm
dziesiętny,

-

różnicę między funkcjami o podobnych nazwach – sqr i sqrt.

Wyrażenia logiczne

Wyrażeniem logicznym może być:

1. stała logiczna: true

≡

prawda, false

≡

fałsz

2. zmienna typu boolean,
3. porównanie w sensie liczbowym lub tekstowym (kolejności alfabetycznej)

według schematu:
wyrażenie

1

operator wyrażenie

2

Porównanie ma wartość logiczną true lub false. Operatorami porównań są:

<

=

>

<=

>=

< > „różny”

Przykłady porównań:

)

3

x

3

sin(

2

1

−

π

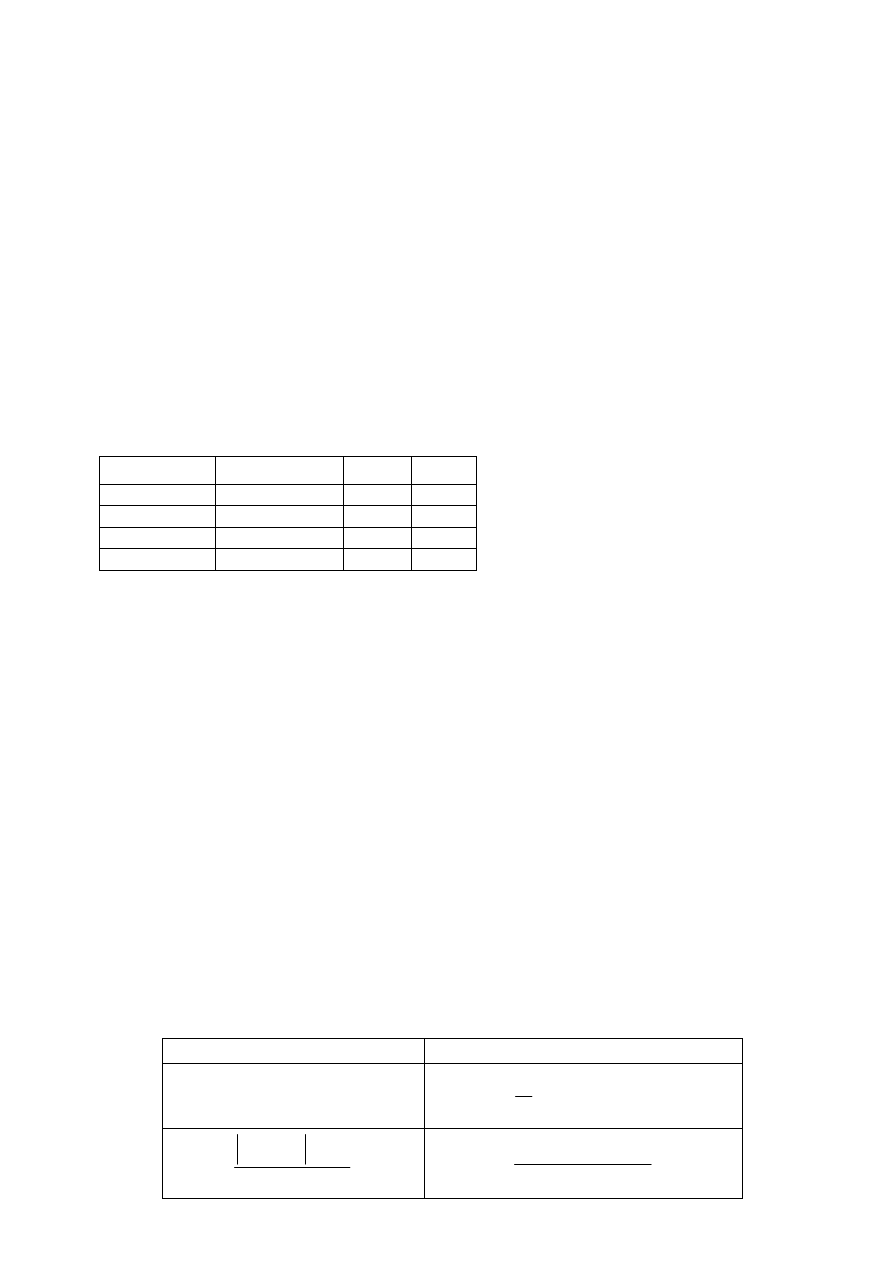
x12 < 2

(4*x+1.5) < 30.7
nazwisko >= 'G'

{nazwiska od litery G do ko

ń

ca alfabetu}

4. stałe logiczne, zmienne logiczne, porównania (w nawiasie!), połączone

operatorami logicznymi:

- jednoargumentowymi:

not(negacja)

np.

not(i < 5)

- dwuargumentowymi:

and (iloczyn logiczny –

"

i

"

–

jednoczesne

spełnienie

warunków)

np.

(x > 0) and (x < 3)

or (suma logiczna –

"

lub

"

–

alternatywne spełnienie warunków)

np.

(x <= 0) or (x >= 100)

Poniższa tabela przedstawia wartości wyrażeń logicznych w zależności od wartości

argumentów:

Argument 1

Argument 2

and

or

false

false

false

false

true

false

false

true

false

true

false

true

true

true

true

true

Wartość wyrażenia logicznego można przypisać zmiennej typu boolean bądź

użyć je w instrukcjach warunkowych lub pętlach repeat i while. Efektem wypisania
na ekranie wyrażenia logicznego lub zmiennej logicznej będzie wartość true lub fal-
se. Przykładowe użycie w programie:

var zm1, zm2: boolean;

x:real;

begin
readln(x);
if (x>0) and (x<100) then

writeln ('cos tam. . . ');

zm1:= not (x>sin(x));
zm2:= (x>0) and (x<>35);
writeln(zm2);
readln;
end.

Ć

wiczenie

1.

Napisać program, w którym dla podanej wartości

x

(np. x=3.45) obliczane są

wartości następujących wyrażeń oraz wyprowadzane wyniki na ekran konsoli
(wykorzystać tabelę funkcji standardowych ):

2sin 2x

2

3e

-2x

cos

3

3x

3

ctg (x-30

o

) 10

-7

)

3

x

3

sin(

1

−

π

4

2

x

tg

5

x

4

x

−

−

56

,

4

x

3

cos

x

x

log

2

2

+

−

2.

Napisać program obliczający wynik dzielenia całkowitego liczby 3456 przez
17 oraz resztę z tego dzielenia.

3.

Napisać program, w którym wymagane jest wprowadzenie przez użytkownika
liczby rzeczywistej, a następnie sprawdzana jest przynależność podanej liczby
do przedziału (0, 10).

4.

Napisać program, w którym:

a)

użytkownik podaje wartość początkową zmiennej

x

,

b)

w "pętli" while..do.. warunek sprawdza czy wartość

x

jest większa od

0.0001 i jeśli tak, to aktualne

x

jest dzielone przez 3,

c)

program oblicza i wyświetla liczbę wykonanych dzieleń oraz wartość koń-
cową

x

(zastosować zmienną typu całkowitego licznik, powiększaną o 1

wewnątrz pętli).

5.

Napisać program, w którym użytkownik podaje dowolne nazwisko, program
wyświetla długość (liczbę znaków) nazwiska (zastosować zmienną typu
string).

6.

Napisać program, w którym użytkownik podaje dwa dowolne nazwiska, pro-
gram podaje informację które nazwisko jest wcześniej w alfabecie (zastosować
porównanie dwóch zmiennych typu string).

7.

Napisać program, w którym znajdujemy kod ASCII wpisanego przez użyt-
kownika znaku. Wyświetlanie kodów wpisywanych znaków odbywa się w pę-
tli, której warunkiem zakończenia jest wpisanie znaku '0'. (zastosować zmien-
ną typu char).