WYDZIAŁ MECHANICZNY ENERGETYKI I LOTNICTWA

POLITECHNIKI WARSZAWSKIEJ

Zakład Teorii Maszyn i Robotów

Laboratorium Podstaw Automatyki i Sterowania IV

Instrukcja do ćwiczenie nr 2

Badania symulacyjne układu napędowego

z silnikiem prądu stałego

1

Cel ćwiczenia

Celem ćwiczenia jest badanie własności modelu stopnia napędowego dla:

• sil

nika obciążonego stałym momentem,

•

silnika obciążonego momentem zmiennym,

Dla każdego z powyższych modeli silnika należy zaobserwować działanie układu przy

różnych wymuszeniach. Ćwiczenie ma na celu pokazanie studentom zastosowania
oprogramowania Matlab Simulink w badaniu modeli rzeczywistych, w tym przypadku

modelu silnika prądu stałego. Wychodząc z modelu fizycznego, poprzez model

matematyczny do różnych sposobów opisu tego samego zjawiska.

1.1

Opis obiektu badań

Przedmiotem fizycznym podlegającym badaniu jest stopień napędowy stosowany
do

sterowania ruchem postępowym lub obrotowym członu konstrukcji mechanicznej

(np. ramienia robota).

W stopniu napędowym stosowany jest elektryczny silnik bezszczotkowy prądu stałego.

Ruch obrotowy wirnika silnika przenoszony przez przekładnię (reduktor) napędza ruch

obrotowy ramienia manipulatora (lub innego członu). Zastosowanie układu zamieniającego

ruch obrotowy na postępowy umożliwia uzyskanie napędu o ruchu postępowym.

W celu sterowania (czyli celowego oddziaływania) ruchem obrotowym obciążenia trzeba

celowo wpływać na obroty wirnika. Sterowanie obrotami wirnika jest możliwe przez zmiany

napięcia (albo natężenia) prądu płynącego w obwodzie elektrycznym silnika. Trzeba wiedzieć

w jaki sposób zmienić napięcie (natężenie) w obwodzie elektrycznym silnika aby uzyskać

pożądane położenie (lub prędkość kątową) obciążenia.

Silnik elektryczny nie jest idealnym układem wykonawczym. Jako układ mechaniczny ma

on pewną bezwładność, w czasie obrotów wirnika występuje tarcie wiskotyczne między

ruchomym wirnikiem a nieruchomą częścią silnika. Tarcie wiskotyczne występuje także
w

przekładni, co daje efekt tłumienia sygnału. Obwód elektryczny silnika ma dodatkowo

m.in. własną indukcyjność (efekt różniczkowania sygnału) oraz oporność (tłumienie sygnału).

Skumulowanie wszystkich dodatkowych oddziaływań „zniekształca” rezultat sterowania.

W szczególności można uzyskać niestabilne zachowanie się układu, a więc

np. oscylujące położenie kątowe obciążenia albo położenie obarczone dużym błędem.

Ze względu na omówione wyżej czynniki, w rzeczywistych stopniach napędowych

wprowadza się regulatory o tak dobranych parametrach aby kompensować wszystkie

niepożądane zjawiska i aby układ regulacji miał pożądane cechy, jak np. określone wartości

zapasu stabilności (np. zapasu modułu, zapasu fazy) czy określony czas regulacji.

Położenie regulatora w układzie sterowania jest zależne od celu jaki chcemy osiągnąć.

Regulat

or włączony w pętlę sprzężenia zwrotnego kształtuje sygnał zwrotny, przed

wzmacniaczem kształtuje sygnału uchybu, przed węzłem sumacyjnym kształtuje wartość

zadaną.

3

2 Model obiektu

2.1 Wprowadzenie

Pierwszym etapem prac przy projektowaniu stopnia napędowego jest sformułowanie jego

modelu matematycznego. Tworząc model powinniśmy pamiętać, które wielkości traktujemy
jako –

wejściowe a które – jako wielkości wyjściowe. W modelu tym powinny być

uwzględnione wartości parametrów rzeczywistego stopnia napędowego (jak np. rezystancja,

pojemność, indukcyjność, moment bezwładności itd.).

2.2

Model obciążonego silnika

Silnik rozpatrujemy jako element wykonawczy układu regulacji prędkości kątowej wirnika

ω.

Wyjściem układu silnika jest prędkość kątowa wirnika.

Tworzony model ob

ciążonego silnika zakładając najłatwiejszy do opisu przypadek, gdy

moment pochodzący od obciążenia i moment bezwładności obciążenia jest stały. Taki model

jest często wykorzystywany przy projektowaniu napędów w robotyce, gdzie nadmiar mocy
silników pozwala

pomijać efekty wynikające ze zmieniających się momentów pochodzących

od obciążeń.

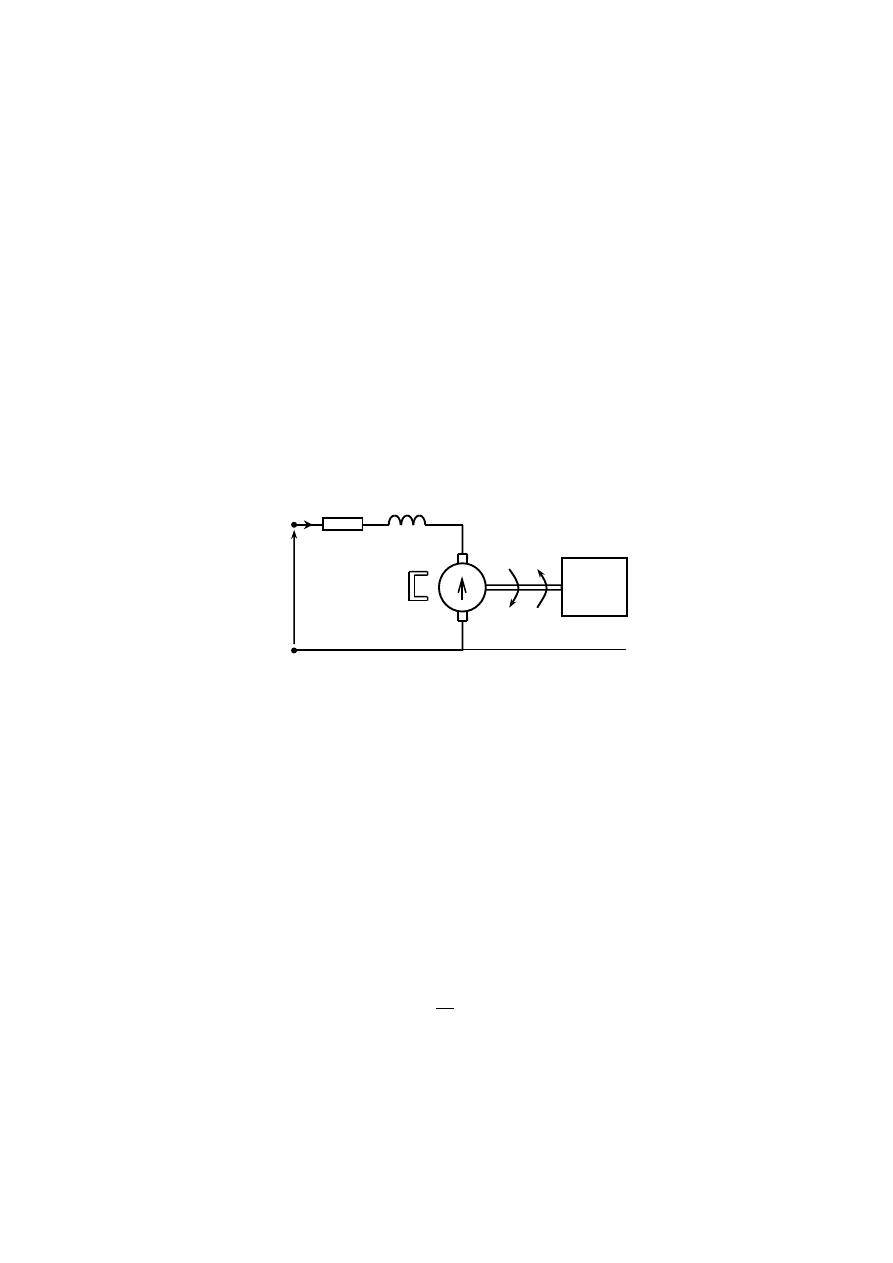
Rys. 1. Schemat ideowy silnika prądu stałego.

Na wejście układu, doprowadzamy napięcie elektryczne u

a

Moment obrotowy silnika powstaje wskutek dynamicznego oddziaływania pola

magnetycznego na przewód z prądem umieszczony w tym polu. Pole magnetyczne jest

wytwarzane przez jedną lub kilka par biegunów elektromagnesów w umieszczonej zwykle

części nieruchomej tzw. magneśnicy (jeśli jest to silnik prądu stałego) lub stojanie (jeśli jest to

silnik prądu przemiennego). W części elektrycznej silnika (obwodzie twornikowym)

wzbudzana jest siła przeciwelektromotoryczna powodująca obrót wirnika (wraz
z

twornikiem). Dla uproszczenia pojemność obwodu twornikowego będzie pomijana,

rezystancja zastępcza tego obwodu (uwzględniająca twornik) niech będzie równa R,
a

indukcyjność L.

(może też być prąd

regulowany), wyjście rozumiane jest w niniejszym przykładzie jako prędkość

ω.

Stosując prawo Kirchoff’a do obwodu twornika, wyznaczamy napięcie sterujące

w obwodzie twornikowym:

e

dt

di

L

Ri

u

a

+

+

=

(1)

gdzie:

u

a =

u

a

R

-

rezystancja tego obwodu (jednostka Ω),

(t)

-

napięcie sterujące w obwodzie twornikowym (jednostka V),

i = i(t)

-

prąd w obwodzie twornikowym (jednostka A),

L

-

indukcyjność obwodu (jednostka H),

R

L

I

E

U

J =J

w

+J

ob

Ω

M

Φ

M

4

e = e(t)

-

siła przeciwelektromotoryczna (jednostka V).

Siła przeciwelektromotoryczna e i prędkość kątowa wirnika ω są zależnością:

ω

b

k

e

=

(2)

gdzie:

k

b

rad

Vs

-

stała elektromotoryczna silnika (jednostka

)

Podstawiając w równaniu 1 prawą stronę równania 2 otrzymujemy:

ω

b

a

k

dt

di

L

Ri

u

+

+

=

(3)

Moment m

w

rozwijany przez wirnik misi równoważyć moment własny silnika i moment

pochodzący od obciążenia m

b

ω

ω

f

dt

d

J

m

w

+

=

. Równanie to można zapisać w postaci:

(4)

gdzie:

J –

łączny moment bezwładności silnika i obciążenia (jednostka

2

/ s

rad

Nm

)

f –

współczynnik tarcia wiskotycznego (jednostka

s

rad

Nm

/

)

Moment obrotowy m

w

i

k

m

t

w

=

rozwijany

przez wirnik silnika jest proporcjonalny do natężenia

prądu płynącego w obwodzie twornika:

(5)

gdzie:

k

t

A

Nm

–

tzw. stała momentu silnika (jednostka

),

Równania 3 i 4 są bazowymi równaniami do dalszych rozważań. Pozwolą one na dalszą

analizę modelu silnika prądu stałego zarówno metodą przestrzeni stanów jak i metodą
transmitancji.

2.3 Model silnika w przestrzeni stanów

Opis modelu silnika w przestrzeni stanów oparty jest na równaniach stanu, które są

równaniami różniczkowymi opisującymi proces ciągły zachodzący w czasie. Zmiennymi

stanu są zmienne zawarte w równaniach stanu. Ogólne równanie stanu ma postać:

(

)

t

u

x

f

x

,

,

=



(6)

lub w postaci macierzowej:

Bu

Ax

x

+

=



(7)

gdzie :

f – funkcja wektorowa,
A, B – macierze funkcyjne,
x – wektor zmiennych stanu,
u –

wektor zmiennych sterujących,

t – czas.

5

W przypadku rozpatrywanego silnika prądu stałego, zmiennymi stanu są prąd silnika i

oraz prędkość obrotowa ω.
Równania 3 i 4 można zapisać w postaci (uwzględniając 5):

L

u

L

k

i

L

R

dt

di

a

b

+

−

−

=

ω

(8)

ω

ω

J

f

i

J

k

dt

d

t

−

=

(9)

Jak można zauważyć równania te są już równaniami stanu, wiec można je zapisać w

postaci macierzowej:

























+

























−

−

−

=













0

)

(

0

0

0

)

(

)

(

1

t

u

t

t

i

a

L

J

f

J

k

L

k

L

R

dt

d

dt

di

t

b

ω

ω

(10)

Równanie macierzowe 10 jest końcowym równaniem i pozwala ono na bezpośrednią

implementacje w programie Matlab Simulink.

2.4

Transmitancja obciążonego silnika

Punktem wyjścia do wyznaczenia transmitancji silnika są równania 3 i 4, na nich to zostanie

wykonana transformat Laplace’a i przekształcenia w celu implementacji modelu w programie
Matlab Simulink.

Po dokonaniu transformaty Laplace’a zależności 3 i takim uporządkowaniu wyrazów, aby

uzyskać zależność natężenia prądu od napięcia U

a

)

(

)

(

)

(

s

sL

R

k

s

U

sL

R

I

s

I

b

a

a

Ω

+

−

+

=

(s)

i prędkości Ω(s) otrzymujemy:

(11)

Dla odróżnienia transformat od ich oryginałów użyliśmy powyżej dużych liter do

oznaczenia transformat zmiennych.

Po dokonaniu transformaty Laplace’a zależność (5) i uwzględnieniu jej w (11)

otrzymujemy zależność między momentem rozwijanym przez silnik a napięciem U

a

)

(

)

(

)

(

s

sL

R

k

k

s

U

sL

R

k

s

M

b

t

a

t

w

Ω

+

−

+

=

(s)

(na

pięciem sterującym) i prędkością Ω(s), której wpływ uwidacznia się przez zwrotne

oddziaływanie siły przeciwelektromotorycznej:

(12)

Podobnie postępujemy z równaniem 4, gdzie po dokonaniu transformaty Laplace’a

otrzymujemy:

)

(

)

(

)

(

s

f

s

s

J

s

M

w

Ω

+

Ω

=

(13)

Zauważamy, że zależność 12 podaje moment M

w

Moment M

rozwijany przez wirnik silnika w funkcji

parametrów obwodu elektrycznego, natomiast w zależności 13 moment ten jest wyrażony
w

funkcji parametrów mechanicznych obciążenia.

w

rozwijany prz

ez silnik (rozumiany w opisie części elektrycznej jako wielkość

wyjściowa) zależy od napięcia sterującego U

a

(wielkość wejściowa) oraz od prędkości

kątowej (przenoszonej zwrotnie), zależność 12. Z drugiej zaś strony moment ten równoważy

obciążenie posiadające prędkość kątową Ω(s) (wielkość wyjściowa), co jest opisane

zależnością 13.

6

Na podstawie wprowadzonych zależności można wyznaczyć transmitancję obciążonego

silnika, porównując stronami 12 oraz 13:

sL

R

s

k

s

U

k

s

f

s

s

J

b

a

t

+

Ω

−

=

Ω

+

Ω

)

(

)

(

)

(

)

(

(14)

Wielkością wejściową silnika jest napięcie U

a

(

)

t

b

t

a

s

k

k

Rf

Lf

RJ

s

JL

s

k

s

U

s

G

+

+

+

+

=

Ω

=

2

)

(

)

(

(s

), wielkością wyjściową prędkość kątowa

Ω(s). Transmitancja obciążonego silnika jest więc równa:

(15)

2.5 Parametry silnika

Jeżeli prowadzący nie poda innych parametrów silnika, należy użyć następujących wartości
(wielk

ości podane są w jednostkach wcześniej sprecyzowanych, podane jednostki zapewniają

zgodność obliczeń, tak więc dalej ich nie piszemy):

U

a

-

napięcie maksymalne zasilania

U

a

L -

indukcja uzwojeń silnika

L = 3.88 * 10

= 35

R - rezystancja u

zwojeń silnika

R = 1.5

-3

k

b

-

stała elektromotoryczna silnika,

k

b

k

= 1.2

t

-

stała momentu silnika

k

t

J

= 0.62

m

-

moment bezwładności silnika

J

m

= 25.5*10

ƒ -

współczynnik tarcia wiskotycznego silnika ƒ

- 4

m

2.6 Schema

t stopnia napędowego zrealizowany w SIMULINKU

= 0.169.

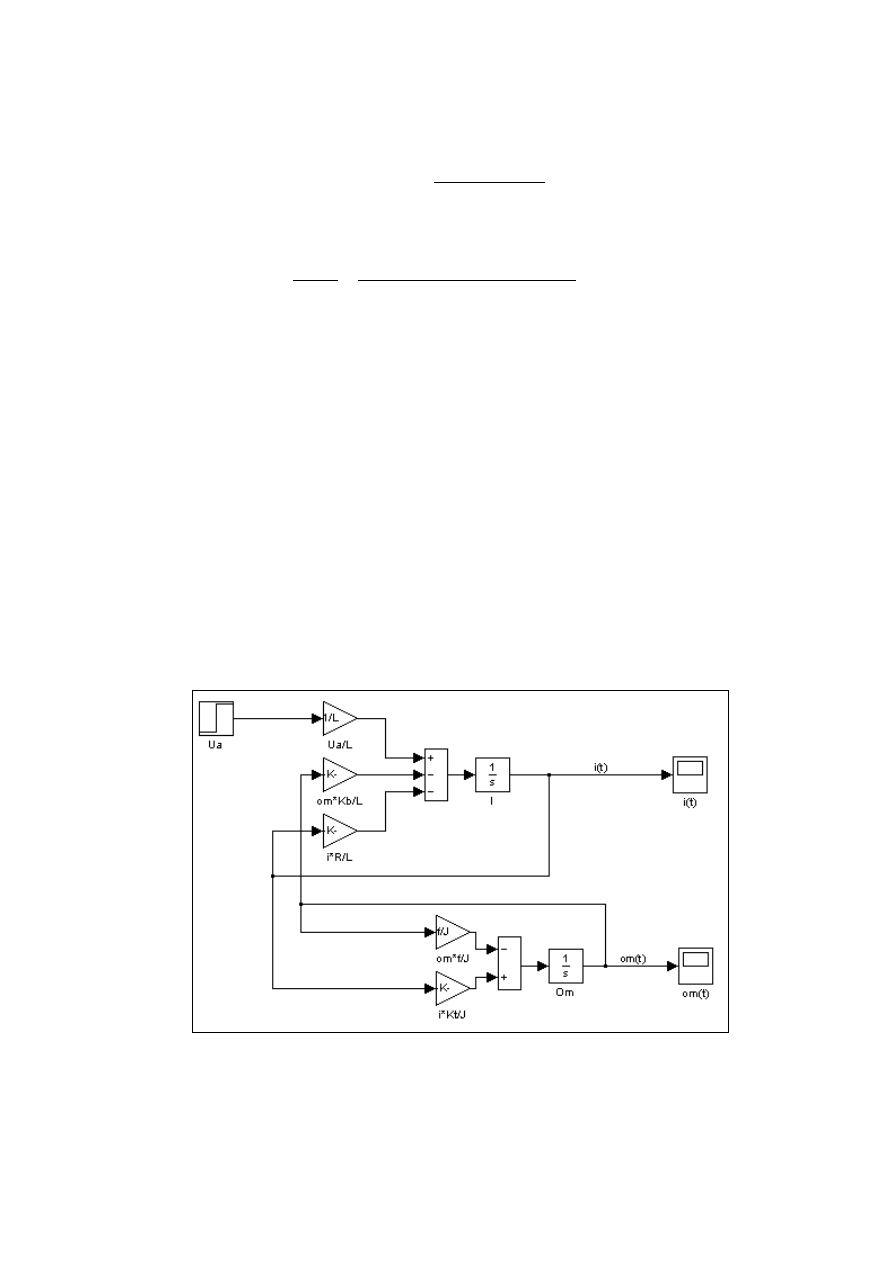
W trakcie ćwiczenia należy zbudować modele silnika prądu stałego na podstawie równań

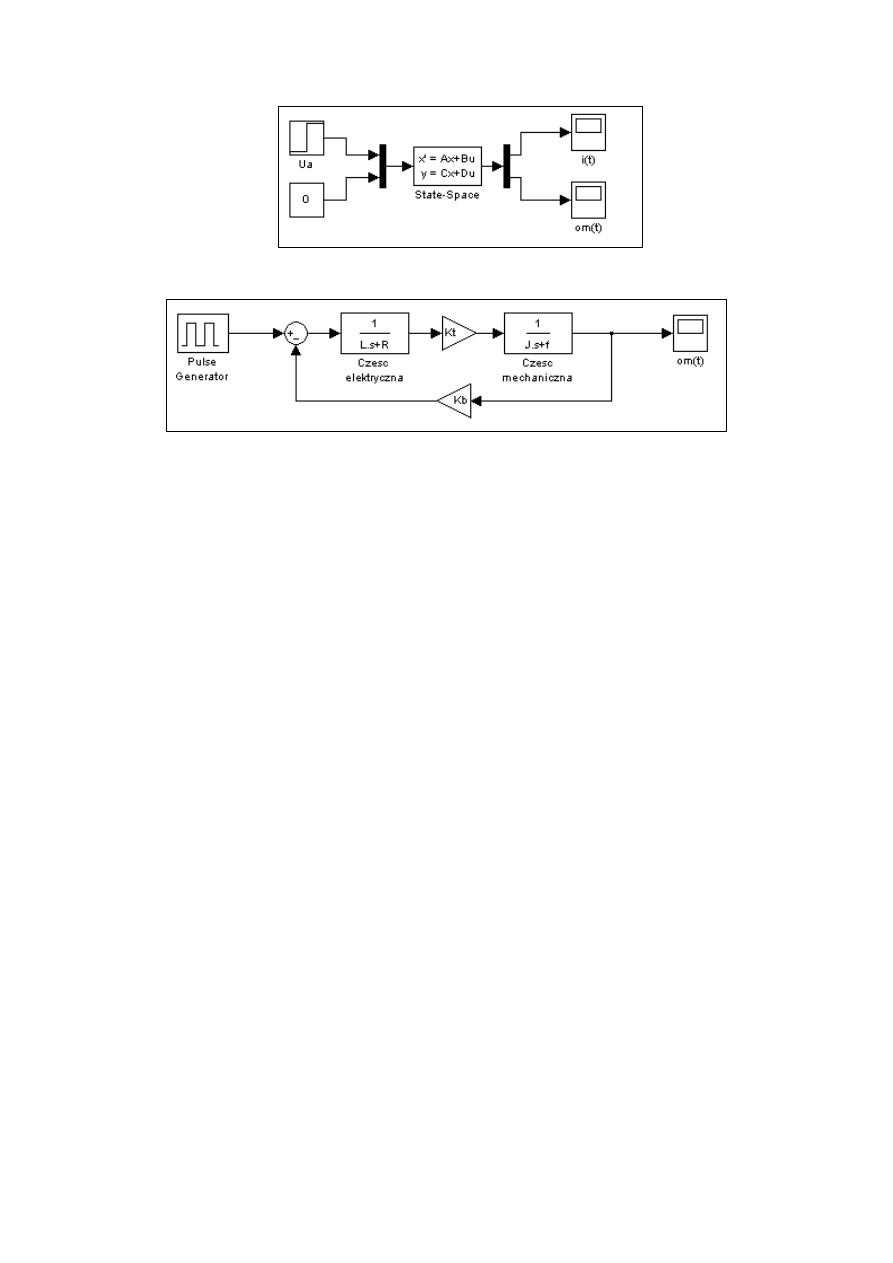
różniczkowych 8 i 9, równań stanu 10 oraz transmitancji 15.

Rys. 2. Schemat blokowy silnika prądu stałego na podstawie równań różniczkowych.

7

Rys. 3. Schemat blokowy silnika prądu stałego z równaniami stanu.

Rys. 4. Schemat transmitancji silnika prądu stałego.

3

PRZEBIEG ĆWICZENIA

CZĘŚĆ I:

1.

Wykonać modele silnika prądy stałego na podstawie :

• rów

nań różniczkowych,

•

równań stanu

• transmitancji

2.

Podłączyć modele silnika do układów pomiarowych.

3.

Wykonać wykresy odpowiedzi silnika na wymuszenie skokowe (skok napięcia
zasilania).

CZĘŚĆ II:

1.

Dla modelu wykonanego w oparciu o równania różniczkowe wykreślić rodzinę

charakterystyk zależności prędkości obrotowej ω i prądu twornika i od

zewnętrznego obciążenia ω = f(J

0

), i = f(J

0

2.

Dla modelu wykonanego w oparciu o równania stanu wykreślić rodzinę

charakterystyk prędkości obrotowej ω i prądu twornika i od napięcia zasilania

ω = f(u

).

a

), i = f(u

a

3. Dla modelu wykonanego w oparciu o transmitancje zasilanego z generatora fali

prostokątnej, wykreślić zależność prędkości obrotowej ω od współczynnika

wypełnienia impulsu ω = f(h).

).

4 SPRAWOZDANIE

W sprawozdaniu należy zamieścić:
1.

Zwięzły opis zadania i schematy połączeń

2. Wyniki obserwacji charakterystyk skokowych dla poszczególnych modeli
3.

Wyniki symulacji przeprowadzonych w trakcie ćwiczenia

4. Wnioski