WOJSKOWA AKADEMIA TECHNICZNA

im. Jarosława Dąbrowskiego

w Warszawie

Wydział Elektroniki

LABORATORIUM SYGNAŁÓW I KODOWANIA

Grupa

............................

Podgrupa

...........................

Data wykonania

ćwiczenia

...........................

Ćwiczenie prowadził

...........................

Ocena:

...........................

Skład podgrupy:

1. ............................................................

2.

............................................................

3.

............................................................

4.

............................................................

5.

............................................................

6.

............................................................

7.

............................................................

8.

............................................................

9.

............................................................

10. ............................................................

Data oddania

sprawozdania

...........................

Podpis prowadzącego

...........................

Temat ćwiczenia: Pomiary parametrów i charakterystyk statystycznych sygnałów losowych




1. Wykaz przyrządów pomiarowych użytych w ćwiczeniu

Lp. Nazwa

przyrządu Typ

Firma

Numer

fabryczny

1.

2.

3.

4.

5.

2. Obserwacja kształtów funkcji gęstości prawdopodobieństwa wartości chwilowych wybranych
sygnałów losowych

Na generatorze funkcyjnym firmy Agilent (HP) ustawić następujące wartości parametrów:

• wartość międzyszczytową (dynamikę sygnału) 500 mVpp [Ampl];

• wartość składowej stałej 0V [Offset];
• wartość częstotliwości podstawowej 1kHz [Freq];

• współczynnik wypełnienia (dla fali prostokątnej) 50% [%Duty].

Następnie, dla poszczególnych sygnałów stochastycznych:

A) sygnał normalny – szum biały [Noise];
B) sygnał harmoniczny z losową fazą;
C) sygnał prostokątny z losową fazą;
D) sygnał trójkątny z losową fazą;
E) sygnał piłokształtny z losową fazą

zaobserwować jak normują się (przy zwiększaniu liczby realizacji pomiarów N) kumulowane
charakterystyki funkcji gęstości prawdopodobieństwa wartości chwilowych sygnałów. Dla N>100
przerysować charakterystyki do odpowiednich ramek. Na osiach nanieść odpowiednie wartości!

A)

B)

C)

D)

E

F)

W ramce F) narysować charakterystykę funkcję gęstości prawdopodobieństwa wartości chwilowych dla
zadanego przez prowadzącego sygnału ……………………………………….……………………… przy
zmienionym jednym z parametrów (wskazanym przez prowadzącego – zaznaczyć, którym):

a) wartość międzyszczytowa (dynamika sygnału) 800 mVpp [Ampl];
b) wartość składowej stałej 250mV [Offset];
c) wartość częstotliwości podstawowej 2kHz [Freq];
d) współczynnik wypełnienia (dla fali prostokątnej) 25% [%Duty].

3. Pomiary parametrów statystycznych sygnałów losowych

Wykonać pomiary parametrów kumulowanych (uśrednionych) mg, Sg i m2g w funkcji liczby realizacji
pomiarów N. Pomiary realizować dla N:

od N =1 do 20 z krokiem co 1,

(1, 2, 3, 4, …, 19, 20)

od N =20 do 100 z krokiem co 5,

(25, 30, 35, …, 95, 100)

od N =100 do 300 z krokiem co 20,

(100, 120, …, 280, 300)

od N =300 do 1000 z krokiem co 50,

(350, 400, …, 950, 1000)

a)
dla

sygnału …………………………..………………………………………………….

b)
dla

sygnału …………………………..………………………………………………….

c)
dla

sygnału …………………………..………………………………………………….

d)
dla

sygnału …………………………..………………………………………………….

Jeżeli badany sygnał był sumą szumu (NOISE) i sygnału zdeterminowanego z losową fazą (SIGNAL)
oceń stosunek SNR mocy sygnału użytecznego (P

SIGNAL

) do mocy szumu (P

NOISE

). Pomiar ten wykonaj

dla każdego z sumowanych sygnałów z osobna na podstawie pomiaru ich średniej mocy kumulowanej
m2g dla N>100. W tym celu skorzystać z zależności:

( )

( )

100

2

2

>

=

=

N

NOISE

SIGNAL

NOISE

SIGNAL

N

g

m

N

g

m

P

P

SNR

Dla sygnału normalnego (szumu) zapisać wartości wszystkich parametrów mg, Sg, m2g dla N>100 (do
wykorzystania w punkcie 5a).


4. Tabela wyników (obliczenia)

Dla każdego z sygnałów wykonać tabelę wyników według wzoru:

N

mg

Sg

m2g

mg

f

[mV]

Sg

f

[mV]

m2g

f

[(mV)

2

]

mg

n

Sg

n

m2g

n

1

2

3

…

950

1000

MAX

MIN

gdzie:
MAX, MIN –

wartości maksymalne i minimalne analizowanego parametru;

mg, Sg, m2g –

wartości parametrów wyznaczonych w trakcie pomiarów;

mg

f

, Sg

f

, m2g

f

– wartości parametrów przeliczone na jednostki fizyczne*;

mg

n

, Sg

n

, m2g

n

– wartości parametrów unormowanych według zależności:

( )

( )

(

)

MIN

MAX

n

mg

mg

mg

N

mg

N

mg

−

−

=

1000

,

( )

( )

(

)

MIN

MAX

n

Sg

Sg

Sg

N

Sg

N

Sg

−

−

=

1000

,

( )

( )

(

)

MIN

MAX

n

g

m

g

m

g

m

N

g

m

N

g

m

2

2

1000

2

2

2

−

−

=

*) Przeliczenie na jednostki fizyczne dokonujemy poprzez porównanie sygnału harmonicznego o zadanej
wartości pik-pik (jej odpowiada określona wartość amplitudy sygnału harmonicznego, a tym samym
określona wartość skuteczna tego sygnału) z odpowiadającą jej wartością skuteczną Sg(N) dla N>100.


5. Charakterystyki normowania się parametrów statystycznych sygnałów losowych

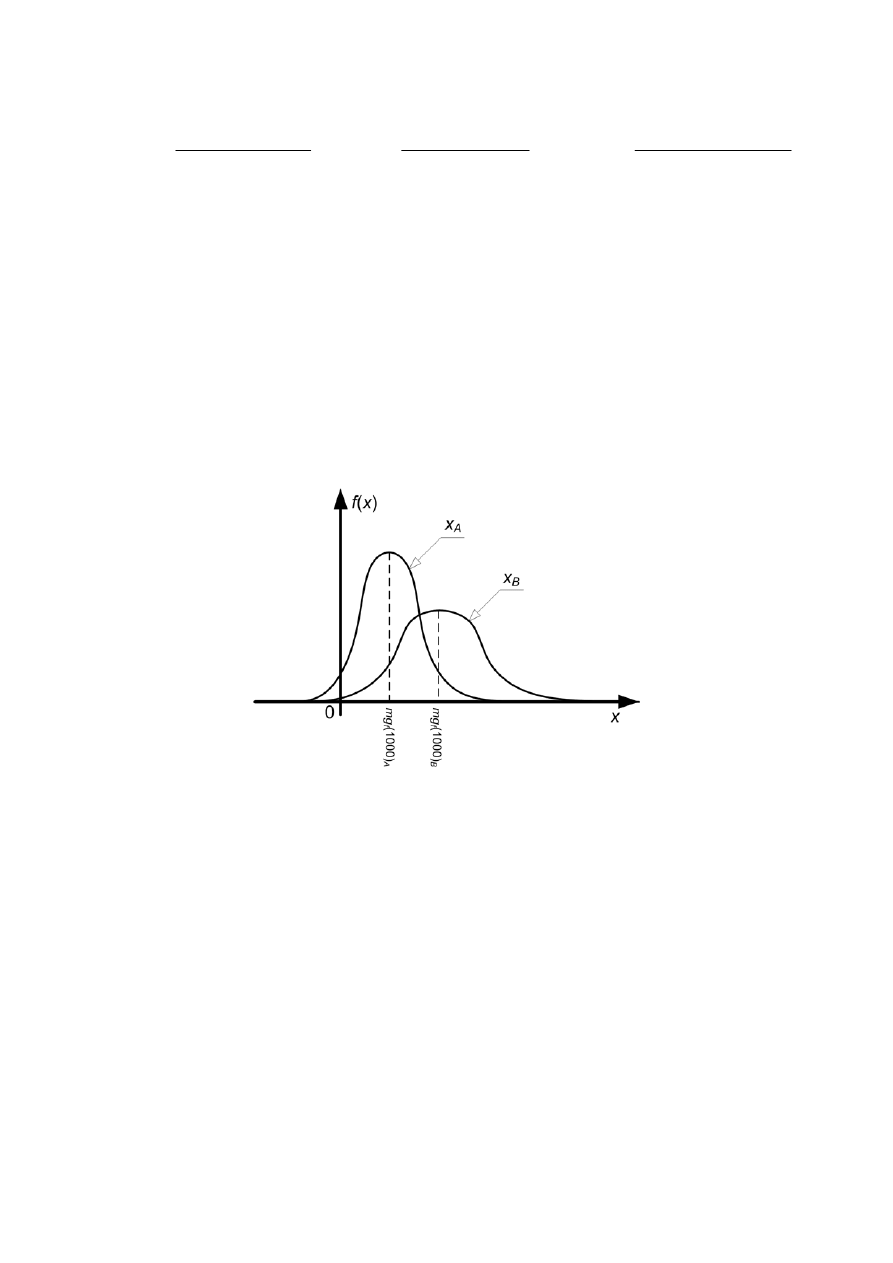
a) Jeżeli badanym sygnałem był sygnał normalny, wykreśl na jednym wykresie funkcje gęstości

prawdopodobieństwa wartości chwilowych dla tych sygnałów, korzystając z wartości parametrów
mg

f

(1000) i Sg

f

(1000).

Jeżeli badanym sygnałem była suma sygnału normalnego i sygnału zdeterminowanego z losową fazą
wykreślić opisane charakterystyki przy wykorzystaniu wartości parametrów zanotowanych w trakcie
obliczania stosunku SNR (N>100). Na osiach nanieść parametry przeliczone na jednostki fizyczne.

b) Wykreślić charakterystyki parametrów mg

f

, Sg

f

, m2g

f

w funkcji N (na trzech wykresach – na każdym

wykresie jeden parametr dla dwóch sygnałów). Na tych charakterystykach zaznaczyć dla każdego
sygnału proste:

–

mg

f

(1000), mg

f

(1000) ± 10%, mg

f

(1000) ± 5%;

–

Sg

f

(1000), Sg

f

(1000) ± 2%, Sg

f

(1000) ± 1%;

–

m2g

f

(1000) , m2g

f

(1000) ± 0, 5%, m2g

f

(1000) ± 0, 25%.

Na podstawie wykreślonych prostych znaleźć dla każdego sygnału i zaznaczyć na odpowiednim

wykresie taką wartość N

i

, że:

%

10

)

1000

(

)

(

%

10

)

1000

(

:

1000

1

1

+

≤

≤

−

∀

≤

≤

mg

N

mg

mg

N

N

N

%

5

)

1000

(

)

(

%

5

)

1000

(

:

1000

2

2

+

≤

≤

−

∀

≤

≤

mg

N

mg

mg

N

N

N

%

2

)

1000

(

)

(

%

2

)

1000

(

:

1000

3

3

+

≤

≤

−

∀

≤

≤

Sg

N

Sg

Sg

N

N

N

%

1

)

1000

(

)

(

%

1

)

1000

(

:

1000

4

4

+

≤

≤

−

∀

≤

≤

Sg

N

Sg

Sg

N

N

N

%

5

.

0

)

1000

(

2

)

(

2

%

5

.

0

)

1000

(

2

:

1000

5

5

+

≤

≤

−

∀

≤

≤

g

m

N

g

m

g

m

N

N

N

%

25

.

0

)

1000

(

2

)

(

2

%

25

.

0

)

1000

(

2

:

1000

6

6

+

≤

≤

−

∀

≤

≤

g

m

N

g

m

g

m

N

N

N

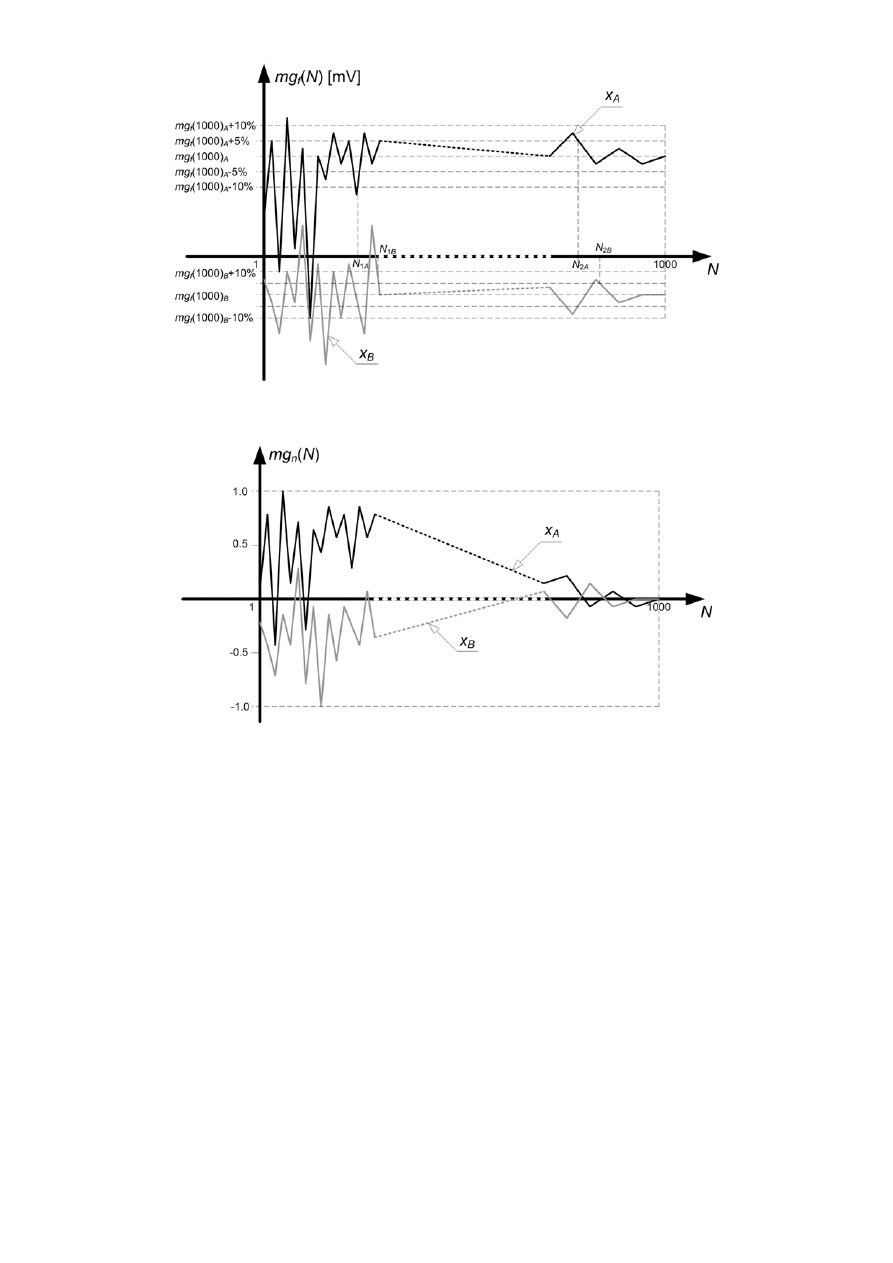
c) Wykreślić charakterystyki parametrów unormowanych mg

n

, Sg

n

, m2g

n

w funkcji N (na trzech

wykresach – na każdym wykresie jeden parametr dla dwóch sygnałów).

d) Dla każdego sygnału z osobna, wykreślić na jednym wykresie trzy charakterystyki parametrów

unormowanych mg

n

, Sg

n

, m2g

n

w funkcji N.

6. Wnioski

We wnioskach zanotować swoje spostrzeżenia. Spróbować odpowiedzieć na poniższe pytania (rozwiązać

zadania / problemy).

a) Czy narysowane w punkcie 2 wszystkie charakterystyki są właściwe? Z czego może wynikać fakt, że

np. w sygnale prostokątnym z losową fazą o współczynniku wypełnienia 50% pojawiające się
dystrybucje mogą nie być jednakowej wielkości?

b) Jak wpływa kształt rozkładu prawdopodobieństwa wartości chwilowych (a tym samym jak wpływają

wartości parametrów statystycznych rozkładu) na szybkość stabilizowania się parametrów?

c) Które parametry stabilizują się najszybciej i dlaczego?
d) Jaki jest sens, z punktu widzenia wykonywania pomiarów, wyznaczania wartości parametru N

i

?

e) Czy z charakterystyk parametrów unormowanych można wyciągnąć inne wnioski dotyczące szybkości

stabilizowania się tych parametrów aniżeli z charakterystyk dla parametrów nieunormowanych? Jeżeli
tak, to dlaczego?

f) Jeżeli badane były minimum dwa sygnały odpowiedzieć jak wpływa miara SNR na stabilizowanie się

parametrów tych sygnałów?

g*) W literaturze znaleźć zależności analityczne opisujące narysowane w punkcie 2. funkcje gęstości

prawdopodobieństwa wartości chwilowych.