WOJSKOWA AKADEMIA TECHNICZNA

im. Jarosława Dąbrowskiego

w Warszawie

Wydział Elektroniki

LABORATORIUM PODSTAW TELEKOMUNIKACJI

Grupa

...........................

Podgrupa

............................

Data wykonania

ćwiczenia

............................

Ćwiczenie prowadził

............................

Ocena:

............................

Skład podgrupy:

1. ............................................................

2.

............................................................

3.

............................................................

4.

............................................................

5.

............................................................

6.

............................................................

7.

............................................................

8.

............................................................

9.

............................................................

10. ............................................................

Data oddania

sprawozdania

............................

Podpis prowadzącego

............................

Temat ćwiczenia: Sposoby opisu i modelowania zakłóceń kanałowych




1. Wykaz przyrządów pomiarowych użytych w ćwiczeniu

Lp. Nazwa

przyrządu Typ

Firma

Numer

fabryczny

1.

2.

3.

4.

5.

2. Realizacja ćwiczenia

2.1 Obserwacja kształtów funkcji gęstości prawdopodobieństwa wartości chwilowych

wybranych sygnałów losowych

Na generatorze funkcyjnym firmy Agilent ustawić następujące wartości parametrów:

-

A

– wartość międzyszczytową (dynamikę sygnału) [Ampl];

-

B

– wartość składowej stałej [Offset];

-

f

– wartość częstotliwości podstawowej (dla sygnałów okresowych) [Freq];

-

WT – współczynnik wypełnienia (dla fali prostokątnej) [%Duty].

Podgrupa I

Podgrupa II

Podgrupa III

Podgrupa IV

ustawienia

podstawowe

ustawienia

dodatkowe

ustawienia

podstawowe

ustawienia

dodatkowe

ustawienia

podstawowe

ustawienia

dodatkowe

ustawienia

podstawowe

ustawienia

dodatkowe

A

[mV]

500 2000 720 2880 400 1600 700 3500

B

[mV]

0 250

1240

1440 0 200

1240

1040

f

[kHz]

1 2 2 4 1 3 2 6

WT

[%]

50 25 50 75 50 30 50 80

Następnie, korzystając z ustawień podstawowych, dla poszczególnych sygnałów stochastycznych:

A) sygnał normalny – szum biały [Noise];

B) sygnał harmoniczny z losową fazą;

C) sygnał prostokątny z losową fazą;

D) sygnał trójkątny z losową fazą;

E) sygnał piłokształtny z losową fazą

zaobserwować jak normują się (przy zwiększaniu liczby realizacji pomiarów N) kumulowane

charakterystyki funkcji gęstości prawdopodobieństwa wartości chwilowych sygnałów. Dla N>100

przerysować charakterystyki do odpowiednich ramek. Na osiach nanieść odpowiednie wartości!

Zachowując skalę, na sąsiednich rysunkach narysować te same charakterystyki dla poszczególnych

sygnałów uwzględniając zmianę jednego z parametrów z ustawień dodatkowych:

A) dla sygnału normalnego – A;

B) dla sygnału harmonicznego z losową fazą – f;

C) dla sygnału prostokątnego z losową fazą – WT;

D) dla sygnału trójkątnego z losową fazą – B;

E) dla sygnału piłokształtnego z losową fazą – f.

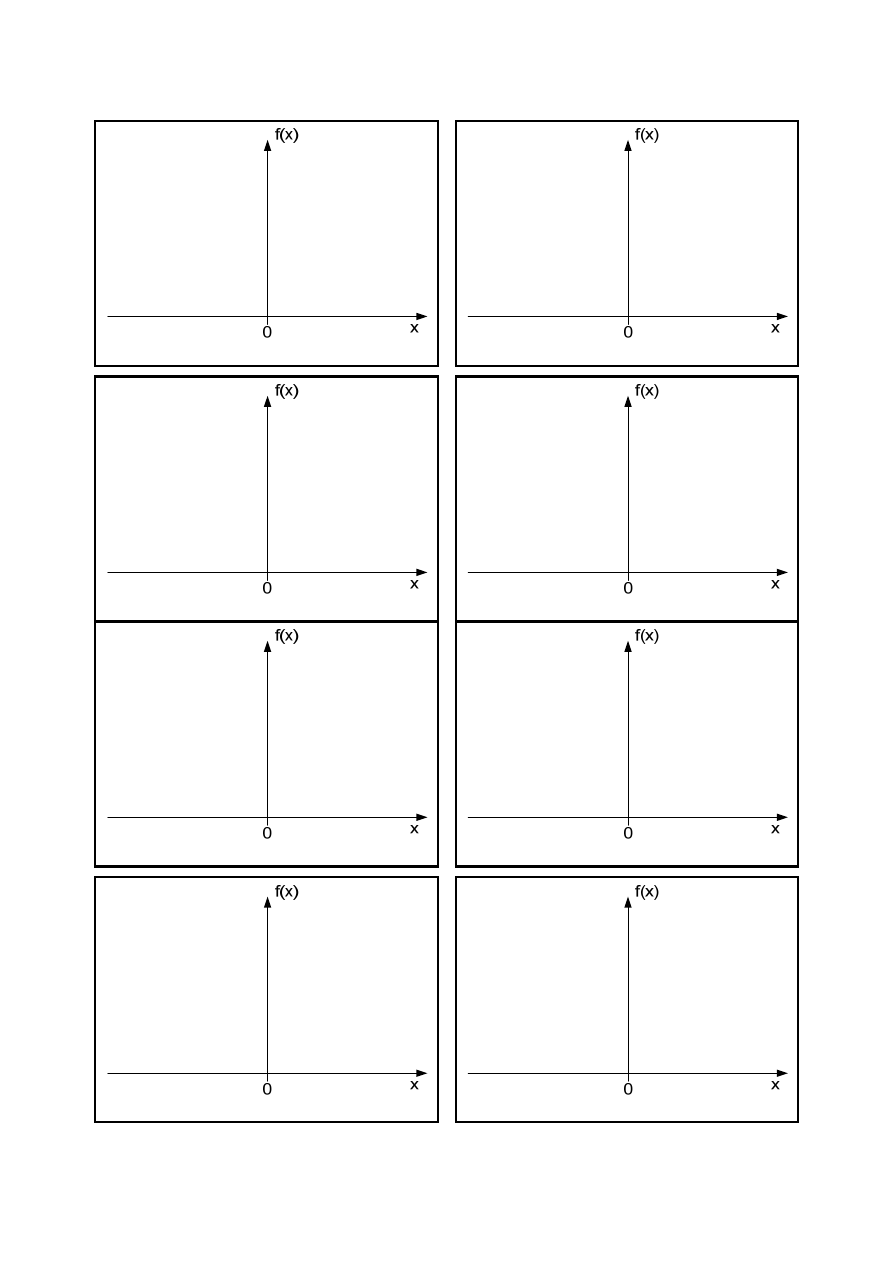
A)

B)

C)

D)

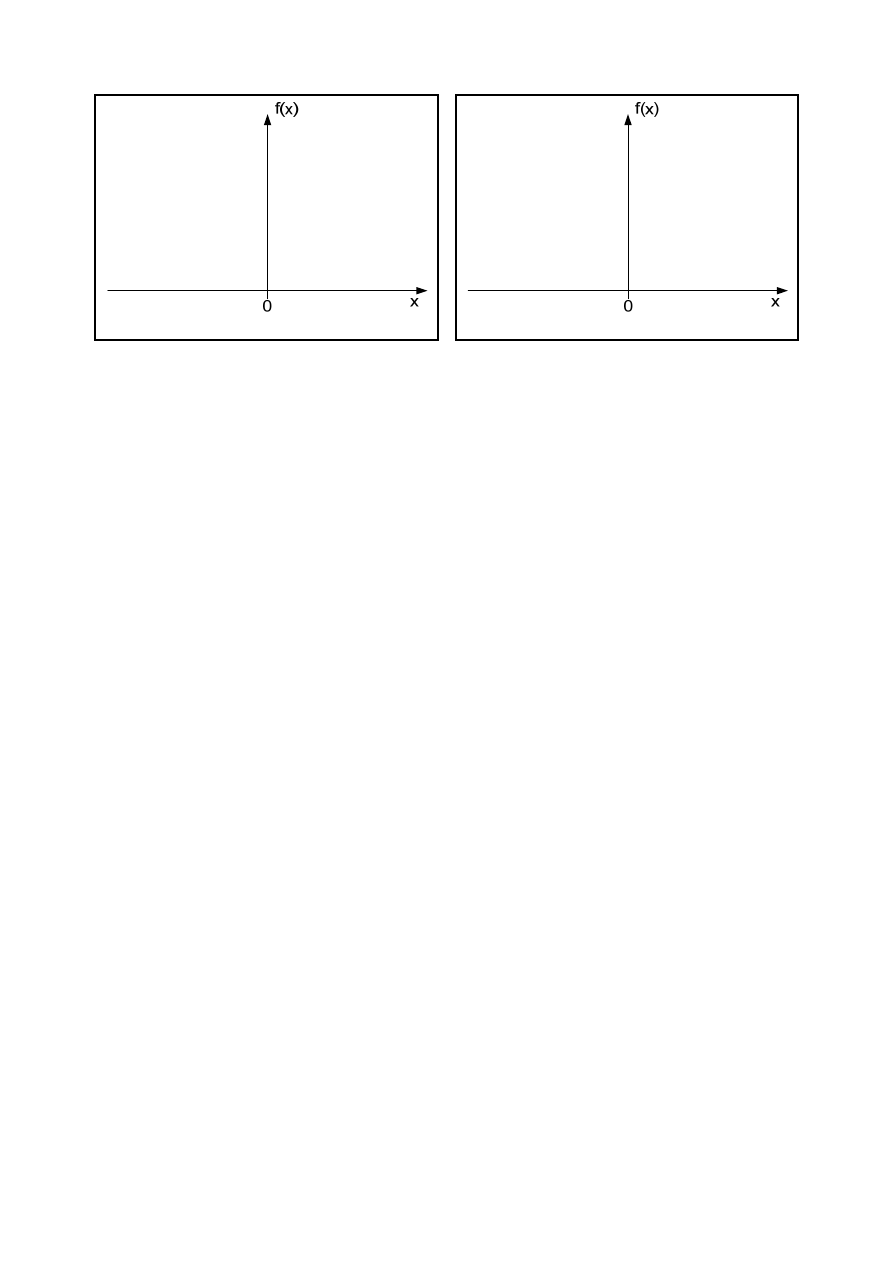
E)

2.2 Pomiary parametrów statystycznych sygnałów losowych

Dla sygnału (którego parametry ustawia prowadzący ćwiczenie):

…………………………………………………..………………………………………………….

zapisać w tabeli w punkcie 4 sto wyników pomiarów parametrów chwilowych m0, S i m2.

Następnie (w domu) dokonać przeliczenia wartości chwilowych parametrów w jednostkach

programu [j] na jednostki fizyczne m0

F

, S

F

i m2

F

– [mV, (mV)

2

]. Obliczyć wartości średnie X

ŚR

(kumulowane dla N=100) oraz określić wartości maksymalne X

MAX

i minimalne X

MIN

poszczególnych parametrów.

X

ŚR

–

wartość średnia (kumulowane dla N=100) analizowanego parametru;

X

MIN

, X

MAX

–

wartości maksymalne i minimalne analizowanego parametru;

m0, S, m2 –

wartości parametrów wyznaczonych w trakcie pomiarów;

m0

F

, S

F

, m2

F

– wartości parametrów przeliczone na jednostki fizyczne*;

*) Przeliczenie na jednostki fizyczne dokonujemy poprzez porównanie sygnału harmonicznego o

zadanej wartości pik-pik (jej odpowiada określona wartość amplitudy sygnału harmonicznego, a

tym samym określona wartość skuteczna tego sygnału) z odpowiadającą jej wartością skuteczną

Sg(N) dla N=200.

A

P-P

= ………… [mVpp] odpowiada Sg(200) = ………… [ j ]

zatem 1 [ j ] odpowiada …………[mV]

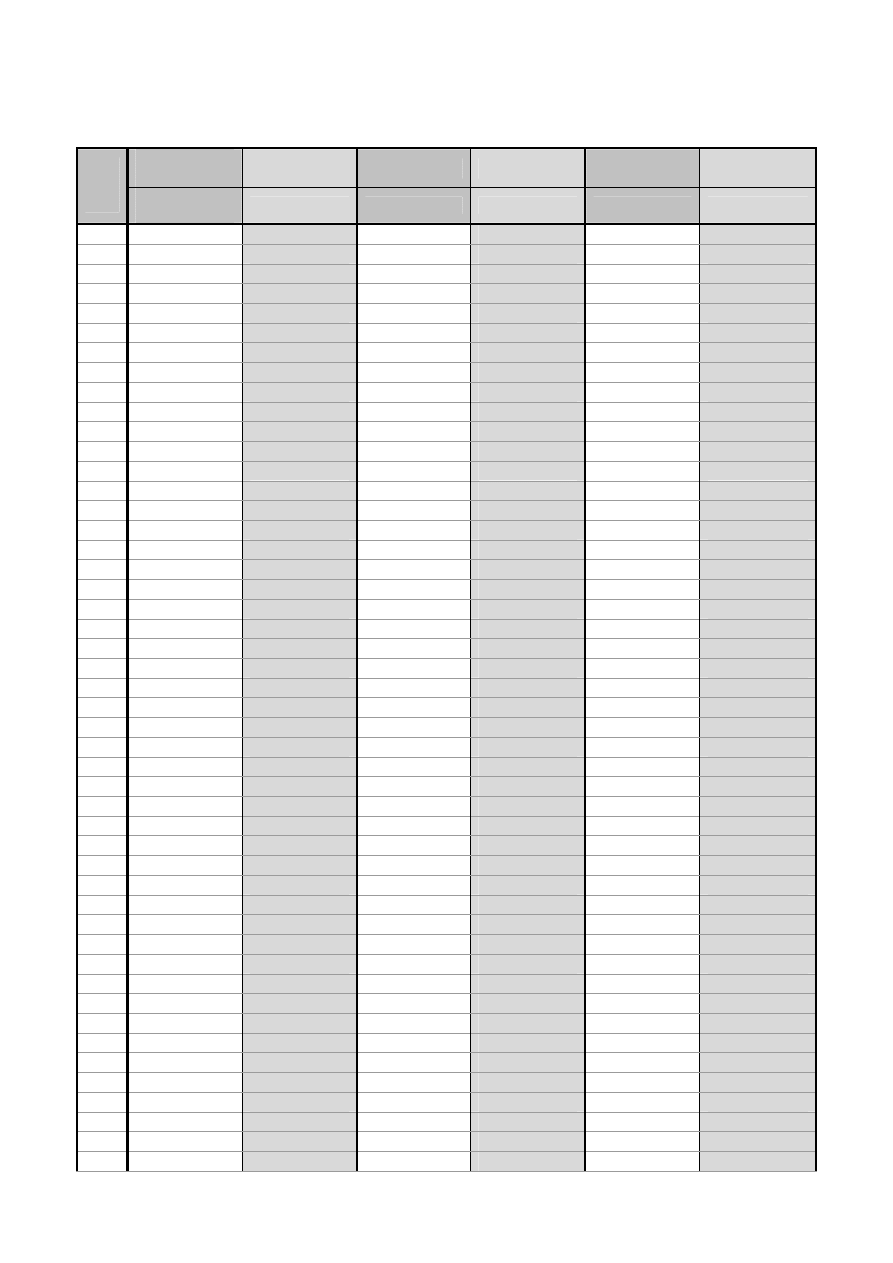
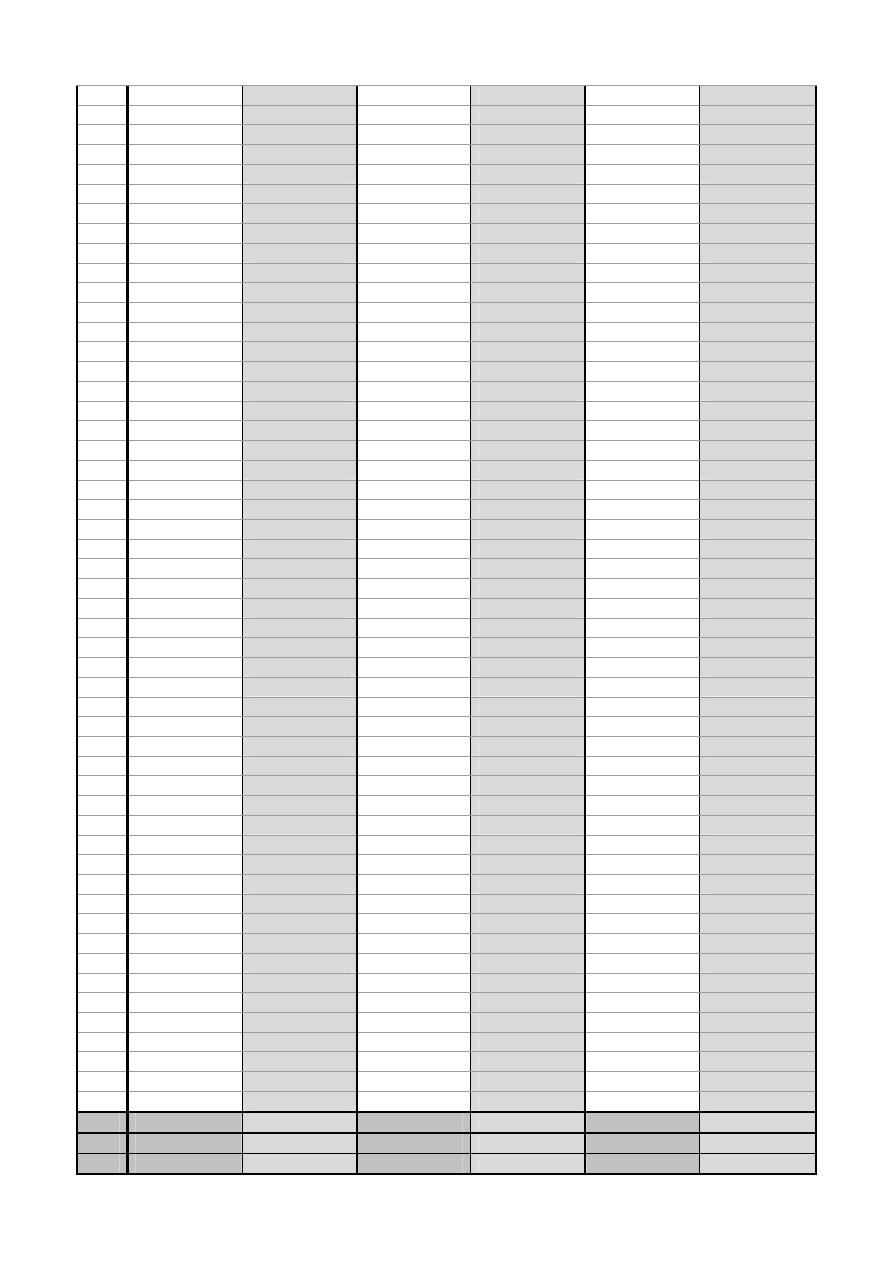
2.3 Wyniki pomiarów

m0

m0

F

S

S

F

m2

m2

F

N

[ j ]

[ mV ]

[ j ]

[ mV ]

[ j

2

]

[ (mV)

2

]

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89

90

91

92

93

94

95

96

97

98

99

100

X

ŚR

X

MIN

X

MAX

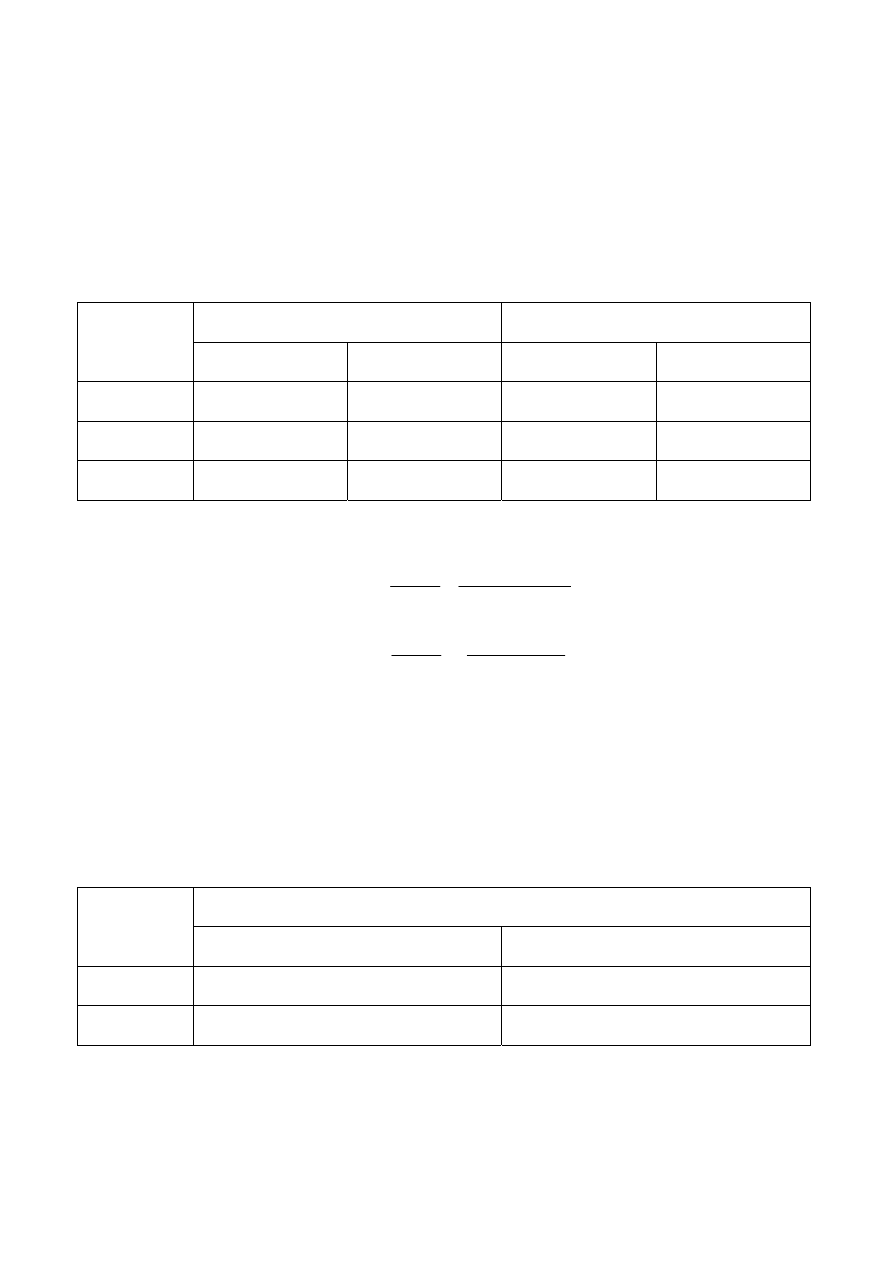
2.4 Określenie stosunku mocy sygnału użytecznego do mocy szumu

Jeżeli badany sygnał był sumą sygnału szumu (NOISE) i sygnału zdeterminowanego z losową fazą

(SIGNAL) wyznaczyć należy miarę SNR, czyli stosunek mocy sygnału użytecznego (P

SIGNAL

) do

mocy szumu (P

NOISE

). Dla każdego z sygnałów (z osobna) należy dokonać pomiaru jego

parametrów dla N=200. które zapisać należy w poniższej tabeli.

Sygnał użyteczny (SIGNAL) Sygnał szumu (NOISE)

Parametry

(przy N=200)

[ j ] / [ j

2

]

[ mV ] / [ (mV)

2

]

[ j ] / [ j

2

]

[ mV ] / [ (mV)

2

]

mg

Sg

m2g

Korzystając z poniższych zależności należy wyznaczyć parametr SNR:

I)

( )

( )

200

2

200

2

NOISE

SIGNAL

NOISE

SIGNAL

I

g

m

g

m

P

P

SNR

=

=

,

II)

( )

( )

2

200

200

⎥

⎦

⎤

⎢

⎣

⎡

=

=

NOISE

SIGNAL

NOISE

SIGNAL

II

Sg

Sg

P

P

SNR

.

Podane zależności są zależnościami w mierze liniowej, tzn. wyznaczane są w jednostkach [W/W].

W ćwiczeniu należy dokonać przeliczenia parametru SNR na mirę logarytmiczną, czyli miarę

określaną w [dB] (czyt. decybelach), korzystając z zależności:

[ ]

[

]

(

)

W/W

log

10

dB

10

SNR

SNR

=

Wyniki wyliczeń zapisać w poniższej tabeli.

SNR

[ W / W ]

[ dB ]

SNR

I

SNR

II

Zastanowić się nad różnicami wartości parametrów SNR

I

i SNR

II

.

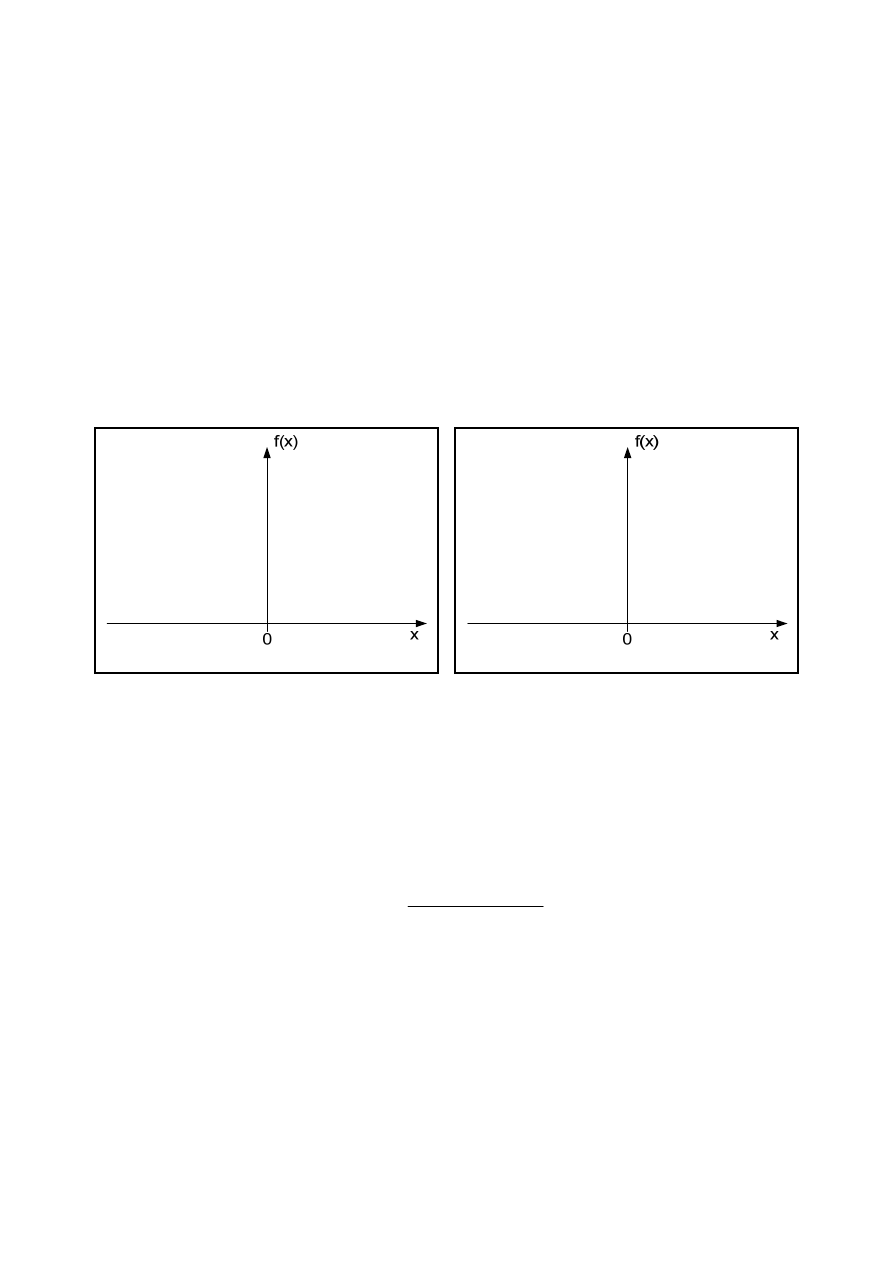
2.5 Określenie stosunku mocy sygnału użytecznego do mocy szumu

Korzystając z zależności analitycznej opisującej funkcję gęstości prawdopodobieństwa wartości

chwilowych sygnału normalnego (rozkład Gaussa) wykreśl tę funkcję korzystając z wartości

mg

F

(200)

i Sg

F

(200)

dla sygnału szumu, zmierzonych i zanotowanych w poprzednim punkcie

ćwiczenia. Jeżeli znana jest zależność analityczna opisująca teoretyczną funkcję gęstość

prawdopodobieństwa wartości chwilowych sygnału użytecznego, wyznacz postać graficzną tej

funkcji nanieś na wykres z rozkładem normalnym. Wykorzystaj w tym celu wartości mg

F

(200)

i Sg

F

(200)

dla sygnału użytecznego, zmierzone w poprzednim punkcie ćwiczenia. Wykresy

przedstaw w jednostkach fizycznych. Na osiach zaznaczyć skalę i jednostki.

2.6. Obliczenia

Dla zebranych pomiarów:

– znaleźć wartość maksymalną X

MAX

i minimalną X

MIN

analizowanego parametru;

– do zakresu zmienności (X

MAX

– X

MIN

) dodać wartość 0.1, a następnie podzielić przedział

zmienności na 5 podprzedziałów o szerokości:

5

1

.

0

+

−

=

Δ

MIN

MAX

X

X

X

;

– wówczas podprzedziały będą miały granice:

I

[

)

X

X

X

MIN

MIN

Δ

+

−

−

05

.

0

;

05

.

0

,

II

[

)

X

X

X

X

MIN

MIN

Δ

+

−

Δ

+

−

2

05

.

0

;

05

.

0

,

III

[

)

X

X

X

X

MIN

MIN

Δ

+

−

Δ

+

−

3

05

.

0

;

2

05

.

0

,

IV

[

)

X

X

X

X

MIN

MIN

Δ

+

−

Δ

+

−

4

05

.

0

;

3

05

.

0

,

V

[

]

X

X

X

X

MIN

MIN

Δ

+

−

Δ

+

−

5

05

.

0

;

4

05

.

0

,

przy czym:

05

.

0

5

05

.

0

+

=

Δ

+

−

MAXx

MIN

X

X

X

;

– określić granice podprzedziałów w jednostkach z programu i w jednostkach fizycznych;

– zliczyć liczbę wartości mierzonego parametru w danym podprzedziale;

– uzupełnić tabele w punkcie 7 – dla każdego parametru wykonać oddzielną tabelę;

– wykreślić histogram prawdopodobieństwa wystąpienia wartości parametru w poszczególnych

podprzedziałach – dla każdego parametru wykonać oddzielny histogram;

– poprowadzić obwiednię na histogramach;

– określić dla danego rozkładu wartość średnią X

ŚR

=

x

i odchylenie standardowe

σ ;

– zaznaczyć wartości wyznaczonych parametrów rozkładu na histogramach;

– wyznaczyć prawdopodobieństwo wystąpienia parametru SNR w przedziale

(

)

σ

σ

+

−

x

x

;

i

porównać ją z wartością prawdopodobieństwa jaka odpowiada temu przedziałowi dla

rozkładu normalnego;

– w miarę możliwości nanieść na histogram krzywą Gaussa – funkcję gęstości

prawdopodobieństwa rozkładu normalnego o wyznaczonych wartościach parametrów;

– określić typ rozkładu analizowanego parametru.

2.7. Wyniki obliczeń

Przedział [ j lub j

2

]

Przedział [mV lub (mV)

2

]

Wartość środkowa przedziału [ j ]

Wartość środkowa przedziału [mV]

Liczba wartości parametru w przedziale

Prawdopodobieństwo wystąpienia wartości
parametru w przedziale

Wartość średnia [ j ] / [mV]

Odchylenie standardowe [ j ] / [mV]

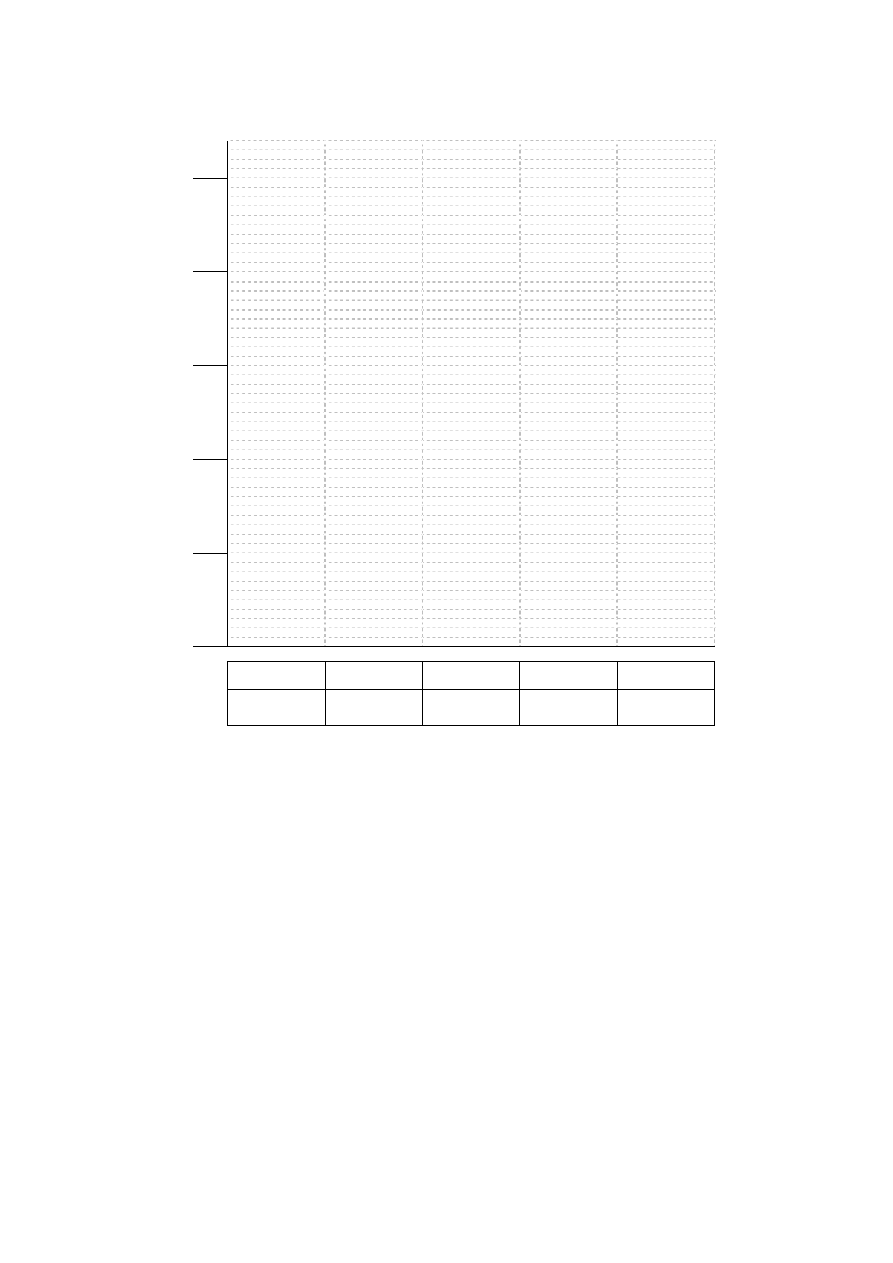
2.8. Histogram

P(X)

0,5

0,5

0,4

0,4

0,3

0,3

0,2

0,2

0,1

0,1

0

0

Przedziały:

Elementów

w przedziale

3. Wnioski