Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

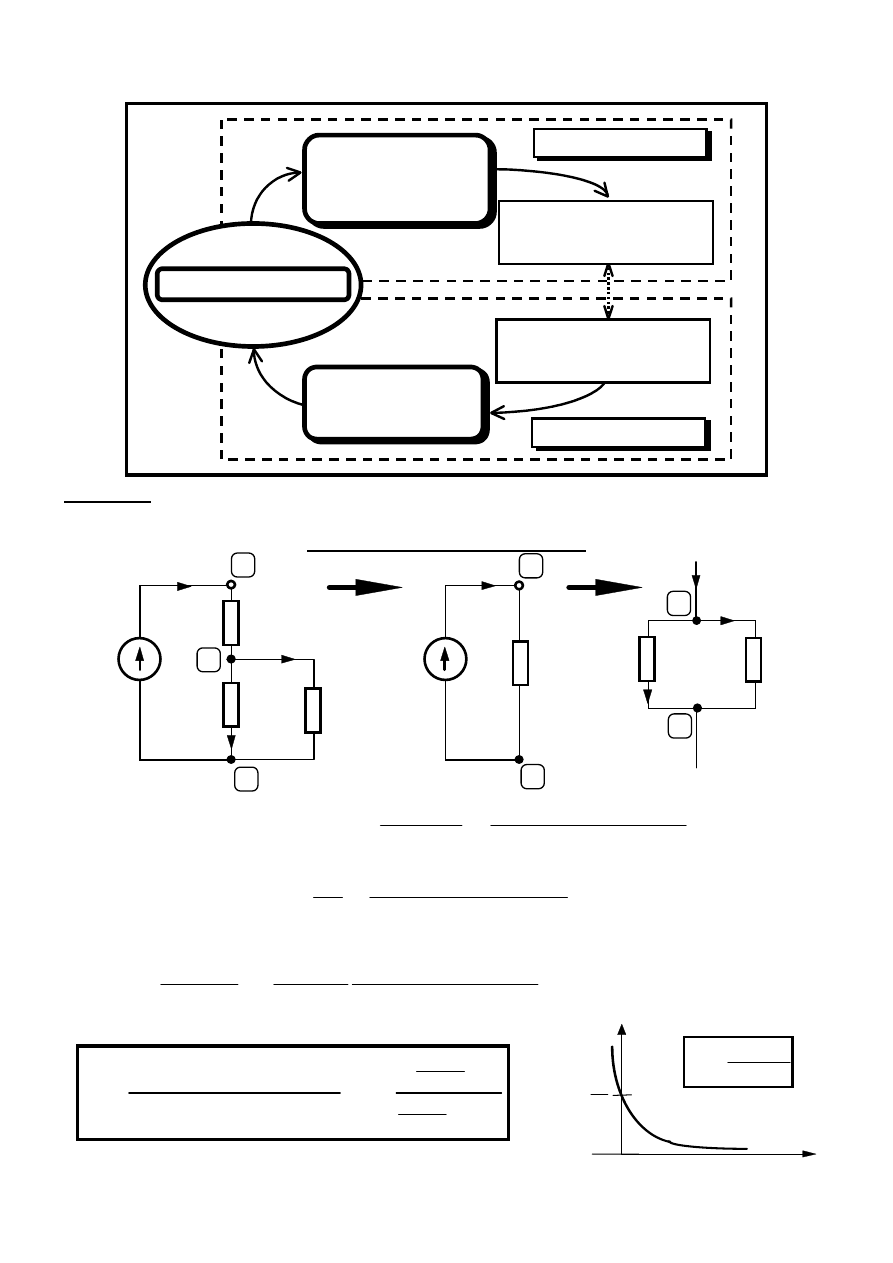
Analiza obwodów elektrycznych

Obwód elektryczny

Synteza

Analiza

Wyznaczenie innych wielkości
charakteryzujących obwód; np.
moce, sprawności itp.

Zadane funkcje obwodowe i in-
ne wielkości charakteryzujące
obwód; np. moce, sprawności
it

Wyznaczenie wartości

parametrów wybranych

elementów obwodu

Określenie minimalnego

zbioru

funkcji obwodowych

F

o

= { u, i }

Przykład

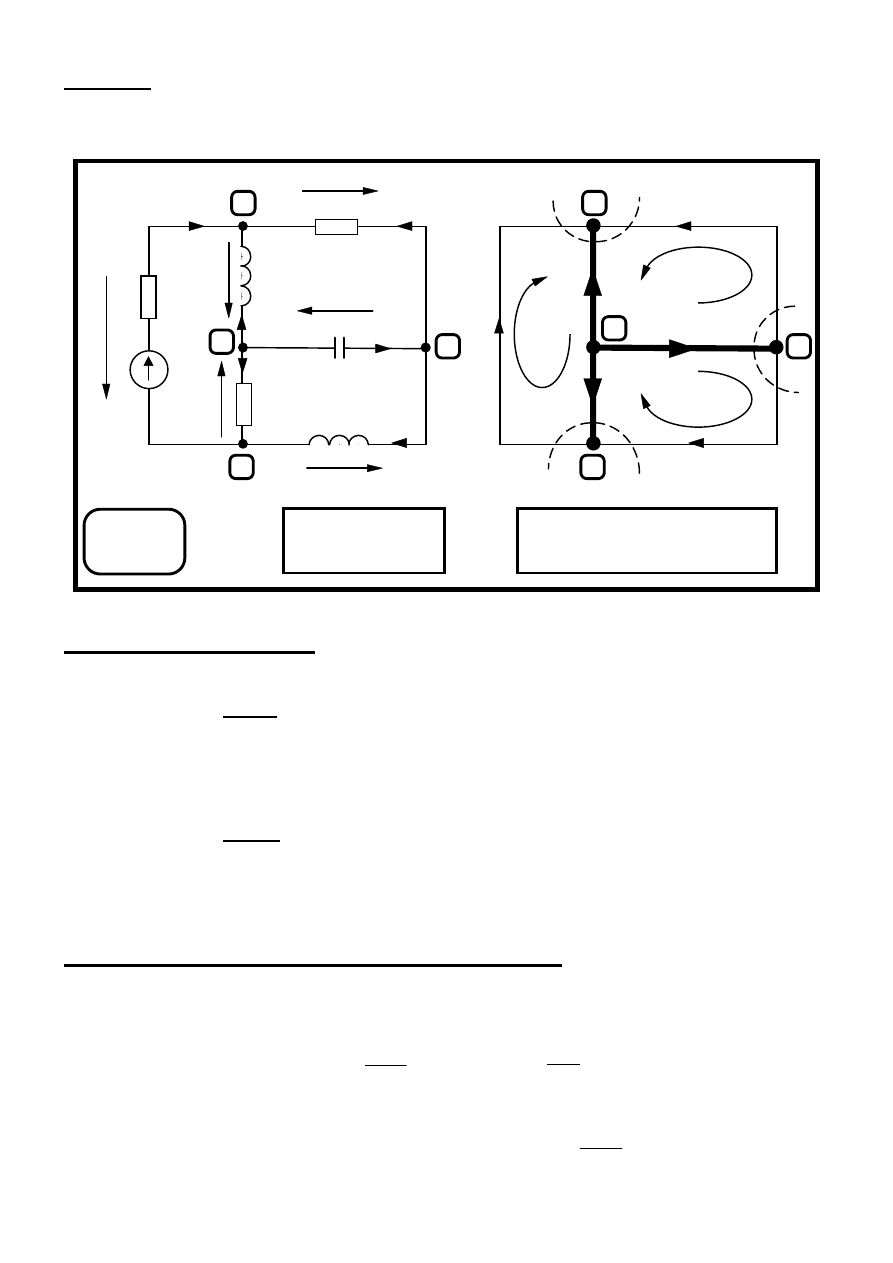
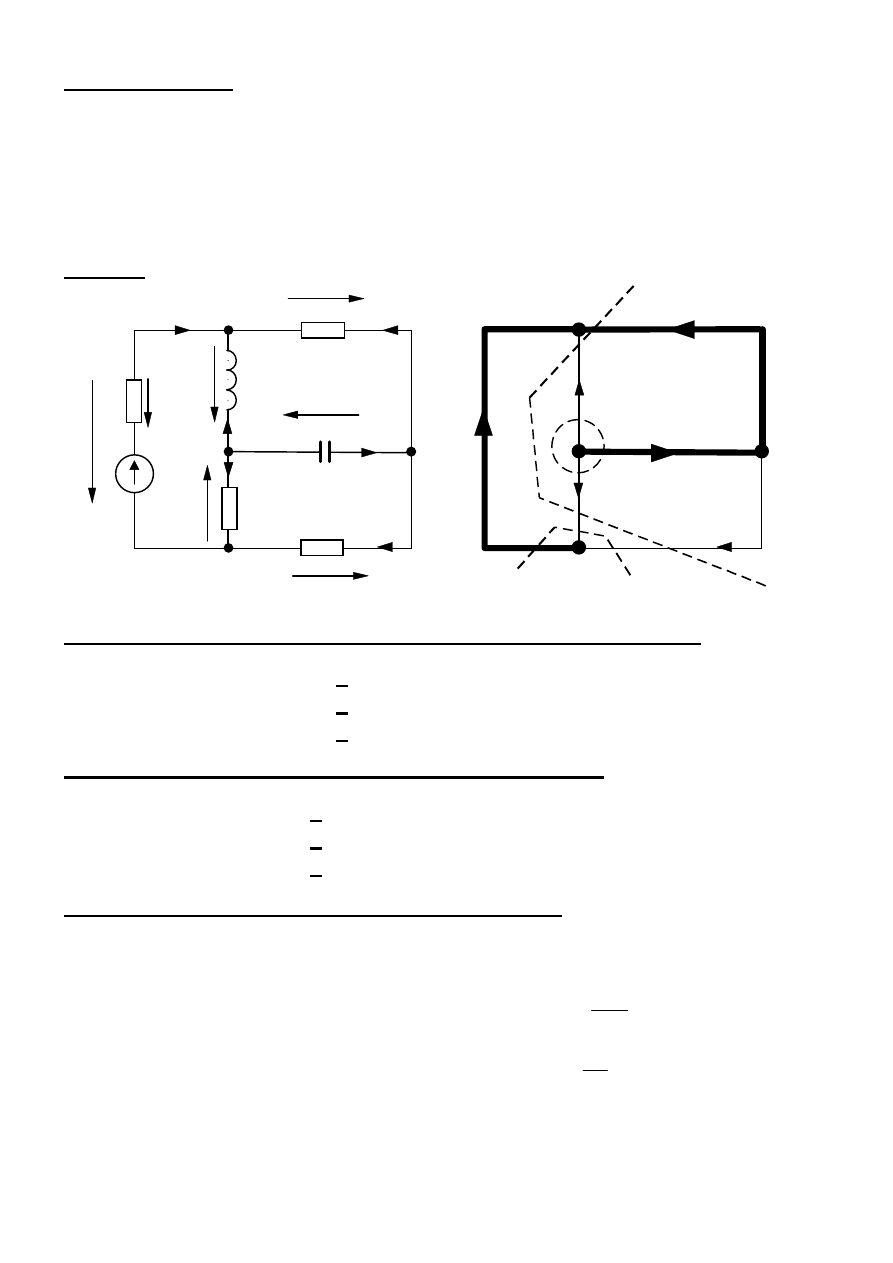
W obwodzie o schemacie pokazanym na rysunku wyznaczyć w postaci

symbolicznej wartość natężenia prądu i

o

.

Analiza obwodu elektrycznego.

R

2

R

1

R

o

u

i

o

i

A

C

B

i

2

R

z

u

i

C

B

R

o

i

2

R

2

i

o

A

C

i

1. Rezystancja zastępcza:

R

R

G

G

R R

R R

R R

R

R

z

=

+

+

=

+

+

+

1

1

o

2

o

1

1

2

2

o

o

2

2. Z Postulatu Ohma:

i

u

R

R

R

R R

R R

R R

u

z

=

=

+

+

+

2

1

1

2

2

o

o

o

3. Konduktancyjny Dzielnik Prądu ( węzeł B lub C ):

i

G

G

G

i

R

R

R

R

R

R R

R R

R R

u

o

o

o

2

2

o

2

o

o

o

=

+

=

+

+

+

+

⋅

2

1

1

2

2

i

R

R R

R R

R R

u

u

R

R

R

R

R R

R

R

o

o

o

o

=

+

+

⋅ =

+

+

+

2

1

1

2

2

2

1

2

1

2

1

2

(1)

R

o

i

o

i

A

B

R

o

o

=

+

u

R

1

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Przykład W obwodzie o schemacie pokazanym na poprzednim rysunku wyznaczyć w taką wartość
r oporu rezystora R

o

aby natężenie prądu i

o

= I

ZAD

.

Synteza obwodu elektrycznego.

Wprost ze wzoru (1) otrzymujemy:

r

I

o

I

ZAD

o

ZAD

=

=

+

−

⎛
⎝

⎜

⎞
⎠

⎟

=

R

R

R

R

u

R

i

2

1

2

1

(2)

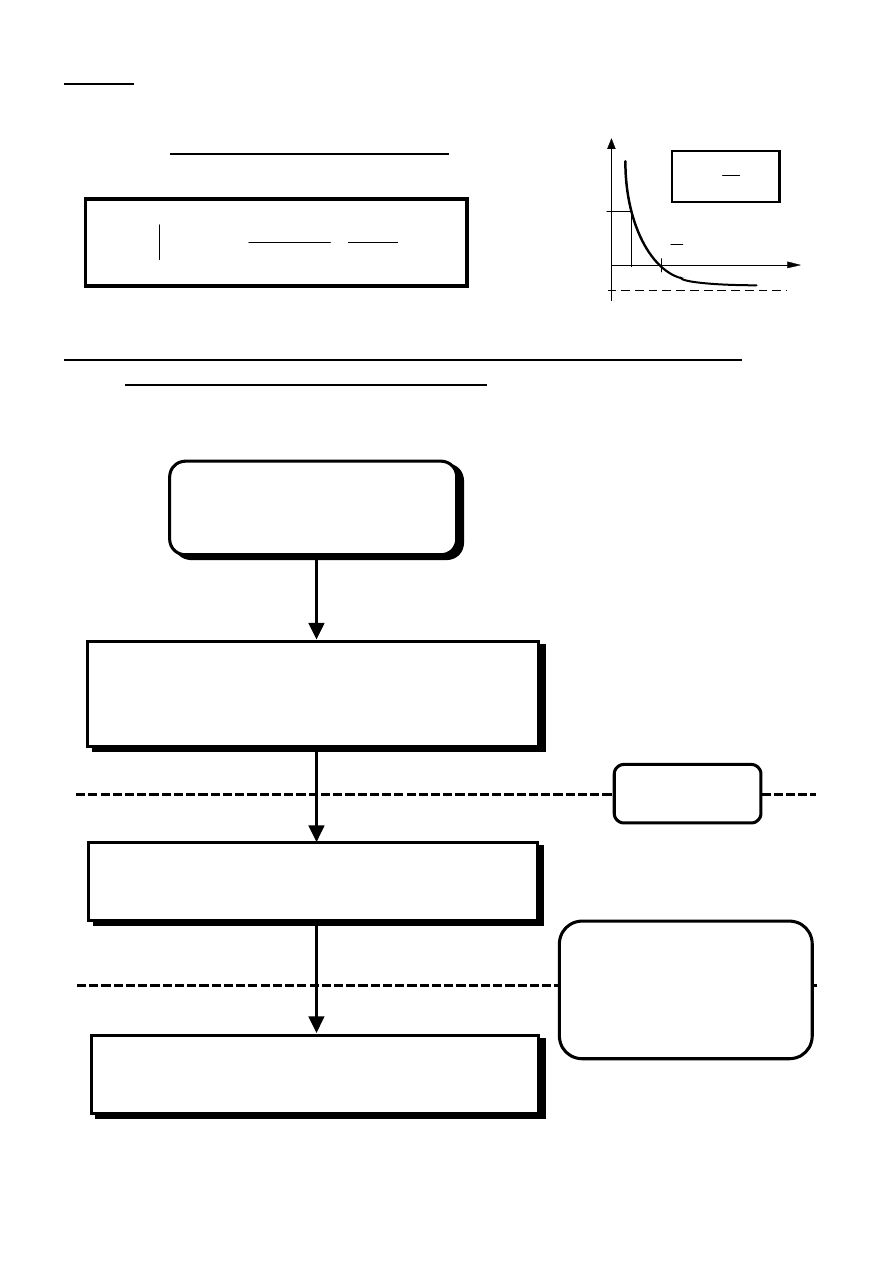
Analiza obwodów elektrycznych ( rozwiązywanie obwodów elektrycznych ) – wyzna-
czenie minimalnego zbioru funkcji obwodowych ( napięć u, prądów i ) pozwalających
w łatwy sposób wyznaczyć także inne wielkości charakteryzujące obwód.

Ułożenie w oparciu o wybraną metodę
minimalnego układu niezależnych rów-
nań równowagi obwodu.

Analiza obwodów

elektrycznych

Rozwiązanie minimalnego układu nieza-
leżnych równań równowagi obwodu.

Dyskusja uzyskanych rozwiązań rów-
nań równowagi obwodu.

Obwód jest już

„rozwiązany” !

Wyniki analizy obwodu

otrzymane w postaci:

– symbolicznej;
– półsymbolicznej;
– numerycznej.

r

I

Z A D

R

o

i

o

R

A

i

B

o

o

=

−

– B

A

B

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

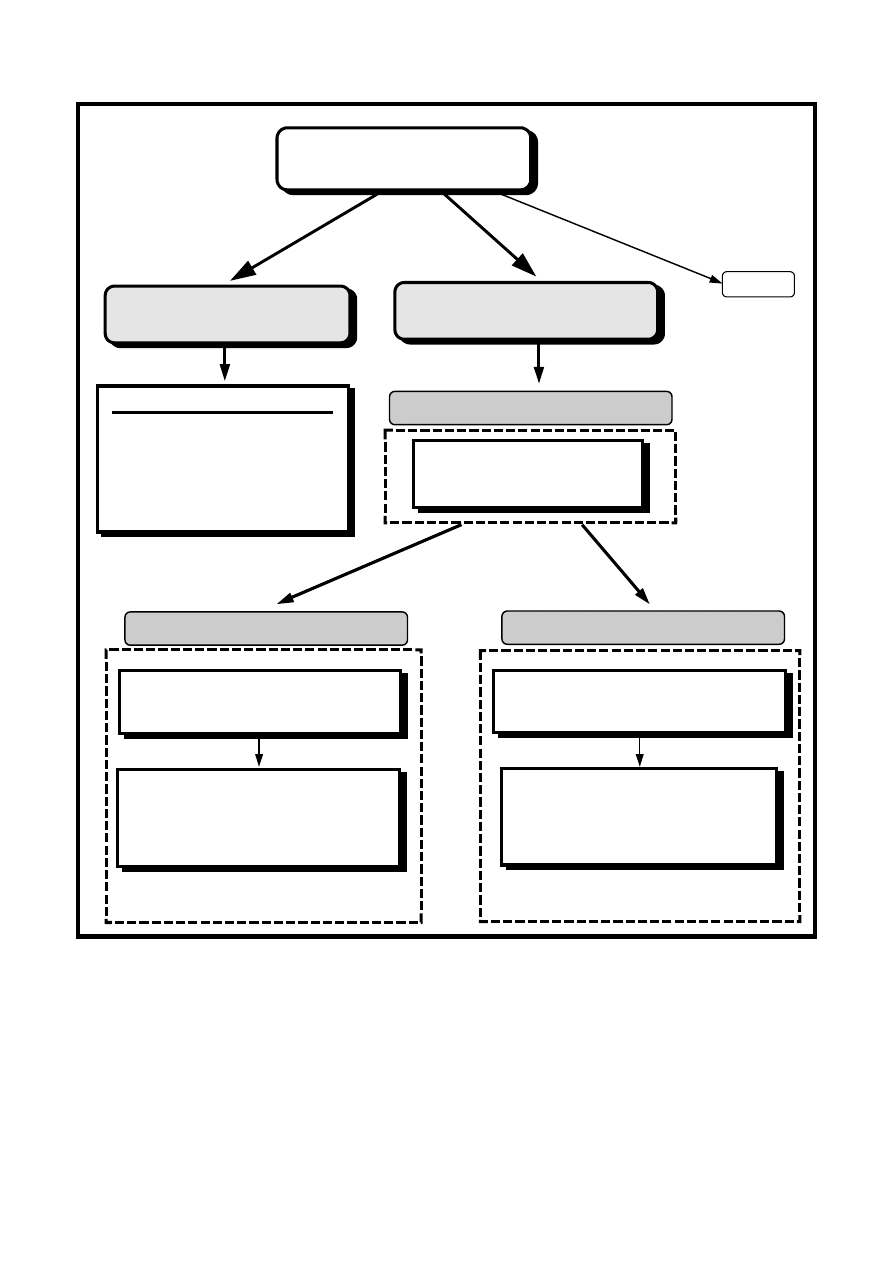
Podstawowe metody analizy obwodów elektrycznych

Metody analizy

obwodów elektrycznych

Zastosowanie różnych:

⇒ transfiguracji obwodu;

⇒ twierdzeń TO;

⇒ gotowych wzorów;

⇒ ………

Metody Pośrednie

( „automatyczne” )

Metody Bezpośrednie

( „na piechotę” )

PPK ⊕ NPK ⊕ PO

„MPK”

Metoda Prądów Strun

„MPS”

Metoda Napięć Konarowych

„MNK”

Metoda Prądów Oczkowych

( metoda Maxwell’a )

„MPO”

Metoda Napięć Węzłowych

( metoda Coltri’ego )

„MNW”

Metody oparte o NPK i PO

Inne

Metody oparte o PK i PO

Metody oparte o PPK i PO

………………

………………

W metodach analizy obwodów SLS dążymy do wyboru minimal-

nej liczby funkcji obwodowych ( prądów i oraz napięć u ) koniecznych
do jego pełnej analizy.

Wybrane funkcje obwodowe są rozwiązaniami wynikającego z

PPK i NPK układu niezależnych równań równowagi obwodu.

Zastosowanie teorii liniowych grafów skierowanych w znaczny

sposób ułatwia i automatyzuje tworzenie poprawnych układów rów-
nań równowagi obwodu.

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

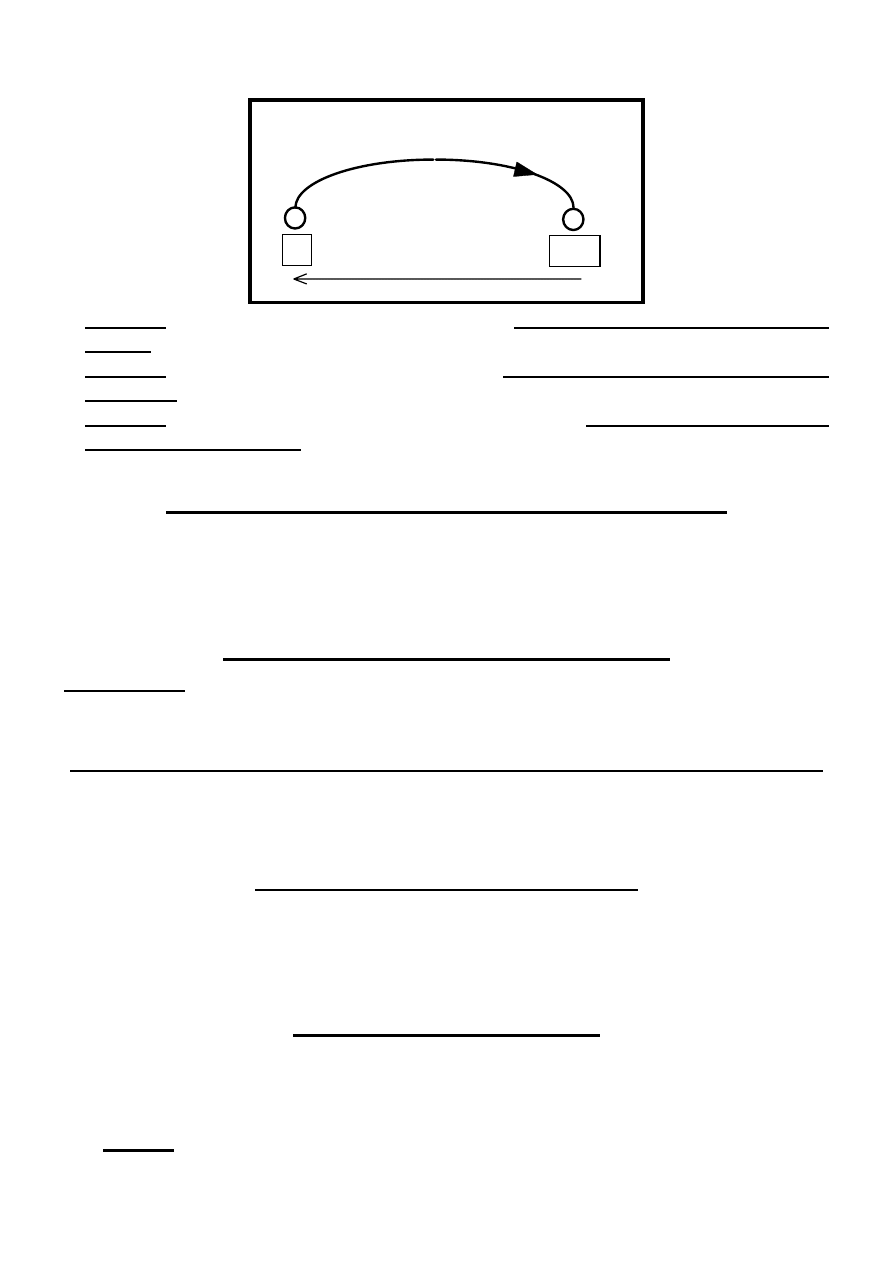
Strzałkowanie gałęzi liniowych grafów skierowanych

u

p

i

p

k

k+1

p

1. Krawędź liniowego grafu skierowanego jest zorientowana zgodnie ze zwrotem

prądu i przyjętym w odpowiadającej jej gałęzi analizowanego obwodu SLS.

2. Krawędź liniowego grafu skierowanego jest zorientowana przeciwnie do zwrotu

napięcia u przyjętego w odpowiadającej jej gałęzi analizowanego obwodu SLS.

3. Krawędź liniowego grafu skierowanego ma taką samą cechę ( R, L, C, e, j …) jak

odpowiadająca jej gałąź analizowanego obwodu SLS.

Metoda Postulatów Kirchhoffa ( MPK )

Metoda Postulatów Kirchhoffa ( MPK ) jest klasyczną, obecnie raczej rzadko stosowaną, metodą anali-
zy obwodów elektrycznych. Modyfikacje MPK prowadzą do innych metod analizy obwodów.

Równania równowagi obwodu

Założenia:

g

– liczba gałęzi obwodu;

w

– liczba węzłów obwodu;

Liczba niewiadomych (napięć gałęziowych i prądów gałęziowych)

L

N

= 2g

Niezależne równania równowagi:

PPK:

r = w – 1

NPK:

n = g – w + 1

Liczba równań równowagi

L

RR

= r + n = g

Uwaga: Równania PPK piszemy dla przekrojów fundamentalnych

Równania NPK piszemy dla oczek fundamentalnych

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Przykład

Napisać równania różniczkowo-całkowe obwodu pokazanego na rysunku. Przy-

jąć zerowe warunki początkowe ( dla t < 0 energia zgromadzona w C oraz w L: w

C

= 0, w

L

=

0 ).

C

4

L

6

L

3

R

5

R

2

u

3

u

2

u

4

u

6

u

1

R

1

e

1

i

5

i

3

i

6

i

4

i

2

i

1

B

C

D

A

i

5

i

3

i

6

i

4

i

2

i

1

B

C

D

A

III

II

I

g = 6

w = 4

L

N

= 2g = 12

L

RR

= g = 6

PPK: r = w – 1 = 3
NPK: n = g – w + 1 = 3

u

5

Równania równowagi

PPK

W

A

:

i

3

+ i

1

+ i

2

= 0

W

C

:

i

4

– i

2

– i

6

= 0

W

D

:

i

5

– i

1

+ i

6

= 0

NPK

O

I

:

u

1

– u

3

+ u

5

= 0

O

II

:

u

2

– u

3

+ u

4

= 0

O

III

:

u

6

+ u

4

– u

5

= 0

PO ( prądy gałęziowe - napięcia gałęziowe ):

u

1

= R

1

i

1

– e

1

u

2

= R

2

i

2

u

d i

d t

3

3

= L

3

u

C

i d

t

4

4

4

0

1

=

∫

τ

u

5

= R

5

i

5

u

d i

d t

6

6

= L

6

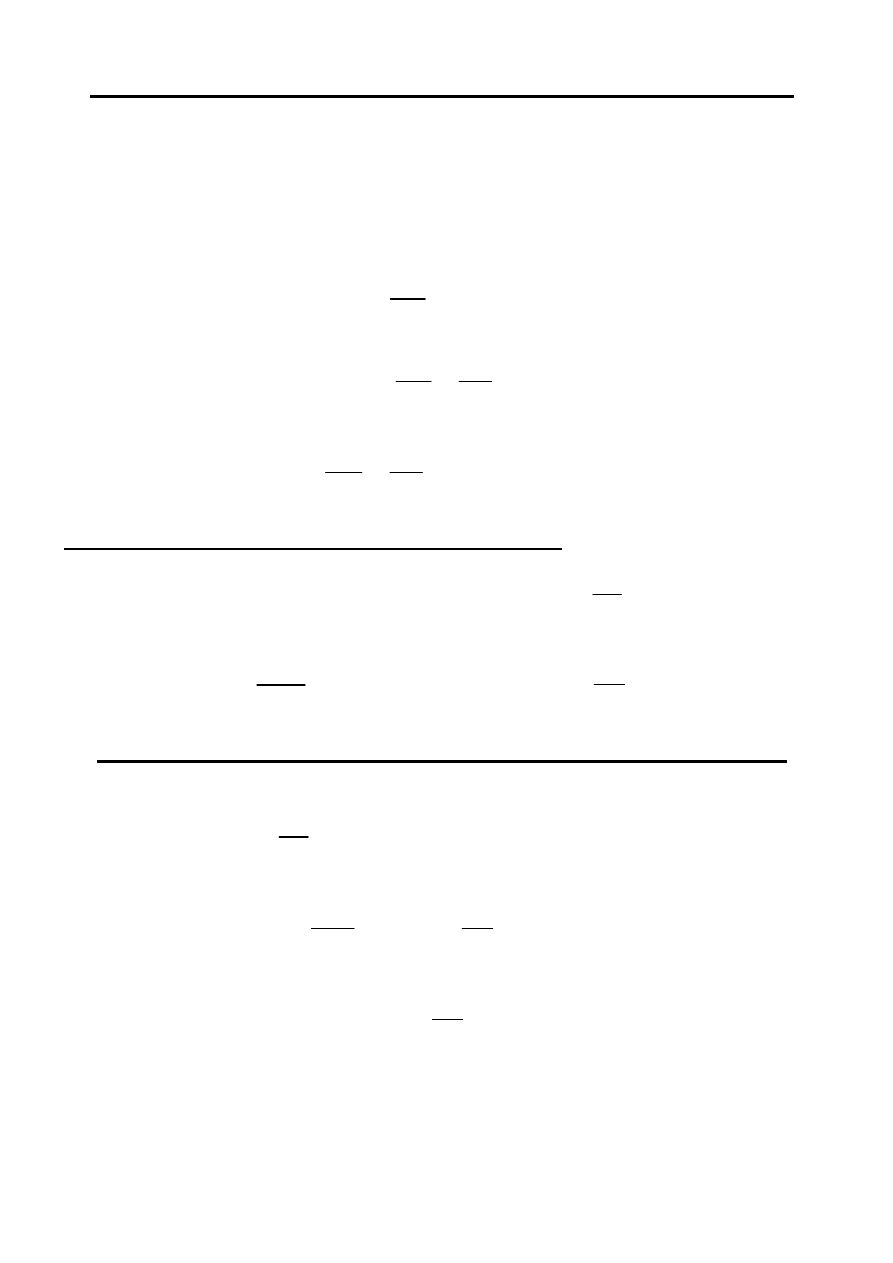
Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Równania różniczkowo–całkowe d

la prądów gałęziowych:

i

i

i

i

i

i

i

i

i

R i

L

di

dt

R i

e

R i

L

di

dt

C

i d

L

di

dt

C

i d

R i

t

t

3

1

2

4

2

6

5

1

6

1 1

3

3

5 5

1

2 2

3

3

4

4

0

6

6

4

4

0

5 5

0

0

0

1

0

1

0

+ + =

− − =

− + =

−

+

= +

−

+

=

+

−

=

⎧

⎨

⎪

⎪

⎪

⎪

⎪⎪

⎩

⎪

⎪

⎪

⎪

⎪

⎪

∫

∫

τ

τ

PO ( napięcia gałęziowe - prądy gałęziowe ):

i

G u

G e

1

1 1

1 1

=

+

i

2

= G

2

u

2

i

L

u d

t

3

3

3

0

1

=

∫

τ

i

d u

d t

4

4

= C

4

i

5

= G

5

u

5

i

L

u d

t

6

6

6

0

1

=

∫

τ

Równania różniczkowo–całkowe d

la napięć gałęziowych:

1

1

0

1

0

0

0

3

3

0

1 1

2 2

1 1

4

4

2 2

6

6

0

5 5

1 1

6

6

0

1 1

1

3

5

2

3

4

6

4

5

L

u d

G u

G u

G e

C

du

dt

G u

L

u d

G u

G u

L

u d

G e

u

u

u

u

u

u

u

u

u

t

t

t

τ

τ

τ

∫

∫

∫

+

+

= −

−

−

=

−

+

= +

− +

=

− +

=

+

−

=

⎧

⎨

⎪

⎪

⎪

⎪

⎪

⎪

⎩

⎪

⎪

⎪

⎪

⎪

⎪

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

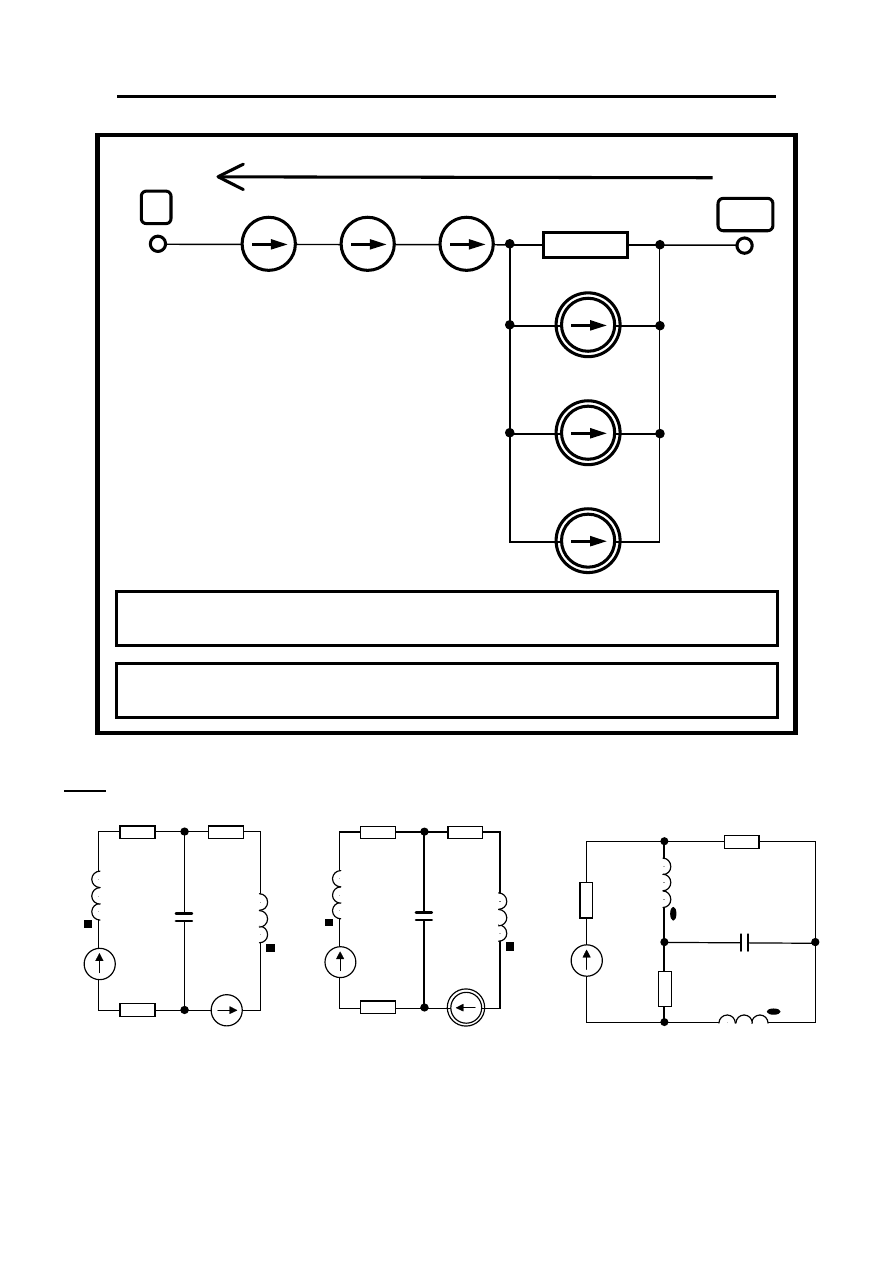
Uogólniona gałąź rezystancyjna ( konduktancyjna )

w

k

w

k+1

i

k

u

k

e

k

r⋅i

sn

R

k

(G

k

)

g⋅u

sp

α⋅i

sp

k⋅u

sn

j

k

u

k

= R

k

i

k

– [R

k

( j

k

+

αi

sp

+ gu

sp

) + (e

k

+ ku

sn

+ ri

sn

)]

i

k

= G

k

u

k

+ [( j

k

+

αi

sp

+ gu

sp

) + G

k

(e

k

+ ku

sn

+ ri

sn

)]

Zadanie Napisać równania różniczkowo-całkowe dla obwodów pokazanych na rysunkach

C

2

L

3

L

1

R

1

R

2

e

3

e

1

R

3

C

2

L

3

L

1

R

1

R

2

j

3

e

1

R

3

C

4

L

6

L

3

R

5

R

2

R

1

e

1

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

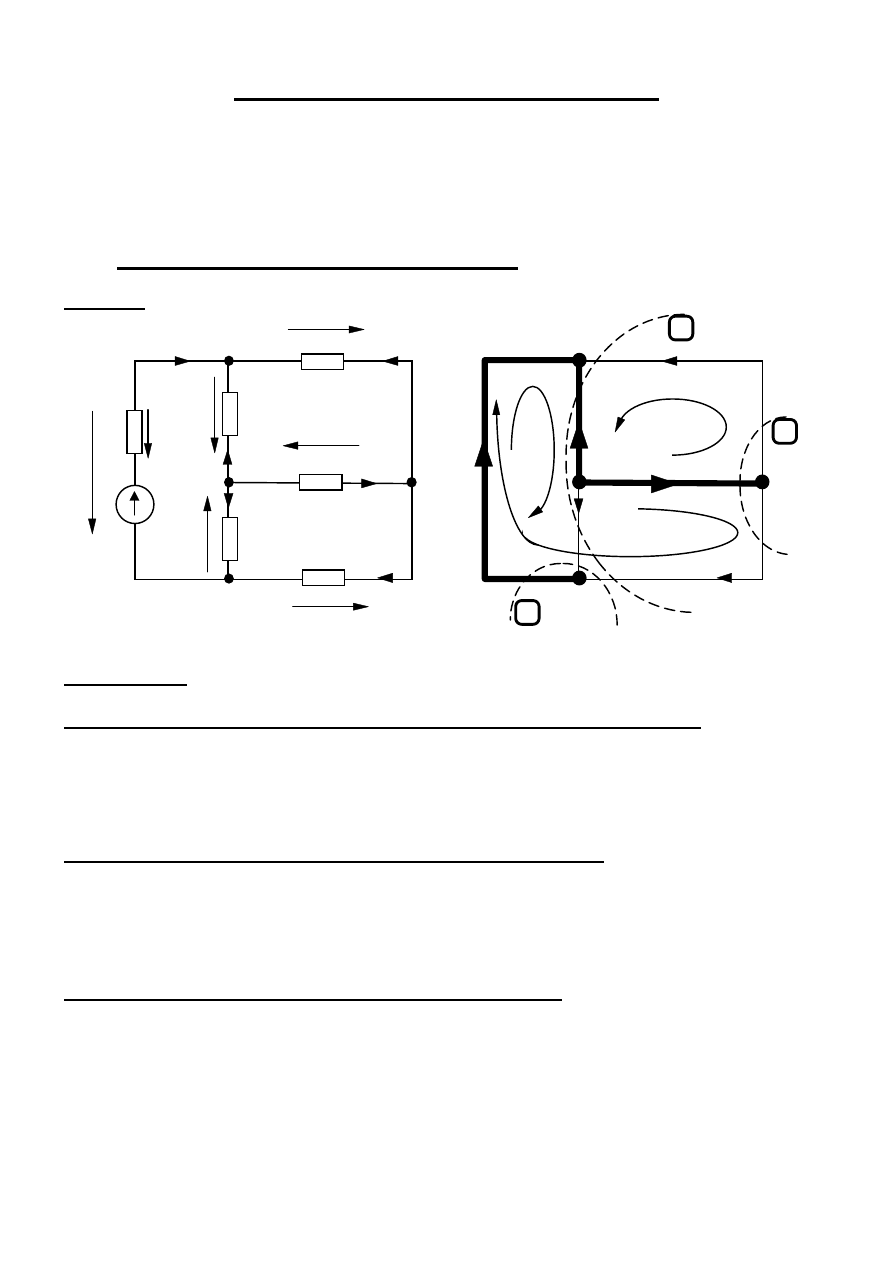
Metoda prądów strun ( MPS )

MPS oparta jest na spostrzeżeniu, że pozostawienie w obwodzie tylko drzewa unie-
możliwia przepływ prądu ( brak konturów ). Dodanie dowolnej (kolejnej) struny ge-
neruje oczko fundamentalne, które pozwala na przepływ w nim prądu dodanej stru-
ny. Z tego wynika, że znajomość prądów strun pozwala wyznaczyć pozostałe funkcje
obwodowe – w pełni rozwiązać obwód.

Liczba strun ( szukanych prądów ):

n = g – w + 1

Przykład Dla obwodu pokazanego na rysunku ułożyć równania MPS

R

4

R

6

R

3

R

5

R

2

u

3

u

2

u

4

u

6

u

1

R

1

e

1

i

5

i

3

i

3

i

6

i

4

i

4

i

2

i

1

i

1

i

5

i

6

i

2

B

C

A

III

II

I

u

5

g = 6;

w = 4;

n = g – w + 1 = 3 = L

RR

Prądy strun: { i

2

, i

5

, i

6

} - niewiadome

Z przekrojów fundamentalnych wyznaczamy prądy konarów:

Przekrój A:

i

3

= – i

2

– i

5

Przekrój B:

i

1

= + i

5

+ i

6

Przekrój C:

i

4

= + i

2

+ i

6

Piszemy równania NPK dla oczek fundamentalnych:

Oczko I:

u

1

– u

3

+ u

5

= 0

Oczko II:

u

4

– u

3

+ u

2

= 0

Oczko III:

u

1

– u

3

+ u

4

+

u

6

= 0

PO ( prądy gałęziowe - napięcia gałęziowe ):

u

1

= R

1

i

1

– e

1

= R

1

( + i

5

+ i

6

) – e

1

u

2

= R

2

i

2

=

R

2

i

2

u

3

= R

3

i

3

=

R

3

( – i

2

– i

5

)

u

4

= R

4

i

4

=

R

4

( + i

2

+ i

6

)

u

5

= R

5

i

5

= R

5

i

5

u

6

= R

6

i

6

=

R

6

i

6

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Równania MPS:

R

3

i

2

+ ( R

1

+ R

3

+ R

5

) i

5

+ R

1

i

6

= + e

1

( R

2

+ R

3

+ R

4

)

i

2

+ R

3

i

5

+ R

4

i

6

= 0

( R

3

+ R

4

)

i

2

+ ( R

1

+ R

3

)

i

5

+ ( R

1

+ R

4

+ R

6

)

i

6

=

+

e

1

Przykład Napisać równania różniczkowo-całkowe MPS

C

4

R

6

L

3

R

5

R

2

u

3

u

2

u

4

u

6

u

1

R

1

e

1

i

5

i

3

i

3

i

6

i

4

i

4

i

2

i

1

i

1

i

5

i

6

i

2

u

5

Z przekrojów fundamentalnych wyznaczamy prądy konarów:

Przekrój { 1, 5, 6 }:

i

1

= + i

5

+ i

6

Przekrój { 4, 3, 5 }:

i

4

= – i

3

– i

5

Przekrój { 2, 3, 5, 6 }:

i

2

= – i

3

– i

5

– i

6

Piszemy równania NPK dla oczek fundamentalnych:

Oczko { 3, 2, 4 }:

u

3

– u

2

– u

4

= 0

Oczko { 5, 1, 2, 4 }:

u

5

+ u

1

– u

2

– u

4

= 0

Oczko { 6, 1, 2 }:

u

6

+ u

1

– u

2

= 0

PO ( prądy gałęziowe - napięcia gałęziowe ):

u

1

= R

1

i

1

– e

1

= + R

1

( i

5

+ i

6

) – e

1

u

2

= R

2

i

2

= – R

2

( i

3

+ i

5

+ i

6

)

u

3

= f

3

(

i

3

)

=

L

d i

d t

3

3

u

4

= f

4

(

i

4

)

= –

(

)

1

4

3

5

0

C

i

i d

t

+

∫

τ

u

5

= R

5

i

5

= R

5

i

5

u

6

= R

6

i

6

=

R

6

i

6

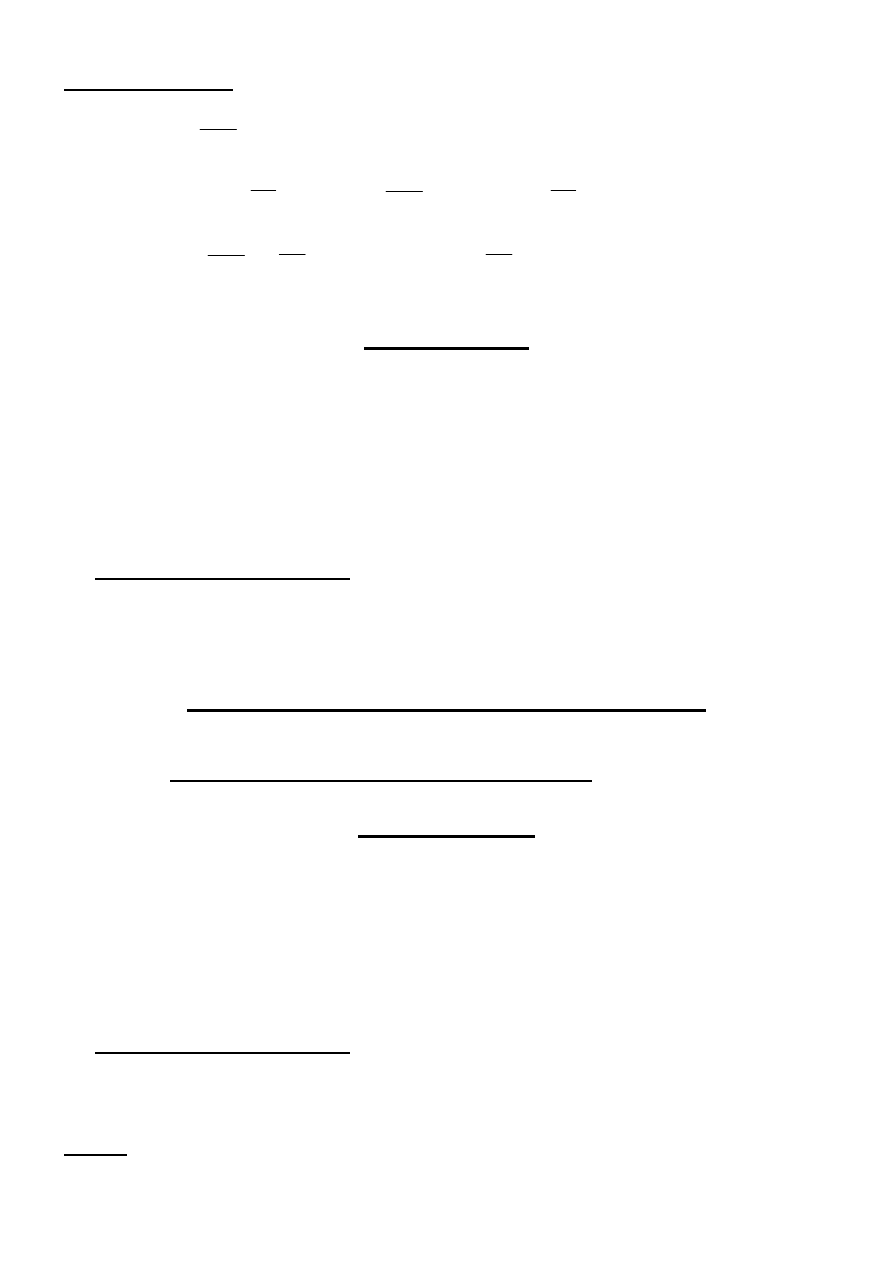
Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Równania MPS:

L

d i

d t

3

3

– ( R

1

+ R

5

)

i

5

– R

1

i

6

= – e

1

( R

2

i

3

+

1

4

3

0

C

i d

t

∫

τ

+

L

d i

d t

3

3

) + ( R

2

i

5

+

1

4

5

0

C

i d

t

∫

τ

) + R

2

i

6

= 0

(

L

d i

d t

3

3

+

1

4

3

0

C

i d

t

∫

τ

) – ( R

1

i

5

–

1

4

5

0

C

i d

t

∫

τ

) – (R

1

+ R

6

)

i

6

= – e

1

MPS – jak ?

1.

Wybieramy r = w – 1 konarów drzewa:

−

wszystkie źródła prądu umieścić w strunach;

−

maksymalną liczbę autonomicznych źródeł napięcia umieścić w konarach;

2.

Z przekrojów fundamentalnych w oparciu o PPK wyliczamy prądy konarów;

3.

Dla oczek fundamentalnych piszemy n = g – w + 1 równań w oparciu o NPK;

4.

Ustalmy związki u-i ( równania PO ) dla wszystkich gałęzi;

5.

Łączymy równania otrzymane w p. 2, 3 i 4 w n = g – w + 1 równań MPS;

Obwód jest już rozwiązany !!!

6.

Rozwiązujemy ze względu na prądy strun układ równań z p. 5;

7.

Wyliczamy prądy konarów i to co nas interesuje w analizowanym obwodzie.

Metoda napięć konarowych ( MNK )

MNK jest metodą dualną do metody MPS.

Liczba konarów (szukanych napięć ):

r = w – 1

MNK – jak ?

1.

Wybieramy r = w – 1 konarów drzewa:

−

wszystkie źródła napięcia umieszczamy w konarach;

−

maksymalną liczbę autonomicznych źródeł prądu umieszczamy w strunach;

2.

Z oczek fundamentalnych w oparciu o NPK wyliczamy napięcia strun;

3.

Dla przekrojów fundamentalnych piszemy r = w – 1 równań w oparciu o PPK;

4.

Ustalmy związki u-i ( równania PO ) dla wszystkich gałęzi;

5.

Łączymy równania otrzymane w p. 2, 3 i 4 w r = w – 1 równań MNK;

Obwód jest już rozwiązany !!!

6.

Rozwiązujemy ze względu na napięcia konarowe układ równań z p. 5;

7.

Wyliczamy napięcia strun i to co nas interesuje w analizowanym obwodzie.

Zadanie Napisać równania MNK dla przykładów związanych z MPS