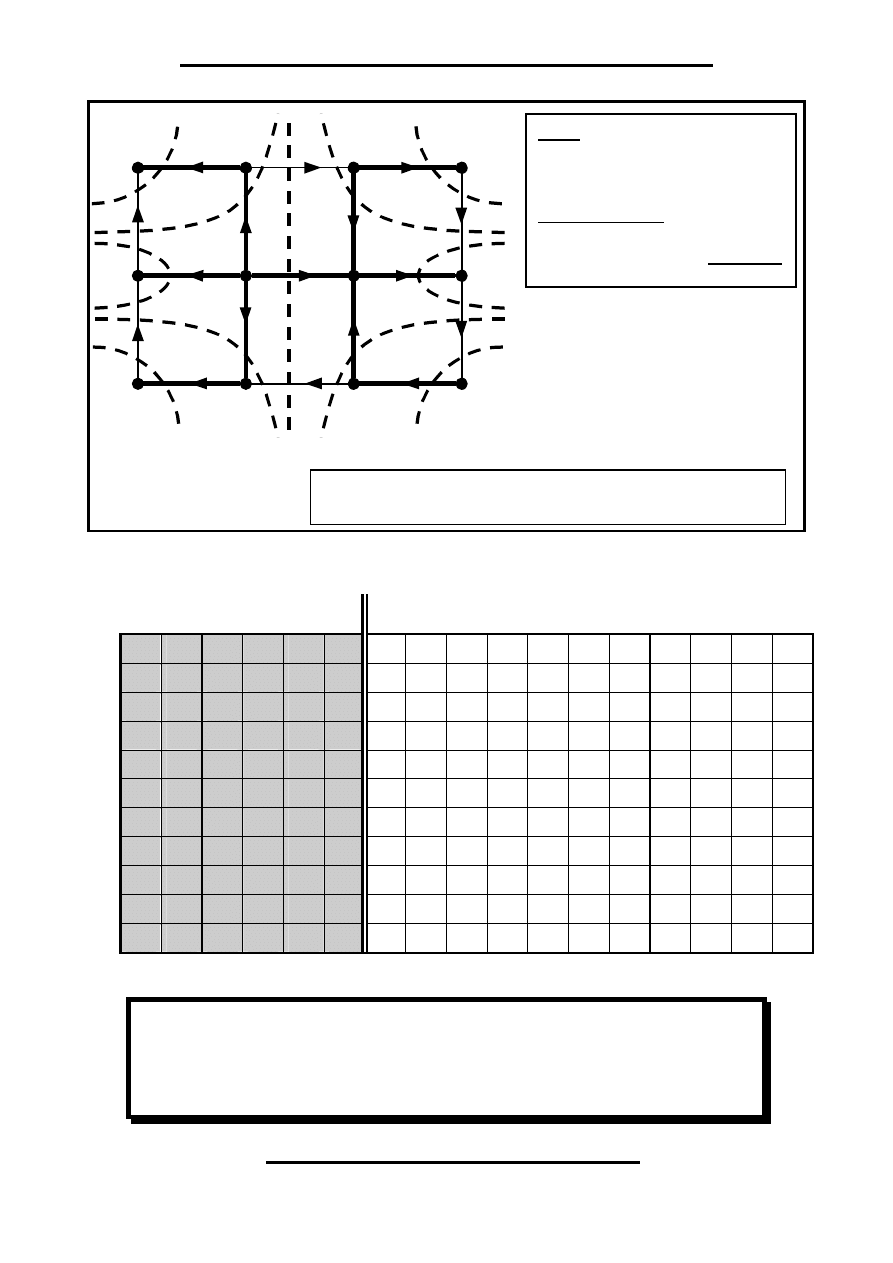
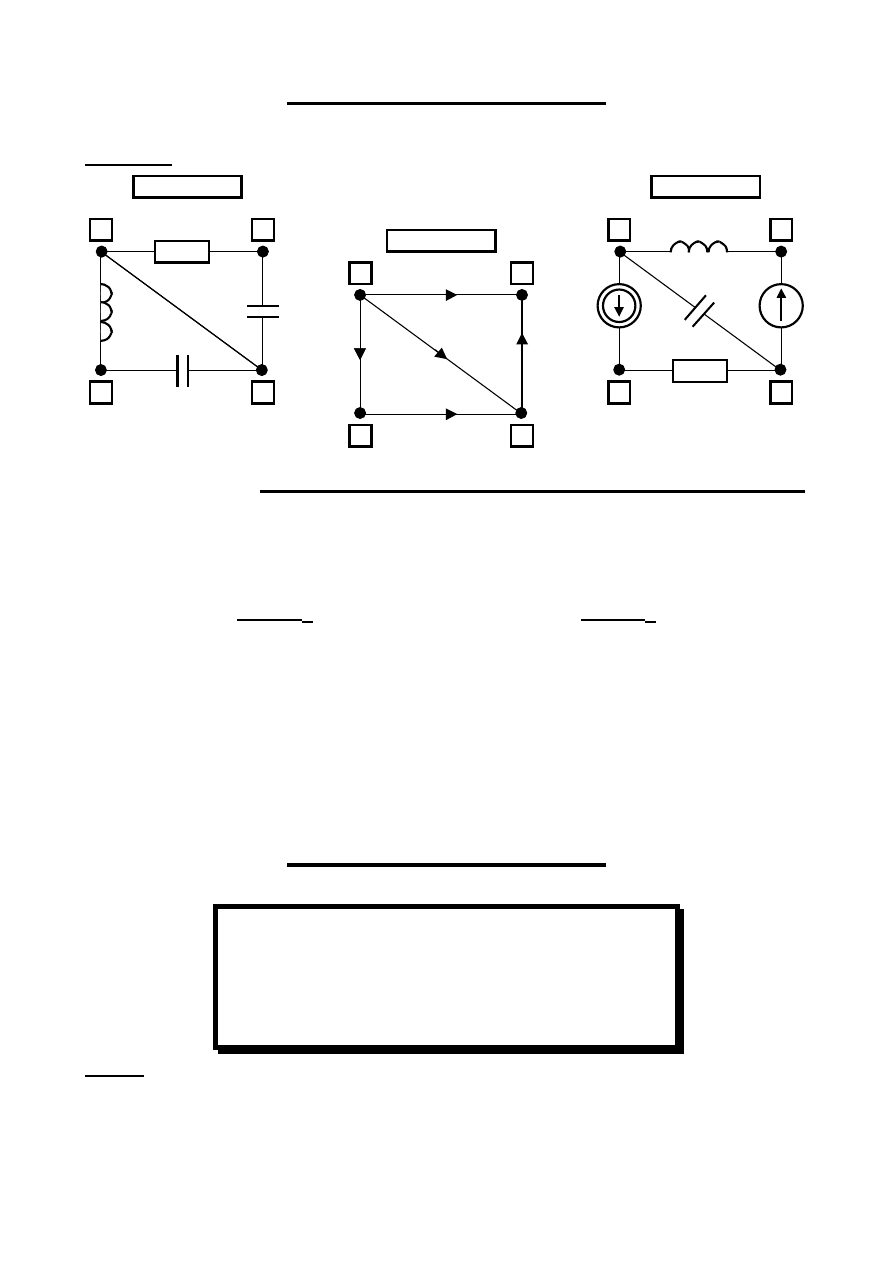
Macierzowy zapis równań równowagi
Przekroje fundamentalne – Macierz Incydencji Węzłowej
1
2
3
4
5
6
a
b
c
d
f
e
g
j
k
h
i
a
b
b
d
e
f
g
h
i
j
k
c
Graf:
g = 17
- gałęzie
w = 12
- węzły
Fundamentalne:
n = g – w +1 = 6
- oczka
r = w – 1
= 11 - przekroje
Drzewo ( konary ):
T = { a, b, c, d, e, f, g, h, i, j, k }
Antydrzewo ( struny ):
Z = { 1, 2, 3, 4, 5, 6 }
Gałęzie: g
Struny: n = g – w + 1
Konary: r = w – 1
1 2 3 4 5 6 a b c d e f g h i j k
R
a
+1
+1
R
b
+1 –1
+1
R
c
–1
+1
+1
R
d
+1
–1
+1
R
e
–1 +1
+1
R
f
–1
+1
R
g
+1
–1
+1
R
h
–1 +1
+1
R
i
+1 –1
+1
R
j
–1
+1
R
k
–1
+1
(
)
(
)
( )
[
]
r
r
n
r
g
r
×
×
×
=
1
|
Q
A
gdzie:
Q
(r
×n)
–
macierz incydencji węzłowej.
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
PPK:
(
)
(
)
(
1
1
g
0
I
A
×
×
×
)
=
⋅
r
g
g
r
(
) ( )
[
]
( )
( )
( )
1
1
k
1
s
0
I
I
1
Q
×
×
×
×
×
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
n
r
n
r
r
n
r
(
) ( )
( )
)
1
(
1
k
1
s
0
I
I
Q
×
×
×
×
=
+
n
r
n
n
r
( )
(
)
(
1
s
1
k
I
Q
I
×
×
×
)
⋅
−
=
n
n
r
r
(
)
( )
( )
(
)
(
)
(
1
s
1
k
1
s
1
g
I
Q
1
I
I
I
×
×
×
×
×
×
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
n
n
r
n
n
r
n
g
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
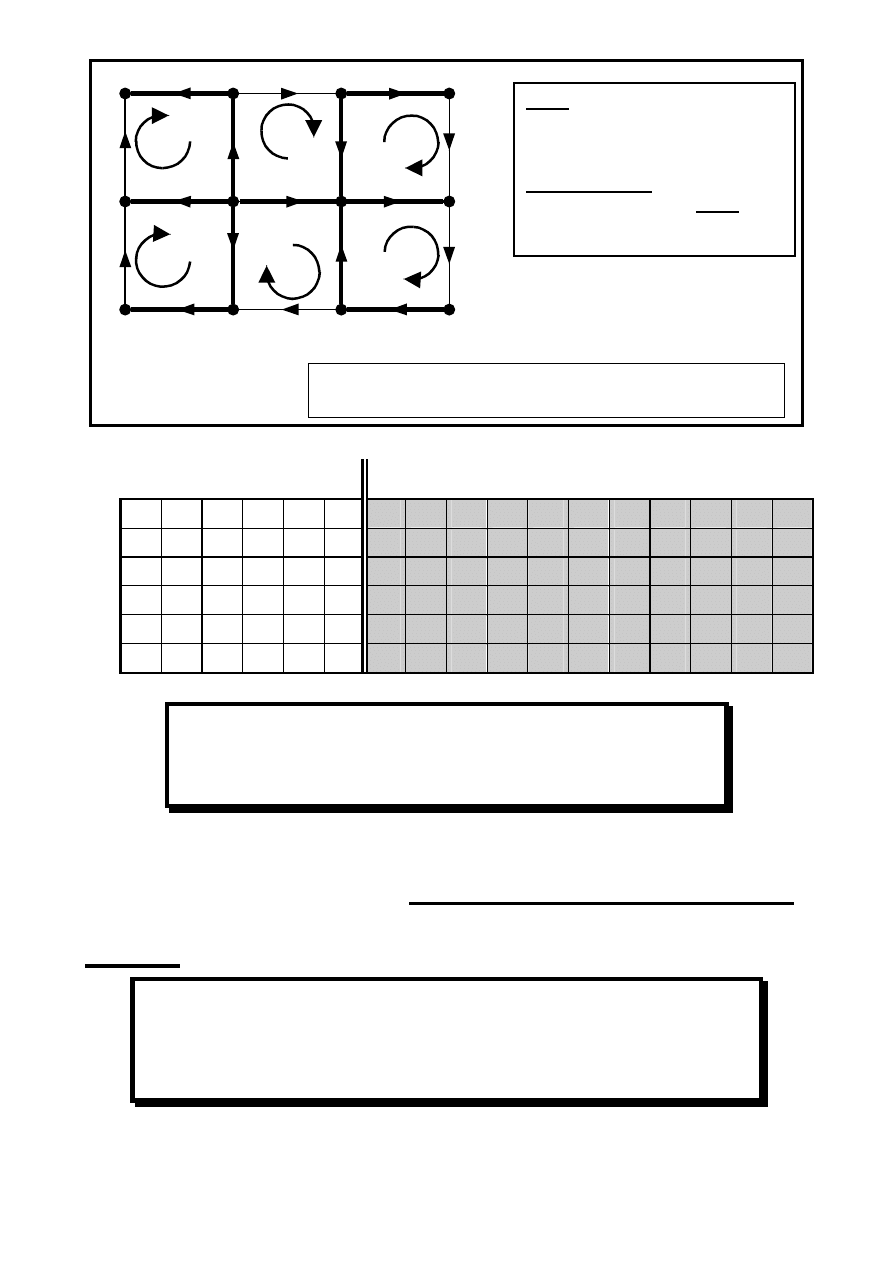
Oczka Fundamentalne – Macierz Incydencji Oczkowej
III
I
II
VI
IV
V
1
2
3
4
5
6
a
b
c
d
f
e
g
j
k
h
i
Graf:
g = 17
- gałęzie
w = 12
- węzły
Fundamentalne:
n = g – w +1 = 6
- oczka
r = w – 1
= 11 - przekroje
Drzewo ( konary ):
T = { a, b, c, d, e, f, g, h, i, j, k }
Antydrzewo ( struny ):
Z = { 1, 2, 3, 4, 5, 6 }
Gałęzie: g
Struny: n = g – w + 1
Konary: r = w – 1
1 2 3 4 5 6 a b c d e f g h i j k
O
I
+1
–1 –1 +1
O
II
+1
+1
–1 +1
O
III
+1
–1 +1 –1
O
IV
+1
–1
+1
+1
O
V
+1
+1
–1 –1
O
VI
+1
+1
+1
+1
(
)
(
)
(
)
[
]
r
n
n
n
g
n
×
×
×
=
P
|
1
B
gdzie:
P
(n
×r)
= –
Q
T
– macierz incydencji oczkowej
NPK:
)
1
(
)
1
(
g
)
(
0
U
B
×
×
×
=
⋅
n
g
g
n
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
(
)
( )
( )
( )
1
1
k
1
s
0
U
U
B
×
×
×
×
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
n
r
n
g
n
[
]
)
1
(
)
1
(
k
)
1
(
s
)
(
)
(
0
U
U
P
1
×
×
×
×
×
=
⎥
⎦
⎤
⎢
⎣
⎡
⋅
n
r
n
r
n
n
n
)
1
(
)
1
(
k
)
(
)
1
(
s
0
U
P
U
×
×
×
×
=
+
n
r
r
n
n
)
1
(
k
)
(
)
1
(
s
U
P
U
×
×
×
⋅
−
=
r
r
n
n
( )
)
1
(
k
)
(
T
)
1
(
s
U
Q
U
×
×
×
⋅
=
r
r
n
n
(
)
)
1
(
k
)
(
)
(
)
1
(
k
)
1
(
s
1
g
U
1
P
U
U
U
×
×
×
×
×
×
⋅
⎥
⎦
⎤
⎢
⎣
⎡−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
r
r
r
r
n
r
n
g
(
)
( )
)
1
(
k
)
(
)
(
T
1
g
U
1
Q
U
×
×
×
×
⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
r
r
r
r
n
g
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
Energia całkowita i moc chwilowa w sieci SLS
Moc chwilowa k-tej gałęzi:
( )
)
(
)
(
t
i
t
u
t
p
k
k
k
⋅
=
Moc chwilowa całej sieci:
( )
g
T
g
g
T
g
1
U
I
I
U
)
(
)
(
⋅
=
⋅
=
=
=
∑
=
g
k
k
t
p
t
d
t
w
d
t
P
gdzie:
∫
=
t
t
d
P
t
w
0
)
(
)
(
τ
τ
energia elektryczna przetworzona przez sieć w przedziale czasu < t
0
, t >.
Zasada zachowania energii w sieci SLS
const
)
(
=
∀ t
w
t
Zasada Tellegena
Jeśli w sieci SLS funkcja w(t) jest klasy C
1
, to:
( )
0
U
I
I
U
)
(
)
(
g
T
g
g
T
g
1
=
=
=
=
=
∀
∑
=
g
k
k
t
t
p
t
d
t
w
d
t
P
Dowód:
[
]
[
]
0
U
1
Q
Q
1
I
U
1
Q
I
Q
1
U
I
0
I
Q
1
1
Q
U
I
Q
1
U
1
Q
I
U
k
T
T
s
k
T
T
s
g
T
g
s
k
s
T
k
T
g
T
g
=
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
⋅
−
⋅
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⋅
=
⋅
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
−
⋅
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
⋅
qed.
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
Twierdzenie Tellegena
Niech
s
ieci S
A
i S
B
mają identyczną strukturę
( topologię )
.
Przykład
Sieć S
A
A
B
C
D
A
B
C
D
Sieć S
B
A
B
C
D
Graf S
A
i S
B
Oznacza to, że macierze incydencji węzłowej sieci są identyczne:
Q
A
≡ Q
B
Także macierze incydencji oczkowej sieci są identyczne:
P
A
= (–
Q
A
)
T
≡ (–
Q
B
)
T
= P
B
.
Sieć S
A
Sieć S
B
s(B)
g(B)
s(A)
g(A)
k(B)
T
g(B)
k(A)
T
g(A)
I
Q
1
I
;
I
Q
1
I
U
1
Q
U
;
U
1
Q
U
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
Twierdzenie Tellegena
Jeśli
s
ieci S
A
i S
B
mają identyczną strukturę
( topologię ), to:
(
)
( )
(
)
( )
;
0
U
I
I
U
;
0
U
I
I
U
g(B)
T
g(A)
g(A)
T
g(B)
g(A)
T
g(B)
g(B)
T
g(A)
=
⋅
=
⋅
=
⋅
=
⋅
Dowód: Jak uprzednio !
Twierdzenie Tellegena jest powszechnie stosowane przy obliczaniu
wrażliwości obwodu na zmiany jego parametrów.
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
Kilka słów o wrażliwości funkcji obwodowych
na zmiany parametrów obwodów SLS
Wrażliwość bezwzględna funkcji obwodowej f:
k
f
x
x
X
f
ametrSieci
WybranyPar
ieci
ParametryS
f
S
k
∂
∂
=
∂
∂
=
)
(
)
(
Bezwzględna tolerancja funkcji obwodowej f:
(
)
∑
∑
=
=
∆
⋅
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
∆
⋅
∂
∂
=
∆
N
k
k
f
x
N
k
k
k
x
S
x
x
X
f
X
f
k
1
1
)
(
)
(
)
(
)
(
)
(
0
X
f
X
f
X
f
∆
+
=
Przykład
Wyznaczyć wrażliwości napięcia wyjściowego U
0
rezystancyjnego
dzielnika
napięcia na zmiany oporu jego rezystorów R
1
i R
2
.
E
R
1
R
2
U
0
E
R
R
R
U
2
1
2
0
+
=
Parametry: x
1
= R
1
, x
2
= R
2
, x
3
= E
Bezpośrednie wyliczenie wrażliwości
(
)
(
)
⎪
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎪
⎨
⎧
⎥⎦
⎤
⎢⎣
⎡
+
+
=
∂
∂
=
⎥⎦
⎤
⎢⎣
⎡
Ω
+
+
=
∂
∂
=
⎥⎦
⎤
⎢⎣
⎡
Ω
+
−
=
∂
∂
=
V
V
V
V
2
1
2
0
2
1
2
1
2
0
2
2
1
2
1
0
0
0
2
0
1
R
R
R
E
U
S
E
R
x
R
R
U
S
E
R
x
R
R
U
S
U
E
U
R
U
R
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
x
1
= R
1
0
1
U
R
S
1
R
E
+
x
2
= R
2
0
2
U
R
S
2
1
2
R
R
R
+
+
x
3
= E
0
U
E
S
2
R
E
−
R
1
= 100 k
Ω; R
2
= 50 k
Ω; E= 12 V: U
0
= 4 V
(
)
(
)
⎪
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎪
⎨
⎧
⎥⎦
⎤
⎢⎣
⎡
+
=
⋅
+
⋅
⋅
+
=
⎥⎦
⎤
⎢⎣
⎡
Ω
+
=
⋅
+
⋅
⋅
+
=
⎥⎦
⎤
⎢⎣
⎡
Ω
−
=
⋅
+
⋅
⋅
−
=
V
V
3
1
10
50
10
100
10
50
mV
75
4
12
10
100
10
50
10
100
mV
75
2
12
10
50
10
100
10
50
3
3
3
2
3
3
3
2
3
3
3
0
0
2
0
1
U
E
U
R
U
R
S
S
S
Tolerancja napięcia wyjściowego dzielnika:
E
S
R
S
R
S
U
0
0
2
0
1
U
E
2
U
R
1
U
R
0
∆
⋅
+
∆
⋅
+
∆
⋅
=
∆
∆R
1
=
± 10 kΩ ( 10 % )
∆R
2
=
± 5 kΩ ( 10 % )
∆E=
± 120 mV ( 1 % )
(
)
( )
(
)
[ ]
[ ]
[ ]
V
)
3
(
57
,
0
V
75
43
75
00
,
3
20
20
V
10
120
3
1
5
75
4
10
75
2
3
0
±
=
±
=
±
±
=
=
⋅
±
+
±
+
±
−
=
∆
−
m
U
U
0
= 4
± 0,57(3) V = < 3,42(6), 4,57(3) > V
∆R
2
=
± 2,5 kΩ ( 5 % )
(
)
(
)
(
)
[ ]
[ ]
[ ]
V
44
,
0
V
75
33
75
00
,
3
20
10
V
10
120
3
1
5
,
2
75
4
10
75
2
3
0
±
=
±
=
±
±
=
=
⋅
±
+
±
+
±
−
=
∆
−
m
U
U
0
= 4
± 0,43 V = < 3,57, 4,43 >
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
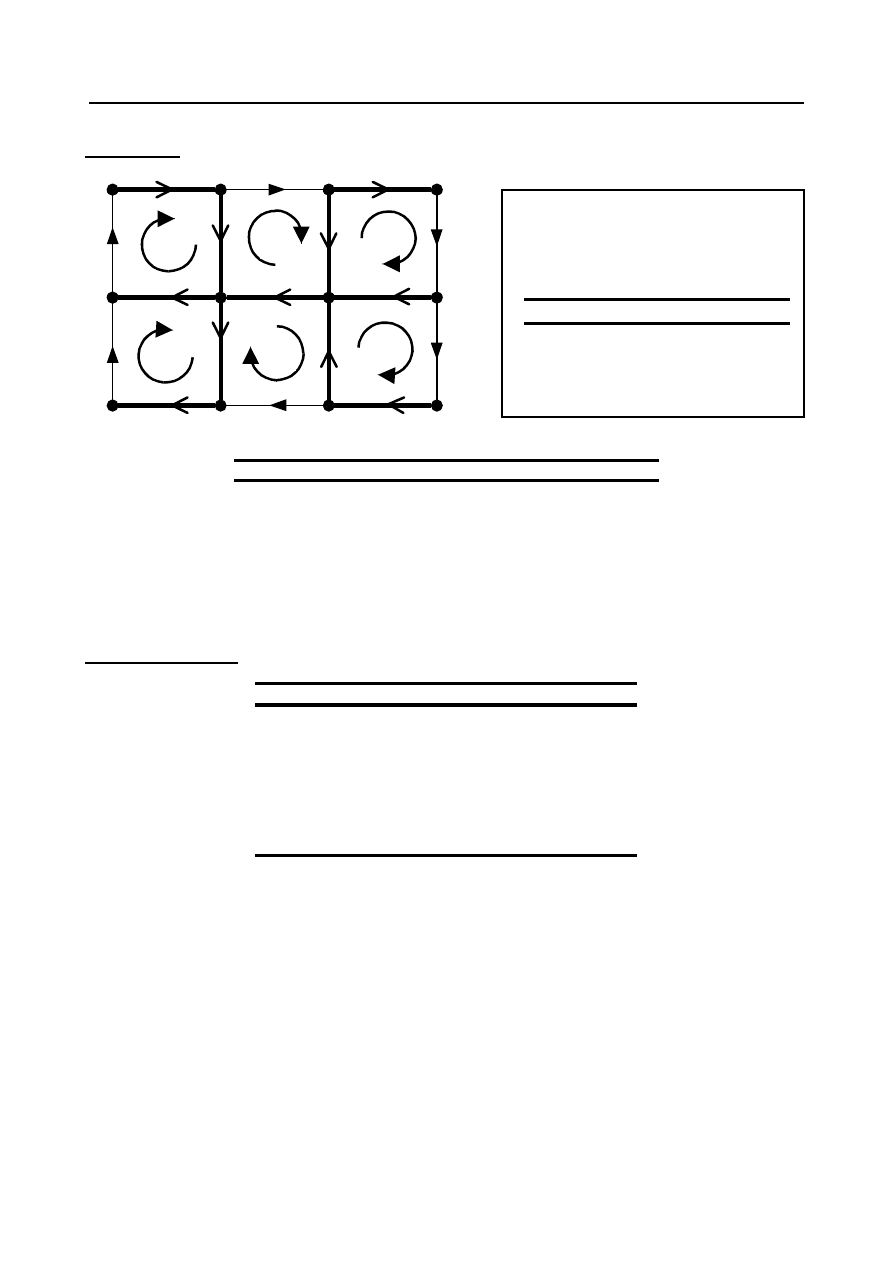
Metoda prądów oczkowych ( MPO ) –
„Metoda Maxwella”
Przykład:
III
I
II
VI
IV
V
1
2
3
4
5
6
a
b
c
d
f
e
g
j
k
h
i
g = 17;
w = 12;
L
N
= 2
⋅g = 34;
Liczby równań różnych metod
Metoda
Liczba równań
MPK
g
= 17
MPS
g – w + 1 = 6
MNK
w – 1
= 11
Prąd
Oczko
Gałęzie Oczkowy
Strunowy
O
I
= { 1; a, b, c } :
i
I
= i
1
O
II
= { 2; b, e, d } :
i
II
= i
2
O
III
= { 3; e, f,
g } :
i
III
= i
3
O
IV
= { 4; c, h,
j
} :
i
IV
= i
4
O
V
= { 5; d, h, i } :
i
V
= i
5
O
VI
= { 6; g, i,
k
} :
i
VI
= i
6
Prądy gałęziowe:
Prąd
Gałąź Gałęziowy Oczkowy
1
i
1g
= i
I
2
i
2g
= i
II
3
i
3g
= i
III
4
i
4g
= i
IV
5
i
5g
= i
V
6
i
6g
= i
VI
a
i
a
= i
I
b
i
b
= i
I
– i
II
c
i
c
= i
I
– i
IV
d
i
d
= i
II
– i
V
e
i
e
= i
II
– i
III
f
i
f
= i
III
g
i
g
= i
III
– i
IV
h
i
h
= i
IV
– i
V
i
i
i
= i
VI
– i
V
j
i
j
= i
IV
k
i
k
= i
VI
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
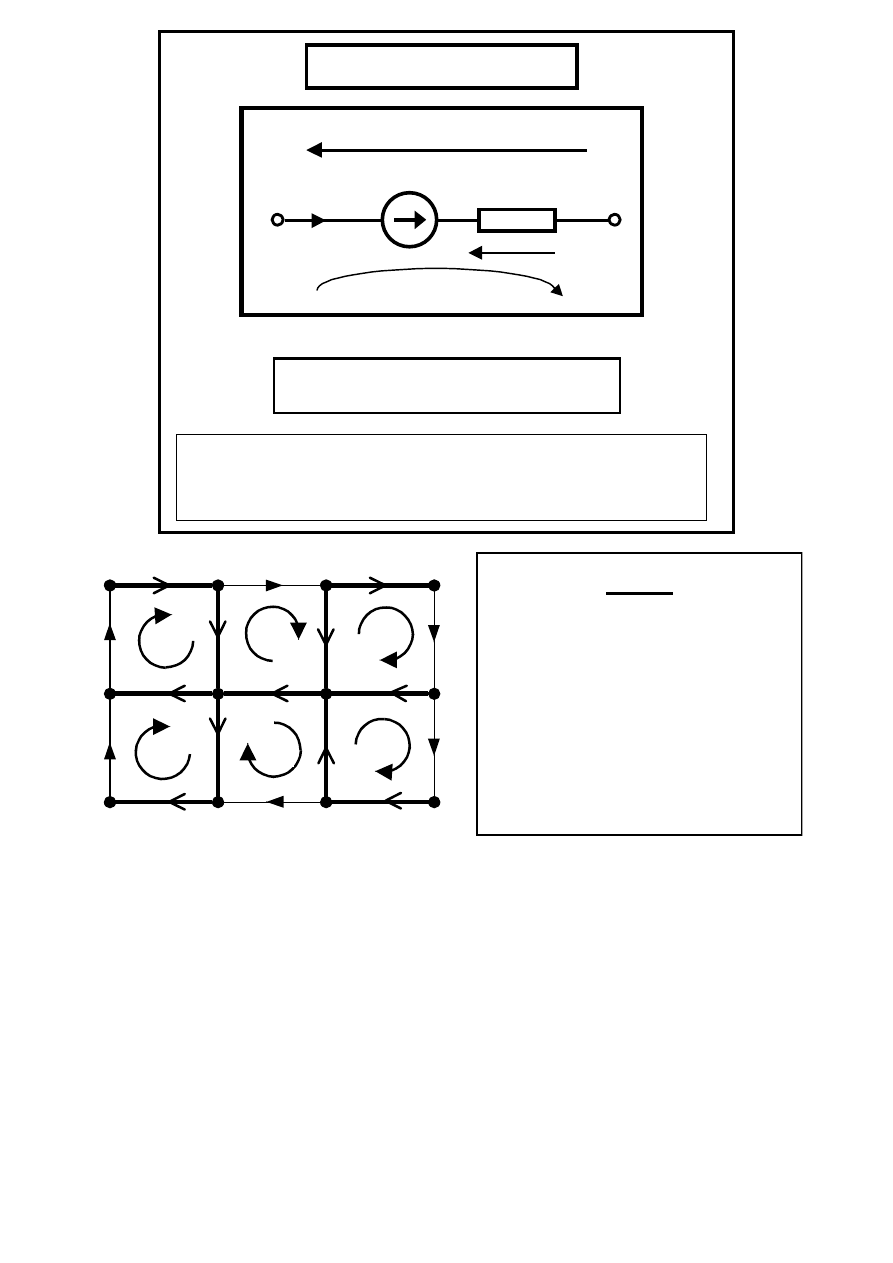
e
g
R
g
i
g
u
g
Postać napięciowa gałęzi
u
g
= R
g
⋅i
g
– e
g
e
g
= (
∑e + R
g
⋅∑j
g
) + (
∑[ri
s
]
g
+ R
g
⋅∑[αi
s
]
g
)
e
g
= e
autonomiczne
+ e
sterowane
O
n
R
g
i
g
III
I
II
VI
IV
V
1
2
3
4
5
6
a
b
c
d
f
e
g
j
k
h
i
NPK
O
I
:
u
1
+ u
a
+ u
b
+ u
c
= 0
O
II
:
u
2
+ u
e
+ u
d
– u
b
= 0
O
III
:
u
3
+ u
g
– u
e
+ u
f
= 0
O
IV
:
u
4
– u
c
+ u
h
+ u
j
= 0
O
V
:
u
5
– u
h
– u
d
– u
i
= 0
O
VI
:
u
6
+ u
k
+ u
i
– u
g
= 0
u
1
= R
1
I
I
–
(
∑e
1
+ R
1
⋅∑j
1
) – (
∑[ri
s
]
1
+ R
1
⋅∑[αi
s
]
1
)
u
2
= R
2
I
II
–
(
∑e
2
+ R
2
⋅∑j
2
) – (
∑[ri
s
]
2
+ R
2
⋅∑[αi
s
]
2
)
u
3
= R
3
I
III
–
(
∑e
3
+ R
3
⋅∑j
3
) – (
∑[ri
s
]
3
+ R
3
⋅∑[αi
s
]
3
)
u
4
= R
4
I
IV
–
(
∑e
4
+ R
4
⋅∑j
4
) – (
∑[ri
s
]
4
+ R
4
⋅∑[αi
s
]
4
)
u
5
= R
5
I
V
–
(
∑e
5
+ R
5
⋅∑j
5
) – (
∑[ri
s
]
5
+ R
5
⋅∑[αi
s
]
5
)
u
6
= R
6
I
VI
–
(
∑e
6
+ R
6
⋅∑j
6
) – (
∑[ri
s
]
6
+ R
6
⋅∑[αi
s
]
6
)
u
a
= R
a
I
I
–
(
∑e
a
+ R
a
⋅∑j
a
) – (
∑[ri
s
]
a
+ R
a
⋅∑[αi
s
]
a
)
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE

u
b
= R
b
(I
I
– I
II
)
–
(
∑e
b
+ R
b
⋅∑j
b
) – (
∑[ri
s
]
b
+ R
b
⋅∑[αi
s
]
b
)
u
c
= R
c
(I
I
– I
IV
)
–
(
∑e
c
+ R
c
⋅∑j
c
) – (
∑[ri
s
]
c
+ R
c
⋅∑[αi
s
]
c
)
u
d
= R
d
(I
II
– I
V
) –
(
∑e
d
+ R
d
⋅∑j
d
) – (
∑[ri
s
]
d
+ R
d
⋅∑[αi
s
]
d
)
u
e
= R
e
(I
II
– I
III
) –
(
∑e
e
+ R
e
⋅∑j
e
) – (
∑[ri
s
]
e
+ R
e
⋅∑[αi
s
]
e
)
u
f
= R
f
I
III
–
(
∑e
f
+ R
f
⋅∑j
f
) – (
∑[ri
s
]
f
+ R
f
⋅∑[αi
s
]
f
)
u
g
= R
g
(I
III
– I
IV
) –
(
∑e
g
+ R
g
⋅∑j
g
) – (
∑[ri
s
]
g
+ R
g
⋅∑[αi
s
]
g
)
u
h
= R
h
(I
IV
– I
V
) –
(
∑e
h
+ R
h
⋅∑j
h
) – (
∑[ri
s
]
h
+ R
h
⋅∑[αi
s
]
h
)
u
i
= R
i
(I
VI
– I
V
)
–
(
∑e
i
+ R
i
⋅∑j
i
) – (
∑[ri
s
]
i
+ R
i
⋅∑[αi
s
]
i
)
u
j
= R
j
I
IV
–
(
∑e
j
+ R
j
⋅∑j
j
) – (
∑[ri
s
]
j
+ R
j
⋅∑[αi
s
]
j
)
u
k
= R
k
I
VI
–
(
∑e
k
+ R
k
⋅∑j
k
) – (
∑[ri
s
]
k
+ R
k
⋅∑[αi
s
]
k
)
Podstawiając do NPK:
O
I
:
u
1
+ u
a
+ u
b
+ u
c
= 0
R
1
I
I
–
(
∑e
1
+ R
1
⋅∑j
1
) +
(
∑[ri
s
]
1
+ R
1
⋅∑[αi
s
]
1
) +
+
R
a
I
I
–
(
∑e
a
+ R
a
⋅∑j
a
) + (
∑[ri
s
]
a
+ R
a
⋅∑[αi
s
]
a
) +
+
R
b
(I
I
– I
II
) –
(
∑e
b
+ R
b
⋅∑j
b
) – (
∑[ri
s
]
b
+ R
b
⋅∑[αi
s
]
b
) +
+
R
c
(I
I
– I
IV
) –
(
∑e
c
+ R
c
⋅∑j
c
) – (
∑[ri
s
]
c
+ R
c
⋅∑[αi
s
]
c
) = 0
i grupując prdy oczkowe:
( R
1
+ R
a
+
R
b
+
R
c
)
I
I
–
R
b
I
II
–
R
c
I
IV
+
– { (
∑[ri
s
]
1
+ R
1
⋅∑[αi
s
]
1
) +
(
∑[ri
s
]
a
+ R
a
⋅∑[αi
s
]
a
) +
(
∑[ri
s
]
b
+ R
b
⋅∑[αi
s
]
b
) +
(
∑[ri
s
]
c
+ R
c
⋅∑[αi
s
]
c
) }
=
=
(
∑e
1
+
∑e
a
+
∑e
b
+
∑e
c
) + ( R
1
⋅∑j
1
+ R
a
⋅∑j
a
+ R
b
⋅∑j
b
+
R
c
⋅∑j
c
)
……………… itd.
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
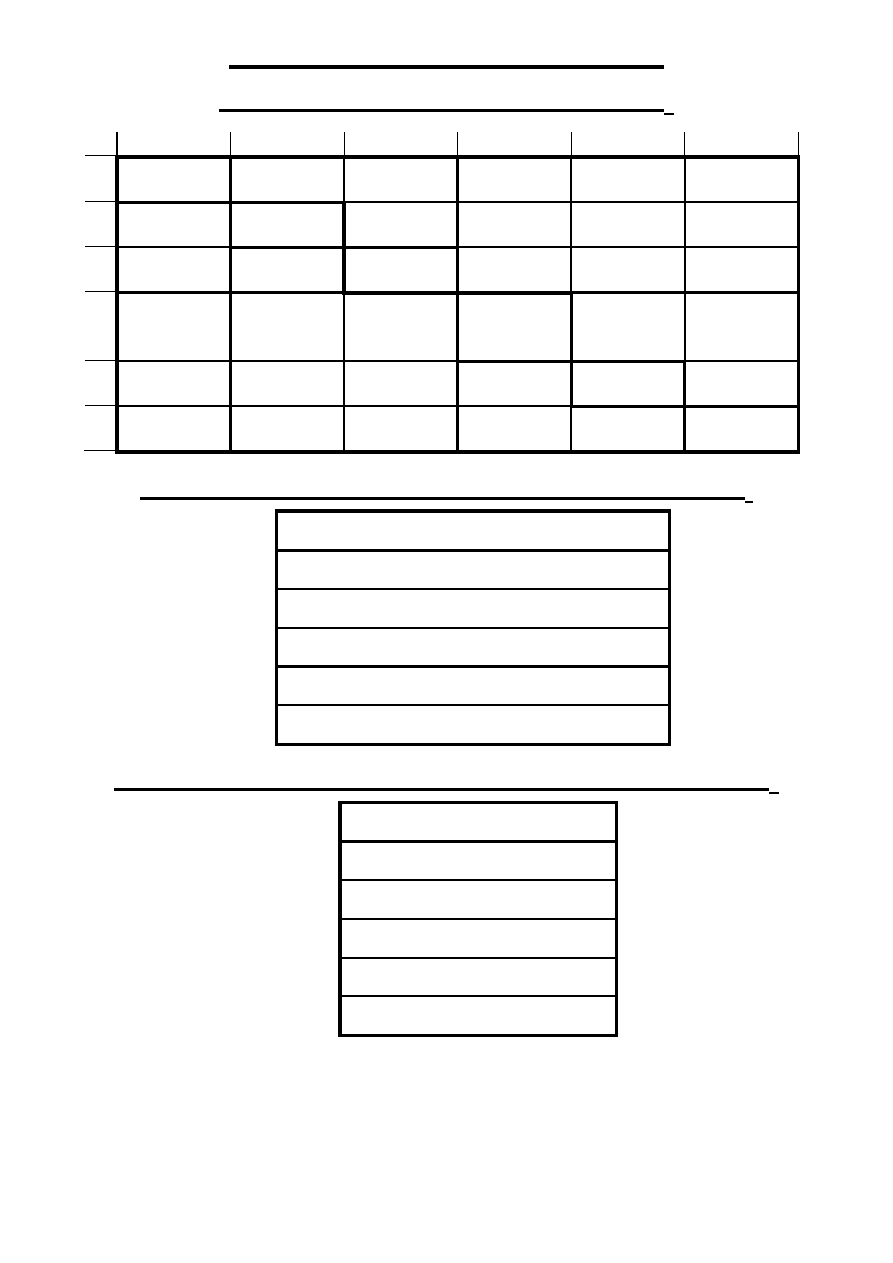
MPO w zapisie macierzowym
Macierz Rezystancji Oczkowych R
o
O
I
O
II
O
III
O
IV
O
V
O
VI
O
I
+
(
∑R)
O I/I
– R
O I/II
–
R
O I/III
–
R
O I/IV
–
R
O I/V
–
R
O I/VI
O
II
– R
O II/I
+
(
∑R)
O II/II
– R
O II/III
–
R
O II/IV
–
R
O II/V
–
R
O II/VI
O
III
– R
O III/I
–
R
O III/II
+
(
∑R)
O III/III
– R
O III/IV
–
R
O III/V
–
R
O III/VI
O
IV
– R
O IV/I
–
R
O IV/II
–
R
O IV/III
+
(
∑R)
O IV/
IV
– R
O IV/V
–
R
O IV/VI
O
V
– R
O V/I
–
R
O V/II
–
R
O V/III
–
R
O V/IV
+
(
∑R)
O V/V
– R
O V/VI
O
VI
– R
O VI/I
–
R
O VI/II
–
R
O VI/III
–
R
O VI/IV
–
R
O VI/V
+
(
∑R)
O VI/VI
Wektor Sterowanych Wymuszeń Oczkowych E
s
(
∑[ri
s
]
g
)
O I
+ (R
g
⋅∑[αi
s
]
g
)
O I
(
∑[ri
s
]
g
)
O II
+ (R
g
⋅∑[αi
s
]
g
)
O II
(
∑[ri
s
]
g
)
O III
+ (R
g
⋅∑[αi
s
]
g
)
O III
(
∑[ri
s
]
g
)
O IV
+ (R
g
⋅∑[αi
s
]
g
)
O IV
(
∑[ri
s
]
g
)
O V
+ (R
g
⋅∑[αi
s
]
g
)
O V
(
∑[ri
s
]
g
)
O VI
+ (R
g
⋅∑[αi
s
]
g
)
O VI
Wektor Autonomicznych Wymuszeń Oczkowych E
o
+
(
∑e)
O I
+ (
∑Rj)
O I
+
(
∑e)
O II
+ (
∑Rj)
O II
+
(
∑e)
O III
+ (
∑Rj)
O III
+
(
∑e)
O IV
+ (
∑Rj)
O IV
+
(
∑e)
O V
+ (
∑Rj)
O V
+
(
∑e)
O VI
+ (
∑Rj)
O VI
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
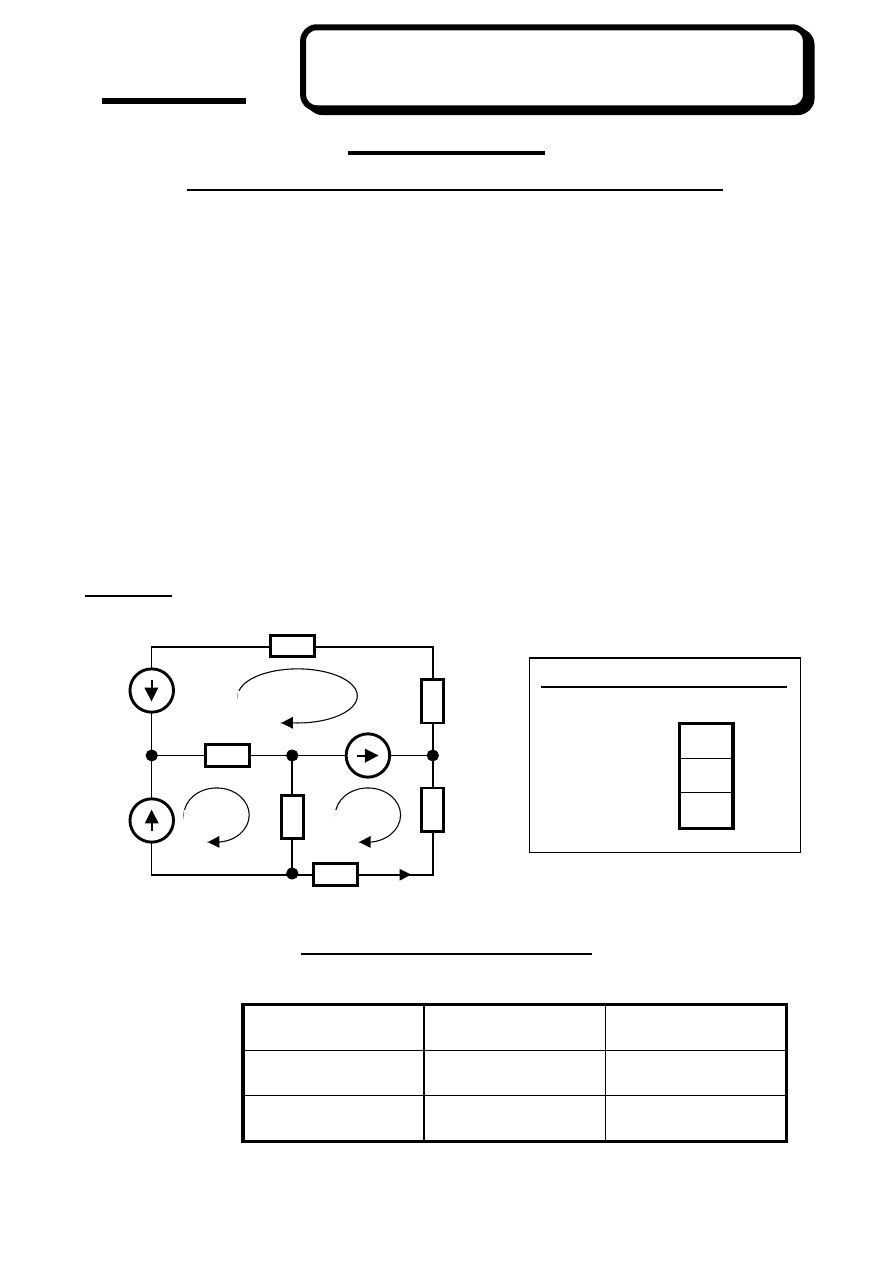
MPO: R
o
⋅I
o
– E
s
(I
o
) = E
o
MPO – jak ?
1.
Wybrać n = g – w + 1 oczek niezależnych i nadać im jednakowe zwroty;
2.
Utworzyć macierz rezystancji oczkowych R
o
:
−
na przekątnej głównej z plusem suma oporów rezystorów w oczku;
−
poza przekątną z minusem opory rezystorów wspólnych sąsiednich oczek;
3.
Utworzyć wektor autonomicznych wymuszeń oczkowych E
o
:
−
zwrot wymuszenie zgodny ze zwrotem oczka - znak plus;
−
zwrot wymuszenie przeciwny do zwrotu oczka - znak minus;
4.
Utworzyć wektor sterowanych wymuszeń oczkowych E
s
:
−
znaki wynikają ze zwrotu wymuszenia sterowanego oraz prądu sterującego w
stosunku do zwrotu oczka;
5.
Zapisać równania MPO i po uporządkowaniu do postaci: R
os
I
o
= E
o
;
gdzie: R
os
- macierz
( niesymetryczna jeśli w obwodzie są ZNSP lub ZPZP )
związana z
wartościami oporów rezystorów wchodzących w skład wybranych oczek
niezależnych oraz wartościami współczynników sprzężeń między oczkami
wynikającymi z istnienia w obwodzie ZNSP oraz ZPSP
6.
Dowolną metodą rozwiązać równania MPO: R
os
I
o
= E
o
→ I
o
= [R
os
]
–1
E
o
.
Przykład
Zapisać równania MPO dla obwodu o schemacie pokazanym na rysunku
R
1
R
2
R
3
R
4
R
5
R
6
E
1
r
I
s
I
s
I
1
I
s
I
2
Wektor prądów oczkowych
O
1
I
1
I
o
=
O
2
I
2
O
s
I
s
E
2
Macierz Rezystancji Oczkowych
O
1
O
2
O
s
O
1
R
1
+ R
2
+ R
5
– R
5
0
R
o
=
O
2
– R
5
R
4
+ R
5
–
R
4
O
s
0 –
R
4
R
3
+ R
4
+ R
6
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
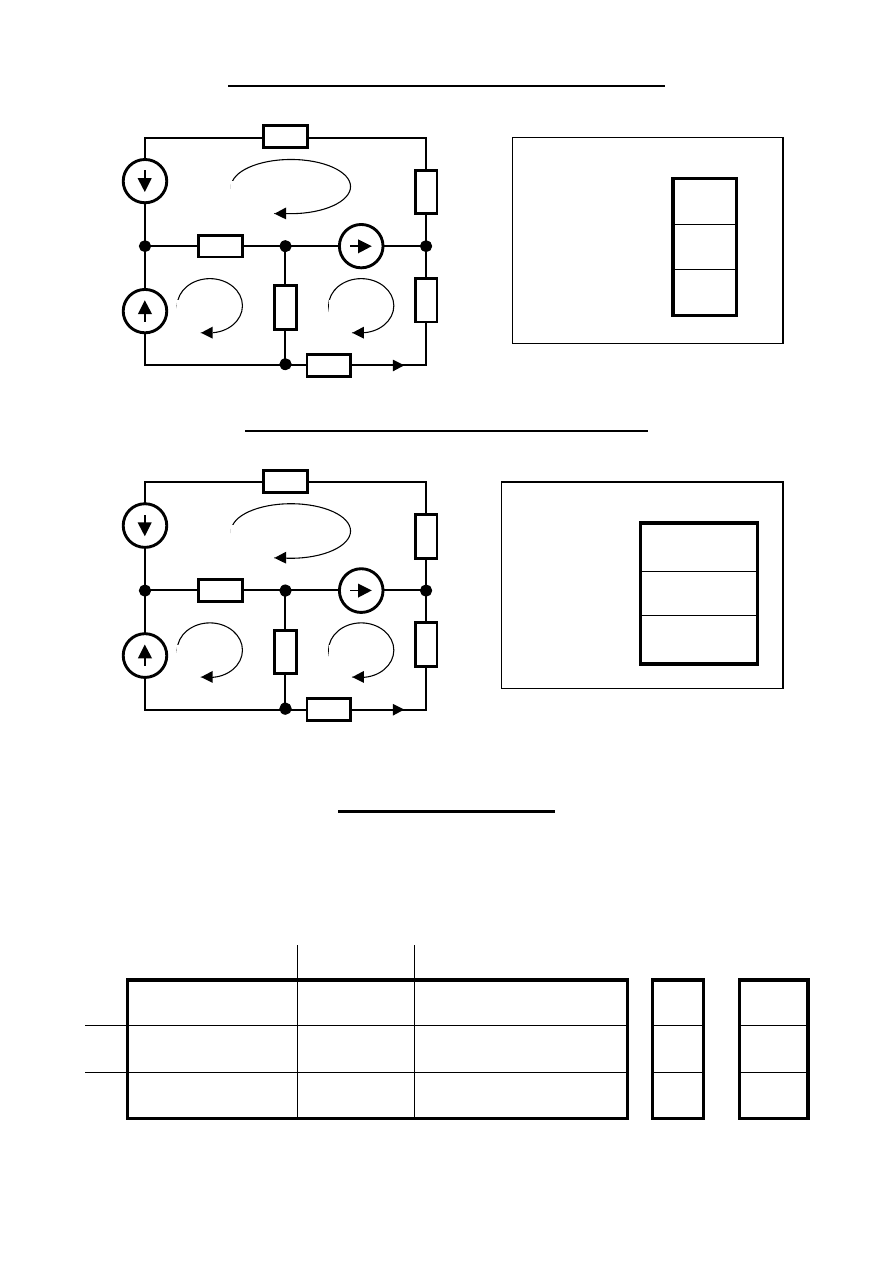
Wektor Autonomicznych Wymuszeń Oczkowych
R
1
R
2
R
3
R
4
R
5
R
6
E
1
r
I
s
I
s
I
1
I
s
I
2
O
1
–E
2
E
o
=
O
2
+E
1
O
s
0
E
2
Wektor Sterowanych Wymuszeń Oczkowych
R
1
R
2
R
3
R
4
R
5
R
6
E
1
r
I
s
I
s
I
1
I
s
I
2
O
1
–
r
⋅(–I
s
)
E
s
=
O
2
0
O
s
+
r
⋅(–I
s
)
E
2
Równania MPO
R
o
I
o
– E
s
= E
o
O
1
O
2
O
s
O
1
R
1
+ R
2
+ R
5
–
R
5
–
r
I
1
–E
2
O
2
– R
5
R
4
+ R
5
– R
4
⋅ I
2
= +E
1
O
s
0 –
R
4
R
3
+ R
4
+ R
6
+r I
s
0
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
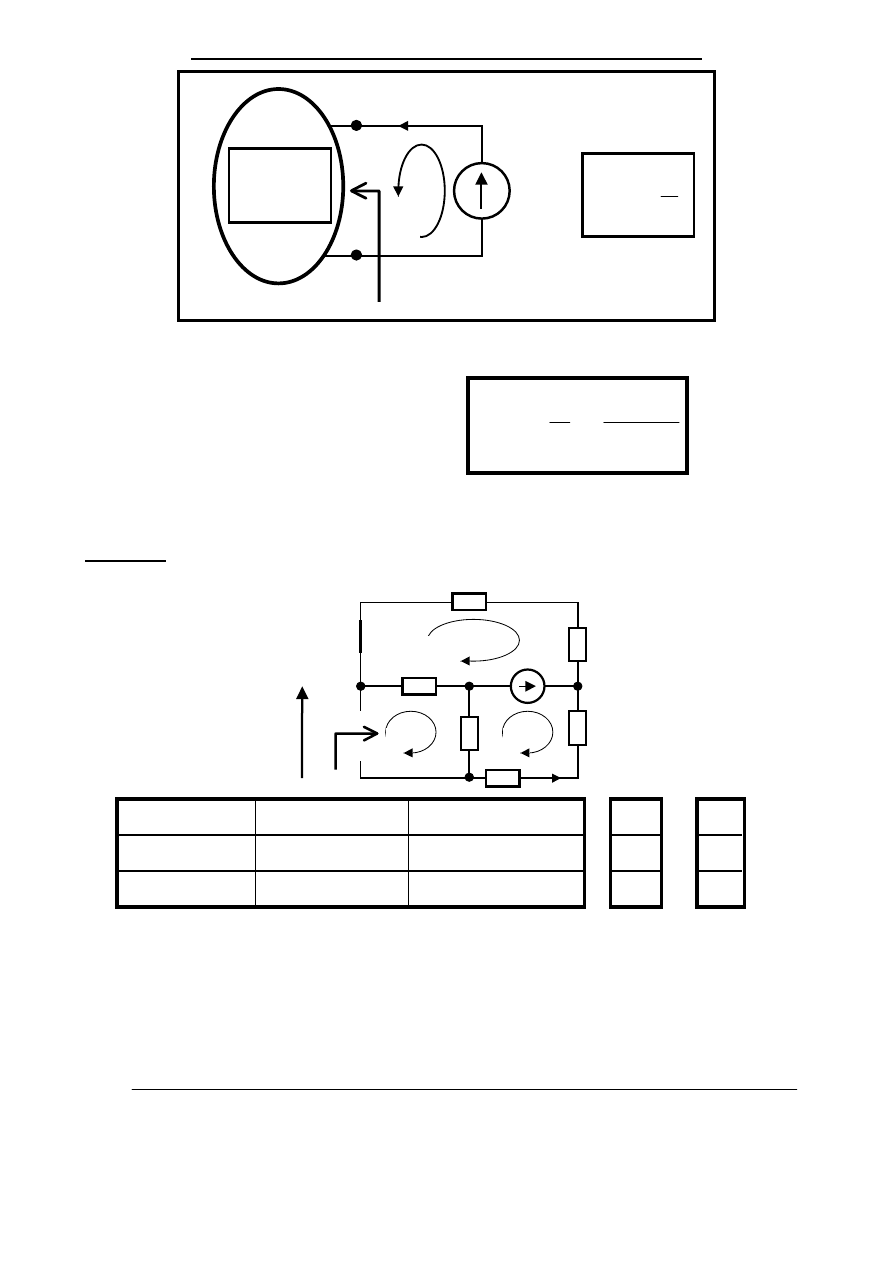
Obliczanie rezystancji złożonych dwójników
Rezystory
ZNSP
ZPSP
u
i
O
I
R
w
i
u
=
w
R
[ ]
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⋅
0
0
0
R
2
1
os
M
M
u
i
i
i
i
n
os
os
R
R
i
∆
w
R
i
u
∆
=
=
Przykład
Jaka rezystancja obciąża źródło E
1
z poprzedniego przykładu ?
R
1
R
2
R
3
R
4
R
5
R
6
r
I
s
I
s
I
1
I
2
I
R
w
u
R
4
+ R
5
–
R
5
–
R
4
i
u
– R
5
R
1
+ R
2
+ R
5
–
r
⋅
I
1
= 0
– R
4
0
R
3
+ R
4
+ R
6
+ r
I
2
0
∆R
os
= (R
4
+ R
5
)( R
1
+ R
2
+ R
5
)( R
3
+ R
4
+ R
6
+ r) – R
4
R
5
r +
– (R
1
+ R
2
+ R
5
)(R
4
)
2
– (R
3
+ R
4
+ R
6
+ r)(R
5
)
2
∆
i
R
os
= ( R
1
+ R
2
+ R
5
)( R
3
+ R
4
+ R
6
+ r)
(
)
(
)
(
)
(
)
5
4
4
2
4
1
4
6
4
3
5
4
5
2
5
1
4
2
4
1
5
2
5
1
4
2
4
1
5
2
1
6
5
6
2
6
1
5
4
5
3
4
2
4
1
3
2
3
1
w
)
(
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
r
R
R
R
R
R
R
R
R
R
R
R
r
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
R
+
+
−
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
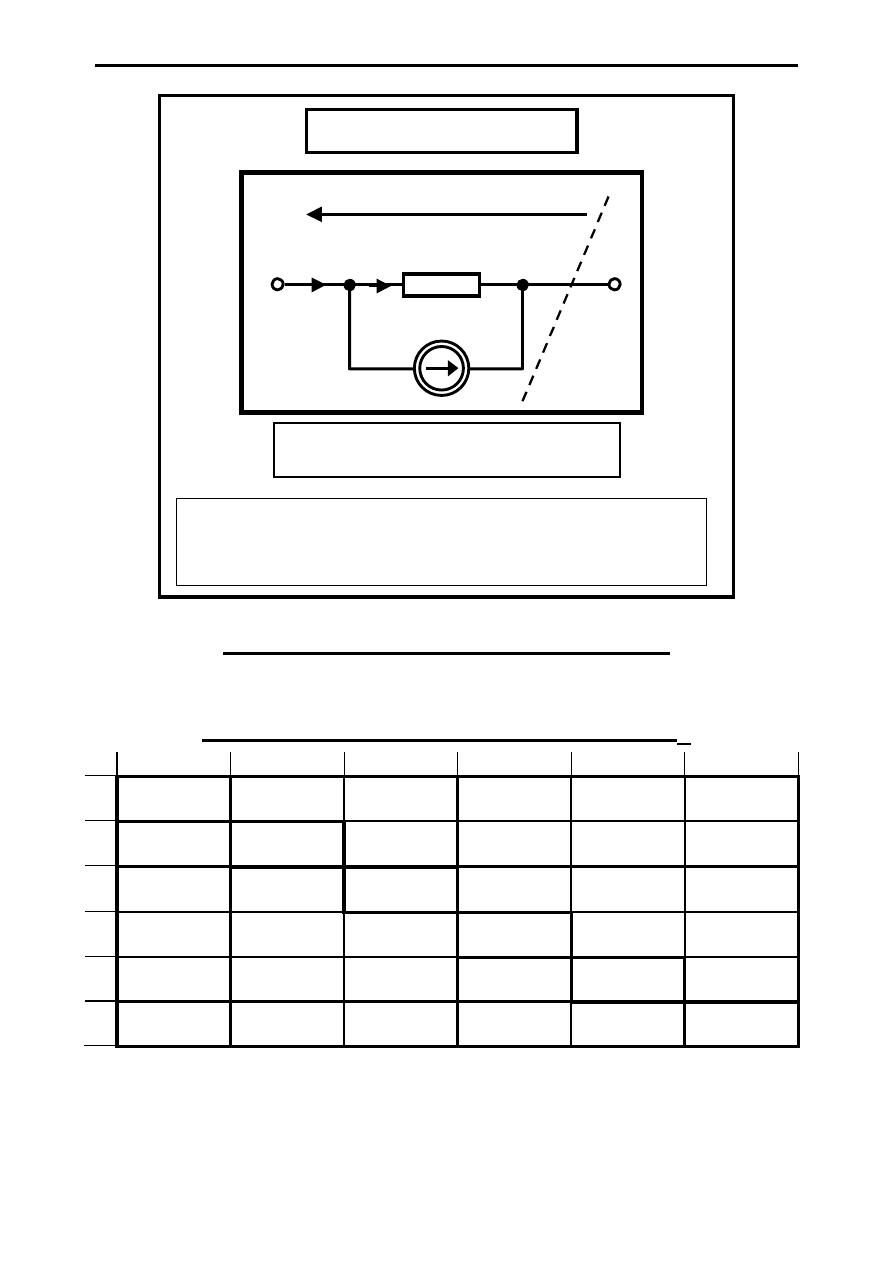
Metoda napięć węzłowych ( MNW ) –
„Metoda Coltriego”
G
g
i
g
u
g
Postać prądowa gałęzi
i
g
= G
g
⋅u
g
+ j
g
j
g
= ( G
g
⋅∑e + ∑j
g
) + (
∑[gu
s
]
g
+ G
g
⋅∑[ku
s
]
g
)
j
g
= j
autonomiczne
+ j
sterowane
j
gk
G
g
u
g
W
n
MNW w zapisie macierzowym
Macierz Konduktancji Węzłowych G
w
W
1
W
2
W
3
W
4
…
…
W
1
+
(
∑G)
W 1/1
– G
W 1/2
–
G
W 1/3
–
G
W ¼
…
…
W
2
– G
W 2/1
+
(
∑G)
W 2/2
– G
W 2/3
–
G
W 2/4
…
…
W
3
– G
W 3/1
–
G
W 3/2
+
(
∑G)
W 3/3
– G
W ¾
…
…
W
4
– G
W 4/1
–
G
W 4/2
–
G
W 4/3
+
(
∑G)
W 4/4
… …
…
… … … … … …
…
… … … … … …
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
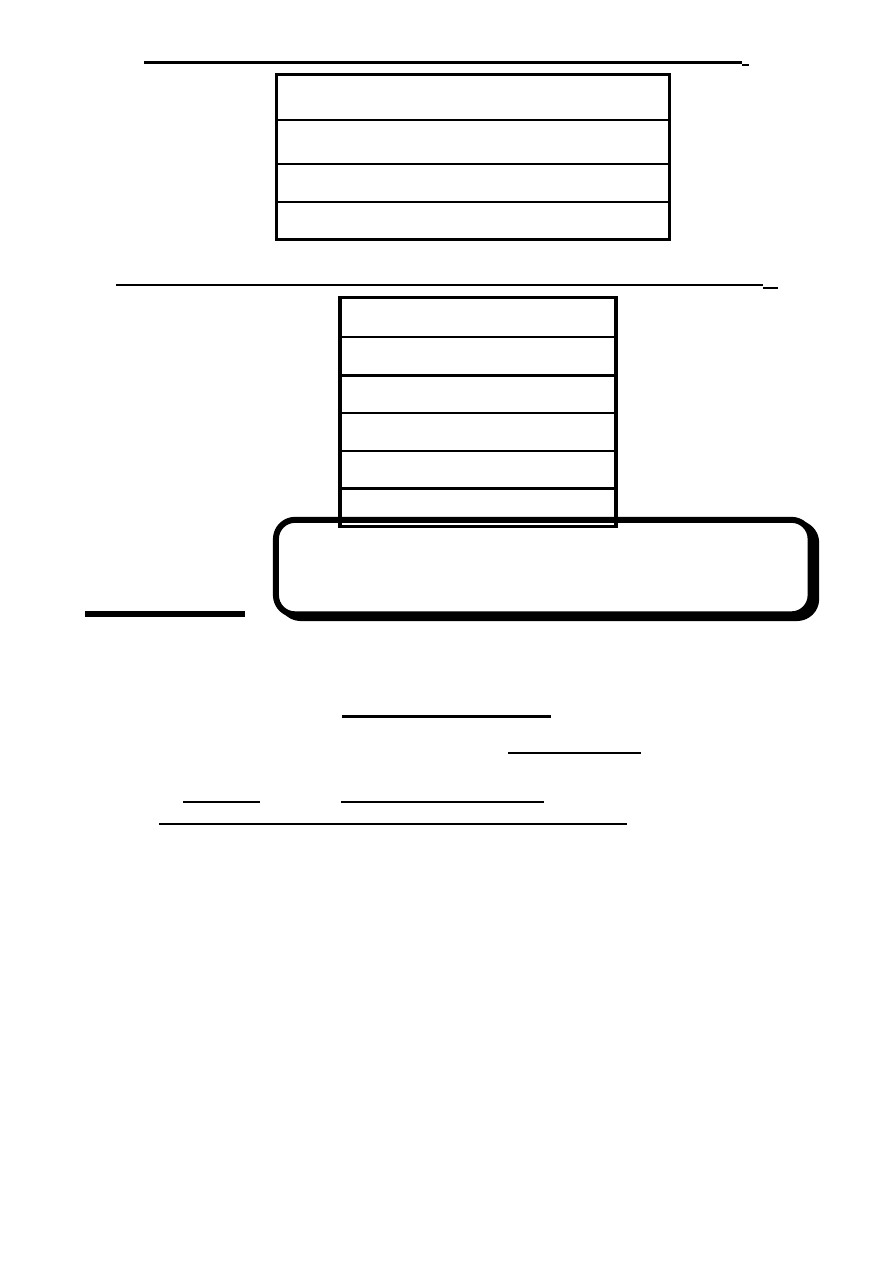
Wektor Sterowanych Wymuszeń Węzłowych J
s
(
∑[gu
s
] )
W 1
+ ( G
g
⋅∑[ku
s
]
)
W 1
(
∑[gu
s
] )
W 2
+ ( G
g
⋅∑[ku
s
]
)
W 2
…
…
Wektor Autonomicznych Wymuszeń Węzłowych J
w
+
(
∑Ge)
W 1
+ (
∑j)
W 1
+
(
∑Ge)
W 2
+ (
∑j)
W 2
…
…
…
MNW: G
w
⋅U
w
– J
s
(U
w
) = J
w
MNW – jak ?
1.
Wybrać węzeł odniesienia V=0, dla pozostałych
r = w – 1 węzłów napisać MNW;
2.
Utworzyć macierz konduktancji węzłowych G
w
:
− na
przekątnej
głównej z
plusem suma przewodności
rezystorów we węźle;
− poza przekątną
z
minusem przewodności rezystorów wspólnych
sąsiednich węzłów;
3.
Utworzyć wektor autonomicznych wymuszeń węzłowych J
w
:
− zwrot do węzła
-
znak plus
;
− zwrot od węzła
-
znak minus
;
4.
Utworzyć wektor sterowanych wymuszeń węzłowych J
s
:
−
znaki wynikają ze zwrotu wymuszenia sterowanego oraz napięcia sterującego w
stosunku do węzła;
5.
Zapisać równania MNW i po uporządkowaniu do postaci: G
ws
U
w
= J
w
;
gdzie: G
ws
- macierz
( niesymetryczna jeśli w obwodzie są ZNSN lub ZPSN )
związana z wartościami
przewodności rezystorów dołączonych do wybranych węwzłów oraz wartościami
współczynników sprzężeń między węzłami wynikającymi z istnienia w obwodzie ZNSN
oraz ZPSN
6.
Dowolną metodą rozwiązać równania MNW: G
ws
U
w
= J
w
→ J
w
= [G
ws
]
–1
J
w
.
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
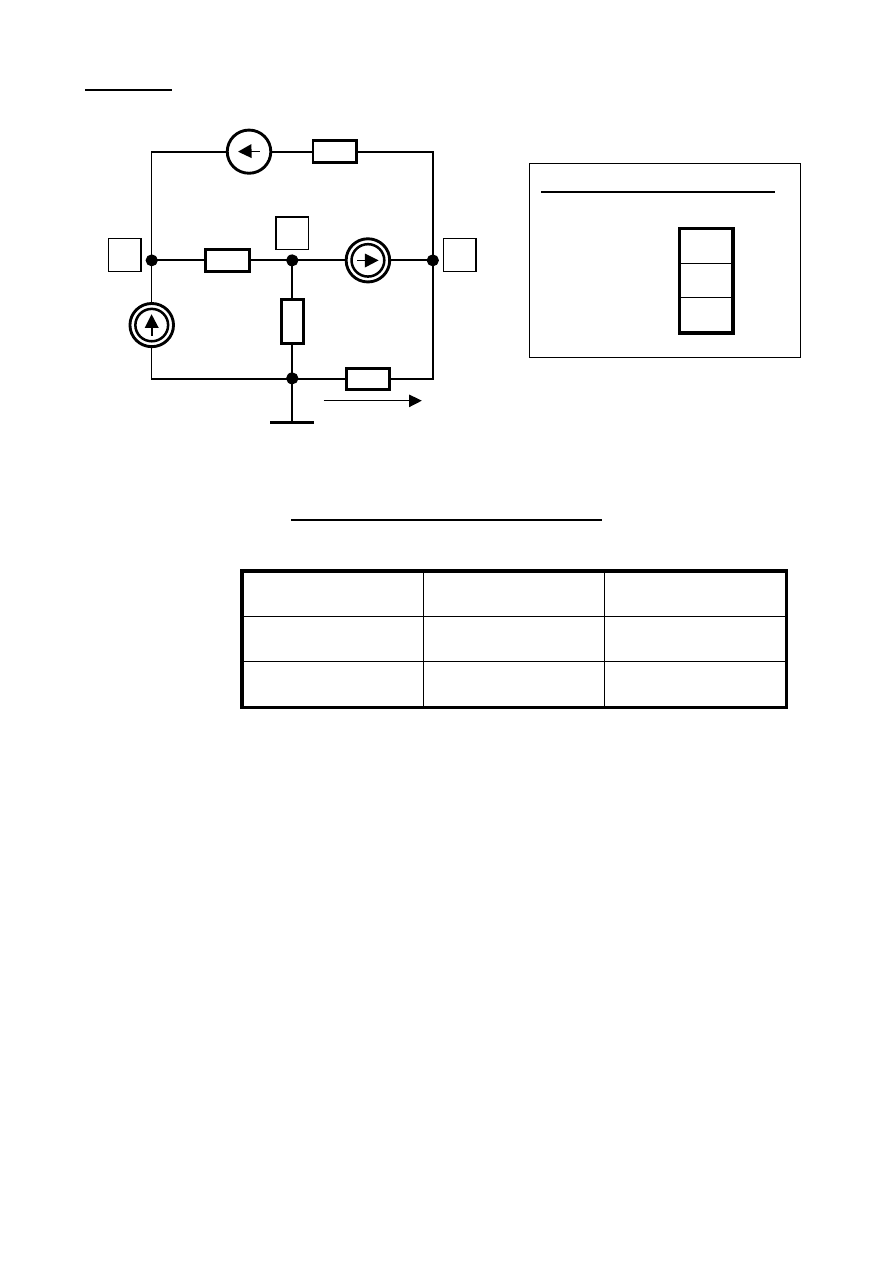
Przykład
Zapisać równania MNW dla obwodu o schemacie pokazanym na rysunku
R
1
R
4
R
5
R
6
J
1
g
U
s
Wektor napięć węzłowych
W
1
V
1
U
w
=
W
2
V
2
W
3
V
3
E
2
U
s
WO
1
2
3
V
1
V
2
V
3
V
0
= 0
Macierz Konduktancji Węzłowych
W
1
W
2
W
3
W
1
G
1
+ G
5
–
G
5
–
G
1
G
w
=
W
2
– G
5
G
4
+ G
5
0
W
3
– G
1
0
G
1
+ G
6
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
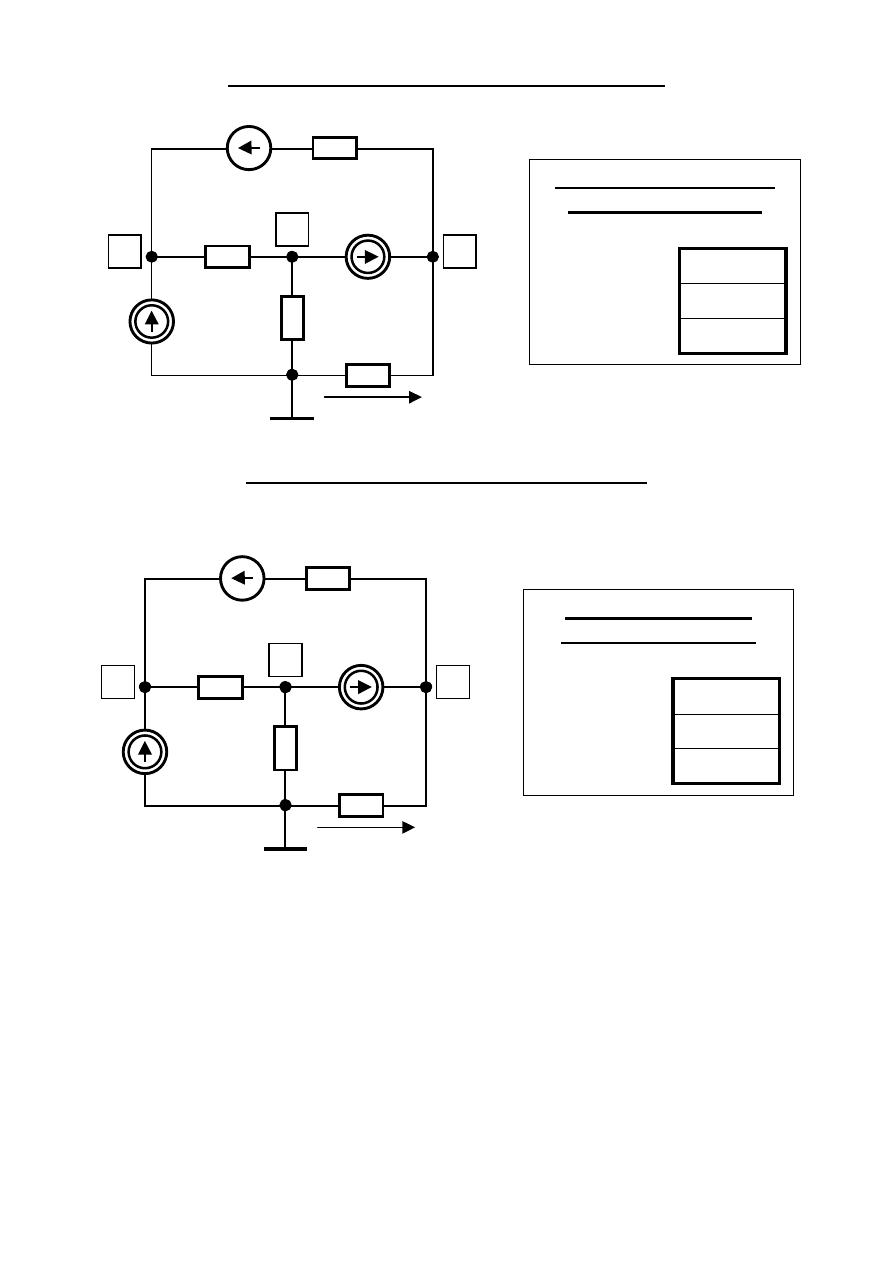
Wektor Autonomicznych Wymuszeń Oczkowych
R
1
R
4
R
5
R
6
J
1
g
U
s
Wektor autonomicznych
wymuszeń węzłowych
W
1
J
1
+ G
1
E
2
J
w
=
W
2
0
W
3
– G
1
E
2
E
2
U
s
WO
1
2
3
V
1
V
2
V
3
V
0
= 0
Wektor Sterowanych Wymuszeń Węzłowych
R
1
R
4
R
5
R
6
J
1
g
U
s
Wektor sterowanych
wymuszeń węzłowych
W
1
0
J
s
=
W
2
– g(+V
3
)
W
3
+ g(+V
3
)
E
2
U
s
WO
1
2
3
V
1
V
2
V
3
V
0
= 0
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
Równania MNW
G
w
U
w
– J
s
= J
w
W
1
W
2
W
3
W
1
G
1
+ G
5
–
G
5
–
G
1
V
1
J
1
+
G
1
E
1
W
2
– G
5
G
4
+ G
5
+
g
⋅ V
2
= 0
W
3
– G
1
0
G
1
+ G
6
– g
V
3
–
G
1
E
1
V
1
E1 g G1 G4
- E1 G1 G4 G6 - E1 G1 G5 G6 + g G4 J1 - G1 G4 J1 + g G5 J1 - G1 G5 J1 - G4 G6 J1 - G5 G6 J
g G1 G4
+ g G4 G5 - G1 G4 G5 - G1 G4 G6 - G1 G5 G6 - G4 G5 G6
V
2
=
E1 G1 G5 G6
-
g G1 J1
-
g G5 J1
+
G1 G5 J1
+
G5 G6 J1
-
g G1 G4
-
g G4 G5
+
G1 G4 G5
+
G1 G4 G6
+
G1 G5 G6
+
G4 G5 G6
V
3
-
E1 G1 G4 G5
+
G1 G4 J1
+
G1 G5 J1
-
g G1 G4
-
g G4 G5
+
G1 G4 G5
+
G1 G4 G6
+
G1 G5 G6
+
G4 G5 G6
Obliczanie konduktancji złożonych dwójników
Rezystory
ZNSN
ZPSN
j
G
w
2
1
w
V
V
G
−
=
=
j
u
j
u
WO
V
2
V
1
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
Przykład
Jaka konduktancja obciąża źródło E
2
z poprzedniego przykładu ?
G
w
R
4
R
5
R
6
g
U
s
U
s
WO
V
1
V
2
V
0
= 0
R
1
u
j
G
1
j
G
5
j
u – (G
1
+ G
5
)
j – (V
2
– V
1
) = 0
(
)
1
2
5
1
w
V
V
j
G
G
G
−
+
+
=
G
4
+
g V
1
=
–j
0 G
6
– g
V
2
+j
(
)
4
6
4
6
5
1
w
G
G
G
G
G
G
G
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
+
+
=
g
przy założeniu: G
6
≠ g !!!
Dr inż. Jacek Czosnowski
Katedra Elektrotechniki AGH Wydział EAIiE
Wyszukiwarka
Podobne podstrony:
4 Analiza obwodów prądu stałego
Analizowanie obwodow elektryczn Nieznany
analizator obwodow ntw7 cz2
Analiza%20obwodow
05 Analizowanie obwodów elektrycznych
5 Analiza obwodów prądu zmiennego(1)
5 Metody operatorowe analizy obwodow SLS
06 Analizowanie obwodow elektry Nieznany (2)
analiza obwodow elektrycznych i Nieznany
6 Analiza obwodow 1
analizator obwodow nwt7cz1
4 Analiza obwodów prądu stałego
06 Analizowanie obwodów elektrycznych i elektronicznych
4 analiza obwodow elektrycznych !!!!!!!!!!!!!!!!!!!!!!!
więcej podobnych podstron