Analiza obwodów SLS, e, i
z
czyli
zaczynamy na dobre
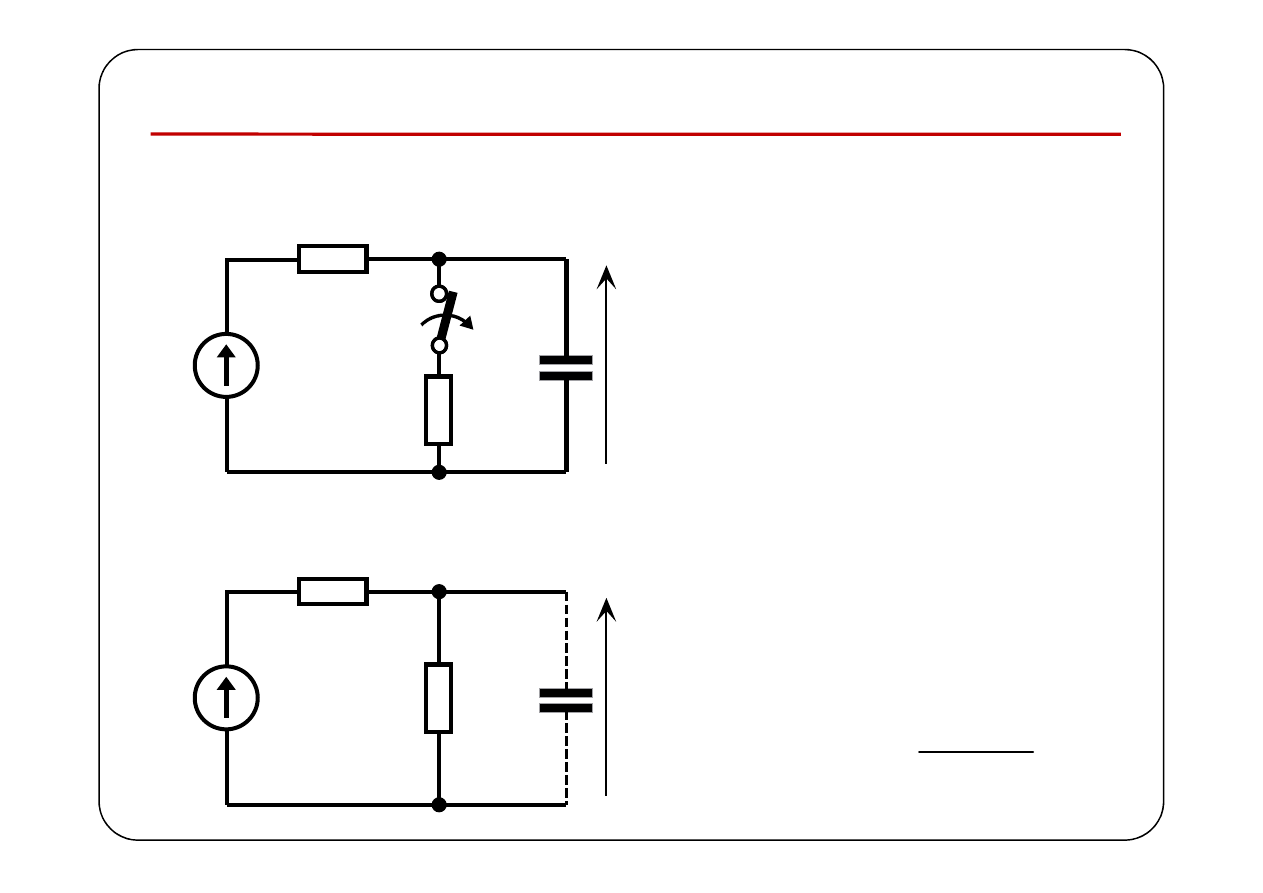
Stany nieustalone w obwodach RL i RC
R
R
0
E
0
C
K
t = 0
u(t)
E
0
= const.
Przykład 1.
R
R
0
E
0
C
U
t < 0
( )
0
0
0
0
R
u
U
E
R
R
= = +
Warunek początkowy
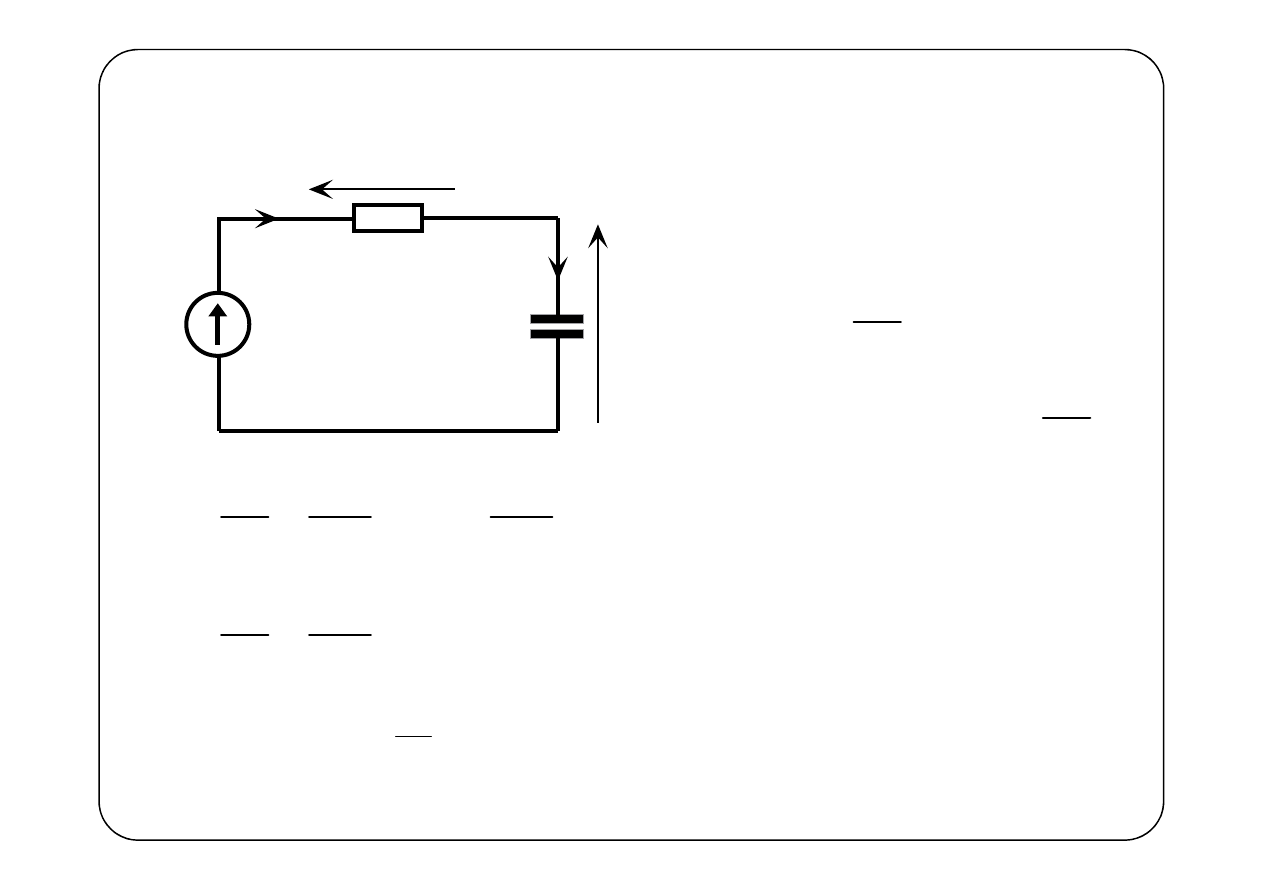
R
E
0
C
u(t)
u
R
(t)
i(t)
i(t)
t > 0
( ) ( )
( )
( )
( )
0
0,
d
,
d
d
.
d
R
R
E
u
t
u t
u
i t
C
t
u
u
t
Ri t
RC
t
− +
+
=
=
=
=
dt
( )
0
d
1
1
d
u
u t
E
t
RC
RC
+
=
( )
d
1
0
d
u
u t
t
RC
+
=
Równanie jednorodne
( )
1
e
t
RC
u t
λ
−
=
Rozwiązanie ogólne równania
jednorodnego,
λ
– dowolna stała
Rozwiązanie
Rozwiązanie
Dowolne rozwiązanie
równania
równania
równania
niejednorodnego
jednorodnego
niejednorodnego
=
+
ogólne
ogólne
szczególne
Rozwiązanie ogólne równania niejednorodnego:
( )
1
0
e
t
RC
u t
E
λ
−
=
+
( )
0
Z warunku początkowego
( )
0
0
0
0
0
0
czyli
0
,
R
u
E
E
R
R
R
E
R
R
λ
λ
= +
= +
= − +
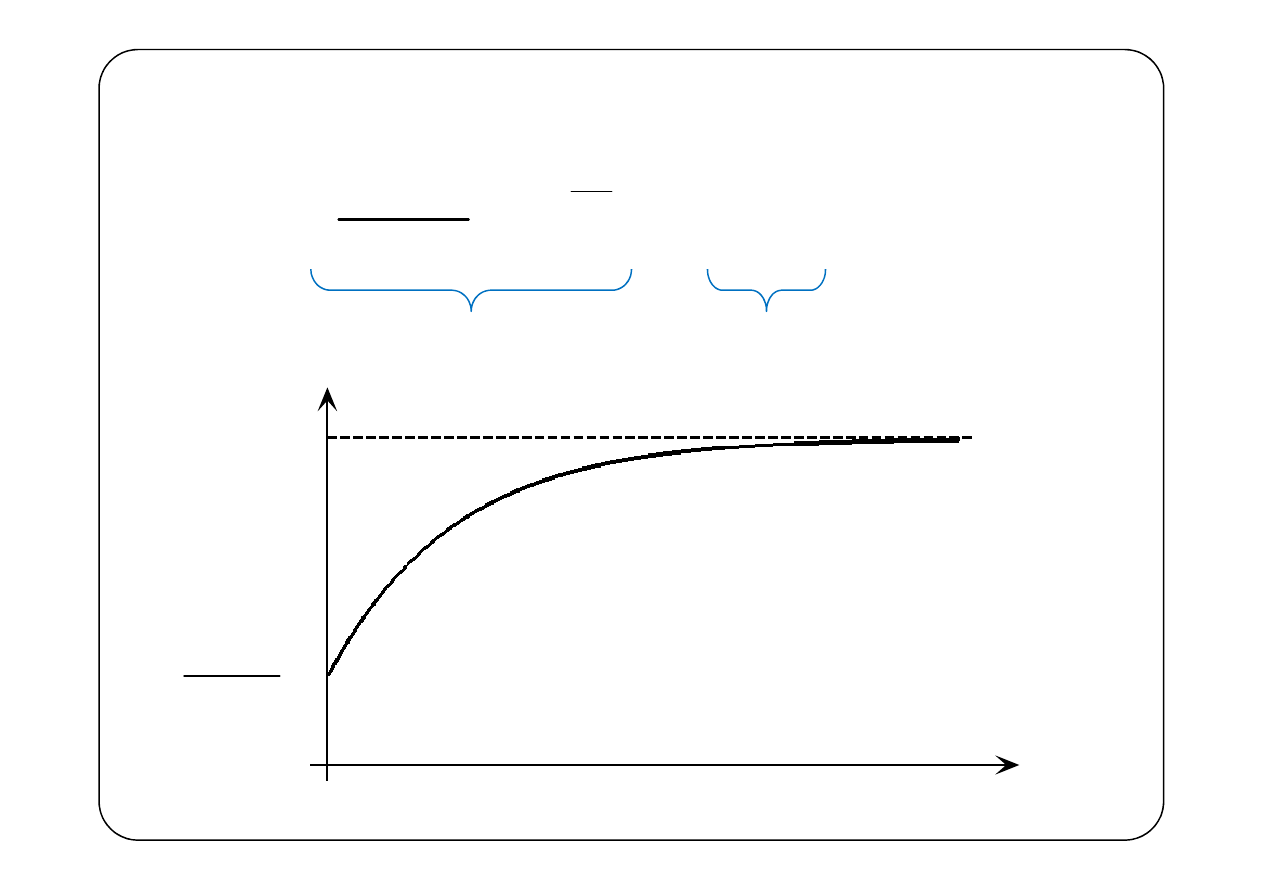
Ostatecznie
( )
1
0
0
0
e
t
RC
R
u t
E
E
R
R
−
= −
+
+
Składowa przejściowa
Składowa ustalona
u(t)
0
E
0
0
0
R
E
R
R
+
0
E
t
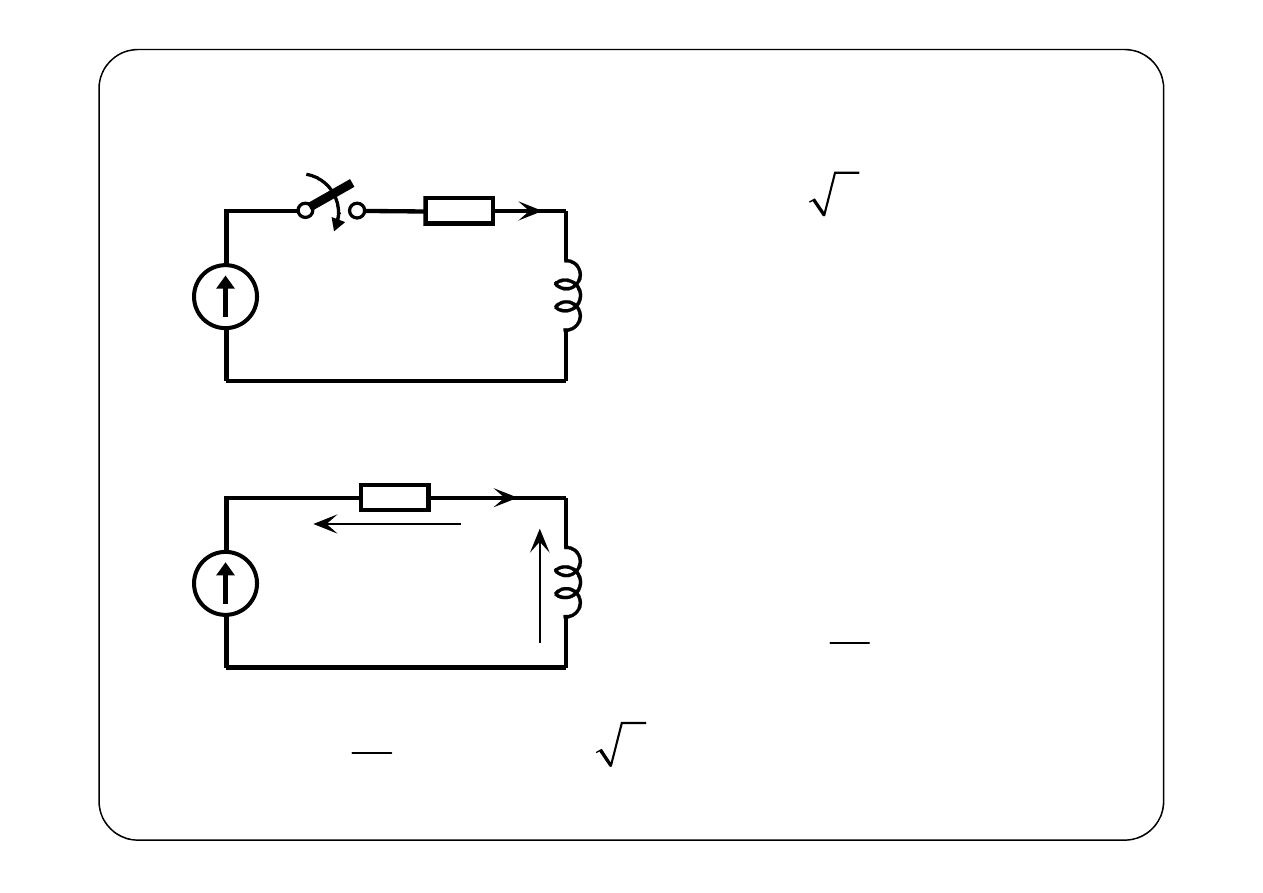
Przykład 2.
e(t)
R
L
i(t)
K
t = 0
( )
(
)
0
2 sin
e t
E
t
ω
θ
=
+
t > 0
( )
0
0
i
=
Warunek początkowy
t > 0
e(t)
R
L
i(t)
u
R
(t)
u
L
(t)
( )
( )
( )
( )
( )
( )
0
d
d
R
L
R
L
e t
u
t
u
t
u
t
R i t
i
u
t
L
t
−
+
+
=
=
=
( )
(
)
0
d
2 sin
d
i
L
Ri t
E
t
t
ω
θ
+
=
+
Rozwiązanie ma postać
( )
( )
u
e
R
t
L
i t
i t
λ
−
=
+
Będziemy poszukiwać rozwiązania szczególnego o postaci
( )
(
)
u
0
2 sin
i t
I
t
ω
ϕ
=
+
( )
(
)
{
}
{
}
j
j
j
2 Im e
2 Im e e
t
t
i t
I
I
ω ϕ
ω
ϕ
+
=
=
co zapiszemy jako
( )
(
)
{
}
{
}
0
0
j
j
j
u
2 Im e
2 Im e e
t
t
i t
I
I
ω ϕ
ω
ϕ
+
=
=
Podobnie
( )
{
}
0
j
j
2 Im
e e
t
e t
E
ω
θ
=
Obliczamy pochodną
{
}
{
}
0
0
j
j
j
j
u
0
d
d
2 Im e e
2 Im j
e e
d
d
t
t
i
I
I
t
t
ω
ω
ϕ
ϕ
ω
=
=
Po podstawieniu do równania niejednorodnego otrzymujemy
{
}
{
}
{
}
0
0
0
j
j
j
j
j
j
0
2 Im j
e e
2 Im e e
2 Im
e e
t
t
t
L
I
R
I
E
ω
ω
ω
ϕ
ϕ
θ
ω
+
≡
(
)
{
}
0
j
j
j
0
Im
j
e
e
e
0
t
R
L I
E
ω
ϕ
θ
ω
+
−
≡
{
}
0
j
Im
e
0
0
t
W
W
ω
≡ ⇔
=
{
}
Im
e
0
0
W
W
≡ ⇔
=
(
)
j
j
0
j
j
0
j
e
e
0
e
e
j
R
L I
E
E
I
R
L
ϕ
θ
θ
ϕ
ω
ω
+
−
=
= +
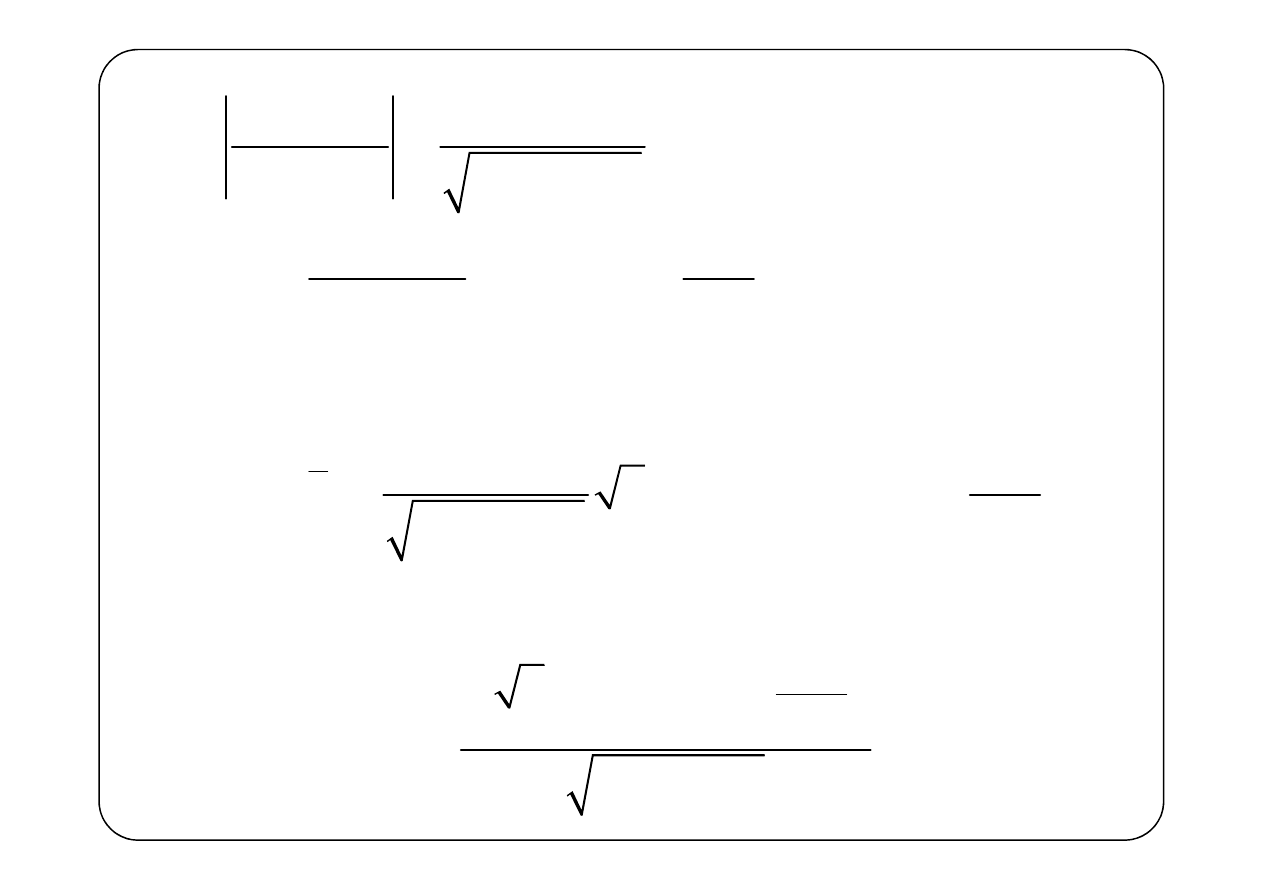
j
2
2
2
0
0
e
j
E
E
I
R
L
R
L
θ
ω
ω
=
=
+
+
j
0
0
e
arg
arctg
j
L
E
R
L
R
θ
ω
ϕ
θ
ω
=
= −
+
R
L
ω
Ostatecznie, jako rozwiązanie ogólne równania niejednorodnego
otrzymujemy
( )
0
0
2
2
2
0
e
2 sin
arctg
R
t
L
L
E
i t
t
R
R
L
ω
λ
ω
θ
ω
−
=
+
+ −
+
Z warunku początkowego i(0) = 0 otrzymamy
0
2
2
2
0
2 sin
arctg
L
E
R
R
L
ω
θ
λ
ω
−
= −
+
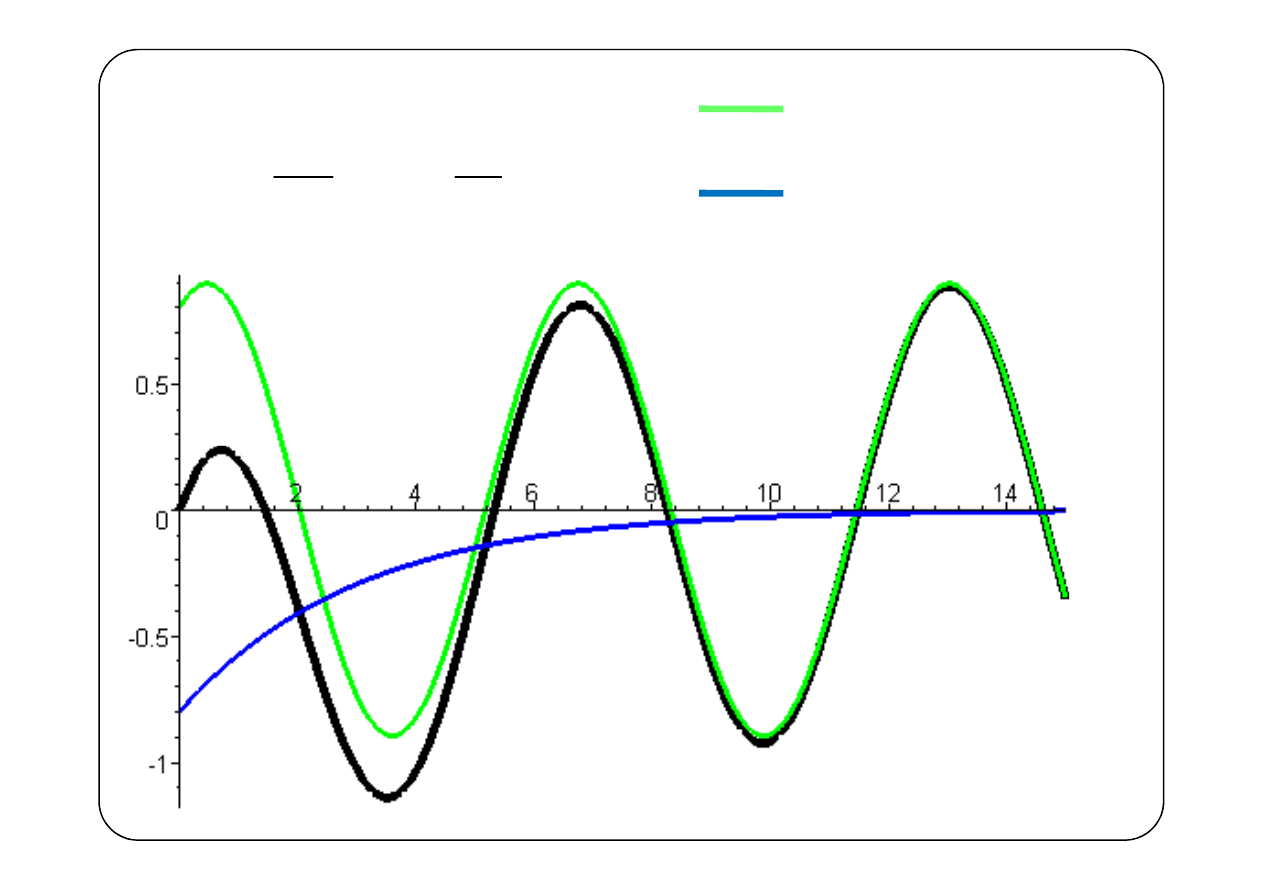
6
0
2 V,
1kΩ,
3mH,
rad
3π
10
,
rad.
s
4
E
R
L
ω
θ
=
=
=
=
=
składowa ustalona
składowa przejściowa
i(t), mA
t,
µ
s
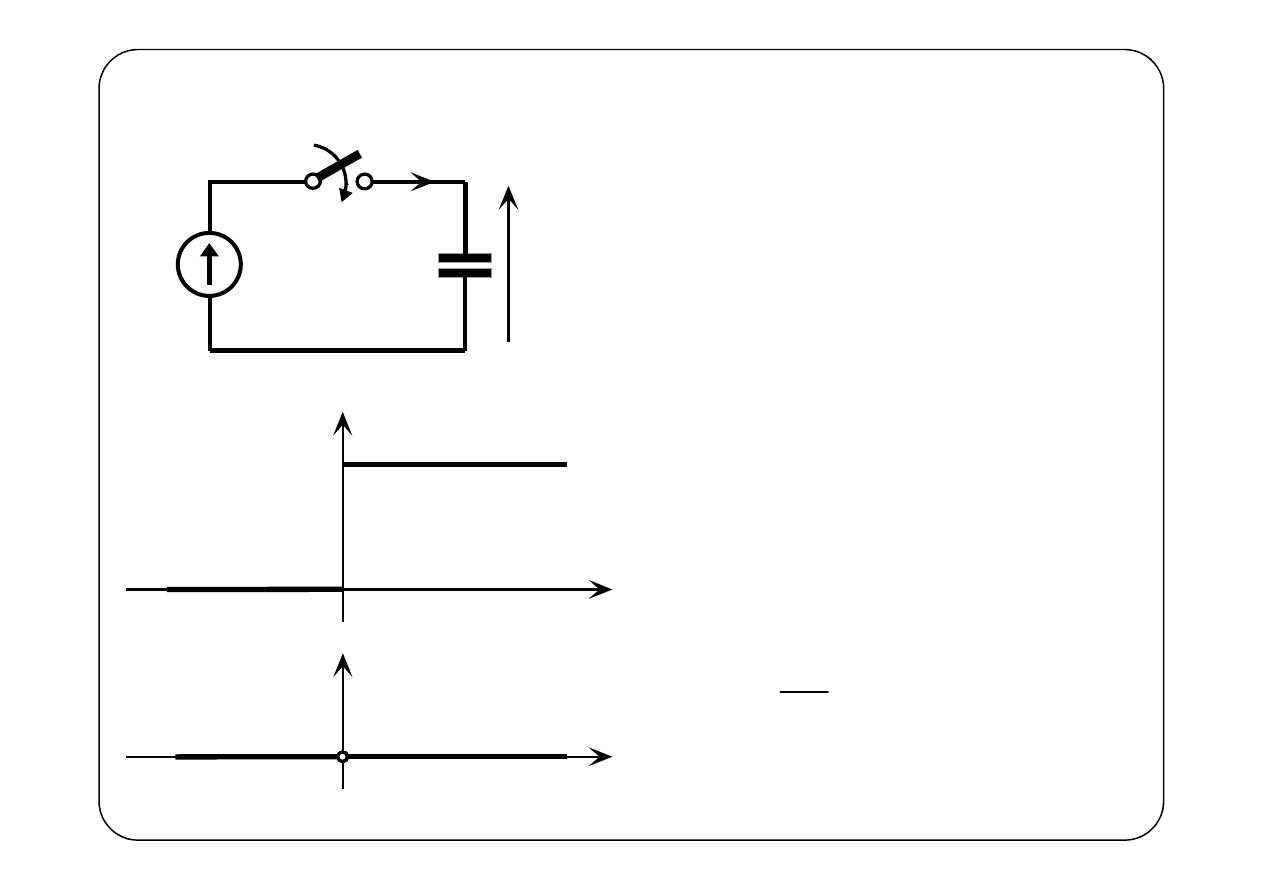
Przykład 3.
E
0
C
K
t = 0
u(t)
i(t)
0
const
E
=
Kondensator nie był naładowany,
czyli u(t) = 0 dla t < 0.
u(t)
E
0
t
i(t)
t
( )
( )
0
u t
E
t
=
1
( )
0
gdy
0
d
d
gdy
0
t
u
i t
C
t
t
≠
=
=
=
?
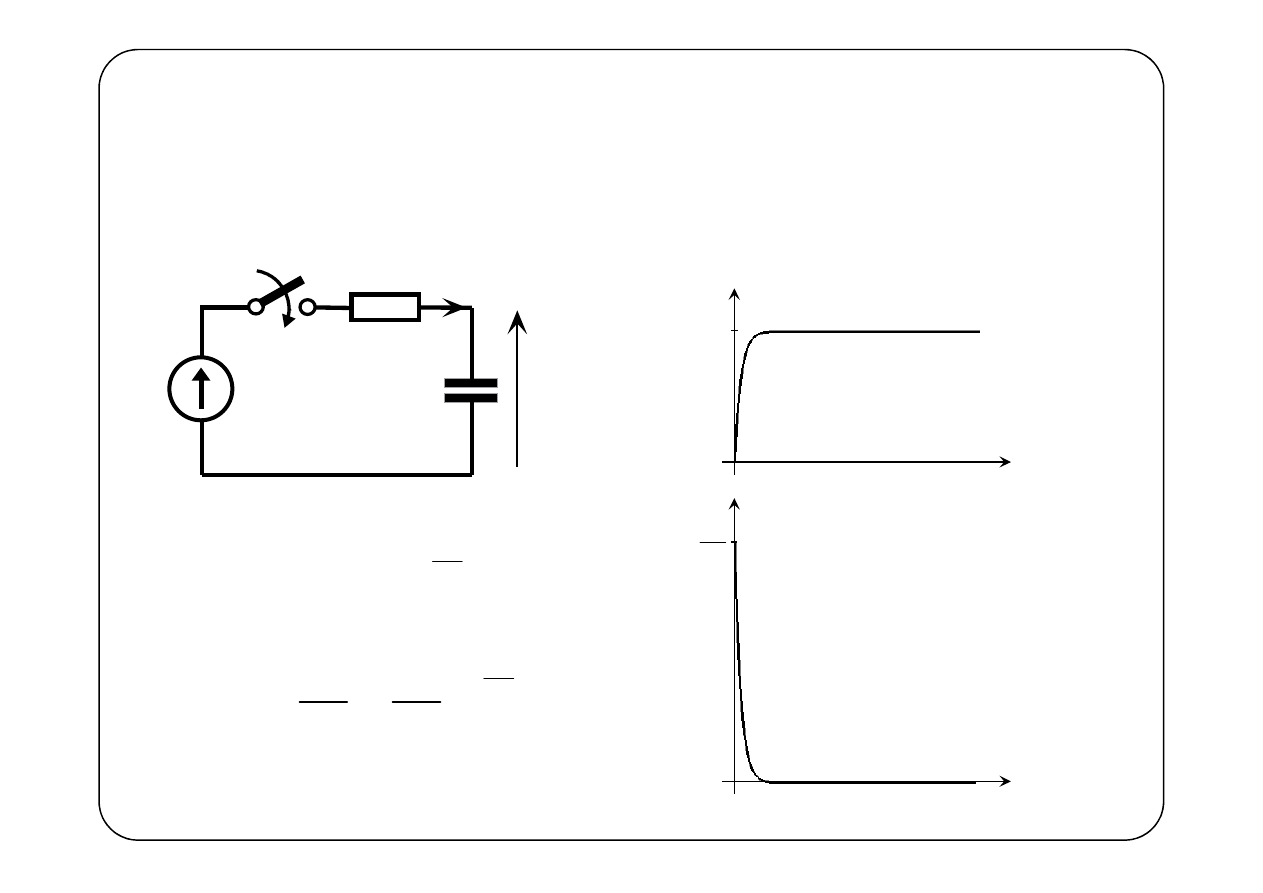
Rozważmy ładunek zgromadzony na okładkach kondensatora
( )
( )
0
0
gdy
0
gdy
0
t
q t
Cu t
CE
t
<
=
=
>
E
0
C
K
t = 0
u(t)
i(t)
r
u(t)
E
0
t
( )
( )
1
0
1
0
1 e
d
e
d
t
rC
t
rC
u t
E
E
u
i t
C
t
r
−
−
=
−
=
=
i(t)
0
E
r
t
t
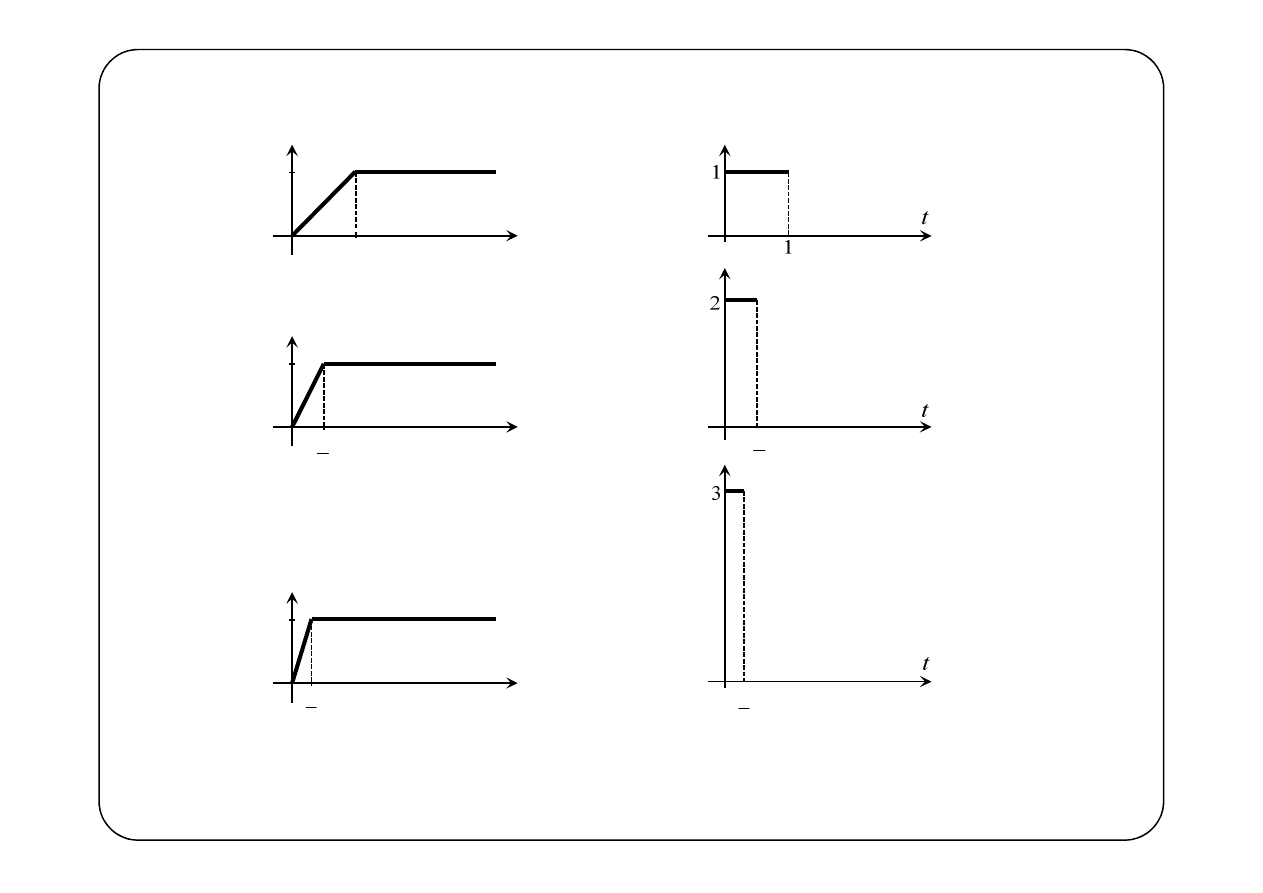
1
t
1
1
1
t
f
n
n
1
2
1
f
n
’
1
3
1
t
1
2
3
∞
i
i
i
( )
t
↓
1
1
3
1
2
↓
?
( )
δ t
↓
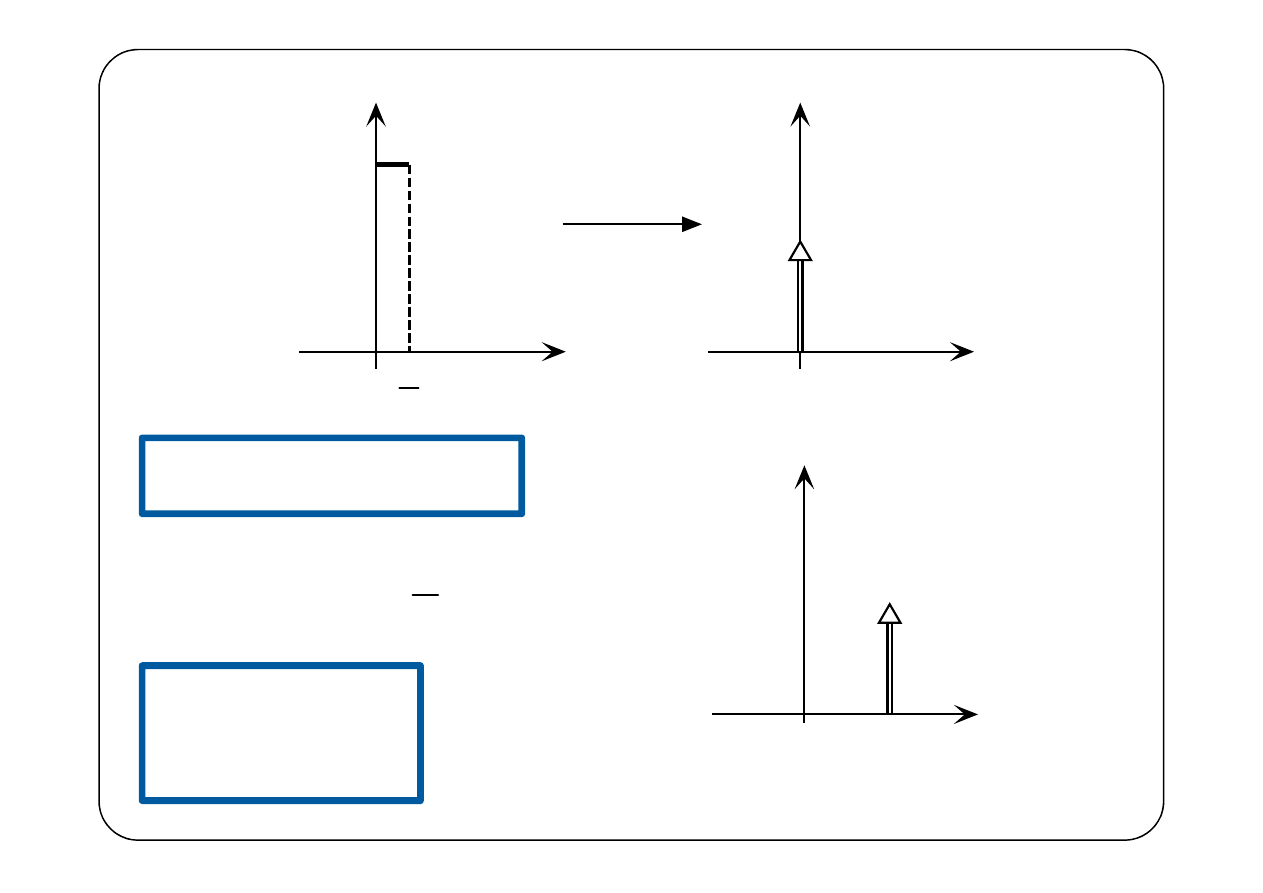
f
n
'
(t)
n
1
n
t
t
( ) ( )
δ
f t
t
=
n
→ ∞
( )
δ
0
dla
0
t
t
=
≠
( )
( )
1
d
1
δ
d
1
n
f
t
t
n
n
t
t
∞
−∞
∞
−∞
′
= ⋅ =
∫
∫
≜
t
( )
f t
(
)
0
δ t
t
−
t
0
( )
( )
( )
( )
0
0
0
0
0
0
0
0
lim
δ
d
δ
d
1
lim
δ
d
δ
d
0
t
t
t
t
t
t
t
t
ε
ε
ε
ε
ε
ε
∞
∞
→
−
−
>
∞
∞
→
+
+
>
=
=
=
=
∫
∫
∫
∫
( )
0
0
δ
d
1
t
t
+
−
=
∫
( )
( )
( )
0
gdy
0
δ
d
δ
d
t
t
t
t
τ τ
τ τ
<
=
=
=
∫
∫
1
( )
( )
( )
0
0
gdy
0
δ
d
δ
d
1 gdy
0
t
t
t
τ τ
τ τ
−∞
−
<
=
=
=
>
∫
∫
1
( ) ( )
d
δ
d
t
t
t
1
≜

Jeżeli f(t) jest ciągła w punkcie t = 0, to
( ) ( )
( ) ( )
( ) ( )
( ) ( )
( )
δ
0 δ
δ
d
0
δ
d
0
f t
t
f
t
f t
t
t
f
t
t
f
∞
∞
−∞
−∞
=
=
=
∫
∫
Własność filtrująca dystrybucji Diraca
−∞
−∞
Ogólniej, jeżeli f(t) jest ciągła w punkcie t = t
0
, to
( )
(
)
( ) (
)
( )
(
)
( ) (
)
( )
0
0
0
0
0
0
0
δ
δ
δ
d
δ
d
f t
t
t
f t
t
t
f t
t
t
t
f t
t
t
t
f t
∞
∞
−∞
−∞
−
=
−
−
=
−
=
∫
∫
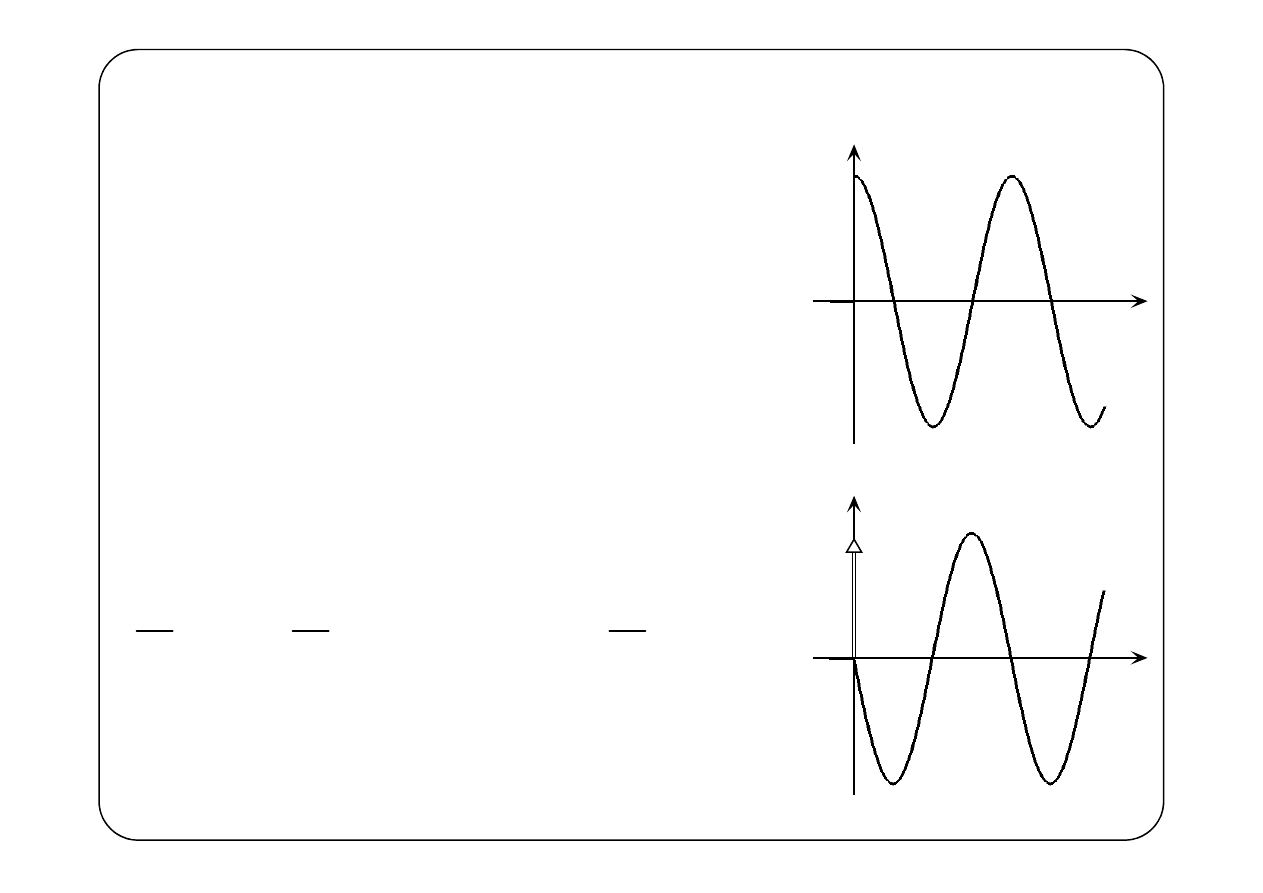
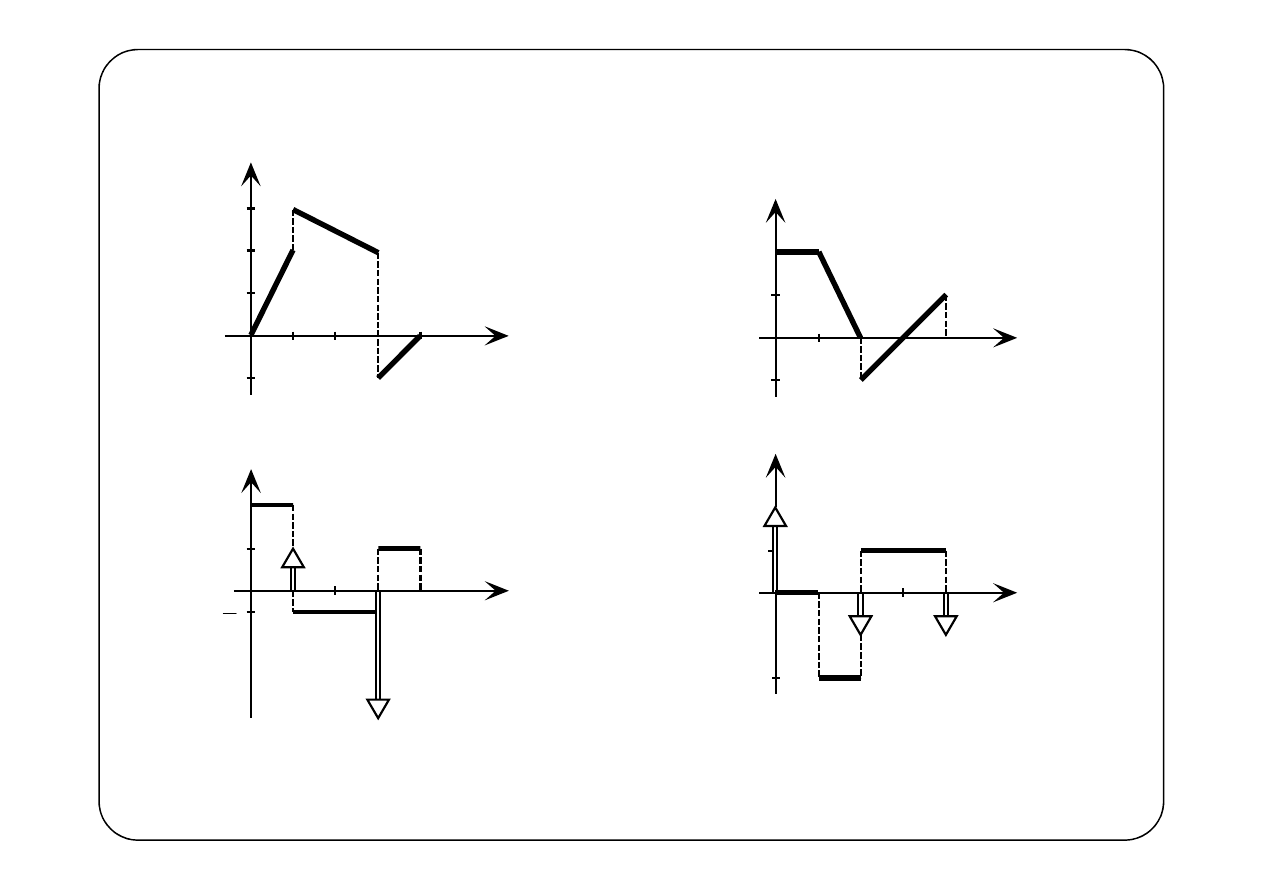
Różniczkowanie funkcji nieciągłych
( )
( )
cos
f t
t
t
=
⋅
1
( )
f t
( )
f
t
′
( )
δ t
( )
( )
( )
( ) ( )
d
d
d
cos
cos
d
d
d
sin
δ
f t
t
t
t
t
t
t
t
t
t
t
=
⋅
+
⋅
=
= −
⋅
+
1
1
1
1
2
3
1
2 3
4
–1
t
( )
f t
4
2
–2
1 2
3 4
t
( )
f t
( )
f
t
′
( )
f
t
′
2
1
1
2
−
1
2
3 4
(
)
δ
1
t
−
(
)
3 δ
3
t
−
−
t
2
–4
1
2
3
4
t
( )
f
t
′
( )
4 δ t
(
)
2 δ
2
t
−
−
(
)
2 δ
4
t
−
−
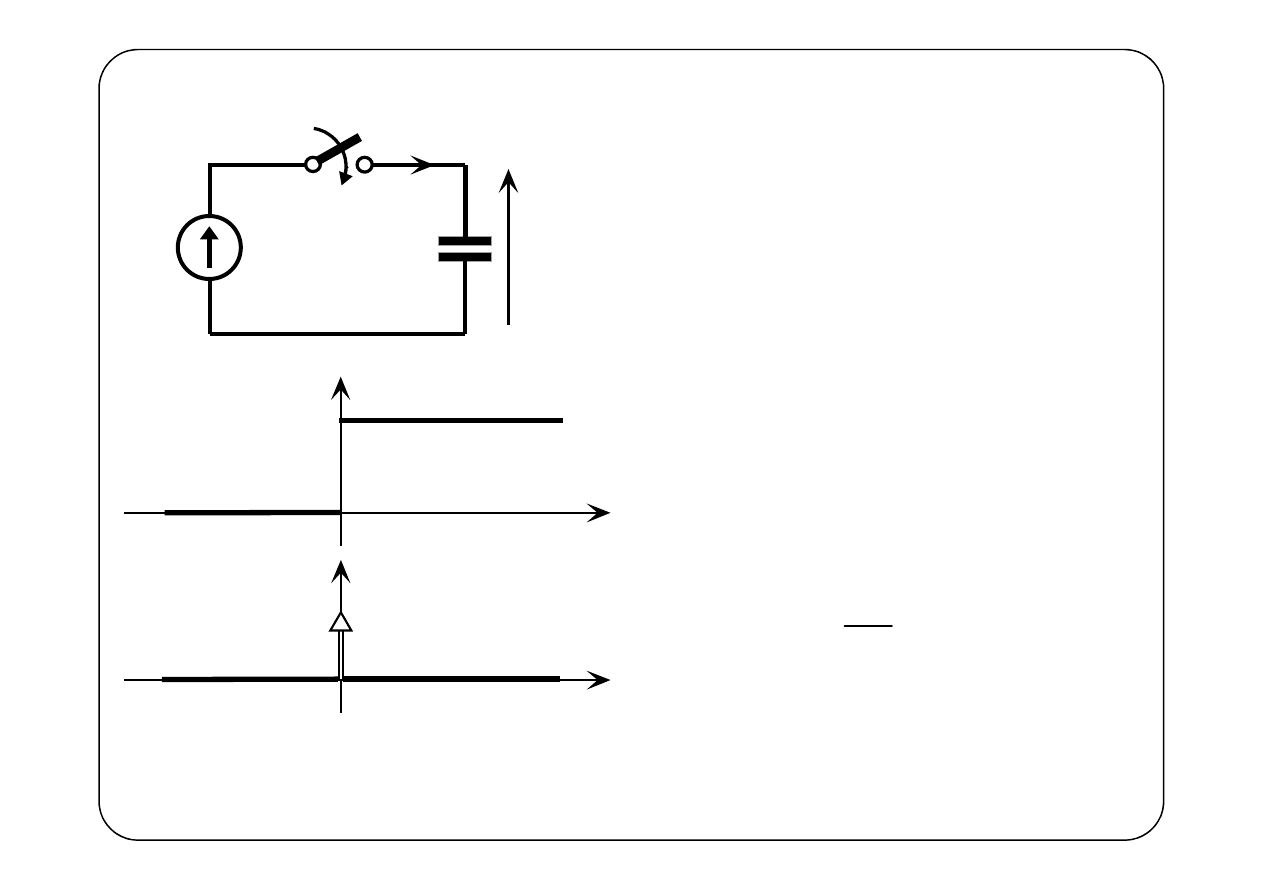
Przykład 3.
E
0
C
K
t = 0
u(t)
i(t)
0
const
E
=
Kondensator nie był naładowany,
czyli u(t) = 0 dla t < 0.
E
0
u(t)
t
i(t)
t
( )
0
δ
CE
t
( )
( )
0
u t
E
t
=
1
( )
( )
0
d
δ
d
u
i t
C
CE
t
t
=
=
( )
( )
( )
( )
0
0
d
δ
d
t
t
q t
i
CE
CE
t
τ τ
τ τ
−∞
−∞
=
=
=
∫
∫
1
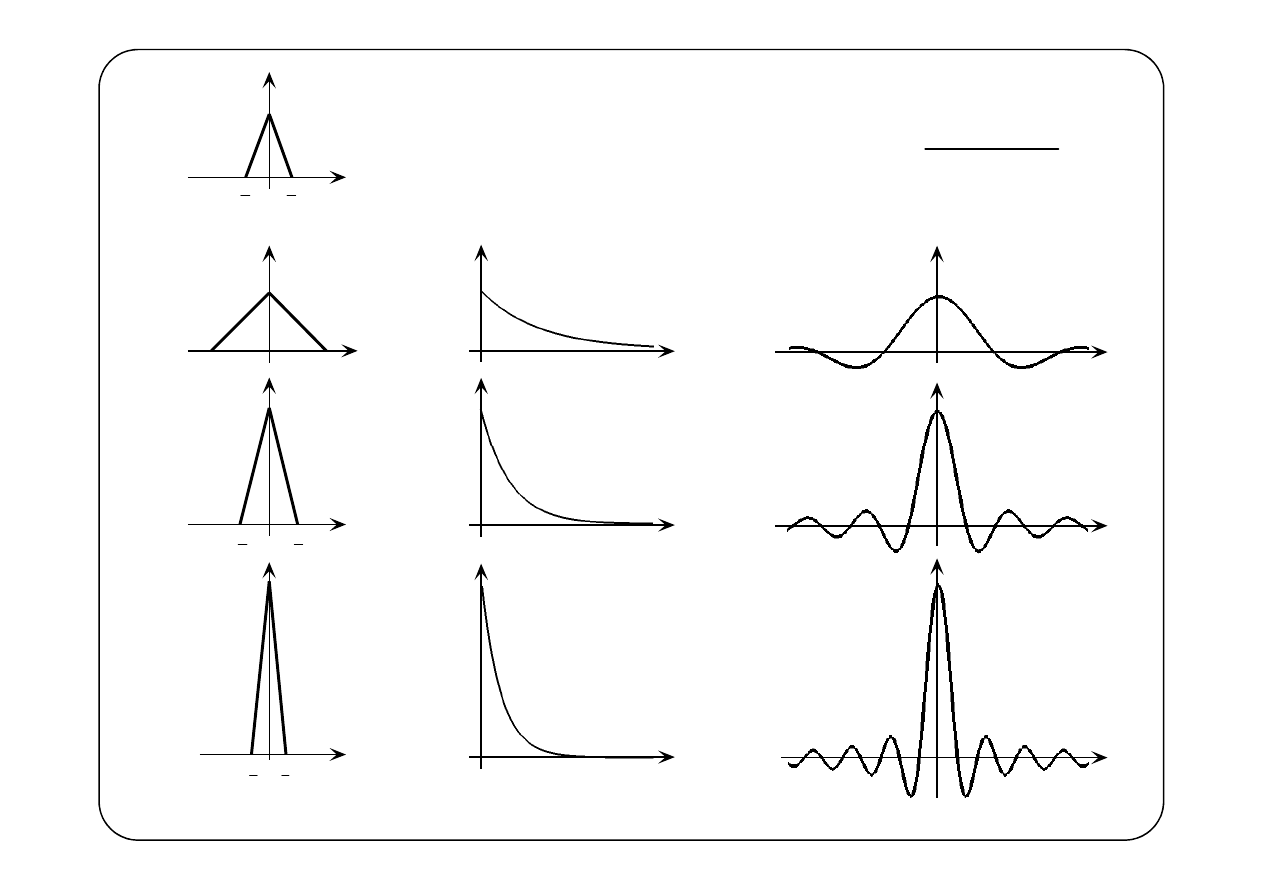
( )
n
f
t
n
1
n
1
n
−
( )
1
f t
1
1
–1
t
t
( )
2
f
t
2
( )
1
f t
1
t
( )
2
f
t
2
( )
( )
e
nt
n
f
t
n
t
−
=
1
( )
1
f t
1
t
( )
2
f
t
2
( )
( )
sin
π
π
n
n t
f
t
t
=
1
2
1
2
−
t
( )
3
f t
3
1
3
−
1
3
t
t
( )
3
f t
3
t
t
( )
3
f t
3
t
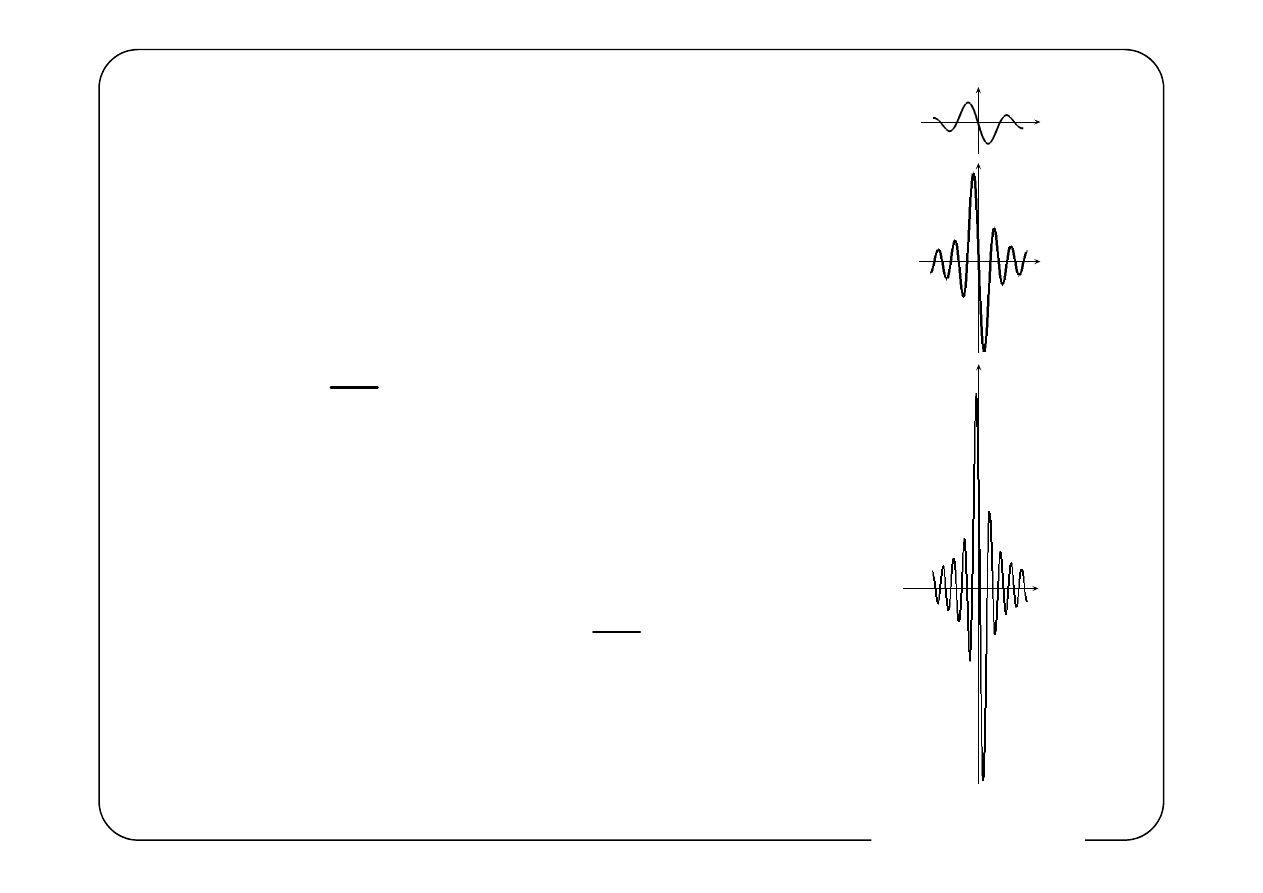
Niech
( )
( )
δ
n
n
f
t
t
→∞
→
Jeżeli dla każdego n istnieje
( )
( )
d
d
n
n
f
t
f
t
t
′
=
to
( )
( )
( )
d
δ
δ
d
n
n
f
t
t
t
t
→∞
′
′
→
≜
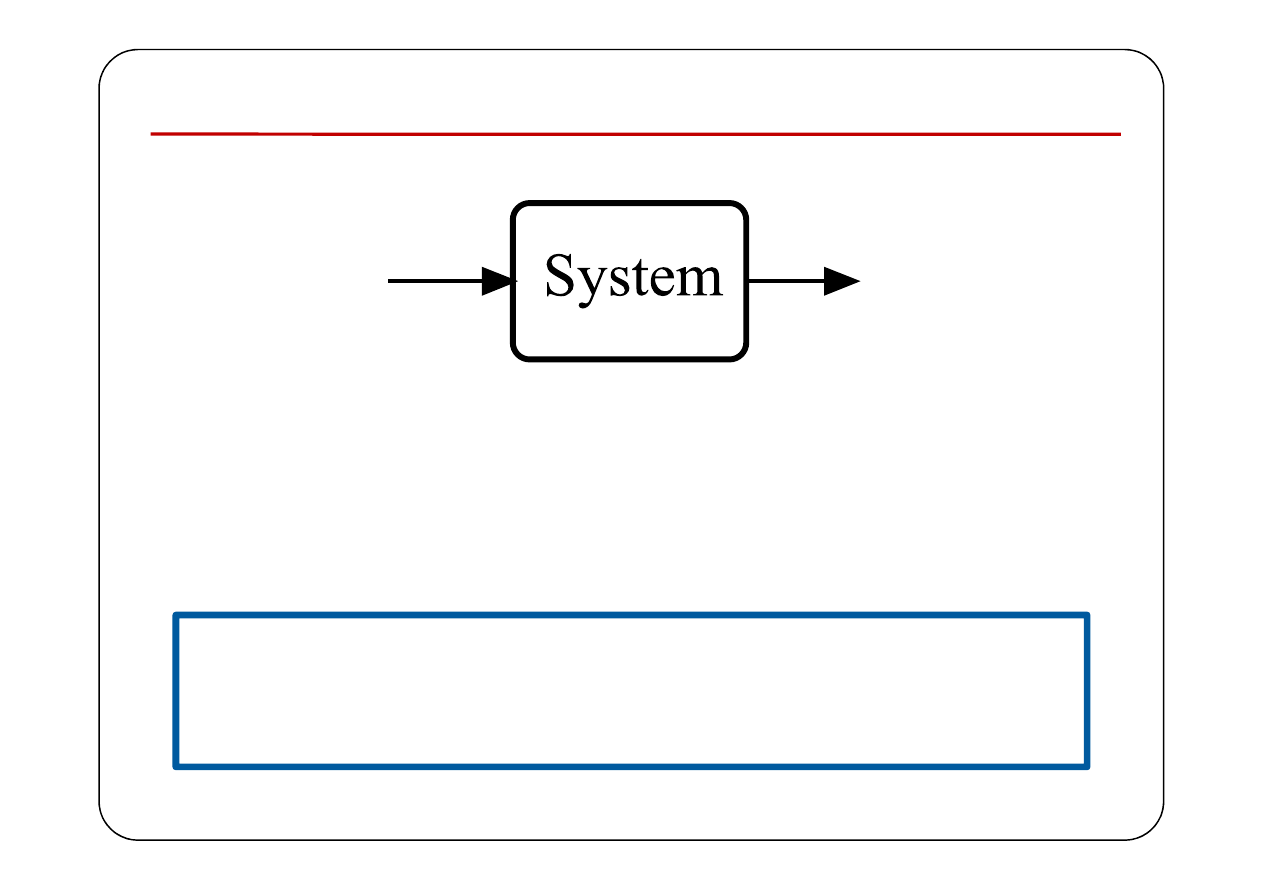
Charakterystyka impulsowa układu SLS
p(t)
r(t)
( )
( )
{ }
r t
p t
=
T
( )
( )
{ }
r t
p t
=
T
( ) ( )
δ
p t
t
=
( )
( )
{ }
δ
h t
t
≜
T
Charakterystyka impulsowa
lub reakcja impulsowa układu
i warunki początkowe są zerowe
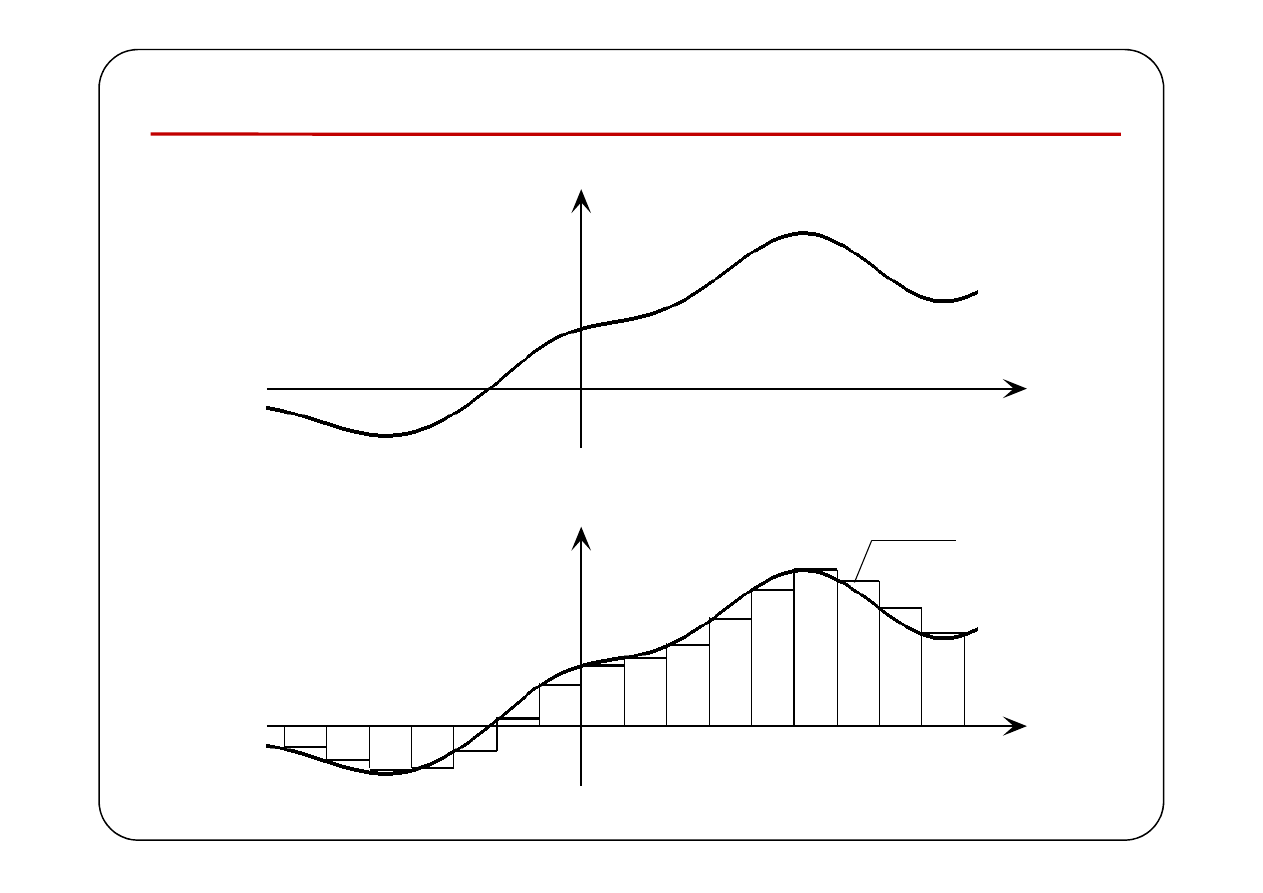
Dowolne pobudzenie
p(t)
t
p(t)
t
t
∆
2 t
∆
k t
∆
t
−∆
⋯
( )
p k t
∆
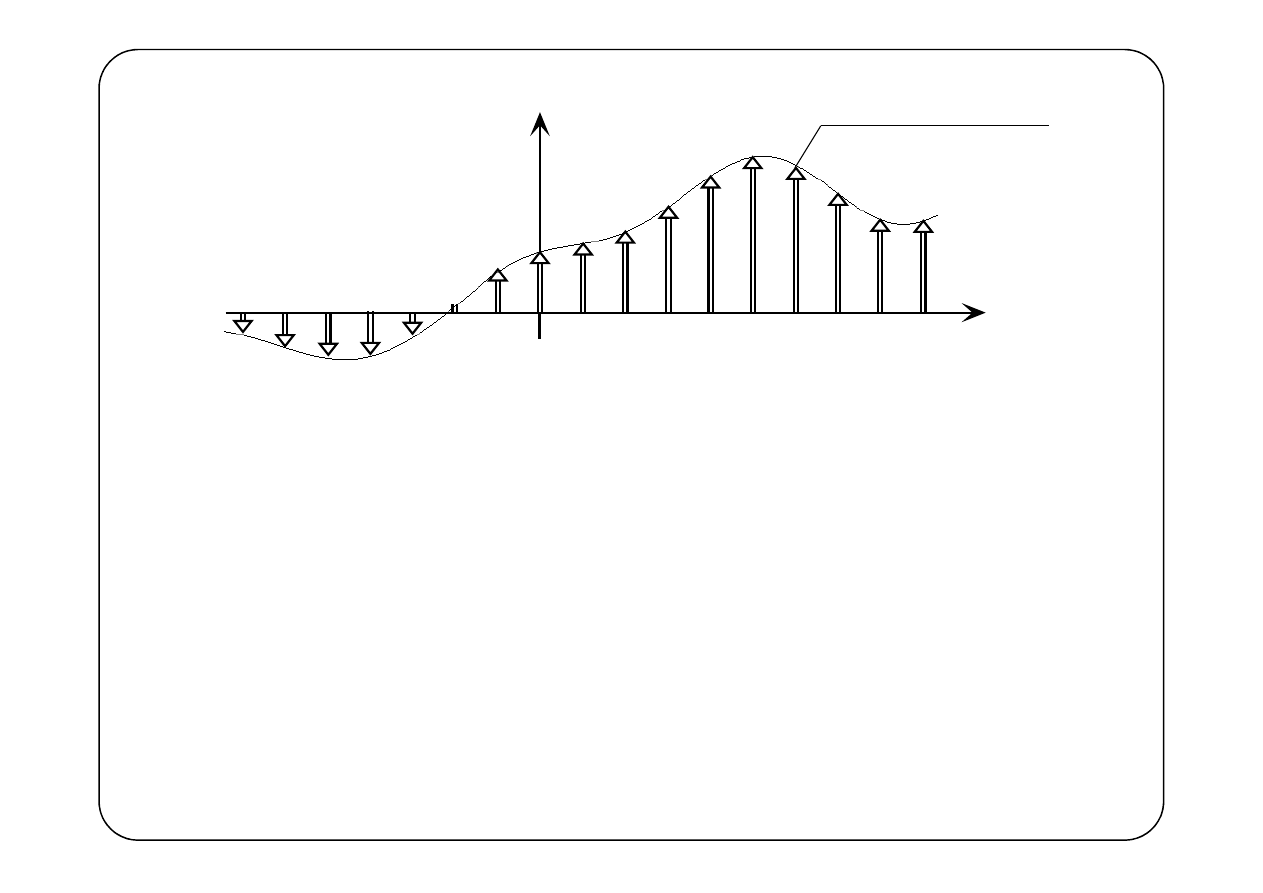
p(t)
t
t
∆
2 t
∆
k t
∆
t
−∆
⋯
( )
(
)
δ
p k t
t
t
k t
∆ ∆
− ∆
( )
( )
(
)
δ
p t
p k t
t
t
k t
∞
≈
∆ ∆
− ∆
∑
( )
( )
(
)
k
=−∞
∑
( )
( )
(
)
(
)
( )
(
)
( )
(
)
( )
(
)
( )
(
)
δ
δ
δ
δ
k
k
t
h t
t
k t
h t
k t
p k t
t
t
k t
p k t
t h t
k t
p k t
t
t
k t
p k t
t h t
k t
∞
∞
=−∞
=−∞
→
− ∆ →
− ∆
∆ ∆
− ∆ →
∆ ∆
− ∆
∆ ∆
− ∆ →
∆ ∆
− ∆
∑
∑

( )
( ) (
)
k
r t
p k t h t
k t
t
∞
=−∞
≈
∆
− ∆ ∆
∑
0
d
k
t
k t
t
τ
τ
τ
−∞< <∞
−∞< <∞
∆ →
∆
⇒
∆
⇒
( )
( )
d
d
k
t
t
τ
τ
∞
∞
=−∞
−∞
∆
⇒
∆
⇒
∑
∫
i
i
( )
( ) (
)
d
r t
p
h t
τ
τ τ
∞
−∞
=
−
∫
Splot funkcji
f(t), g(t) — dowolne funkcje
( ) ( )
( ) (
)
(
) ( )
( ) ( )
d
d
f t
g t
f
g t
f t
g
g t
f t
τ
τ τ
τ
τ τ
∞
−∞
∞
∗
=
−
=
=
−
=
∗
∫
∫
(
) ( )
( ) ( )
d
f t
g
g t
f t
τ
τ τ
−∞
=
−
=
∗
∫
( )
( ) ( )
r t
p t
h t
=
∗

Własności splotu
( ) ( ) ( ) ( )
( )
( )
( )
( ) ( )
( ) ( )
( ) ( )
( )
( )
( )
( )
1
2
1
2
f t
g t
g t
f t
f t
f
t
g t
f t
g t
f
t
g t
a f t
g t
af t
g t
f t
ag t
∗
=
∗
+
∗
=
∗
+
∗
∗
=
∗
=
∗
( ) ( )
( )
( )
( )
( )
( ) ( )
( )
( ) ( )
( )
δ
δ
a f t
g t
af t
g t
f t
ag t
t
f t
f t
t
f t
f
t
∗
=
∗
=
∗
∗
=
′
′
∗
=

Rozpatrujemy układy liniowe przyczynowe, czyli
( )
0
dla
0
h t
t
≡
<
( )
( ) ( )
( ) (
)
(
) ( )
0
d
d
t
r t
p t
h t
p
h t
p t
h
τ
τ τ
τ
τ τ
+
∞
−∞
−
=
∗
=
−
=
−
∫
∫
Jeżeli dodatkowo
Jeżeli dodatkowo
i warunki początkowe dla są zerowe
( )
0
dla
0
p t
t
≡
<
( )
( ) ( )
( ) (
)
( ) (
)
0
0
d
d
0
t
t
r t
p t
h t
p
h t
h
p t
t
τ
τ τ
τ
τ τ
+
+
−
−
=
∗
=
−
=
−
≥
∫
∫
0
t
= −
Przykład 1.
( )
( )
( ) ( )
( ) ( ) ( )
( ) (
)
e sin
e sin
d
t
h t
t
t
p t
t
r t
h t
p t
t
τ
τ τ
τ τ
−
∞
−
=
⋅
=
=
∗
=
−
=
∫
1
1
1
1
( ) ( ) ( )
( ) (
)
( )
(
) ( )
(
) ( )
0
0
e sin
d
1
e sin d
e
cos
sin
2
1
1
e
cos
sin
2
2
t
t
t
r t
h t
p t
t
t
t
t
t
t
τ
τ
τ τ
τ τ
τ τ
τ
τ
−∞
−
−
−
=
∗
=
−
=
=
= −
+
=
=
−
+
∫
∫
1
1
1
1
1
Przykład 2.
( )
( )
e
t
h t
t
−
=
1
1
1
2
p(t)
t
( )
( ) ( ) ( ) (
) (
)
2
1
1
2
2
p t
t
t
t
t
t
t
= ⋅
−
− ⋅
− + − ⋅
−
1
1
1
( )
( ) ( )
r t
p t
h t
=
∗
=
( )
( ) ( )
( ) (
) (
) (
) (
)
( )
(
)
2
1
1
2
2
e
d
t
r t
p t
h t
t
τ
τ
τ
τ
τ
τ
τ
τ τ
∞
− −
−∞
=
∗
=
=
⋅
−
− ⋅
− + − ⋅
−
−
=
∫
1
1
1
1
( )
(
)
( )
(
)
(
)
0
1
2
e
e d
2
1 e d
1
2 e d
2
t
t
t
t
t
t
t
τ
τ
τ
τ
τ
τ
τ
τ
τ
−
=
−
−
− +
−
−
=
∫
∫
∫
1
1
1
( )
( )
( )
( )
(
)
1
2
1 e
2
2
e
1
3 e
2
t
t
t
t
t
t
t
t
t
− −
− −
−
= − +
−
− +
− + − +
−
1
1
1
BIBO stabilność
Reakcja na dowolne ograniczone pobudzenie jest ograniczona
( )
( )
p t
M
r t
N
≤
< ∞
⇒
≤ < ∞
Twierdzenie
Układ SLS jest stabilny w sensie BIBO wtedy i tylko wtedy gdy
jego charakterystyka impulsowa ma postać
jego charakterystyka impulsowa ma postać
gdzie
jest funkcją (nie zawiera składników dystrybucyjnych),
oraz
( )
( )
( )
0
δ
,
h t
a
t
h t
=
+
( )
0
h t
( )
0
0
d
a
h t
t
K
∞
+
+
≤ < ∞
∫
Dowód
1. Dostateczność
Zakładamy, że oraz
( )
0
0
d
a
h t
t
K
∞
+
+
≤ < ∞
∫
Wówczas
( )
( )
( )
0
δ
h t
a
t
h t
=
+
( )
( ) (
)
( )
( ) (
)
( )
0
0
0
0
0
d
d
d
r t
h
p t
a p t
h
p t
t
a M
M
h
a M
MK
N
τ
τ τ
τ
τ
τ τ
∞
∞
−
+
∞
+
=
−
≤
+
−
≤
≤
+
≤
+
= < ∞
∫
∫
∫
c.b.d.o.
2. Konieczność
Załóżmy, że (czyli a = 0)
oraz
( )
( )
0
h t
h t
=
( )
0
0
d
,
h t
t
∞
+
→ ∞
∫
czyli dla każdego K > 0 istnieje T > 0, takie że
( )
T
( )
0
0
d
T
h
K
τ τ
+
>
∫
Niech
( )
(
)
(
)
(
)
0
0
0
1
gdy
0
1 gdy
0
0
gdy
0
h T
t
p t
h T
t
h T
t
− >
= −
− <
− =
Po podstawieniu
(
)
( )
( )
( )
0
0
0
, czyli
1
gdy
0
1
gdy
0
0
gdy
0
T
t
t
T
h
p T
h
h
τ
τ
τ
τ
τ
τ
− =
= −
>
− = −
<
=
Wówczas
Wówczas
( )
( ) (
)
( )
0
0
0
0
d
d
T
T
r T
h
p T
h
K
τ
τ τ
τ τ
+
+
=
−
=
>
∫
∫
gdzie K może być dowolnie dużą liczbą,
czyli reakcja nie jest ograniczona.
Załóżmy, że
( )
( )
( )
( )
0
δ
δ
h t
a
t
b
t
h t
′
=
+
+
Rozważmy drugi składnik
( )
δ
b
t
′
( )
( ) ( )
( )
δ
r t
b
t
p t
bp t
′
′
=
∗
=
Niech
( )
( )
sin
,
1
p t
t
p t
ω
=
≤ < ∞
( )
( )
0
sin
,
1
p t
t
p t
ω
=
≤ < ∞
Wówczas
( )
0
0
cos
r t
b
t
ω
ω
=
Niech K będzie dowolną liczbą. Wówczas
( )
0
max
K
r t
K
b
ω
>
⇒
>
c.b.d.o.
Wyszukiwarka
Podobne podstrony:
4 Analiza obwodów prądu stałego
Analizowanie obwodow elektryczn Nieznany
analizator obwodow ntw7 cz2
05 Analizowanie obwodów elektrycznych
5 Analiza obwodów prądu zmiennego(1)
5 Metody operatorowe analizy obwodow SLS
6 Analiza obwodow 2
06 Analizowanie obwodow elektry Nieznany (2)
analiza obwodow elektrycznych i Nieznany
6 Analiza obwodow 1
analizator obwodow nwt7cz1
4 Analiza obwodów prądu stałego
06 Analizowanie obwodów elektrycznych i elektronicznych
4 analiza obwodow elektrycznych !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
więcej podobnych podstron