Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
1
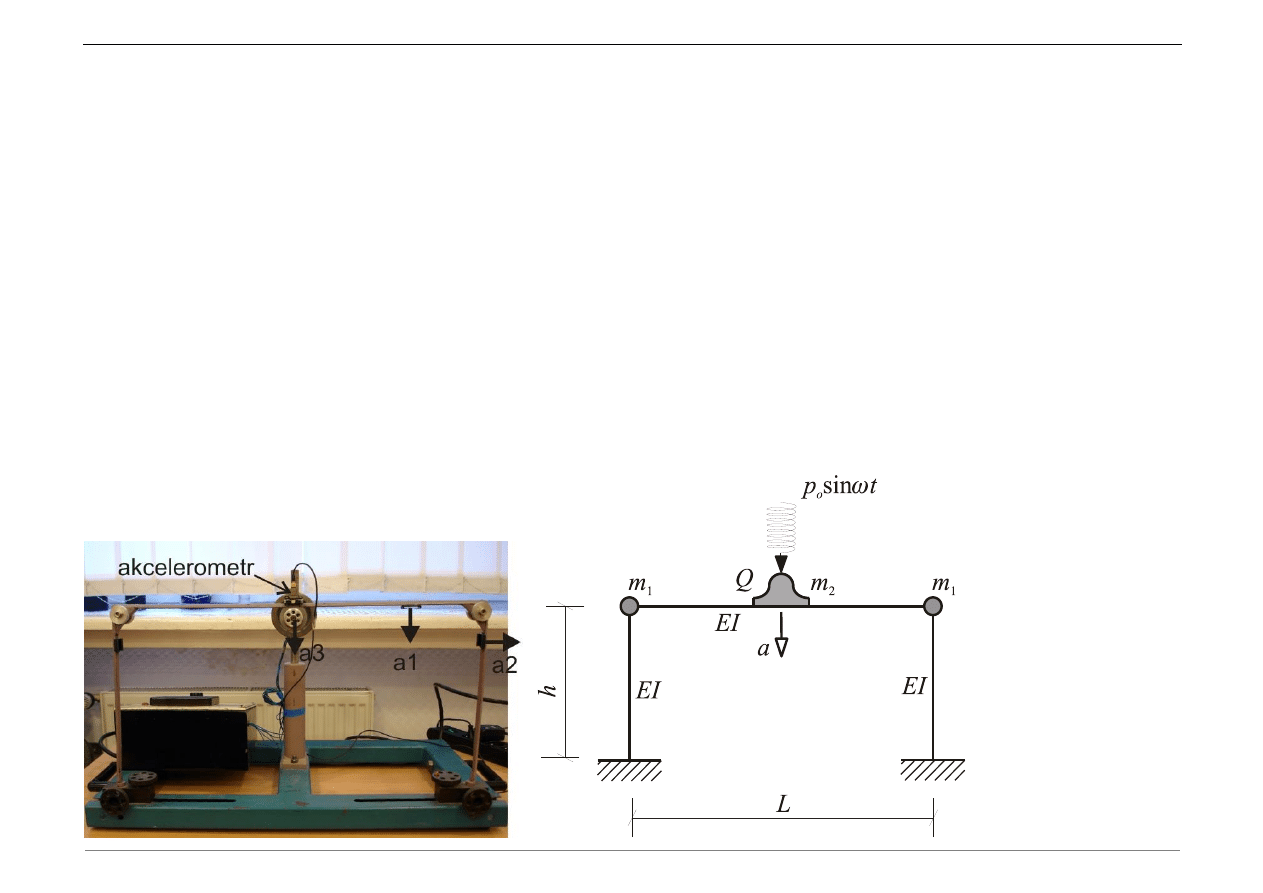
A. Dokonać analizy Fouriera sygnałów pomiarowych zarejestrowanych podczas
doświadczenia przeprowadzonego na ramie portalowej. Drgania (przyspieszenia) zostały
zarejestrowane za pomocą akcelerometru umieszczonego kolejno w trzech pozycjach (a1,
a2, a3), jak zaznaczono na rysunku.
Opis sygnałów:
a1.txt – sygnał przyspieszenia [m/s
2
]
(drgania swobodne, wymuszenie przyłożone w kierunku pionowym)
t1.txt – wektor czasu [s] odpowiadający sygnałowi a1.txt
a2.txt – sygnał przyspieszenia [m/s
2
]
(drgania swobodne, wymuszenie przyłożone w kierunku poziomym)
t2.txt – wektor czasu [s] odpowiadający sygnałowi a2.txt
a3.txt – sygnał przyspieszenia [m/s
2
]
(drgania wymuszone harmonicznie)
t3.txt – wektor czasu [s] odpowiadający sygnałowi a3.txt
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
2
Rozwiązanie:
Transformata Fouriera przekształca sygnał czasowy w sygnał częstotliwościowy oraz
umożliwia wyznaczenie zawartości częstotliwościowej sygnału. Do analizy Fouriera
w programie MATLAB zastosować funkcję fourik.
[base,fx,mag,Amp]=fourik(x,t);
%----------------------------------------------------------
% WEJSCIE:
% x - pomierzony sygnal
% t - wektor czasu
%----------------------------------------------------------
% WYJSCIE:
% base - os czestotliwosci [Hz]
% fx - szybka transformata Fouriera (FFT)
% mag - amplituda transformaty FFT
% Amp - znormalizowana amplituda transformaty FFT
Uwaga: funkcję fourik ściągnąć na dysk i umieścić w katalogu bieżącym.
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
3
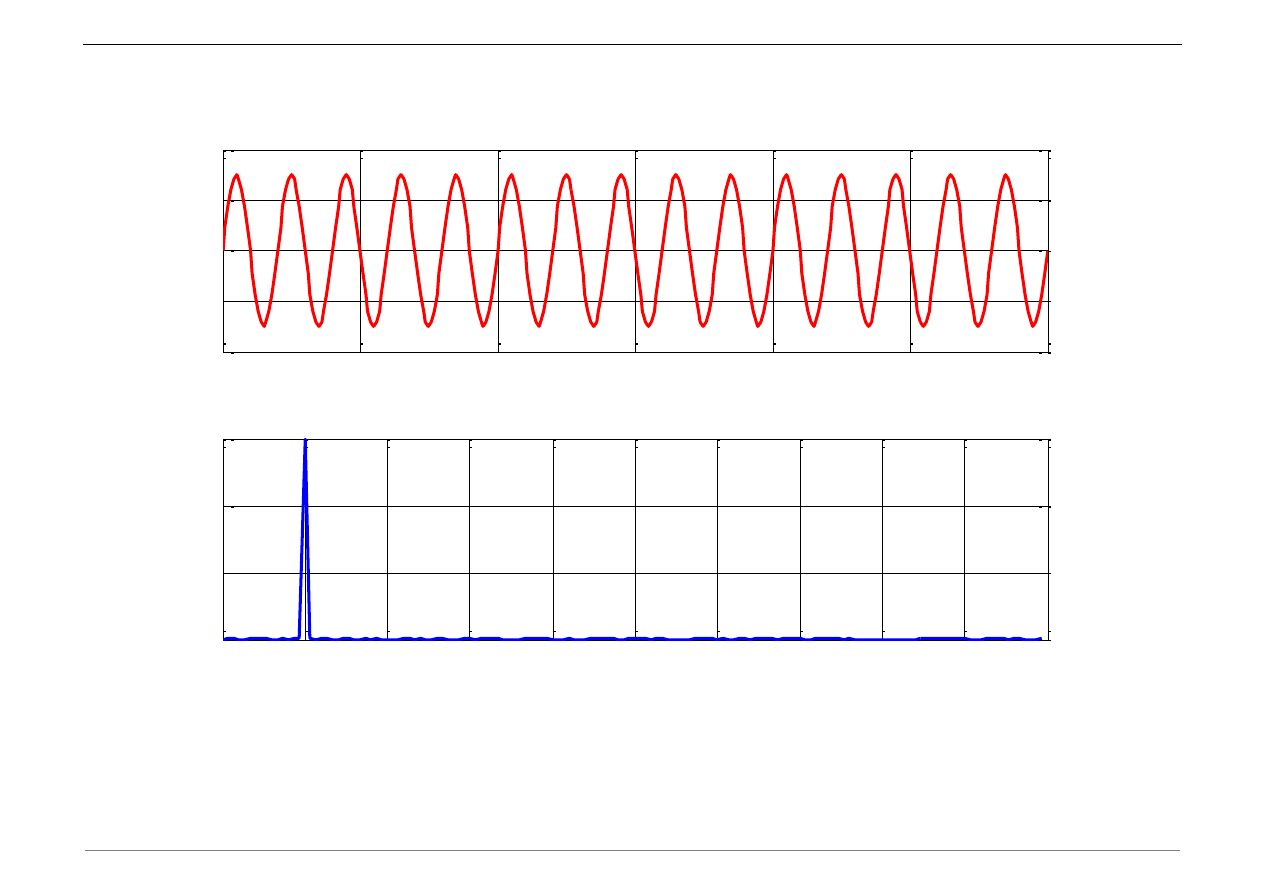
Transformata Fouriera sygnału sinusoidalnego o częstotliwości 5 Hz
a) Zdefiniować wektor czasu t i funkcję u(t):
t=[0:0.01:3];
% [s]
u=3*sin(2*pi*5*t);
% [m]
b) Dokonać transformaty Fouriera sygnału przemieszczenia u(t):
[f,fx,mag,Amp]=fourik(u,t);
c) Wykreślić przebieg sygnałów w dziedzinie czasu i częstotliwości:
figure(1);
subplot(211);grid
on
plot(t,u,
'r'
)
xlabel(
't [s]'
);ylabel(
'u(t) [m]'
);
subplot(212); grid
on
plot(f,Amp,
'b')
xlabel(
'f [Hz]'
)
ylabel(
'znormalizowana amplituda FFT'
)
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
4
0
0.5
1
1.5
2
2.5
3
-4
-2
0
2
4
t [s]
u
(t
)
[m
]
0
5
10
15
20
25
30
35
40
45
50
0
1
2
3
f [Hz]
z
n
o
rm
a
liz
o
w
a
n
a
a
m
p
lit
u
d
a
F
F
T
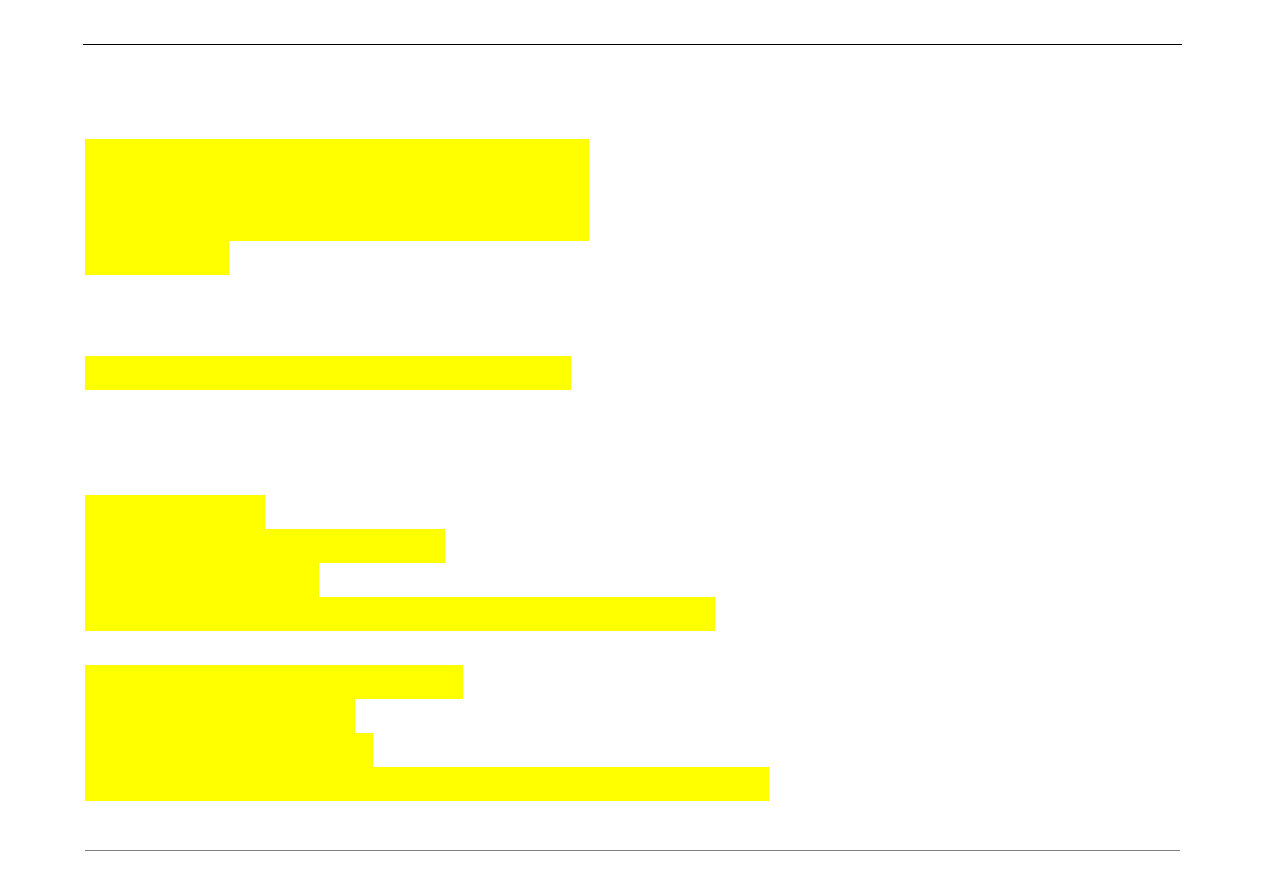
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
5
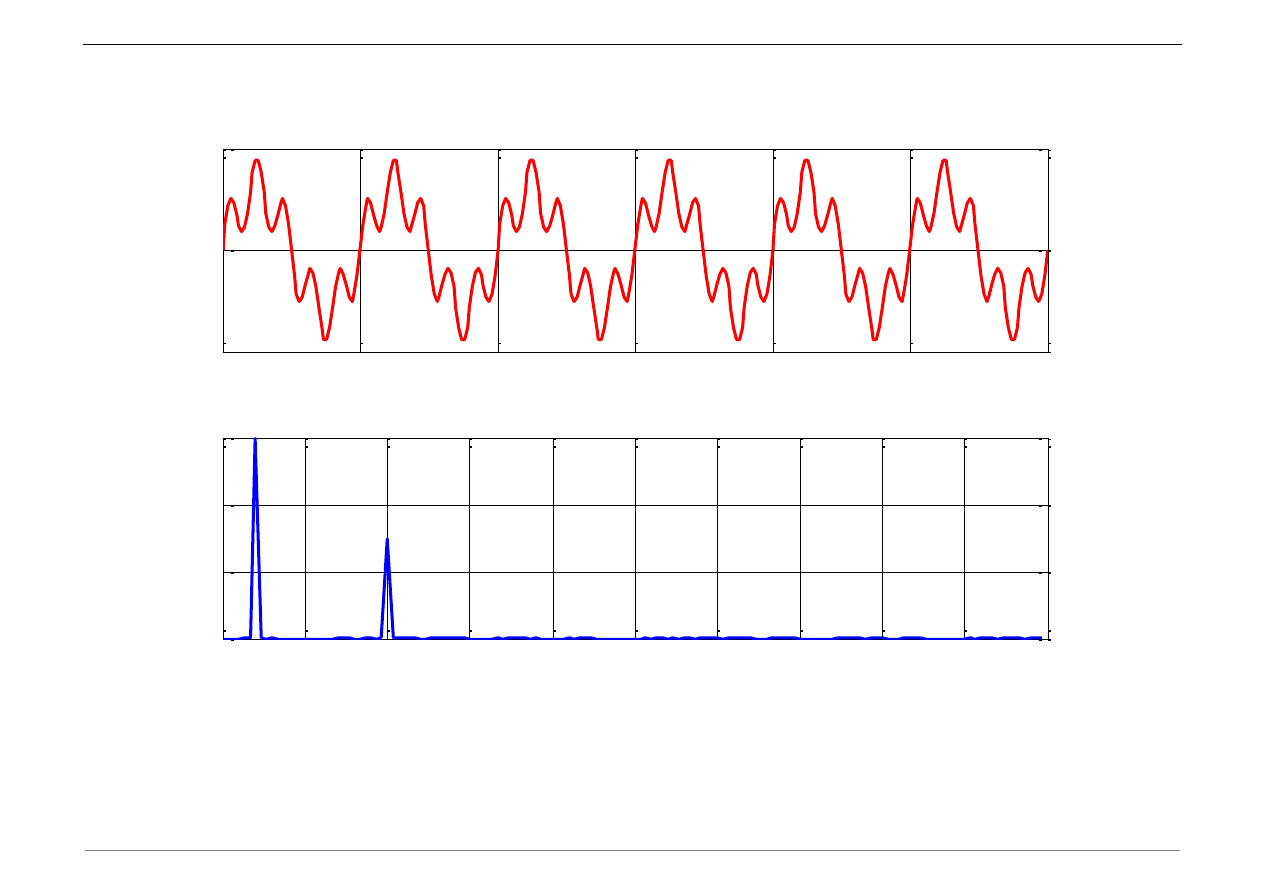
Transformata Fouriera sygnału sinusoidalnego o częstotliwości 2 Hz i 10 Hz
a) Zdefiniować wektor czasu t i funkcję u(t) = u
1
(t) + u
2
(t):
t=[0:0.01:3];
% [s]
u1=3*sin(2*pi*2*t);
% [m]
u2=1.5*sin(2*pi*10*t);
% [m]
u=u1+u2;
b) Dokonać transformaty Fouriera sygnału przemieszczenia u(t):
[f,fx,mag,Amp]=fourik(u,t);
c) Wykreślić przebieg sygnałów w dziedzinie czasu i częstotliwości:
figure(1);
subplot(211);grid
on
plot(t,u,
'r'
)
xlabel(
't [s]'
);ylabel(
'u(t) [m]'
);
subplot(212); grid
on
plot(f,Amp,
'b')
xlabel(
'f [Hz]'
)
ylabel(
'znormalizowana amplituda FFT'
)
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
6
0
0.5
1
1.5
2
2.5
3
-5
0
5
t [s]
u
(t
)
[m
]
0
5
10
15
20
25
30
35
40
45
50
0
1
2
3
f [Hz]
z
n
o
rm
a
liz
o
w
a
n
a
a
m
p
lit
u
d
a
F
F
T
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
7
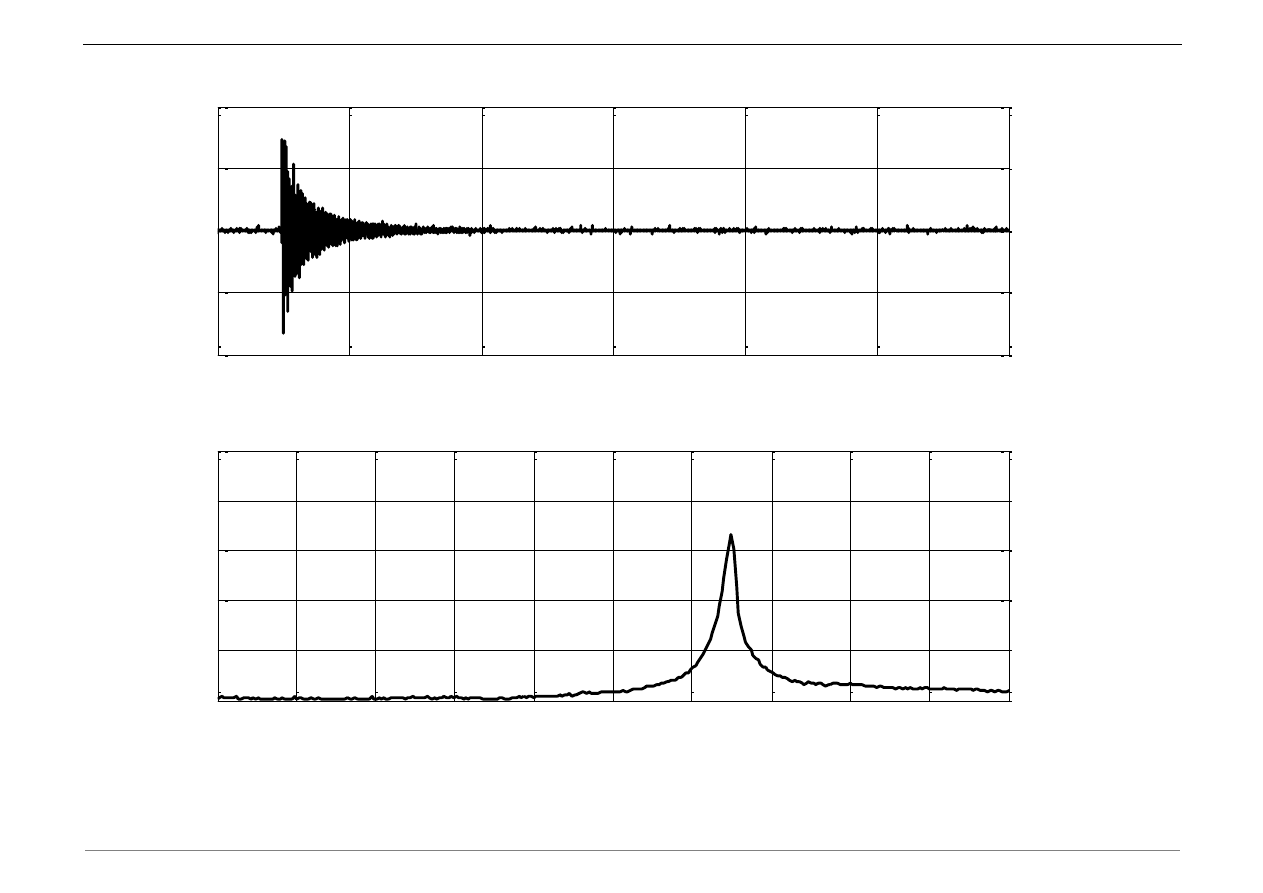
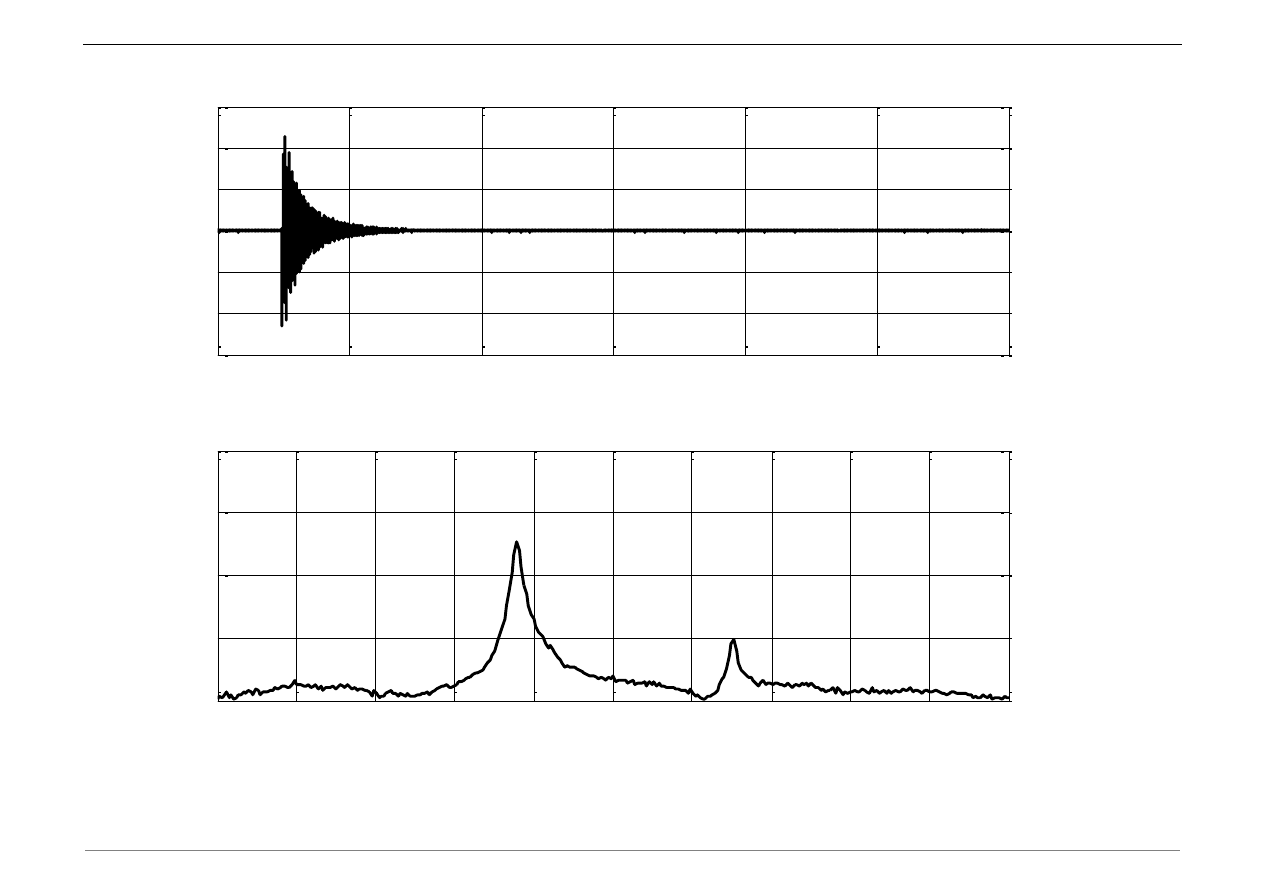
Transformata Fouriera sygnałów pomiarowych
a) Wczytać dane. Do wczytania danych pomiarowych w programie MATLAB zastosować
funkcję load. Uwaga: pliki danych ściągnąć na dysk i umieścić w katalogu bieżącym.
a1=load(
'a1.txt'
); t1=load(
't1.txt'
);
b) Wykreślić przebieg przyspieszenia w czasie:
figure(1)
plot(t1,a1)
xlabel(
't [s]'
)
ylabel(
'a [m/s^2]'
)
c) Dokonać transformaty Fouriera pomierzonego sygnału przyspieszenia:
[base_1,fx,mag,Amp_1]=fourik(a1,t1);
d) Wykreślić rozkład częstotliwościowy sygnału:
figure(2)
plot(base_1,Amp_1)
xlabel(
'f [Hz]'
)
ylabel(
'znormalizowana amplituda FFT'
)
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
8
0
1
2
3
4
5
6
-100
-50
0
50
100
t [s]
a
1
[
m
/s
2
]
0
5
10
15
20
25
30
35
40
45
50
0
0.2
0.4
0.6
0.8
1
f [Hz]
z
n
o
rm
a
liz
o
w
a
n
a
a
m
p
lit
u
d
a
F
F
T
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
9
0
1
2
3
4
5
6
-300
-200
-100
0
100
200
300
t [s]
a
2
[
m
/s
2
]
0
5
10
15
20
25
30
35
40
45
50
0
0.1
0.2
0.3
0.4
f [Hz]
z
n
o
rm
a
liz
o
w
a
n
a
a
m
p
lit
u
d
a
F
F
T
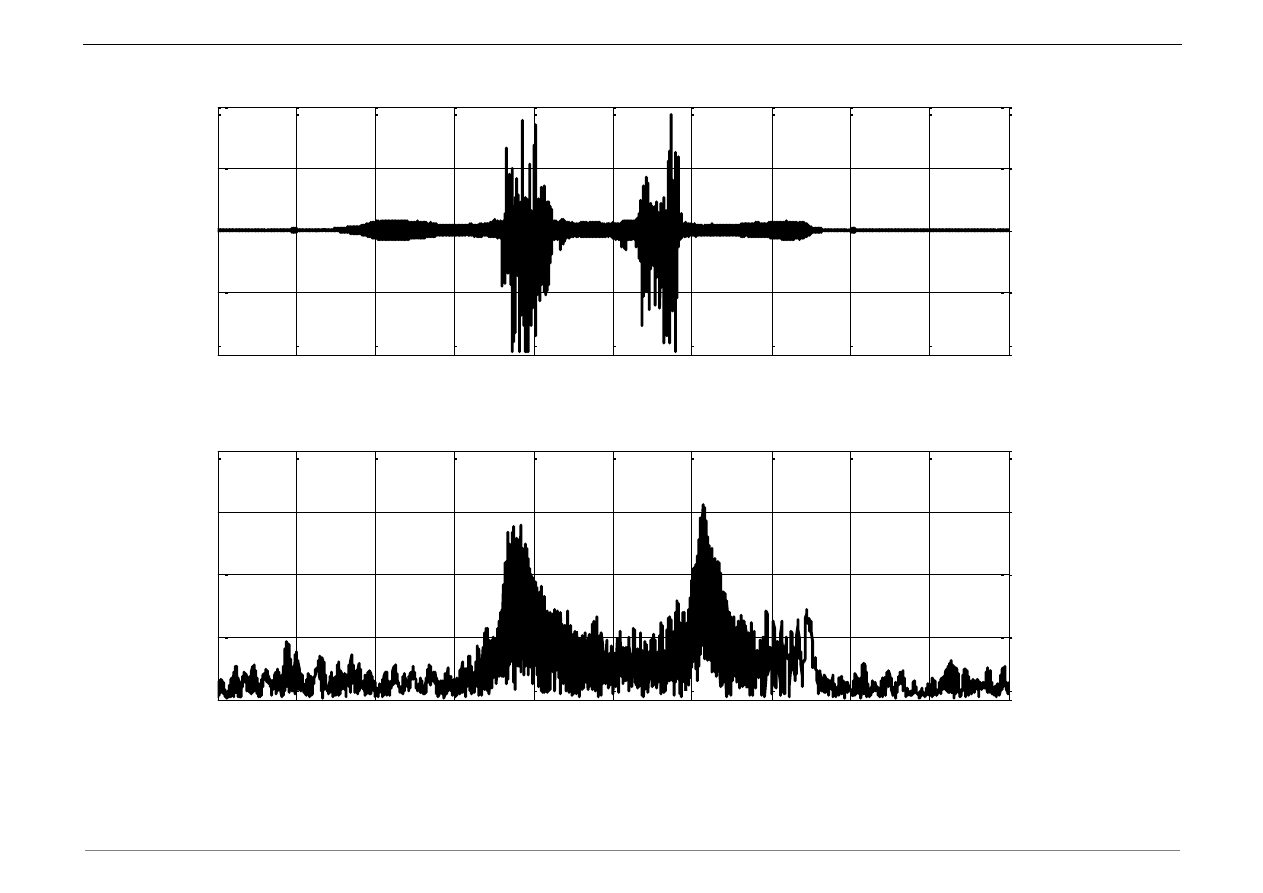
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
10
0
5
10
15
20
25
30
35
40
45
50
-100
-50
0
50
100
t [s]
a
3
[
m
/s
2
]
0
5
10
15
20
25
30
35
40
45
50
0
0.1
0.2
0.3
0.4
f [Hz]
z
n
o
rm
a
liz
o
w
a
n
a
a
m
p
lit
u
d
a
F
F
T
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
11
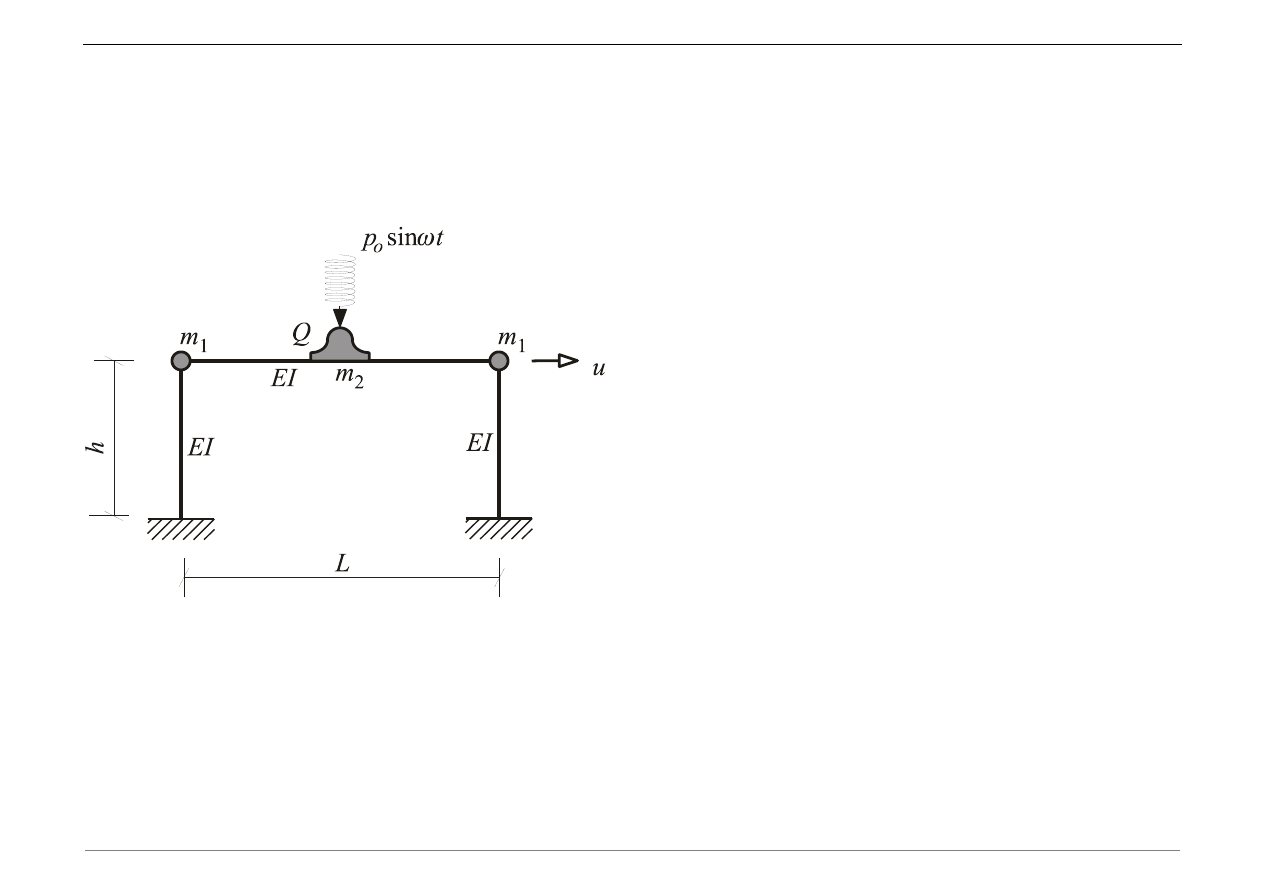
B. Wyznaczyć boczną (poziomą) częstotliwość drgań ramy portalowej, modelując ją za
pomocą układu o jednym stopniu swobody.
Dane: E = 200 GPa, I
x
= 1.26·10
-10
m
4
, A = 3.2·10
-5
m
4
,
= 7850 kg/m
3
,
L = 0.6 m, H = 0.3 m, m
1
= 177 g, m
2
= 270 g.
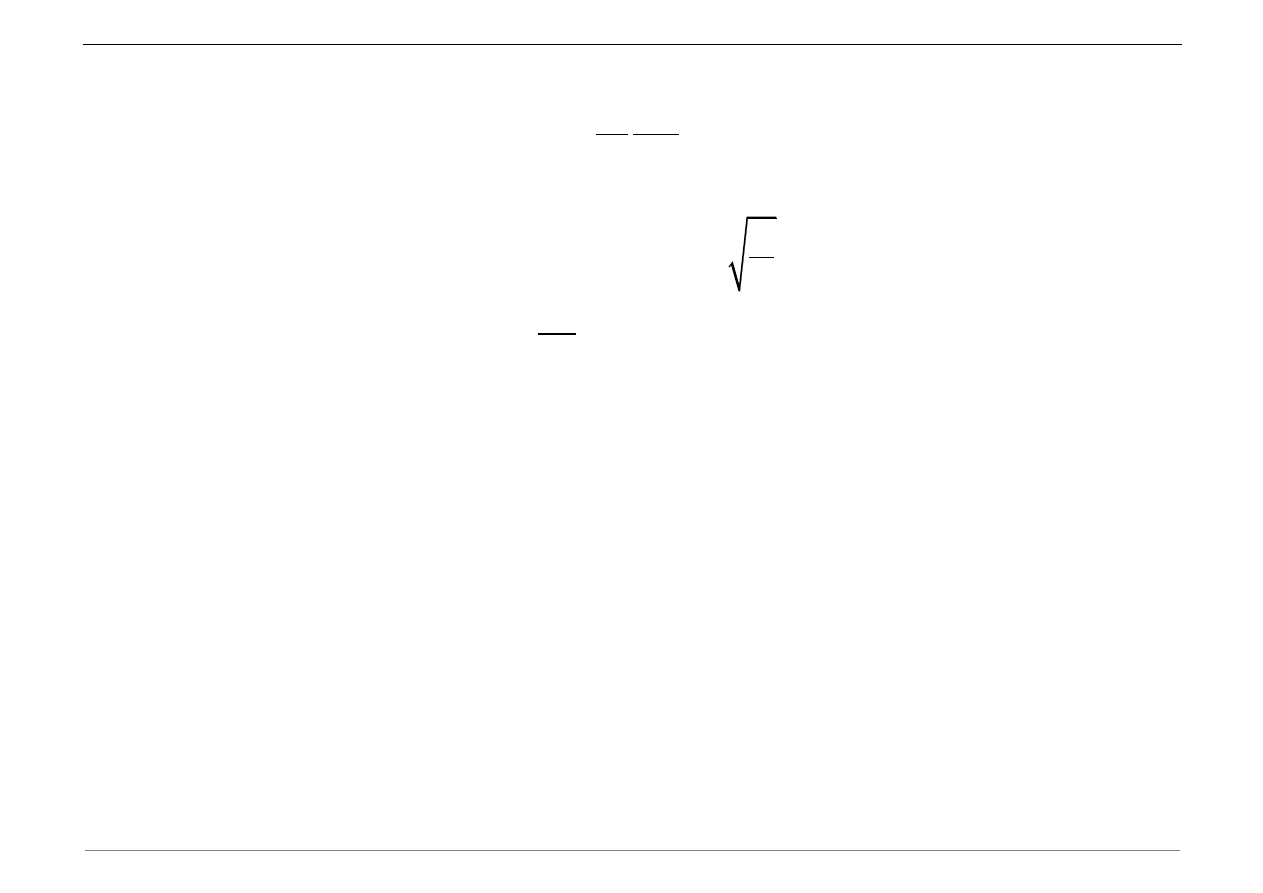
Dynamika Budowli
– laboratorium
Ćwiczenie 3
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
12
Rozwiązanie:
a) Obliczyć boczną sztywność układu
3
96
7
x
EI
k
h
b) Obliczyć masę m
c) Wyznaczyć częstość kołową drgań własnych
n
k
m
[rad/s]
d) Obliczyć częstotliwość drgań
2
n
n
f
[Hz]
e) Porównać obliczoną częstotliwość z częstotliwością uzyskaną z transformaty Fouriera
pomierzonego sygnału