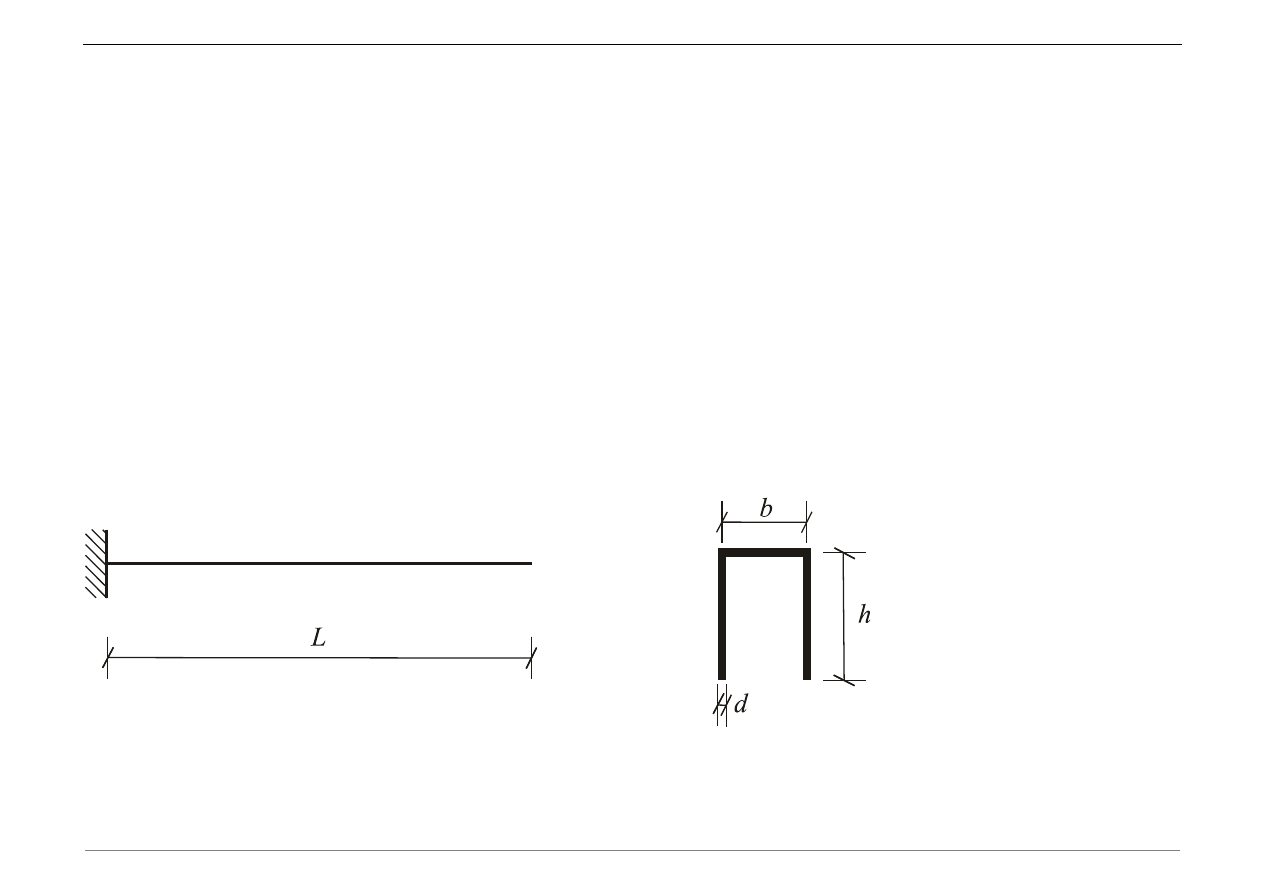
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
1
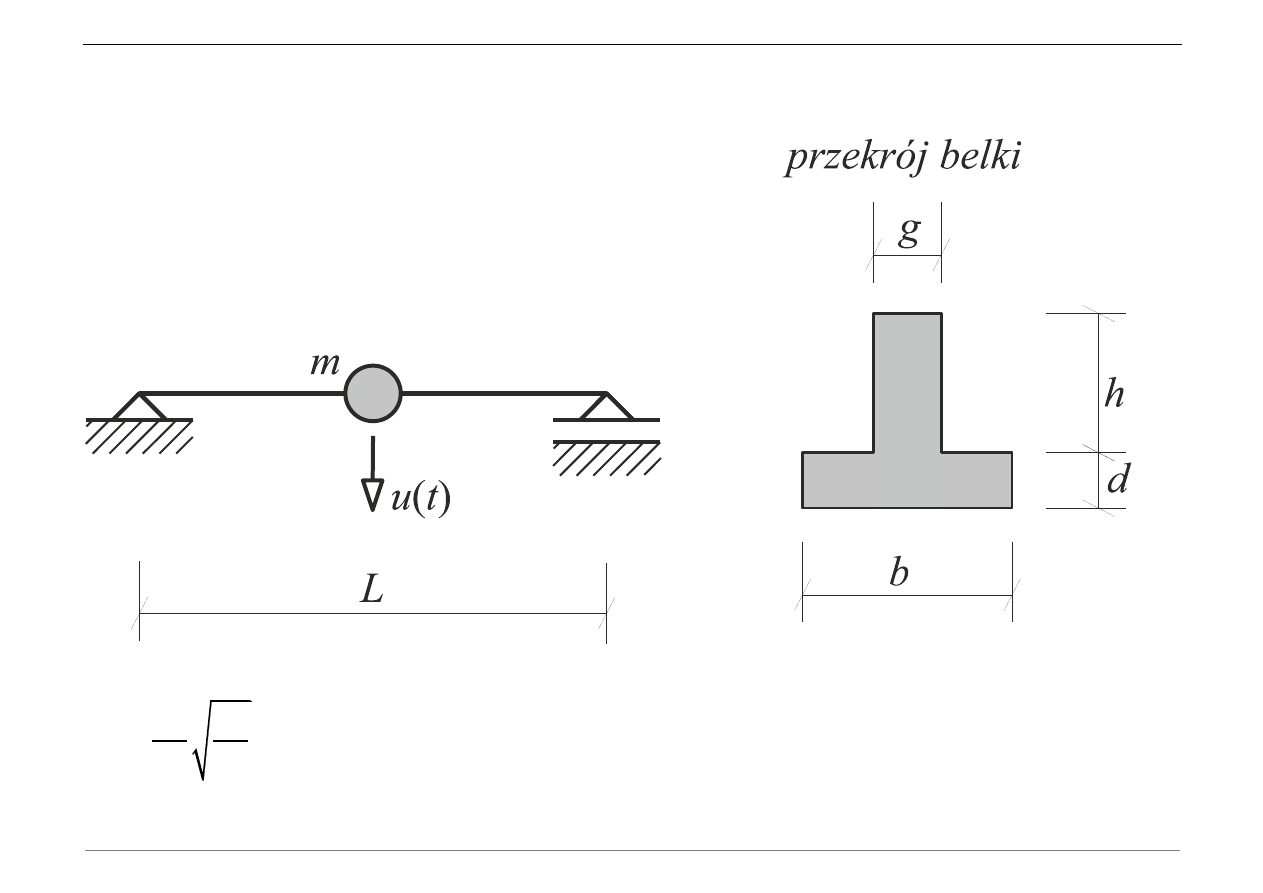
Dana jest belka wspornikowa jak na rysunku:
1. Wymodelować belkę za pomocą układu o jednym stopniu swobody (układ bez
tłumienia), wyznaczyć wartości liczbowe masy m oraz sztywności k.
2. Obliczyć częstotliwość drgań własnych nietłumionych oraz porównać ją
z częstotliwością uzyskaną dla modelu ciągłego.
3. Obliczyć częstotliwość drgań własnych tłumionych.
4. Napisać w środowisku MATLAB program rysujący wykres przemieszczenia u(t)
w funkcji czasu dla drgań nietłumionych i tłumionych. Wykreślić wykresy dla
3 różnych zestawów warunków początkowych. Warunki początkowe dobrać
samodzielnie.
Dane: b, h, d, L, E,
,
, u
0,
v
0
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
2
Rozwiązanie:
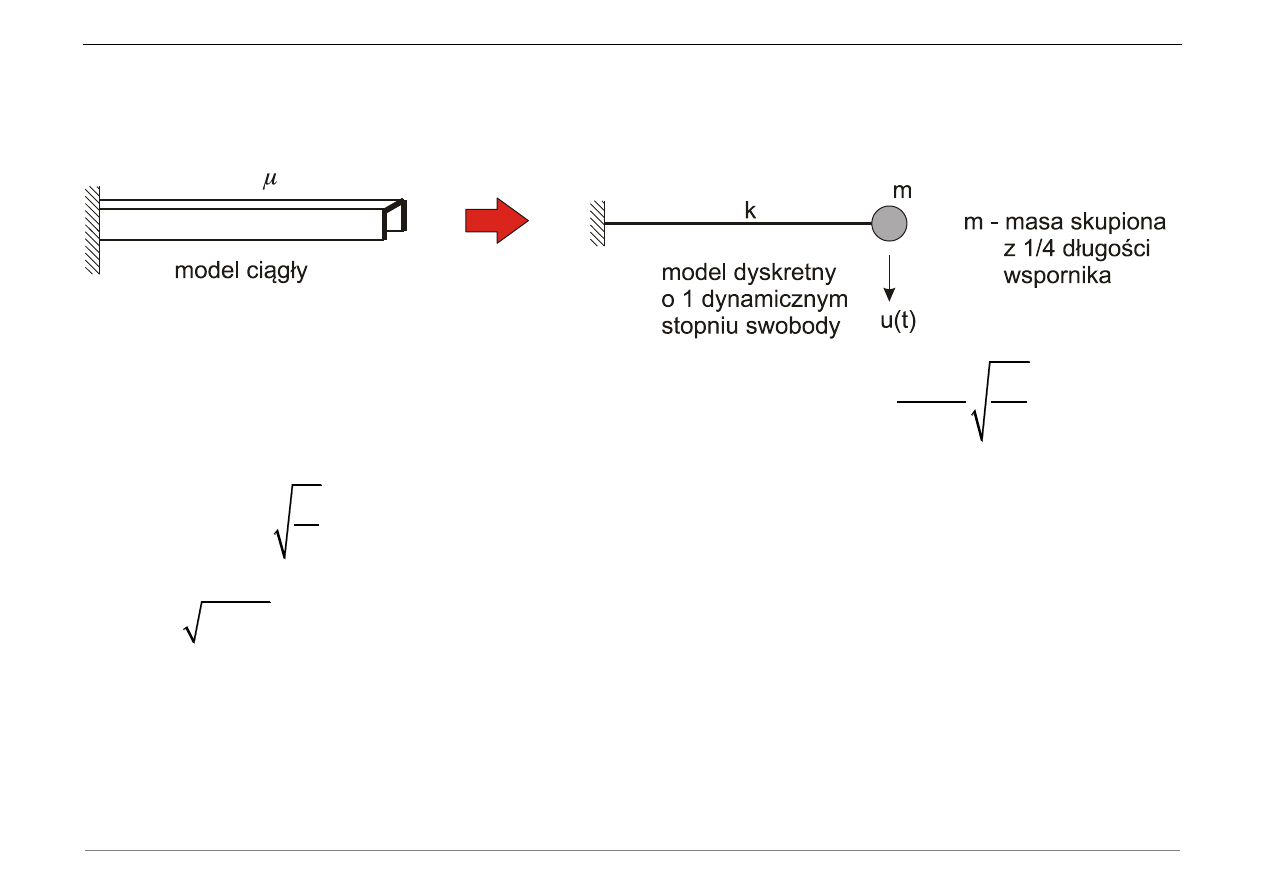
Układ ciągły można zamienić na układ dyskretny o jednym stopniu swobody poprzez
skupienie masy m
Częstość kołowa drgań nietłumionych dla modelu ciągłego:
2
3.516
a
n
EI
L
Częstość kołowa drgań nietłumionych dla modelu dyskretnego o jednym stopniu
swobody:
n
k
m
Częstość kołowa drgań tłumionych dla modelu dyskretnego o jednym stopniu swobody:
2
1
d
n
n
- częstość kołowa drgań własnych nietłumionych [rad/s]
d
- częstość kołowa drgań własnych tłumionych [rad/s]
- masa na jednostkę długości [kg/m]
m - masa skupiona [kg]
- bezwymiarowa liczba tłumienia
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
3
Drgania swobodne zapoczątkowane są poprzez wytrącenie układu z pozycji równowagi, to
znaczy przez przyłożenie w czasie t = 0 przemieszczenia początkowego
0
(0)
u
u
i/lub
prędkości początkowej
0
(0)
u
u
.
Drgania nietłumione opisane są równaniem: ( )
cos
sin
n
n
u t
A
t
B
t
,
(0)
A
u
,
(0)
n
u
B
Drgania tłumione opisane są równaniem:
( )
cos
sin
n
t
d
d
u t
e
A
t
B
t
,
0
0
0
,
.
n
d
u
u
A
u
B
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
4
Kolejność obliczeń:
a) Zadeklarować zmienne b, h, d, L, E,
,
, u
0,
v
0
b=30/100;
% szerokosc [m]
h=50/100;
% wysokosc [m]
d=2/100;
% grubosc [m]
L=12.5;
% dlugosc [m]
E=200e+9;
% modul sprezystosci [Pa]
ro=7900;
% gestosc [kg/m3]
u_0=0.1;
% przemieszczenie poczatkowe [m]
v_0=5;
% predkosc poczatkowa [m/s]
ksi=0.05;
% liczba tłumienia
b) Obliczyć moment bezwładności przekroju
x
I .
% moment statyczny przekroju wzgledem gornej krawędzi [m3]
Sx=2*h*d*h/2;
% pole przekroju [m2]
A=b*d+2*h*d;
% odleglosc [m] srodka ciezkosci przekroju od gornej krawedzi
yc=Sx/A;
% glowny centralny moment bezwladnosci przekroju [m4]
Ix=2*d*h^3/12+b*d*yc^2+2*d*h*(yc-h/2)^2;
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
5
c) Obliczyć masę skupioną m (z ¼ długości belki).
m=1/4*A*L*ro;
% [kg]
d) Obliczyć podatność belki wspornikowej
3
11
3
x
L
EI
(wykresy momentów zginających +
całkowanie graficzne).
dw=L^3/(3*E*Ix);
e) Obliczyć sztywność belki
11
1
k
.
k=1/dw;
f) Obliczyć częstość kołową drgań własnych nietłumionych
n
k
m
(układ o 1 stopniu
swobody).
wn=sqrt(k/m)
g) Obliczyć częstotliwość drgań
2
n
n
f
.
fn=wn/2/pi
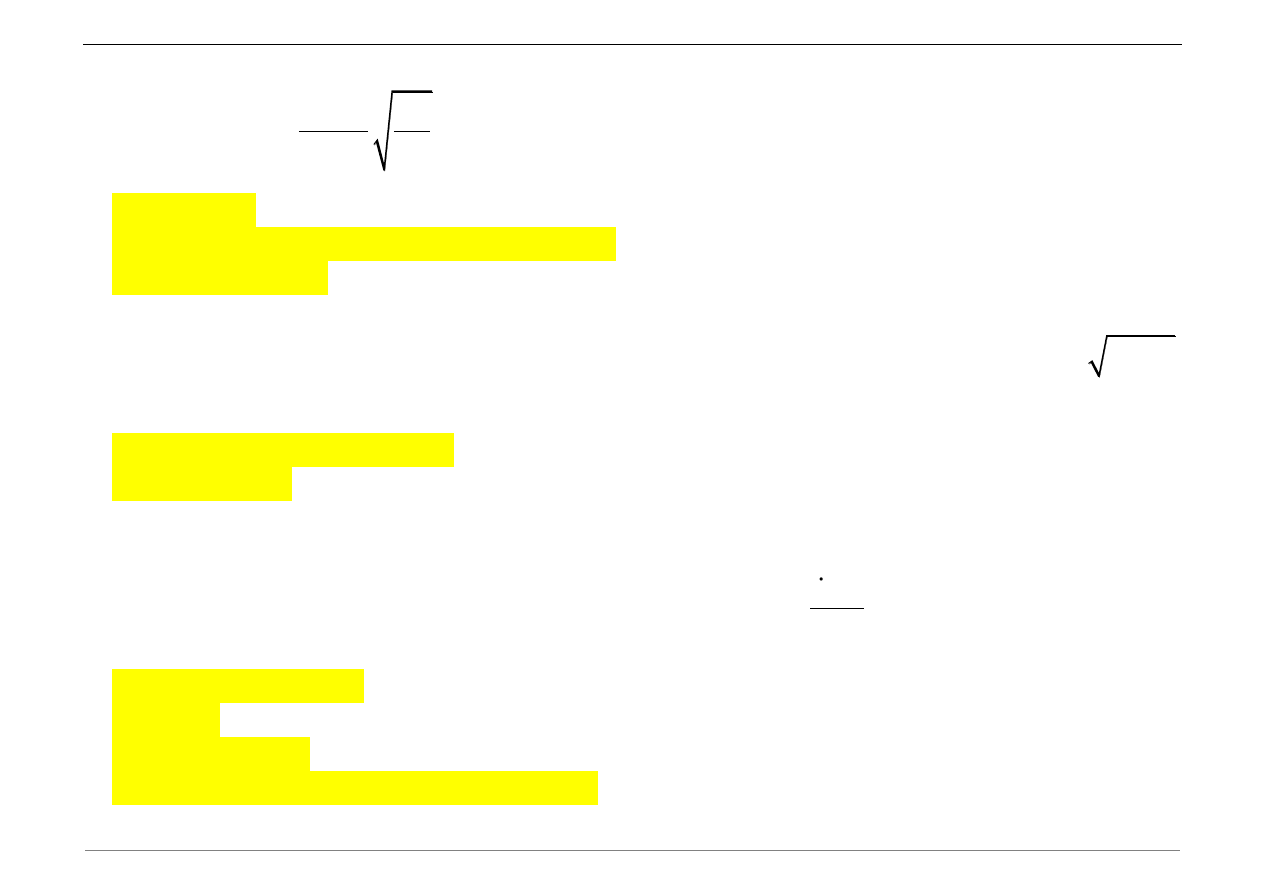
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
6
h) Obliczyć częstość kołową i częstotliwość drgań własnych nietłumionych modelu
ciągłego:
2
3.516
n
EI
L
.
mi=ro*A;
wna=3.516/L^2*sqrt(E*Ix/mi);
fna=wna/2/pi
i) Obliczyć częstość kołową i częstotliwość drgań własnych tłumionych
2
1
d
n
(układ o 1 stopniu swobody).
wd=wn*sqrt(1-ksi^2)
fd=wd/2/pi
j) W programie MATLAB narysować wykres krzywej opisującej drgania swobodne
nietłumione ( )
cos
sin
n
n
u t
A
t
B
t
,
(0)
A
u
,
(0)
n
u
B
.
t=[0:0.001:5];
% definicja wektora czasu
A=u_0;
B=(v_0)/wn;
un=A*cos(wn*t)+B*sin(wn*t);
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
7
k) W programie MATLAB narysować wykres krzywej opisującej drgania swobodne
tłumione
( )
cos
sin
n
t
d
d
u t
e
A
t
B
t
,
0
0
0
,
n
d
u
u
A
u
B
.
A=u_0; B=(v_0+ksi*wn*u_0)/wd;
ut=[A*cos(wd*t)+B*sin(wd*t)].*exp(-ksi*wn*t);
figure(1);
plot(t,un,
'k'
);grid
on
;hold
on
plot(t,ut,
'r'
)
xlabel(
't [s]'
);ylabel(
'u [m]'
)
0
0.5
1
1.5
2
2.5
3
3.5
4
-0.4
-0.2
0
0.2
0.4
t [s]
u
[
m
]
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
8
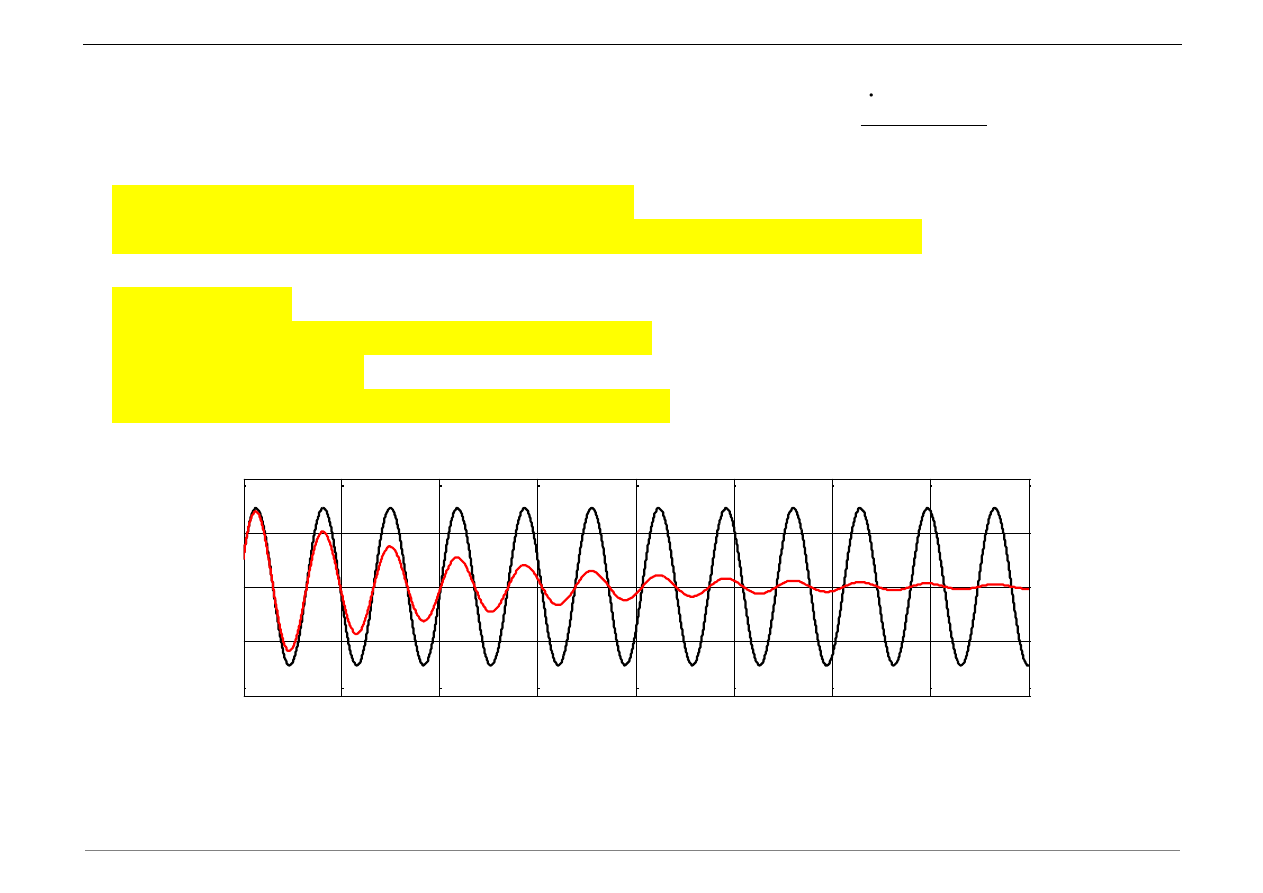
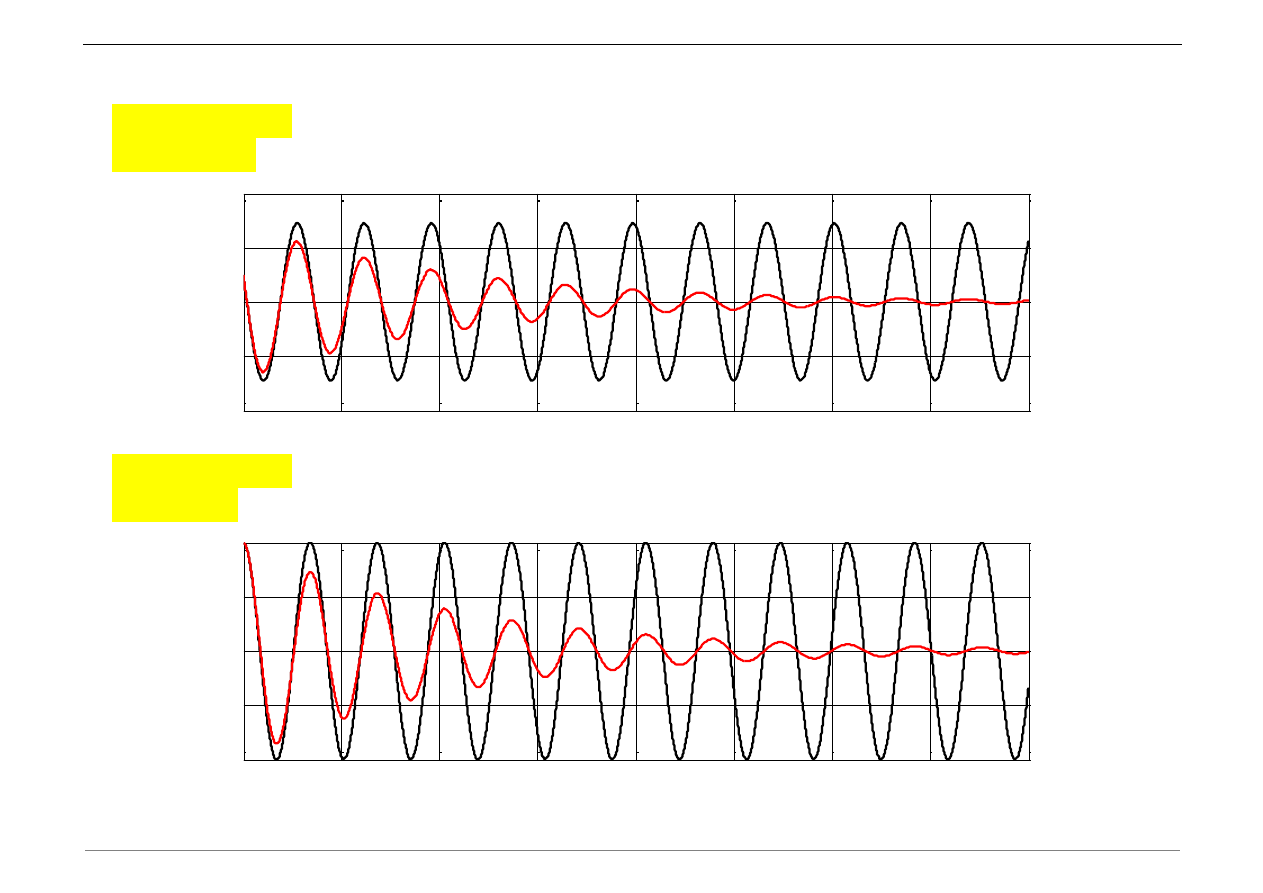
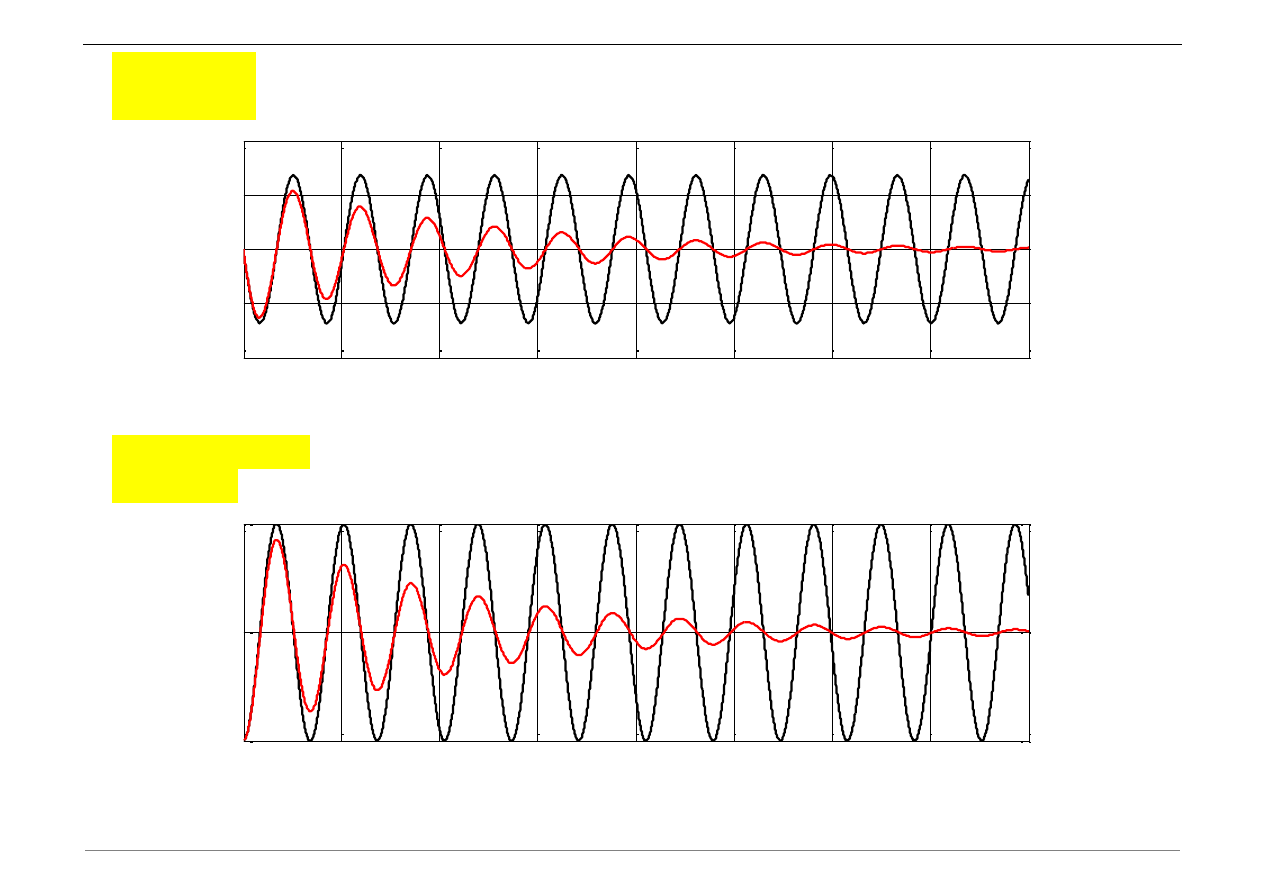
l) Skomentować wpływ różnych warunków początkowych na wykresy drgań.
u_0= 0.1;
v_0= -5;
0
0.5
1
1.5
2
2.5
3
3.5
4
-0.4
-0.2
0
0.2
0.4
t [s]
u
[
m
]
u_0= 0.2;
v_0= 0;
0
0.5
1
1.5
2
2.5
3
3.5
4
-0.2
-0.1
0
0.1
0.2
t [s]
u
[
m
]
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
9
u_0= 0;
v_0= -5;
0
0.5
1
1.5
2
2.5
3
3.5
4
-0.4
-0.2
0
0.2
0.4
t [s]
u
[
m
]
u_0= -0.5;
v_0= 0;
0
0.5
1
1.5
2
2.5
3
3.5
4
-0.5
0
0.5
t [s]
u
[
m
]
Dynamika Budowli
– laboratorium
Ćwiczenie 2
Magdalena Rucka
Politechnika Gdańska, Wydział Inżynierii Lądowej i Środowiska, Katedra Wytrzymałości Materiałów
10
Zadanie do samodzielnego rozwiązania:
2
2
a
n
EI
L